1. Introduction
In most of the developed world, EPSs are known for their robustness, efficiency and extremely high reliability. It comes as no surprise that throughout the decades, this reputation eventually resulted in most of the population taking the electrical energy supply for granted. If it were not for the significant environmental impact of associated activities, such as electrical energy generation and its transmission, no noteworthy changes would be imposed on EPSs in the near future. However, the reality of climate-related concerns has driven the need for technological development to such a level that the conventional electrical energy supply paradigm was placed in front of a challenge none of us had ever faced before. Among others, the sector of electrical energy generation is the most notable example. In a relatively short period of time, significant portions of conventional centralized generating capacities were replaced by distributed renewable energy sources, mostly interfacing with EPSs via semi-conductive power converters [
1]. This can be seen as both a blessing and a curse, since power converters are indeed able to provide a convenient fast-acting intervention, but unfortunately not inherently.
The transition towards converter-based generation caused the vast amount of energy temporarily stored within rotating masses of conventional power plants in the form of rotational kinetic energy to decrease quickly [
2]. This energy serves as a buffer when sudden active power imbalances occur in the EPS, providing a limited energy source for a temporary load supply [
3]. Withdrawing the rotating energy causes generators to decelerate. The deceleration rate depends on the amount of power imbalance and the overall stored rotational kinetic energy. As a consequence, conventional EPSs are not prone to significant
RoCoF. Consequently, the more we advance toward the smart grid paradigm, the more frequency (among several others quantities), measured from electrical signals (voltage, current), becomes affected [
4,
5].
For decades, frequency stability was of no concern to transmission system operators (TSOs). An evident proof of this is the applied UFLS schemes in most developed networks around the world. Apart from a few exceptions in countries whose isolated EPS of smaller dimensions is asynchronously connected to larger interconnections, the great majority of them still use an approach introduced decades ago (known as the conventional or traditional UFLS concept). The research community recognized the problem of neglecting UFLS development quite some time ago, which resulted in an impressive number of scientific publications (e.g., the latest [
6,
7,
8,
9,
10,
11]). Yet, most of those published methods appear complex and require the use of advanced mathematical techniques, several of which are non-transparent. Many of the methods rely either on real-time communication between a vast number of protective devices all across the EPS [
12,
13] or the assumption of having accurate enough information about the involved EPS inertia [
14,
15,
16]. As a result, apart from a few individual pilot projects, no significant progress has been made in this field so far, especially concerning practical applicability.
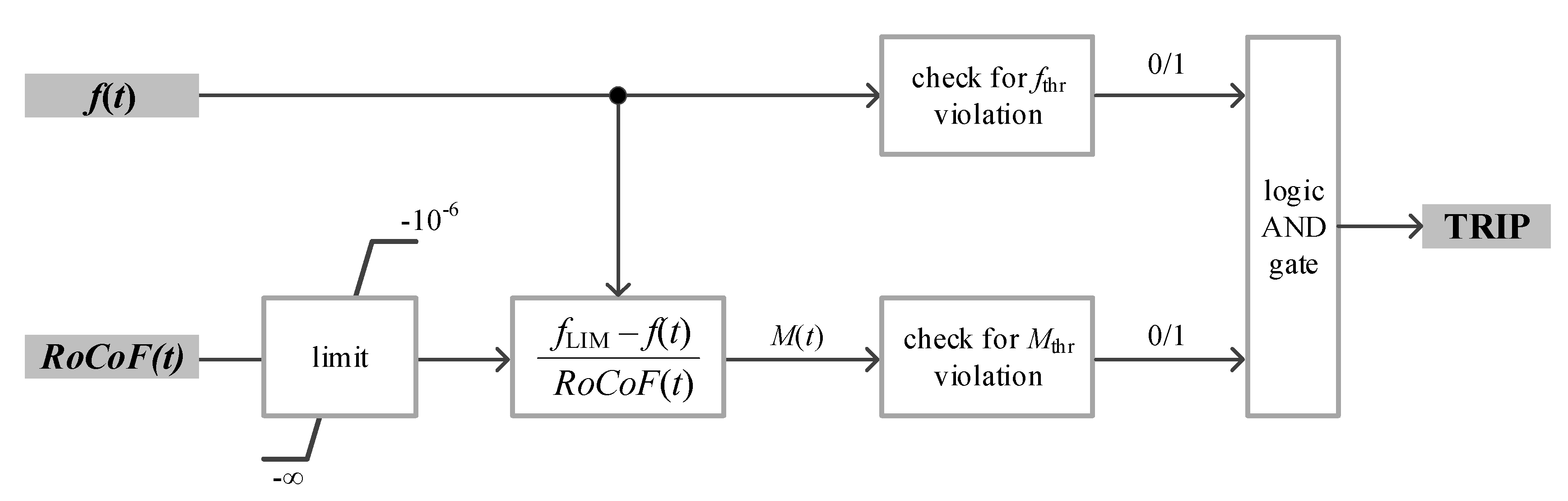
In this paper, we present a procedure for proving the concept of an innovative and practically feasible UFLS [
17] in terms of HIL simulations. For this purpose, a real-time digital simulator (RTDS) was applied together with an IED selected for running a local UFLS algorithm. IED is a commonly used term in the electric power industry to describe microprocessor-based controllers of EPS equipment [
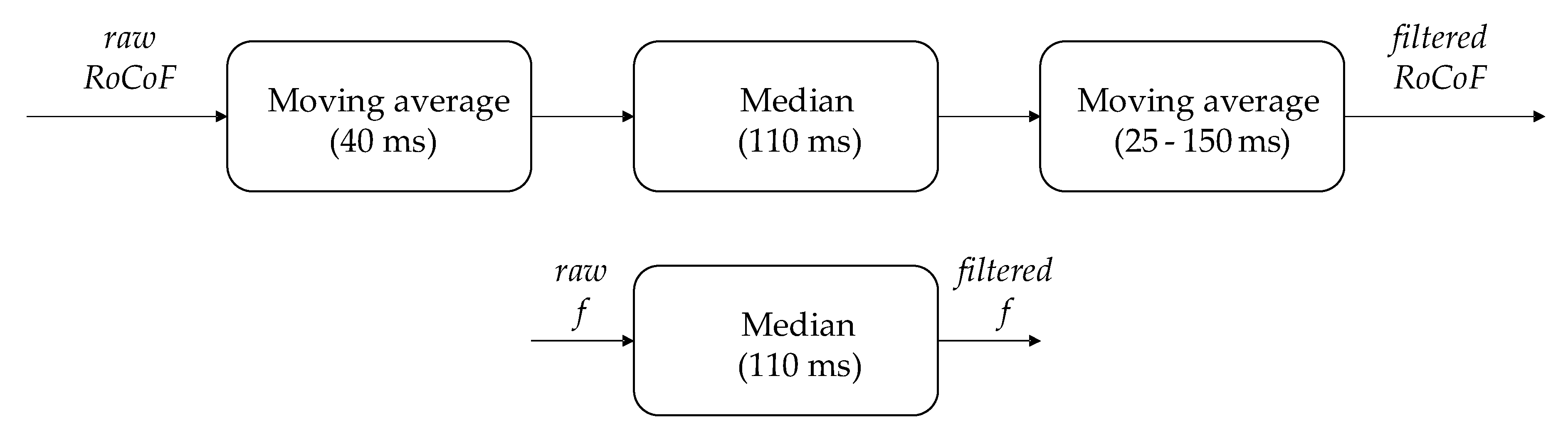
18]. During the HIL testing of the innovative UFLS method, we have developed a few improvements related to a more straightforward deployment of the method: (i) improved filtering for better resolution and filtering of anomalies, (ii) a proof that despite the
RoCoF filtering, introduced time delays do not diminish the speed of UFLS, and (iii) easy deployment of the method on the existing IED-based devices. For the reader’s convenience, a brief summary of the new UFLS methodology from [
17] is provided in
Section 2, together with the IED-related implementation challenges and provided solutions for the applicability of the method in a real environment. This is followed by the specifics of the experimental HIL setup in
Section 3 and the simulation results in
Section 4. Finally, the conclusions are drawn in
Section 5.
4. Results
Both the conventional six-stage UFLS scheme currently used in Slovenia and the innovative UFLS scheme were applied in simulation scenarios. Specifics of both UFLS settings are provided in
Table 1. Frequency thresholds
fthr are taken from the Slovenian Grid code [
27], and additional frequency stability margin thresholds
Mthr are selected with a one-second span between them since the analysis showed there are no special differences when selected otherwise.
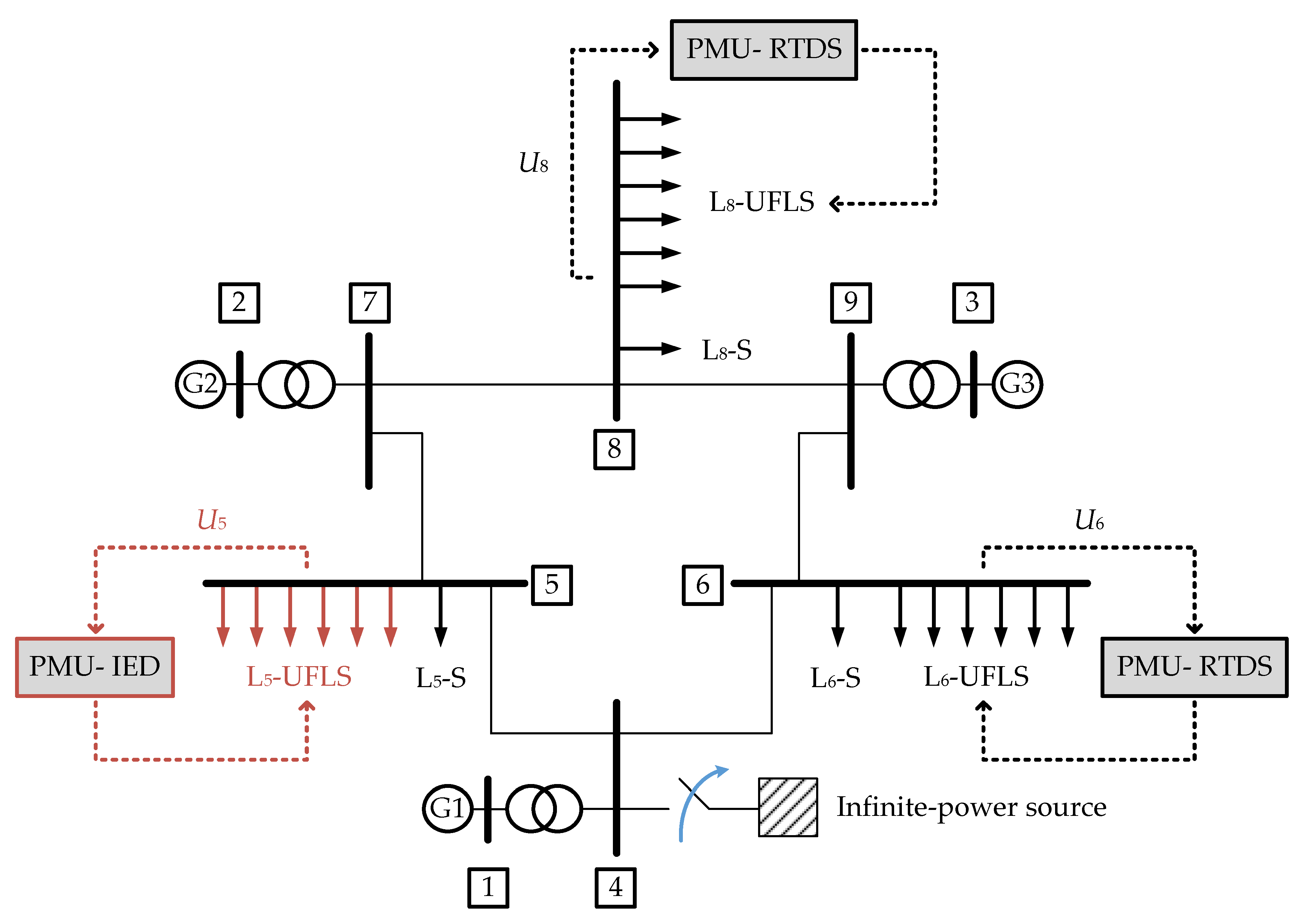
In the base case, steady-state conditions before the main event were set so that the total loading of the benchmark IEEE 9-bus system model (
Figure 9) was 315 MW and the overall generating power was 319.6 MW. Apart from the base case, this research included 65 additional simulated cases (66 altogether), in which the total generation capacity before the main event was gradually decreased by 1% per case. In this way, the amount of power provided by the power source (and consequently power mismatch between the generation and the consumption) in the moment of a simulated switching event increased with each consecutive case. This was repeated to the point where all available frequency control and protection mechanisms (primary frequency control and UFLS) were insufficient to prevent frequency decay bellow the
fLIM.
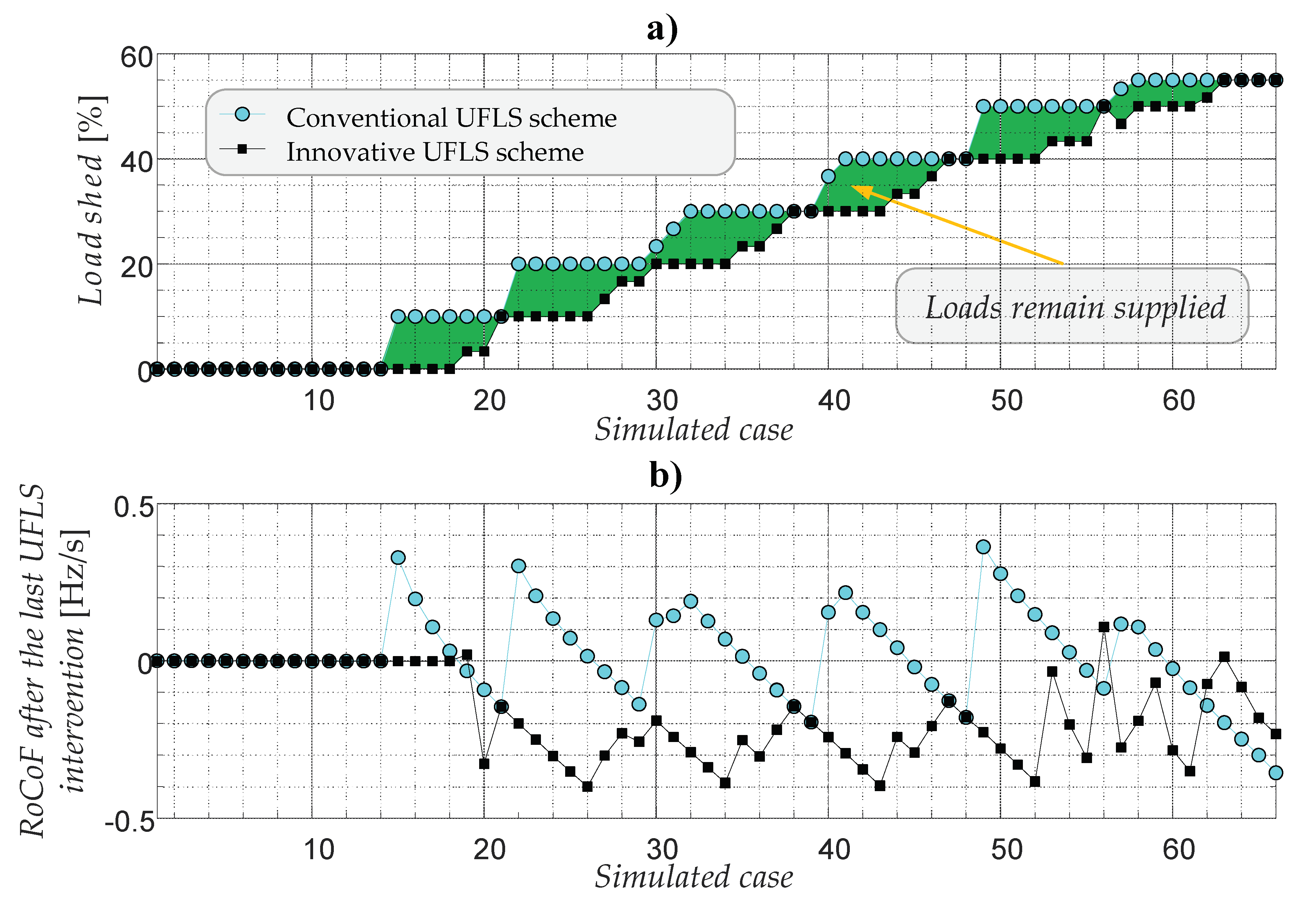
In
Figure 10, an overview of the results extracted from the entire set of 66 simulated cases is provided. Cases are listed on the horizontal axis. Conventional UFLS results are depicted with cyan markers, whereas black markers correspond to innovative UFLS.
Figure 10a shows the percentage of the EPS de-loading due to UFLS. Conventional UFLS is activated in 79% of all cases (52 out of 66). Among these, innovative UFLS keeps more load supplied in 81% of cases (42 out of 52) while still being successful in achieving frequency stabilization. This is marked by a green-shaded area between the two curves in
Figure 10a.
Another thing worth mentioning is that with a conventional UFLS scheme, shedding in all three busses will nearly always take place simultaneously (92% of cases/48 out of 52 cases) and, consequently, the entire UFLS stage will be tripped. However, partial UFLS activation is much more frequent for the innovative UFLS scheme (31% of cases/16 out of 52), as can be observed in
Figure 10a. The reason for this is that even though the
fthr and
Mthr values are set to same values for all three devices participating in a UFLS scheme, the variety of calculated
M(
t) values is much higher across the network than the variety of calculated
f(t) values. With three load busses, we therefore introduced three ‘’substages’’ for each of the UFLS stages, which can be seen as fine-tuning power imbalance with UFLS. Furthermore, in systems with more load busses, even finer tuning could be achieved due to those inherently introduced substages.
However, observing the amount of disconnected load is only one of several ways to highlight the superiority of innovative UFLS. When evaluating the efficiency of UFLS, different authors took different approaches in the existing literature (established in [
28]), ranging from ranking the schemes according to the time required before the frequency is returned back to the nominal value, to comparing post-event steady-state frequency offset or by observing frequency overshoots that might appear after UFLS is activated. It was concluded in [
28] that there is no unified scoring metric for this. One thing is for certain though: the main objective of UFLS, by its definition, is to prevent a further frequency drop [
29] or, in other words, restore the balance [
30] between generated and consumed active power in the EPS in due time. Plainly speaking, this means that UFLS is to stabilize the frequency and bring
RoCoF to a value as close as possible to zero.
For this reason,
Figure 10b shows the
RoCoF value after the last UFLS intervention took place for each case (this might be any of the stages, depending on the imbalance conditions). This observation is independent of any other influential mechanisms, especially specifics of the governor and its control, that often have a significant impact on frequency response after UFLS is activated. The value of zero was dedicated to
RoCoF results when UFLS was not activated at all. When conventional UFLS was activated, the re-balancing was unsuccessful in 52% of the cases (29 out of 52), since the last shedding resulted in having a surplus of power generation. One might treat this as if dealing with a flip of a coin, i.e., pure guessing. On the other hand, innovative UFLS paused its intervention in the time since it successfully recognized that the frequency is about to be stabilized without triggering the last stage. The
RoCoF values after the last UFLS intervention are kept below zero (average value around −0.25 Hz/s) in 98% of the cases (46 out of 47) and frequency control is left to continuously fine-tune the power balance. At this point, it should be stressed that the paused stage triggering does not mean that the stage is permanently blocked. Quite the opposite; shedding hibernates until conditions for its triggering are met. This means that if the available frequency control is exhausted, the stage will be triggered later on, once the
M(
t) value becomes low enough. An example of such conditions is simulated case no. 56. However, as can be seen from
Figure 10, such situations are extremely rare and yet, they nevertheless successfully solve under-frequency conditions.
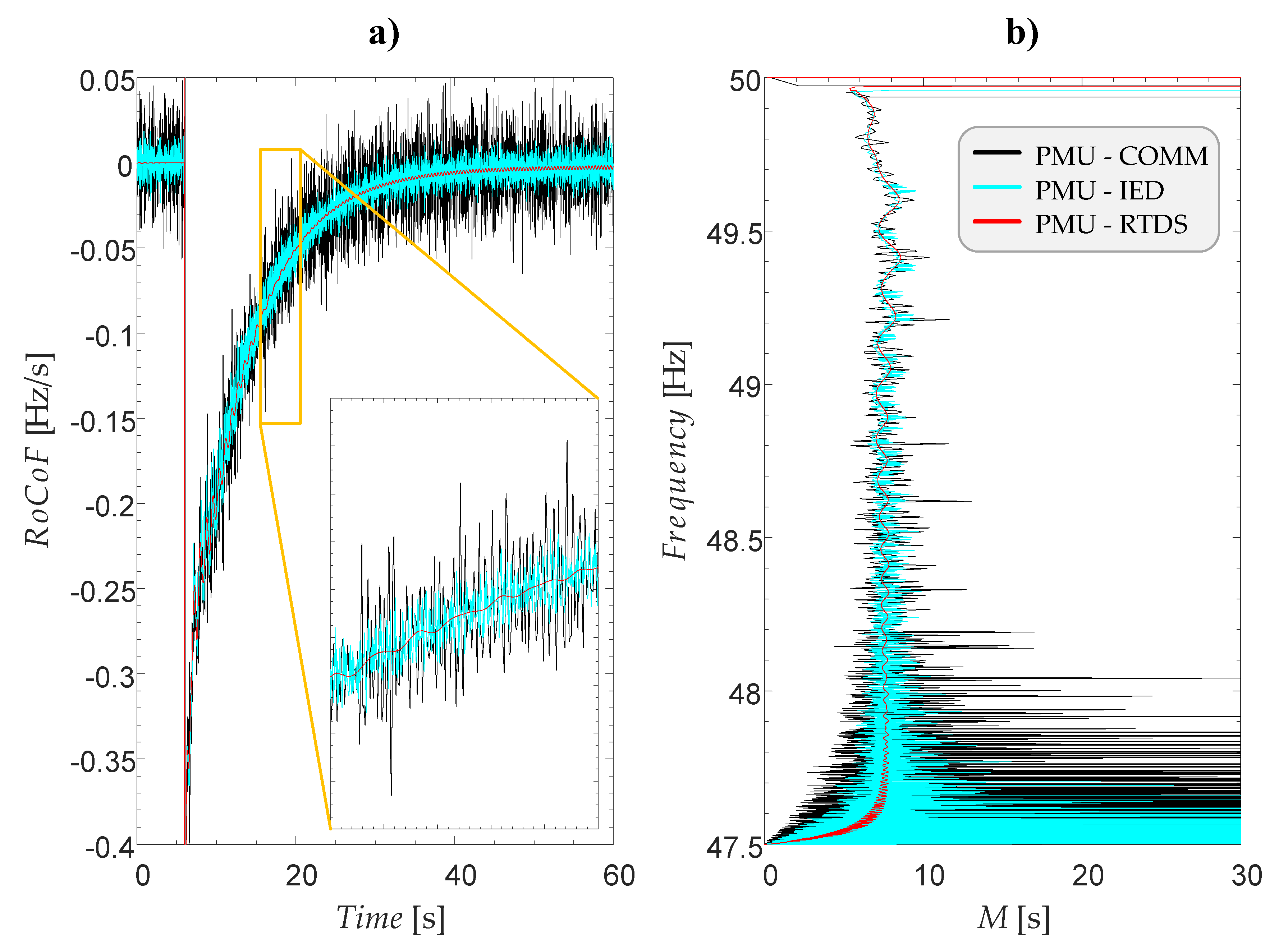
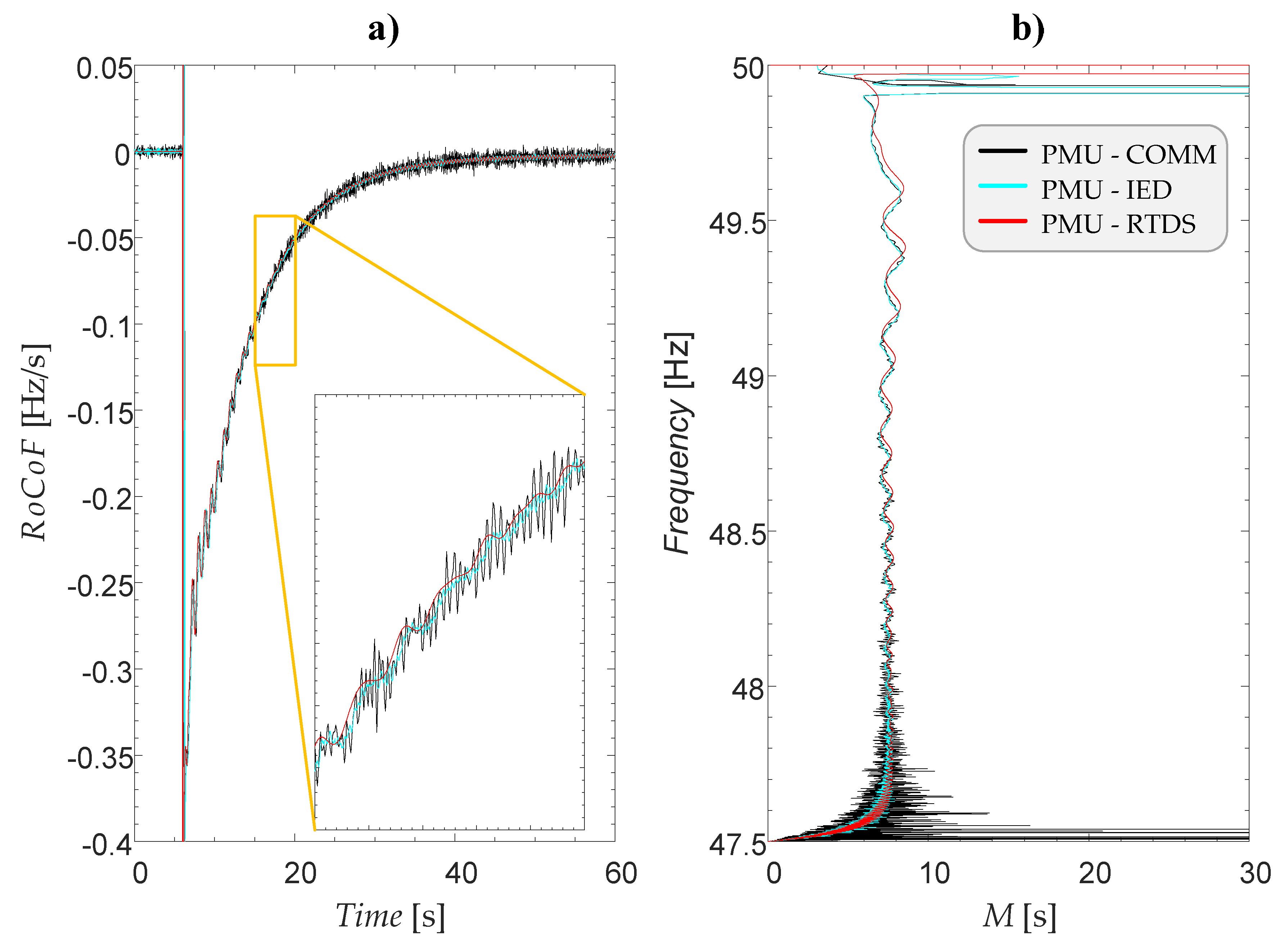
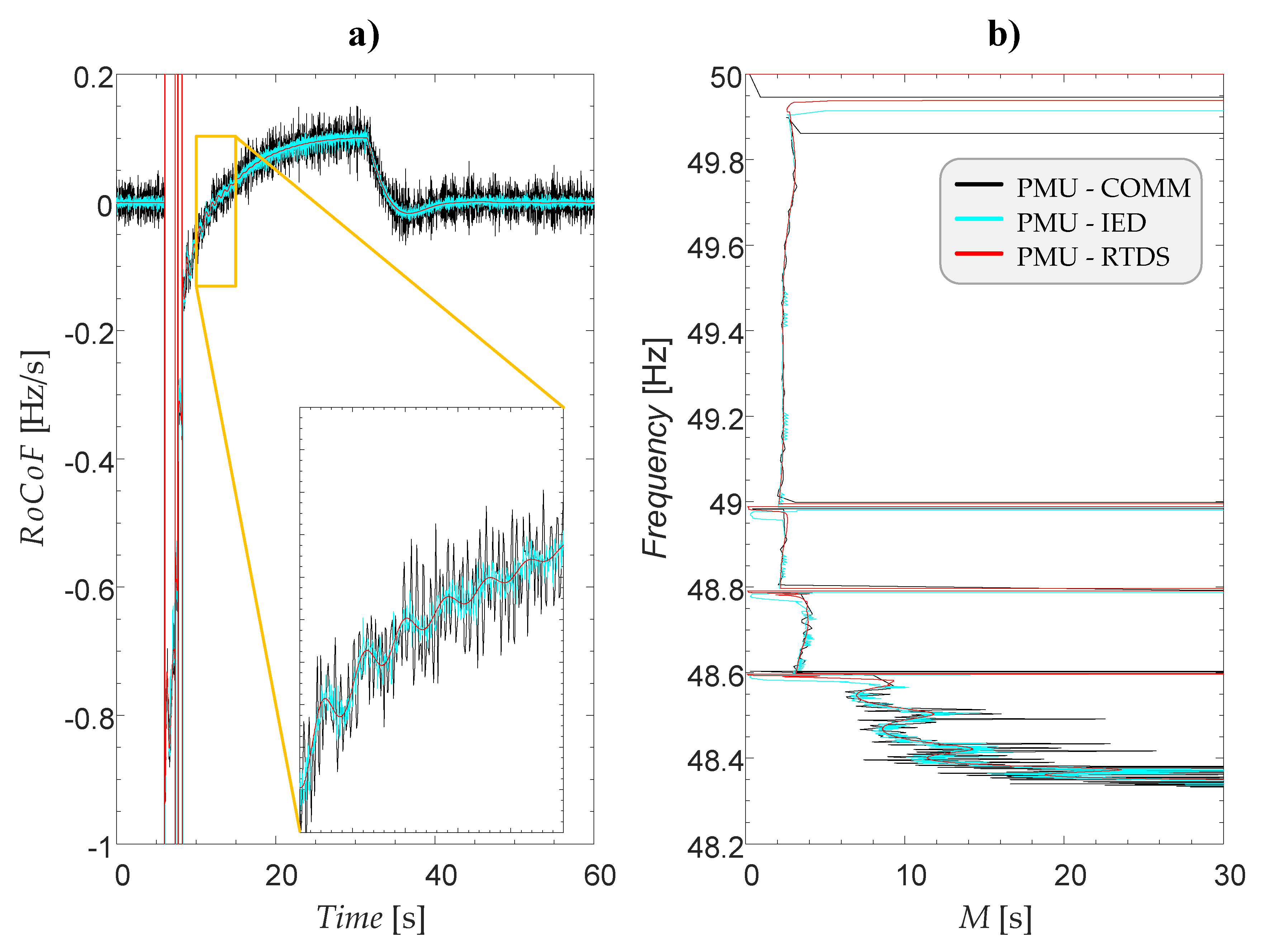
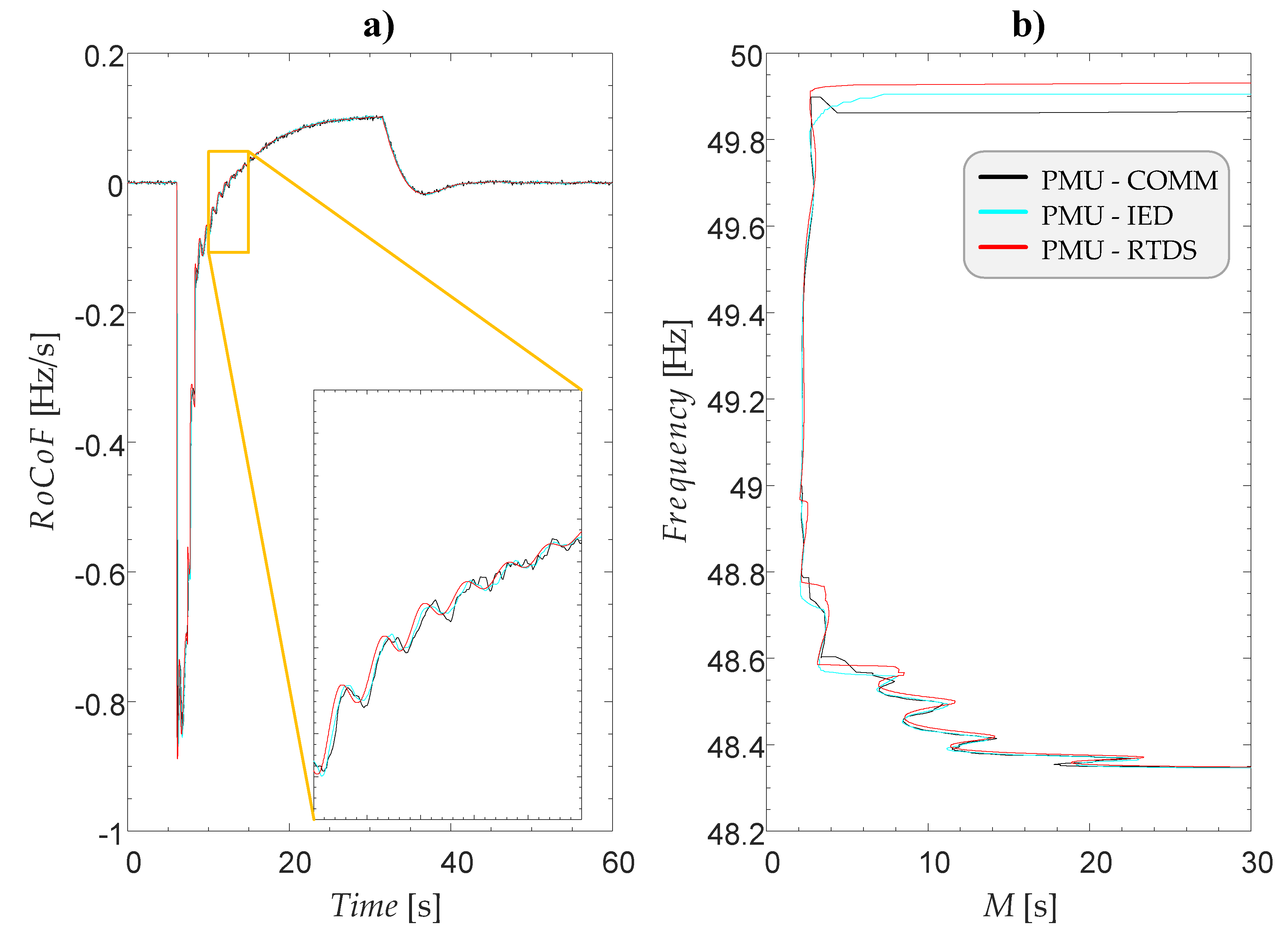
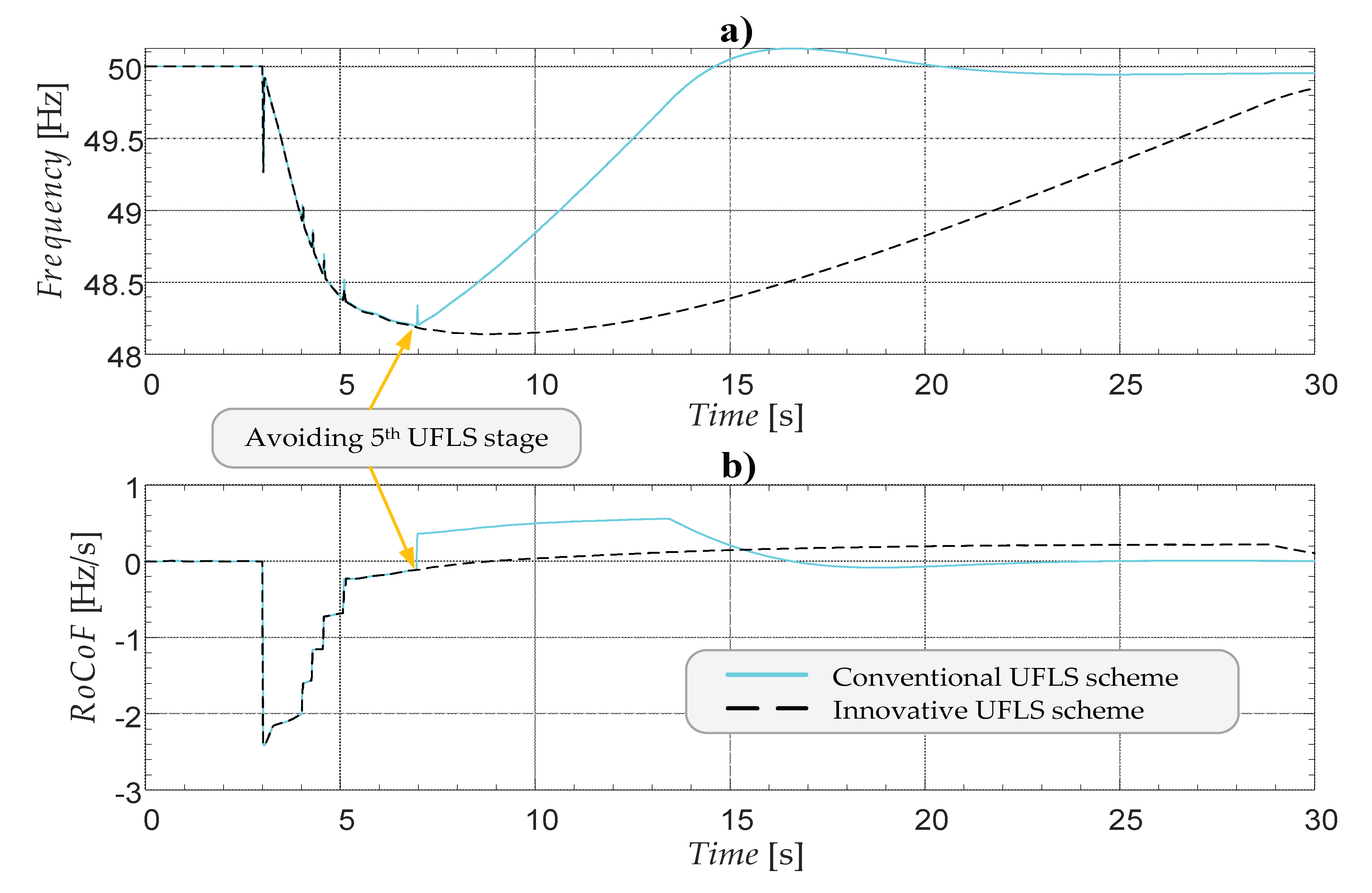
For simulated case no. 49, a time-domain response of the EPS frequency and
RoCoF is depicted in
Figure 11a and
Figure 11b respectively. From observing the diagrams, it becomes evident that at the moment of reaching the frequency threshold of the fifth UFLS stage, innovative UFLS detects that there is still enough time available before frequency instability is endangered (
M 8 s,
Figure 12). As a result, the fifth UFLS stage is paused, which allows the frequency control to finish the frequency stabilization process by itself. If that was not the case, the fifth UFLS stage would have been triggered later on when the frequency would have approached the selected frequency stability limit
fLIM and, consequently, the
M criterion of the fifth stage would have been triggered.
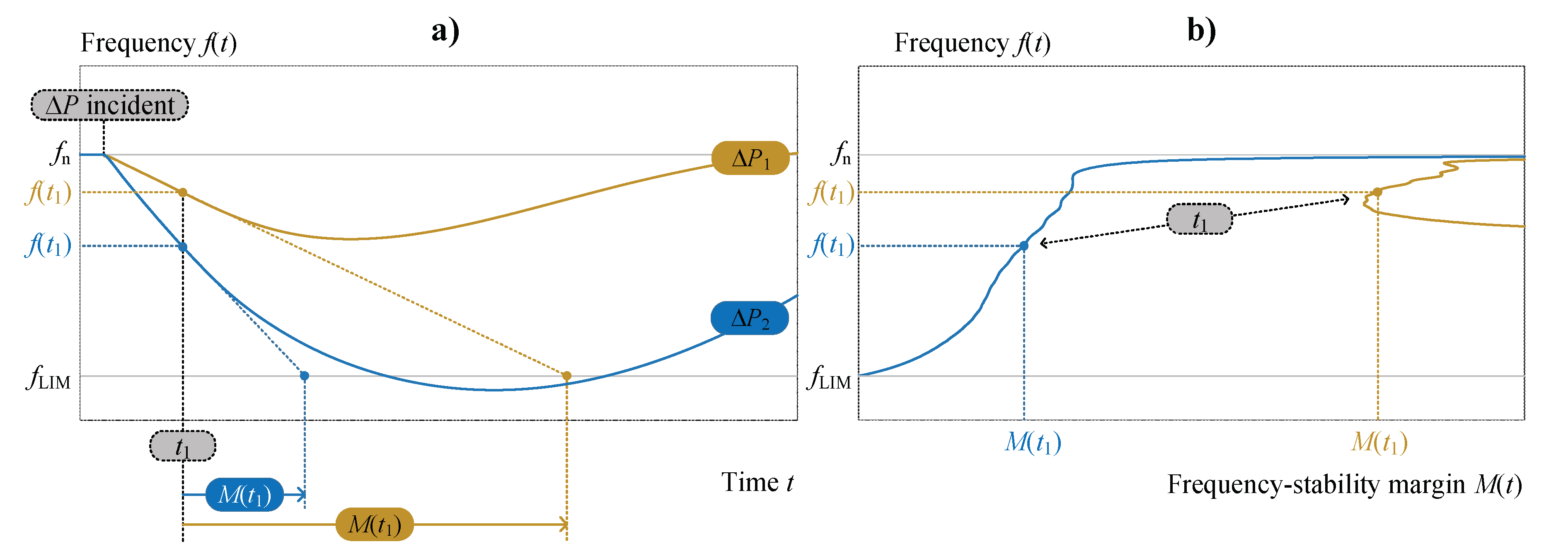
There is another essential thing that has to be discussed. When the frequency is decreasing with a significant
RoCoF(t), a prompt triggering of UFLS is required since any additional time delay might be unacceptable. This is inherently achieved in conventional UFLS (triggering solely according to the frequency criterion
fthr) and it is vital to be aware that this is also the case with innovative UFLS. The initial concern with the innovative UFLS scheme was related to extreme scenarios, in which the curve on the
f(t)-M(t) plane is expected to make a rather abrupt jump from the upper right corner (steady-state conditions) to the upper left corner of the diagram once power imbalance appears. The delayed recognition of such critical conditions due to two additional moving average filters (
Figure 7) could, therefore, translate into
fthr of a certain stage being violated before the corresponding
Mthr. This would in turn be observed as shedding at lower frequency compared to a conventional UFLS scheme. However, our testing proved that even when dealing with an extreme initial
RoCoF −10 Hz/s), the
Mthr criterion is still violated sufficiently prior to the
fthr criterion. In
Table 2, the actual frequency at which the
Mthr was met is given for each UFLS stage. Evidently,
M criteria of all UFLS stages were met before the frequency even reached the
fthr value of the first UFLS stage (0.483 Hz margin in a worst-case scenario—see the last column in
Table 2). This proves that the innovative UFLS scheme would respond to such an extreme event identically as the conventional scheme, with no additional time delay.
5. Conclusions
In the most common viewpoint of smart grids, the decentralization of electric power generation is usually accompanied by the centralization of protection functions. In this paper, we proved the concept of a RoCoF-based innovative UFLS which does not require centralization, yet still provides a high level of efficiency and flexibility. The main conclusion of this paper is that the innovative UFLS is deemed feasible and robust in practical applications. A proposed transition from conventional towards innovative UFLS is extremely simple; (i) an exceptionally simple logic based on RoCoF has to be incorporated in each under-frequency relay and (ii) a second criterion has to be added (parallel to the existing frequency threshold) for real-time monitoring. This new criterion is based on a patent-pending frequency stability margin calculated in real-time from the RoCoF and frequency values.
HIL simulations proved that innovative UFLS is feasible for real-world scenarios and that applying RoCoF does not affect its robustness in any of the tested conditions if the correct filtering techniques are selected. The main advantages of the innovative UFLS can be observed in moderate RoCoF conditions, being such from the very moment of a power deficit occurrence or decreased later on by UFLS intervention.
To summarize the main contributions of this research which all relate to the practical aspects of the implementation of an innovative UFLS scheme under test: (i) a multi-stage
RoCoF filtering procedure that enables using
RoCoF for local frequency stability margin calculation and monitoring in real-time for UFLS purposes. Filtering improves the resolution (linear filter stages) and filters out the anomalies (non-linear filter stage) in
RoCoF measurements, (ii) a proof that despite
RoCoF filtering, introduced time delays do not diminish the speed of UFLS operation during fast-occurring events (tested for −10 Hz/s) as long as
RoCoF is used in an appropriate manner as suggested in [
17], (iii) a proof that IEDs with specifications similar to the PMU can be used for UFLS, which decreases cost (i.e., using the same device for EPS observability and UFLS protection) and opens up numerous possibilities, including building business and market models for UFLS as a part of the end consumer response and other market opportunities related to Smart Grids, and (iv) a new criterion for comparison between several UFLS methods, being the remaining
RoCoF after UFLS stops intervening.
The analysis revealed that the diversity of IEDs (e.g., relays) and RoCoF-measuring techniques present in an EPS is beneficial to the UFLS method under test. Further optimization of RoCoF filtering is possible to reduce time delays, but one has to keep in mind that optimization, according to the noise requirements, has to be appropriately considered. Future work will be directed towards the development of the UFLS concept in which bulk load shedding is left to conventional UFLS, whereas handling the remaining power imbalance is left to smart devices (e.g., smart meters) located at end consumers and, therefore, widespread within the entire EPS.