Active Charge Balancing Strategy Using the State of Charge Estimation Technique for a PV-Battery Hybrid System
Abstract
1. Introduction
2. Modeling Approach
2.1. Photovoltaic (PV) Mathematical Modeling
2.2. Maximum Power Point Tracking (MPPT)
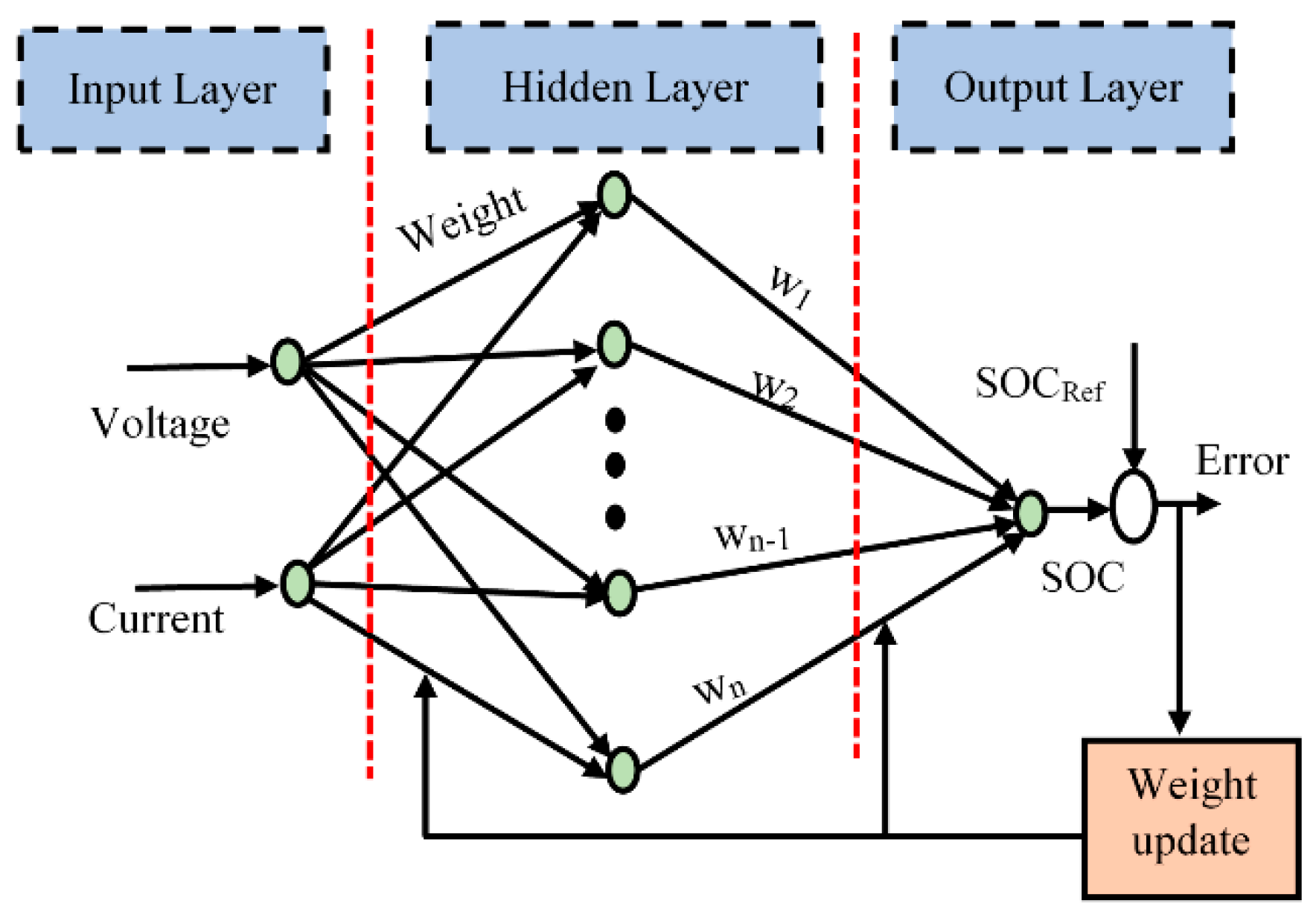
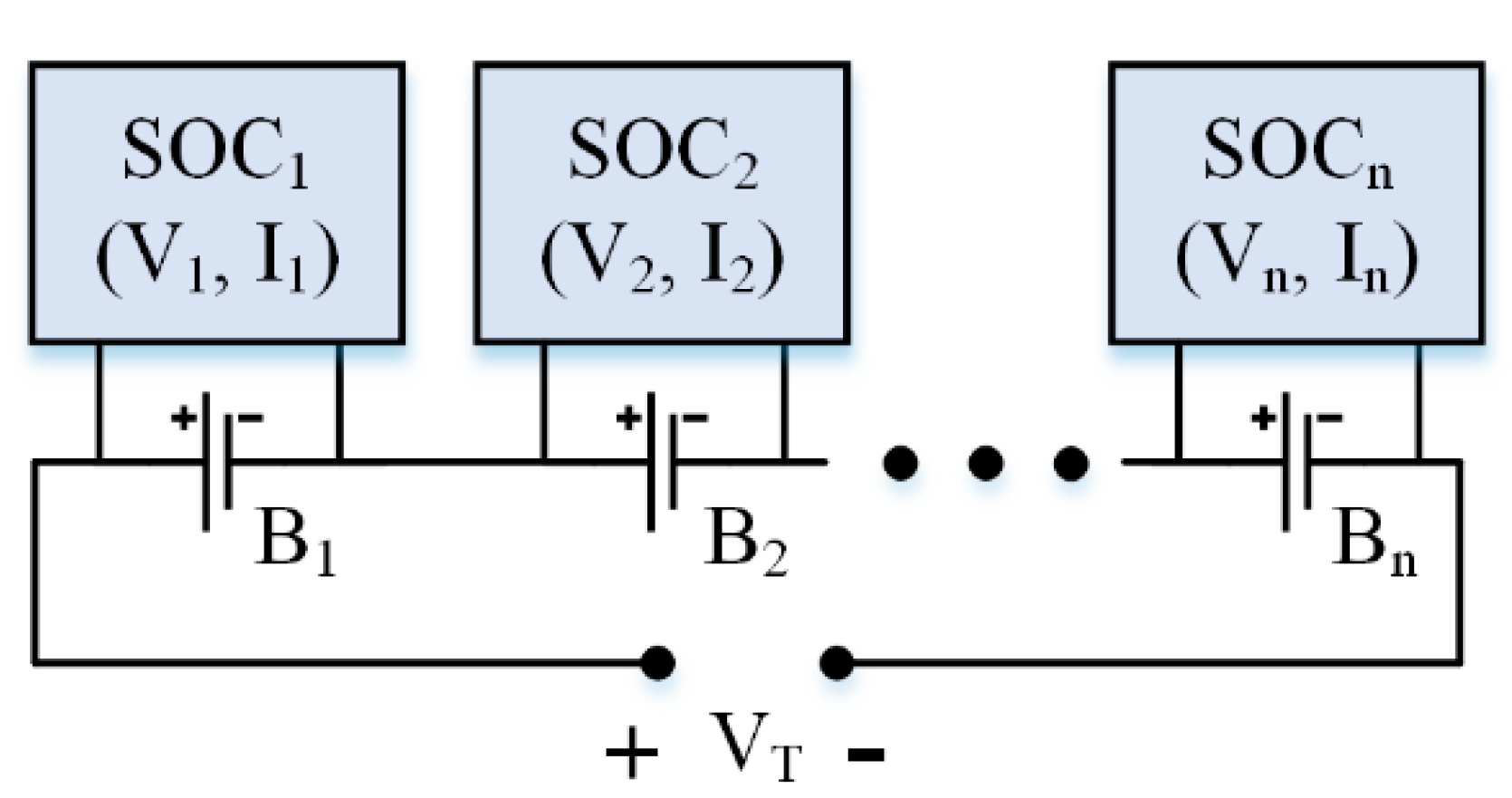
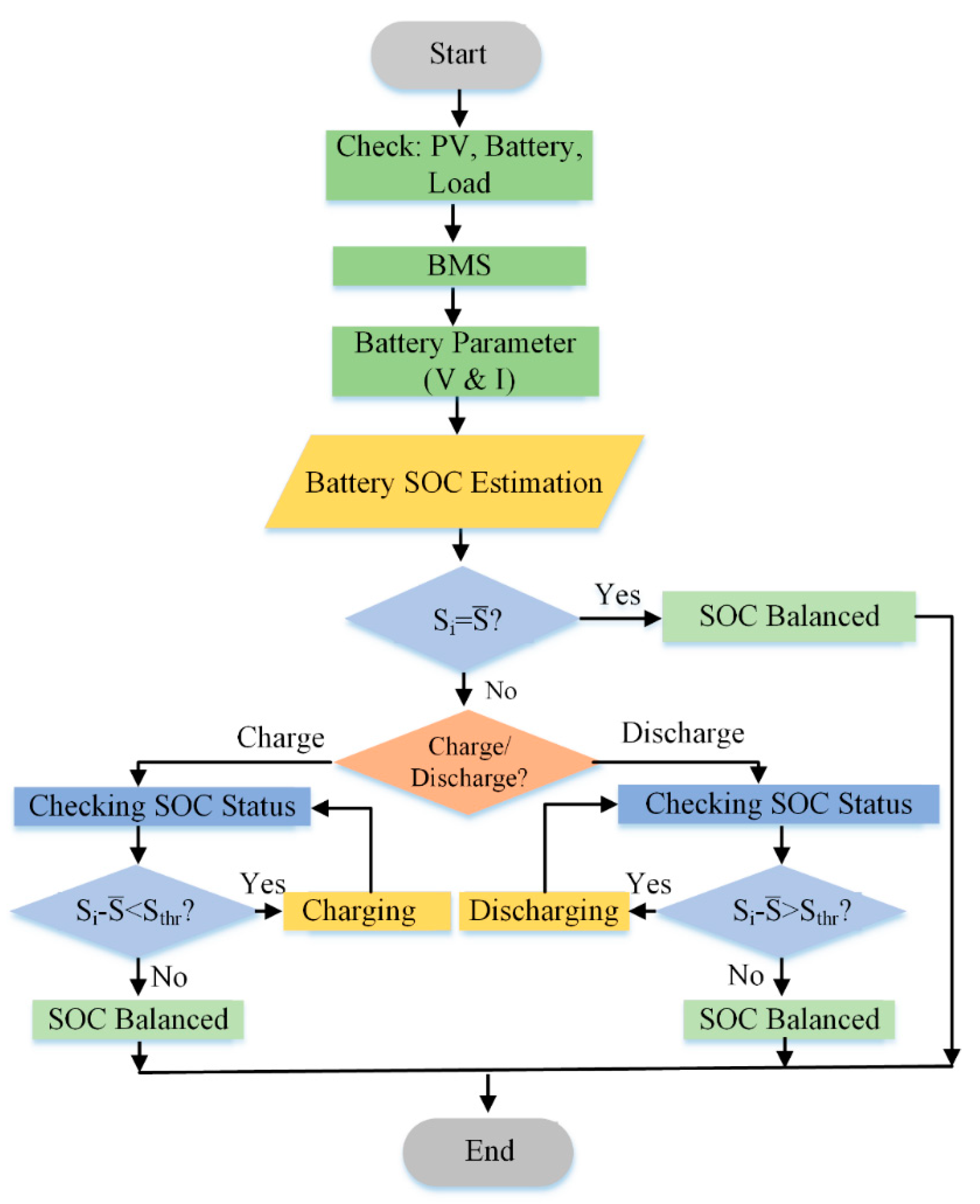
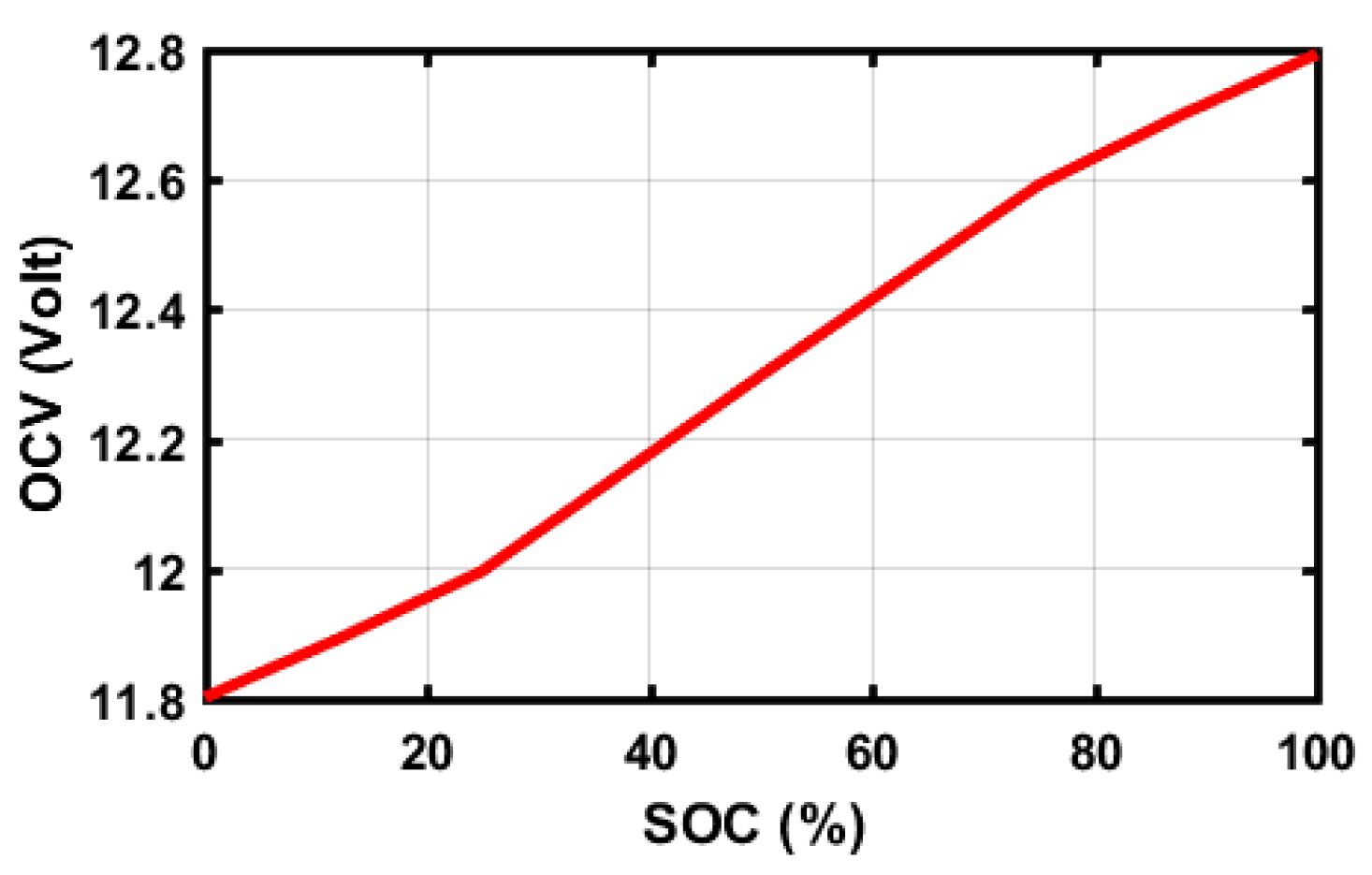
2.3. State of Charge (SOC) Estimation
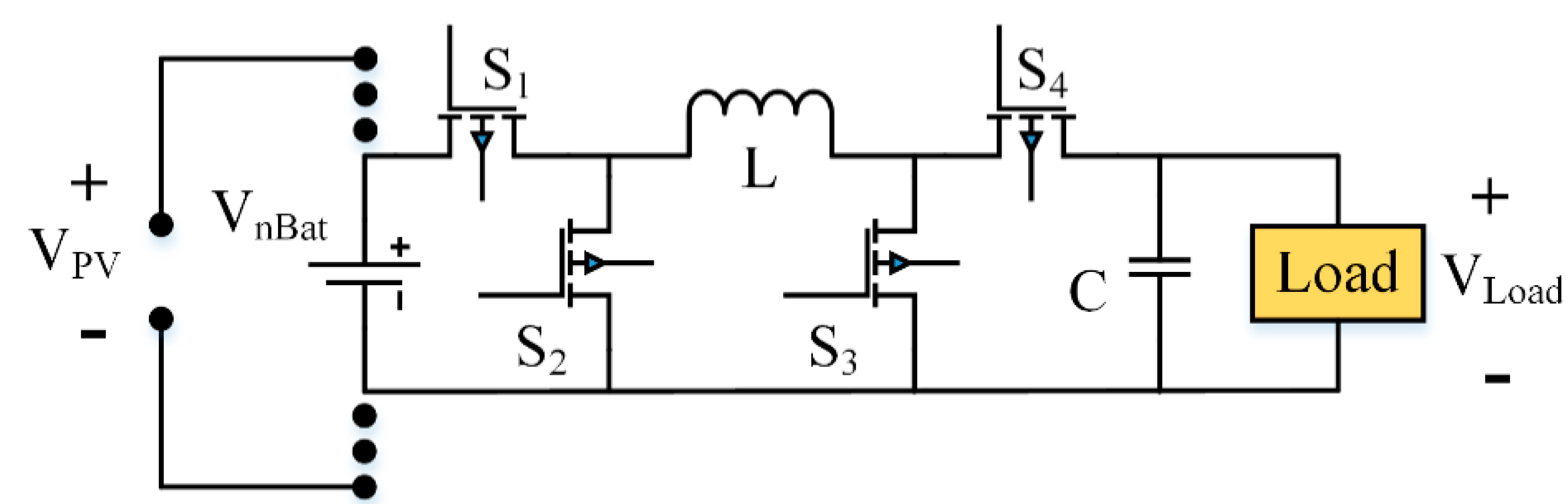
2.4. DC/DC Buck-Boost Converter
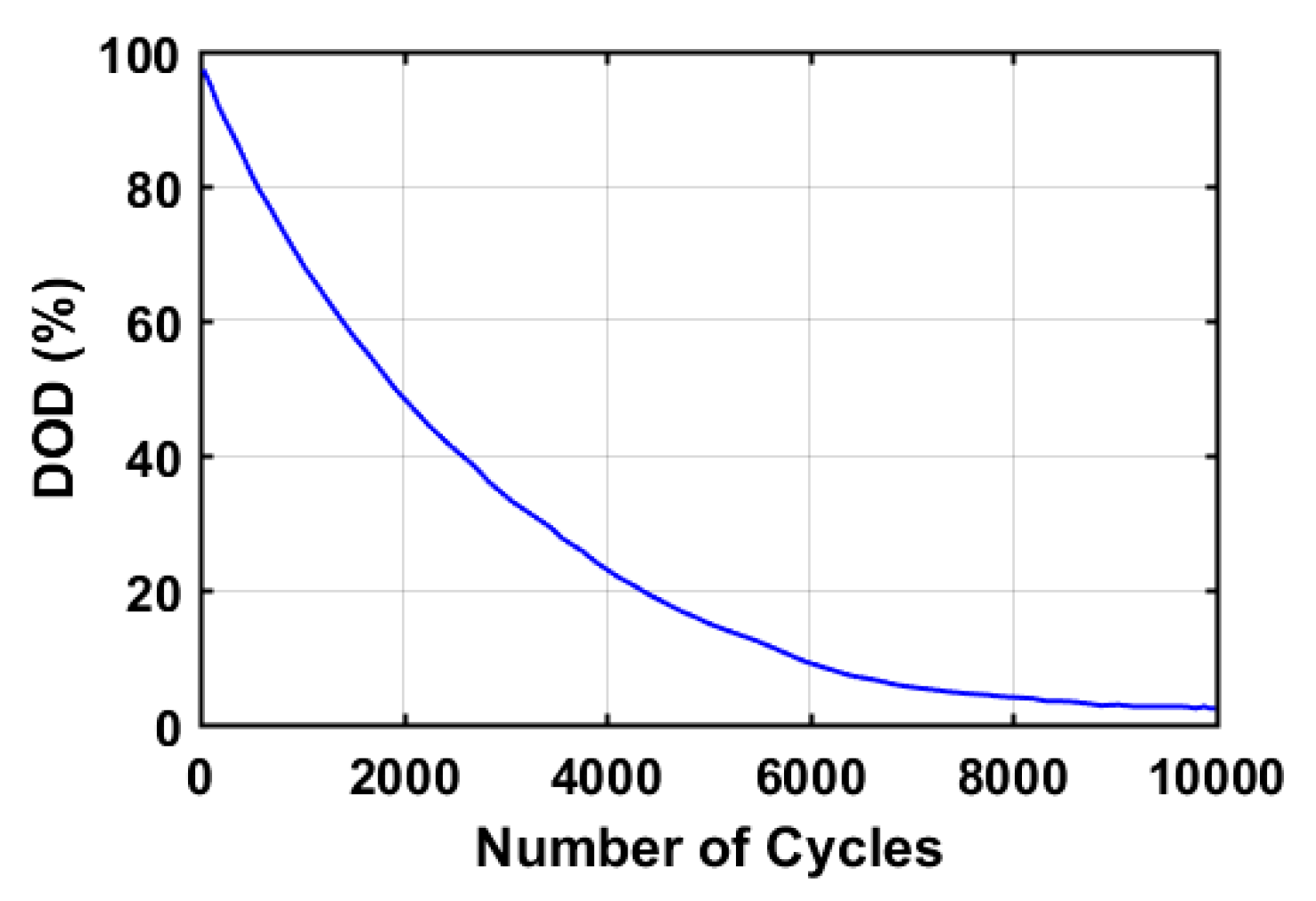
2.5. Battery Lifetime Estimation
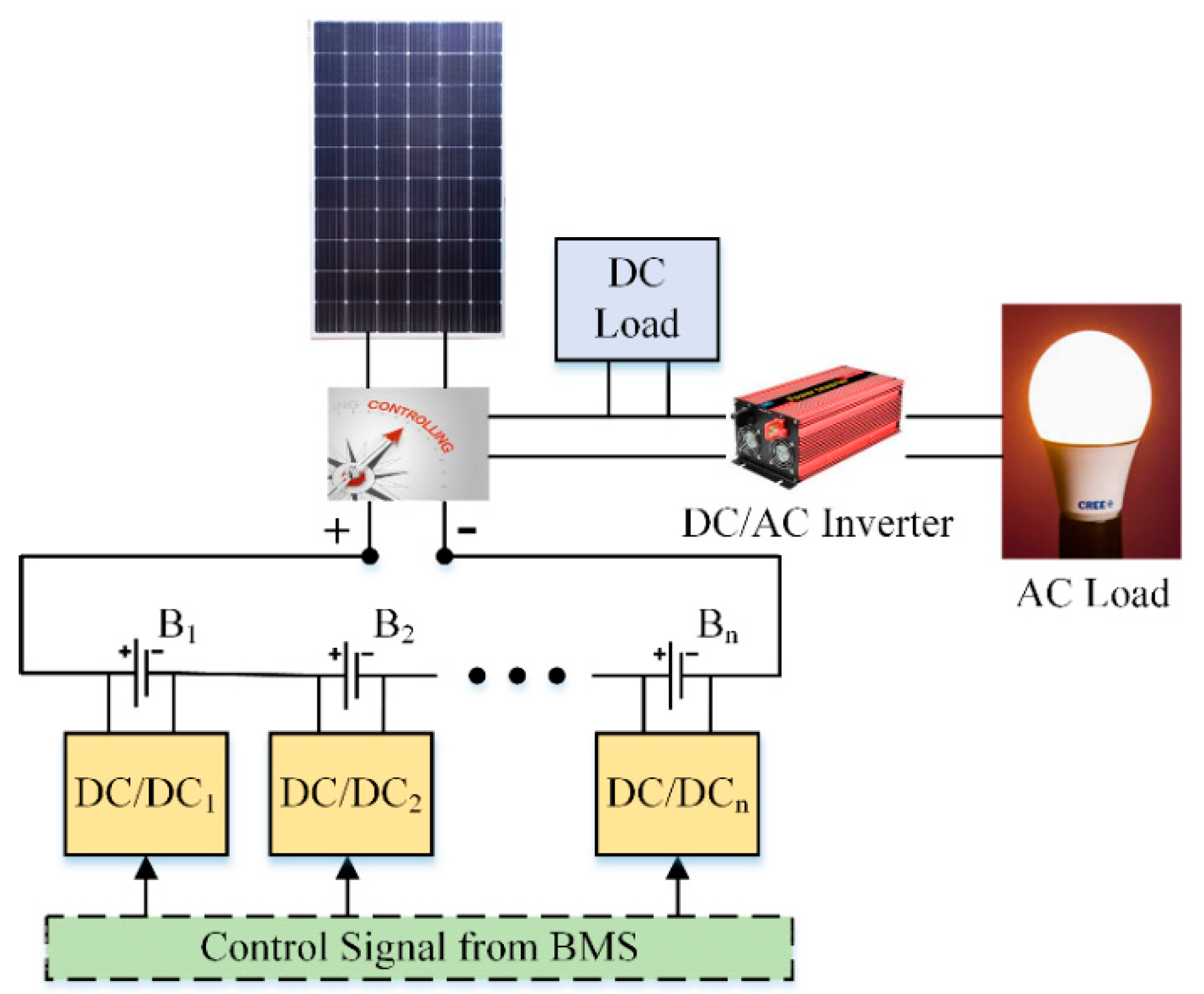
3. Proposed Methodology
3.1. Simulation Model
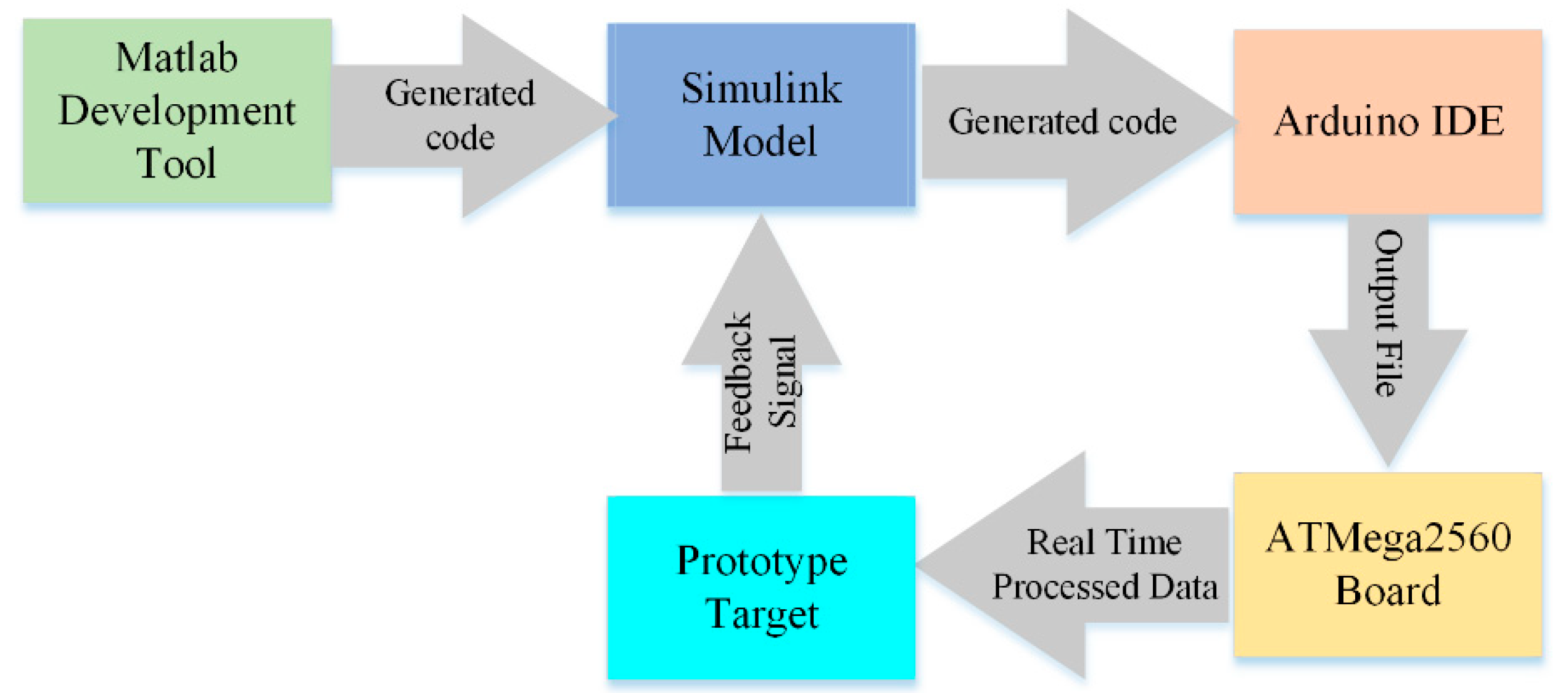
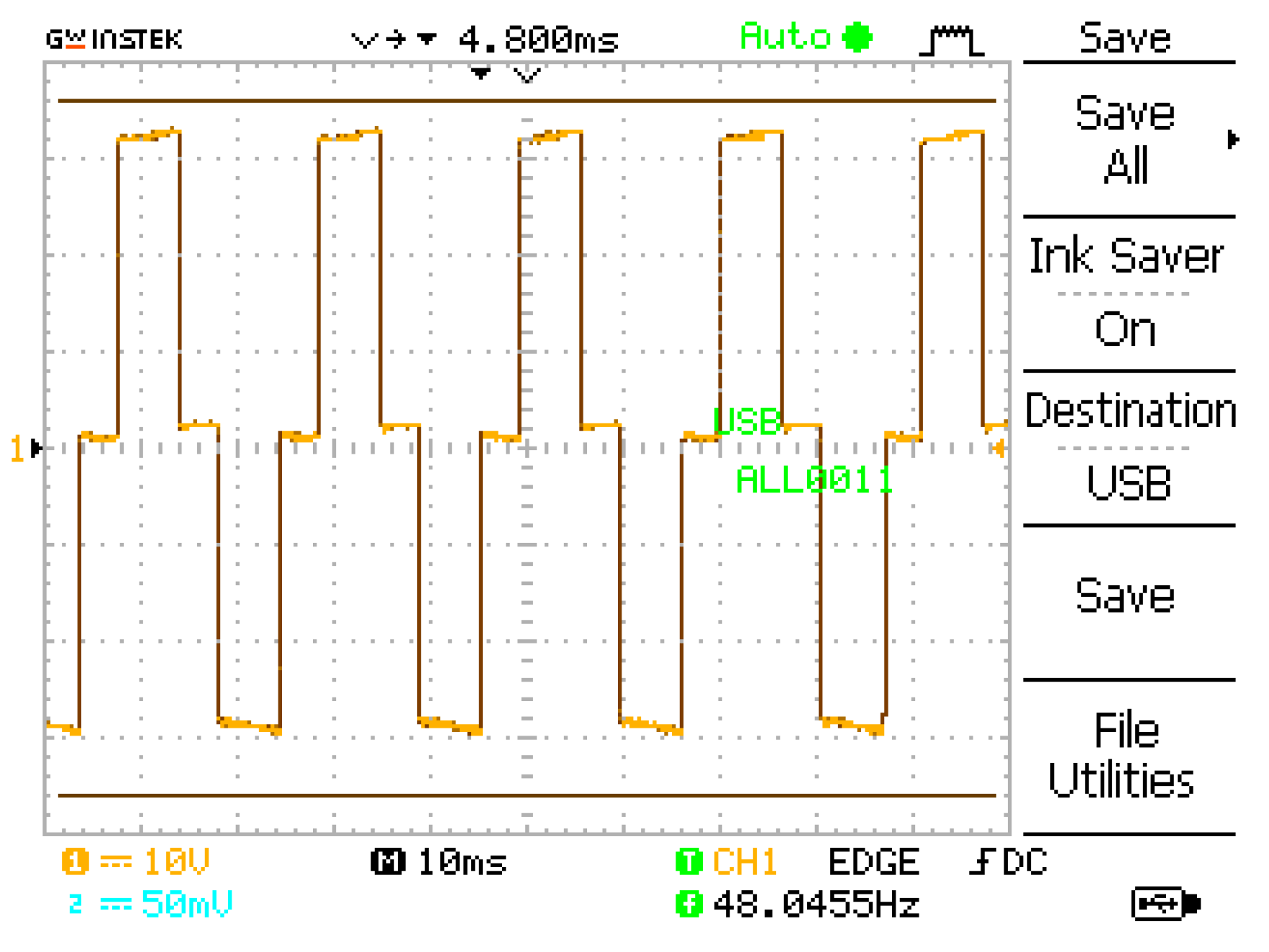
3.2. Experimental Model
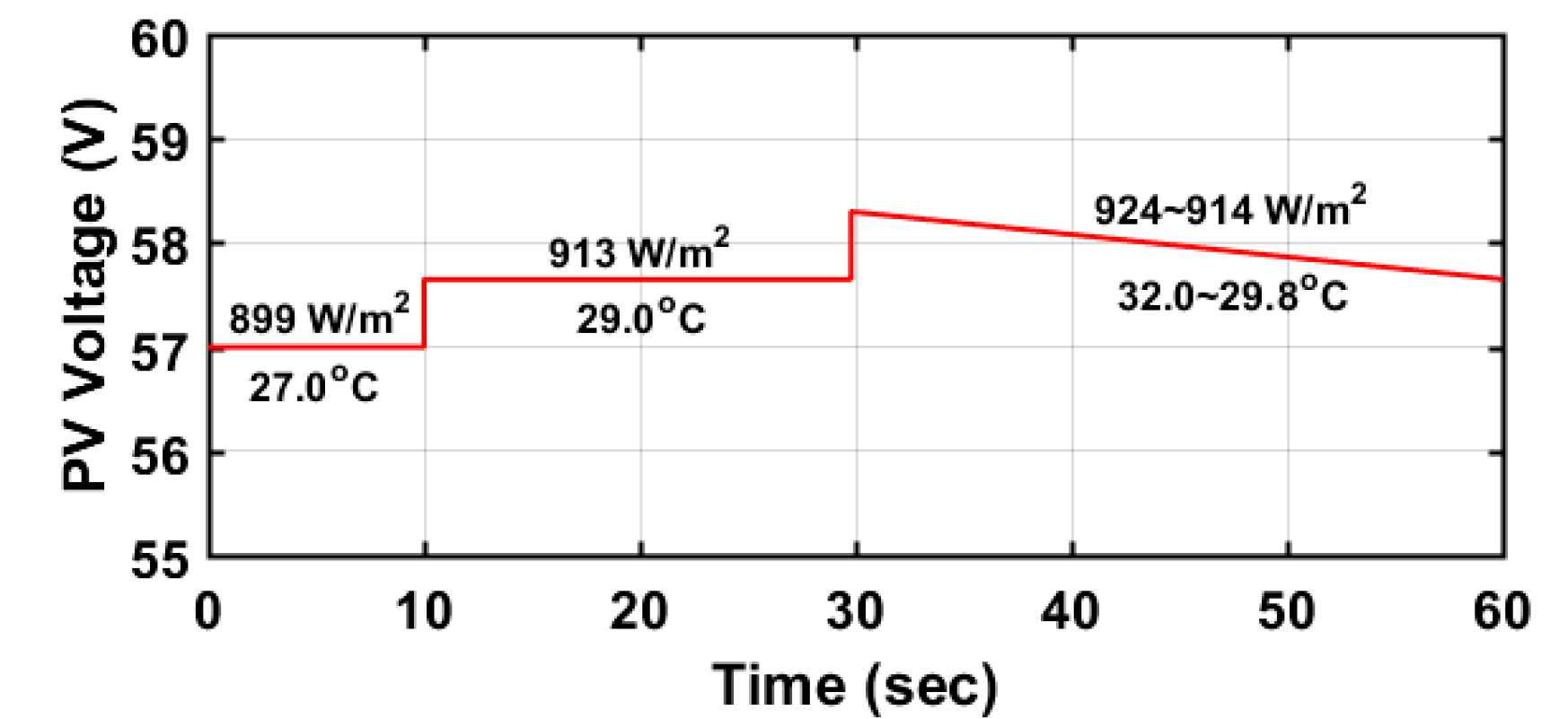
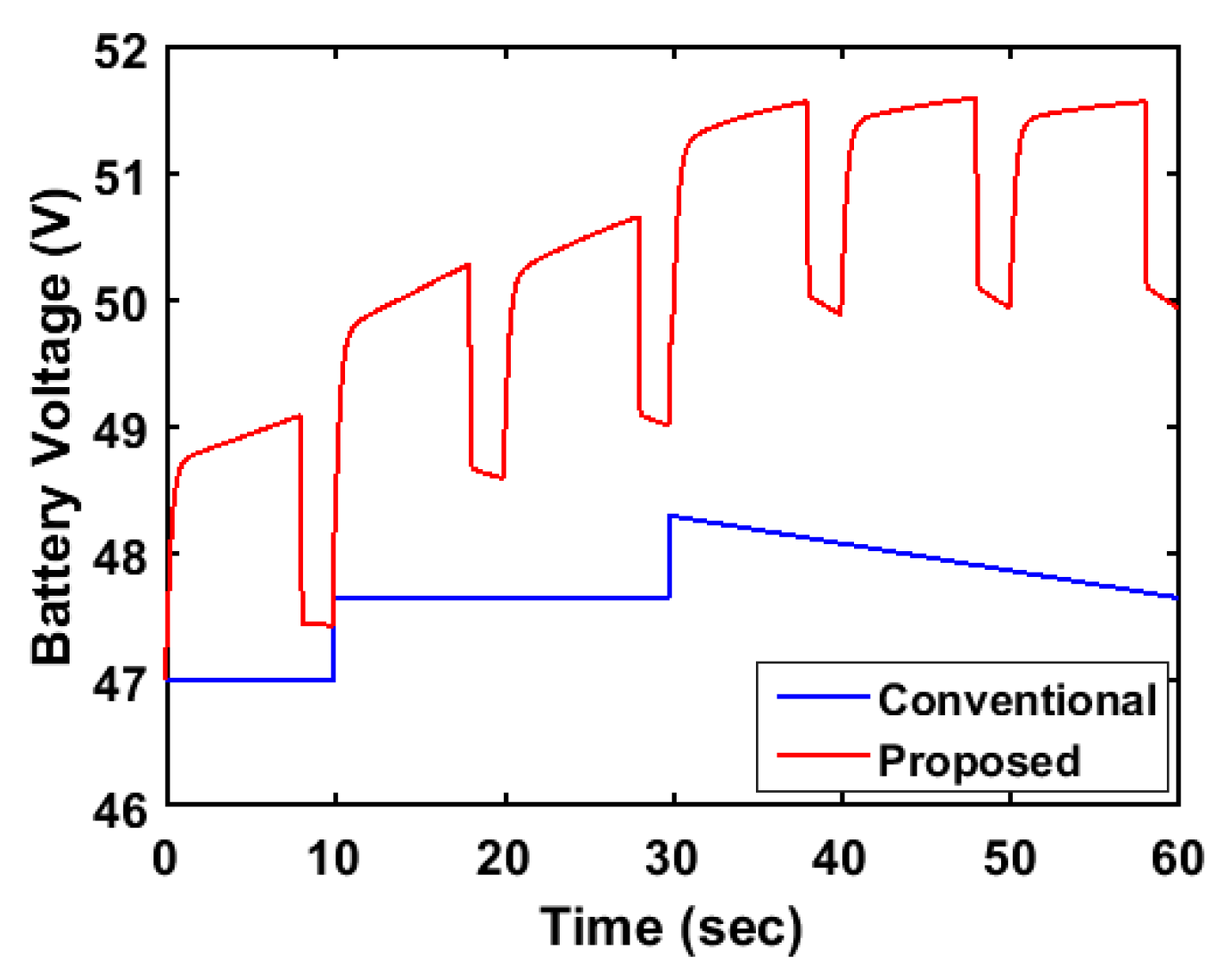
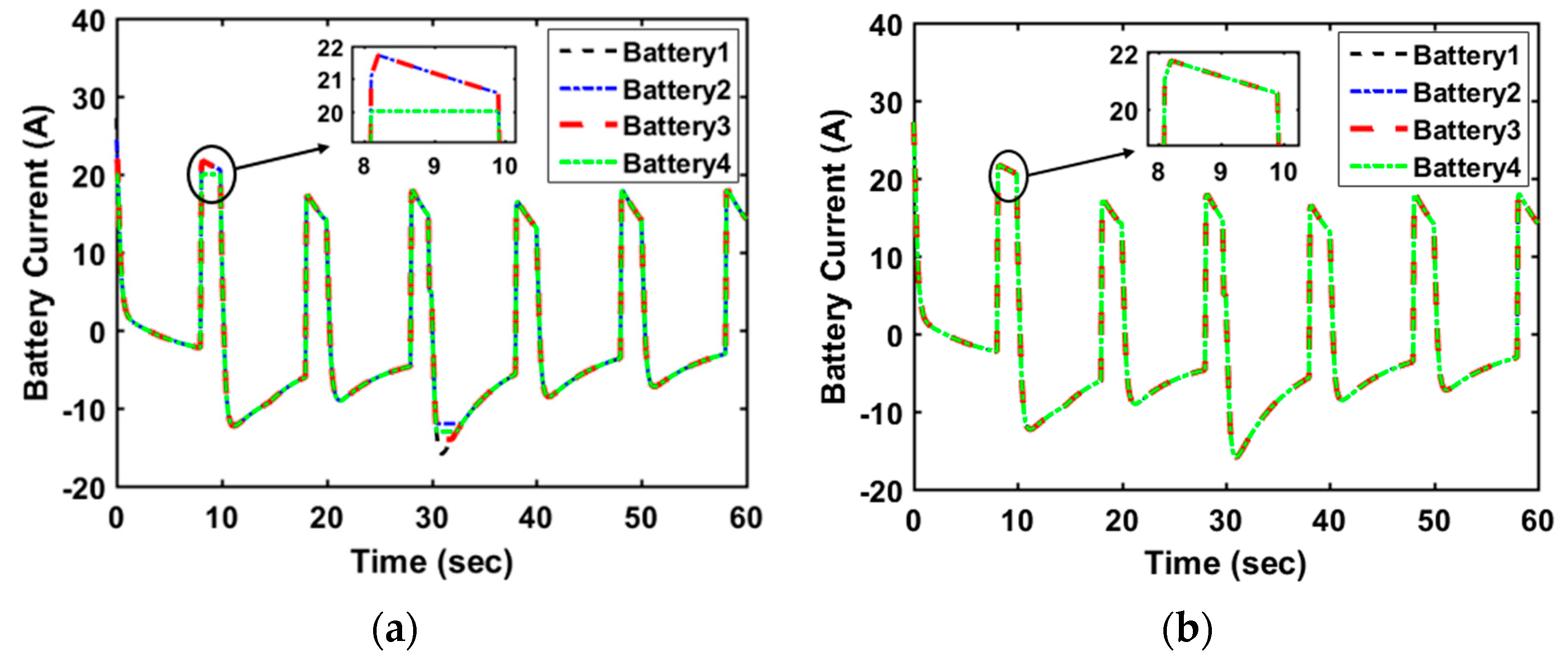
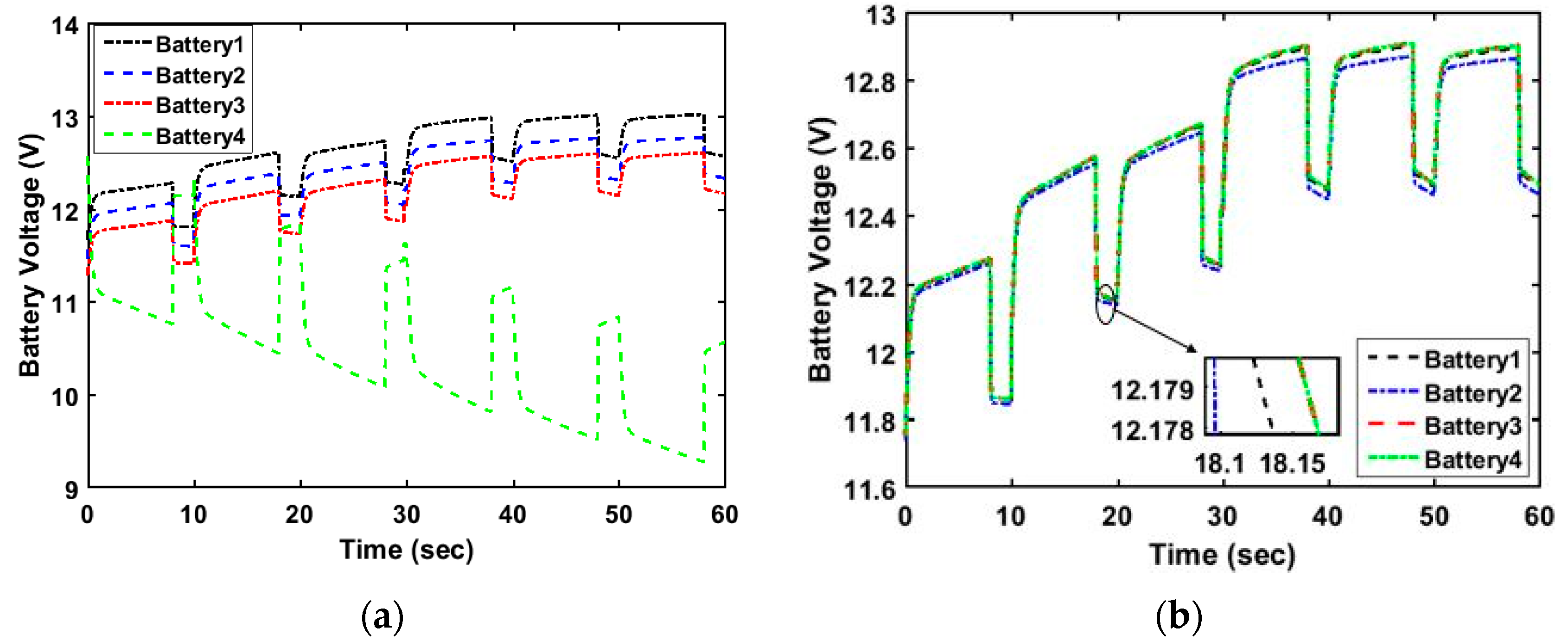
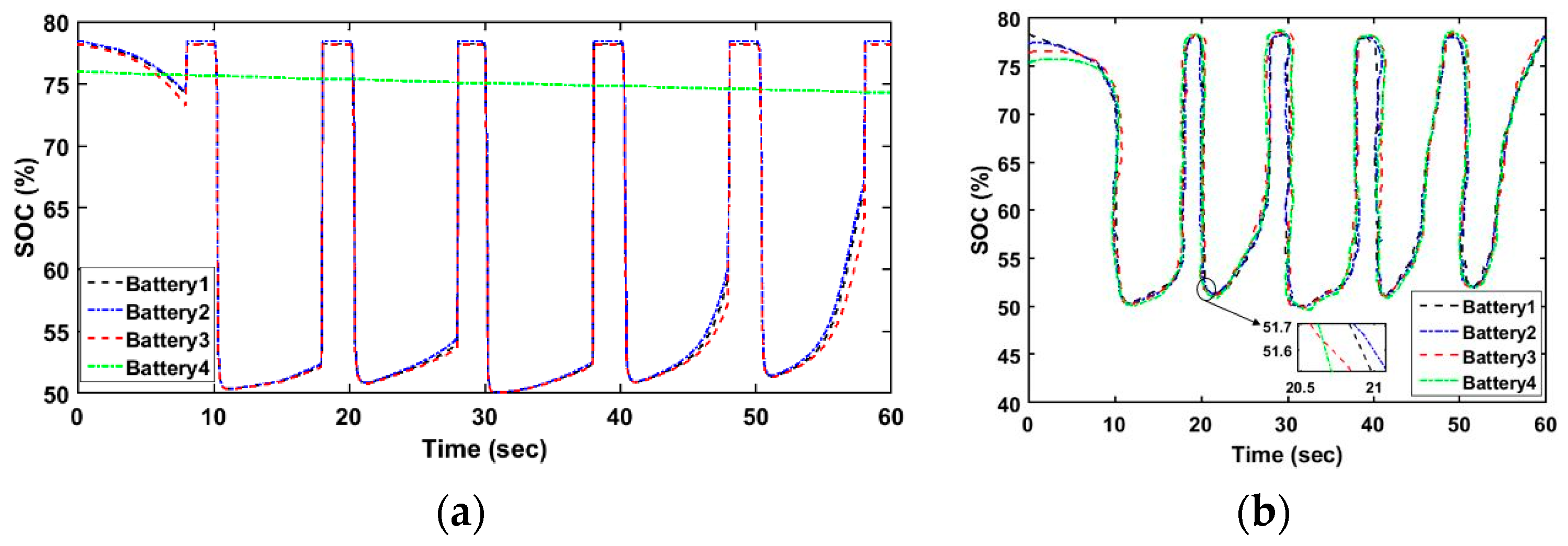
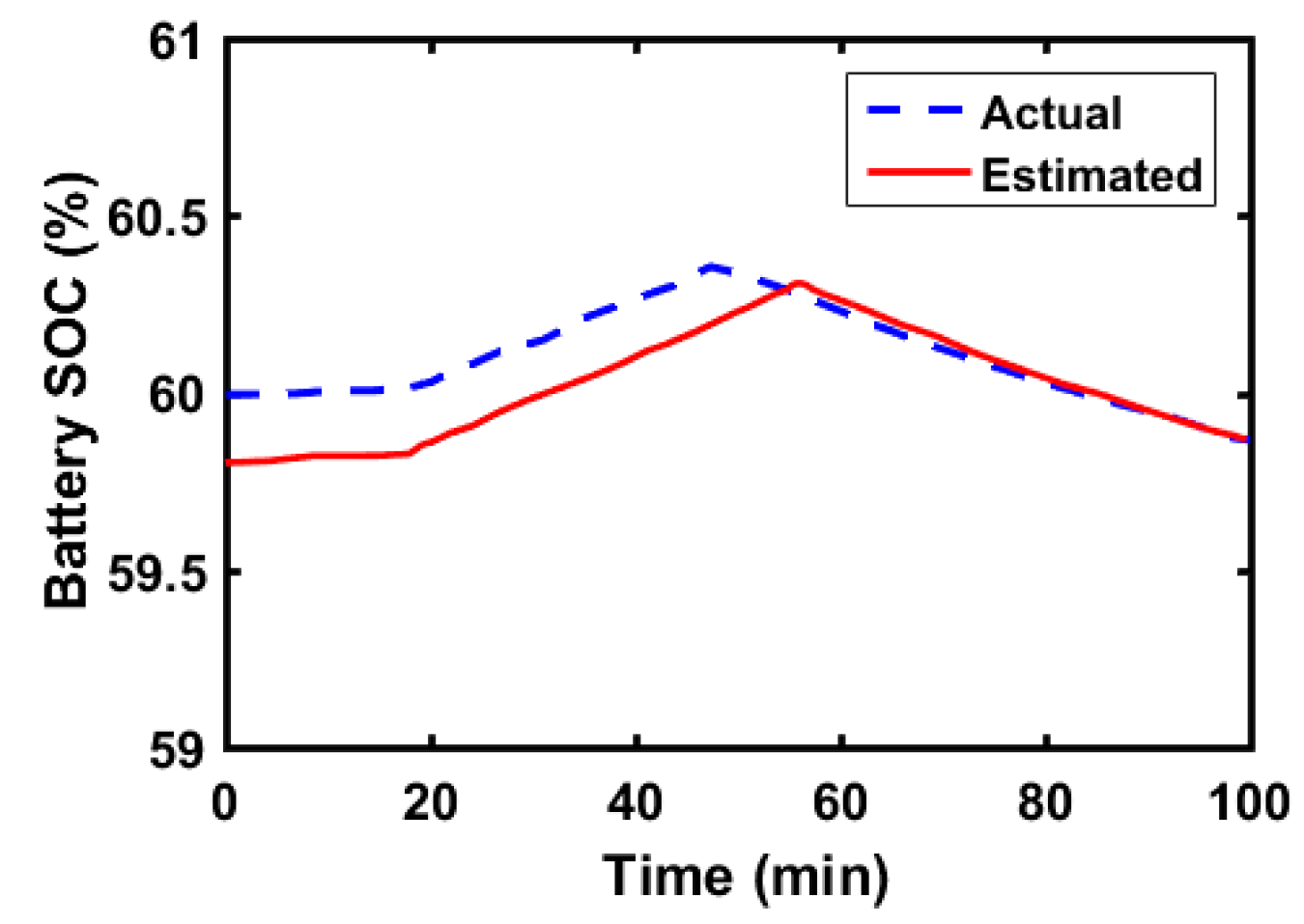
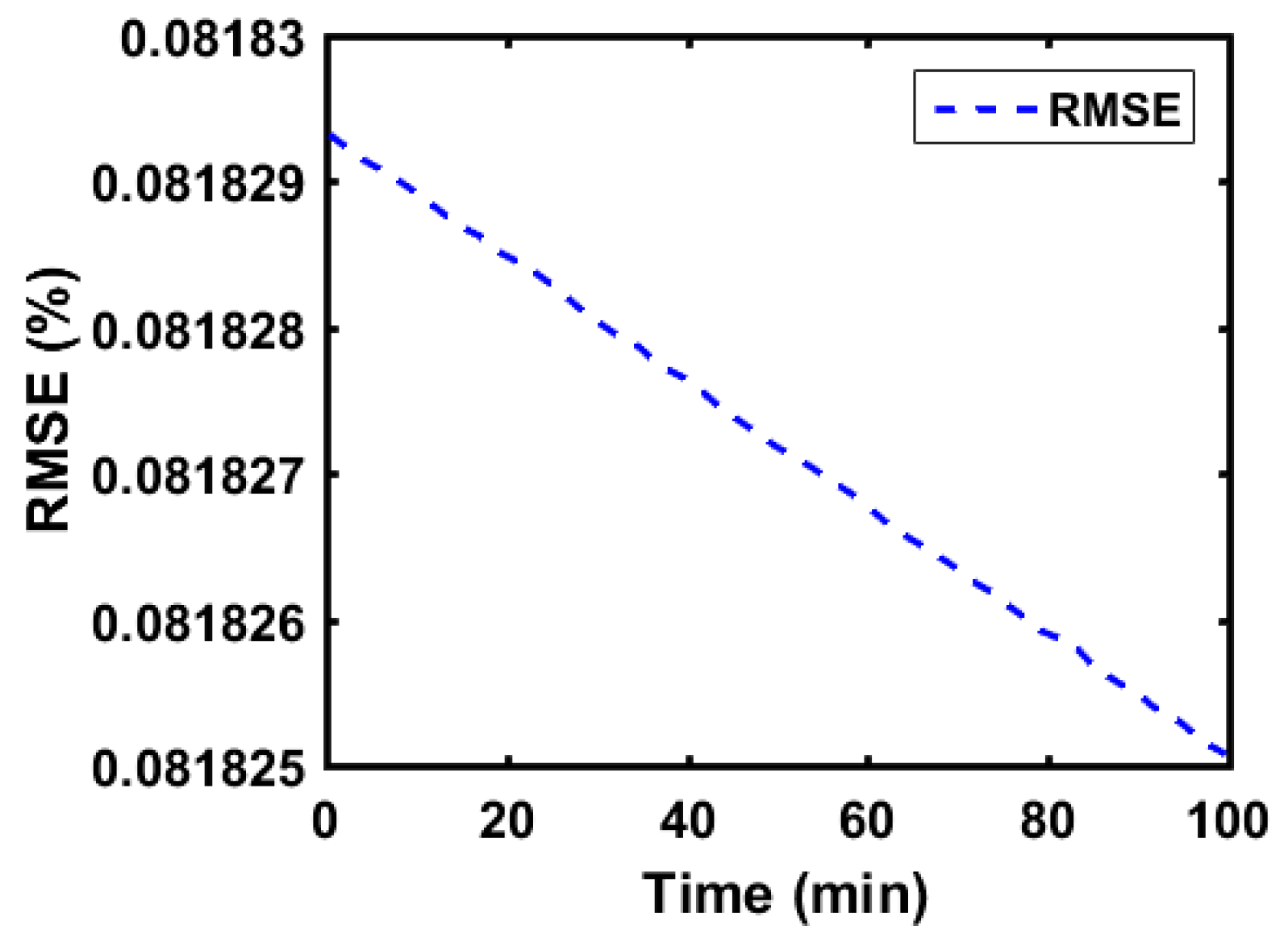
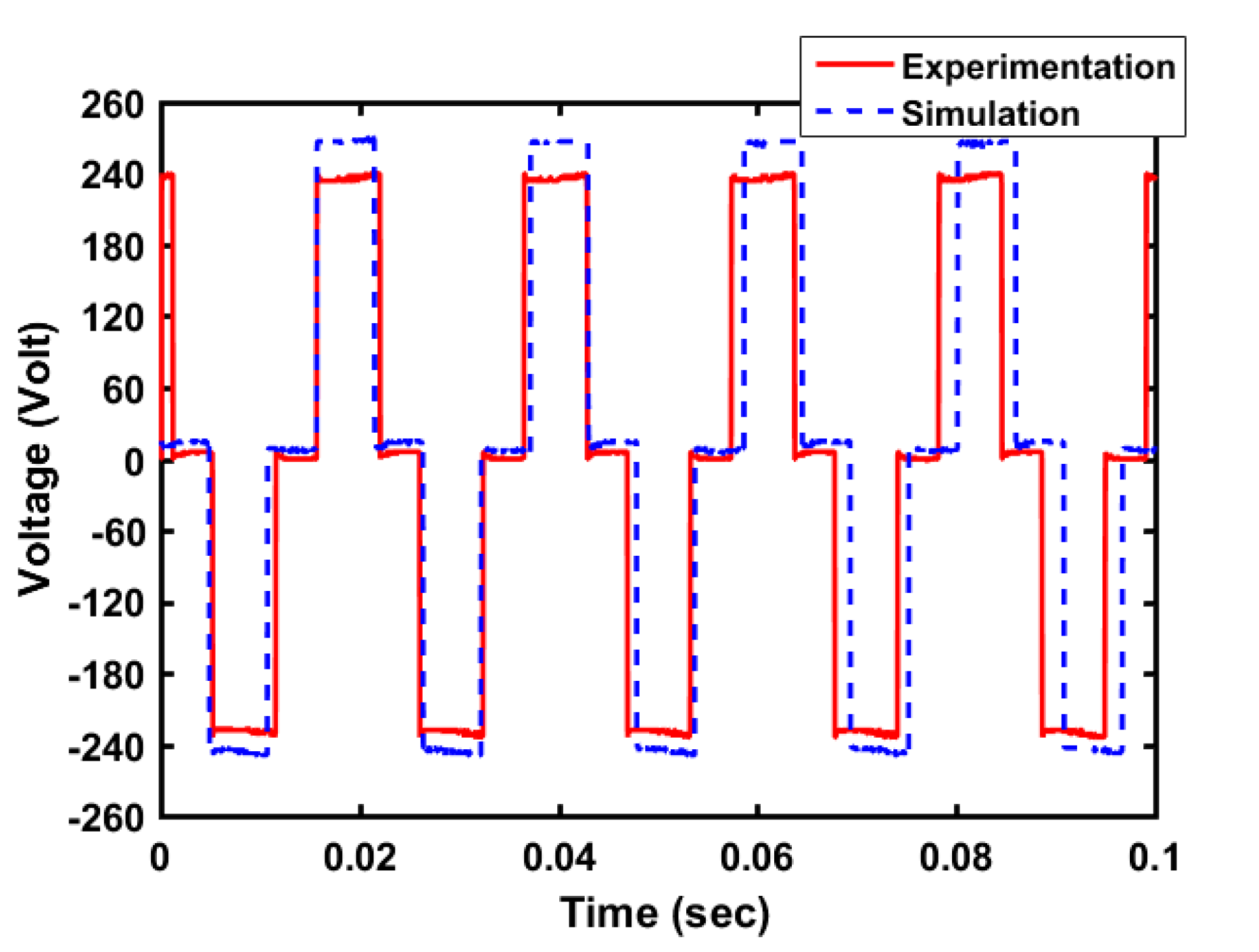
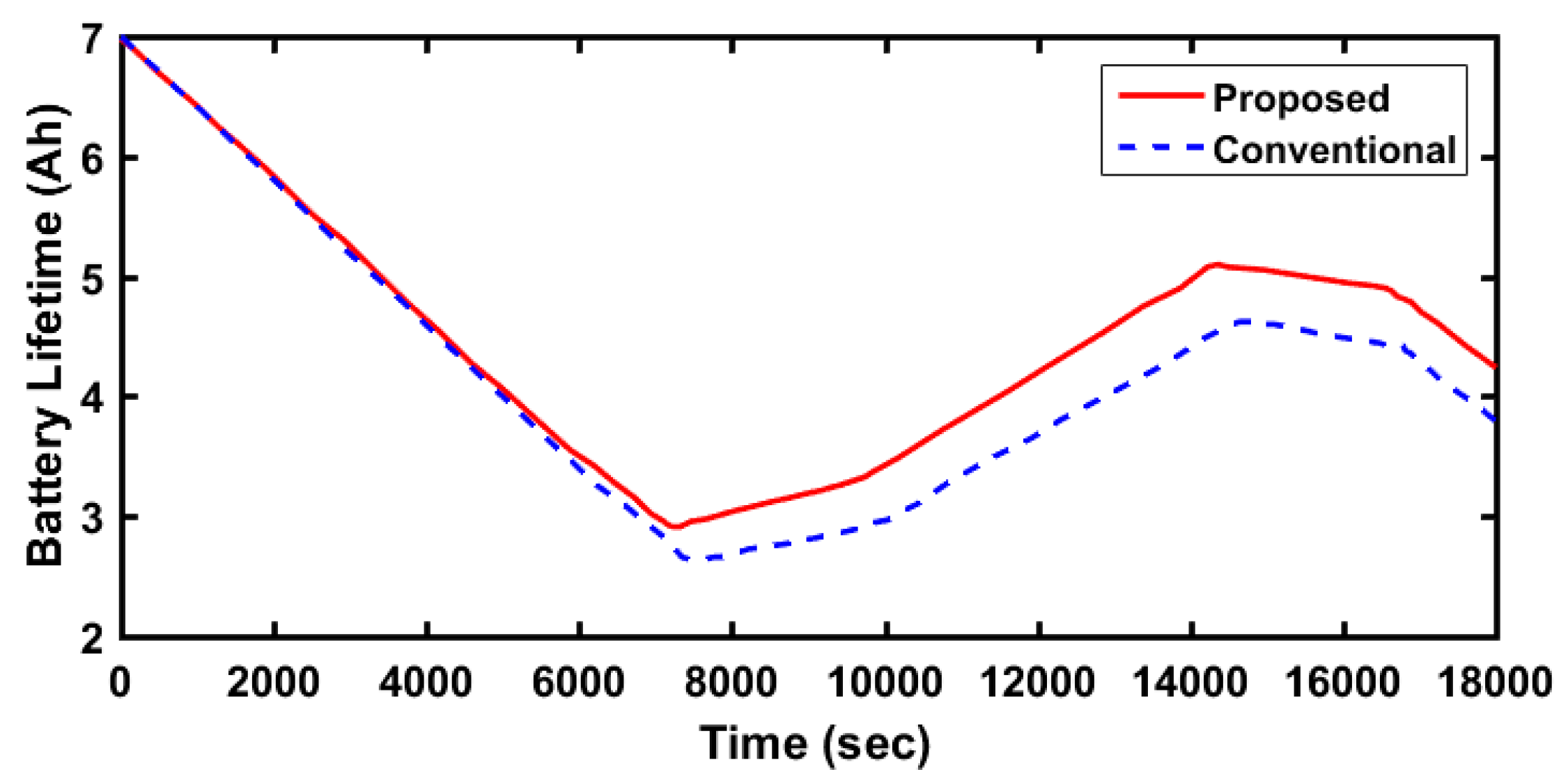
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghenai, C.; Bettayeb, M. Modelling and performance analysis of a stand-alone hybrid solar PV/Fuel Cell/Diesel Generator power system for university building. Energy 2019, 171, 180–189. [Google Scholar] [CrossRef]
- Castro, R. Data-driven PV modules modelling: Comparison between equivalent electric circuit and artificial intelligence based models. Sustain. Energy Technol. Assess. 2018, 30, 230–238. [Google Scholar] [CrossRef]
- Lasheen, M.; Abdel-Salam, M. Maximum power point tracking using Hill Climbing and ANFIS techniques for PV applications: A review and a novel hybrid approach. Energy Convers. Manag. 2018, 171, 1002–1019. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An enhanced adaptive P&O MPPT for fast and efficient tracking under varying environmental conditions. IEEE Trans. Sustain. Energy 2018, 9, 1487–1496. [Google Scholar]
- Essa, M. Management of charging cycles for grid-connected energy storage batteries. J. Energy Storage 2018, 18, 380–388. [Google Scholar] [CrossRef]
- Correa-Florez, C.A.; Gerossier, A.; Michiorri, A.; Kariniotakis, G. Stochastic operation of home energy management systems including battery cycling. Appl. Energy 2018, 225, 1205–1218. [Google Scholar] [CrossRef]
- Hossain, E.; Zawad, M.; Rakibul Islam, K.H.; Akash, M.Q. Design a novel controller for stability analysis of microgrid by managing controllable load using load shaving and load shifting techniques; and optimizing cost analysis for energy storage system. Int. J. Renew. Energy Res. 2016, 6, 772–786. [Google Scholar]
- Akinyele, D.; Belikov, J.; Levron, Y. Battery storage technologies for electrical applications: Impact in stand-alone photovoltaic systems. Energies 2017, 10, 1760. [Google Scholar] [CrossRef]
- Kujundzic, G.; Vasak, M.; Matusko, J. Estimation of VRLA battery states and parameters using Sigma-point Kalman filter. In Proceedings of the 2015 International Conference on Electrical Drives and Power Electronics (EDPE), High Tatras, Slovakia, 21–23 September 2015; pp. 204–211. [Google Scholar]
- Cui, X.; Shen, W.; Zhang, Y.; Hu, C.; Zheng, J. Novel active LiFePO4 battery balancing method based on chargeable and dischargeable capacity. Comput. Chem. Eng. 2017, 97, 27–35. [Google Scholar] [CrossRef]
- Caspar, M.; Eiler, T.; Hohmann, S. Systematic Comparison of Active Balancing: A Model-Based Quantitative Analysis. IEEE Trans. Veh. Technol. 2018, 67, 920–934. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, D.; He, H.; Cao, W.; Dong, G. A noise-tolerant model parameterization method for lithium-ion battery management system. Appl. Energy 2020, 268, 114932. [Google Scholar] [CrossRef]
- Herrera, V.I.; Martinez-laserna, E.; Milo, A.; Gaztañaga, H. Techno-economic assessment of Lithium-ion battery lifetime estimation methods for sizing and operation conditions definition in railway applications. In Proceedings of the 14th IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017. [Google Scholar]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Noise-Immune Model Identification and State of Charge Estimation for Lithium-ion Battery Using Bilinear Parameterization. IEEE Trans. Ind. Electron. 2020, 67, 417–426. [Google Scholar] [CrossRef]
- Liu, V.T.; Chen, J.R. Balancing for Lead-Acid Batteries of Electric Motorcycles. Appl. Mech. Mater. 2015, 764–765, 491–495. [Google Scholar] [CrossRef]
- Knap, V.; Stroe, D.I.; Christensen, A.E.; Propp, K.; Fotouhi, A.; Auger, D.J.; Schaltz, E.; Teodorescu, R. Self-balancing feature of Lithium-Sulfur batteries. J. Power Sources 2017, 372, 245–251. [Google Scholar] [CrossRef]
- Duan, C.; Wang, C.; Li, Z.; Chen, J.; Wang, S.; Snyder, A.; Jiang, C. A solar power-assisted battery balancing system for electric vehicles. IEEE Trans. Transp. Electrif. 2018, 4, 432–443. [Google Scholar] [CrossRef]
- Rauniyar, A.; Irfan, M.; Saputra, O.; Kim, J.; Lee, A.; Jang, J.; Shin, S. Design and development of a Real-Time monitoring system for multiple lead–acid batteries based on Internet of things. Futur. Internet 2017, 9, 28. [Google Scholar] [CrossRef]
- Gopi, R.R.; Sreejith, S. Converter topologies in photovoltaic applications—A review. Renew. Sustain. Energy Rev. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Vigneshkumar, V.; Palani, S. Development of a hybrid genetic algorithm/perturb and observe algorithm for maximum power point tracking in photovoltaic systems under non-uniform insolation. IET Renew. Power Gener. 2015, 9, 757–765. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar]
- Bendib, B.; Belmili, H.; Krim, F. A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 45, 637–648. [Google Scholar] [CrossRef]
- Alik, R.; Jusoh, A. Modified Perturb and Observe (P&O) with checking algorithm under various solar irradiation. Sol. Energy 2017, 148, 128–139. [Google Scholar]
- Ishaque, K.; Salam, Z.; Lauss, G. The performance of perturb and observe and incremental conductance maximum power point tracking method under dynamic weather conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Bani Ahmad, A.; Ooi, C.A.; Ishak, D.; Teh, J. State-of-Charge Balancing Control for ON/OFF-Line Internal Cells Using Hybrid Modular Multi-Level Converter and Parallel Modular Dual L-Bridge in a Grid-Scale Battery Energy Storage System. IEEE Access 2019, 7, 131–147. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Shiau, J.K.; Ma, C.W. Li-Ion battery charging with a buck-boost power converter for a solar powered battery management system. Energies 2013, 6, 1669–1699. [Google Scholar] [CrossRef]
- Chang, F.; Roemer, F.; Baumann, M.; Lienkamp, M. Modelling and Evaluation of Battery Packs with Different Numbers of Paralleled Cells. World Electr. Veh. J. 2018, 9, 8. [Google Scholar] [CrossRef]
- Id, E.M.; Id, V.I.H.; Gandiaga, I.; Milo, A. Li-Ion Battery Lifetime Model ’ s Influence on the Economic Assessment of a Hybrid Electric Bus’s Operation. World Electr. Veh. J. 2018, 9, 28. [Google Scholar]
- Kavousi-Fard, A.; Niknam, T.; Fotuhi-Firuzabad, M. Stochastic Reconfiguration and Optimal Coordination of V2G Plug-in Electric Vehicles Considering Correlated Wind Power Generation. IEEE Trans. Sustain. Energy 2015, 6, 822–830. [Google Scholar] [CrossRef]
- Devarakonda, L.; Hu, T. Effects of rest time on discharge response and equivalent circuit model for a lead-acid battery. J. Power Sources 2015, 282, 19–27. [Google Scholar] [CrossRef]
- Pavlov, D. Invention and Development of the Lead–Acid Battery. In Lead-Acid Batteries: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2017; pp. 3–32. [Google Scholar]
- Dell, R.M.; Moseley, P.T.; Rand, D.A.J. Batteries and Supercapacitors for Use in Road Vehicles. In Towards Sustainable Road Transport; Elsevier: Amsterdam, The Netherlands, 2014; pp. 217–259. [Google Scholar]
- Lee, S.; Cherry, J.; Safoutin, M.; McDonald, J. Modeling and Validation of 12V Lead-Acid Battery for Stop-Start Technology. In Proceedings of the SAE INTERNATIONAL, Michigan, MI, USA, 4–6 April 2017; pp. 1–11. [Google Scholar]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Campestrini, C.; Kosch, S.; Jossen, A. Influence of change in open circuit voltage on the state of charge estimation with an extended Kalman filter. J. Energy Storage 2017, 12, 149–156. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.; Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.E. Ben Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Xiang, C.; Wei, C.; Zhao, Y. Unscented kalman filter-based battery SOC estimation and peak power prediction method for power distribution of hybrid electric vehicles. IEEE Access 2018, 6, 35957–35965. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, Y.; Chen, S.; Wang, T. Design and implementation of a battery management system with active charge balance based on the SOC and SOH online estimation. Energy 2019, 166, 908–917. [Google Scholar] [CrossRef]
- Qays, O.; Buswig, Y.; Anyi, M. Active Cell Balancing Control Method for Series-Connected Lithium-Ion Battery. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 2424–2430. [Google Scholar]
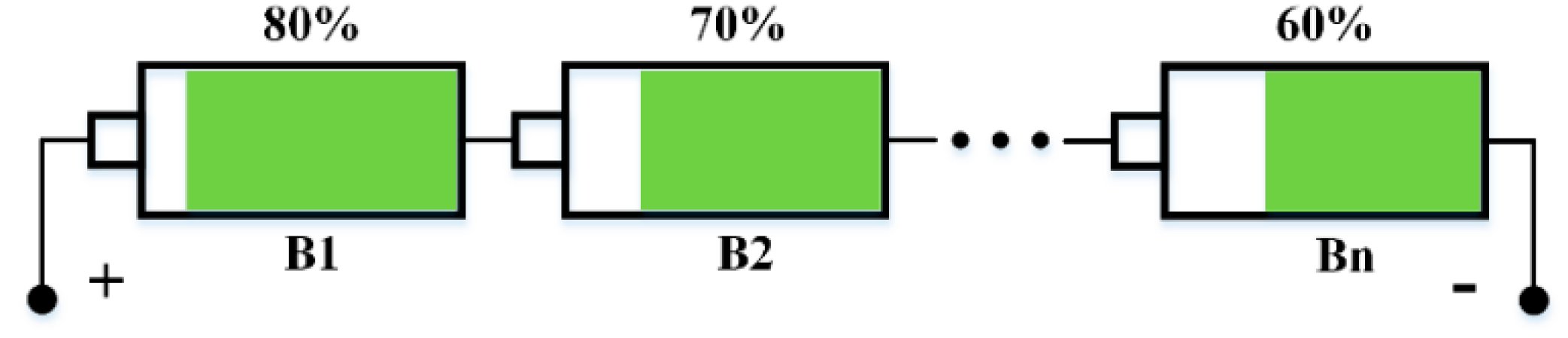
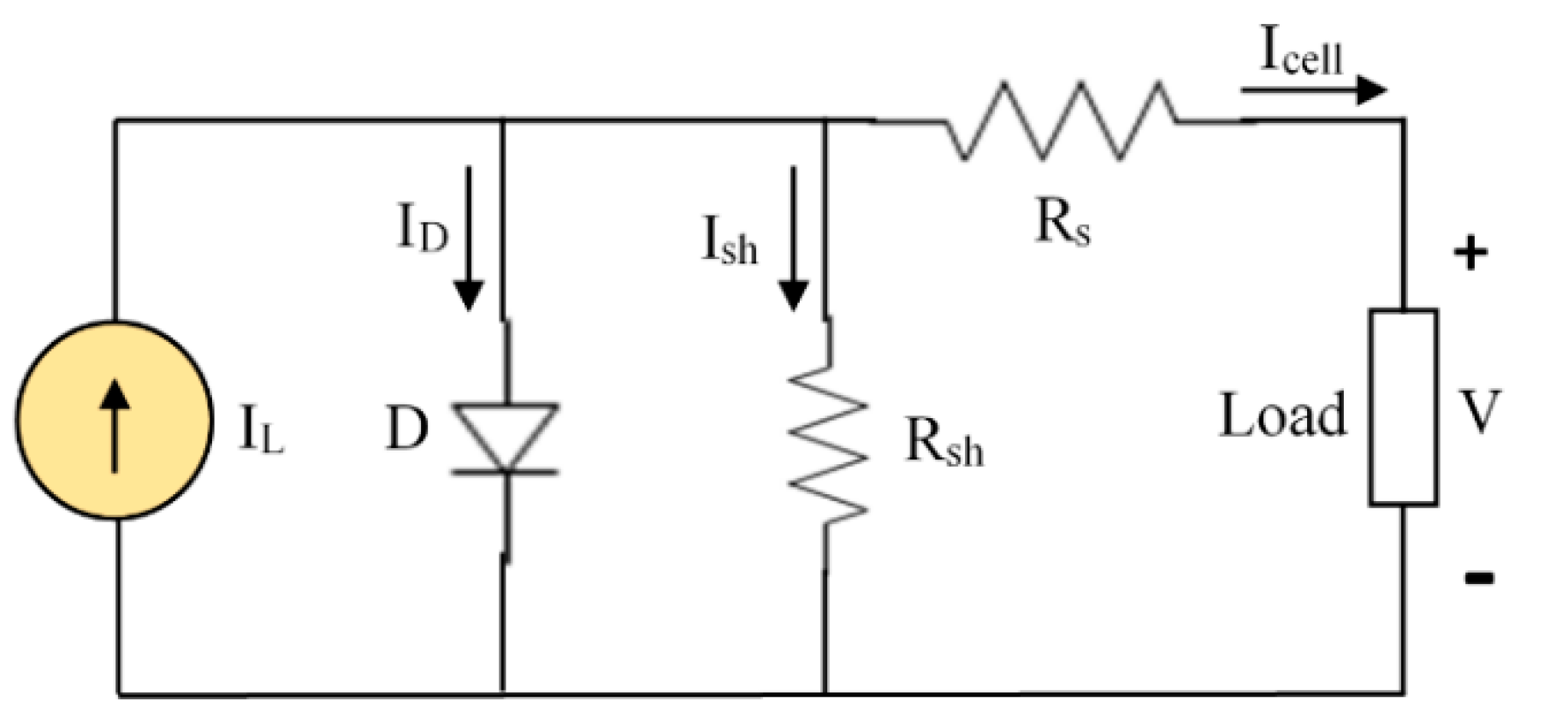
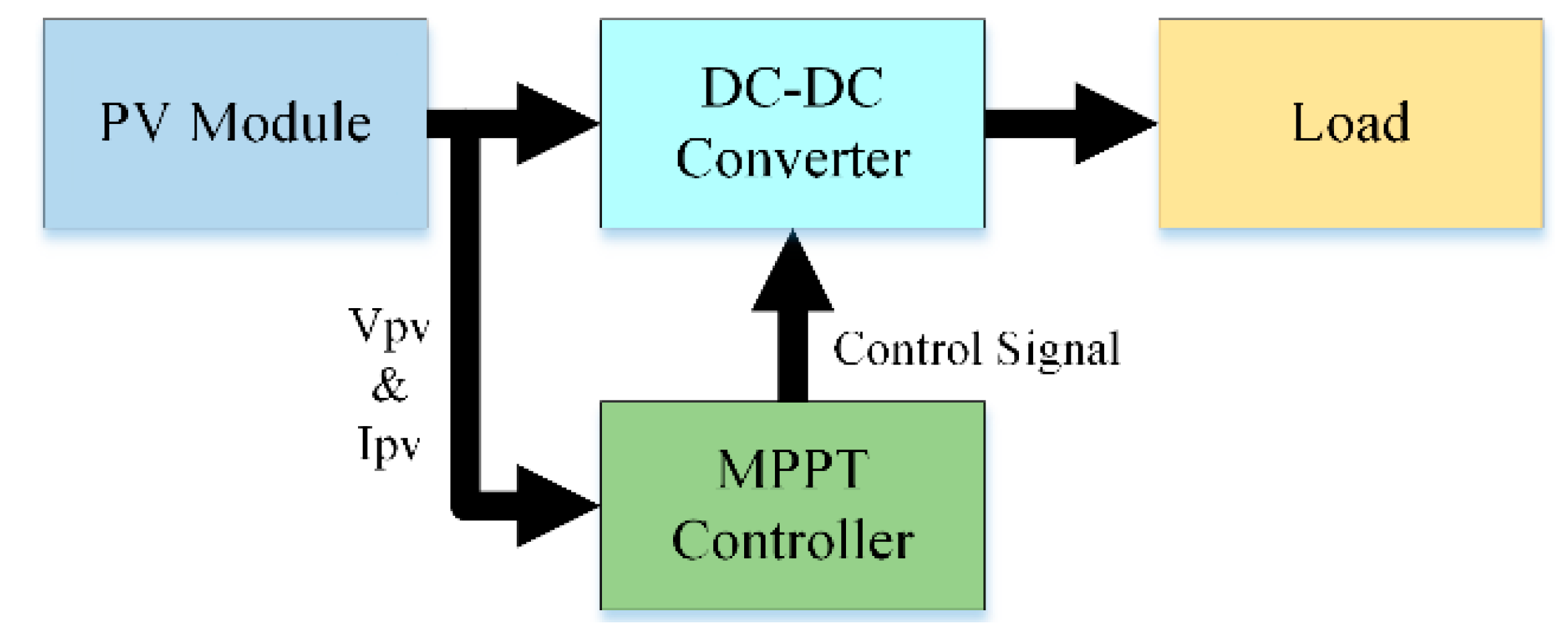
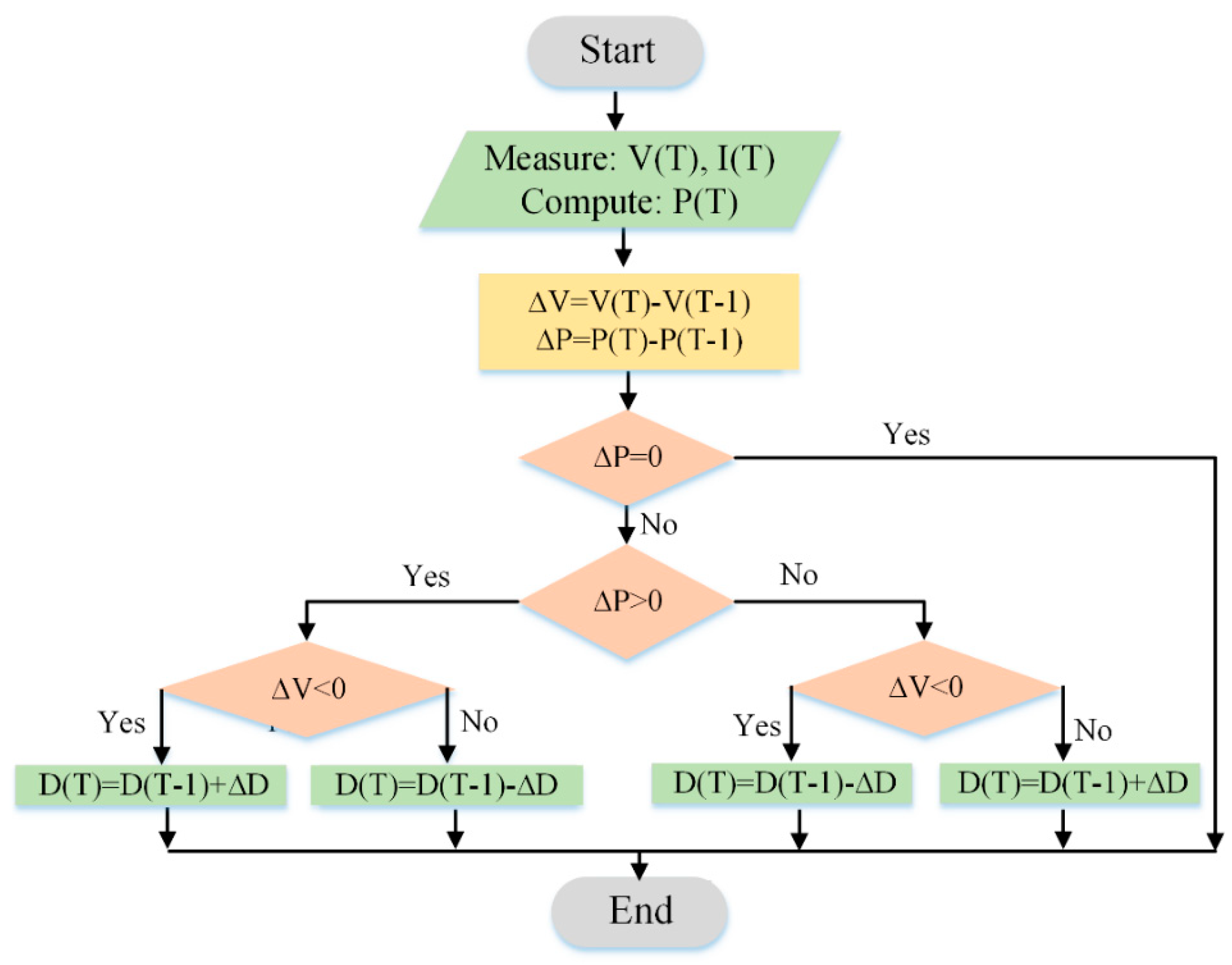


| Perturbation | ∆P | Resultant Perturbation |
|---|---|---|
| +ve | +ve | +ve |
| +ve | −ve | −ve |
| −ve | +ve | −ve |
| −ve | −ve | +ve |
| MOSFET Switch | Inductor Condition | Buck Mode | Boost Mode | Buck-Boost Mode |
|---|---|---|---|---|
| S1 | Charge | ON | ON | ON |
| Discharge | OFF | OFF | ON | |
| S2 | Charge | OFF | OFF | OFF |
| Discharge | ON | ON | OFF | |
| S3 | Charge | OFF | ON | ON |
| Discharge | OFF | OFF | OFF | |
| S4 | Charge | ON | OFF | OFF |
| Discharge | ON | ON | ON | |
| Average Load Voltage |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohirul Qays, M.; Buswig, Y.; Hossain, M.L.; Abu-Siada, A. Active Charge Balancing Strategy Using the State of Charge Estimation Technique for a PV-Battery Hybrid System. Energies 2020, 13, 3434. https://doi.org/10.3390/en13133434
Ohirul Qays M, Buswig Y, Hossain ML, Abu-Siada A. Active Charge Balancing Strategy Using the State of Charge Estimation Technique for a PV-Battery Hybrid System. Energies. 2020; 13(13):3434. https://doi.org/10.3390/en13133434
Chicago/Turabian StyleOhirul Qays, Md, Yonis Buswig, Md Liton Hossain, and Ahmed Abu-Siada. 2020. "Active Charge Balancing Strategy Using the State of Charge Estimation Technique for a PV-Battery Hybrid System" Energies 13, no. 13: 3434. https://doi.org/10.3390/en13133434
APA StyleOhirul Qays, M., Buswig, Y., Hossain, M. L., & Abu-Siada, A. (2020). Active Charge Balancing Strategy Using the State of Charge Estimation Technique for a PV-Battery Hybrid System. Energies, 13(13), 3434. https://doi.org/10.3390/en13133434