1. Introduction
Wind energy is one of the fastest-growing renewable energy technologies around the world [
1]. Power from wind produces no air pollution or carbon dioxide emissions, no water consumption, and it is an inexhaustible renewable energy source [
2]. In addition, operational costs of wind generators are close to zero once turbines have been built [
3]. Global efforts to mitigate climate change and environmental restrictions have motivated an increase of wind power participation in electricity markets in many countries and it will continue growing. In fact, annual capacity additions for onshore wind power are expected to increase to more than 200 GW around the world until 2050, that is, more than four times the wind power added to the operation in 2018 [
4].
In this context, generating realistic scenarios for wind power production in the medium and long term is fundamental to guide decision-making in power systems. Accurate scenarios are needed to design support schemes for wind energy promotion and to define wind power integration targets. Moreover, these scenarios are needed to attract new investments, to achieve a proper level of deployment according to wind resource availability, and to assess possible impacts on the energy mix [
5]. Likewise, these scenarios are used by firms to mitigate the risk exposure, to design energy portfolios, to estimate electricity prices and to build realistic expansion planning scenarios in power systems [
6].
In general, the high variability of renewable energies makes it difficult to predict their energy output. This supposes big challenges to firms and system operators. In fact, the intermittence of renewable resources could produce power curtailments and reduce system reliability of power systems. Moreover, an increase of the operational cost could be expected if more reserves are required to cover sudden energy decreases [
2]. Consequently, additional support mechanisms are needed to deal with renewable energies uncertainty [
7]. In this way, many countries have been making efforts to increase cross-border interconnections and to improve the market integration with other areas [
8]. These actions not only boost the security of electricity supply, but also increase market competition, reduce the need to build new power plants and allow to integrate more renewable technologies into electricity markets.
The current trend towards market integration is changing the paradigm in which power systems are operated. As the interconnection among different areas increases, wind power generation will not only be dependent on the resource availability in local markets, but will also be affected by wind power behavior in other interconnected areas both in the short and the long term. However, in most instances, scenario generation methodologies have been proposed at local scales and just a few works include spatial-temporal dependencies among areas [
9]. Particularly, the works presented in [
10,
11] propose methodologies to generate multiple scenarios considering spatial-temporal correlations among time series of wind turbines at different locations. Nevertheless, these approaches analyze time series from wind turbines and a whole market analysis is not performed.
Two kinds of strategies have been widely reported in the literature to generate wind power scenarios: direct and indirect [
12]. In direct approaches, wind power generation is predicted from historical power data of turbines. In contrast, indirect approaches predict the wind speed in a first step, and then wind power is forecasted through the curves that relates wind speed and wind power for each turbine [
12]. Classic forecasting techniques include physical and statistical approaches. While physical approaches are based on fundamental physical principles like conservation of mass and energy, statistical approaches generally use previous historical data to build statistical models [
1]. Most of these approaches are proposed for a period of less than one year [
13,
14], and just a few are focused on scenario generation with longer time horizons [
3]. Particular examples of these kinds of work have been reported in [
15] and [
16].
Recently, forecasting techniques based on Artificial Intelligence (AI) and hybrid models have been tested [
3,
17,
18,
19,
20,
21]. Usually, AI-based and hybrid models have shown less prediction errors than classic techniques [
22,
23]. However, classic techniques are easier to interpret and are less intensive from a computational point of view [
18,
24]. These characteristics are valuable, especially when the objective is to generate many scenarios that simulate the hourly behavior of wind generation in the long term. In fact, an hourly resolution in long-term scenarios could help to better deal with the problems originated by wind energy intermittence.
Most of the literature proposes methodologies to generate scenarios for wind power in a turbine or a group of turbines located in one area, and a whole system analysis is not performed. Actually, there is a lack of scenario generation methodologies capable of capturing the spatial-temporal dependencies of wind power in multi-area electricity markets. This paper fills this gap in the literature. The proposed approach is focused on generating realistic scenarios for wind power as local methodologies fail to reproduce properly the dependency relationships of wind power behavior among areas and markets. In fact, aggregated wind power time series from several systems not only include implicit information of wind behavior in all interconnected markets, but also network status and firm strategies. In addition, generating wind power scenarios from a market-aggregated perspective decreases the error when compared with desegregated approaches [
25]. In particular, this approach with an hourly resolution allows system operators to simulate the operation of power systems and to assess wind energy production in a more effective way [
16]. Finally, an hourly resolution allows to evaluate the quality of scenarios generated at different temporal scales, which has received little attention in the literature.
Based on the previous considerations, a new methodology to generate realistic scenarios for wind power in the long term in interconnected electricity markets is proposed in this paper. This approach considers spatial-temporal dependencies among different electricity markets. Furthermore, the effectiveness of this proposal has been assessed by backtesting approaches at distinct temporal scales. Finally, several tests have been made using real time series of wind power generation for Spain, Portugal and France. The contrast between the size of each market and its wind installed capacity allows to capture a wide range of scenarios from a local and global perspective.
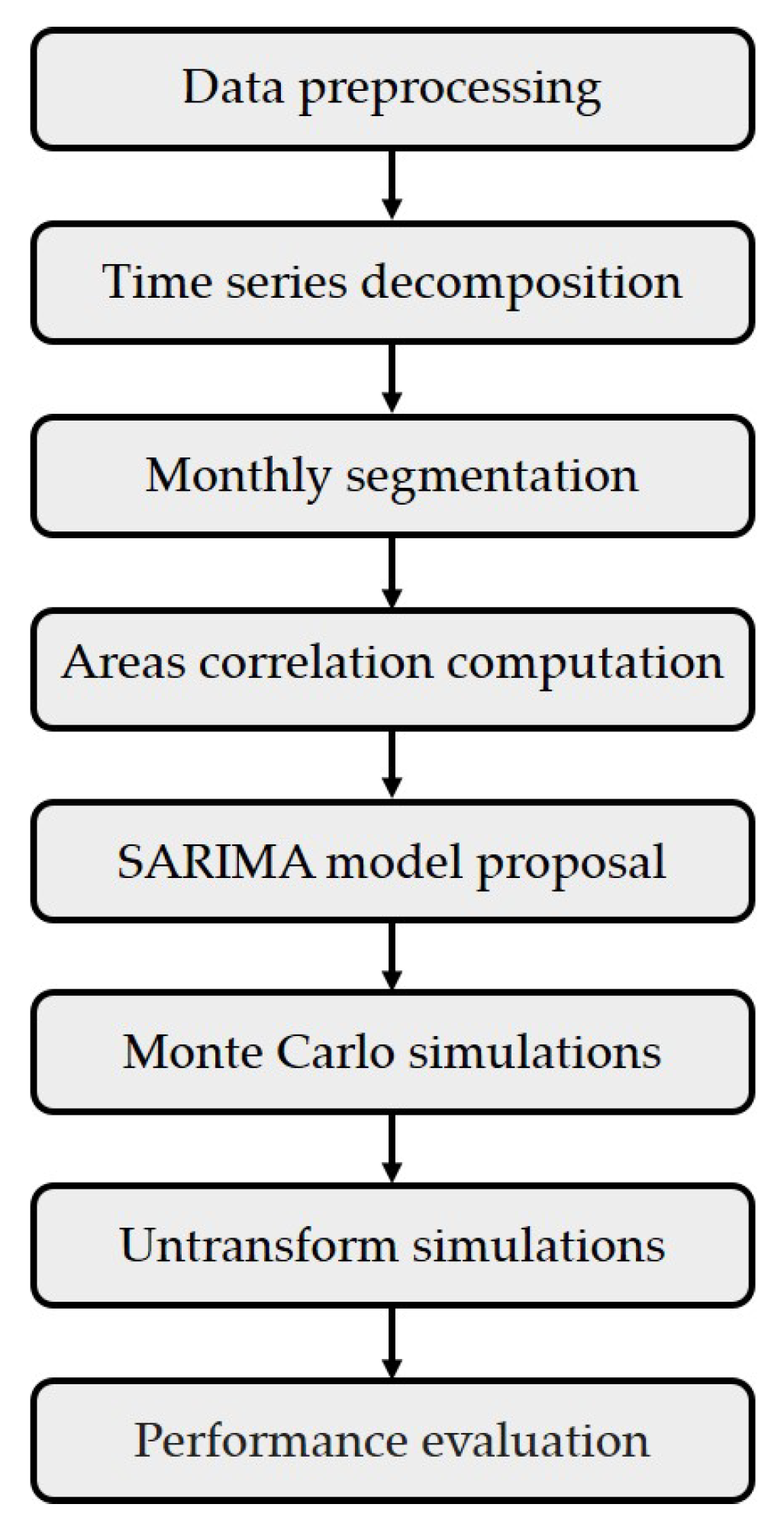
This proposal is divided into five main steps. In the first two steps, a data pre-processing and a time series decomposition is performed for each market. Four data normalization transformations are assessed, and trends and seasonality are captured for each area. In a third step, the temporal dependencies for each area are identified for wind power through Seasonal Auto Regressive Integrated Moving Average models (SARIMA). In this step, the dynamic of wind power for each area is captured and dependencies among areas are treated in detail. Moreover, in order to identify the best model, two approaches for SARIMA have been compared. In the fourth step, the estimation of probability distribution functions considering dependencies, found at the third stage, is conducted through correlated and multivariate Monte Carlo simulations. With this, the idiosyncrasy of wind generation dynamics for each time series and the dependencies among areas are replicated in each market. Finally, backtesting and benchmarking strategies are proposed to assess the effectiveness of the two proposed approaches at different time scales.
Summarizing, the main contributions of this paper are:
A new methodology to obtain realistic scenarios for wind power generation considering spatial-temporal dependencies among electricity markets is proposed. There is a lack of methodologies to generate realistic scenarios of wind power from a whole market perspective. The proposed methodology contributes to filling this gap.
Two approaches to generate realistic wind power scenarios are proposed for the long term with a statistical approach. Most forecasting statistical approaches tackles the wind power forecasting problem from a short-term perspective. In this paper, a long-term approach with an hourly resolution is proposed.
Finally, different strategies to evaluate the accuracy of generated scenarios are proposed and assessed at different time scales. Statistical properties of distribution functions of generated scenarios have been compared with historical data on an hourly, daily, weekly and monthly scale.
This paper is organized as follows. In
Section 2, the methodology is detailed. In
Section 3, the results obtained with the proposed methodology are analyzed and compared. Finally, in
Section 4, the main conclusions are presented and discussed.
2. Methodology
As mentioned, five steps have been proposed in this paper to generate scenarios of wind power production. The first step includes data pre-processing, i.e., the treatment of data mistakes, removing the dependencies between wind power and installed capacity for each area, and the transformation to a Gaussian-normalized time series. Second, a time series decomposition is performed. In this step, trends, seasonality and residuals for each area have been identified. Third, SARIMA models have been fitted to the historical data to detect temporal dependencies. Fourth, in order to generate wind power scenarios, several paths of multivariate and correlated Monte Carlo simulation of SARIMA models has been simulated. At last, backtesting and benchmarking stages are carried out from a bottom-up approach in order to compare Monte Carlo simulations with the original data. A description of each one of these steps is included in the next sections.
2.1. Data Pre-Processing
Missing data from time series for each area were avoided using linear interpolation methods and all outliers were considered for the study cases. Moreover, possible mistakes in historical data have been identified and amended. Contrary to short-term approaches, installed capacity of wind power needs to be removed from the time series of each area. Thus, the trend of the time series will only depend on the dynamics of wind power generation in each market. In addition, a better representation of spatial-temporal correlations among areas is obtained. In this paper, dependencies of generated wind power due to the installed capacity are removed using per unit values, i.e., time series are built using the utilization of wind power instead of real power. In this way, the generated scenarios could be easily scaled by multiplying by new capacity expansions.
As mentioned in [
2], wind power shows more variability than wind speed. In fact, the time series of wind power reflects the joint effects of the high variability of wind speed, the controllability in wind turbines and the network status. Moreover, wind power is proportional to the cube of wind speed in the operational region of turbines. Still, some events could decrease the power output of wind turbines to zero suddenly, like maintenance activities and low wind speed conditions. In addition, aggregated time series reflects the dynamics of multiple geographical areas with different weather characteristics.
In this context, wind power data shows a non-normal distribution. This asymmetrical and nonlinear behavior may distort time series decomposition, add spurious interactions in data, and complicate the model analysis. Several transformations have been proposed to normalize time series [
26]. In this paper, four of the most popular transformations have been compared: Box-Cox, Yeo-Johnson, Logit, and Ordered Quantile [
27]. To the best of our knowledge, these transformations have not been compared for data normalization of wind power generation in electricity markets. However, applications of these transformations can be found in [
27,
28,
29,
30].
Table 1 shows each one of the transformations considered in this paper:
y refers to the original data, both
and
z are transformed data,
is a parameter adjusted in both cases via maximum likelihood,
represents the standard normal of the cumulative distribution function, and rank and length are the observation’s rank and the number of samples of data series, respectively.
In order to select the best transformation, the Pearson P statistic (divided by its degrees of freedom) is calculated for each approach. Pearson P statistic allows to compare among transformations as an absolute distance of the departure of normality and it is a relatively interpretable goodness-of-fit measure. In this case, the closer the data is to a normal distribution, the closer the Pearson P value will be 1.
2.2. Time Series Decomposition
Time series decomposition refers to deconstructing a time series into different components; typically, trend, seasonality and residuals. In particular, additive decomposition is appropriated when the magnitude of seasonal variations or the fluctuation around the trend-cycle do not vary with the level of the series [
31]. In this step, the deterministic components of time series are identified. Additive decomposition models are represented by (
1):
where
,
,
and
denotes the normalized time series, the trend, seasonality, and residuals of time series at period
t, respectively. A linear trend, if any, is fitted by using a least-square approach. Annual and/or daily seasonality could be included in time series decomposition. Thus, the seasonality is given by (
2):
where
and
are the annual and daily seasonality at time
t, respectively. The annual seasonality may be represented through Fourier series [
32,
33,
34], since this fits better than, for example, quadratic models [
35]. It can be calculated as (
3):
where
s is the number of hours of the year, and
and
are constants optimized from historical data for each area using a least-squares approach. In addition, daily seasonality is calculated for each hour
i of the day as shown in (
4):
where
is the mean for each of the twenty four hours of the day in the series and
is the mean of
, that is (
5)–(
6):
being
the number of data for hour
i,
the set of the existing data for hour
i, and
N the number of data for hour
i in all the data series of the same area.
2.3. Detection of Spatial-Temporal Dependencies
Wind is produced by differences in the atmospheric pressure. In fact, air moves from higher to lower pressure areas developing different wind speeds. These differences in atmospheric pressures are mainly due to unequal solar heating around the world. Because of this, the dynamics of wind power depends on the season of the year and the hour of the day. In order to capture time dependencies of wind power, a SARIMA has been fitted for each area. In general, a SARIMA
process is represented as [
36]:
where
S is the periodicity, and
p and
q are integers that indicates the non-seasonal autoregressive and moving average polynomial orders, respectively.
B is the backward shift operator, satisfying
and
, and
is white noise with mean equal to zero and variance
. In addition,
P and
Q are integers representing the seasonal autoregressive and moving average polynomial orders, and
d and
D are non-seasonal and seasonal differencing orders, respectively.
and
are polynomials in
B of degrees
p and
q, respectively, and are given by:
Finally,
and
are polynomials in
B of degrees
P and
Q, respectively, as is shown in (
10) and (
11):
To fit the best SARIMA model, the Box-Jenkins method has been followed [
37]. This method consists of an iterative process that can be summarizedin three main steps [
36]: model identification, parameter estimation, and diagnostic checking. In the model identification, suitable values for SARIMA orders are established. With this aim, an analysis of the Autocorrelation Function (ACF) and Partial Autocorrelation Functions (PACF) is performed. In the parameter estimation, the polynomial coefficients of the SARIMA are calculated. These parameters are estimated via maximum likelihood for all the suitable values found in the model identification. At last, the fitted models are checked for inadequacies. In addition to the visual inspection of residual autocorrelations for each series, the Bayesian Information Criterion (BIC) have been used to select the best final structure of the SARIMA models that allows us to capture the conditional mean. In this way, BIC is given by [
38]:
where
is the maximized value of the likelihood function for the estimated model,
are the values that maximize the likelihood function,
m is the number of parameters to be estimated, and
n is the number of observed data. In this context, for a set of possible SARIMA models, the preferred is the one with the minimum BIC value.
Capturing the wind power behavior throughout the year and the spatial-temporal dependencies at a multidimensional level, the question arises whether it may be interesting to use a dynamic model that is specifically calibrated for different periods of time throughout the year. Because of this, two kinds of SARIMA models have been fitted to be compared. First, one static SARIMA is fitted for each area. With this approach, the dependencies of all historical data have been considered in each SARIMA. That means that the scenarios will be generated using this only model for the whole time horizon. However, as data dependencies could change according to the time of the year, a dynamic methodology to fit one SARIMA per month is accomplished in the second approach. In this case, one time series for each month and area is built with historical data of the same month and area. In other words, twelve SARIMA have been fitted for each area using monthly time series. In contrast to the first approach, the SARIMA fitted for each area considers only information of the historical data for the same month. This way, the scenarios will be generated month to month through the twelve fitted SARIMA.
2.4. Scenario Generation
In traditional wind power forecasting approaches, each scenario is generated from uncorrelated and univariate normal distributions. However, time series in multi-area electricity markets could be strongly correlated, not only due to weather condition in near areas, but to the status of the grid, the load profiles, and firms’ strategies, among others. Moreover, these dependency relationships may change throughout the year when a modeling at market or country level is performed. To capture these correlations, hourly multivariate and correlated residuals with normal distribution functions have been generated. That is, the generated residuals include spatial correlations through covariance matrices obtained from monthly historical data series:
where
k is the number of residuals generated,
is a real
k dimensional vector,
is the symmetric covariance matrix,
is the determinant of
and
is the mean of the residuals.
Once temporal dependencies have been modeled with SARIMA, and spatial relationships among areas have been included in residuals, Monte Carlo simulations are performed to generate the wind power scenarios. Contrary to deterministic approaches, Monte Carlo simulations allow to generate complete distribution functions for each hour. Moreover, each generated scenario includes temporal dependencies identified with the SARIMA model. In the case of the dynamic approach, presample responses and innovations for initial values of Monte Carlo simulation have been included from each path belonging to the previous month. Thus, scenarios are coherent among months and more realistic paths are achieved. Furthermore, the source of uncertainty that is related to the random error term is incorporated in the process of generating scenarios. Therefore, the variation in the errors has been considered. In the static case, the last values of historical data have been considered. Finally, in both approaches, trend and seasonality are added to simulated residuals, data series are inversely transformed, and a performance evaluation is carried out.
2.5. Performance Evaluation
As mentioned before, there is a lack of methodologies to assess the quality of wind power scenarios generated at different time scales, such as daily, weekly or monthly. Usually, a global benchmarking between distribution functions of generated scenarios and historical data is performed for an hourly scale. However, this approach does not give information about the performance of wind power scenario generator to model the behavior of historical data at different temporal scales. This information is essential when realistic wind paths are needed on a larger scale, for example, in generation planning, maintenance scheduling, and security analysis.
Hourly resolution for long-term scenarios as proposed in this paper allows to assess bottom-up analysis. In order to evaluate the generated scenarios, a comparison between the main statistical properties of the historical time series and the proposed scenarios is carried out at different time scales with a bottom-up approach. Moreover, a comparison between different SARIMA approaches was accomplished. In order to assess the quality of the scenarios, two stages have been used. In the first stage, distribution functions and the two first moments of the distribution have been contrasted to assess the global performance for each approach. In a second stage, the Pinball Loss Function (PLF) and the Winkler Score (WS) have been used to evaluate each approach at different intervals.
PLF and WS have been widely used to assess a forecast through a probabilistic approach [
39]. In particular, PLF is an error measure for a quantile forecast [
6,
39]. Unlike other measures, a score is assigned according to the differences between the real values of a time series and the quantile values obtained in a forecast. The lower the score, the better the forecast. Let
be the percentil of scenarios generated with
. Then, PLF is given by [
40,
41]:
Unlike PLF, WS enables to compare between prediction intervals that takes into account both “sharpness” and “calibration” [
42]. The WS penalizes when the forecasted value lies outside a predefined interval, and rewards a narrow prediction. As with PLF, the lower the achieved scores are, the better is the forecast. If the
prediction interval for time
t is given by
, then the WS is calculated as [
6,
39]:
It should be noted that these parameters depend on the number of Monte Carlo simulations. However, as the number of simulations increase, the difference tends to be lower. To contrast the obtained results, a global benchmarking is first performed. Secondly, a monthly evaluation is conducted, and, finally, a weekly and an hourly comparison for each month are assessed. Furthermore, the monthly covariances of the generated scenarios have been assessed to ensure that spatial dependencies are accurately captured. Finally,
Figure 1 shows a flow chart that summarizes the methodology proposed in this paper.
3. Results
The proposed methodology has been tested in a real study case using Matlab®, in particular, the 2018b version. For this purpose, real hourly wind power data for Spain from 2008 to 2019, and from 2012 to 2019 for Portugal and France have been analyzed. In this way, 105,192 samples for Spain and 70,128 for Portugal and France have been considered. This study case reflects the different dynamics in terms of wind resources in different regions. Data are available with the authors.
There are remarkable particularities that make this study case interesting to generate wind power scenarios with a multi-area approach. First, while electricity markets of Spain and Portugal are joined in the Iberian Electricity Market (MIBEL), energy exchange between MIBEL and France is limited by the market clearance of each area. In this way, energy exchanges not only depend on wind resource availability in the three areas, but also on the balance between offer and supply in the MIBEL and French markets. Second, the energy flow among areas is limited by the interconnection capacity. To date, these areas are joined through a cross-border interconnection, up to about 3000 MW between Spain and France and close to 4000 MW between Spain and Portugal [
43]. Both market clearance and cross-boarder capacity could be inducing spatial-temporal correlations in wind power generation, as opposed to others produced by climate. These correlations are expected to be captured with the proposed approaches. Finally, the electricity mix is different in each country. Currently, France, Spain and Portugal have an installed generation capacity close to 130, 105, and 20 GW, respectively. From these values, 9%, 22% and 25% are from wind power [
44]. The contrast between the size of each market and its wind installed capacity allows to capture a wide range of scenarios from a local and global perspective. This section shows the main findings for each step proposed in the Methodology section.
3.1. Data Pre-Processing
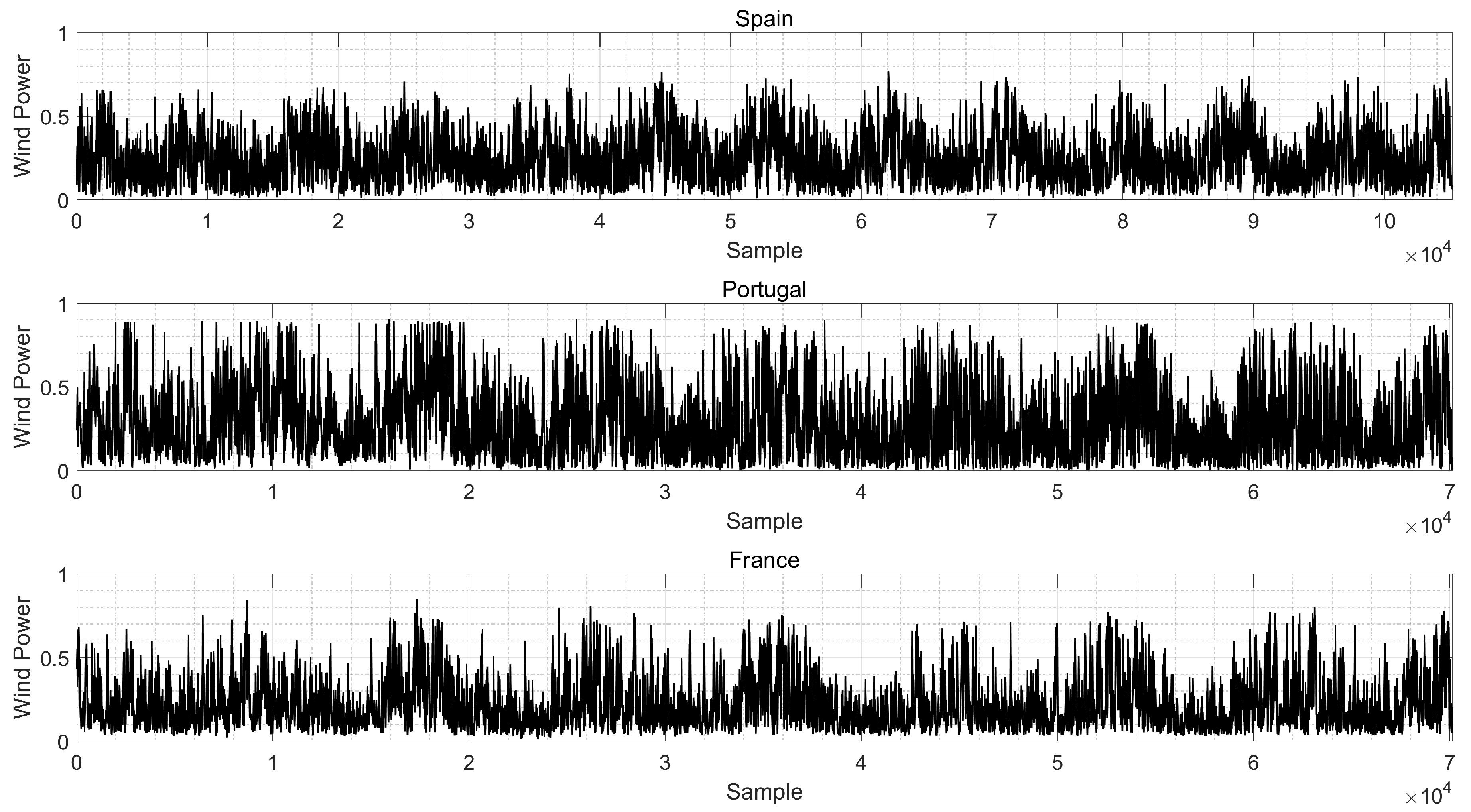
Figure 2 shows the real historical data of wind power per unit for each area. As it was expected, temporal series show an annual seasonal behavior for the three countries. Moreover, the differences among wind power utilization are evident, with Portugal being the country with the highest utilization.
To normalize data series Box-Cox, Yeo-Johnson, Logit and Ordered quantile transformation have been evaluated. As an example,
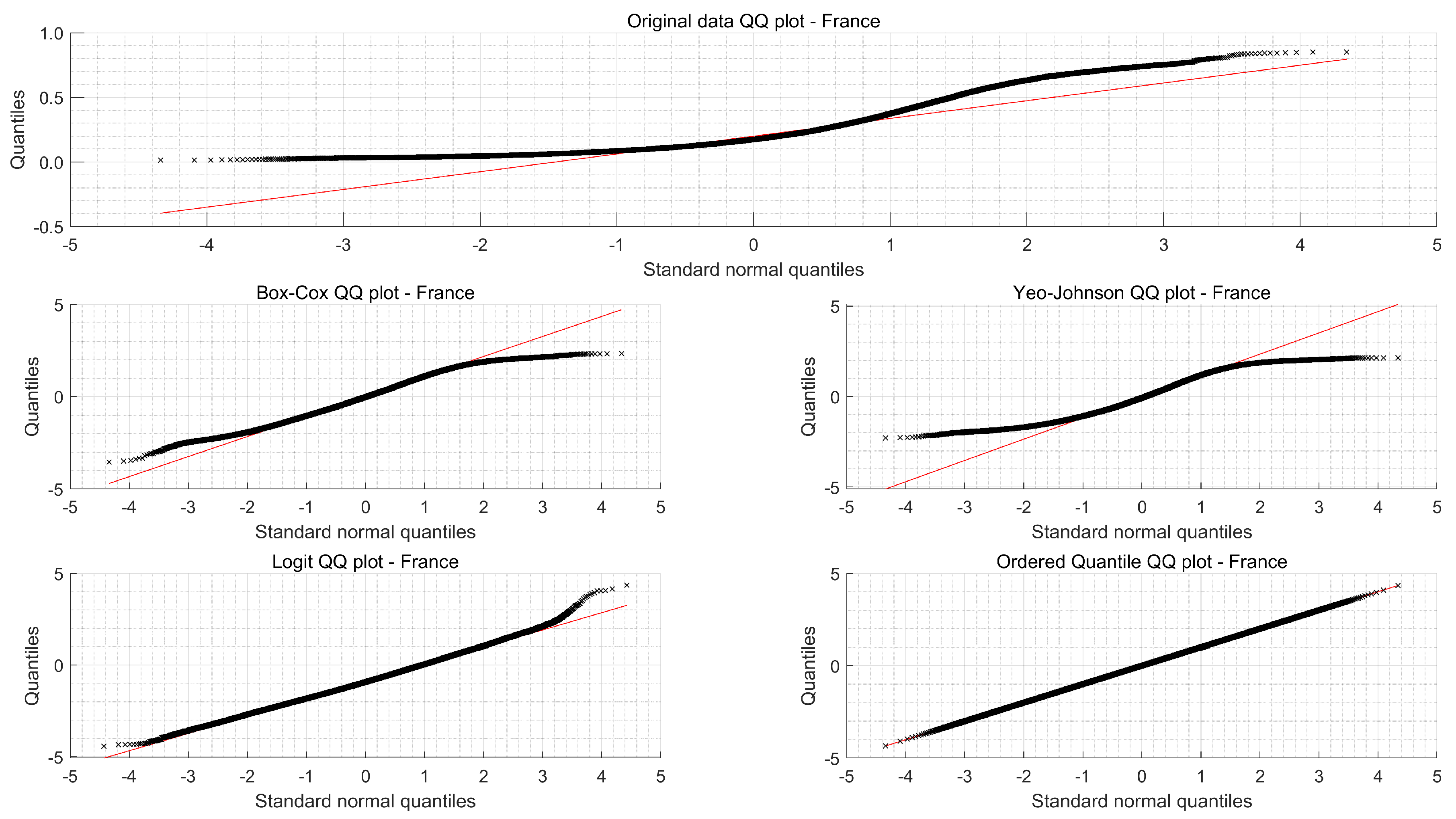
Figure 3, shows at the top quantile-quantile (QQ) plots for original data, and below, the normalized time series obtained with each transformation for France. A visual inspection on these figures indicates that while tails remain in Box-Cox, Yeo-Johnson and Logit transformation, asymmetries have been removed with Ordered quantile transformation, showing the best normalized data. Similar plots were obtained for the other areas. To complement the visual inspection of these figures, the Pearson P statistic has been calculated for each transformation. The obtained results are shown in
Table 2 for each area. It is clear that the Ordered quantile transformation shows the lowest value for the Pearson P statistic for all the areas. Based on these results, the Ordered quantile transform has been selected for data normalization in all areas.
Figure 4 shows the real data histograms and kernel density approaches for each area, as well as the same histograms and kernel densities for ordered quantile transformed series. Histograms of real data show asymmetries. In particular, long tails to the right for each area and heavy tails to the left are identified. In contrast, transformed data are much closer to a normal distribution and these asymmetries have been removed in all areas by means of ordered quantile transformation.
3.2. Time Series Decomposition
After the transformation, seasonality and trends from data series of each area have been removed. As an example,
Figure 5 shows the data decomposition for Spain. Similar results have been obtained for Portugal and France. The horizontal and vertical axis of each graph represent the hours and the wind power, respectively. The first graph at the top shows time series transformed with ordered quantile. The second figure shows annual seasonality obtained from Equation (
3). Usually, a few terms of Fourier transformation are needed to estimate seasonality. In this paper, they have been obtained from a harmonic function with order two. In this case, the daily component has not been included. The third graph identifies a trend with a low positive slope for Spain. This could be explained by the installation of wind turbines with a higher performance in recent years. Finally, at the bottom, the white noise obtained after seasonality and trend subtraction is shown according to Equation (
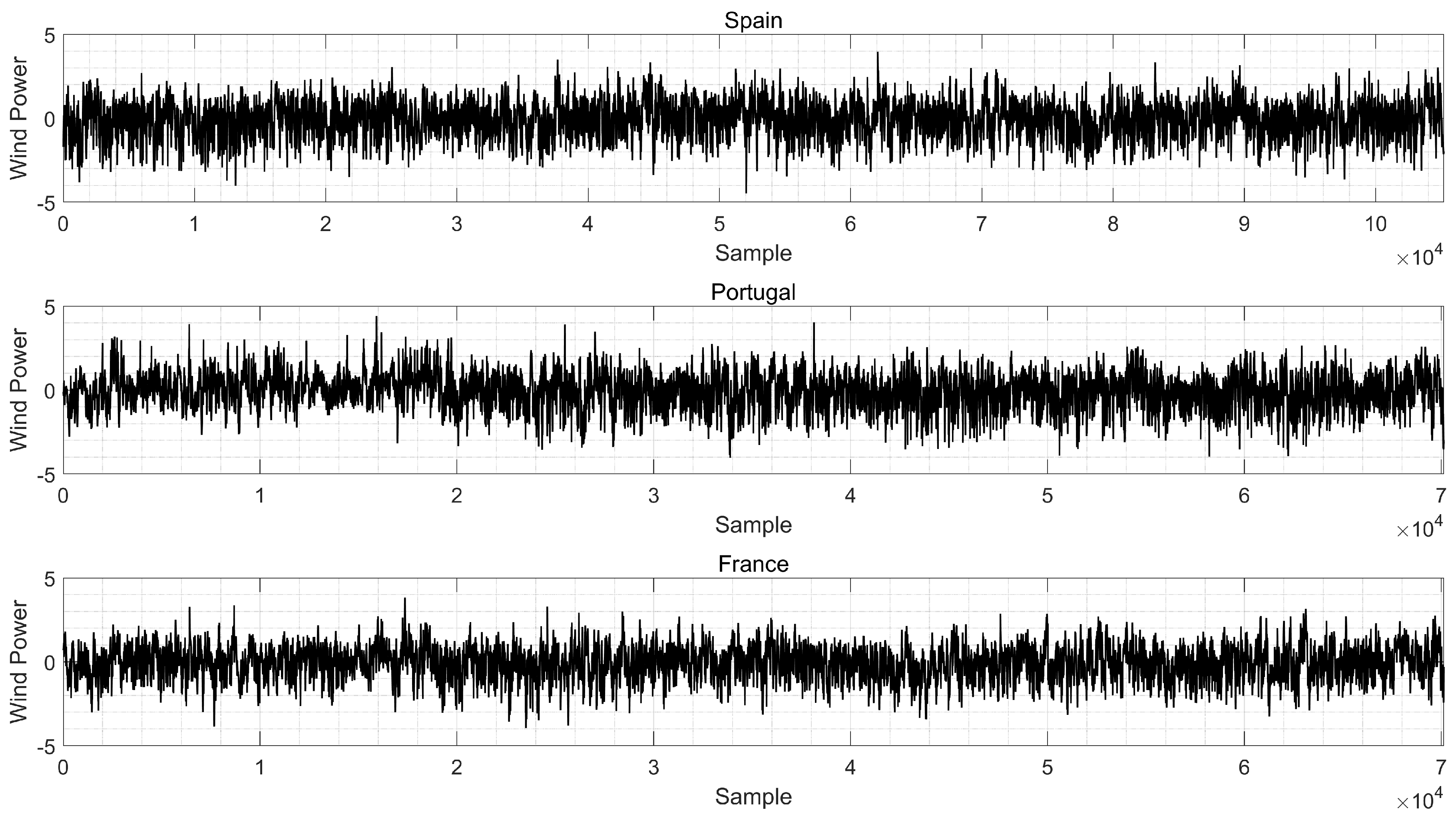
1). In this figure, a highly random behavior is identified after the decomposition when compared with the data series shown at the top of the figure.
Figure 6 shows the obtained residuals for each area after the data decomposition.
3.3. Detection of Spatial-Temporal Dependencies
Weather and geographical aspects are internalized in aggregated form through the SARIMA models and the correlations among areas. As previously mentioned, two approaches have been proposed to evaluate spatial-temporal dependencies of wind power for each area at different time scales. While in the first approach, dynamics of wind power are captured along the whole time series, in the second approach a dynamic segmentation is proposed to consider only dependencies among historical data within the same month. To find the order of the best SARIMA model, the Box-Jenkins methodology has been used [
37]. In a first stage, a visual inspection of ACF and PACF has been carried out to find possible SARIMA orders. In a second stage, an exhaustive combination of these values and different autoregressive and moving average orders for seasonal and non-seasonal components of the SARIMA model was carried out. The differentiation has not been taken into account. Subsequently, BIC values are evaluated to select the SARIMA orders that produce the best fit for the data. Moreover, the residuals have been evaluated to ensure a white noise behavior. Finally, to calculate the coefficients of the polynomials
,
,
, and
for selected SARIMA, a maximum likelihood estimation has been implemented.
3.4. Scenario Generation
Random and correlated paths have been simulated for static and dynamic approaches. With this aim, multivariate residuals with mean zero and considering the covariances among areas have been generated from the same normal distribution through Monte Carlo simulations. As a result, 1000 paths for each month m have been generated with a number of innovations equal to the number of hours of the historical data. The last values of each path in have been used as starting points for pre-sample responses and innovations of each path of month m, respectively. Once these scenarios are generated, the trend and seasonality are added to the simulated residuals and, finally, the data series are inversely transformed.
3.5. Performance Evaluation
The performance of the static and dynamic approach have been evaluated with a bottom-up approach. In the first stage, the results have been compared on an hourly basis. In order to quantify the differences between both approaches, PLF and WS have been evaluated. The results obtained for each area are shown in
Table 3 and
Table 4, respectively. The best results are highlighted in bold. Both tables suggest a superior performance of the dynamic approach in all the percentiles and intervals.
In the second stage, an evaluation of hourly data for each month has been performed.
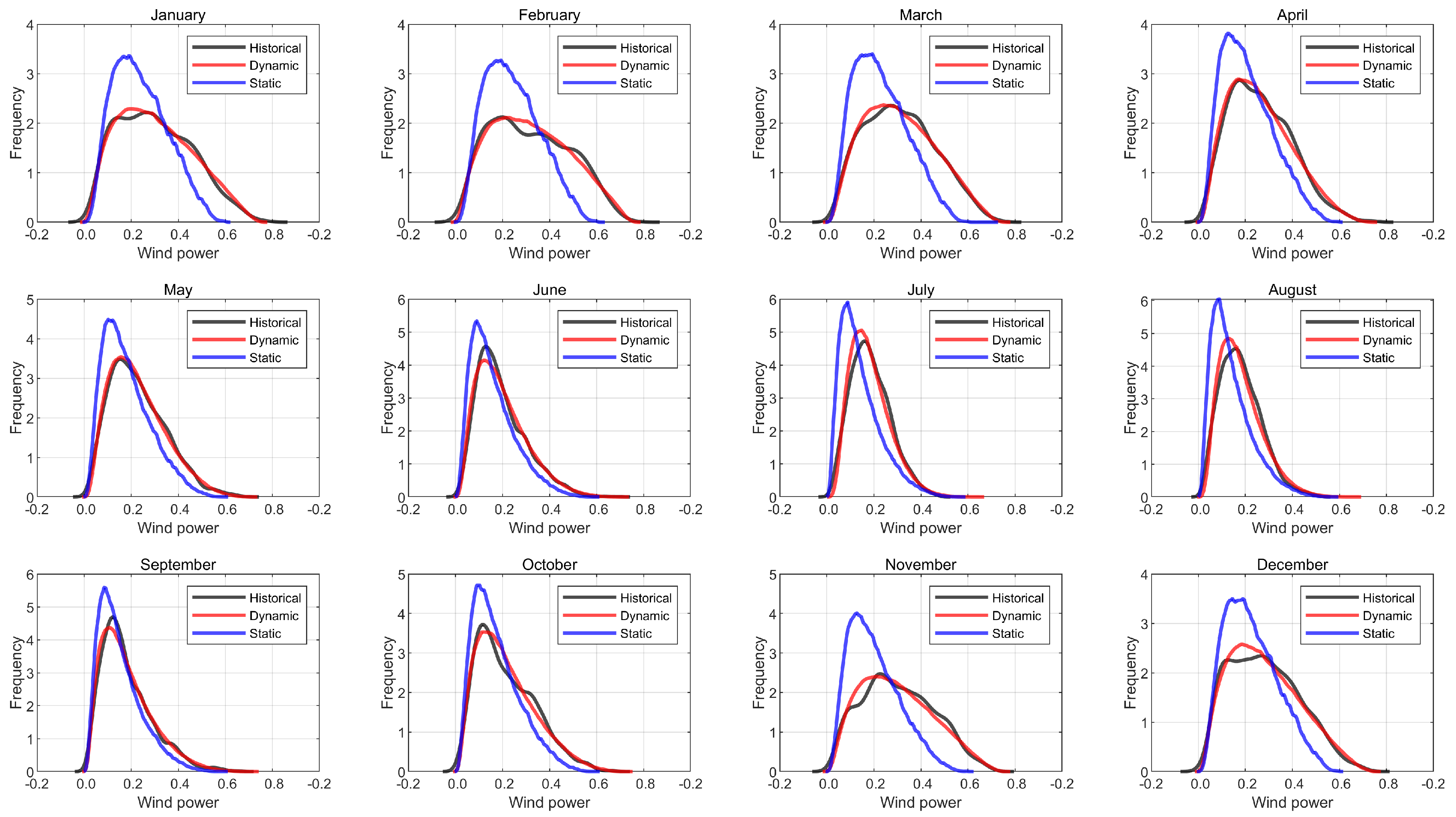
Figure 7 shows the mean of the hourly historical data for each month, as well as the values obtained for the dynamic approach in all the areas. The vertical axis shows the value for each month indicated on the horizontal axis. It can be seen from this figure that the dynamic approach is close to historical data the whole horizon. The obtained results suggest that the temporal relations are well captured with the dynamic approach from a monthly point of view. In other words, the dynamic approach not only captures appropriately the distribution function of all historical data (as shown in
Table 3 and
Table 4), but also captures better the mean of each month. As an example,
Figure 8 shows the monthly density distribution functions obtained with both approaches for Spain. A comparison with historical distribution functions indicates that the dynamic approach reproduces more accurately the behavior of the time series than the static approach.
Likewise the results obtained for PLF at percentiles P5, P30, P50, P70 and P95, and the mean are provided in
Table 5. The best results are highlighted in bold. In all cases, a higher score is obtained with the static approach. That means that the dynamic approach represents more accurately the distribution function of wind power than the static approach at different quantiles, when monthly distribution functions are considered. In addition,
Table 6 shows the WS with intervals of 50%, 80%, 90% and 98%. Again, as it can be seen in bold, the dynamic approach shows a superior performance to reproduce the monthly historical behavior of the time series for each area at different intervals.
In the third stage, the scenarios generated with both approaches have been evaluated on a weekly basis. With this aim, two-year scenarios have been generated and contrasted with the two last years of historical data. The mean for each week has been calculated both for the historical data and for each path of the dynamic and static approaches.
Table 7 and
Table 8 show the results obtained for PLF and WS, respectively. The values of PLF and WS are always lower for the dynamic approach, as it is shown in bold values.
Figure 9 shows the mean obtained for each scenario and area compared with historical data, both for the dynamic and static approach. It can be seen that the dynamic model better reproduces the changes in the weekly behavior of the time series. This can be clearly evidenced between weeks 20 to 40, and 70 and 90.
In the fourth stage, a daily evaluation has been performed. In this case, the scenarios have been generated for one year, and the mean of the wind generation for each day has been calculated for all the paths. The obtained results are shown in
Table 9 and
Table 10. The best results are highlighted in bold. In both PLF and WS, the dynamic approach captures better the behavior of the time series at different percentiles and intervals on a daily scale. This can also be seen in
Figure 10, where the daily means for each approach are shown and compared with the historical behavior. The figure shows that, for all the areas, the dynamic approach better follows the historical time series behavior.
Finally, a comparison of the correlations among areas have been performed. In particular, the time series of Spain and Portugal show the highest correlations, as expected due to the similarities among wind climate and topographical conditions [
45]. However, these correlations could not be only due to the similarities in wind behavior but also because both are coupled in the MIBEL market. In contrast, energy exchanges with France are less coupled and they are limited by cross-border interconnections. Unlike the static approach, the dynamic model is able to capture the changes in dependency relationships at different scales throughout the year.
Table 11 shows the correlations for the historical data and the dynamic approach, both on an hourly, daily, weekly, and monthly basis. It can be seen that the dynamic approach reproduces better the monthly correlations between Spain and Portugal than in the other scales. That is because the scenarios have been generated considering those monthly correlations. However, hourly, daily and weekly correlations are close to those observed in the historical data. Moreover, the lower correlations between Spain and Portugal with France are well captured with the dynamic approach as well.
To summarize, in this section, it has been shown that the dynamic approach proposed in this paper reproduces better than the static approach, the dynamics and the spatial-temporal dependencies observed in the historical data at different time scales. While the low value obtained for the PLF in the dynamic approach indicates that the distribution of the scenarios generated reproduces more accurately the historical behavior at different quantiles, and the low value obtained for the WS suggests that the forecasted scenarios achieve less error when different prediction intervals are considered. In this way, the proposed model evidenced the robustness to simulate the idiosyncrasy of the historical time series of each area at different intervals, even when time series with dynamics so different as that have been used for the study case are considered. Finally, it is shown that the dynamic approach simulates closely the sudden changes observed in the mean of the historical data at different time scales with the highest reliability and that the scenarios generated preserve the correlation among areas observed in the historical data.