Cogeneration Economics for Greenhouses in Europe
Abstract
1. Introduction
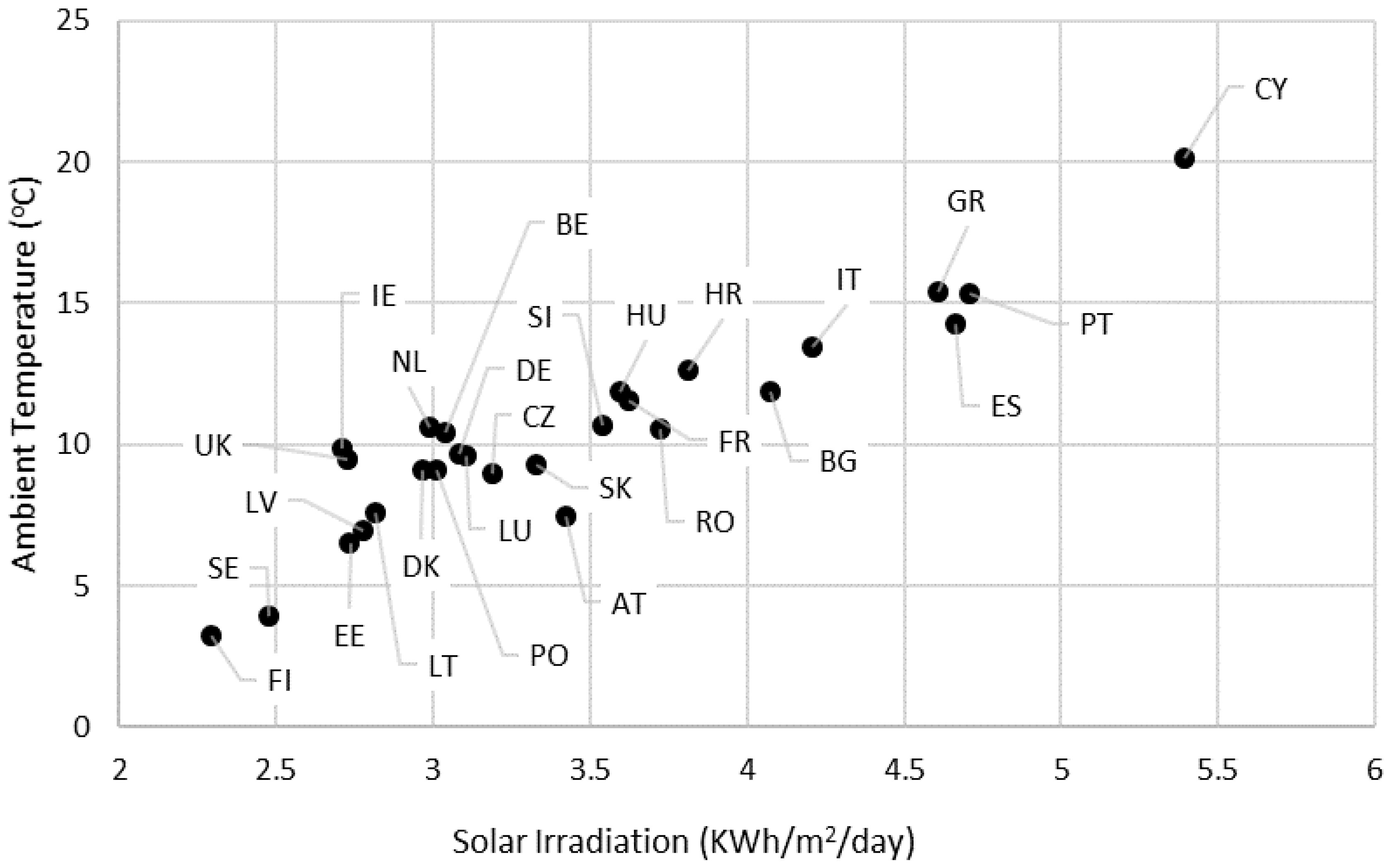
2. European Countries: Basic Climatic and Energy Cost Characteristics
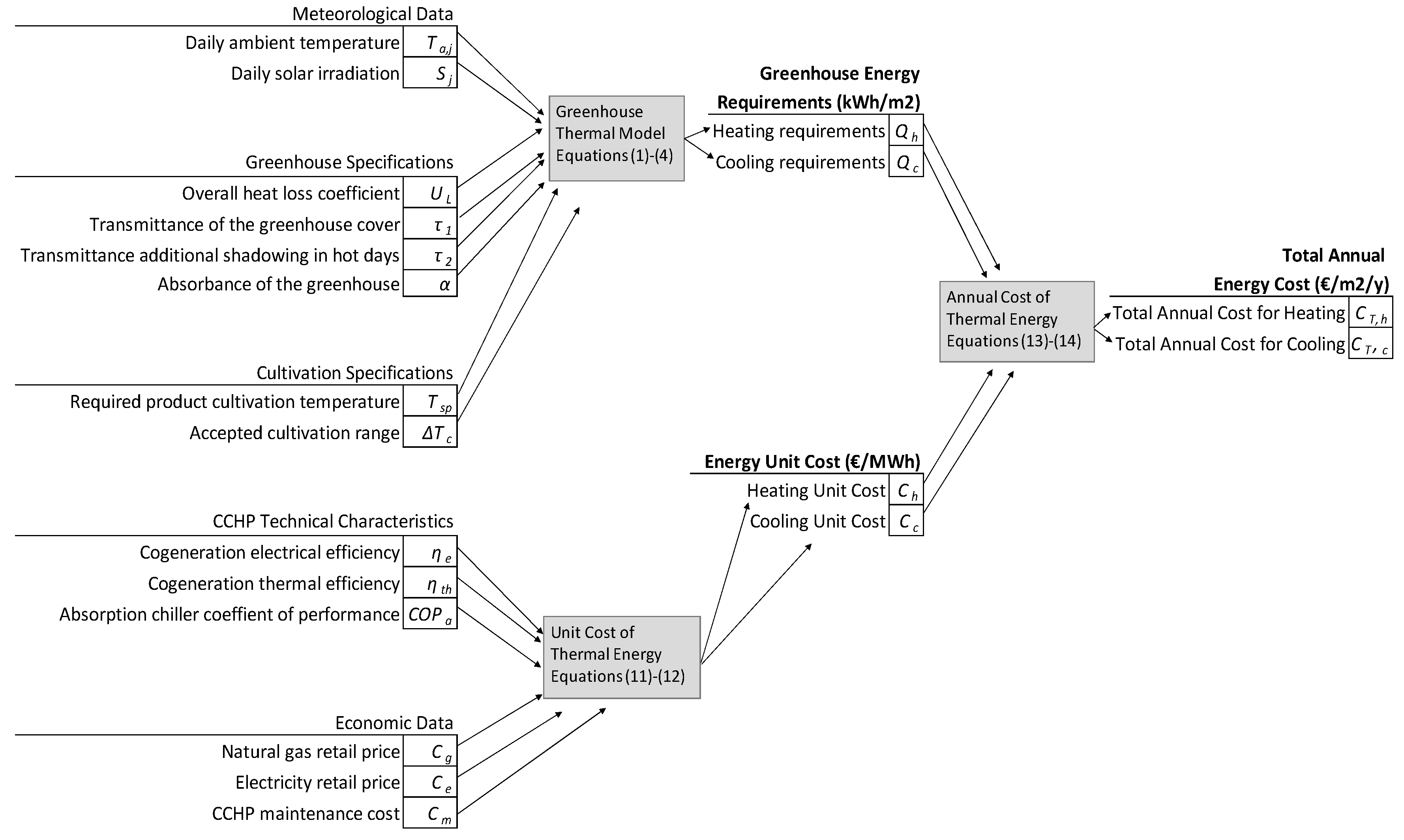
3. Greenhouse Model
3.1. Greenhouse Thermal Load Model
- (1)
- meteorological conditions (ambient air temperature, solar irradiation);
- (2)
- product cultivation species; and
- (3)
- greenhouse design parameters (structure, size, etc.).
- (kWh/m2/d) is the greenhouse daily heating load during day j;
- (kWh/m2/d) is the greenhouse daily cooling load during day j;
- (-) is the number of the day of the year (;
- (kW/m2K) is the greenhouse effective overall heat loss coefficient;
- (°C) is the set point greenhouse temperature (the required product cultivation temperature);
- (°C) is the accepted temperature difference from set point temperature (cultivation range);
- (°C) is the daily ambient temperature during day j;
- (kWh/m2/d) is the daily average solar irradiation on a horizontal surface during day j;
- (-) is the transmittance of the greenhouse cover;
- (-) is the transmittance of the additional shadowing cover during hot days; and
- (-) is the absorbance of the greenhouse.
3.2. Cost of Thermal Energy with Cogeneration
- (MWh(gas)) is the annual natural gas consumption by the cogeneration system to cover the required greenhouse heating load ;
- (MWh(gas)) is the annual natural gas consumption by the cogeneration system to cover the required greenhouse cooling load ;
- (MWh(el)) is the electricity produced by the cogeneration during heating season;
- (MWh(el)) is the electricity produced by the cogeneration during cooling season;
- (€/MWh(gas)) is the natural gas retail price;
- (€/MWh(th)) is the cost of the useful heating produced by the CCHP system (unit cost for heating);
- (€/MWh(el)) is the electricity retail price;
- (€/MWh(el)) is the cogeneration maintenance cost relative to the electricity produced; and
- (€/MWh(co)) is the cost of the useful cooling produced by the CCHP system (unit cost for cooling).
- (-) is the CCHP thermal efficiency;
- (-) is the CCHP electrical efficiency; and
- (-) is the coefficient of performance of the heat driven absorption chiller.
4. Results and Discussion
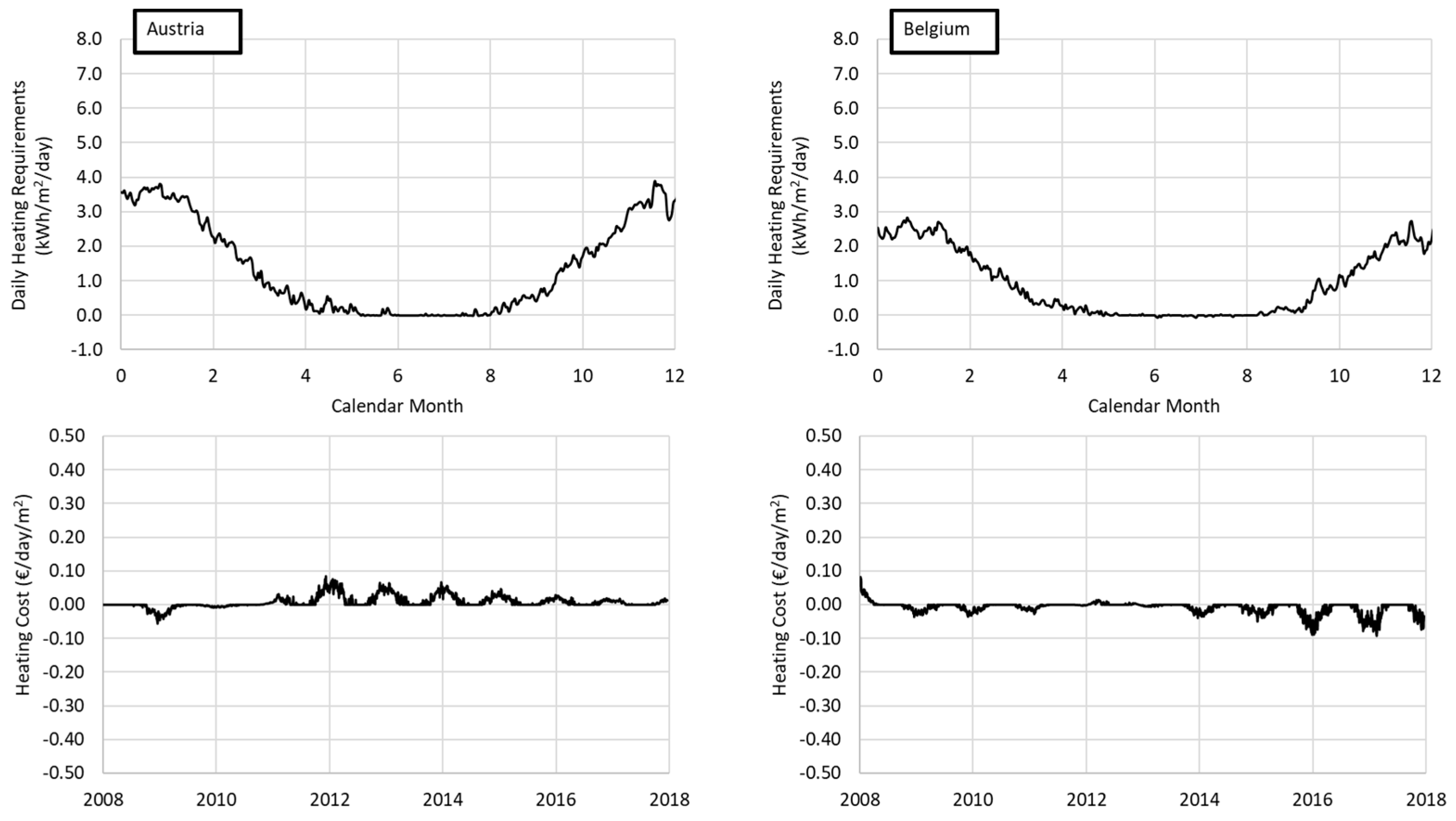
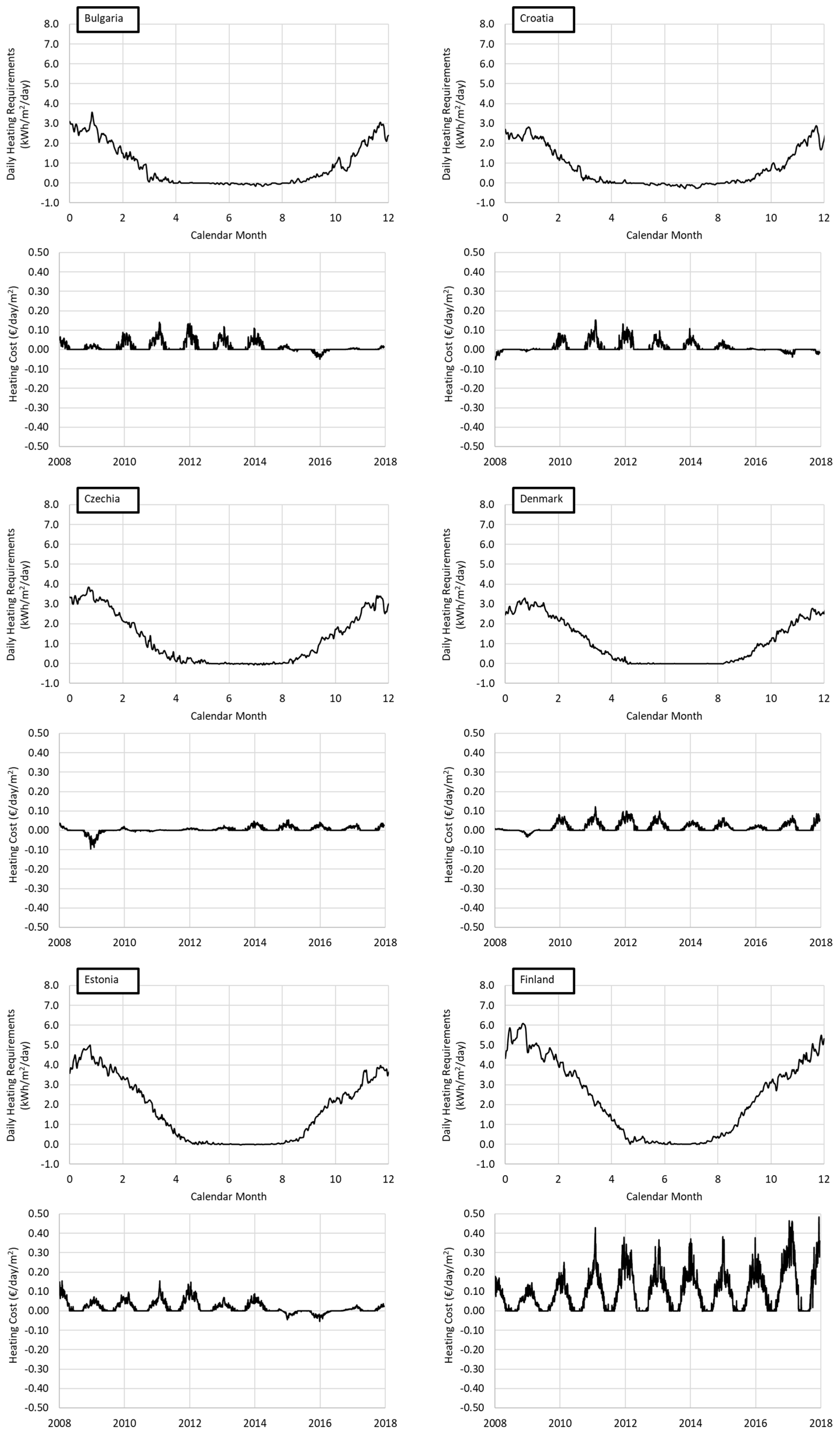
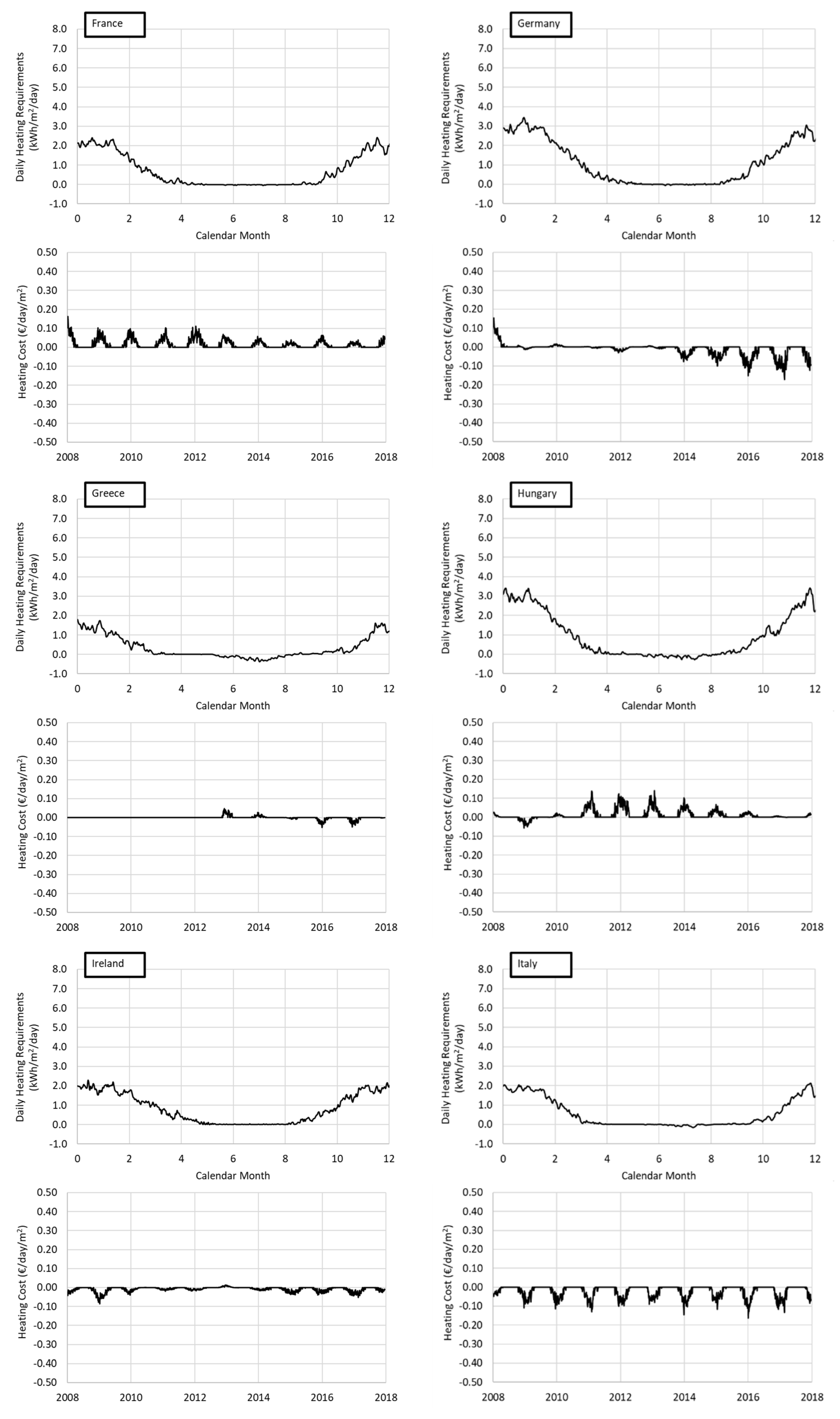
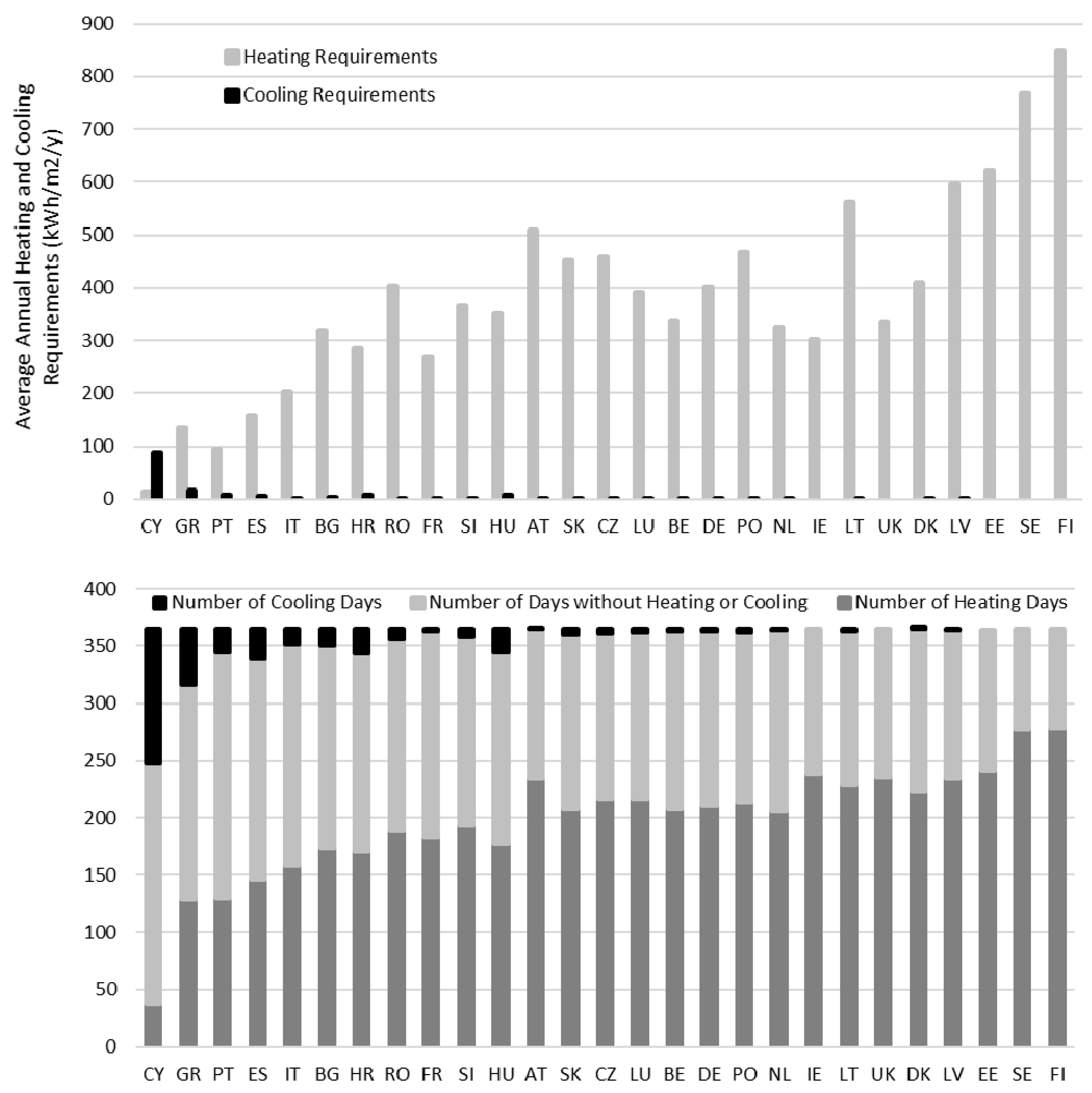
4.1. Greenhouse Energy Requirements
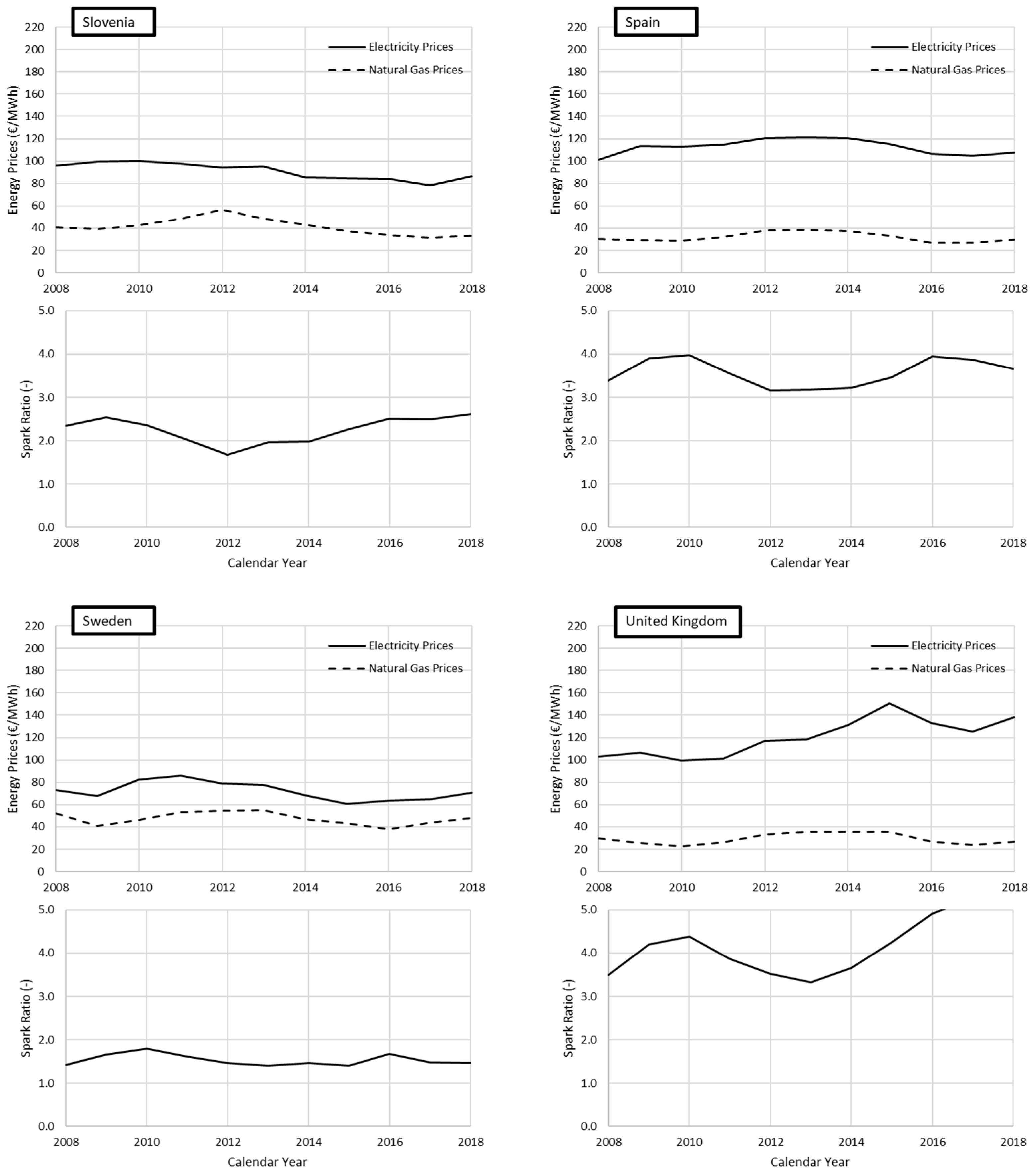
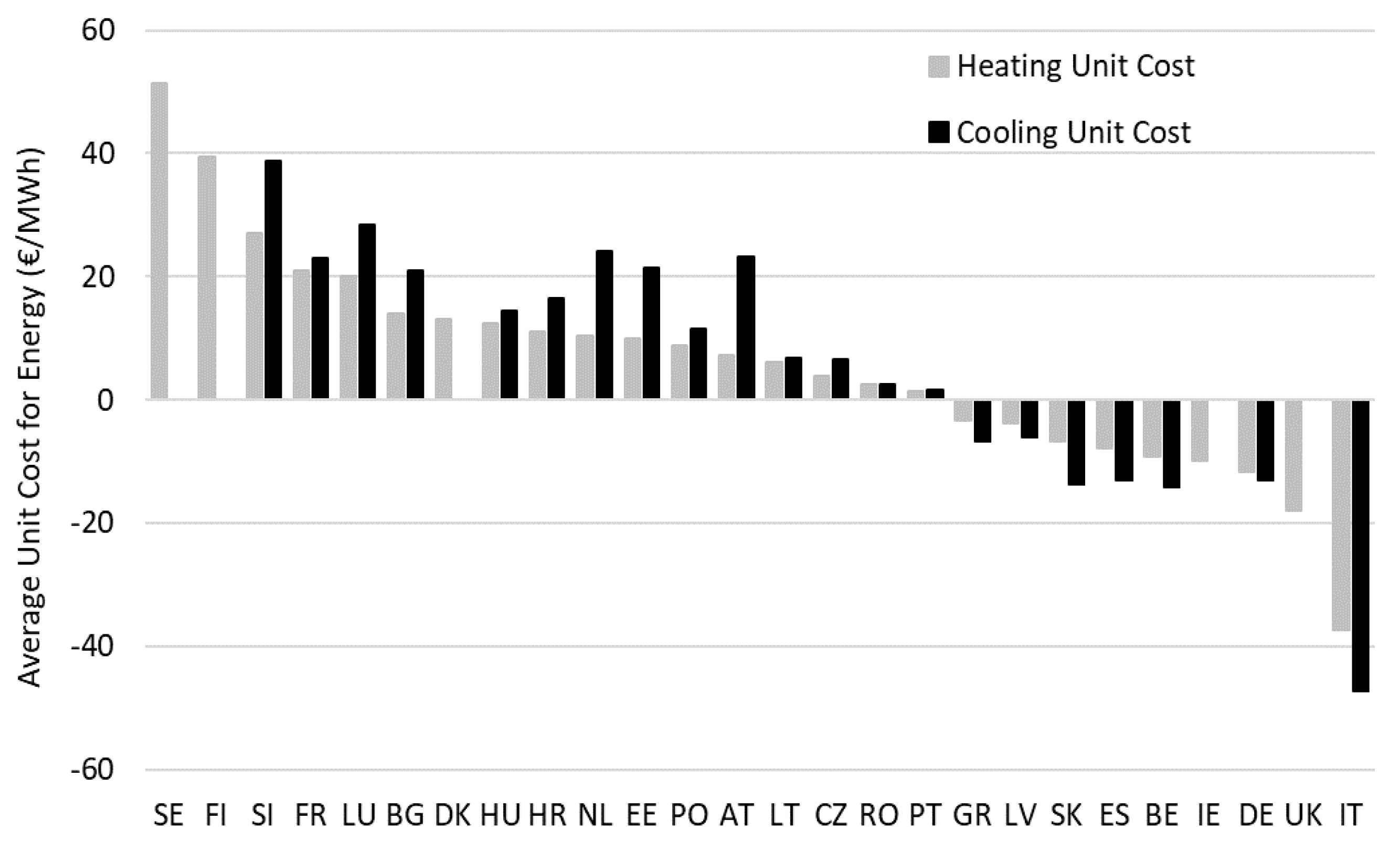
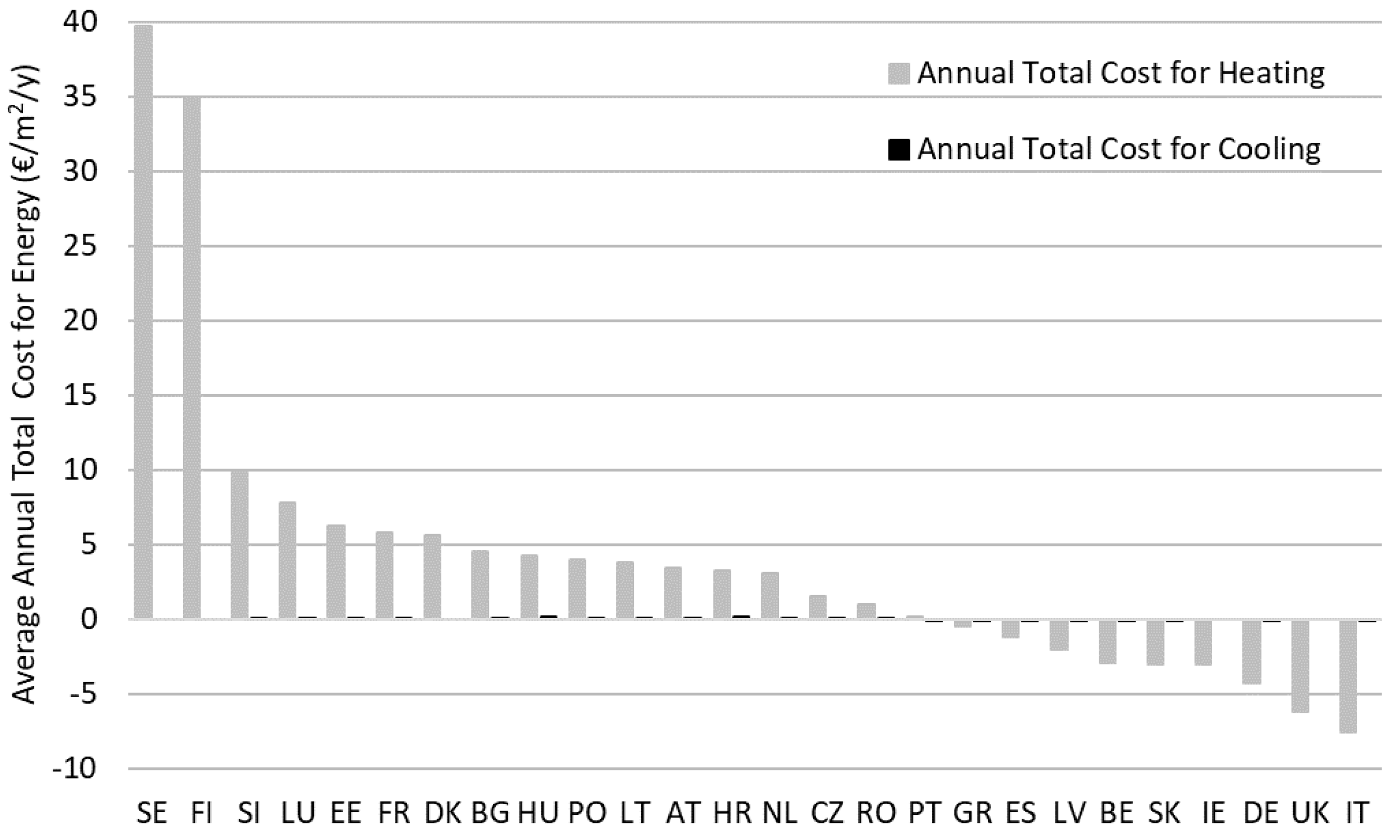
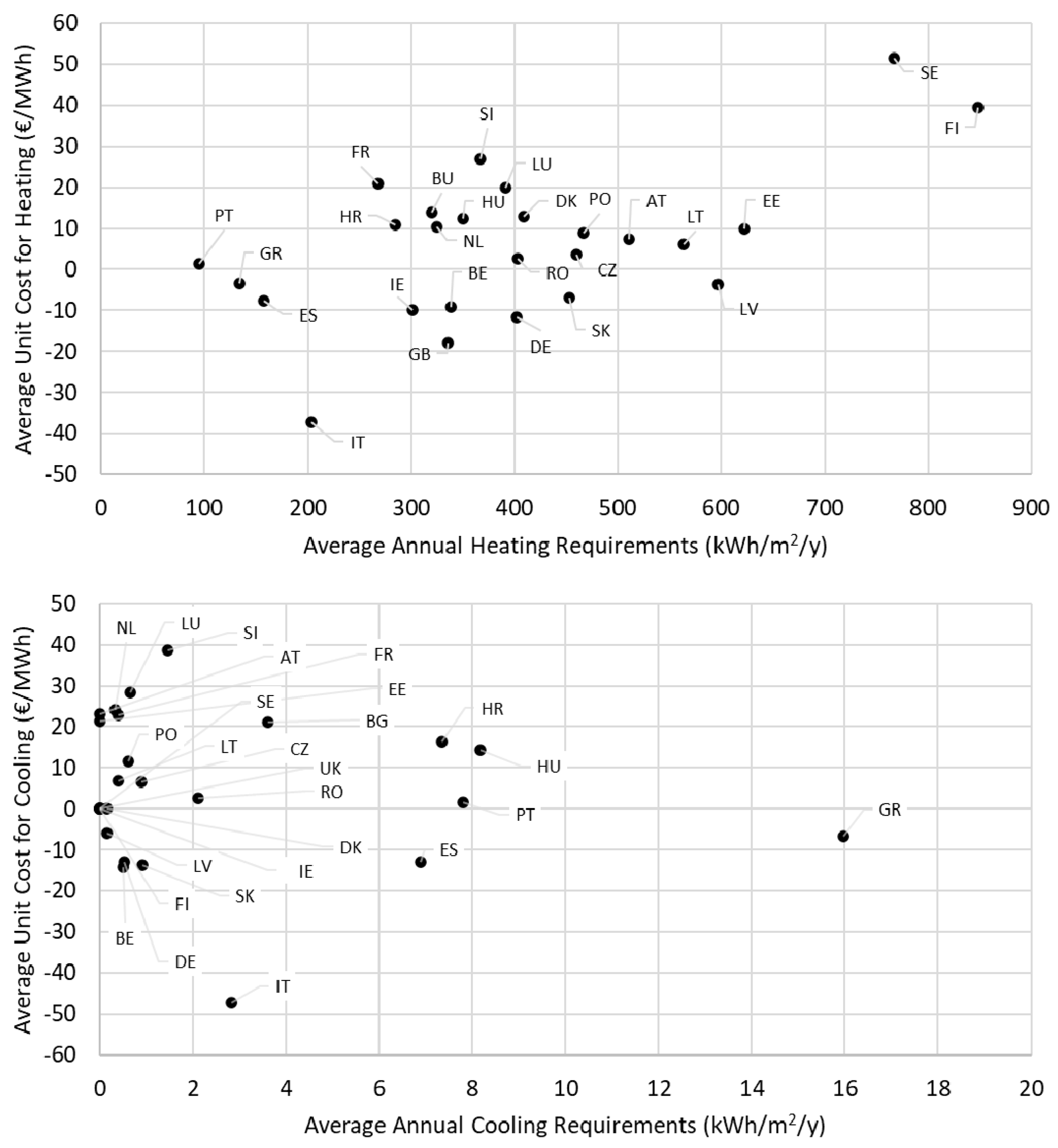
4.2. Cost of Greenhouse Energy
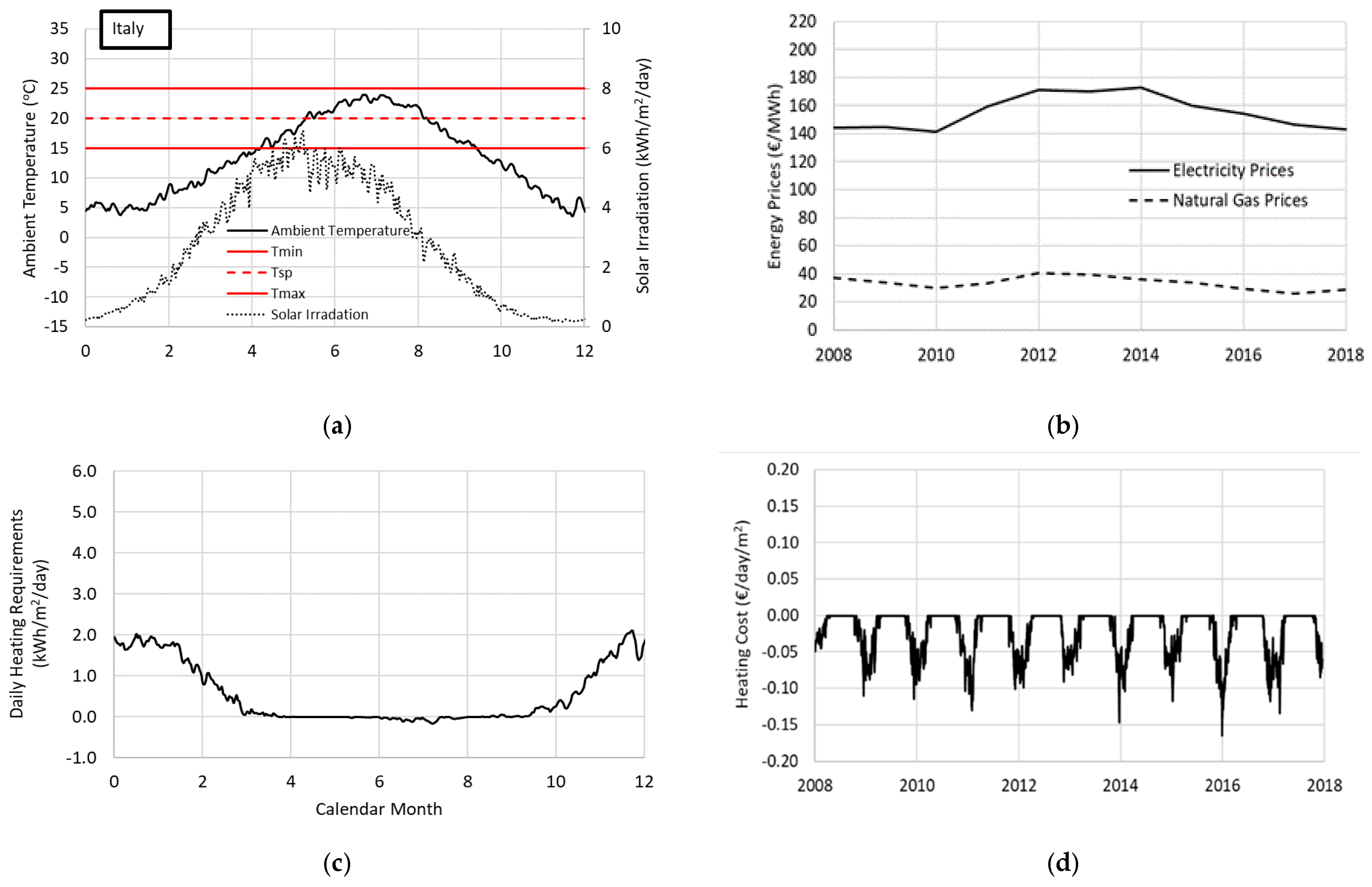
4.3. Seasonal Representation of the Effects of Energy Prices on Energy Greenhouse Costs: Estonia, The Netherlands, and Italy
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| the cost of the produced useful heating by the CCHP system (unit cost for heating) (€/MWh(th)) | |
| the coefficient of performance of the heat driven absorption chiller (-) | |
| the cost of the produced useful cooling by the CCHP system (unit cost for cooling) (€/MWh(co)) | |
| the electricity retail price (€/MWh(el)) | |
| the natural gas retail price (€/MWh(gas)) | |
| the CCHP maintenance cost (€/MWh(el)) | |
| the annual total heating cost (€/m2/y) | |
| the annual total cooling cost (€/m2/y) | |
| the electricity produced by the cogeneration during heating periods (kWh(el)) | |
| the electricity produced by the cogeneration during cooling periods (kWh(el)) | |
| the number of the day of the year ( (-) | |
| the annual natural gas consumption by the cogeneration system to cover the required greenhouse heating load (kWh(th)) | |
| the annual natural gas consumption by the cogeneration system to cover the required greenhouse cooling load (kWh(co)) | |
| the greenhouse daily heating load (kWh(th)/m2/d) | |
| the annual heating requirements of the greenhouse (kWh(th)/m2) | |
| the greenhouse daily cooling load (kWh(co)/m2/d) | |
| the annual cooling requirements of the greenhouse (kWh(co)/m2) | |
| the daily average solar irradiation on a horizontal surface (kW/m2) | |
| the daily ambient air temperature (°C) | |
| the set point greenhouse temperature (the required product cultivation temperature) (°C) | |
| the greenhouse effective overall heat loss coefficient (kW/m2K) | |
| the accepted temperature difference from set point temperature (cultivation range) (°C) | |
| the CCHP electrical efficiency (-) | |
| the CCHP thermal efficiency (-) | |
| the transmittance of the greenhouse cover (-) | |
| the transmittance of the additional shadowing cover during hot days (-) | |
| the absorbance of the greenhouse (-) | |
| AT | Austria |
| BE | Belgium |
| BG | Bulgaria |
| CCHP | Combined cooling heat and power |
| CHP | Combined heat and power |
| CY | Cyprus |
| CZ | Czech Republic |
| DE | Germany |
| DK | Denmark |
| EE | Estonia |
| ES | Spain |
| FI | Finland |
| FIP | Feed-in premium |
| FR | France |
| GR | Greece |
| HR | Croatia |
| HU | Hungary |
| ICE | Internal combustion engine |
| IE | Ireland |
| IT | Italy |
| LT | Lithuania |
| LU | Luxembourg |
| LV | Latvia |
| NL | Netherlands |
| PO | Poland |
| PT | Portugal |
| RO | Romania |
| SE | Sweden |
| SI | Slovenia |
| SK | Slovakia |
| UK | United Kingdom |
Appendix A
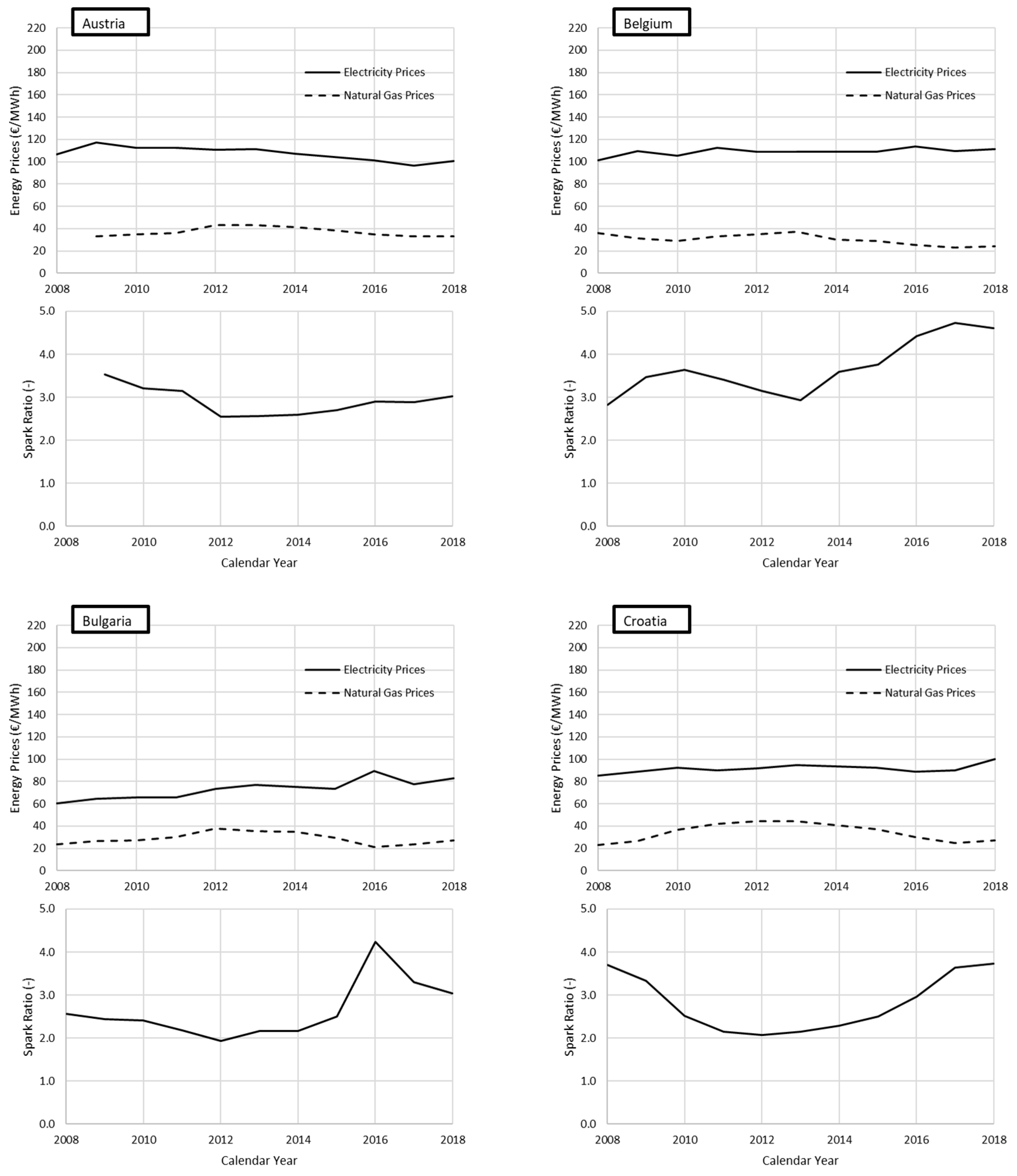
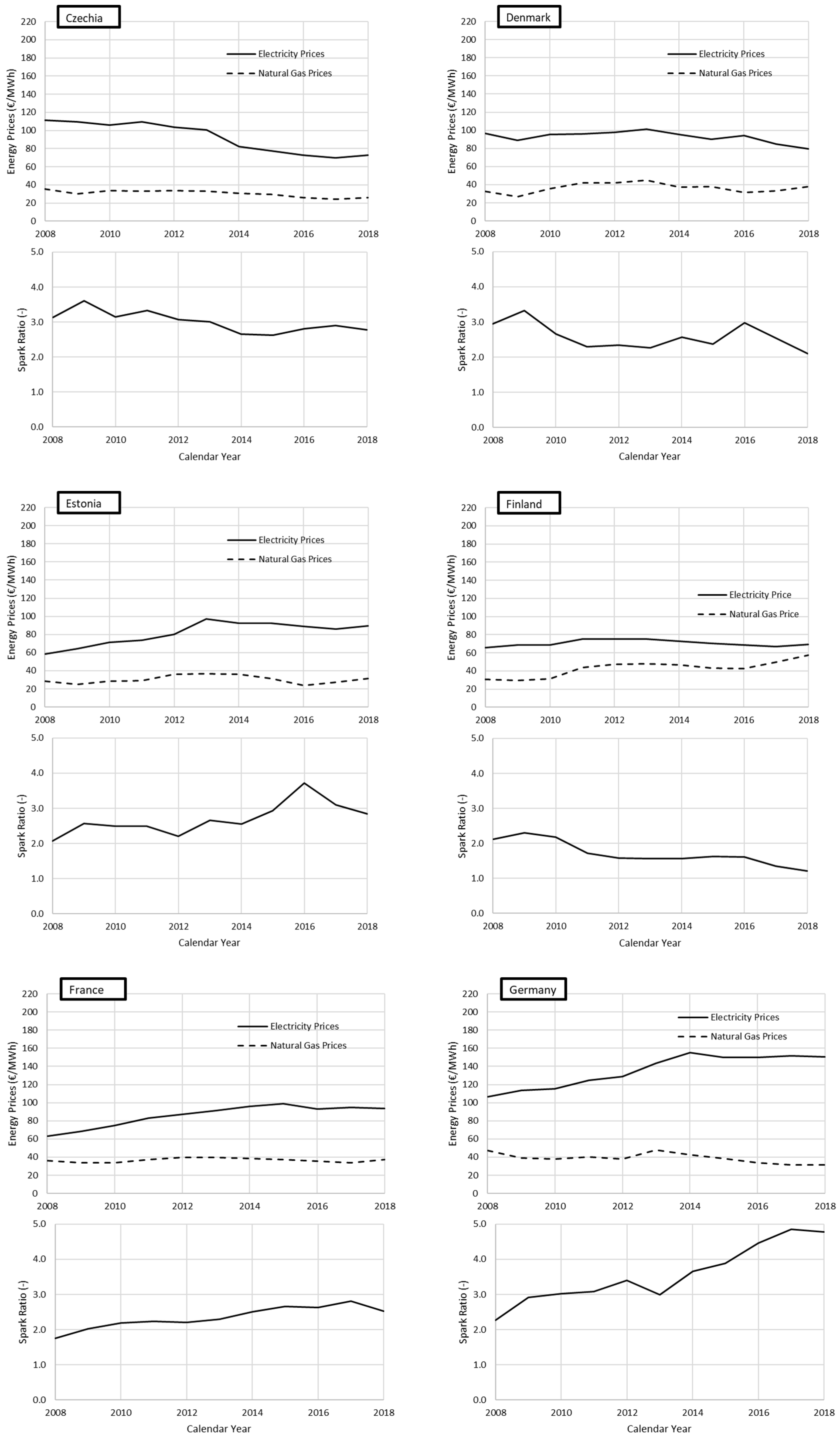
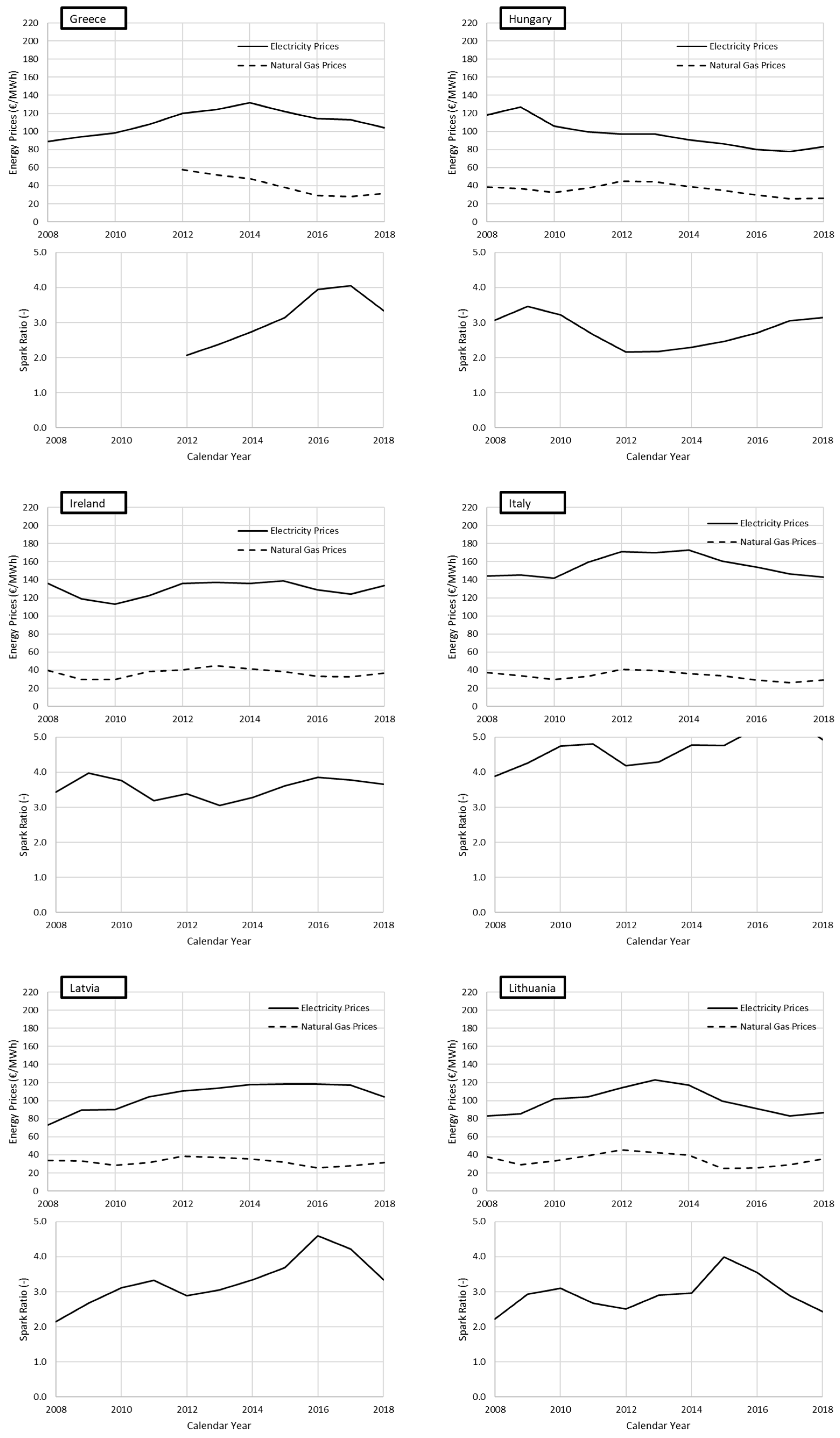
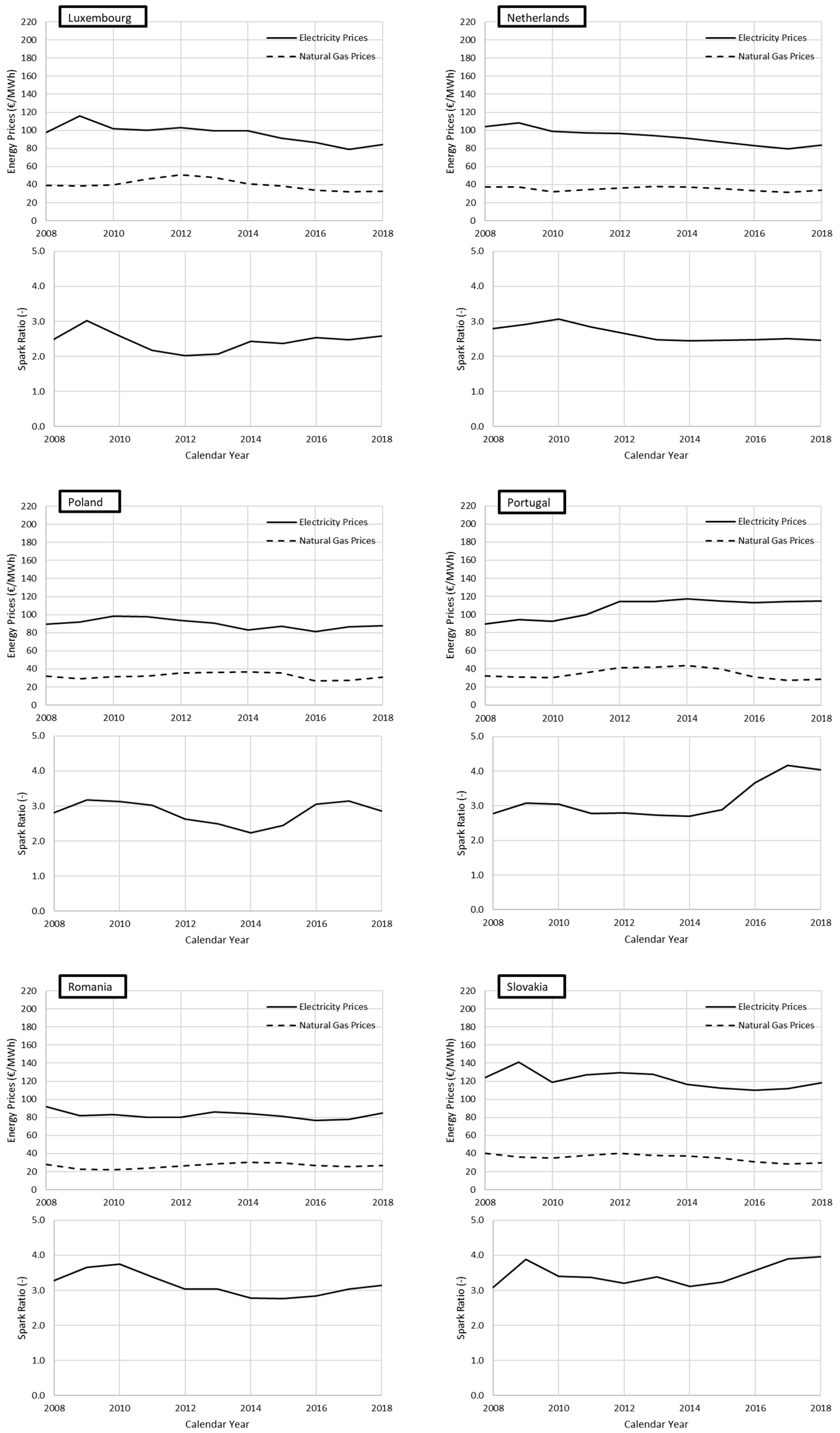


References
- Bibbiani, C.; Fantozzi, F.; Gargari, C.; Campiotti, C.A.; Schettini, E.; Vox, G. Wood Biomass as Sustainable Energy for Greenhouses Heating in Italy. Agric. Agric. Sci Procedia 2016, 8, 637–645. [Google Scholar] [CrossRef]
- European Comission. EIP-AGRI Focus Group Circular Horticulture. Final Report. February 2019, pp. 1–36. Available online: https://ec.europa.eu/eip/agriculture/sites/agri-eip/files/eip-agri_fg_circular_horticulture_final_report_2019_en.pdf (accessed on 1 May 2020).
- Fernández, J.A.; Orsini, F.; Baeza, E.; Oztekin, G.B.; Muñoz, P.; Contreras, J.; Montero, J.I. Current trends in protected cultivation in Mediterranean climates. Eur. J. Hortic. Sci. 2018, 83, 294–305. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Taylor, L.; Tanino, K. Heating demand and economic feasibility analysis for year-round vegetable production in Canadian Prairies greenhouses. Inform. Process. Agric. 2019, 6, 81–90. [Google Scholar] [CrossRef]
- Marsh, L.S.; Singh, S. Economics of greenhouse heating with a mine air-assisted heat pump. Trans. Am. Soc. Agric. Eng. 1994, 37, 1959–1963. [Google Scholar] [CrossRef]
- Kantor Management Consultants & Embassy of the Kingdom of The Netherlands. Greece-Market Special. Developments in the Greek Horticulture Sector: Greenhouses and Agro Logistics; Rijksdienst voor Ondernemend: The Hague, The Netherlands, 2015. [Google Scholar]
- Santamouris, M.; Argiriou, A.; Vallindras, M. Design and operation of a low energy consumption passive solar agricultural greenhouse. Sol. Energy 1994, 52, 371–378. [Google Scholar] [CrossRef]
- Sethi, V.P.; Sharma, S.K. Survey and evaluation of heating technologies for worldwide agricultural greenhouse applications. Sol. Energy 2008, 82, 832–859. [Google Scholar] [CrossRef]
- Adaro, J.A.; Galimberti, P.D.; Lema, A.I.; Fasulo, A.; Barral, J.R. Geothermal contribution to greenhouse heating. Appl. Energy 1999, 64, 241–249. [Google Scholar] [CrossRef]
- Vourdoubas, J. Overview of Heating Greenhouses with Renewable Energy Sources a Case Study in Crete- Greece. J. Agric. Environ. Sci. 2015, 4, 70–76. [Google Scholar] [CrossRef][Green Version]
- Compernolle, T.; Witters, N.; Van Passel, S.; Thewys, T. Analyzing a self-managed CHP system for greenhouse cultivation as a profitable way to reduce CO2-emissions. Energy 2011, 36, 1940–1947. [Google Scholar] [CrossRef]
- Tataraki, K.G.; Kavvadias, K.C.; Maroulis, Z.B. Combined cooling heating and power systems in greenhouses. Grassroots and retrofit design. Energy 2019, 189, 116283. [Google Scholar] [CrossRef]
- Singh, S.; Mittal, J.P.; Singh, M.P.; Bakhshi, R. Energy-use patterns under various farming systems in Punjab. Appl. Energy 1988, 30, 261–268. [Google Scholar] [CrossRef]
- Esengun, K.; Erdal, G.; Gündüz, O.; Erdal, H. An economic analysis and energy use in stake-tomato production in Tokat province of Turkey. Renew. Energy 2007, 32, 1873–1881. [Google Scholar] [CrossRef]
- Singh, S.; Singh, S.; Pannu, C.J.S.; Singh, J. Energy input and yield relations for wheat in different agro-climatic zones of the Punjab. Appl. Energy 1999, 63, 287–298. [Google Scholar] [CrossRef]
- Yilmaz, I.; Akcaoz, H.; Ozkan, B. An analysis of energy use and input costs for cotton production in Turkey. Renew. Energy 2005, 30, 145–155. [Google Scholar] [CrossRef]
- Çetin, B.; Vardar, A. An economic analysis of energy requirements and input costs for tomato production in Turkey. Renew. Energy 2008, 33, 428–433. [Google Scholar] [CrossRef]
- Singh, G.; Singh, S.; Singh, J. Optimization of energy inputs for wheat crop in Punjab. Energy Convers. Manag. 2004, 45, 453–465. [Google Scholar] [CrossRef]
- Ozkan, B.; Kurklu, A.; Akcaoz, H. An input-output energy analysis in greenhouse vegetable production: A case study for Antalya region of Turkey. Biomass Bioenergy 2004, 26, 89–95. [Google Scholar] [CrossRef]
- Mohammadi, A.; Omid, M. Economical analysis and relation between energy inputs and yield of greenhouse cucumber production in Iran. App. Energy 2010, 87, 191–196. [Google Scholar] [CrossRef]
- Ozkan, B.; Fert, C.; Karadeniz, C.F. Energy and cost analysis for greenhouse and open-field grape production. Energy 2007, 32, 1500–1504. [Google Scholar] [CrossRef]
- De Felice, M.; Kavvadias, K. ERA-NUTS: Time-series based on C3S ERA5 for European Regions (Version 1980–2018) Zenodo. 2019. Available online: http://doi.org/10.5281/zenodo.2650191 (accessed on 1 April 2020).
- Eurostat. Statistics Explained. Natural Gas Prices Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Natural_gas_price_statistics (accessed on 12 March 2020).
- Eurostat. Statistics Explained. Electricity Prices Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics (accessed on 12 March 2020).
- European Cogeneration Roadmap, Cogeneration Observatory and Dissemination Europe 2-CODE 2. Belgium. January 2015. Available online: https://ec.europa.eu/energy/intelligent/projects/en/projects/code2 (accessed on 12 March 2020).
- Moreton, O.R.; Rowley, P.N. The feasibility of biomass CHP as an energy and CO2source for commercial glasshouses. Appl. Energy 2012, 96, 339–346. [Google Scholar] [CrossRef][Green Version]
- American Society of Agricultural and Biological Engineers. Heating, Ventilating and Cooling Greenhouses; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2008. [Google Scholar]
- Kittas, C.; Katsoulas, N.; Bartzanas, T. Energy needs and energy saving in Mediterranean greenhouses. Acta Hortic. 2014, 1054, 25–30. [Google Scholar] [CrossRef]
- Kittas, C.; Katsoulas, N.; Bartzanas, T. Structures: Design, technology and climate control, Part II. In Good Agricultural Practices for Greenhouse Vegetable Production in the South East European Countries for Greenhouse Vegetable; Food and Agriculture Organization of the United Nations: Rome, Italy, 2017; pp. 29–51. [Google Scholar]
- Agrawal, V. Climate and Soil Requirements for Vegetable Crops, Chapter 9. In Vegetable Crops at a Glance; Scientific Publishers: New Pali Road, Jodhpur, India, 2018. [Google Scholar]
- Wu, D.W.; Wang, R.Z. Combined cooling, heating and power: A review. Prog. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- Jradi, M.; Riffat, S. Tri-generation systems: Energy policies, prime movers, cooling technologies, configurations and operation strategies. Renew. Sustain. Energy Rev. 2014, 32, 396–415. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration, U.S. Department of Energy. Distrib-Uted Generation and Combined Heat & Power System Characteristics and Costs in the Buildings Sector; U.S. Department of Energy: Washington, DC, USA, 2017; Report.
- ILF Consulting Engineers Austria GmbH, and AIT Austrian Institute of Technology GmbH. European Commission. Long Term (2050) Projections of Techno-Economic Performance of Large-Scale Heating and Cooling in the E.U.; Report 2017; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar] [CrossRef]
- García, J.L.; De La Plaza, S.; Navas, L.M.; Benavente, R.M.; Luna, L. Evaluation of the feasibility of alternative energy sources for greenhouse heating. J. Agric. Eng. Res. 1998, 69, 107–114. [Google Scholar] [CrossRef]



| Technical Data | |||
|---|---|---|---|
| Greenhouse Characteristics | |||
| Overall heat loss coefficient | 9.0 | W/m2K | |
| Transmittance of the greenhouse cover | 0.50 | - | |
| Transmittance of greenhouse additional shadowing cover during hot days | 0.10 | - | |
| Absorbance of the greenhouse | 0.40 | - | |
| Product Characteristics | |||
| Required product cultivation temperature | 20.0 | °C | |
| Accepted cultivation range | ±5.0 | °C | |
| Equipment Characteristics | |||
| Cogeneration electrical efficiency | 0.35 | - | |
| Cogeneration thermal efficiency | 0.50 | - | |
| Coefficient of performance of the heat driven absorption chiller | 0.70 | - | |
| Economic Characteristics | |||
| Cogeneration maintenance cost | 10 | €/MWh(el) | |
| Country | Heating Needs in This Work (kWh/m2/y) | Heating Needs in García et al. (kWh/m2/y) |
|---|---|---|
| United Kingdom | 335 | 444 (Bedford) |
| Netherlands | 325 | 424 (De Bilt) |
| Germany | 402 | 453 (Braunschweig) |
| Italy | 203 | 406 (Milano) |
| France | 268 | 239 (Montpellier) |
| Spain | 158 | 88 (Almeria) |
| Greece | 134 | 198 (Aliartos) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tataraki, K.; Giannini, E.; Kavvadias, K.; Maroulis, Z. Cogeneration Economics for Greenhouses in Europe. Energies 2020, 13, 3373. https://doi.org/10.3390/en13133373
Tataraki K, Giannini E, Kavvadias K, Maroulis Z. Cogeneration Economics for Greenhouses in Europe. Energies. 2020; 13(13):3373. https://doi.org/10.3390/en13133373
Chicago/Turabian StyleTataraki, Kalliopi, Eugenia Giannini, Konstantinos Kavvadias, and Zacharias Maroulis. 2020. "Cogeneration Economics for Greenhouses in Europe" Energies 13, no. 13: 3373. https://doi.org/10.3390/en13133373
APA StyleTataraki, K., Giannini, E., Kavvadias, K., & Maroulis, Z. (2020). Cogeneration Economics for Greenhouses in Europe. Energies, 13(13), 3373. https://doi.org/10.3390/en13133373





