Design Synchronous Generator Using Taguchi-Based Multi-Objective Optimization

Abstract

The extensive use of finite element models accurately simulates the temperature distribution of electrical machines. The simulation model can be quickly modified to reflect changes in design. However, the long runtime of the simulation prevents any direct application of the optimization algorithm. In this paper, research focused on improving efficiency with which expensive analysis (finite element method) is used in generator temperature distribution. A novel surrogate model based optimization method is presented. First, the Taguchi orthogonal array relates a series of stator geometric parameters as input and the temperatures of a generator as output by sampling the design decision space. A number of stator temperature designs were generated and analyzed using 3-D multi-physical field collaborative finite element model. A suitable shallow neural network was then selected and fitted to the available data to obtain a continuous optimization objective function. The accuracy of the function was verified using randomly generated geometric parameters to the extent that they were feasible. Finally, a multi-objective genetic optimization algorithm was applied in the function to reduce the average and maximum temperature of the machine simultaneously. As a result, when the Pareto front was compared with the initial data, these temperatures showed a significant decrease.

1. Introduction

Electrical machine is one of the most promising solution to reduce energy crisis, air pollution and global warming. Recently, research on temperature field of electrical machine is attracting more and more attention since it is one of the major obstacles to the performance improvement. Excessively high temperatures will cause accelerated insulation aging and deterioration within some essential components, such as winding conductors. In addition, the electrical resistivity of the winding conductors are proportion to the temperature, which creates a positive feedback that in turn accelerates the loss and temperature rise that occurs in the winding. Thermal effects on the geometrical dimensions of the machine’s physical structure, such as a narrowing within the air gap, may alter the machine’s nominal performance, or even result in faults and failures. To tackle the above thermal challenges in an electric machine, the optimal design of the heat dissipation mechanism in order to obtain a balanced heat distribution across different components is required [1,2,3,4,5].

The optimization design process can be divided into three stages: the sampling and calculation of data, the definition of the optimization objective function, and the application of the optimization algorithm. In the first stage, the data used to reflect the relationship between the inputs and outputs of the specified system are sampled and any computational or experimental means used to generate the corresponding response. Commonly used data sampling methods include full-factorial sampling, Latin hypercube sampling, and orthogonal array, with different sampling methods determined depending on the system being analyzed. For the temperature design of the electrical machine, it is necessary to have as few sample points as possible and a uniform distribution of sample points in the design space, as well as to avoid projection overlap. The Taguchi orthogonal array is a desirable choice because of the orthogonal characteristics between the columns in the array.

The definition of the objective function determines the efficiency of the optimization. The accuracy of this function largely affects the optimization quality, and the complexity of its computation affects the time taken to update and iterate the solution during the optimization process. Evaluation of the temperature performance of electrical machine involves the use of expensive computer simulations (finite element analysis, computational fluid dynamics), which means that only a limited number of simulations are usually affordable. Due to the long running times of simulations (often overnight), almost any optimization algorithm applied directly to the simulation will be slow [6]. The proposed surrogate model approach provides a solution that avoids investing in a computational budget in answering questions, and instead invests in developing fast mathematical approximations to long running computer code. This approach bridges the variables and their response with the form of black box which is convenient for studying systems with complex internal mechanisms.

In the last stage, a suitable and effective optimization algorithm will be applied to the defined objective function for finding the optimal results. There are two main types of multi-objective optimization methods in common use, one based on weighting factors and the other on heuristic algorithms. The first method assigns different weight values to each objective performance according to the optimization requirements to establish the weight function as the optimization objective function. It simplifies the multi-objective function problem into a single objective function for solving. Butat the same time, the problem of weighting factor also arises how to choose the exact weighting factor to clearly describe the relationship between the objective performance. It’s a challenge for the designer. And this approach is not well adapted to non-linear problems. The second approach constructs Pareto solutions based on population search, such as multi-objective optimization genetic algorithm (MOGA). In such approach a set of designs is worked on concurrently and evolved towards the final Pareto set in one process. In doing this, designs are compared to each other and progressed if they are of high quality and if they are widely spaced apart from other competing designs [6].

Literature Review

Since Dr. Genichi Taguchi [7] developed the Taguchi method, it has been used extensively in industrial optimization, including electrical machine applications. The existing motor optimization approaches based on the Taguchi method [8,9,10] are “point-like”, where the designer chooses a fixed level for each factor and then selects the “optimal” value among known results. The level values of the factors are mostly subjective, which makes the optimization results more favorable to the designer’s expectations. It is more convincing to find the optimal value for each factor with continuous variations in the range of values taken. The objective function is the basis for continuous optimization within the feasible interval.

In recent years, surrogate model methods have been increasingly used in electrical machine optimization research. Ziyan et al. compared Kriging method, response surface method, and radial basis function, three surrogate model building methods, in optimizing electrical machine electromagnetic problems [11]. Weile et al. creates the surrogate model between output performance and design parameters of a coreless axial flux permanent magnet synchronous machine (AFPMSM) using support vector machine [12]. Neural networks as non-parametric models can also ignore the internal principles of the system and directly establish the relationship between inputs and outputs. However, the accuracy of the models usually built is related to the amount of training data, which limits their application to surrogate models.

The popularity of multi-objective genetic algorithm (MOGA) has led to its increasing use in electrical machines, from the accuracy aspect of the optimization model to the adaptation of the optimization algorithm. Abdelhadi et al. proposed a novel adaptive GA scheme design to accurately solve nonlinear fitting optimization problem within a reduced computing time [13]. Mallik et al. designed an efficiency-optimized squirrel cage induction motor, where genetic algorithm was chosen as the tool for optimization. And the objective function is typical theory formula of electrical machine [14].

From the above discussion, existing optimization methods have the following limitations:

• Most existing designs evaluate performance by means of a limited sample of data without a continuous objective function, which selects the “optimal solution” among existing combinations of variables. Such an optimization is undoubtedly inaccurate and subjectively biased by the designers.
• During the optimization process, it takes a lot of simulation time to evaluate the performance of a large number of sampling points, which increases the difficulty of engineering practical applications.

In this paper, to solve the above problem, a novel optimization method based on a surrogate model is proposed. The geometric parameters and temperatures of the stator are the optimization variables and objectives, respectively. Taguchi orthogonal arrays were used for sampling, and the corresponding responses for each experiment were simulated using a three-dimensional multi-physics field synergistic finite element model. The data from the orthogonal array and the additional sets of randomly generated data used for the test are jointly trained as surrogate model of shallow neural networks, which build direct mathematical relationship between geometric variables and temperature, greatly reducing the computational burden of optimization. In the last, a multi-objective genetic algorithm was applied to the function to reduce the maximum and average temperature of stator. The highlights of the paper can be summarized as:

• The Taguchi orthogonal array was used for the sampling process in the surrogate model building process, which ensures that sampling is spread throughout the design space while reducing the number of expensive performance analyses;
• The combination of Taguchi orthogonal array with a shallow artificial neural network was used to approximate the optimization objective function, ignoring the internal mechanism of the system and simplifying the industrial optimization process;
• The multi-objective optimization in thermal and fluid field of generator to simultaneously reduce the maximum and average temperature of the stator.

The rest of this article is organized as follows. Section 2 introduces prototype synchronous generator and the process of multi-physical field collaborative conjugate heat transfer model. The proposed Taguchi orthogonal array and neural network based optimization methods are presented in Section 3. Section 4 summarizes the results. The adaptation of the proposed optimization method to practical engineering applications is discussed in Section 5.

2. Optimization Objective

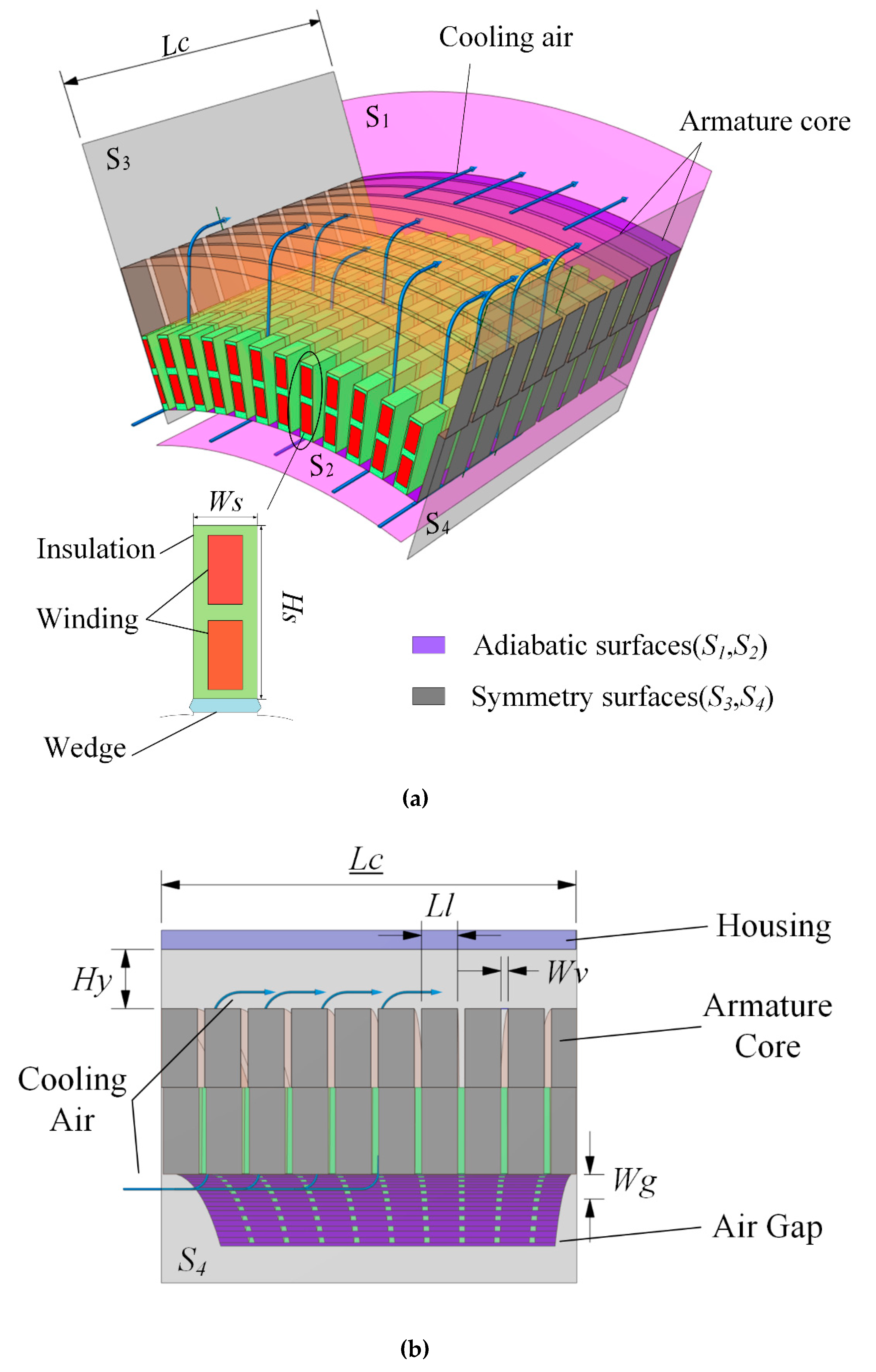
In this paper, the optimization objective is a diesel-driven salient synchronous generator. The stator of this generator consists of armature core, winding and their insulation, slot wedge, and housing, as shown in Figure 1. The stator is divided into sections by radial ventilation duct to allow a cooling air medium to cool the inside of the generator. The cooling air driven by the shaft-mounted fan sequentially passed through the end of the stator, the air gap, the radial vent duct, and the back of the yoke to the other end of the stator in turn (see Figure 1a, blue arrowed curve). It brings heat out of the stator to lower the internal temperature. There are 120 slots evenly distributed around the circumference of the inner diameter of the stator, and double-wound windings with the same number of strands and cross-section are distributed in the slots.

Table 1. Design specifications of the generator.

Parameter	Value (Unit)
Rated output power	8600 (kW)
Rated operating speed	720 (rpm)
Rated output voltage	13.8 (kV)
Rated frequency	60 (Hz)
Insulation class	H
Poles/Phases/Slots	10/3/120

shows the design specifications of the generator.

Considering that the focus of this paper is on the process of optimization, the following simplifications and assumptions were made in the model.

• Since the heat generated by the stator winding losses is much greater than the heat generated by the rotor winding losses, this paper only optimizes the stator temperature for this generator.
• As the given solving region of 3-D multi-physical field collaborative model, the half of axial length and one-tenth circumferential stator is determined because of its geometric structure axial and circumferential symmetrical.
• In terms of heat generation in the winding, the temperature difference within the winding is negligible. Here it is assumed that the winding generates heat uniformly. Considering that the complex structure of the end windings can impose a heavy computational burden on the multi-physics field coupled simulation calculations, the heating and cooling of the winding ends are not considered in this paper.
• Under steady-state motor operating conditions, the heat inflow and outflow at the stator axial center plane as well as at the stator air gap are equal. It is assumed that there is no heat transfer in the axial center section and there is no heat exchange between the stator and the rotor.

In the multi-physical field collaborative conjugate heat transfer model, the electromagnetic and fluid fields were simulated based on the above assumptions. In electromagnetic field, various losses are intrinsic to the heat generation of the machine. The losses were calculated at constant output power and output voltage. Based on the loss results, the heat source density is calculated as the initial condition of the fluid field and the temperature distribution of the stator was then evaluated. In this paper, the heat of the stator mainly comes from the winding loss and the core loss. The heat source density of the winding loss q_cu is [15],

$$q_{cu}{=k}_F{\rho }_0{j}^2\frac{235+T_1}{235+T_0}\times {10}^6=k_F{j}^2{\rho }_0[1+(T_1-T_0){\beta }_0\times {10}^6]$$

(1)

where T₁, T₀ are temperature of the winding and the initial temperature (in °C), k_F is the additional loss factor of copper (k_F ≈ 1.2), j is the current density (in A/mm²), ρ₀ is the coefficient of resistance of the copper wire, and β₀ is the temperature coefficient of resistance of the copper wire relative to initial temperature. The heat source density of the core loss q_Fe is [15],

$$q_{Fe}=\frac{p_{Fe}}{V_l}=\frac{p_{Fe}}{F\cdot a}$$

(2)

where a is the length of stator lamination (in m), F is the effective area of the lamination (in m²).

In thermal field, this design uses an open cooling circuit to achieve a critical temperature balance within an electrical machine. Heat from the inner components is conducted to the outer surface of the machine and then is subjected to the convective cooling [16]. The process can be expressed as followed.

$$\{\begin{array}{l}\lambda \frac{{\partial }^{2}T}{\partial x^2}+\lambda \frac{{\partial }^{2}T}{\partial y^2}+\lambda \frac{{\partial }^{2}T}{\partial z^2}=-q_v\\ \lambda \frac{\partial T}{\partial n}|{}_{{}_{S_1,S_2}}=0\\ \lambda \frac{\partial T}{\partial n}=-\alpha (T-T_f)\end{array}$$

(3)

where T is the temperature of stator (in °C); T_f is the ambient temperature (in °C); λ is thermal conductivity (in W/(m·K)); q_ν is heat source density (in W/m³); α is coefficient of convection (in W/(m²·K)). S₁ is the adiabatic surface between the rotor yoke and the air gap; S₂ is adiabatic surface of the central cross section of the axial, as shown in Figure 1. Except for those faces, the other outer surfaces of the stator are set to natural convection. The thermal conductivity is temperature dependent and the coefficients of convection are related to the fluid velocity. The thermal conductivity λ is,

$$\lambda ={\lambda }_0(1+bT)$$

(4)

where λ₀ is the thermal conductivity when the temperature is 0 °C;T is temperature and b is a constant depending on material. And, in this paper, the materials are set to isotropic in thermal conductivity. The coefficient of convection α_δ from the armature surface to the air gap is [15],

$${\alpha }_{\delta }=28(1+V_{\delta }{}^{0.5})$$

(5)

and the coefficient of convection α_B of insulated copper winding is [14],

$${\alpha }_B=12(1+V_B{}^{0.5})$$

(6)

where V_δ, V_B is the fluid velocity (in m/s).

3. Proposed Method

3.1. Structure

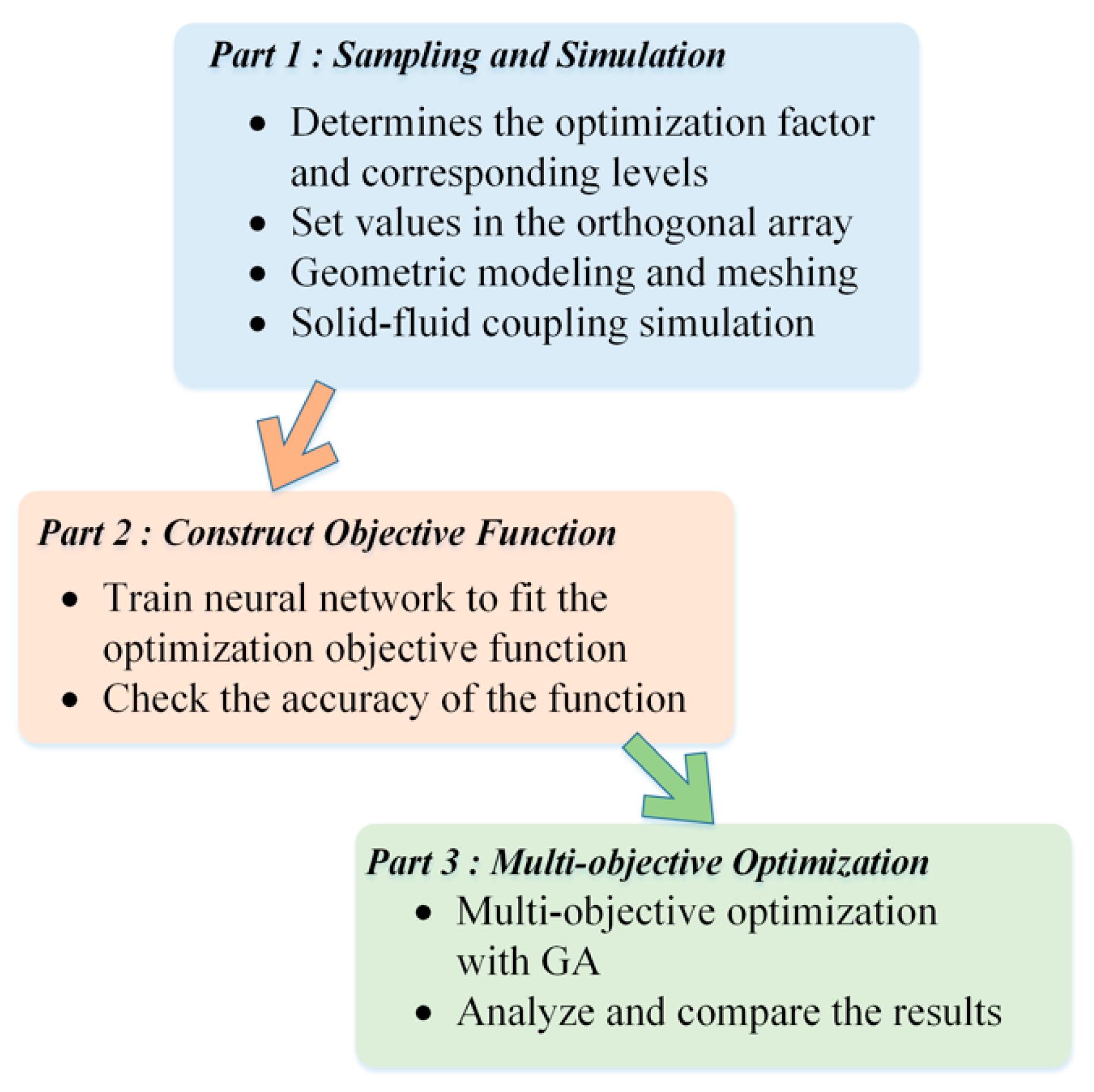
In this paper, the design process is composed of three parts, as shown in Figure 2.

Part 1: This part determines the optimization factor and corresponding levels. And the experiment data is organized in an appropriate Taguchi orthogonal array. For calculating the average and maximum temperatures of these experiments in the array, a 3-D multi-physical field collaborative conjugate heat transfer model can be established using the code of ANSYS, Inc. (Pittsburgh, PA, USA)

Part 2: To define the optimization objective function that directly reveals the mathematical relationship between stator geometric parameters and temperatures, a shallow neural network model was trained to fit the function. The experiment data were divided into three subsets. Two of them were used to fit the function and the other was used to evaluate the accuracy of the function.

Part 3: By optimizing the fitted objective function with a multi-objective genetic algorithm as far as practicable, a Pareto front that provides a series of solutions for project is obtained.

3.2. Background of Taguchi Method

Design of Experiments (DoE) is a statistical technique for planning, conducting, analyzing, and interpreting controlled tests [17]. It identifies the factors that control the value of a parameter or group of parameters [18]. The Taguchi method is a DoE that improves quality and reduces loss by reducing variation in the design of a product or process. The Taguchi method has a wide range of applications, such as battery charging [19,20] or the power systems [21,22].

3.2.1. Process of System

The process of the Taguchi method is that the system outputs quality characteristic under the influence of different kinds of factors. Figure 3 [20] presents in detail the process, which includes the following parts.

• The system is the heart of a process and describes the mechanisms of applications. In this paper, the engineering system is the generator stator’s temperature field.
• Signal factors are the input values at the start-up of the system. Only dynamic systems have input factors.
• Control factors are the design parameters that significant affect system performance. In this work, the control factors are the geometric parameters of the stator.
• Noise factors are uncontrolled factors that cause the characteristics of a product to deviate from its target values. There is not the focus of this study and so are ignored.
• Quality characteristic is the output of the system, which is used to indicate the performance of a system. In this paper, one tends to find the minimum temperatures in the feasible range.

3.2.2. Orthogonal Array

In the Design of Experiments, the most commonly used experimental designs are full factorial design, Box Behnken design, and Latin Hypercube sampling method. Full factorial design uses all possible combinations of levels of factors in each complete trial or replication of experiments [18]. Box Behnken design specifies special points in the space. If 3 three-level factors are considered, the number of full-factorial experiments is 9, and the number of Box Behnken design is 15. Latin Hypercube Sampling method belongs to the stratified sampling [23], which number depends on the selection of interval. Therefore, these methods are often costly and prohibitive, especially when applied industrially.

The Taguchi method constructs a special set of orthogonal arrays for collecting experiment data. It effectively reduces the number of experiments that must be performed. For example, an orthogonal array (L₄2³) of three two-level factors requires four experiments, as indicated in

Table 2. Taguchi orthogonal array L₄2³ [21].

Experiments	Levels of Each Factor
	Factor A	Factor B	Factor C
1	1	1	1
2	1	2	2
3	2	1	2
4	2	2	1

. Three factors A, B, C are set to levels 1 and 2. In the array, the columns are balanced within themselves such that they all have an equal number of levels of factor. And the columns are balanced between any two columns such that together they form an equal number of possible combinations. Two two-level factors combine in four possible ways, such as (1, 1), (1, 2), (2, 1), and (2, 2). When two columns of an array form these combinations the same number of times, the columns are said to be orthogonal [24]. Accordingly, the orthogonal array reduces the number of experiments that have to be carried out to obtain all necessary information.

3.3. Taguchi Training Data

In this paper, the maximum and average temperature of the stator were selected as optimization objectives, which the maximum temperature determines the life-span of insulation, and the average temperature reflects the distribution of temperature. In order to optimize the performance of the stator thermal field, the structure of the stator was altered to decrease the losses of each part or enhance the cooling effect.

The choice of stator geometry variables takes into account not only the heat generated by the electromagnetic losses of the individual components, but also the flow of cooling air. In the stator cooling system, the velocity of cooling air flow and the temperature difference between it and the heat source determine the efficiency of cooling. For reducing the maximum and average temperature of the stator, the following factors that significantly affect the performance of the heat generation and cooling system are selected as the optimization variables: stator core length (Lc), lamination length (Ll), vent ducts width (Wv), air gap width (Wg), stator slot width (Ws), stator slot height (Hs) and yoke vent duct height (Hy). The diagram of each factor is shown in Figure 1. The levels of above factors are listed in

Table 3. Levels of each factor.

Parameters	Level 1	Level 2	Level 3
Stator core length (mm) A	1000	1150	1300
Lamination length (mm) B	40	50	60
Vent duct width (mm) C	8	10	12
Air gap width (mm) D	8	10	12
Stator slot width (mm) E	22	24	26
Stator slot height (mm) F	113	116	119
Yoke vent duct height (mm) G	80	90	100

, where level 2 of each factor are their original values. Except for the above seven variables, the number of ventilation ducts as the eighth variable is added. It’s relevance as follow:

$$N_{vent}=\mathrm{Round}(\frac{Lc-Ll}{Ll-Wv})$$

(7)

where N_vent is the number of vent ducts, Lc is the length of the stator core, Ll is the length of lamination, and Wv is the width of the vent ducts.

Based on the Taguchi orthogonal array, an array of 13 three-level factors (L₂₇3¹³) is used to collect training data. Owing to the orthogonal characteristic of the array, as mentioned in the Section 3 Background of Taguchi method, any two columns are orthogonal. Thus, in this array, the first seven columns (A to G) that represent seven control factors are used and the redundant parts thereof are ignored (see

Table A1. Taguchi orthogonal array L₂₇3¹³.

Experiments	1	2	3	4	5	6	7	8	9	10	11	12	13
1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	1	1	1	2	2	2	2	2	2	2	2	2
3	1	1	1	1	3	3	3	3	3	3	3	3	3
4	1	2	2	2	1	1	1	2	2	2	3	3	3
5	1	2	2	2	2	2	2	3	3	3	1	1	1
6	1	2	2	2	3	3	3	1	1	1	2	2	2
7	1	3	3	3	1	1	1	3	3	3	2	2	2
8	1	3	3	3	2	2	2	1	1	1	3	3	3
9	1	3	3	3	3	3	3	2	2	2	1	1	1
10	2	1	2	3	1	2	3	1	2	3	1	2	3
11	2	1	2	3	2	3	1	2	3	1	2	3	1
12	2	1	2	3	3	1	2	3	1	2	3	1	2
13	2	2	3	1	1	2	3	2	3	1	3	1	2
14	2	2	3	1	2	3	1	3	1	2	1	2	3
15	2	2	3	1	3	1	2	1	2	3	2	3	1
16	2	3	1	2	1	2	3	3	1	2	2	3	1
17	2	3	1	2	2	3	1	1	2	3	3	1	2
18	2	3	1	2	3	1	2	2	3	1	1	2	3
19	3	1	3	2	1	3	2	1	3	2	1	3	2
20	3	1	3	2	2	1	3	2	1	3	2	1	3
21	3	1	3	2	3	2	1	3	2	1	3	2	1
22	3	2	1	3	1	3	2	2	1	3	3	2	1
23	3	2	1	3	2	1	3	3	2	1	1	3	2
24	3	2	1	3	3	2	1	1	3	2	2	1	3
25	3	3	2	1	1	3	2	3	2	1	2	1	3
26	3	3	2	1	2	1	3	1	3	2	3	2	1
27	3	3	2	1	3	2	1	2	1	3	1	3	2

for orthogonal array L₂₇3¹³).

After completing the above selection, assignment, and combination of stator geometry variables, each group of experiments in Taguchi orthogonal array is simulated under the specified conditions. In this paper, the variables are controlled for comparison and the experiments for each group are performed with constant output power and output voltage. A three-dimensional multi-physics field collaborative model conforming to the engineering error after comparison with experiments is used for the temperature evaluation of each set of experiments. So far, the Taguchi training data are all prepared, in which the stator geometry variables are the input of the neural network, and the stator temperature obtained from the simulation calculation is the output.

3.4. Neural Network

Neural networks are used for processing information. They have a wide range of applications across almost all areas of science and engineering. Unlike conventional data processing methods, which require extensive expert knowledge when used in the modelling of electrical machines, neural networks provide a model-free, adaptive, fault-tolerant, parallel, and distributed processing solution [25].

In this work, a neural network is a black box that directly learns the function that captures the relationship between geometric parameters and temperatures without guessing the internal relations of a generator temperatures system.

3.4.1. Structure

In this work, to construct the surrogate model of objective function, a feedforward network is trained by backpropagation. The most exciting thing when it comes to backpropagation is training recurrent neural networks (RNNs), which has significant advantages for dealing with problems with errors or problems containing noisy signals. In this study, to simplify the modeling process, all experimental data are assumed to be accurate and without noise factors. The feedforward network arranged in the form of eight inputs, one hidden layer with 20 neurons and the output layer with two neurons. The process begins with the receipt of inputs by the input layer neurons, which are processed by each layer sequentially to the output layer. The connections between neurons are unidirectional and neurons in the same layer are unconnected to each other, as shown in Figure 4 [25].

In the training process, the objective function is constructed. The weight and bias from the input layer to the hidden layer are denoted as W₁ and b₁ respectively, while those from the hidden layer to the output layer are W₂ and b₂. The activation functions of the two layers are the hyperbolic tangent sigmoid function Φ from the input to the hidden, and the linear function Ψ from the hidden to the output layer the function can be expressed as follows.

$$T=\Phi [W_2\Psi (W_{1}X+b_1)+b_2],$$

(8)

$$T=\left[\begin{array}{l}{T}_{\mathit{Avg}}\\ T_{\mathit{Max}}\end{array}\right]X=\left[\begin{array}{l}{X}_1\\ X_2\\ M\\ X_8\end{array}\right],$$

(9)

where X is an input geometric parameters matrix and T is an output temperatures objective functions matrix. W₁ and W₂ are weights matrixes; b₁ and b₂ are bias vectors.

3.4.2. Training, Testing, and Validation

In the fitting process, experiment data are divided into three subsets. The first subset is the training data set, which is used to fit to the initial model. The second subset is the testing data set, which is used to adjust the weights and biases to reduce the difference between the outputs of the model and the target with monitoring of the error in the training process [26]. It also used to choose the number of hidden units in the neural network, which can avoid overfitting. The third subset is the validation data set, which is used to check the accuracy of the fitted model [27]. The validation data set is not used in the training process.

In the training data set, the input variables are those eighth variables that organized in the Taguchi orthogonal array. The input variables value of the validation and testing data set are generated by pseudo-random numbers in the feasible range for each variable.

3.5. Multi-objective Optimization

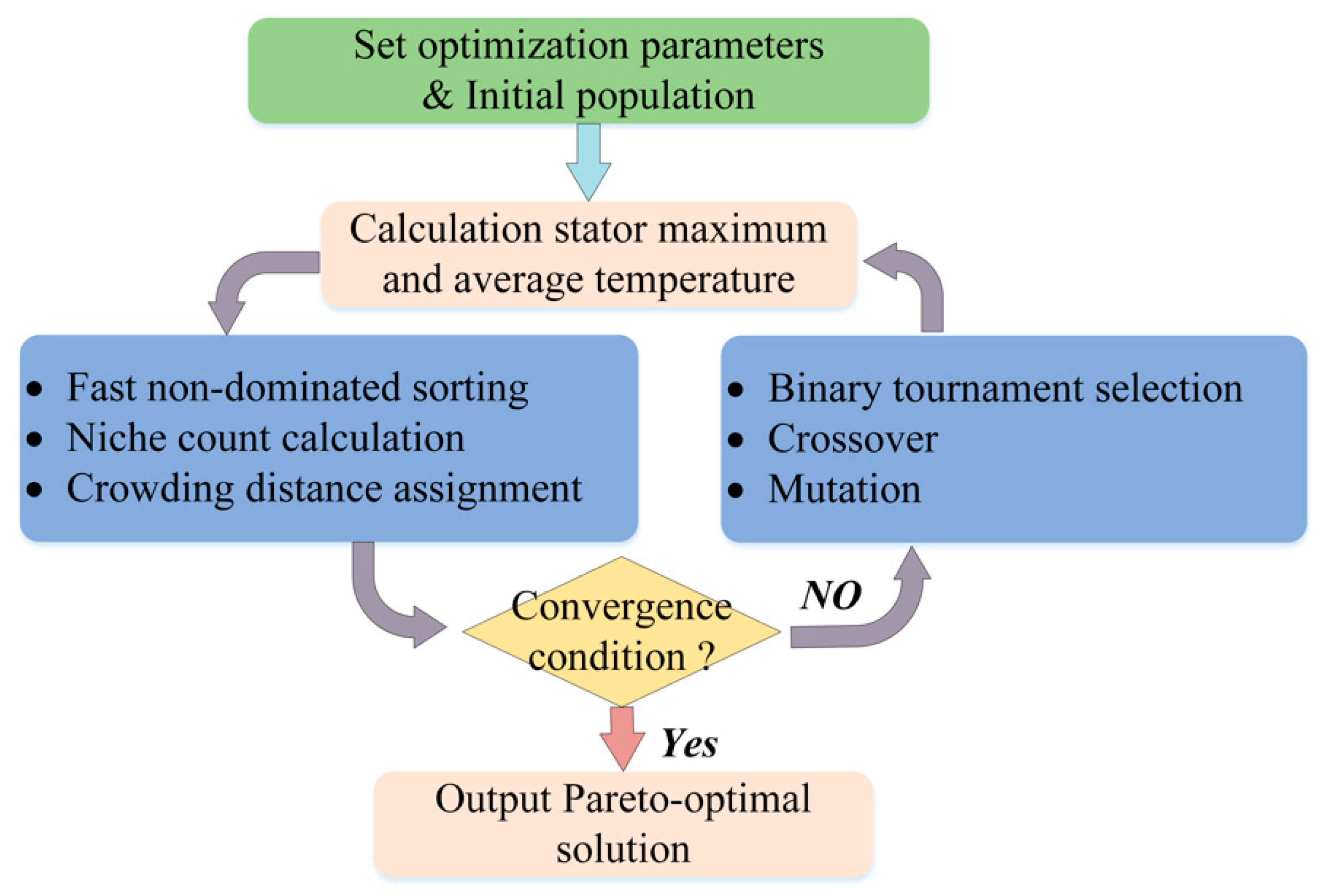
To minimize simultaneously the maximum temperature and the average temperature of the generator stator, the fast non-dominated sorting genetic algorithm (NSGA-Ⅱ) [28,29] was applied to the neural network fitted function (7). Its features are fast non-dominated sorting, crowding distance assignment, a crowded comparison operator, and the elitism strategy. Figure 5 presents the optimization process. Fast non-dominated sorting reduces the high computational complexity and the crowd distance approach is used to obtain a more uniform spread of solutions on the best-known Pareto front without using fitness sharing.

In this study, as mentioned, the optimization variables are the geometric parameters and the optimization objectives are the maximum and average temperature. The optimization objective function is the trained shallow neural network model; refer to (7) and (8). And the mathematical expression of optimization can be expressed as followed

$$\begin{array}{ll}Minimize& T(X),X\in D\subset R^8\\ subjectto& T_{\mathit{Avg}}(X)\le T_{\mathit{Max}}(X)\end{array}$$

(10)

where D is eight dimension feasible design region; R⁸ is eight dimension space; T(X) is the objective functions matrix that fitted by neural network; T_Avg(X) and T_Max(X) are average and maximum temperatures objective function, respectively; and X = [x¹, x², …, x⁸]^T is optimization variables.

4. Results

4.1. Finite Element Simulation Result

Through 3-D multi-physical field collaborative model, the temperatures of three subsets are simulated and the results of the training subset are shown in

Table 4. Simulation results of training data set.

Experiments	Average Temperature	Maximum Temperature	Experiments	Average Temperature	Maximum Temperature
1	85.5	114.7	15	95.1	137.1
2	91.8	125.9	16	91.3	133.1
3	98.9	134.2	17	83.2	116.1
4	81.6	112.8	18	80.4	113.9
5	86.1	120.5	19	94.8	129.0
6	96.1	137.2	20	90.2	117.1
7	77.8	109.6	21	93.1	121.4
8	82.4	116.4	22	79.7	105.1
9	87.9	125.1	23	76.9	111.1
10	83.3	117.5	24	83.4	122.1
11	87.3	124.7	25	89.9	119.5
12	87.5	126.2	26	80.1	117.7
13	97.4	126.0	27	98.3	134.1
14	92.1	128.7	-	-	-

, and other subset results are in

Table A2. Simulation results of the data set.

Experiments	A	B	C	D	E	F	G	Vent Duct Numbers	Average Temperature (°C)	Maximum Temperature (°C)
1	1202	40	11	8	22	117	93	23	94.6	126.2
2	1129	54	9	9	25	114	92	17	86.8	119.3
3	1209	57	10	12	22	118	83	17	80.3	112.6
4	1077	60	8	9	24	119	81	15	84.4	114.4
5	1002	41	8	9	25	118	85	20	91.3	123.1
6	1160	49	12	8	23	116	98	18	94.3	126.9
7	1084	52	9	9	24	114	99	17	84.2	115.2
8	1284	54	10	9	24	118	94	19	93.6	127.6
9	1272	55	12	8	22	114	95	18	88.1	120.2
10	1118	53	8	10	24	119	84	17	81.1	111.7

and

Table A3. Simulation results of validation data set.

Experiments	A	B	C	D	E	F	G	Vent Duct Numbers	Average Temperature (°C)	Maximum Temperature (°C)
1	1128	42	10	8	25	114	99	21	92.4	122.6
2	1241	55	11	11	25	118	80	18	88.9	127.3
3	1062	55	8	11	26	116	84	16	92.9	125.8
4	1197	42	9	11	23	115	87	23	86.7	119.1
5	1087	60	12	8	23	115	98	14	89.0	121.3
6	1206	44	12	8	24	114	90	21	88.6	121.5
7	1092	45	10	9	26	118	84	19	99.8	135.3
8	1283	50	10	10	23	113	86	21	85.8	119.0
9	1071	46	12	12	26	115	98	18	83.7	122.4
10	1210	55	12	12	24	113	80	17	89.0	120.4

.

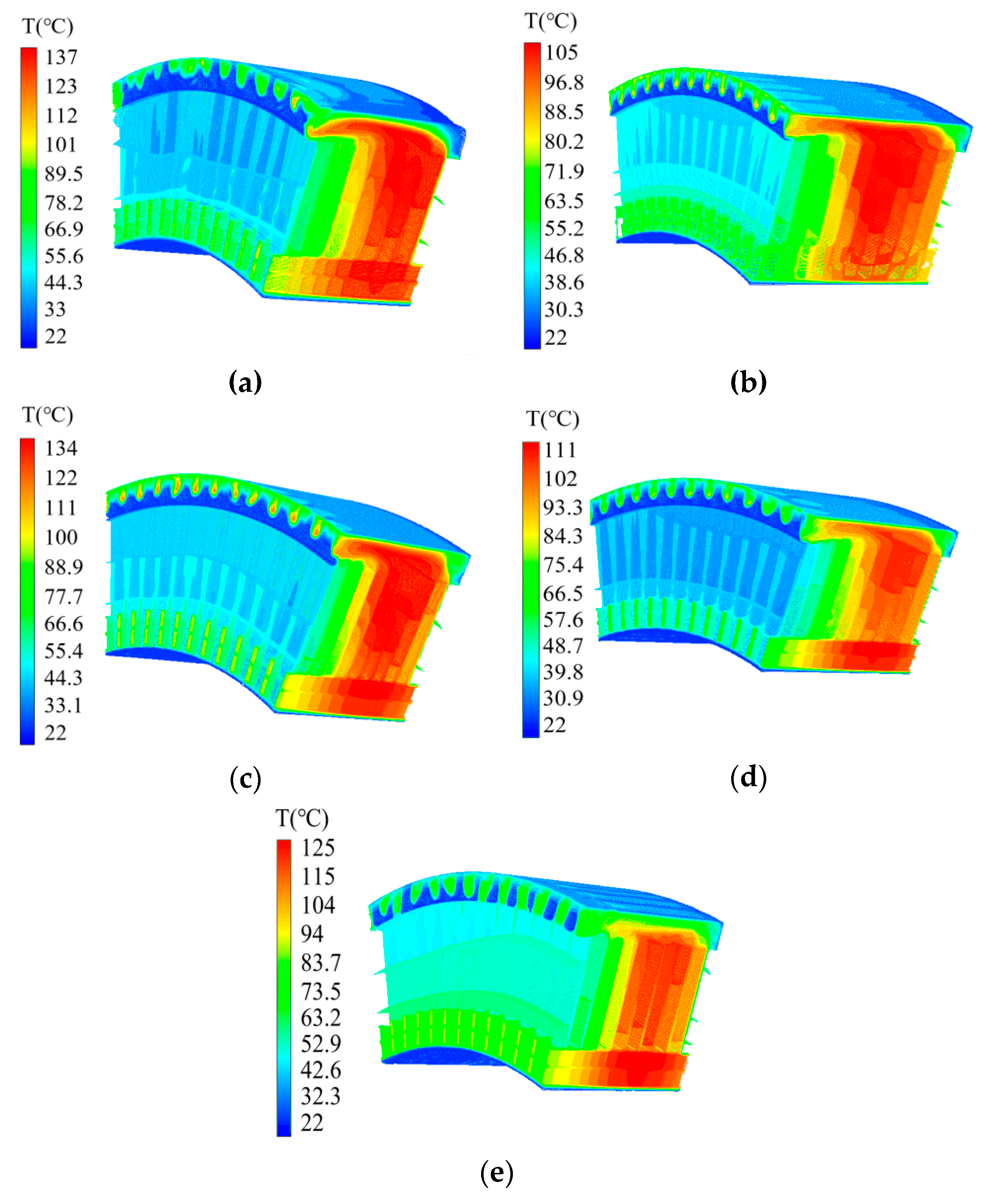
In the results, the maximum temperatures are in the range 105.1 °C to 137.2 °C and the mean value is 121.8 °C; the highest value of the average temperature is 99.8 °C and the lowest is 76.9 °C with a mean of 87.5 °C. For analysis, five experiments of training subset, including the highest and lowest maximum temperature, the highest and lowest average temperature, and the original temperature, are selected and their temperature contours are shown in Figure 6. Compared with the end of the stator where ventilate well, the temperature of the center part is higher. Meanwhile, since the copper loss difference of those experiments is little, the volume of the iron segments has a significant effect on the temperature, which the larger the volume, the lower the temperature.

4.2. Accuracy Assessment

To validate the accuracy of the fitted model, the validation set was used to check the error between the results of the fitted function and thee simulation. In Figure 7, the temperatures of the calculated and simulated, including the average and maximum temperature of the fitted model and that of the finite element simulation model, are compared (detailed errors in

Table A4. Errors between the neural network model and simulation results.

-	1	2	3	4	5	6	7	8	9	10	Mean Value
Average Temperature Error (%)	4.05	2.02	2.4	0.68	2.56	0.75	4.96	0.41	2.48	3.82	2.41
Maximum Temperature Error (%)	2.19	0.70	4.2	3.66	2.02	0.52	4.45	2.7	0.28	4.71	2.54

). All error values were below 5%. And the mean error values of the average and the maximum temperatures were 2.41% and 2.54% respectively. From the results above, the accuracy of the fitted model sufficed for industrial application.

4.3. Optimization Result

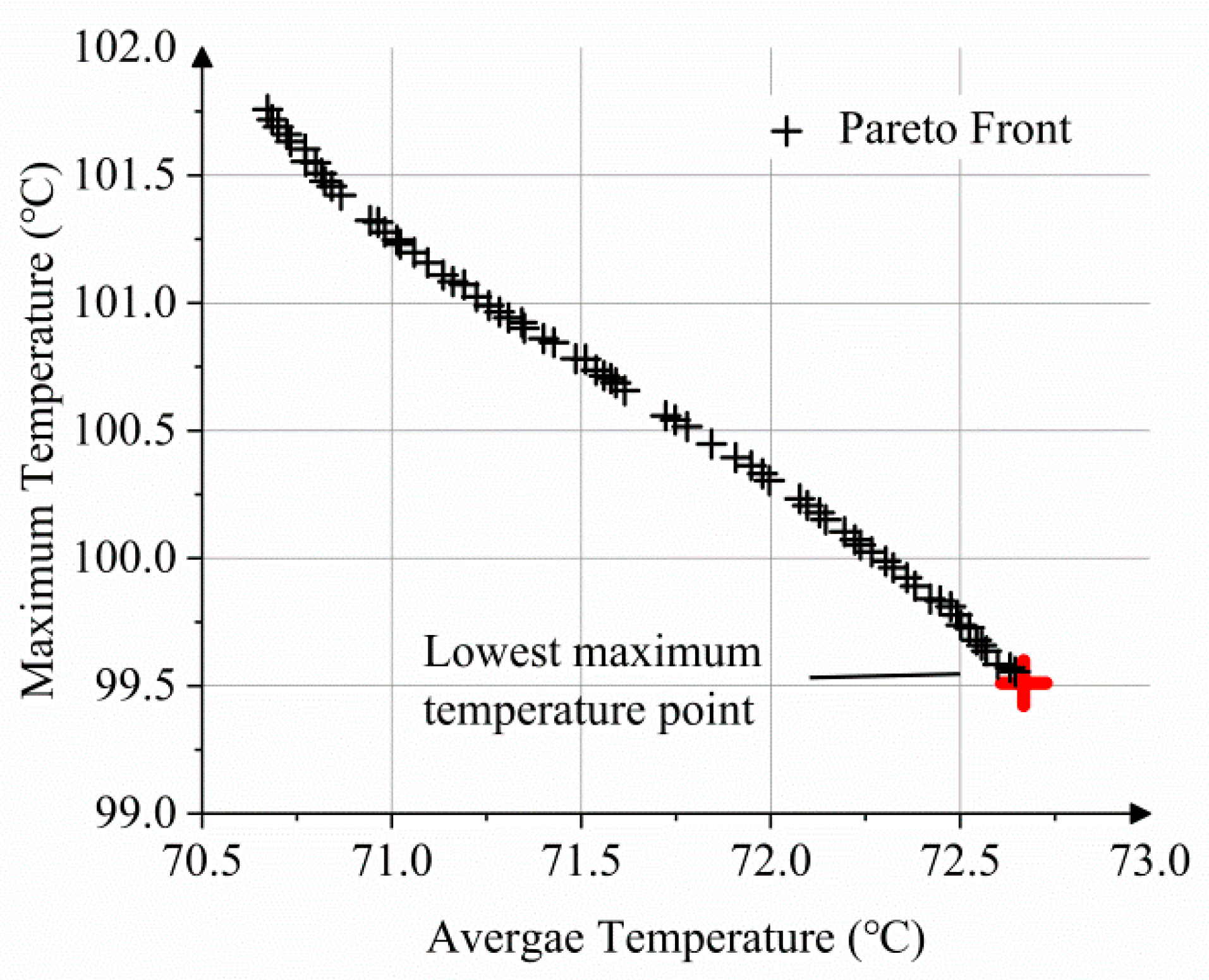
As the result of multi-objective optimization based on GA, Pareto front is a set of solutions that are non-dominated with respect to each other. It can be examined for trade-off and the choice of a solution according the actual needs of engineering. In Figure 8, the Pareto front is shown, wherein the mean value of the optimized average temperature is 71.7 °C and that of the optimized maximum temperature is 100.6 °C. There both lower than the corresponding value of the three-subset data. Compared with the original values that before the optimization, the optimized maximum temperature reduced by up to 27.5 °C and the average temperature reduced by up to 20.1 °C.

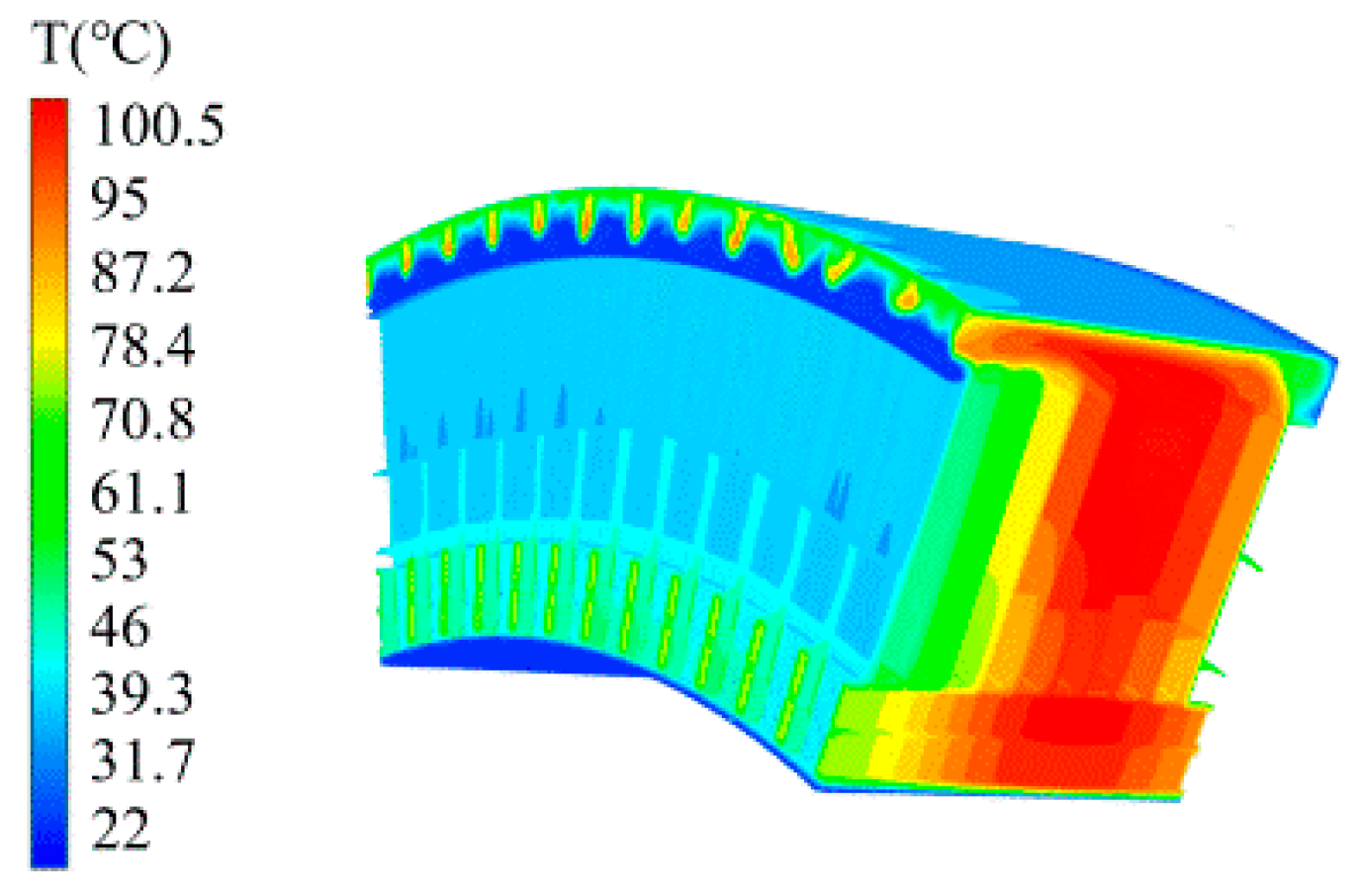
Due to the difficulty of the experiment, the finite element simulation method was used to verify the calculation results. In this paper, the lowest maximum temperature point was selected and its finite element simulation result is shown in Figure 9. The simulation result was compared with the calculated results with the average temperature error of 2.5% and the maximum temperature error of 0.99%, both of which lower than 5%.

5. Discussion

In this study, a multi-objective optimization method for multi-physics fields of a generator based on surrogate model is proposed. The geometric structure of the generator stator was optimized under the consideration of electromagnetic field and thermal field to reduce the maximum and average temperature of the stator. In the optimization process, the use of simulation calculations in the iterative process is avoided by building surrogate model of the optimization objective function, which greatly reduces the cost of expensive calculations. The different methods included in the study were Taguchi orthogonal array, shallow neural network, and multi-objective genetic algorithm.

Taguchi orthogonal array provides the sampling plan for training the initial model of the neural network. The Taguchi orthogonal array distributes the sampling points uniformly and interconnectedly across the sampling space due to the orthogonal characteristic of the factors, which is advantageous for neural networks that learn using only input and output data. In the process of sampling using the Taguchi orthogonal array, the most critical aspect is the choice of factors and their level values. The number of factors determines the dimensionality of the target system, while their level values affect the distribution of sampling points in the design space. The seven factors in this paper are selected from the factors that affect the heating and cooling effect of the stator, and to be more accurate, the significance of each candidate factor for the optimization objectives and the correlation between the factors can be analyzed, which is useful for further optimization, although it also increases the expense in the acquisition of experimental data. As for the level values of each factor, there is no doubt that these values should be reasonable, and the maximum and minimum values determine the upper and lower bounds of each factor in the optimization process. In this paper, the selection of the upper and lower bounds for each factor is based on the empirical range of values used in motor design, and Level 2 is the median value of this interval.

For the calculations of the groups of experiments in the Taguchi orthogonal array, this study uses the three-dimensional finite element calculation method of magnetic thermal coupling. Many assumptions and model simplifications were made in the calculations considering the current computational power. In the electromagnetic calculation process, the power and voltage were set to constant values for the control variables to calculate the losses of the machine at steady state. The variations in the stator geometry only have an effect on the current density of each part. Actually, the research of transient electromagnetic state with time and the machine under different operating conditions will be more relevant for practical applications. Of course, the study of current density as the main cause of electrical machine losses is still relevant for practical engineering purposes. In the temperature field of the motor, the assumption of no heat transfer to the axial center surface of the stator applies only to the steady-state, where the inflow and outflow of heat to and from that surface are equivalent. For the heat transfer between the stator and the rotor, the influence of the positional change of the salient pole rotor over time on the cooling air flow can be accurately calculated in the transient study. During the simulation calculations, it is feasible to make certain assumptions about the boundary conditions depending on the purpose of the study.

What is also important to consider in the optimization process based on Taguchi orthogonal array and neural network is the process of establishing the surrogate model, the selection of its parameters, and the training method, which largely determines the quality of the subsequent optimization. For example, overfitting problems due to small amounts of data can be controlled or prevented by selecting an appropriate number of network layers and number of neurons to limit the fitting ability of the neural network. The Bayesian method was also used to prevent overfitting during the training of neural networks.

6. Conclusion

This paper proposed a novel method to optimize the structure of the stator of a synchronous generator based on Taguchi method and neural network. And a multi-objective genetic algorithm was employed to reduce the maximum and average temperature of stator. The important contributions of the proposed method are summarized as follows:

• A novel continuous optimization objective function based on a shallow neural network was constructed, which directly reveals the relationship between the geometric parameters of interest and the operating temperatures of stator. It can be accurately used as a surrogate model to finite element model to reduce the computational burden of simulation calculations in the optimization process to a great extent.
• This paper employed Taguchi orthogonal array to organize data bridging the geometric variables and temperature objectives, which require few amount of the sampling point. It is beneficial for time-consuming and expensive experiments in industrial optimization.
• The multi-objective optimization problem of the electrical machines was solved, and the result is a set of solutions that can be examined for the trade-off and the choice of a solution according the actual needs of engineering.

In future research, more flexibility in the selection of performance and independent variables of the electrical machine can be made, not only in steady-state operation conditions, but rather extends to transient systems to make the calculations more relevant to engineering reality. At the same time, sampling points more in line with system characteristics can be added to collect design space information in the form of non-uniform sampling. In terms of the development of surrogate models, their fitting accuracy and fit models need to be further developed to evaluate the solution through a more suitable model.