Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation
Abstract
:1. Introduction
- Proposition of PCCOPF formulation by using QCQP with the matpower environment.
- Proposition of CCCOPF formulation in the matpower environment that ensures the same voltage magnitude at all nodes in the system (pre- and post-contingency).
2. Problem Formulation
2.1. Objective Function
2.2. Equality Constraints
2.3. Inequality Constraints
2.4. Contingency Constrained Optimal Power Flow Problem
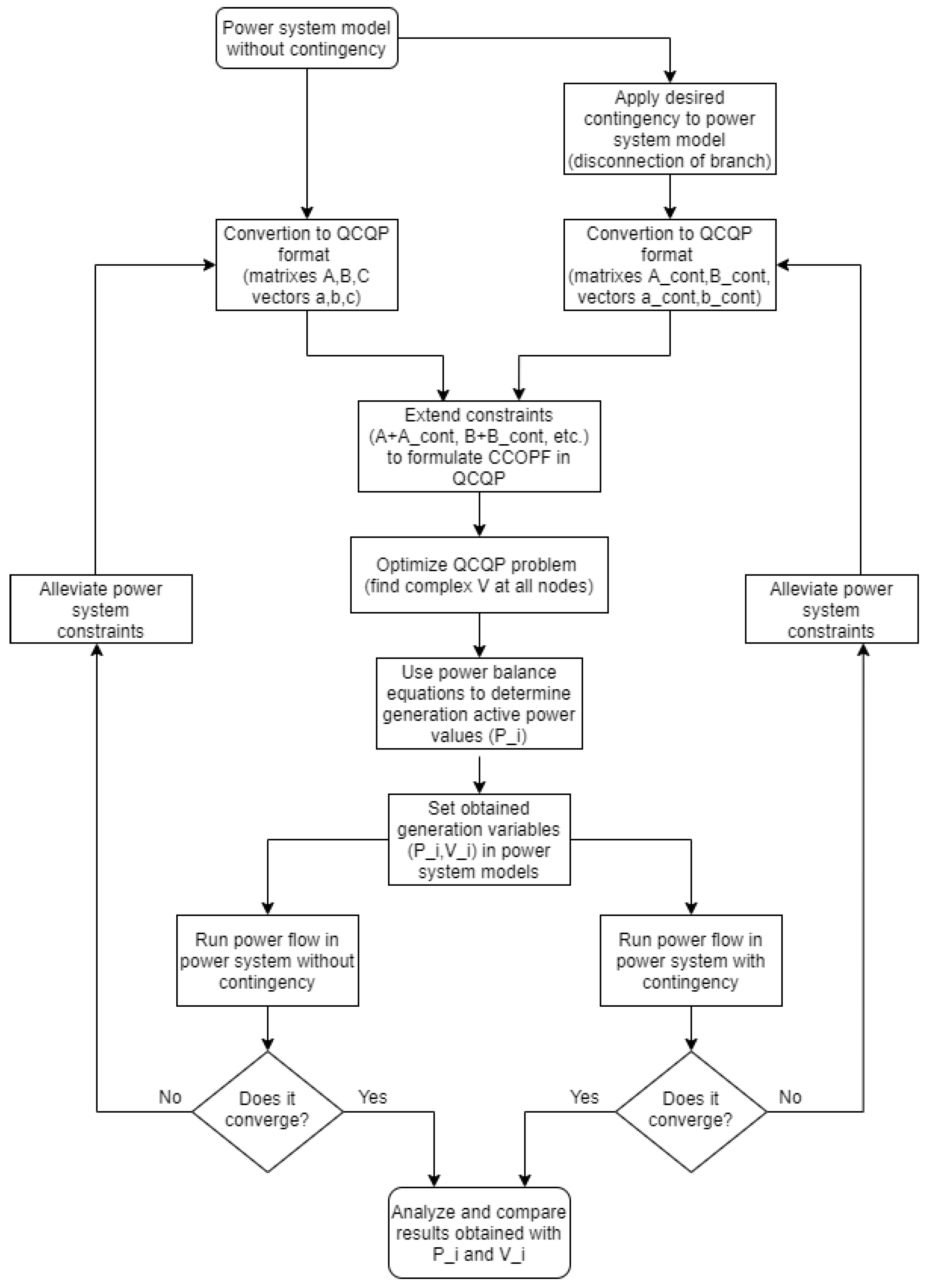
3. Strategies for Solving Contingency Constrained Optimal Power Flow Problems
3.1. QCQP Formulation of Preventive CCOPF Problem
- The state variable that is iterated to find the solution is, for every node, the complex voltage at the node.
- As the injected active power can be expressed as a function of the voltage angle and voltage magnitude squared. High order terms of Equations (1) and (2) are omitted to keep a quadratic format in the objective function:
- The operation cost function (13) could also be used to represent the cost of Photovoltaic generation by changing the coefficient sign to negative.
- Loadability line constraints are rewritten in terms of current square. In doing so, all constraints are quadratic as well.
- A contingency in the test network is carried out (e.g., disconnection of specific branch)
- The equivalent QCQP instance of the previous edited (under contingency) power system is calculated ().
- The original power system (without contingencies) is transformed into a QCQP instance.
- In the QCQP instance of the original power system (), equality constraints matrix and vector of the power system under contingency () are indexed to the original ones ().
- This final system is optimized and, due to its constraints, the resulting dispatch allows the system to work with their variables between limits in both cases: with and without contingencies.
3.2. Optimal Power Flow of Extended Network
4. Results and Comparison
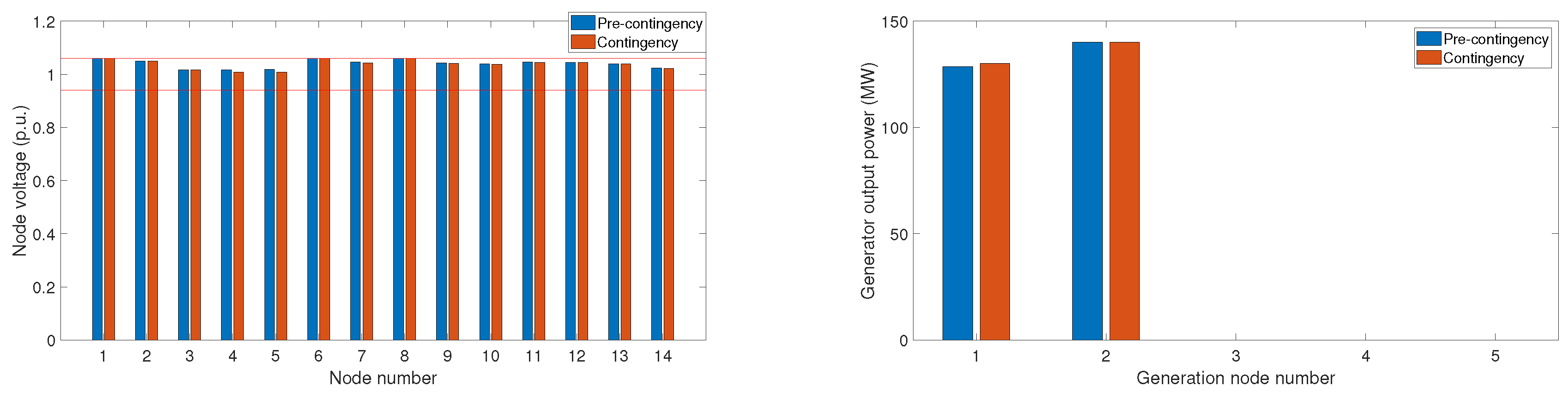
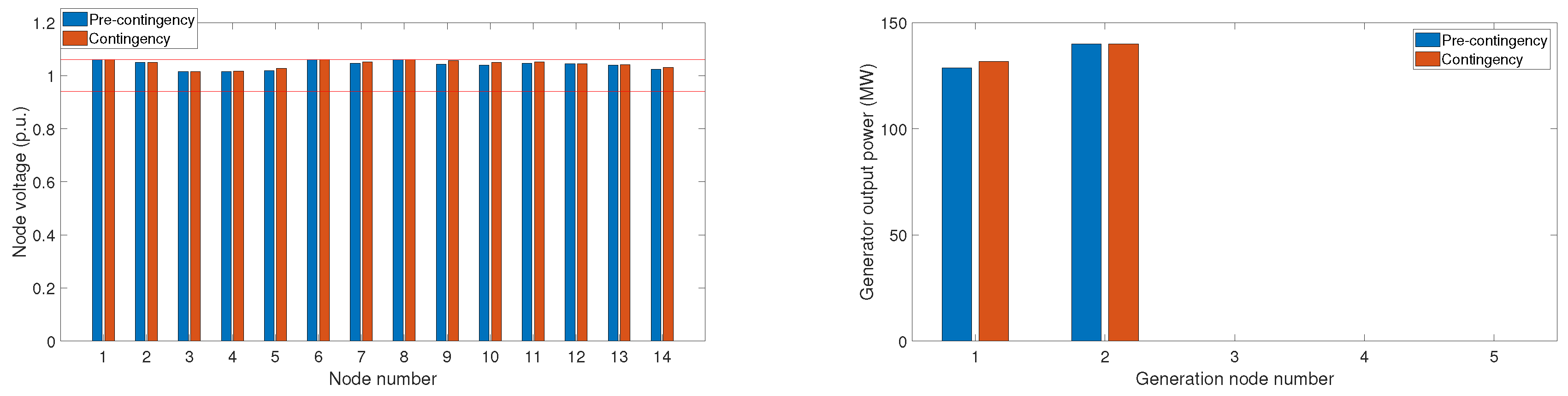
4.1. Quadratically Constrained Quadratic Programming Formulation
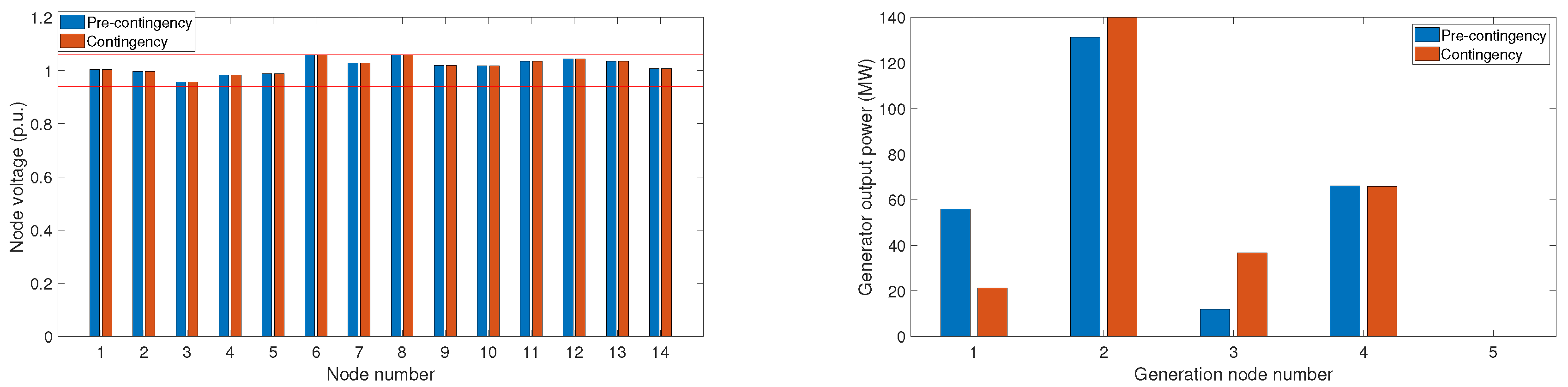
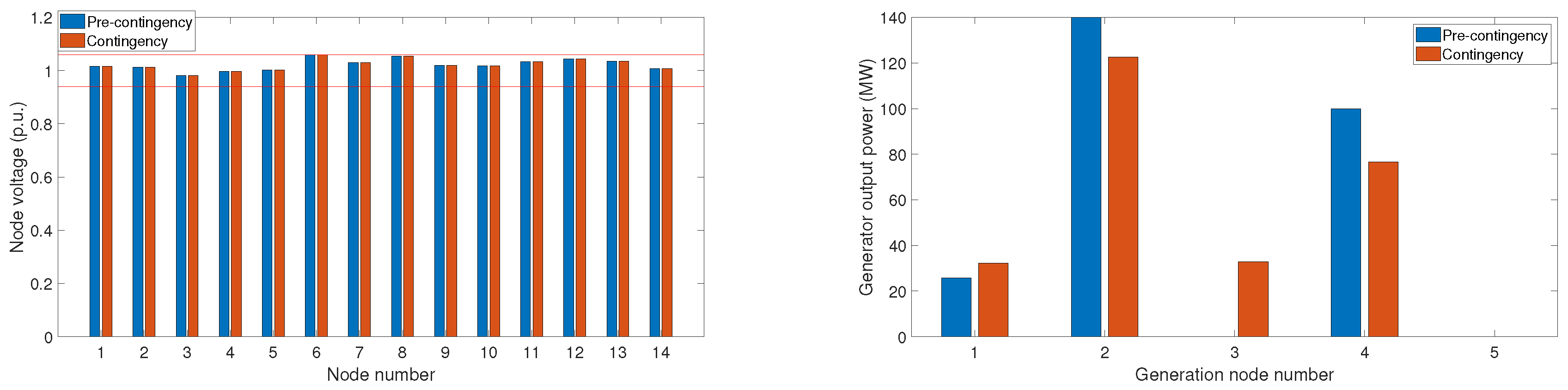
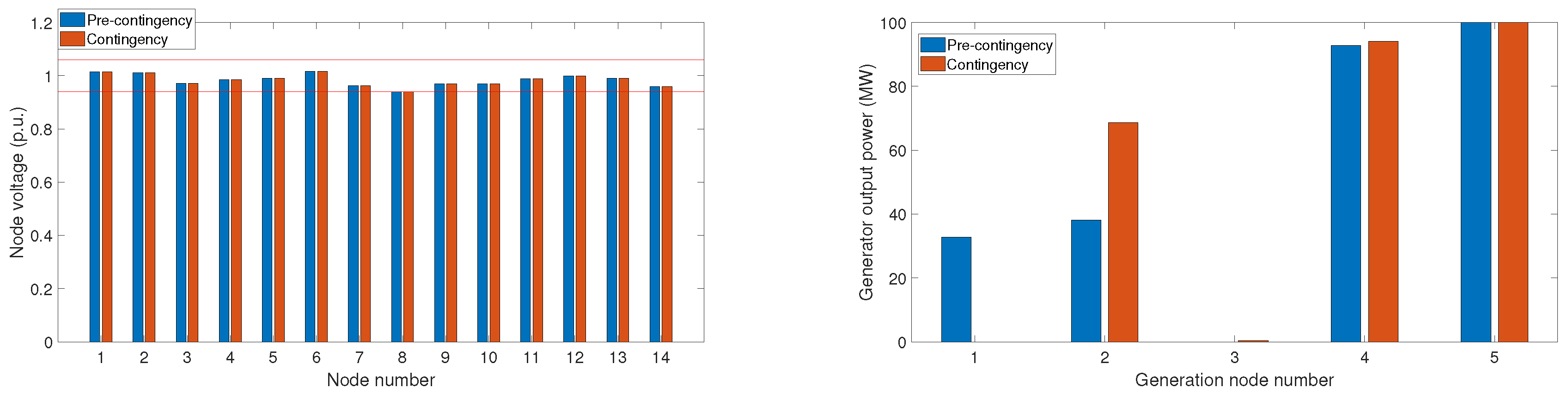
4.1.1. Thermal Generation Only
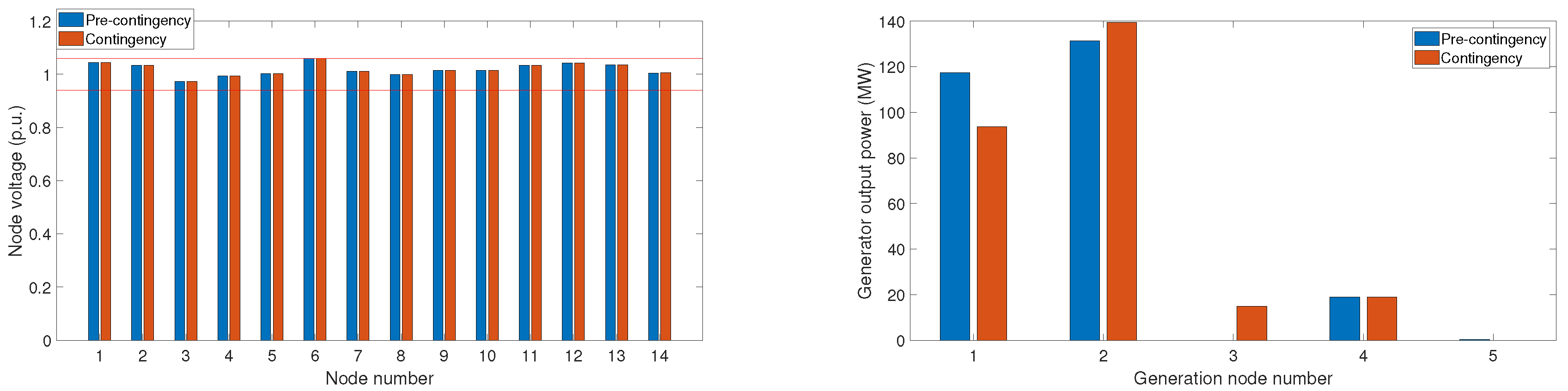
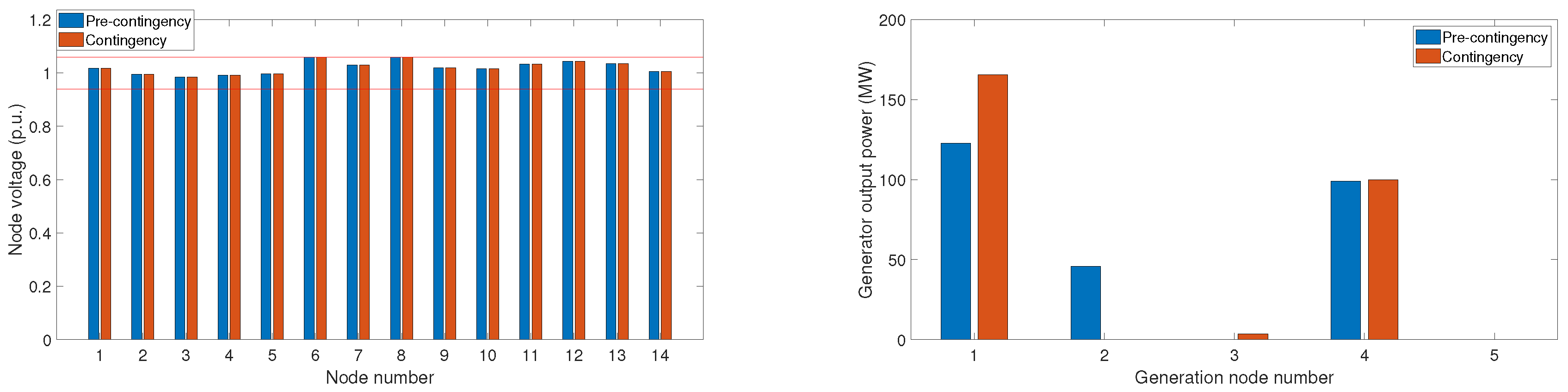
4.1.2. Thermal and Photovoltaic Generation
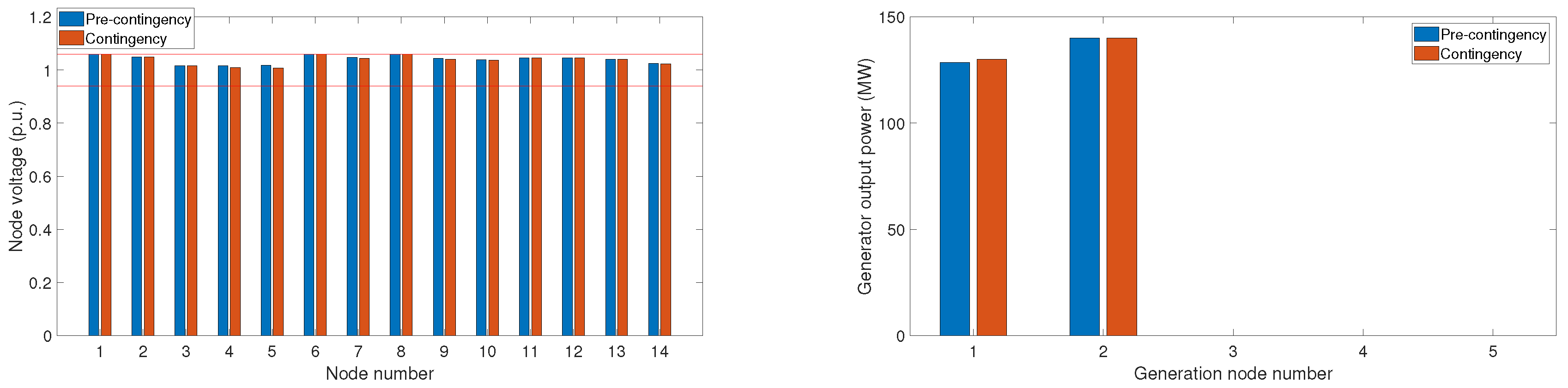
4.2. Optimal Power Flow of the Extended Network
4.2.1. Thermal Generation Only
4.2.2. Thermal and Photovoltaic Generation
4.3. Results Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Bus Number | [MW] | [MW] | [p.u.] | [p.u.] |
|---|---|---|---|---|
| 1 | 0 | 0 | 1.06 | 0.94 |
| 2 | 21.7 | 12.7 | 1.06 | 0.94 |
| 3 | 94.2 | 19 | 1.06 | 0.94 |
| 4 | 47.8 | −3.9 | 1.06 | 0.94 |
| 5 | 7.6 | 1.6 | 1.06 | 0.94 |
| 6 | 11.2 | 7.5 | 1.06 | 0.94 |
| 7 | 0 | 0 | 1.06 | 0.94 |
| 8 | 0 | 0 | 1.06 | 0.94 |
| 9 | 29.5 | 16.6 | 1.06 | 0.94 |
| 10 | 9 | 5.8 | 1.06 | 0.94 |
| 11 | 3.5 | 1.8 | 1.06 | 0.94 |
| 12 | 6.1 | 1.6 | 1.06 | 0.94 |
| 13 | 13.5 | 5.8 | 1.06 | 0.94 |
| 14 | 14.9 | 5 | 1.06 | 0.94 |
| Bus Number | [MVAr] | [MVAr] | [MW] | [MW] | [] | [] | [$] |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 0 | 332.4 | 0 | 0 | 20 | 0 |
| 2 | 50 | −40 | 140 | 0 | 0 | 20 | 0 |
| 3 | 40 | 0 | 100 | 0 | 0 | 40 | 0 |
| 6 | 24 | −6 | 100 | 0 | 0 | 40 | 0 |
| 8 | 24 | −6 | 100 | 0 | 0 | 40 | 0 |
| Branch Number | ||
|---|---|---|
| 1 | 1 | 2 |
| 2 | 1 | 5 |
| 3 | 2 | 3 |
| 4 | 2 | 4 |
| 5 | 2 | 5 |
| 6 | 3 | 4 |
| 7 | 4 | 5 |
| 8 | 4 | 7 |
| 9 | 4 | 9 |
| 10 | 5 | 6 |
| 11 | 6 | 11 |
| 12 | 6 | 12 |
| 13 | 6 | 13 |
| 14 | 7 | 8 |
| 15 | 7 | 9 |
| 16 | 9 | 10 |
| 17 | 9 | 14 |
| 18 | 10 | 11 |
| 19 | 12 | 13 |
| 20 | 13 | 14 |
References
- Capitanescu, F.; Ramos, J.M.; Panciatici, P.; Kirschen, D.; Marcolini, A.M.; Platbrood, L.; Wehenkel, L. State of the art, challenges, and future trends in security constrained optimal power flow. Electr. Power Syst. Res. 2019, 81, 1731–1741. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Sun, W. An automated transient stability constrained optimal power flow based on trajectory sensitivity analysis. IEEE Trans. Power Syst. 2016, 32, 590–599. [Google Scholar] [CrossRef]
- Nguyen-Duc, H.; Tran-Hoai, L.; Ngoc, D.V. A novel approach to solve transient stability constrained optimal power flow problems. Turkish J. Electr. Eng. Comput. Sci. 2017, 25, 4696–4705. [Google Scholar] [CrossRef]
- Hinojosa, V.H. An improved corrective security constrained OPF for meshed AC/DC grids with multi-terminal VSC-HVDC. Energies 2020, 13, 516. [Google Scholar] [CrossRef] [Green Version]
- Stott, B.; Alsaç, O. Optimal power flow: Basic requirements for real-life problems and their solutions. In Proceedings of the SEPOPE XII Symposium, Rio de Janeiro, Brazil, 20–23 May 2012. [Google Scholar]
- Gunda, J.; Djokic, S.; Langella, R.; Testa, A. On convergence of conventional and meta-heuristic methods for security-constrained OPF analysis. In Proceedings of the 31st Annual ACM Symposium on Applied Computing, Pisa, Italy, 3–6 April 2016; pp. 109–111. [Google Scholar]
- Karbalaei, F.; Shahbazi, H.; Mahdavi, M. A new method for solving preventive security-constrained optimal power flow based on linear network compression. Int. J. Electr. Power Energy Syst. 2018, 96, 23–29. [Google Scholar] [CrossRef]
- Cao, J.; Du, W.; Wang, H.F. An improved corrective security constrained OPF for meshed AC/DC grids with multi-terminal VSC-HVDC. IEEE Trans. Power Syst. 2015, 31, 485–495. [Google Scholar] [CrossRef]
- Capitanescu, F.; Wehenkel, L. A new iterative approach to the corrective security-constrained optimal power flow problem. IEEE Trans. Power Syst. 2008, 23, 1533–1541. [Google Scholar] [CrossRef] [Green Version]
- Gunda, J.; Djokic, S.; Langella, R.; Testa, A. Comparison of conventional and meta-heuristic methods for security-constrained OPF analysis. In Proceedings of the AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015; pp. 1–6. [Google Scholar]
- Fang, D.; Gunda, J.; Djokic, S.Z.; Vaccaro, A. Security-and time-constrained OPF applications. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Kaur, M.; Dixit, A. Newton’s Method approach for Security Constrained OPF using TCSC. In Proceedings of the IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar]
- Wu, X.; Zhou, Z.; Liu, G.; Qi, W.; Xie, Z. Preventive security-constrained optimal power flow considering UPFC control modes. Energies 2017, 10, 1199. [Google Scholar] [CrossRef] [Green Version]
- Nycander, E.; Söder, L. Comparison of stochastic and deterministic security constrained optimal power flow under varying outage probabilities. In Proceedings of the IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Gao, X.; Lu, X.; Chan, K.W.; Hu, J.; Xia, S.; Xu, D. Distributed Coordinated Management for Multiple Distributed Energy Resources Optimal Operation with Security Constrains. In Proceedings of the IEEE Power and Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019; pp. 1–5. [Google Scholar]
- Cao, J.; Liu, Y.; Ge, Y.; Cai, H.; Zhou, B.W. Enhanced corrective security constrained OPF with hybrid energy storage systems. In Proceedings of the UKACC 11th International Conference on Control (CONTROL) IEEE, Belfast, UK, 31 August–2 September 2016; pp. 1–7. [Google Scholar]
- Nasr, M.A.; Nikkhah, S.; Gharehpetian, G.B.; Nasr-Azadani, E.; Hosseinian, S.H. A multi-objective voltage stability constrained energy management system for isolated microgrids. Int. J. Electr. Power Energy Syst. 2020, 117, 105646. [Google Scholar] [CrossRef]
- Alzalg, B.; Anghel, C.; Gan, W.; Huang, Q.; Rahman, M.; Shum, A.; Wu, C.W. Contingency constrained optimal power flow solutions in complex network power grids. In Proceedings of the IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; pp. 1636–1639. [Google Scholar]
- Wang, Q.; McCalley, J.D.; Zheng, T.; Litvinov, E. A computational strategy to solve preventive risk-based security-constrained OPF. IEEE Trans. Power Syst. 2012, 28, 1666–1675. [Google Scholar] [CrossRef]
- Van Acker, T.; Van Hertem, D. Linear representation of preventive and corrective actions in OPF models. In Proceedings of the Young Researchers Symposium, Eindhoven, The Netherland, 12–13 May 2016. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.D.; Murillo-Sánchez, C.E. Matpower User’s Manual, Version 7.0. 2019. Available online: https://matpower.org/docs/MATPOWER-manual-7.0.pdf (accessed on 2 May 2020).
- Bernal, J.; Neira, J.; Rivera, S. Mathematical Uncertainty Cost Functions for Controllable Photo-Voltaic Generators considering Uniform Distributions. WSEAS Trans. Math. 2019, 18, 137–142. [Google Scholar]
- Gaing, Z.; Lin, C. Contingency-Constrained Optimal Power Flow Using Simplex-Based Chaotic-PSO Algorithm. In Applied Computational Intelligence and Soft Computing; Hindawi Publishing Corporation: London, UK, 2011; p. 13. [Google Scholar]
- Low, S.H. Convex relaxation of optimal power flow—Part I: Formulations and equivalence. IEEE Trans. Control Netw. Syst. 2014, 1, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Josz, C.; Fliscounakis, S.; Maeght, J.; Panciatici, P. AC Power Flow Data in MATPOWER and QCQP Format: ITesla, RTE Snapshots, and PEGASE. arXiv 2016, arXiv:1603.01533. [Google Scholar]
- Vargas, A.; Saavedra, O.; Samper, M.; Rivera, S.; Rodriguez, R. Latin American Energy Markets: Investment Opportunities in Nonconventional Renewables. IEEE Power Energy Mag. 2011, 14, 38–47. [Google Scholar] [CrossRef]






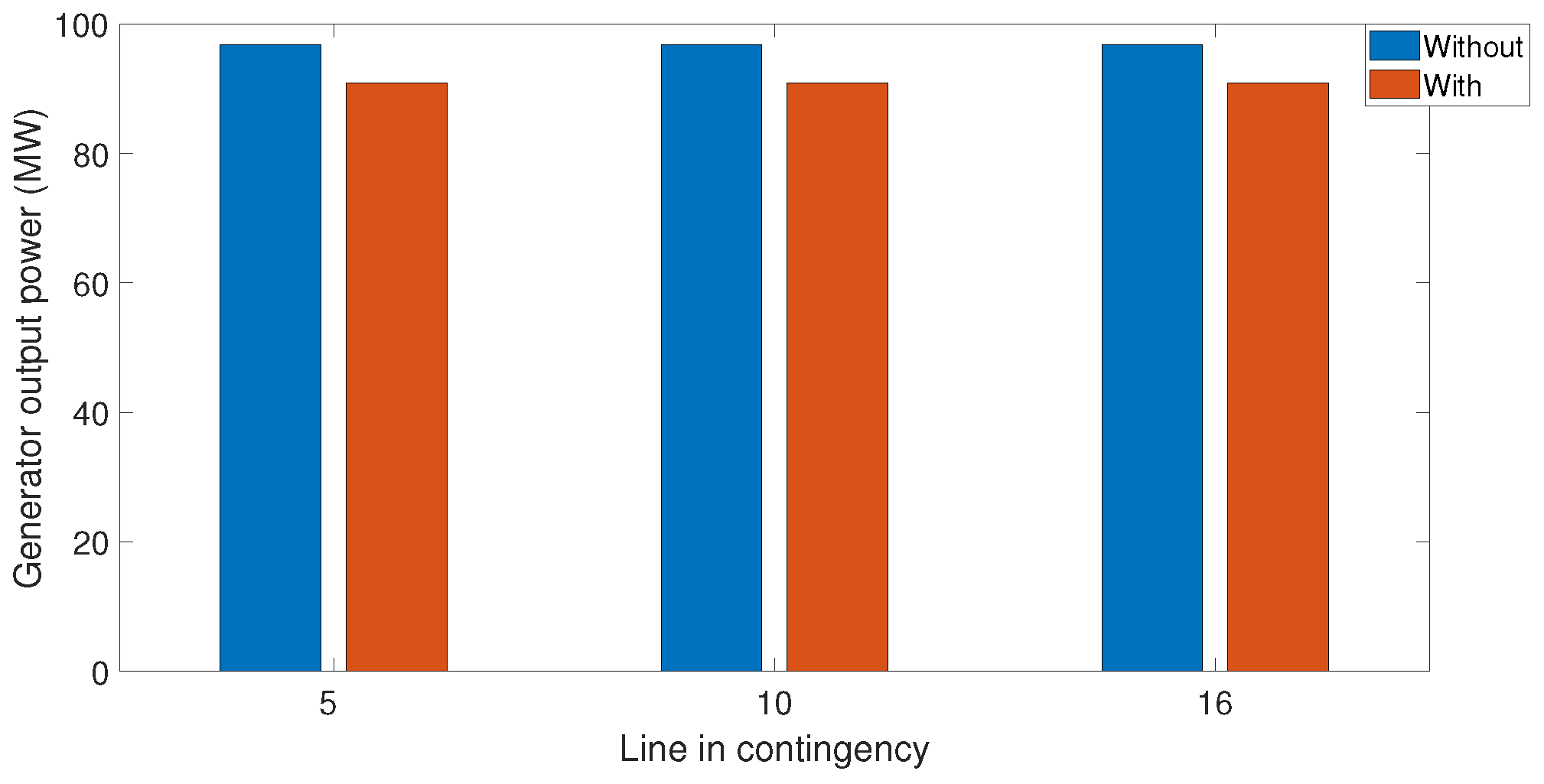


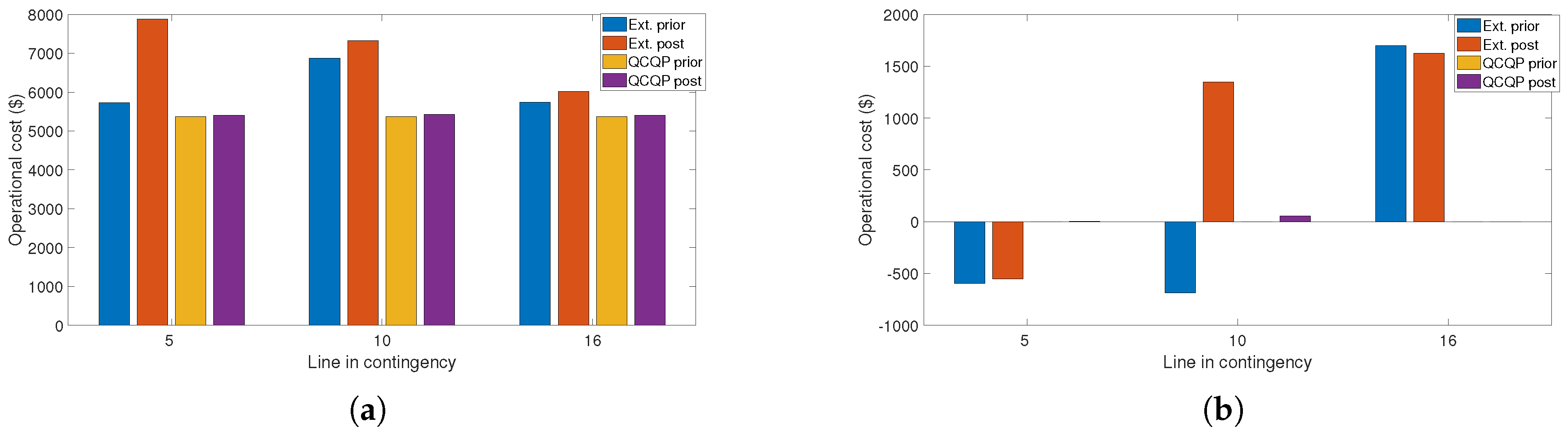
| Variable | Meaning |
|---|---|
| nVAR | Number of state variables (node voltages) |
| nEQ | Number of equality constraints |
| nINEQ | Number of inequality constraints |
| C, c | Objective function coefficient matrix, constant terms vector |
| A, a | Equality constraints coefficient matrix, constant terms vector |
| B, b | Inequality constraints coefficient matrix, constant terms vector |
| QCQP | Extended OPF | |||
|---|---|---|---|---|
| Execution Time (s) | Execution Time (s) | |||
| Contingency Located at | Thermal Generation Only | Thermal Generation + PV Generation and Battery Storage | Thermal Generation Only | Thermal Generation + PV Generation and Battery Storage |
| Branch 5 | 0.531975 | 1.253313 | 0.412515 | 0.507896 |
| Branch 10 | 0.501589 | 0.939263 | 0.435760 | 0.517546 |
| Branch 16 | 0.588455 | 0.938105 | 0.439151 | 0.469477 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon, L.M.; Bretas, A.S.; Rivera, S. Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation. Energies 2020, 13, 3310. https://doi.org/10.3390/en13133310
Leon LM, Bretas AS, Rivera S. Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation. Energies. 2020; 13(13):3310. https://doi.org/10.3390/en13133310
Chicago/Turabian StyleLeon, Luis M., Arturo S. Bretas, and Sergio Rivera. 2020. "Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation" Energies 13, no. 13: 3310. https://doi.org/10.3390/en13133310
APA StyleLeon, L. M., Bretas, A. S., & Rivera, S. (2020). Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation. Energies, 13(13), 3310. https://doi.org/10.3390/en13133310






