Towards a Real-Time Predictive Management Approach of Indoor Air Quality in Energy-Efficient Buildings
Abstract
1. Introduction
2. System Model and Methods
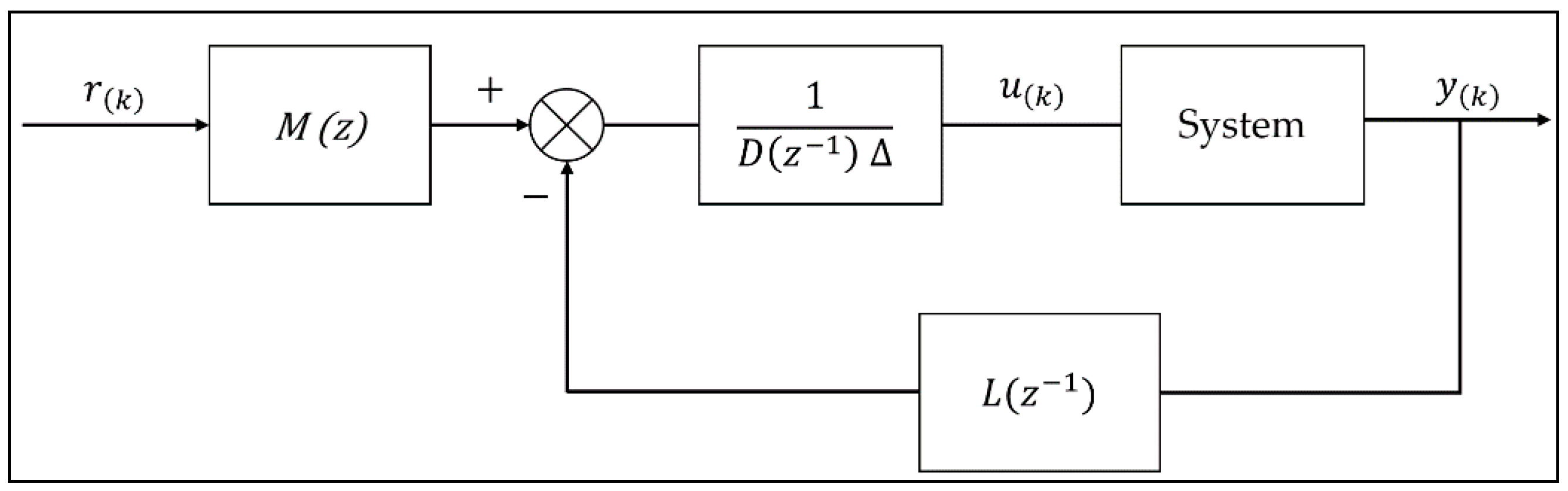
2.1. Ventilation System Modeling
2.2. Predictive Controllers Design
2.2.1. MPC Controller Design
2.2.2. GPC Controller Design
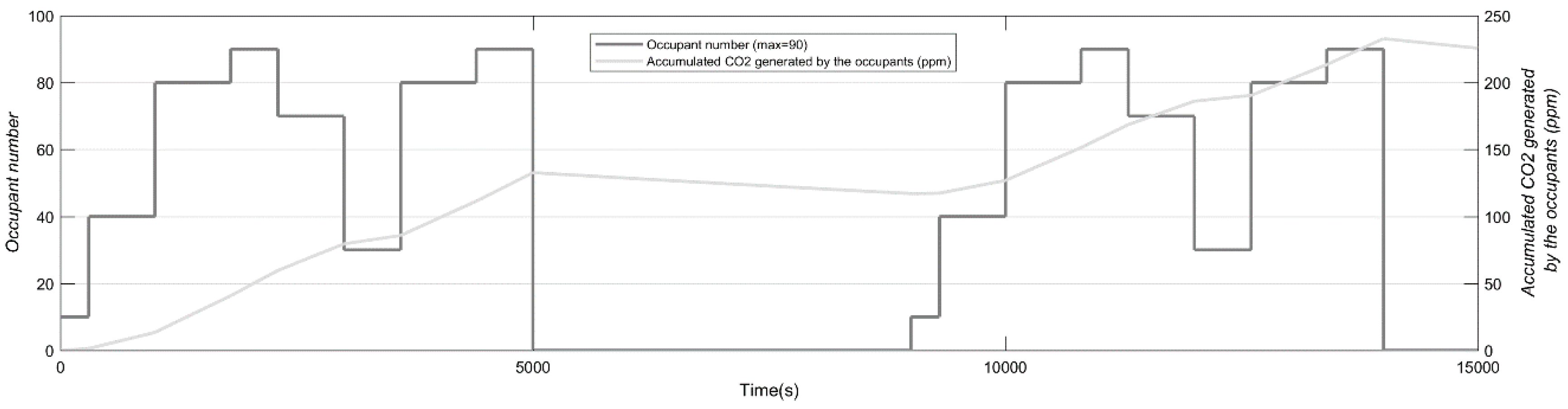
3. Results and Discussion
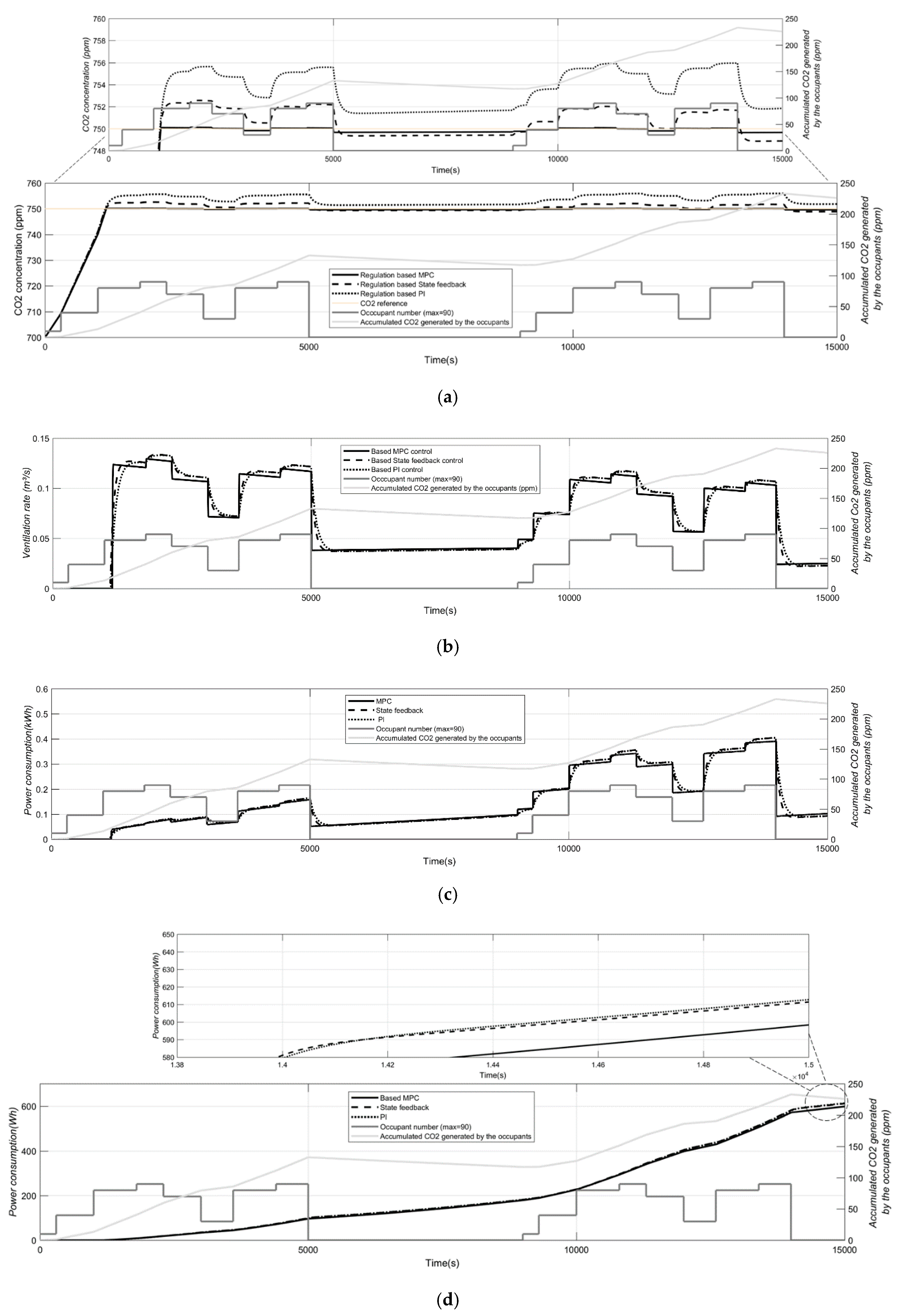
3.1. MPC vs. PI and SF
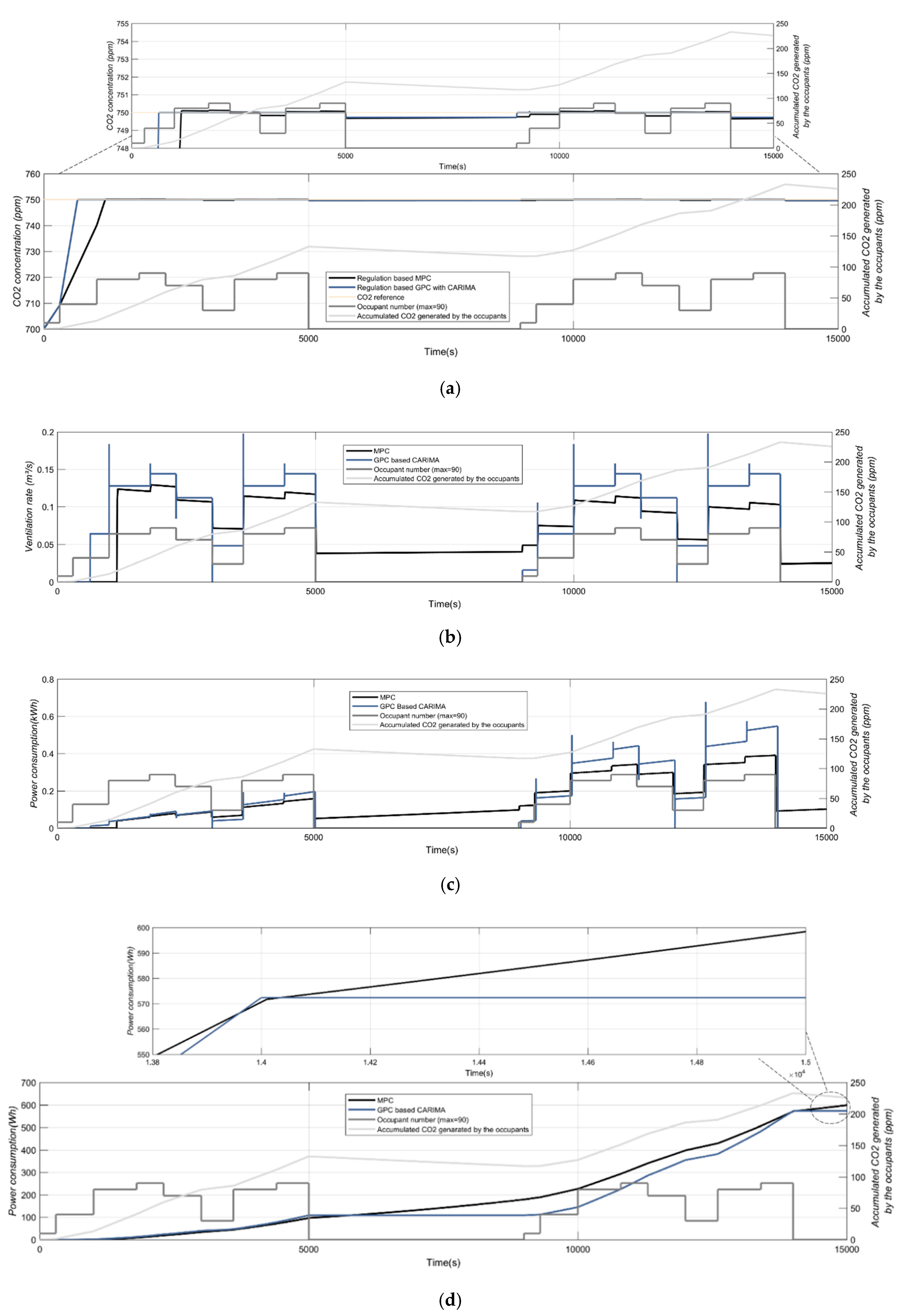
3.2. GPC vs. MPC Performance
4. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Del Mar-Castilla, M.; Álvarez, J.D.; Normey-Rico, J.E.; Rodríguez, F.; Berenguel, M. A multivariable nonlinear MPC control strategy for thermal comfort and indoor-air quality. In Proceedings of the IECON 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7908–7913. [Google Scholar]
- ASHRAE. Ventilation for Preservation of Occupants’ Health, Safety and Wellbeing-Specify Indoor Air Quality, Minimum Ventilation Rate Acceptable for Human Occupants and will not Impair Health; 62-1990; ASHRAE: Atlanta, GA, USA, 1990. [Google Scholar]
- European Committee for Standardization. Ventilation for Non-Residential Buildings. Performance Requirements for Ventilation and Room-Conditioning Systems; prEN-13779; CEN: Geneva, Switzerland, 2003. [Google Scholar]
- Atthajariyakul, S.; Leephakpreeda, T. Real-time determination of optimal indoor-air condition for thermal comfort, air quality and efficient energy usage. Energy Build. 2004, 36, 720–733. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 15251-Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics; European Committee for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- Redlich, C.A.; Sparer, J.; Cullen, M.R. Sick-building syndrome. Lancet 1997, 349, 1013–1016. [Google Scholar] [CrossRef]
- Kharbouch, A.; Naitmalek, Y.; Elkhoukhi, H.; Bakhouya, M.; De Florio, V.; El Ouadghiri, M.D.; Latre, S.; Blondia, C. IoT and big data technologies for monitoring and processing real-time healthcare data. IJDST 2019, 10, 17–30. [Google Scholar] [CrossRef]
- Kukadia, V.; Palmer, J. The effect of external atmospheric pollution on indoor air quality: A pilot study. Energy Build. 1998, 27, 223–230. [Google Scholar] [CrossRef]
- Coley, D.A.; Beisteiner, A. Carbon dioxide levels and ventilation rates in schools. Int. J. Vent. 2002, 1, 45–52. [Google Scholar] [CrossRef]
- Seppänen, O.A.; Fisk, W.J.; Mendell, M.J. Association of ventilation rates and CO2 concentrations with health andother responses in commercial and institutional buildings. Indoor Air 1999, 9, 226–252. [Google Scholar] [CrossRef]
- El Mankibi, M. Indoor air quality control in case of scheduled or intermittent occupancy based building: Development of a scale model. Build. Environ. 2009, 44, 1356–1361. [Google Scholar] [CrossRef]
- Chao, C.Y.; Hu, J.S. Development of an enthalpy and carbon dioxide based demand control ventilation for indoor air quality and energy saving with neural network control. Indoor Built Environ. 2004, 13, 463–475. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Z.; Sun, Y.; Zhu, N. Online optimal ventilation control of building air-conditioning systems. Indoor Built Environ. 2011, 20, 129–136. [Google Scholar] [CrossRef]
- Lachhab, F.; Bakhouya, M.; Ouladsine, R.; Essaaidi, M. Context-driven monitoring and control of buildings ventilation systems using big data and internet of things-based technologies. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 276–288. [Google Scholar] [CrossRef]
- Thosar, A.; Patra, A.; Bhattacharyya, S. Feedback linearization based control of a variable air volume air conditioning system for cooling applications. ISA Trans. 2008, 47, 339–349. [Google Scholar] [CrossRef] [PubMed]
- Arguello-Serrano, B.; Velez-Reyes, M. Nonlinear control of a heating, ventilating, and air conditioning system with thermal load estimation. IEEE Trans. Control Syst. Technol. 1999, 7, 56–63. [Google Scholar] [CrossRef]
- Lachhab, F.; Ouladsine, R.; Bakhouya, M.; Essaidi, M. An energy-efficient approach for controlling heating and air-conditioning systems. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017; pp. 1–7. [Google Scholar]
- Guo, W.; Zhou, M. Technologies toward thermal comfort-based and energy-efficient hvac systems: A review. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 3883–3888. [Google Scholar]
- Zhang, J.; Zhang, K. A particle swarm optimization approach for optimal design of PID controller for temperature control in HVAC. ICMTMA 2011, 1, 230–233. [Google Scholar]
- Lim, D.; Rasmussen, B.P.; Swaroop, D. Selecting PID control gains for nonlinear HVAC&R systems. HVACR Res. 2009, 15, 991–1019. [Google Scholar]
- Song, Y.; Wu, S.; Yan, Y.Y. Control strategies for indoor environment quality and energy efficiency—A review. Int. J. Low Carbon Technol. 2013, 10, 305–312. [Google Scholar] [CrossRef]
- Behrooz, F.; Mariun, N.; Marhaban, M.H.; Radzi, M.; Amran, M.; Ramli, A.R. Review of control techniques for HVAC systems—Nonlinearity approaches based on Fuzzy cognitive maps. Energies 2018, 11, 495. [Google Scholar] [CrossRef]
- Berouine, A.; Akssas, E.; Naitmalek, Y.; Lachhab, F.; Bakhouya, M.; Ouladsine, R.; Essaaidi, M. A fuzzy logic-based approach for HVAC systems control. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1510–1515. [Google Scholar]
- Oldewurtel, F.; Parisiob, A.; Jones, N.C.; Gyalistrasa, D.; Gwerderd, M.; Stauche, V.; BeatLehmann, B.; Morari, M. Use of model predictive control and weather forecasts for energy efficient building climate control. Energy Build. 2012, 45, 15–27. [Google Scholar] [CrossRef]
- Bălan, R.; Cooper, J.; Chao, K.M.; Stan, S.; Donca, R. Parameter identification and model based predictive control of temperature inside a house. Energy Build. 2011, 43, 748–758. [Google Scholar] [CrossRef]
- Ma, J.; Qin, J.; Salsbury, T.; Xu, P. Demand reduction in building energy systems based on economic model predictive control. Chem. Eng. Sci. 2011, 67, 92–100. [Google Scholar] [CrossRef]
- Moroşan, P.D.; Bourdais, R.; Dumur, D.; Buisson, J. Building temperature regulation using a distributed model predictive control. Energy Build. 2010, 42, 1445–1452. [Google Scholar] [CrossRef]
- Huang, G. Model predictive control of VAV zone thermal systems concerning bi-linearity and gain nonlinearity. Control Eng. Pract. 2011, 19, 700–710. [Google Scholar] [CrossRef]
- Xu, M.; Li, S. Practical generalized predictive control with decentralized identification approach to HVAC systems. Energy Convers. Manag. 2007, 48, 292–299. [Google Scholar] [CrossRef]
- Privara, S.; Široký, J.; Ferkl, L.; Cigler, J. Model predictive control of a building heating system: The first experience. Energy Build. 2011, 43, 564–572. [Google Scholar] [CrossRef]
- Yuan, S.; Perez, R. Multiple-zone ventilation and temperature control of a single-duct VAV system using model predictive strategy. Energy Build. 2006, 38, 1248–1261. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Bakhouya, M.; NaitMalek, Y.; Elmouatamid, A.; Lachhab, F.; Berouine, A.; Boulmrharj, S.; Ouladsine, R.; Felix, V.; Zinedine, K.; Khaidar, K.; et al. Towards a context-driven platform using IoT and big data technologies for energy efficient buildings. In Proceedings of the 2017 3rd International Conference of Cloud Computing Technologies and Applications (CloudTech), Rabat, Morocco, 24–26 October 2017; pp. 1–5. [Google Scholar]
- Berrabah, S.; Moussa, M.O.; Bakhouya, M. Towards a thermo-mechanical characterization approach of buildings’ envelope. Energy Rep. 2020, 6, 240–245. [Google Scholar] [CrossRef]
- Elmouatamid, A.; NaitMalek, Y.; Bakhouya, M. An energy management platform for micro-grid systems using internet of things and big-data technologies. J. Syst. Control Eng. 2019, 233, 904–917. [Google Scholar] [CrossRef]
- Boulmrharj, S.; Nait-Malek, Y.; Elmouatamid, A.; Bakhouya, M.; Ouladsine, R.; Zine-Dine, K.; Khaidar, M.; Siniti, M. Battery characterization and dimensioning approaches for micro-grid systems. Energies 2019, 12, 1305. [Google Scholar] [CrossRef]
- Elkhoukhi, H.; Nait-Malek, Y.; Bakhouya, M.; Berouine, A.; Kharbouch, A.; Lachhab, F.; Hanifi, M.; El Ouadghiri, D.; Essaaidi, M. A platform architecture for occupancy detection using stream processing and machine learning approaches. Concurr. Comput. Pract. Exp. 2019, e5651. [Google Scholar] [CrossRef]
- Berouine, A.; Ouladsine, R.; Bakhouya, M.; Lachhab, F.; Essaaidi, M. A model predictive approach for ventilation system control in energy efficient buildings. In Proceedings of the 2019 4th World Conference on Complex Systems (WCCS), Ouarzazate, Morocco, 22–25 April 2019; pp. 1–6. [Google Scholar]
- Allard, F.; Dorer, V.B.; Feustel, H.E. Fundamentals of the Multizone Air Flow Model-COMIS; Air Infiltration and Ventilation Centre: Coventry, UK, 1990; p. 115. [Google Scholar]
- Zannetti, P. Air Pollution Modeling: Theories, Computational Methods and Available Software; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—Part I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Yang, S.H.; Wang, X.Z.; McGreavy, C. A multivariable coordinated control system based on predictive control strategy for FCC reactor-regenerator system. Chem. Eng. Sci. 1996, 51, 2977–2982. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Gunnar, B.; Folkesson, K. Recommendations for Calculations of Energy Consumption for Air Handling Units; Eurovent/Cecomaf WG 6C; Eurovent: Brussels, Belgium, 2005. [Google Scholar]
- Benech, P.; Haessig, P. Estimation du Nombre de Personnes Presentes Dans Une Piece a Partir de la Concentration En Dioxyde De Carbone; Institute of Electronics and Telecommunications of Rennes: Rennes, France, 2015. [Google Scholar]
| Input Parameters | Control Horizon (Nu) | Prediction (Np) | Sampling Time (Ts) | Weighting Control (λ) |
|---|---|---|---|---|
| Value | 3 | 15 | 10s | 0.6 |
| Parameters Name | Parameter Description | Value | Unit |
|---|---|---|---|
| Simulated space volume | 400 | m3 | |
| CO2 generation rate per person | 0.0086 | l/s | |
| Minimum ventilation rate | 1/3600 | m3/s | |
| Maximum ventilation rate | 0.6 | m3/s | |
| Outdoor CO2 concentration | 450 | ppm | |
| Initial indoor CO2 concentration | 700 | ppm | |
| Setpoint of CO2 concentration | 750 | ppm | |
| Maximum number of occupants | 100 | - | |
| Fan inlet/outlet increment total pressure | 1500 | Pa | |
| Overall efficiency | 0.65 | - |
| Energy (Wh) | PI | SF | MPC |
|---|---|---|---|
| Total | 1225.52 | 1222.8 | 1196.74 |
| Gain | 2.35% | 2.13% | - |
| Energy (Wh) | MPC | GPC |
|---|---|---|
| Total | 1196.74 | 1144.78 |
| Gain | 4.34% | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berouine, A.; Ouladsine, R.; Bakhouya, M.; Essaaidi, M. Towards a Real-Time Predictive Management Approach of Indoor Air Quality in Energy-Efficient Buildings. Energies 2020, 13, 3246. https://doi.org/10.3390/en13123246
Berouine A, Ouladsine R, Bakhouya M, Essaaidi M. Towards a Real-Time Predictive Management Approach of Indoor Air Quality in Energy-Efficient Buildings. Energies. 2020; 13(12):3246. https://doi.org/10.3390/en13123246
Chicago/Turabian StyleBerouine, Anass, Radouane Ouladsine, Mohamed Bakhouya, and Mohamed Essaaidi. 2020. "Towards a Real-Time Predictive Management Approach of Indoor Air Quality in Energy-Efficient Buildings" Energies 13, no. 12: 3246. https://doi.org/10.3390/en13123246
APA StyleBerouine, A., Ouladsine, R., Bakhouya, M., & Essaaidi, M. (2020). Towards a Real-Time Predictive Management Approach of Indoor Air Quality in Energy-Efficient Buildings. Energies, 13(12), 3246. https://doi.org/10.3390/en13123246






