Wideband DOA Estimation on Co-prime Array via Atomic Norm Minimization

Abstract

This paper introduces a low complexity wideband direction-of-arrival (DOA) estimation algorithm on the co-prime array. To increase the number of the detectable signal sources and to prevent an unnecessary increase in complexity, the low dimensional co-prime array vector is constructed by arranging elements of the correlation matrix at every frequency bin. The atomic norm minimization (ANM)-based approach resolves the grid-mismatch, which causes an inevitable error in the compressive sensing (CS)-based DOA estimation. However, the complexity surges when the ANM is exploited to the wideband DOA estimation on the co-prime array. The surging complexity of the ANM-based wideband DOA estimation on the co-prime array is handled by solving the time-saving semidefinite programming (SDP) motivated by the ANM for multiple measurement vector (MMV) case. Simulation results show that the proposed algorithm has high accuracy and low complexity compared to compressive sensing (CS)-based wideband DOA estimation algorithms that exploit the co-prime array.

1. Introduction

A direction-of-arrival (DOA) estimation has been studied for decades in array signal processing and has been adopted in a various applications such as localization and radar [1]. In addition, the DOA estimation can take an essential role in cooperative localization for vehicular networks, where the cooperative localization between vehicles requires the relative distances and DOAs of neighboring vehicles [2,3]. Direction-of-arrival (DOA) estimation algorithms can be distinguished according to the bandwidth of the signal: a narrowband DOA estimation and a wideband DOA estimation. When the bandwidth is narrow compared to the carrier frequency of the signal, the phase difference between antennas is only dependent on the DOA as in [4]. On the other hand, when the signal has a wide bandwidth, the narrowband DOA estimation algorithms cannot be used since the phase difference between antennas also varies with the temporal frequency [5]. For this reason, the wideband systems such as automotive radar [6] and other ultra-wideband (UWB) applications [7] require the wideband DOA estimation. The standard approach for the wideband DOA estimation is to decompose the wideband signal into multiple narrowband signals using discrete Fourier transform (DFT) and make narrowband DOA estimation applicable [8,9,10]. However, the complexity of the algorithm may surge as the number of narrowband signals increases [11]. Thus, one of the challenges in wideband DOA estimation is to prevent complexity from getting high.

In the past few years, compressive sensing (CS)-based wideband DOA estimation algorithms have been proposed [11,12,13]. Although different types of CS such as basis pursuit (BP) [14] and sparse Bayesian learning (SBL) [15] are exploited, CS-based DOA estimation algorithms are commonly robust against fewer snapshots and correlation between signal sources [16]. However, in a practical situation, a real DOA does not match perfectly with the basis of the finite search grid, which is used in CS-based DOA estimation. This problem is widely known as grid-mismatch and causes inevitable estimation error [17]. Among [11,12,13], the algorithm in [11] suffers from the grid-mismatch and has high complexity that surges as the number of decomposed narrowband signals increases. On the other hand, the algorithms in [12,13] alleviate the grid-mismatch by using the approximation method in [18] that models the distance from the true DOA to the nearest grid basis. However, [12] experiences high complexity while [13] reduces the complexity by eliminating the useless grid basis at every iteration.

The atomic norm minimization (ANM)-based narrowband DOA estimation is first proposed in [19], where the theoretical base of the atomic norm is established in [20]. The ANM-based DOA narrowband estimation works directly on continuous DOA and completely resolves the grid-mismatch. After the proposal of the ANM, the ANM for multiple measurement vector (MMV) case has been studied in [21], and the robustness of the ANM-based algorithm against noise [22] and the gain-phase error [23] have been discussed. The ANM-based algorithm also extended to 2D-DOA estimation, including azimuth and elevation estimation [24] and multiple-input-multiple-output (MIMO) radar [25]. The ANM-based wideband DOA estimation has been studied in [26]. However, the idea of reducing complexity has not been discussed. In addition, [26] targets linear frequency modulated (LFM) signals and thus is difficult to be used in the general scenario.

Along with the study on the DOA estimation algorithms, the sparse array metrics such as the nested array [27] and the co-prime array [28] have been introduced for an underdetermined case, where the underdetermined case denotes a scenario in which the number of signal sources exceeds the number of antennas. The sparse array creates the virtual array whose cardinality is much larger than that of the physical array and enables detecting more signal sources. The sparse array has been exploited in the seminal works of the CS-based narrowband and wideband DOA estimation [11,12,29] and the ANM-based narrowband and wideband DOA estimation [26,30].

In this paper, we propose a low complexity wideband DOA estimation via ANM which is free from grid-mismatch. The wideband signal is decomposed into multiple narrowband signals, and the low dimensional co-prime array vector is constructed by arranging elements of a correlation matrix at each frequency bin. A problem that encompasses the decomposed narrowband signals of all frequency bins is derived. However, the computational complexity of the derived problem is exceptionally high. Thus, the complexity is reduced by exploiting the semidefinite programming (SDP) in [21], assuming that the co-prime array vectors from all frequency bins are MMVs. The main contributions of the proposed algorithm can be summarized as follows:

• An approach based on ANM resolves the grid-mismatch and enables achieving higher accuracy when the signal sources have a wide bandwidth.
• To reduce the complexity of the ANM-based wideband DOA estimation, the time-saving SDP is derived, which is motivated by the ANM for MMV case.

2. Signal Model

We assume that P uncorrelated wideband signals impinging on the antenna array with M elements. The DOAs of the signal sources are noted as $\mathbf{\Theta }={\left[{\theta }_1,\dots ,{\theta }_P\right]}^T$. The bandwidth of the signals span over the frequency range $[f_l,f_u]$, where $f_l$ and $f_u$ denote the lower and upper frequency bound respectively. For a wideband analysis, the wideband signal is decomposed into K narrowband signals by DFT. The frequency range $[f_l,f_u]$ is sectorized into K bins, and the center frequency of the k-th bin is defined as $f_k$. An array manifold vector of the k-th frequency bin whose DOA is $\theta$, ${\mathbf{a}}_k(\theta )$ can be given as

$${\mathbf{a}}_k(\theta )={\left[e^{j2\pi (d_1/{\lambda }_k)cos\theta },\dots ,e^{j2\pi (d_M/{\lambda }_k)cos\theta }\right]}^T,$$

(1)

where $d_m$ denotes a distance between the m-th antenna and the reference antenna. Note that the first antenna is the reference antenna, and hence $d_1=0$. ${\lambda }_k=c/f_k$, where c is the speed of light. An array manifold matrix of the k-th frequency bin, ${\mathbf{A}}_k(\mathbf{\Theta })$ is

$${\mathbf{A}}_k(\mathbf{\Theta })=\left[{\mathbf{a}}_k({\theta }_1),\dots ,{\mathbf{a}}_k({\theta }_P)\right]\in {\mathbb{C}}^{M\times P}.$$

(2)

The received signal of the k-th frequency bin, ${\mathbf{X}}_k$ can be written as

$${\mathbf{X}}_k={\mathbf{A}}_k(\mathbf{\Theta }){\mathbf{S}}_k+{\mathbf{N}}_k\in {\mathbb{C}}^{M\times T},$$

(3)

where T is the number of snapshots. ${\mathbf{S}}_k={\left[{\mathbf{s}}_k^1,\dots ,{\mathbf{s}}_k^P\right]}^T$, where ${\mathbf{s}}_k^p\in {\mathbb{C}}^{T\times 1}$ denotes the p-th signal vector of the k-th frequency bin. ${\mathbf{N}}_k$ is a noise matrix whose columns follow $\mathcal{CN}(\mathbf{0},{\sigma }^2{\mathbf{I}}_M)$, where ${\sigma }^2$ denotes the power of the noise which is assumed to be known and is equivalent for all k. ${\mathbf{I}}_M$ is a $M\times M$ identity matrix. ${\mathbf{R}}_k^{\mathbf{X}}$, the correlation matrix of ${\mathbf{X}}_k$, can be defined as

$$\begin{array}{cc}\hfill {\mathbf{R}}_k^{\mathbf{X}}& =\mathbb{E}\left[{\mathbf{X}}_k{\mathbf{X}}_k^H\right]\hfill \\ \hfill & ={\mathbf{A}}_k(\mathbf{\Theta }){\mathbf{R}}_k^{\mathbf{S}}{\mathbf{A}}_k{(\mathbf{\Theta })}^H+{\sigma }^2{\mathbf{I}}_M\approx \frac{{\mathbf{X}}_k{\mathbf{X}}_k^H}{T},\hfill \end{array}$$

(4)

where ${\mathbf{R}}_k^{\mathbf{S}}=\mathbb{E}\left[{\mathbf{S}}_k{\mathbf{S}}_k^H\right]\approx {\mathbf{S}}_k{\mathbf{S}}_k^H/T$. Since every signal source is uncorrelated with each other, ${\mathbf{R}}_k^{\mathbf{S}}$ is a diagonal matrix where its p-th diagonal element equals to the power of the p-th signal source. We define ${\mathbf{z}}_k$ such that ${\mathbf{z}}_k=\mathrm{diag}({\mathbf{R}}_k^{\mathbf{S}})$, where $\mathrm{diag}(·)$ denotes a vector whose entries are diagonal elements of a given matrix. The $(i,j)$-th element of ${\mathbf{R}}_k^{\mathbf{X}}$, ${\mathbf{R}}_k^{\mathbf{X}}(i,j)$ can be given as

$$\begin{array}{cc}\hfill & {\mathbf{R}}_k^{\mathbf{X}}(i,j)=\hfill \\ \hfill & \left\{\begin{array}{cc}{\displaystyle \sum _{p=1}^P{\mathbf{z}}_k(p)e^{j2\pi \{(d_i-d_j)/{\lambda }_k\}cos{\theta }_p}}\hfill & \mathrm{for}i\ne j,\hfill \\ {\displaystyle \sum _{p=1}^P{\mathbf{z}}_k(p)e^{j2\pi \{(d_i-d_j)/{\lambda }_k\}cos{\theta }_p}+{\sigma }^2}\hfill & \mathrm{for}i=j,\hfill \end{array}\right.\hfill \end{array}$$

(5)

where ${\mathbf{z}}_k(p)$ is the p-th element of ${\mathbf{z}}_k$.

3. Wideband DOA Estimation on Co-Prime Array via Atomic Norm Minimization

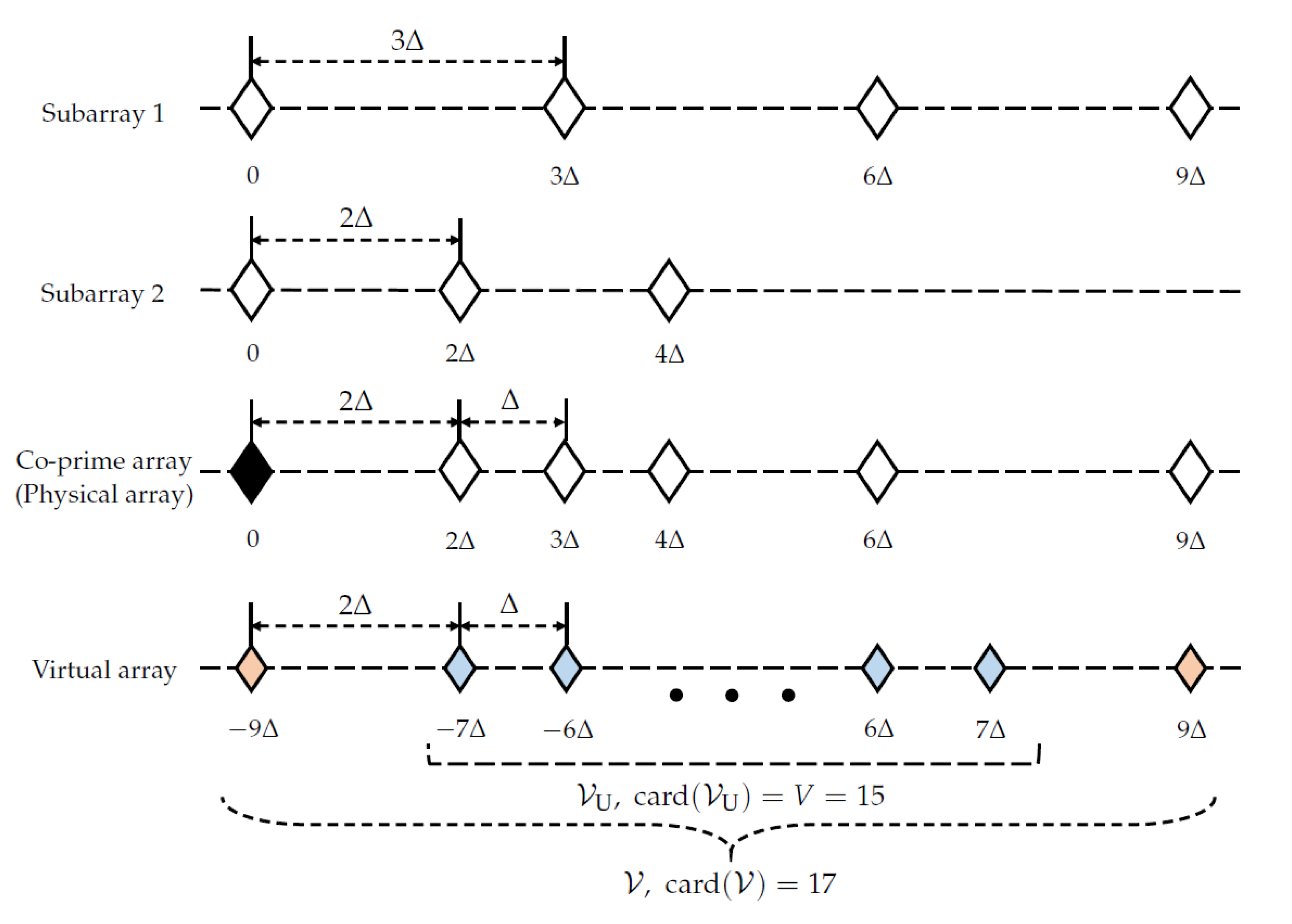
3.1. Construction of Co-Prime Array Vector

To increase the number of the detectable signal sources by using co-prime array, the placement of the antennas should follow the rule in [28] and the co-prime array vector needs to be constructed by rearranging the elements of the correlation matrix. The co-prime array vectors in the previous works [11,12,29] are the vectorized correlation matrix so that the dimension of the co-prime array vector becomes excessively large, causing an unnecessary increase in complexity. In this subsection, the procedure of constructing low dimensional co-prime array vector is introduced.

The co-prime array is a combination of two sparse subarrays, where one subarray consists of $2M_1$ antennas spaced $M_2\Delta$ apart, while the other consists of $M_2$ antennas spaced $M_1\Delta$ apart. $\Delta$ is set to a half-wavelength of the signal whose frequency equals to the center frequency of the range $[f_l,f_h]$, such that $\Delta =c/(f_l+f_h)$. The structure of co-prime array and its virtual array $\mathcal{V}$ are given in Figure 1, where $M=2M_1+M_2-1$. The virtual array is the notion that is used in the seminal works of the co-prime array [12,29,31], where it does not exist physically, yet we can obtain the effect of using a larger array. The set $\mathcal{V}$ indicates the placement of antennas in the virtual array [28], and is defined as

$$\mathcal{V}=\left\{d_i-d_j|i,j=1,2,\dots ,M\right\}.$$

(6)

Note that some elements can repeat, and additional repeating elements are removed in $\mathcal{V}$. V denotes the cardinality of $\mathcal{V}$ and is smaller than $M^2$ as the repeating elements are removed. Figure 1 shows two subarrays, the co-prime array and the virtual array when $M_1=2$ and $M_2=3$. $\mathcal{V}$ can be split into two subsets as in Figure 1: the placement of antenna elements which constitutes a large uniform linear array (ULA) at the center, ${\mathcal{V}}_{\mathrm{U}}$ and the remaining placement. V denotes the cardinality of ${\mathcal{V}}_{\mathrm{U}}$.

The co-prime array vector of the k-th frequency bin, ${\mathbf{y}}_k\in {\mathbb{C}}^{V\times 1}$ is constructed to obtain the cardinality of ${\mathcal{V}}_{\mathrm{U}}$ using ${\mathbf{R}}_k^{\mathbf{X}}$. The construction of ${\mathbf{y}}_k$ using ${\mathbf{R}}_k^{\mathbf{X}}$ is depicted in Figure 2. For clearer understanding, we define the term virtual position of ${\mathbf{R}}_k^{\mathbf{X}}(i,j)$ as $d_i-d_j$. Given the elements of ${\mathbf{R}}_k^{\mathbf{X}}$ and their virtual position in Figure 2a, the procedure of constructing ${\mathbf{y}}_k$ can be broken down into three steps:

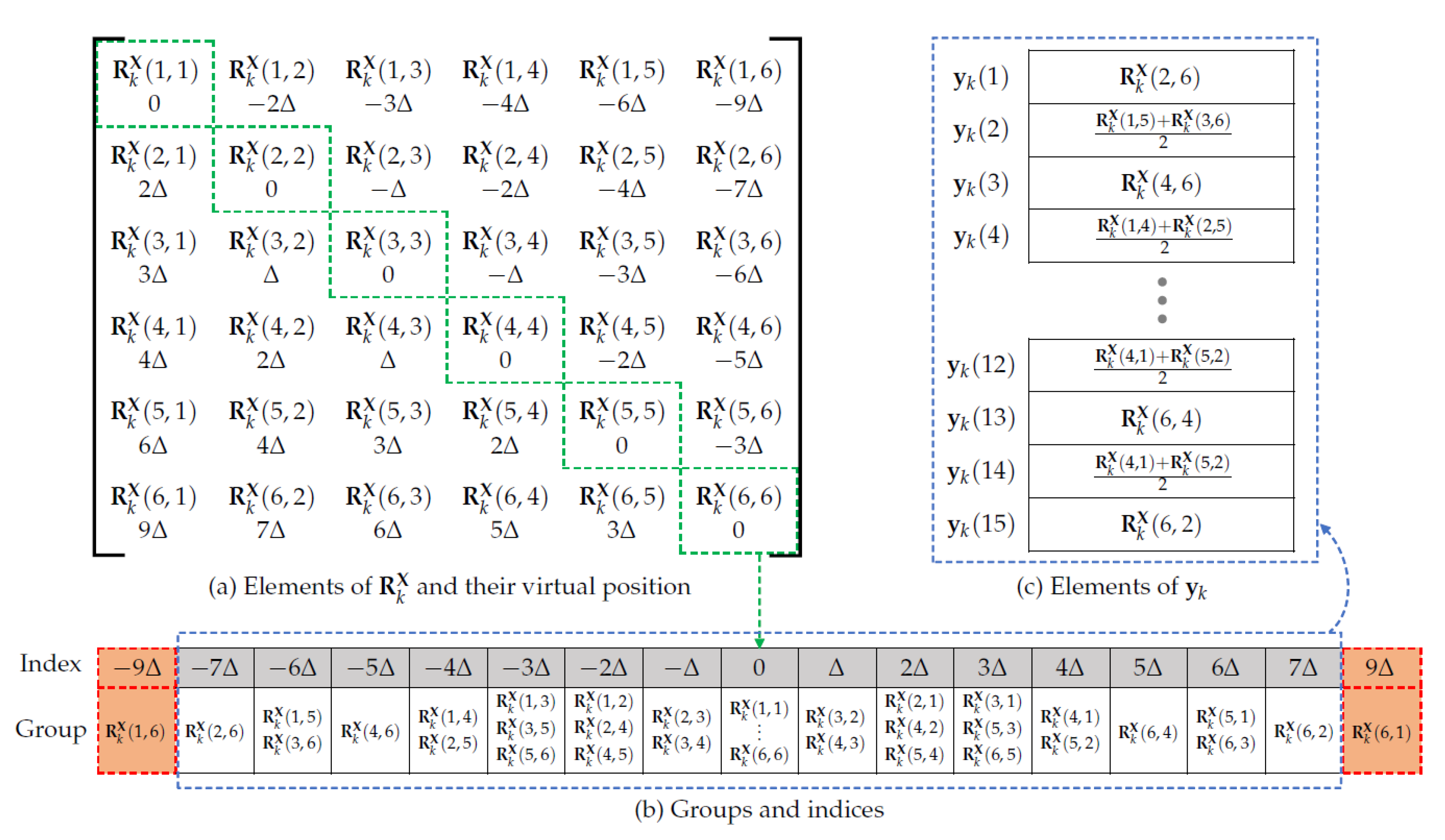
• Group the elements of ${\mathbf{R}}_k^{\mathbf{X}}$ with the same virtual position as in Figure 2b.
  Note that the index in Figure 2b denotes the common virtual position of the elements within the group.
• Leave only the groups whose indices are equivalent to the elements of ${\mathcal{V}}_{\mathrm{U}}$ as in Figure 2b.
• Average the elements in remaining groups and vectorize the averaged elements to obtain ${\mathbf{y}}_k$ as in Figure 2c.

Note that the dimension of ${\mathbf{y}}_k\in {\mathbb{C}}^{V\times 1}$ is smaller than that of the co-prime array vector in [12,29,31], where the dimension of the co-prime array vector in [12,29,31] equals $M^2$. ${\mathbf{y}}_k$ can also be rewritten as

$$\begin{array}{cc}\hfill {\mathbf{y}}_k& ={\mathbf{A}}_k^v(\mathbf{\Theta }){\mathbf{z}}_k+\mathbf{e}={\widehat{\mathbf{y}}}_k+\mathbf{e}.\hfill \end{array}$$

(7)

${\mathbf{A}}_k^v(\mathbf{\Theta })=\left[{\mathbf{a}}_k^v({\theta }_1),\dots ,{\mathbf{a}}_k^v({\theta }_P)\right]\in {\mathbb{C}}^{V\times P}$. ${\mathbf{a}}_k^v(\theta )$ is the array manifold vector of the k-th frequency bin whose antenna placement follows ${\mathcal{V}}_{\mathrm{U}}$, such that

$${\mathbf{a}}_k^v(\theta )={\left[e^{j\pi (-V+1)\frac{\Delta }{{\lambda }_k}cos\theta },e^{j\pi (-V+3)\frac{\Delta }{{\lambda }_k}cos\theta },\dots ,e^{j\pi (V-1)\frac{\Delta }{{\lambda }_k}cos\theta }\right]}^T.$$

(8)

Note that V is an odd number since ${\mathcal{V}}_{\mathrm{U}}$ is symmetric for the reference antenna at the center. $\mathbf{e}={[0,\dots ,0,{\sigma }^2,0,\dots ,0]}^T\in {\mathbb{C}}^{V\times 1}$, where the element located in the middle of $\mathbf{e}$ is ${\sigma }^2$ and the other elements are 0. ${\widehat{\mathbf{y}}}_k={\mathbf{A}}_k^v(\mathbf{\Theta }){\mathbf{z}}_k$, where ${\widehat{\mathbf{y}}}_k$ can be recovered since $\sigma$ is known.

3.2. Wideband DOA Estimation via Atomic Norm Minimization

The atomic norm of ${\widehat{\mathbf{y}}}_k$, ${\parallel {\widehat{\mathbf{y}}}_k\parallel }_{{\mathcal{A}}_k}$ can be given as follows [20].

$$\begin{array}{cc}\hfill {\parallel {\widehat{\mathbf{y}}}_k\parallel }_{{\mathcal{A}}_k}& =\inf \left\{g>0:g\mathrm{conv}({\mathcal{A}}_k)\right\}\hfill \\ \hfill & =\inf \left\{\left.\sum _l|h_l|\right|{\widehat{\mathbf{y}}}_k=\sum _l{h}_l{\mathbf{a}}_k^v({\theta }_l)\right\},\hfill \end{array}$$

(9)

where g is an arbitrary positive real number, $\mathrm{conv}(·)$ denotes a convex of hull of a set, ${\mathcal{A}}_k$ is a set that consists of the atoms of the k-th frequency bin, and ${\mathbf{a}}_k^v({\theta }_l)$ is the l-th atom of the k-th frequency bin. $h_l$ is a complex number which satisfies ${\widehat{\mathbf{y}}}_k={\sum }_l{h}_l{\mathbf{a}}_k^v({\theta }_l)$ for arbitrary $\{{\theta }_l\}$, where $\{{\theta }_l\}$ denotes ${\theta }_l$ for $l=1,\dots ,L$. ${\parallel {\widehat{\mathbf{y}}}_k\parallel }_{{\mathcal{A}}_k}$ can also be represented as SDP in [19]:

$$\begin{array}{cc}\hfill {\parallel {\widehat{\mathbf{y}}}_k\parallel }_{{\mathcal{A}}_k}=& \underset{{\mathbf{u}}_k,t_k}{min}\left\{\frac{1}{2V}\mathrm{Trace}(\mathrm{Toep}({\mathbf{u}}_k))+\frac{1}{2}{t}_k\right\}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left[\begin{array}{cc}\mathrm{Toep}({\mathbf{u}}_k)& {\widehat{\mathbf{y}}}_k\\ {\widehat{\mathbf{y}}}_k^H& t_k\end{array}\right]\ge 0,\hfill \end{array}$$

(10)

where ${\mathbf{u}}_k,t_k$ are optimization variables in (10), $\mathrm{Trace}(·)$ denotes a trace of the matrix, and $\mathrm{Toep}(·)$ denotes a Hermitian Toeplitz matrix whose first column equals to the given vector. For $k=1,\dots ,K$, K different problems can be originated from (10). By summing the objective functions of K problems and integrating K constraints, the SDP that encompasses K frequency bins can be given as

$$\begin{array}{c}\underset{\begin{array}{c}{\mathbf{u}}_1,\dots ,{\mathbf{u}}_K\\ t_1,\dots ,t_K\end{array}}{min}\sum _{k=1}^K\left\{\frac{1}{2V}\mathrm{Trace}(\mathrm{Toep}({\mathbf{u}}_k))+\frac{1}{2}{t}_k\right\}\hfill \\ \mathrm{s}.\mathrm{t}.\left[\begin{array}{cc}\mathrm{Toep}({\mathbf{u}}_1)& {\widehat{\mathbf{y}}}_1\\ {\widehat{\mathbf{y}}}_1^H& t_1\end{array}\right]\ge 0,\dots ,\left[\begin{array}{cc}\mathrm{Toep}({\mathbf{u}}_K)& {\widehat{\mathbf{y}}}_K\\ {\widehat{\mathbf{y}}}_K^H& t_K\end{array}\right]\ge 0.\hfill \end{array}$$

(11)

The complexity of solving (11) is $O\left(K^{3.5}{(V+1)}^{3.5}\right)$, where the complexity can be calculated using the analysis in [32]. Letting D be the size of the search grid used in CS, the complexity of other CS-based wideband algorithms such as [11,12] can be given as $O\left(K^3{D}^3\right)$. Since the sum of exponents in $O\left(K^{3.5}{(V+1)}^{3.5}\right)$ is larger than that of $O\left(K^3{D}^3\right)$, it can be seen that the complexity of solving (11) is generally higher than that of [11,12].

To reduce the complexity, we regard that the atoms and the atomic sets of $\{{\widehat{\mathbf{y}}}_k\}$ are equivalent. When $\{{\widehat{\mathbf{y}}}_k\}$ share equivalent atoms and atomic sets, $\{{\widehat{\mathbf{y}}}_k\}$ are considered as MMV. Since the ANM for MMV case is well-studied in [21], we exploit the SDP formulation in [21], which has far less complexity than (11). To use the SDP in [21], $\mathbf{Y}$ is defined as $\mathbf{Y}=\left[{\widehat{\mathbf{y}}}_1,\dots ,{\widehat{\mathbf{y}}}_K\right]\in {\mathbb{C}}^{V\times K}$, where ${\widehat{\mathbf{y}}}_k$ is regarded as the k-th measurement vector. Then, the time-saving SDP for the wideband signal that is divided into K frequency bins can be given as the dual problem of the SDP in [21]:

$$\begin{array}{c}\underset{\mathbf{Q},\mathbf{H}}{max}\Re \left(\mathrm{Trace}({\mathbf{Q}}^H\mathbf{Y})\right)\hfill \\ \mathrm{s}.\mathrm{t}.\left[\begin{array}{cc}\mathbf{H}& -\mathbf{Q}\\ -{\mathbf{Q}}^H& {\mathbf{I}}_K\end{array}\right]\ge 0,\mathbf{H}\mathrm{is}\mathrm{a}\mathrm{Hermitian}\mathrm{matrix},\hfill \\ \sum _{i=1}^{V-s}{\mathbf{H}}_{i,i+s}=\left\{\begin{array}{cc}K,\hfill & s=0,\hfill \\ 0,\hfill & s=1,\dots ,V-1,\hfill \end{array}\right.\hfill \end{array}$$

(12)

where $\mathbf{Q},\mathbf{H}$ are optimization variables in (12), and $\Re (·)$ denotes the real part of the variable. Letting the optimal solution of $\mathbf{Q}$ in (12) be denoted as ${\mathbf{Q}}^{\star }$, the DOAs can be estimated by finding $\theta$ that yields the large correlation between ${\mathbf{Q}}^{\star }$ and $\mathbf{B}(\theta )$, where $\mathbf{B}(\theta )=\left[{\mathbf{a}}_1^v(\theta ),\dots ,{\mathbf{a}}_K^v(\theta )\right]\in {\mathbb{C}}^{V\times K}$. The correlation between ${\mathbf{Q}}^{\star }$ and $\mathbf{B}(\theta )$ can be represented as the spectrum $f(\theta )$ for $0\le \theta <\pi$ as follows.

$$f(\theta )=\mathrm{Trace}\left(\mathbf{B}{(\theta )}^H{\mathbf{Q}}^{\star }\right),\mathrm{for}0\le \theta <\pi .$$

(13)

Here, the DOAs can be estimated by finding P largest peaks from $f(\theta )$. Let ${\widehat{\theta }}_p$ denote the p-th estimated DOA, the pseudocode of the proposed algorithm can be given as Algorithm 1.

Algorithm 1 A low complexity wideband DOA estimation on co-prime array via ANM

Input:${\mathbf{X}}_k,k=1,\dots ,K$ Output: : ${\widehat{\theta }}_p,p=1,\dots ,P$  for all k do   ${\mathbf{R}}_k^{\mathbf{X}}\approx {\mathbf{X}}_k{\mathbf{X}}_k^H/T$;   Construct ${\mathbf{y}}_k$ according to the steps in Figure 2;   ${\widehat{\mathbf{y}}}_k={\mathbf{y}}_k-\mathbf{e}$;  end for  $\mathbf{Y}=\left[{\widehat{\mathbf{y}}}_1,\dots ,{\widehat{\mathbf{y}}}_K\right]$;  Calculate ${\mathbf{Q}}^{\star }$ via (12);  $f(\theta )={\left\{\mathrm{vec}({\mathbf{Q}}^{\star })\right\}}^H\mathbf{b}(\theta ),\mathrm{for}0\le \theta <\pi$;  Find P largest peaks from $f(\theta )$ to estimate ${\widehat{\theta }}_p,p=1,\dots ,P$;

The spectrum of $f(\theta )$ on noiseless case where $\sigma =0$ is presented in Figure 3. Here, the co-prime array with $M_1=3$, $M_2=5$ is used, such that $M=10$. The figure confirms that the proposed algorithm can successfully estimate the DOAs in the underdetermined case.

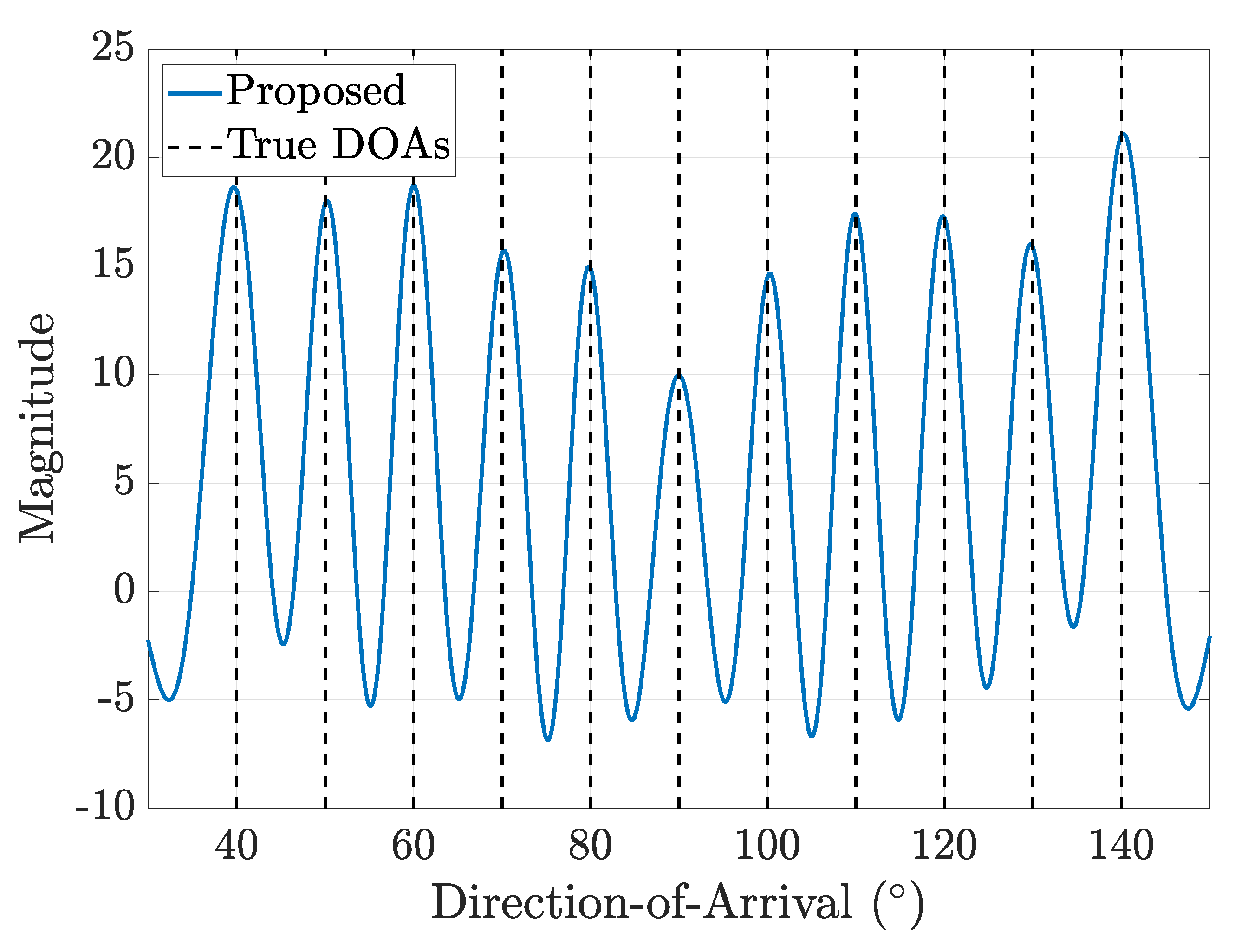
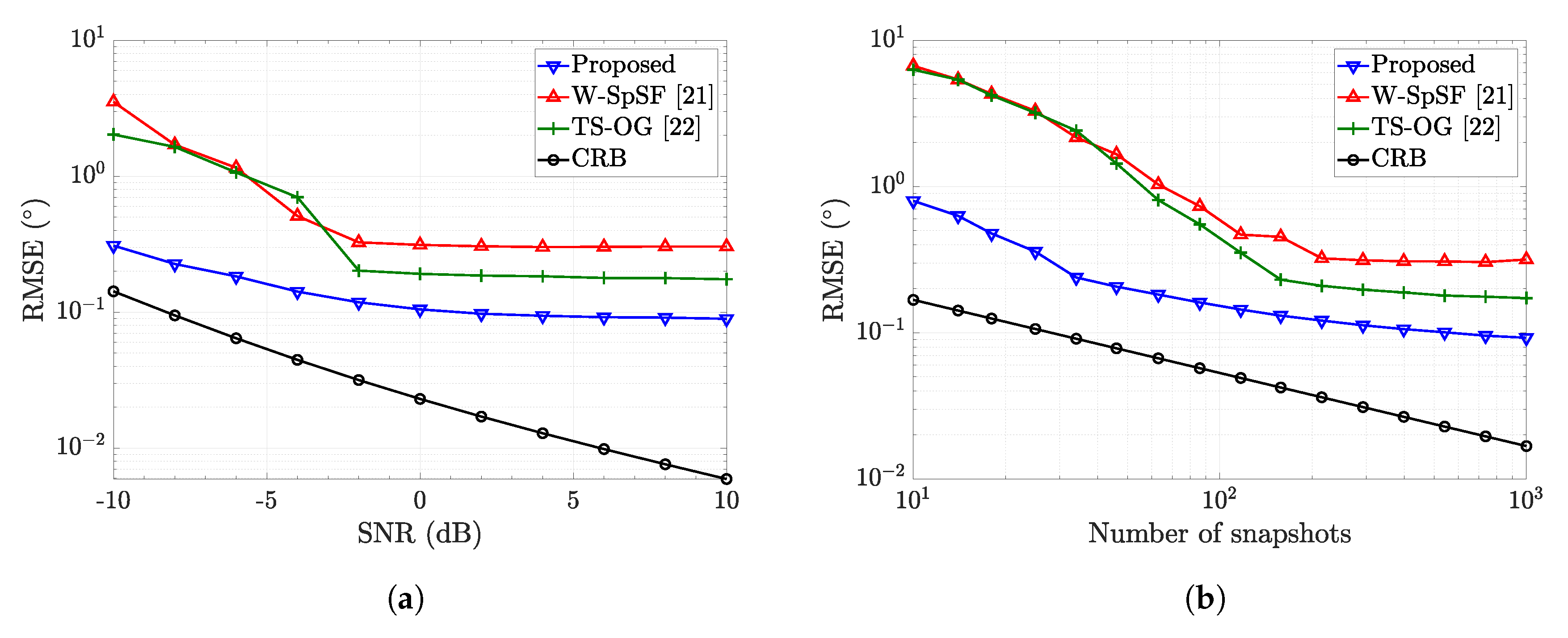
4. Simulation Result

Two other CS-based wideband DOA estimation algorithms are tested for comparison: wideband sparse spectrum fitting (W-SpSF) [11] and two step off-grid (TS-OG) approach [12]. Note that W-SpSF and TS-OG also exploit the co-prime array as the proposed algorithm does. For the simulation settings, the frequency of wideband signals span over $[f_l,f_h]$, where $f_h=1.5f_l$. The frequency range is divided into 10 bins, such that $K=10$. The number of signal sources P is set to 5. $M_1=3$ and $M_2=5$, thus the antenna elements are located as $\left[0,3,5,6,9,10,12,15,20,25\right]\Delta$, where $\Delta =c/(f_l+f_h)$. The power of all signal sources are equal, and each signal source is assumed to have a flat power spectral density (PSD) over $[f_l,f_h]$, such that ${\mathbf{R}}_1^{\mathbf{S}}={\mathbf{R}}_2^{\mathbf{S}}=\dots ={\mathbf{R}}_K^{\mathbf{S}}$. For W-SpSF and TS-OG, the grid spacing is set to $1^{\circ }$, so that the size of the grid $D=181$. To solve (12), CVX [33] is used for the optimization. The signal-to-noise ratio (SNR) of the k-th frequency bin, ${\gamma }_k$ is set as follows.

$${\gamma }_k=\frac{\mathrm{Trace}({\mathbf{R}}_k^{\mathbf{S}})}{{\sigma }^2}.$$

(14)

Since ${\mathbf{R}}_1^{\mathbf{S}}={\mathbf{R}}_2^{\mathbf{S}}=\dots ={\mathbf{R}}_K^{\mathbf{S}}$, ${\gamma }_1={\gamma }_2=\dots ={\gamma }_K$. The root mean square error (RMSE) is defined as

$$\mathrm{RMSE}=\sqrt{\frac{1}{PQ}\sum _{q=1}^Q\left\{\sum _{p=1}^P{\left({\theta }_p^q-{\widehat{\theta }}_p^q\right)}^2\right\}},$$

(15)

where Q is the number of Monte Carlo iterations for RMSE calculation, and ${\theta }_p^q$, ${\widehat{\theta }}_p^q$ respectively denote the real DOA and the estimated DOA of the p-th signal source on the q-th Monte Carlo run. For each iteration, DOAs are chosen randomly between $\left[{30}^{\circ },{150}^{\circ }\right]$ with all DOAs separated at least ${15}^{\circ }$.

Figure 4 shows the accuracy of estimation when SNR and the number of snapshots vary. Cramer-Rao bound (CRB) is presented along with the RMSE of wideband DOA estimation algorithms, where the derivation of CRB is given in Appendix A. In Figure 4, the RMSE of W-SpSF does not fall below $\sqrt{1/12}$, where $\sqrt{1/12}$ is the average estimation error induced by the grid-mismatch when the step size is $1^{\circ }$. In Figure 4a, the proposed algorithm has better accuracy than W-SpSF and TS-OG at all SNR. The RMSE of W-SpSF stops improving even when the SNR is high enough, while the proposed algorithm and TS-OG can break the accuracy limit induced by the grid-mismatch. In Figure 4b, the performance of the proposed algorithm remains robust to a fewer number of snapshots, while W-SpSF and TS-OG shows a large vulnerability compared to the proposed algorithm. Similar to in Figure 4a, the W-SpSF experiences the accuracy limit induced by the grid-mismatch even when the snapshots are abundant, while the others can break the limit induced by the grid-mismatch.

The complexity and the average computation time of all wideband DOA algorithms are given in

Table 1. The complexity and the average computation time of wideband DOA algorithms.

Algorithm	Complexity	Computation Time
Proposed	$O\left(V{(V+K)}^{3.5}\right)$	1.16 s
W-SpSF [11]	$O(K^3{D}^3)$	1.86 s
TS-OG [12]	$O(K^3{D}^3)$	2.59 s

. For computation, Intel CPU i5-7500 (3.40 GHz) and 16 GB RAM are used. The complexity of the proposed algorithm is calculated by using the analysis in [32]. Since the sum of exponents of $O\left(V{(V+K)}^{3.5}\right)$ is lower than that of $O(K^3{D}^3)$, we can tell that the proposed algorithm is generally less complex than [11,12]. Table 1 also shows that the proposed algorithm has the lowest computation time.

5. Conclusions

In this paper, we have proposed the wideband DOA estimation on co-prime array via ANM. To increase the number of the detectable signal sources, the co-prime array vector is constructed by arranging elements of the correlation matrix at every frequency bin. The high complexity of the ANM-based wideband DOA estimation is tackled by using the SDP targeted for MMV, assuming the co-prime array vectors of different frequency bins share the equivalent atoms. Simulation results exhibit that the proposed algorithm has notable merits in both accuracy and complexity compared to other CS-based wideband algorithms that exploit the co-prime array. We expect the proposed algorithm to be extended to 2D-DOA estimation, such as azimuth and elevation estimation on the planar array or to the practical applications, including localization and radar.