Super-Resolution DoA Estimation on a Co-Prime Array via Positive Atomic Norm Minimization
Abstract
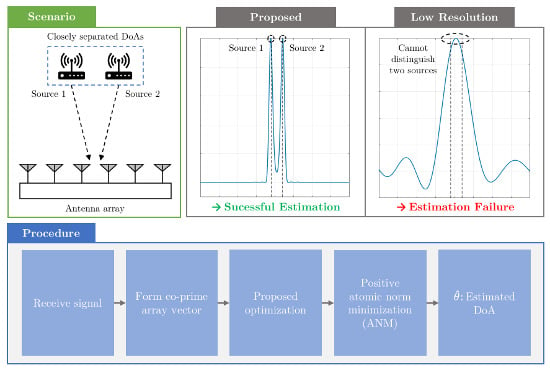
1. Introduction
2. Signal Model
3. Super-resolution DoA Estimation on Co-Prime Array via Positive Atomic Norm Minimization
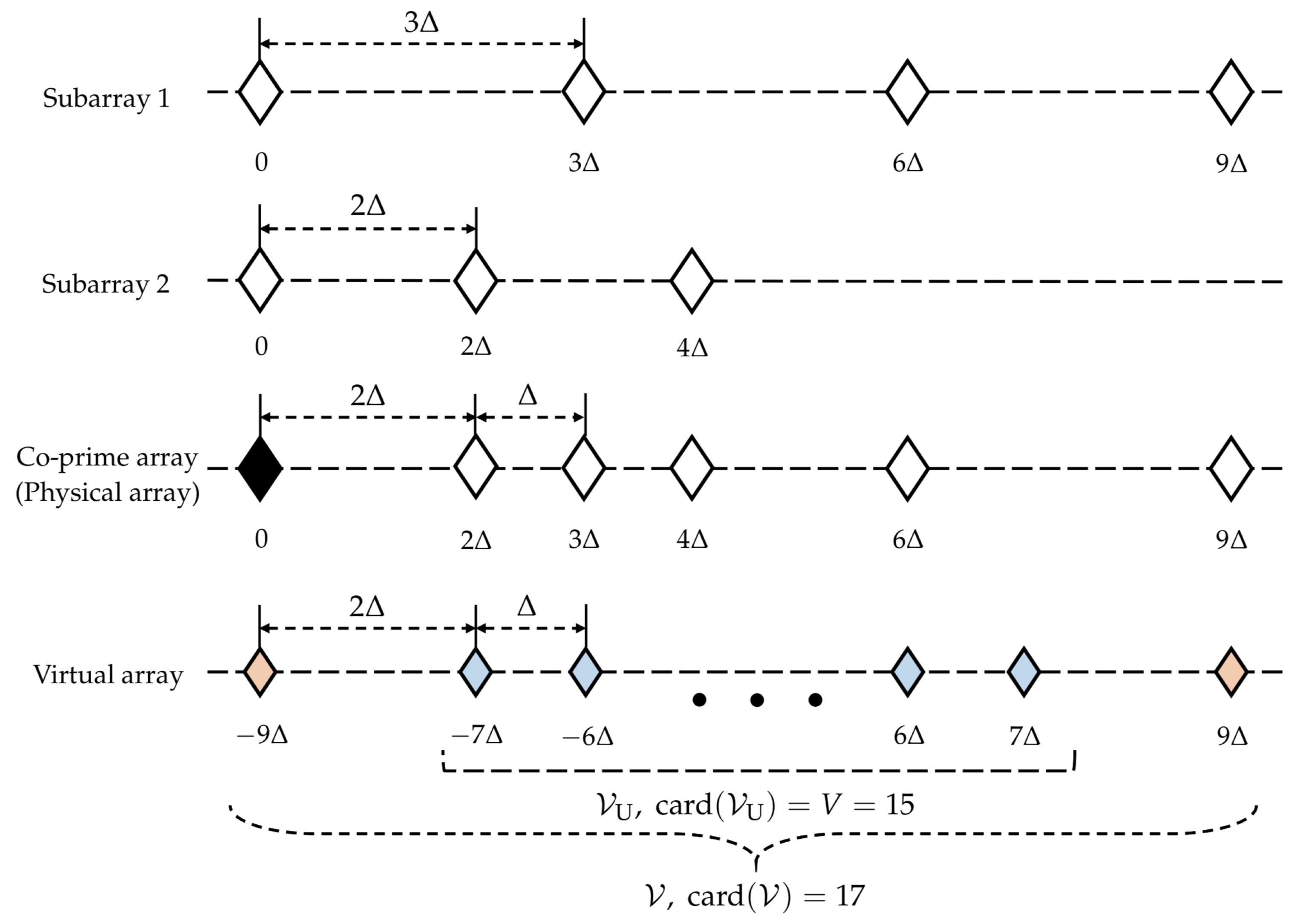
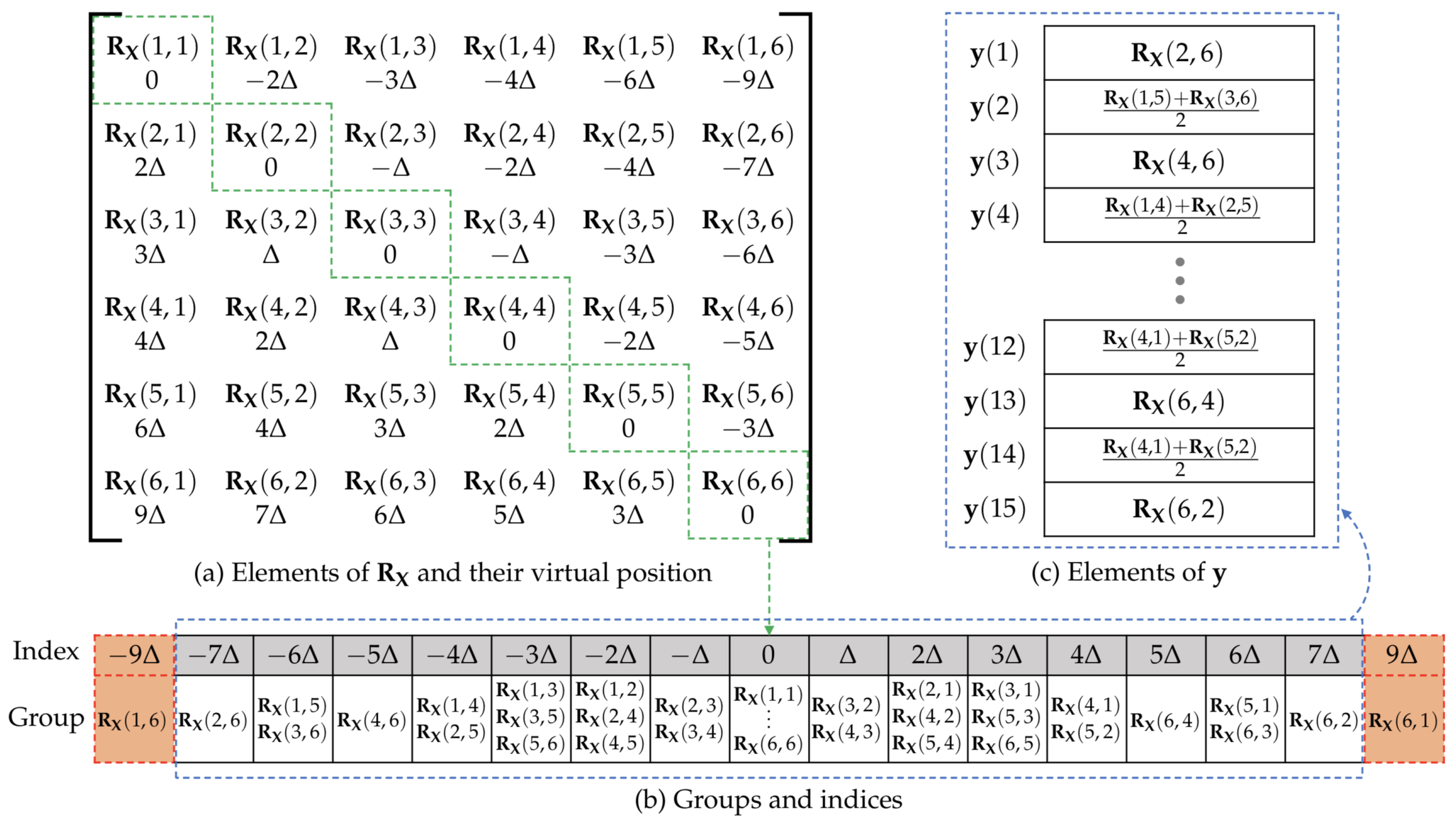
3.1. Construction of Co-Prime Array Vector
3.2. Super-Resolution DoA Estimation via Positive ANM
| Algorithm 1 A super-resolution DoA estimation on a co-prime array via positive ANM. |
| Input: : Output: : ; Construct according to the steps in Figure 3; Calculate via (12); Calculate via (15); ; Find P largest peaks from to estimate ; |
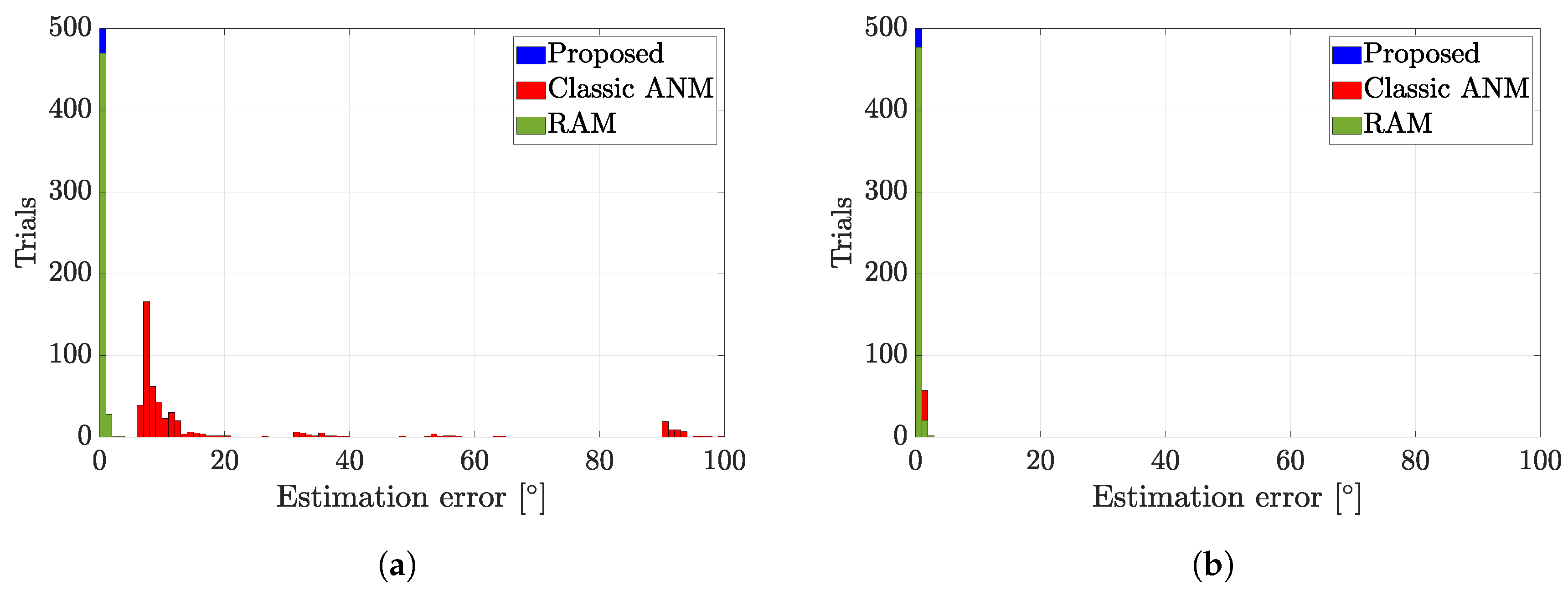
4. Simulation Results and Discussion
4.1. Simulation Settings
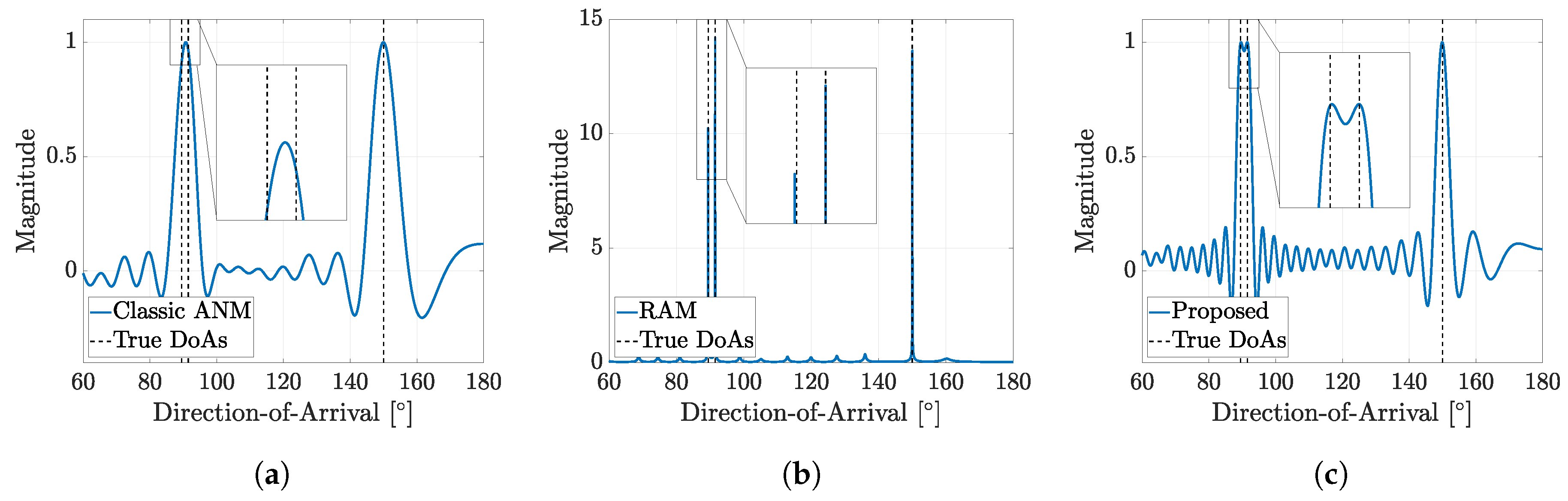
4.2. Analysis of Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.C.; Yao, K.; Hudson, R.E. Source localization and beamforming. IEEE Signal Process. Mag. 2002, 19, 30–39. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Ant. Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Z.; Zhou, Y. Direction-of-arrival estimation of wideband signals via covariance matrix sparse representation. IEEE Trans. Signal Process. 2011, 59, 4256–4270. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S. Underdetermined DOA estimation under the compressive sensing framework: A review. IEEE Access 2016, 4, 8865–8878. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1999, 20, 33–61. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to basis mismatch in compressed sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Tang, G.; Bhaskar, B.N.; Shah, P.; Recht, B. Compressed sensing off the grid. IEEE Trans. Inf. Theory 2013, 59, 7465–7490. [Google Scholar] [CrossRef]
- Chandrasekaran, V.; Recht, B.; Parrilo, P.A.; Willsky, A.S. The convex geometry of linear inverse problems. Found. Comput. Math. 2012, 12, 805–849. [Google Scholar] [CrossRef]
- Bhaskar, B.N.; Tang, G.; Recht, B. Atomic norm denoising with applications to line spectral estimation. IEEE Trans. Signal Process. 2013, 61, 5987–5999. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z. A new atomic norm for DOA estimation with gain-phase errors. arXiv 2019, arXiv:eess.SP/1910.02207. [Google Scholar]
- Tang, W.; Jiang, H.; Pang, S. Grid-free DOD and DOA estimation for MIMO radar via duality-based 2D atomic norm minimization. IEEE Access 2019, 7, 60827–60836. [Google Scholar] [CrossRef]
- Tsai, Y.; Zheng, L.; Wang, X. Millimeter-wave beamformed full-dimensional MIMO channel estimation based on atomic norm minimization. IEEE Trans. Commun. 2018, 66, 6150–6163. [Google Scholar] [CrossRef]
- Chu, H.; Zheng, L.; Wang, X. Super-resolution mmwave channel estimation for generalized spatial modulation systems. IEEE J. Sel. Topics Signal Process. 2019, 13, 1336–1347. [Google Scholar] [CrossRef]
- Candès, E.; Fernandez-Granda, C. Towards a mathematical theory of super-resolution. Commun. Pure Appl. Math. 2014, 67. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Shen, Q.; Cui, W.; Liu, W.; Wu, S.; Zhang, Y.D.; Amin, M.G. Underdetermined wideband DOA estimation of off-grid sources employing the difference co-array concept. Signal Process. 2017, 130, 299–304. [Google Scholar] [CrossRef]
- Shi, Y.; Mao, X.; Zhao, C.; Liu, Y. Underdetermined DOA estimation for wideband signals via joint sparse signal reconstruction. IEEE Signal Process. Lett. 2019, 26, 1541–1545. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-arrival estimation for coprime array via virtual array interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, J.; Qi, J.; Zhang, Z.; Zhu, J. Underdetermined DOA estimation of wideband LFM signals based on gridless sparse reconstruction in the FRF domain. Sensors 2019, 19, 2383. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. Enhancing sparsity and resolution via reweighted atomic norm minimization. IEEE Trans. Signal Process. 2016, 64, 995–1006. [Google Scholar] [CrossRef]
- Chi, Y.; Ferreira Da Costa, M. Harnessing sparsity over the continuum: Atomic norm minimization for superresolution. IEEE Signal Process. Mag. 2020, 37, 39–57. [Google Scholar] [CrossRef]
- Chi, Y. Convex relaxations of spectral sparsity for robust super-resolution and line spectrum estimation. In Proceedings of the Wavelets and Sparsity XVII, San Diego, CA, USA, 6–9 August 2017; Volume 10394, pp. 314–321. [Google Scholar] [CrossRef]
- He, Z.; Shi, Z.; Huang, L.; So, H.C. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting. IEEE Signal Process. Lett. 2015, 22, 435–439. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Stoica, P. Vandermonde decomposition of multilevel Toeplitz matrices with application to multidimensional super-resolution. IEEE Trans. Inf. Theory 2016, 62, 3685–3701. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 7 October 2019).
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]
- Pólik, I.; Terlaky, T. Interior point methods for nonlinear optimization. In Nonlinear Optimization; Di Pillo, G., Schoen, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 215–276. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, H.; Park, Y.M.; Kim, S. Super-Resolution DoA Estimation on a Co-Prime Array via Positive Atomic Norm Minimization. Energies 2020, 13, 3609. https://doi.org/10.3390/en13143609
Chung H, Park YM, Kim S. Super-Resolution DoA Estimation on a Co-Prime Array via Positive Atomic Norm Minimization. Energies. 2020; 13(14):3609. https://doi.org/10.3390/en13143609
Chicago/Turabian StyleChung, Hyeonjin, Young Mi Park, and Sunwoo Kim. 2020. "Super-Resolution DoA Estimation on a Co-Prime Array via Positive Atomic Norm Minimization" Energies 13, no. 14: 3609. https://doi.org/10.3390/en13143609
APA StyleChung, H., Park, Y. M., & Kim, S. (2020). Super-Resolution DoA Estimation on a Co-Prime Array via Positive Atomic Norm Minimization. Energies, 13(14), 3609. https://doi.org/10.3390/en13143609