1. Introduction
Low voltage dc grids have gained attention due to the potential advantages over low voltage ac grids when power electronic devices are proliferated in the system. Firstly, in such systems, the required number of conversion steps is generally reduced leading to improved system efficiency. Secondly, because the switching frequencies of power electronic converters are typically much higher than the native 50/60 Hz frequency of ac grids, the size of passive components can be reduced. Lastly, the absence of frequency and phase can make the control of dc grids significantly simpler [
1,
2,
3,
4,
5].
The protection of low voltage dc grids is more challenging than the protection of conventional low voltage ac systems. Fundamentally, it is more difficult to interrupt inductive currents and extinguish arcs, since the voltages and currents in dc grids do not have a natural zero crossing [
6,
7]. Furthermore, these grids are often meshed and subjected to bi-directional power flows, complicating the detection and selectivity compared to conventional radial networks [
8]. Moreover, in order to prevent high fault currents and blackouts, low voltage dc grids usually require fast fault interruption [
9,
10].
Because of the limited overload capability of power electronic devices, being able to withstand short-circuit conditions for milliseconds leads to oversized components in terms of current-carrying capability [
10,
11,
12]. Furthermore, for dc systems with low inertia, a blackout is inevitable when a fault is sustained for a longer period of time. Fuses, electromechanical devices and hybrid circuit breakers provide solutions for clearing faults in the order of milliseconds to seconds, but faster fault detection and interruption is required for low voltage dc systems [
10,
13,
14,
15]. To achieve this, the low voltage dc systems can be protected with solid-state circuit breakers (SSCBs), which can detect and interrupt faults within microseconds [
16,
17].
Several non-unit and unit protection schemes for low voltage dc grids have been reported in literature [
18,
19,
20]. Non-unit protection schemes utilize local measurements in order to detect faults. Many of these protection schemes measure the current and current rate-of-change, and circuit breakers are opened when preset thresholds are exceeded, but the utilization of higher order derivatives of the current and the grid’s voltage are also reported [
21,
22,
23]. The main advantages of non-unit protection schemes are their simplicity, and their resilience to the failure of protection devices when a hierarchical structure of circuit breakers is used. However, these schemes have difficulty isolating only the faulted areas of the grid and thus achieving selectivity. Therefore, protection schemes were proposed that utilize knowledge about the system’s topology in order to achieve selectivity. For example, faults can be located by measuring the grid’s impedance and comparing it to known line parameters, or a wavelet transform can be used to identify faults by comparing them to simulations of the system [
24,
25,
26,
27,
28]. Furthermore, a handshaking protection scheme was introduced, which locates and isolates a fault by temporarily powering down the dc system [
29]. Nevertheless, these methods struggle to ensure selectivity when system parameters are uncertain or the system topology is changing. On the other hand, unit protection schemes achieve selectivity by utilizing a communication infrastructure. For instance, differential protection schemes locate faults by comparing the currents at different locations in the system, and event-based protection schemes ensure selectivity by combining local detection with central decision-making [
30,
31,
32,
33,
34,
35,
36] However, since fast fault detection and interruption is required in low voltage dc grids, utilizing a communication infrastructure is not desirable.
The main contribution of this paper is a decentralized plug-and-play protection scheme, which contrary to other protection schemes, ensures selectivity without utilizing communication and only requires minimal knowledge about the system. Selectivity is achieved by augmenting the standard solid-state circuit breaker topology with RC dampers and by utilizing the proposed time-current characteristic. The protection scheme is plug-and-play in the sense that selective protection is provided on both sides of the circuit breakers in the system, regardless of the system’s configuration or where the circuit breakers are located in the system and without requiring (re)configuration of the circuit breakers. Furthermore, the protection scheme is experimentally validated, showing the effectiveness of the protection scheme for different low voltage dc systems under various conditions.
This paper is structured as follows. In
Section 2, it is discussed that current limiting inductances and fast fault interruption are crucial for the protection of low voltage dc grids. In
Section 3, the experimental setup is presented and the operation of the designed solid-state circuit breaker (SSCB) is validated. In
Section 4, it is experimentally shown that fast fault propagation and the commutation of inductive currents pose two challenges for the selectivity of non-unit protection schemes. In
Section 5, it is proposed to add an RC damper to the output terminals of the SSCBs in order to delay fault propagation and smoothe current commutation. Furthermore, a time-current characteristic is proposed that coordinates upstream and downstream circuit breakers and also prevents tripping due to current commutation. In
Section 6, the proposed plug-and-play protection scheme is experimentally validated. Finally, in
Section 7, conclusions are drawn.
2. Short-Circuit Fault Currents in Low Voltage DC Grids
In low voltage dc grids overvoltages can occur when, for instance, lightning strikes one of the conductors. Therefore, surge arresters such as Metal Oxide Varistors (MOVs) or spark gaps should be used to clamp the voltage. Furthermore, short-circuits can occur when, for example, a tree falls on one of the overhead lines or the insulation deteriorates in one of the underground lines. In those cases, one or more conductors are short-circuited to each other or to the ground [
37].
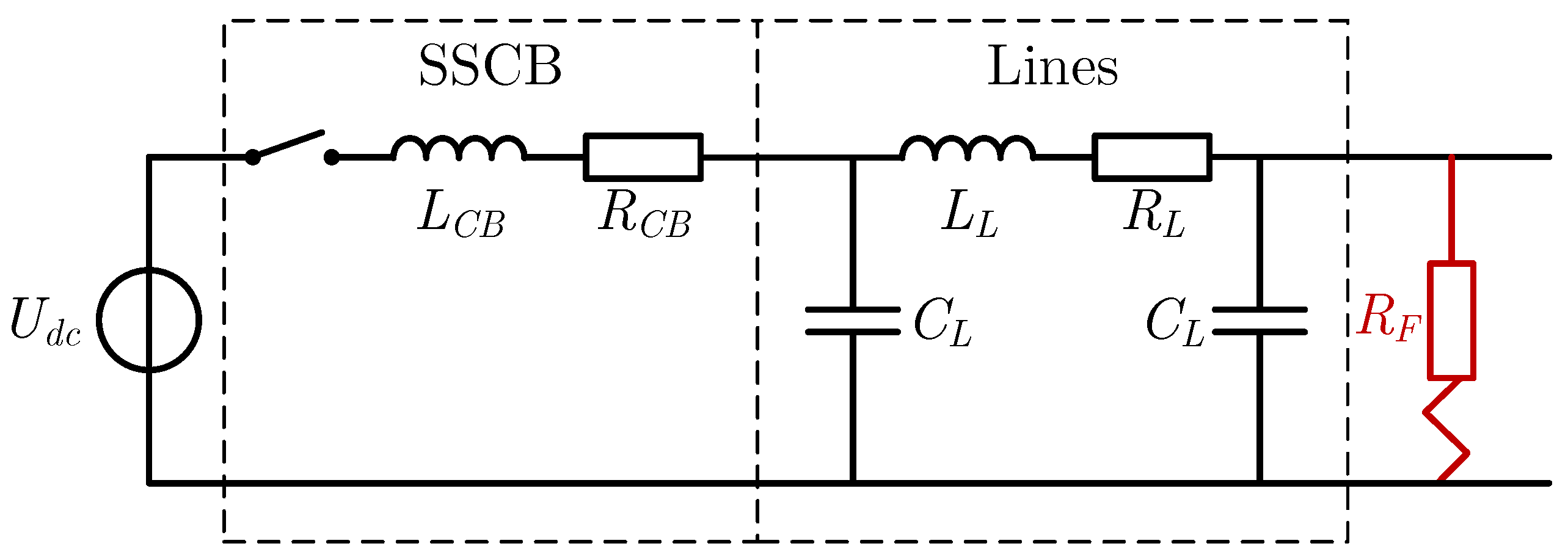
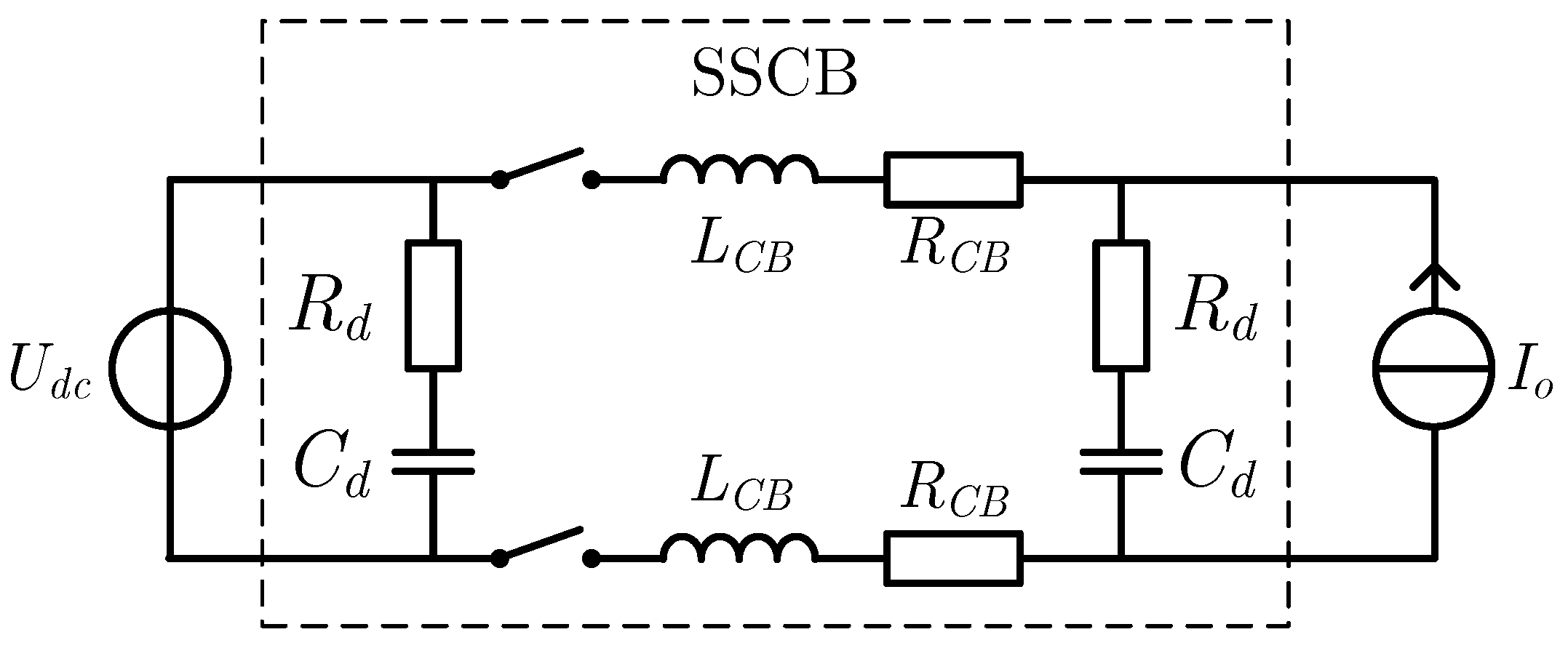
To calculate the short-circuit fault current in a monopolar dc grid, the equivalent circuit in
Figure 1 is used [
18,
21,
25]. The fault current is highest when the voltage on the non-faulted part of the system remains constant, and therefore this part of the system is modelled by a voltage source
. Furthermore, the SSCB is modelled by an ideal switch, its on-state resistance
and its (intrinsic) inductance
. Since the lines in low voltage dc grids are short, the propagation delay can be neglected and lumped element models are sufficiently accurate [
38]. Therefore, the overhead or underground line(s) between the SSCB and the short-circuit are modelled by a lumped element
-model.
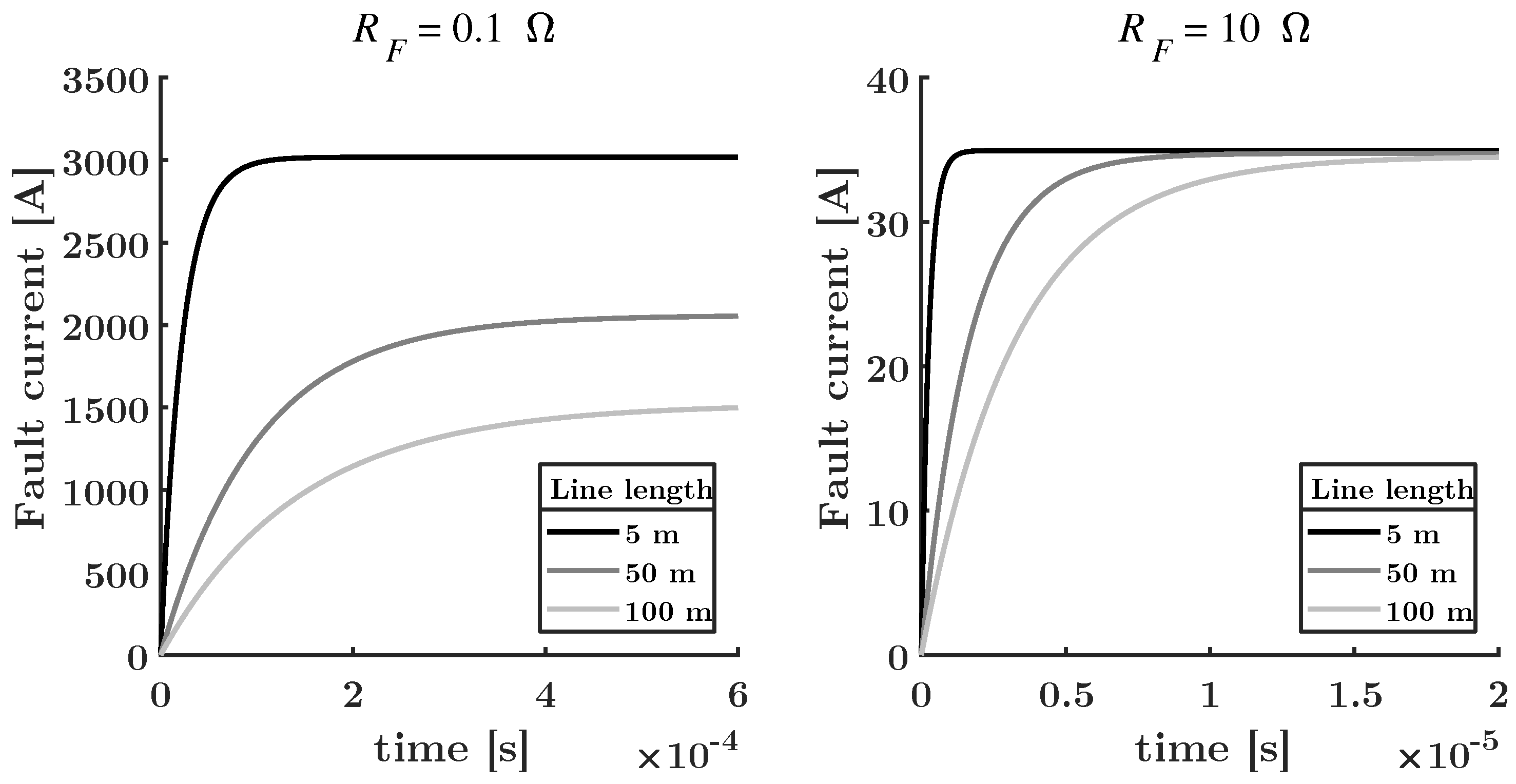
Simulation results for the current during a low resistance fault (0.1
) and a high resistance fault (10
) are shown in
Figure 2. The fault current is shown for different lengths of the distribution line between the SSCB and the fault, which have a typical resistance of 1
/km, an inductance of 0.25 mH/km and a capacitance of 0.5
F/km. Furthermore, during these simulations the grid voltage
is 350 V, the on-resistance
is 0.1
, and the SSCB’s inductance
is 1
H.
Since the capacitance of the line
is small, the fault current can be approximated by
where
is the resistance of the fault.
Note that the steady-state fault current is only determined by the total resistance, which is the reason short-circuit currents are so high in dc grids. Moreover, the line length only has a significant influence on the steady-state current when the fault resistance is low. Furthermore, by differentiating (
1) it becomes clear that the current rate of change is only determined by the sum of the inductances in the system.
The thermal and electrical design of the SSCBs and other components in the grid are dependent on the duration and magnitude of the worst-case fault current that they need to be able to sustain. In the worst case, the short-circuit occurs close to the terminals of the SSCB, making the total inductance close to
. Furthermore, SSCB’s are designed to have as low on-state resistance as possible in order to improve the system’s efficiency. Therefore, if the current before the fault was the nominal current
, the worst-case fault current can be approximated by
where
is the maximum time that the SSCB needs to detect the fault and open its switches.
From (
2) it is clear that, in order to reduce the worst-case fault current, fast fault detection and interruption are essential. Furthermore, even though SSCBs can detect and clear faults within 1
s, a current limiting inductance is often added to SSCBs in order to further limit the maximum fault current. For example, assuming a grid voltage of 350 V, an SSCB clearing time of 1
s, a nominal current of 20 A, and a current limiting inductance of 1
H, the maximum fault current is 370 A.
Since the worst-case fault current develops when the short-circuit occurs at the SSCB’s terminals, this worst-case fault current is not dependent on the system’s parameters or uncertainty in the system. Furthermore, pole-to-pole faults in (grounded) unipolar and bipolar grids exhibit similar behavior to the behavior described in this section, although the resistance and inductance of the return path has to be taken into account. However, because ground faults in these grids have an identical equivalent circuit and behavior, the maximum fault currents in these grids are the same.
4. Non-Unit Protection Scheme Challenges
In the previous section it was shown that faults can be cleared within 1 s by utilizing overcurrent and current rate-of-change detection in combination with an SSCB. Fast and robust fault interruption is possible with such an approach, since no communication infrastructure is utilized. However, in this section it will be shown that achieving selectivity can be challenging when using these non-unit protection methods.
4.1. Fast Fault Propagation
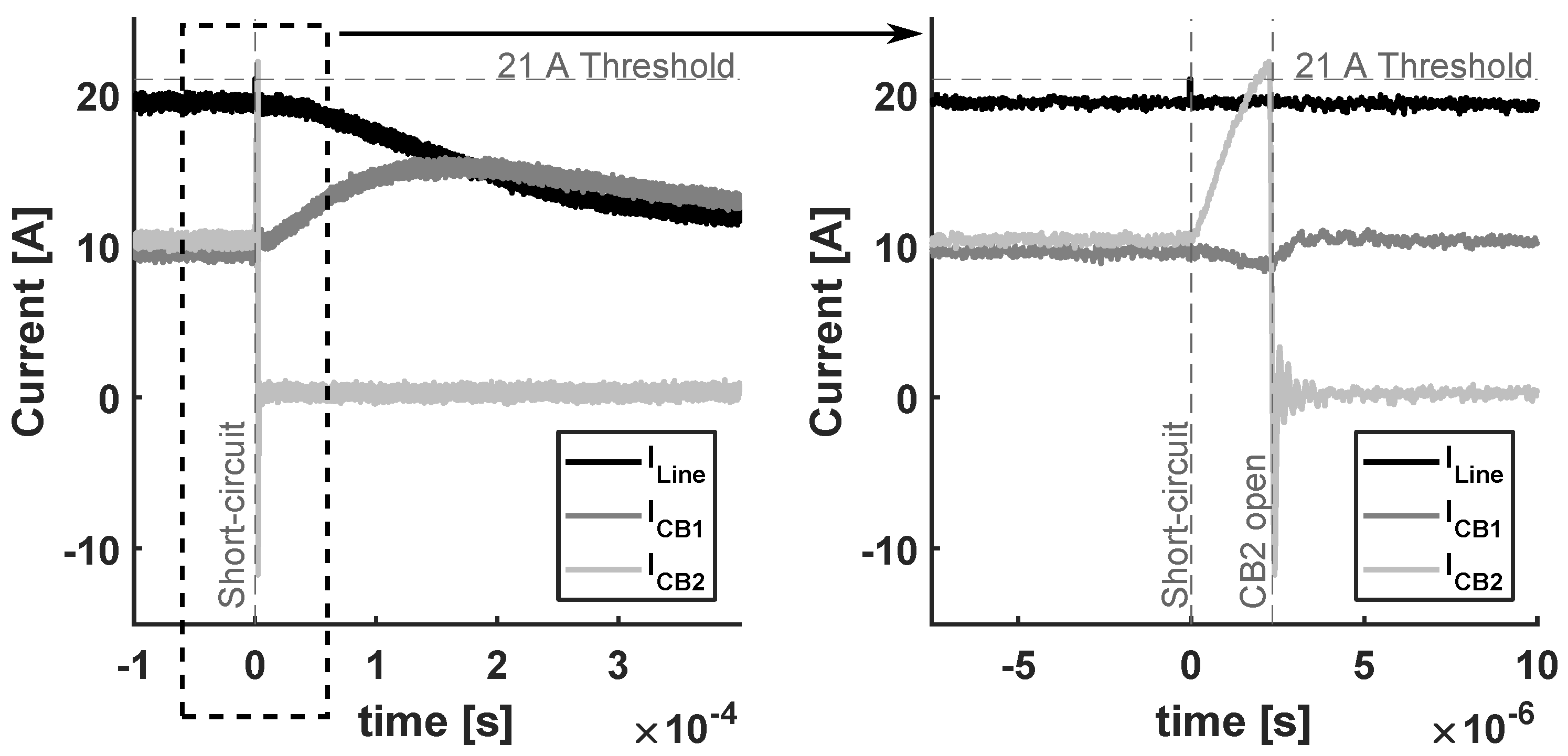
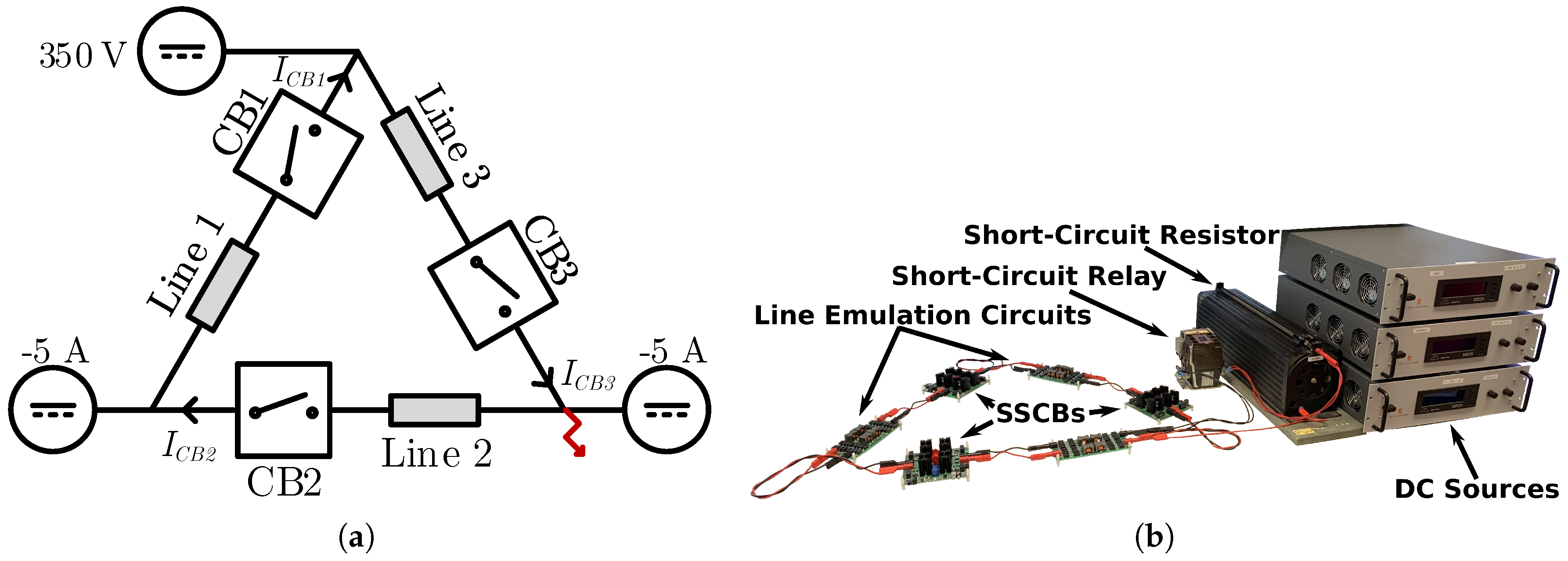
Although the SSCBs current limiting inductance ensures a maximum fault current magnitude, it does not always prevent the fault from propagating through the system and tripping multiple protection devices. To show this the experimental setup shown in
Figure 10 is used.
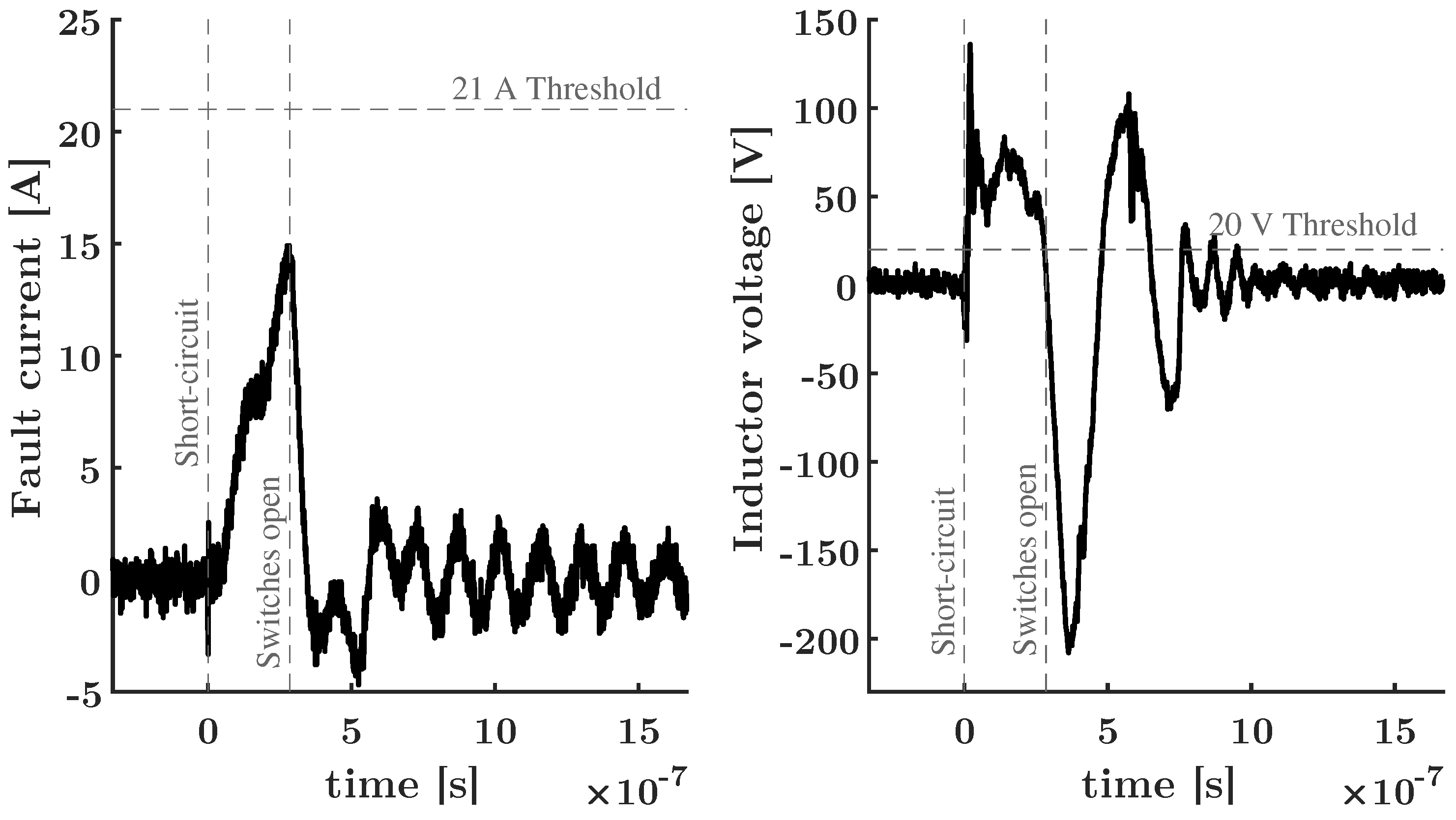
In this setup, a constant voltage source of 350 V and two constant current loads of 5 A are connected to a low inductive dc bus via three SSCBs. This situation can occur, for example, in a dc household that is disconnected from the main grid, where the photovoltaic (PV) panels are providing the energy for loads in two other groups inside the house.
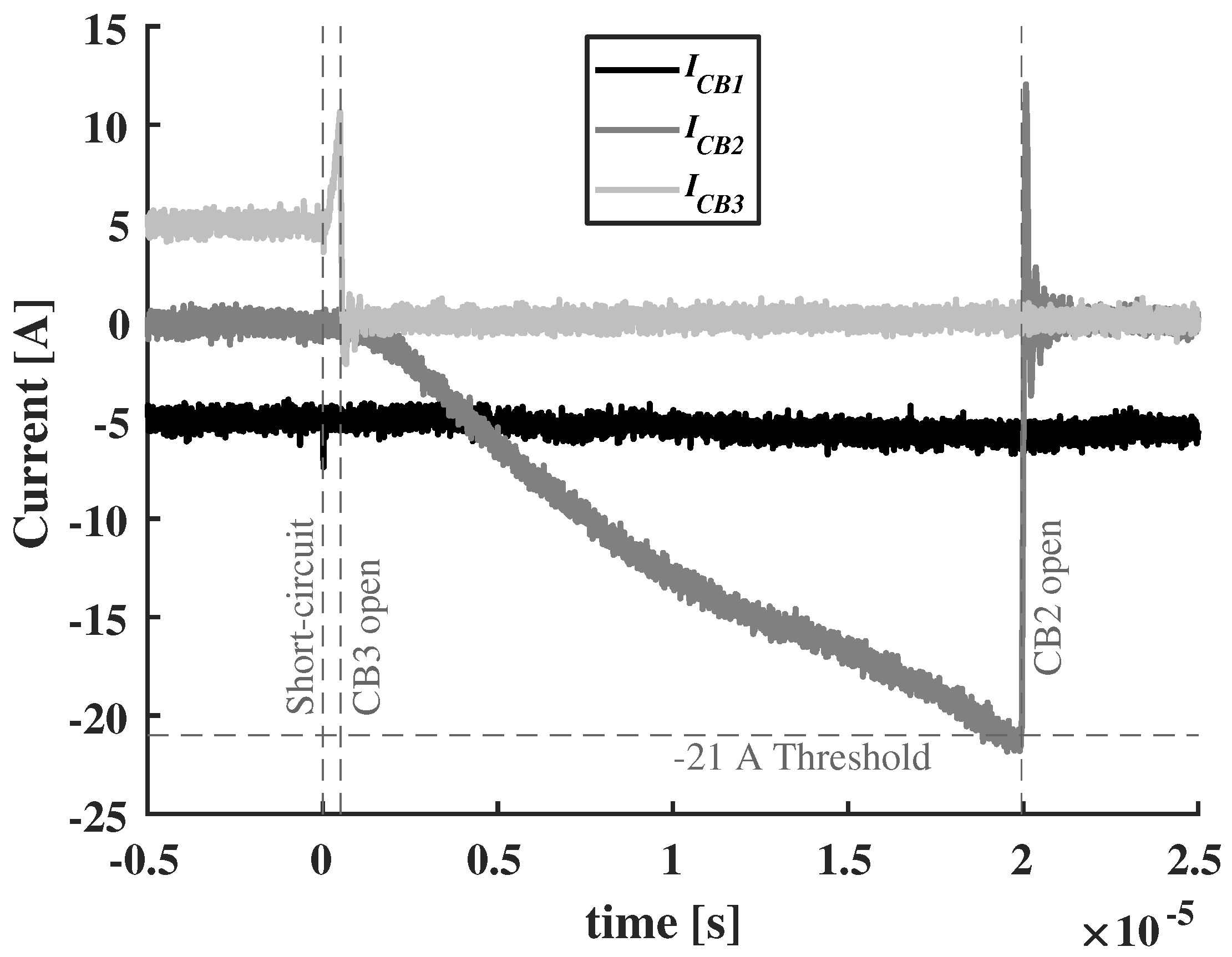
To show that, in some cases, the fault propagates through the system and trips all the SSCBs before the SSCB in the faulted group can react, a short-circuit with a very low fault resistance (0.75
) is induced at the load-side terminal of CB3. The experimental results for the voltage over the current limiting inductance of CB2
and the currents flowing in each circuit breaker are shown in
Figure 11.
Observe that after the short-circuit is induced, the fault current starts flowing from the converters’ output capacitances to the fault. Therefore, the current in CB3 is increasing rapidly, while the currents in CB2 and CB1 are decreasing rapidly. Also note that, although CB2 feeds a load, the discharge of the load converter’s capacitance contributes to the fault current. Furthermore, even though the fault occurs at the load side of CB3, the voltage over the current limiting inductance and CB2 exceeds its threshold before CB3 can act and selectivity is lost.
It is important to realize this is not a consequence of utilizing di/dt detection. If only overcurrent detection is used, the currents in CB1 and CB2 would exceed their limits by the time CB3 clears the fault, because of the high current rate-of-change. Therefore, a challenge for the selectivity of non-unit protection schemes is the fast propagation of low impedance faults through low inductive sections of grids. In radial grids, directional detection can be used to overcome this challenge, but for meshed grids this does not work.
4.2. Commutation of Inductive Currents
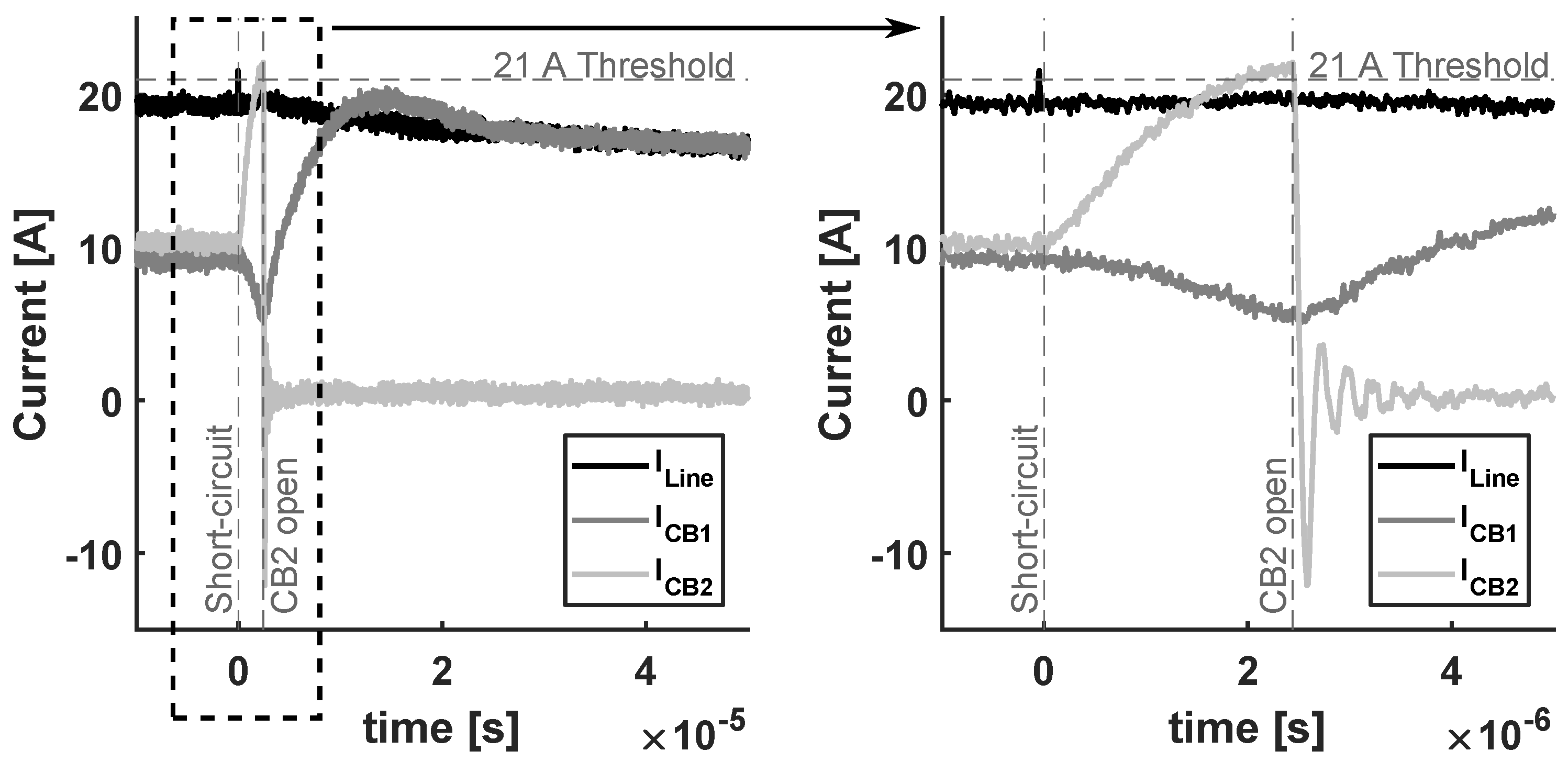
If the current has an alternative path, the interrupting SSCB does not always dissipate the excess inductive energy after clearing the fault. Consequently, for a transient period, the inductive current will flow through the remainder of the system, which can trip other SSCBs in the system. To show this the experimental setup shown in
Figure 12 is used.
For this experiment, a constant voltage source of 350 V is connected to two constant current loads, each consuming 10 A, via an inductive line and two SSCBs. This situation can occur, for example, when a dc household is connected to a main grid. The line in this experiment is emulated by the
-equivalent emulation circuit presented in
Section 3.
To show that, in some cases, commutated inductive currents can trip SSCBs in non-faulted parts of the system, a short-circuit with a short-circuit resistance of 4.0
is induced at the load side of CB2. The current in the line and the currents in the circuit breakers for this experiment are shown in
Figure 13.
Note that, after the short-circuit occurs, the fault current starts flowing from the output capacitances of the converters. Therefore, the currents in the line and CB2 rise quickly, while the current in CB1 decreases rapidly, until the threshold of CB2 is exceeded. Subsequently, after CB2 opens, the inductive current in the line (that was first shared by CB1 and CB2) is commutated to CB1 almost immediately and its di/dt detection is tripped and selectivity is lost. However, if the di/dt measurement was not tripped, the overcurrent detection would have also been tripped since the current through CB1 also briefly exceeds 21 A. Afterwards, since the inductive line current does not have an alternative path, the inductive energy is dissipated in CB1’s MOV’s.
When SSCBs are operating near their rated current, the commutation of inductive currents would likely cause a cascade tripping circuit breakers in the system. Moreover, this challenge cannot be solved by directional detection, even in radial systems. Therefore, the commutation of inductive currents poses a challenge for the selectivity of non-unit protection schemes.
5. Proposed Plug-and-Play Protection Scheme
The previous section presented two challenges for the selectivity of non-unit protection schemes. These challenges can be tackled by utilizing communication, but communication will likely slow down fault detection. Furthermore, (directional) thresholds could be designed to prevent unnecessary tripping, but doing so would require knowledge about the system’s topology and parameters. Therefore, in order to achieve selective protection for plug-and-play low voltage dc grids, an alternative approach is proposed.
5.1. Proposed SSCB Topology to Delay Fault Propagation
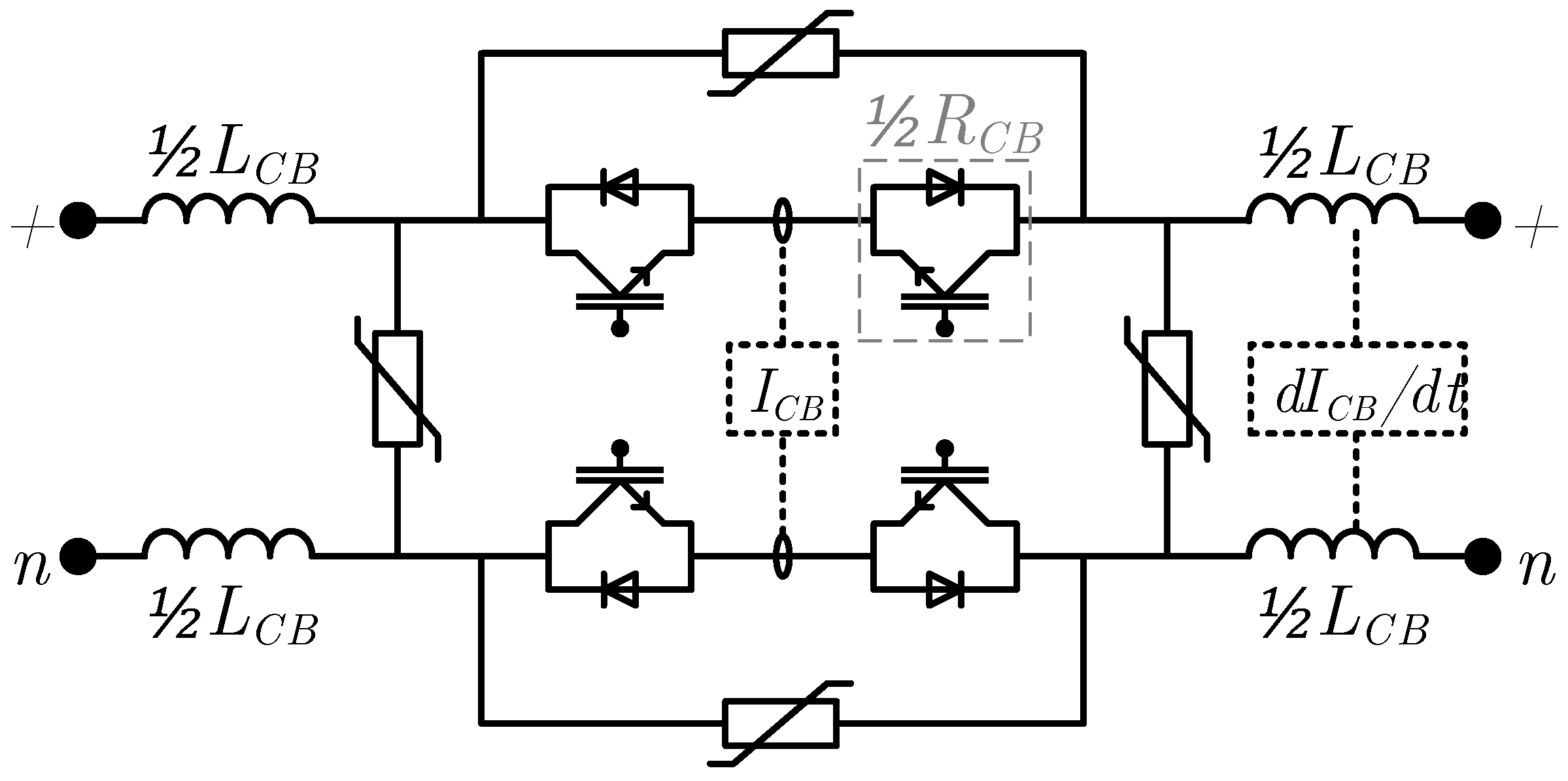
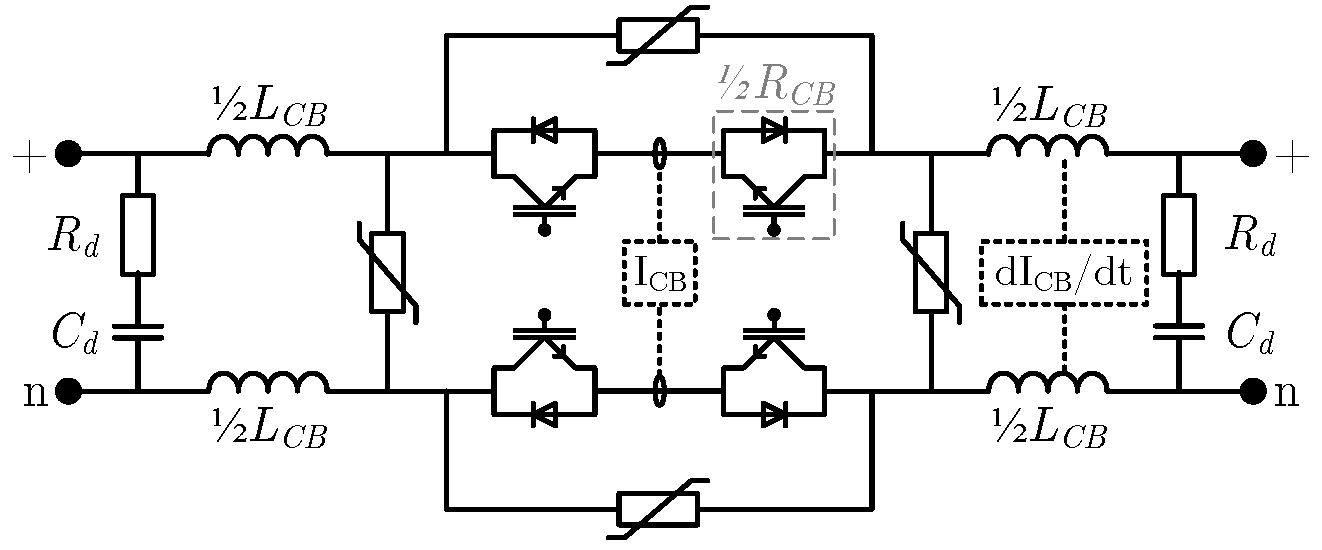
It is proposed to append the SSCB topology with an RC damper on each terminal, as is shown in
Figure 14. The purpose of the dampers’ capacitance is to temporarily provide a low impedance path for fault currents and commutated inductive currents, delaying their propagation. Consequently, before a fault current can flow on the non-faulted side of the SSCB the damper capacitor on the non-faulted side of the SSCB must be discharged through the current limiting inductance. Similarly, a (commutated) current must first charge the damper capacitor before current can flow in the current limiting inductance. Therefore, the propagation of these currents is delayed, providing time for the SSCBs in the faulted areas to clear the fault and smoothing the commutation of inductive currents. However, if just a capacitance was added, high frequency oscillations with low damping could occur between the damper capacitors through the current limiting inductance, since the on-state resistance of the switches is small. Therefore, resistances are added to the dampers in order to attenuate these oscillations.
In the proposed topology, the RC dampers together with the current limiting inductance essentially form a low-pass LCR filter. The inductance, resistance and capacitance of this LCR filter are
,
and
respectively. Making a loop inside the SSCB, the sum of the voltages over the damper capacitors, damper resistors, on-state resistances and current limiting inductances must be zero. Therefore, the differential equation for the inductor current is given by
Differentiating this equation, and dividing by
yields
Applying the Laplace transform on this equation results in
where
s is a complex variable representing attenuation and frequency in the Laplace domain (
), and
is the initial condition for the first derivative of the current. Consequently, the transfer function of this system is given by
The resonant frequency
and attenuation frequency
of this standard second-order system are
which will be used later in this section to provide design guidelines for the damper parameters.
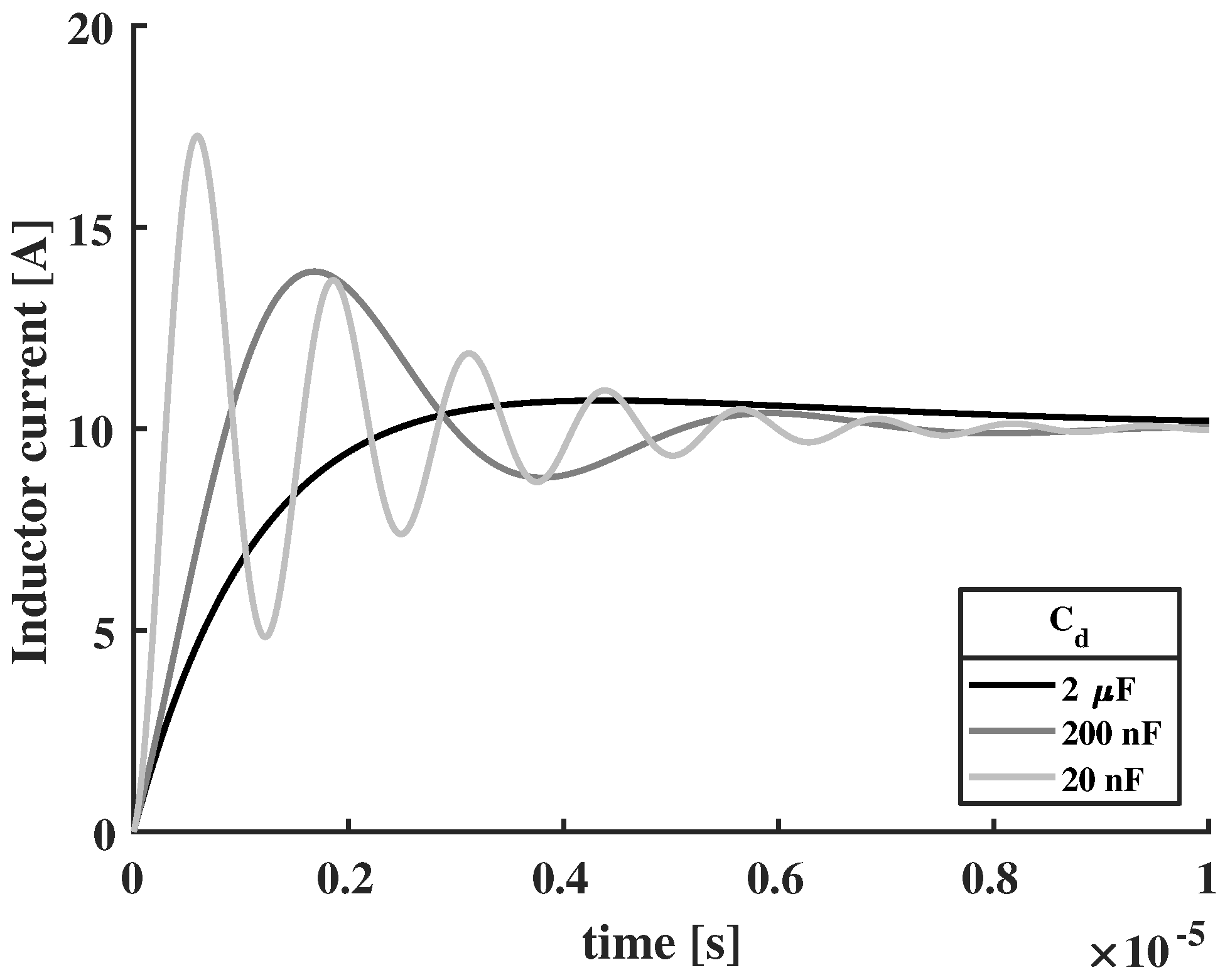
Note that, the higher damper capacitor, the lower the resonant frequency of the SSCB’s LCR circuit and the longer the SSCB will delay the propagation of fault currents. From a different perspective, a higher damper capacitance can provide the energy for the fault current for a longer time.
An additional benefit of the damper capacitance is that it delays and smoothes the commutation of an (inductive) current. This is illustrated by simulating the inductor current in the circuit from
Figure 15. For the simulations the grid voltage
is 350 V, the on-resistance
is 0.1
, the SSCB’s inductance
is 1
H, and the damper resistance
is 2
. The simulation results for the current in the SSCB’s inductors, when the current
is stepped up from 0 to 10 A at
, are given in
Figure 16.
The simulation results show that the damper capacitance absorbs the forced current, delaying the current from flowing inside the SSCB. It also illustrates that, at lower damper capacitances, current overshoot and underdamped high frequency oscillations can occur.
5.2. Proposed Time-Current Characteristic
In ac systems selective coordination between upstream and downstream circuit breakers is often achieved in radial systems by using time-current characteristics for the protection devices. Time-current characteristics depict how long a protection device allows a current to flow before it interrupts it, and they are mainly determined by the thermal and magnetic characteristics of the circuit breakers. The upstream and downstream time-current characteristics are chosen in such a way that the downstream circuit breaker clears the fault first, and the upstream circuit breaker only clears the fault when the downstream circuit breaker fails.
It was shown in the previous section that the commutation of inductive currents can cause the undesired tripping of SSCBs in non-faulted sections. Therefore, coordination among downstream circuit breakers is also required, not just between upstream and downstream SSCBs. Furthermore, since this paper aims for a plug-and-play protection scheme, the coordination must also achieve selectivity in meshed low voltage dc grids.
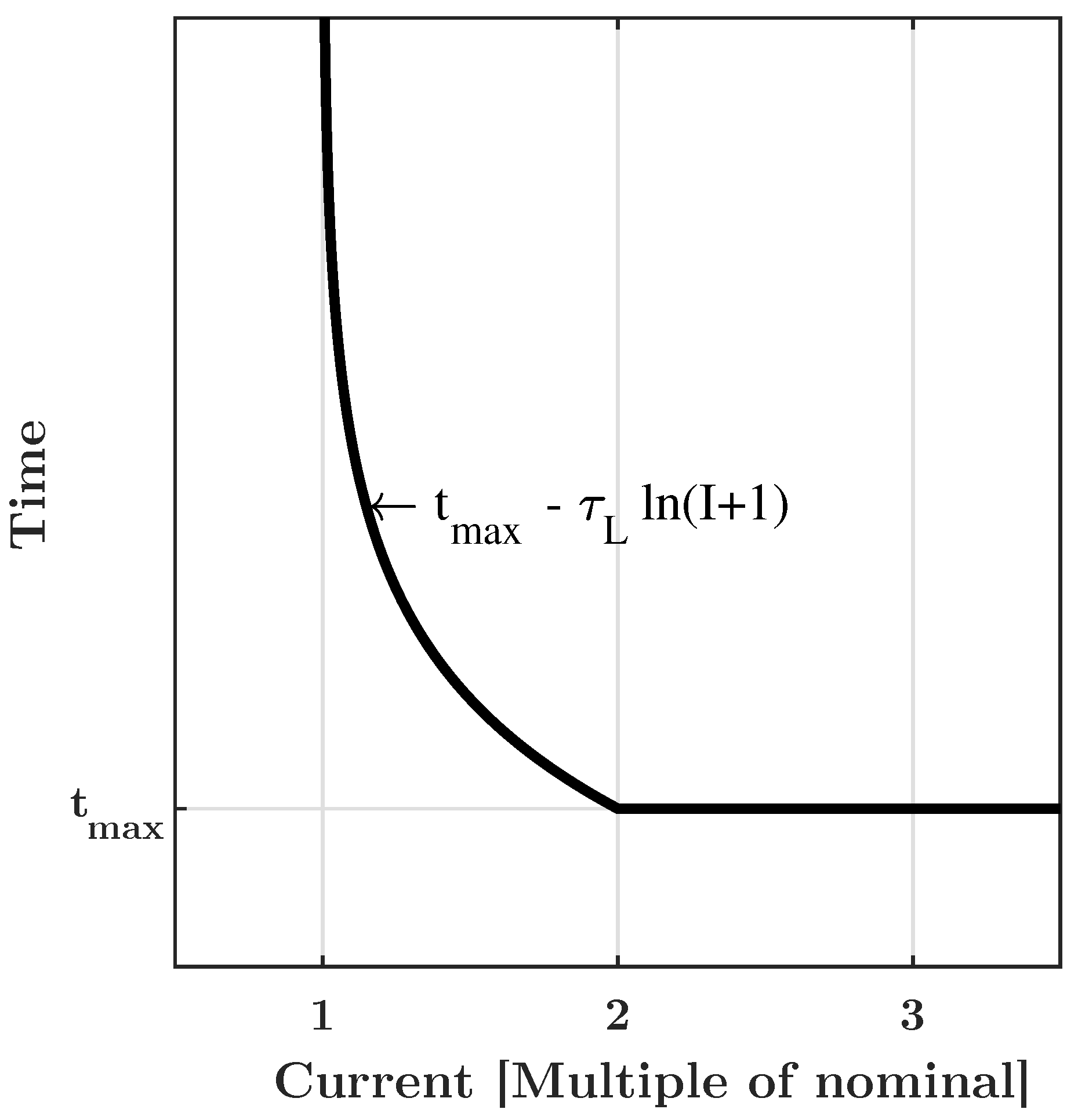
To prevent unnecessary tripping due to commutated currents, the time-current current characteristic must take this current and its decay into account. In the worst-case, the commutated current is the nominal current and this current decays with the time constant of the line. If the SSCB is carrying the nominal current before commutation, the worst-case current after commutation is characterized by the LR time constant and is given by
Therefore, in order to prevent the SSCB from tripping unnecessarily from commutated inductive currents, the proposed characteristic only interrupts immediately if the current exceeds twice the nominal current. Furthermore, between
and
, the time-current characteristic is chosen as
where
is the maximum time the SSCB takes to detect and clear an overcurrent, and
I is the current in the SSCB in multiple of the nominal current.
Note that it is only necessary to know the slowest expected time constant of the lines in the system. Therefore, knowledge about the length of the lines in the system or their interconnection is not required. Moreover, a safety margin can be implemented in order to anticipate uncertainty in the system parameters. The proposed time-current characteristic for SSCBs is shown in
Figure 17.
Because the time-current characteristic scales with nominal current, the proposed time-current characteristic inherently coordinates upstream and downstream SSCBs. To illustrate this, imagine the system of
Figure 12 with an upstream SSCB that has a nominal current of 32 A and two downstream SSCBs that have a nominal current of 16 A. Now if all the SSCBs operate at their nominal current and a fault occurs downstream, the downstream SSCB will trip immediately when the current reaches 32 A. In this case the upstream current is 48 A, for which the upstream breaker will wait a significant time.
5.3. Plug-and-Play Design Guidelines
In the previous subsections a solid-state circuit breaker topology and time-current characteristic were proposed in order to ensure selectivity. In this subsection it is described how these concepts can be incorporated in an SSCB, with a nominal current of and a nominal voltage of , in order to achieve system-wide plug-and-play protection selectivity.
The SSCB’s di/dt detection is tripped if the voltage over the current limiting inductance is more than
. However, in the worst case the voltage is still
for
. Therefore, assuming a sawtooth shaped pulse, the required current limiting inductance is determined by
where
is the current carrying capability of the semiconductor switches for a
pulse, which usually is several times higher than then nominal current of the switches.
When the current is above two times the nominal current, the clearing time is given by
, while for currents between one and two times the nominal current (
10) is used to determine the clearing time. Consequently, the maximum current when the overcurrent protection is tripped is given by
Although lowering the di/dt threshold
decreases the maximum fault current, the detection will also become more sensitive to, for example, electromagnetic interference. The authors found a reasonable threshold voltage to be around
In general, changes in load current will not trigger the di/dt detection with this threshold, since the time constants of distribution lines and power electronic converters are several orders of magnitude higher than the time constant of the SSCB.
The topology that is used for the SSCB is shown in
Figure 14, where the MOVs clamp the voltage to below the maximum rating of the switches. Alternatively, other circuits can be used to limit the voltage on the switches. Regardless, the rating of the clamping circuits determines the maximum inductive energy that the SSCBs can dissipate.
To size the damper components (
7) and (
8) are used. To ensure a smooth commutation of inductive current and prevent instant fault propagation, the resonant frequency of the SSCB is chosen to be an order of magnitude lower than the inverse of the maximum clearing time
(in this paper a factor of 10 is chosen). The damper capacitor is then given by
For a damped response, the damper resistance is sized such that the attenuation frequency is higher than the resonant frequency. Therefore,
If possible, in order to clamp the voltage over the inductor to below the threshold voltage during commutation, the damper resistance should also be
Utilizing these guidelines, the parameters of the SSCB in this paper are given in
Table 2. As a consequence of the damper capacitance and damper resistance, the resonant frequency
of the SSCB is 113 kHz and the attenuation frequency
is 170 kHz. Furthermore, the maximum steady-state losses in the SSCB are 26 W, which is only around 0.7% of the conducted power. Moreover, the losses in the SSCB can be reduced even further by, for example, parallelling multiple semiconductors.
6. Experimental Validation of the Plug-and-Play Protection Scheme
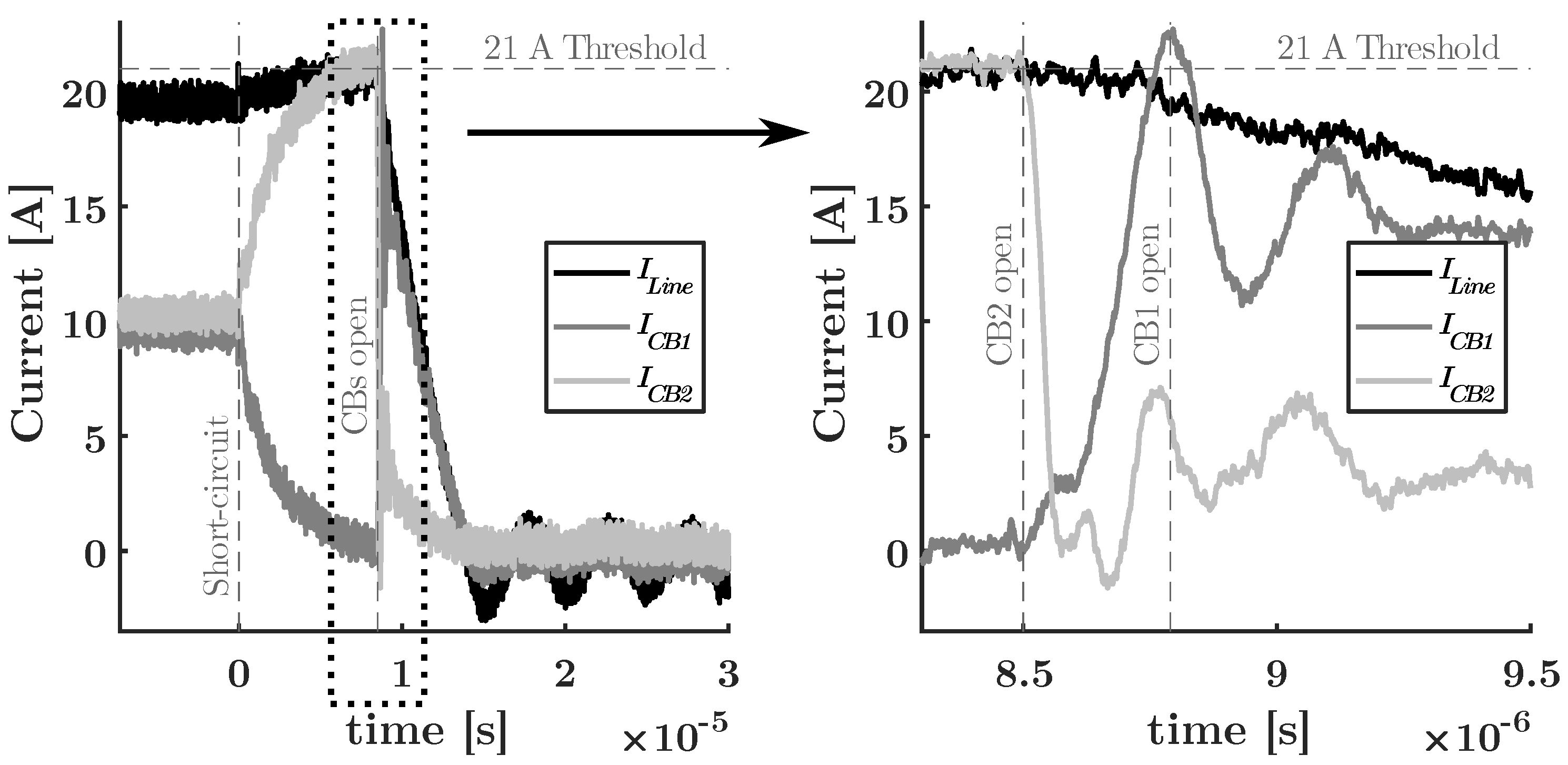
To show that the plug-and-play SSCBs delay the propagation of the fault, the experiment shown in
Figure 10 is repeated. The experimental results for the currents in the SSCBs for this experiment are shown in
Figure 18. Observe that, contrary to the experiment in
Figure 11, only CB3 is tripped, while the currents in the other SSCBs are largely unaffected by the whole process. The current rises fast until the switches of CB3 are opened, after which CB1 and CB2 remain closed. Furthermore, it is seen that the oscillations in the system are attenuated significantly because of the RC dampers.
To show that the plug-and-play SSCBs ensure smooth commutation and selectivity, the experiment shown in
Figure 12 is repeated. The experimental results for the SSCBs’ currents for this experiment are shown in
Figure 19. Note that the commutation of the inductive current is smoothed out over roughly a 10
s interval, which is an order of magnitude longer than in
Figure 13. Furthermore, although the inductive current is commutated to CB1, its thresholds are not exceeded and therefore its fault detection is not tripped.
From the previous experiment, it is clear that the plug-and-play protection scheme accounts for commutated currents, but does not prevent them. The addition of a significant capacitance at the interface of the SSCBs can reduce the commutated current by (temporarily) storing the inductive energy. The experimental results for the same experiment, but with an added 240
F capacitance at the interface of the SSCBs, is shown in
Figure 20. The commutated current is reduced, but applying this solution in a plug-and-play fashion is impractical, since information about the system’s capacitances and inductances is required. Therefore, this paper adopted the proposed time-current characteristic.
To show that the decentralized plug-and-play protection scheme also works for meshed systems, the experiment shown in
Figure 21 is used. The setup consists of a constant voltage source of 350 V connected to two 5 A constant current loads in a ring configuration. The lines in this system are emulated by equivalent
-circuits described in
Section 3. This situation can occur, for example, when dc households are interconnected.
The experimental results for the currents inside the SSCBs, when a short-circuit with a fault resistance of 2.5
is induced at the load-side terminals of CB3, are given in
Figure 22. Observe that the fault current is first mostly supplied by the damper capacitances of CB3 because this path contains the lowest inductance, and consequently CB3’s di/dt detection is triggered. Subsequently, the fault current is supplied mainly by the capacitance of the load in the non-faulted part of the system through CB2 and its overcurrent detection is triggered after around 20
s. Most importantly, CB1 is not triggered and the non-faulted section of the grid remains operational.
Discussion
The experimental results show that the proposed decentralized plug-and-play protection scheme ensures selectivity for different dc grids under various conditions. Firstly, the systems were tested with varying impedance between the sources and the faults. In the experiments, short-circuits with low fault impedance generally trip the di/dt detection, while short-circuits with high fault impedance generally trip the overcurrent detection. Secondly, the experiments showed that the SSCBs are capable of interrupting non-inductive and inductive fault currents, dissipating the inductive energy in the MOV’s when there is no alternative path for inductive currents. Thirdly, it is shown that the protection scheme achieves this for both radial and meshed systems.
The main advantages of the proposed protection scheme are that no communication infrastructure is required and that only minimal knowledge about the system is needed. Furthermore, because the SSCBs are designed for the worst-case scenario, the approach is not sensitive to uncertainties and disturbances in the system. Moreover, the protection scheme is resilient to failures, since upstream circuit breakers trip if downstream circuit breakers fail. Additionally, it is important to note that the RC dampers do not increase the steady state losses of the SSCBs, although they slightly increase losses during transient situations.
The main disadvantage of the proposed protection scheme is that the components in the system need to sustain twice the nominal current for up to . Furthermore, the worst-case time constant of the lines in the system need to be known, although this is not influenced by the length of the lines or their configuration. Moreover, care must be taken that the normal behavior of sources and loads, such as inrush currents, does not cause unnecessary tripping. However, the time-current characteristic can be adapted to avoid tripping on these events. Additionally, although solid-state circuit breakers solve a lot of challenges with regards to the protection of dc grids, they are still relatively inefficient and expensive compared to mechanical circuit breakers.
For the industrial application of the proposed plug-and-play SSCBs, different design considerations can be made. For example, the SSCB’s current can be measured utilizing the voltage over the switches instead of using a high-bandwidth hall-sensor, or the di/dt measurement can be omitted in order to reduce complexity. Furthermore, semiconductor switches with lower cost or lower on-state resistance can be used, or multiple switches can be put in parallel or series. Overall, trade-offs can be made for the electrical performance of the SSCB versus its cost. However, detailed cost analysis and optimization of SSCBs were outside of the scope of this paper.
The proposed plug-and-play protection scheme provides a solid foundation for the protection of low voltage dc systems. In future research, the scheme’s applicability to systems with longer distribution lines, such as medium and high voltage transmission systems, can be investigated. In those studies the impact of the propagation delay on the effectiveness of the approach must be examined. Furthermore, more cost and energy efficient solid-state circuit breaker topologies must be explored. Moreover, it can be researched how the SSCBs can provide additional functionality, such as controlling the power flow and black-starting dc grids. Additionally, a communication infrastructure can be used to improve performance or add functionality.
7. Conclusions
The lack of a zero-crossing makes interrupting inductive currents more challenging in dc grids than in conventional ac grids. Furthermore, fast fault interruption is often required for low voltage dc grids in order to reduce the current stress on the components in the grid and prevent blackouts. Moreover, meshed topologies and bi-directional power flow complicate fault detection and selectivity. To ensure selectivity, literature presents several schemes that rely on communication, or knowledge about the system’s topology and parameters. However, fast fault interruption is difficult when communication is used, and systems are subject to uncertainty and change.
Because of the fast fault interruption and meshed system structures, it is difficult to ensure protection selectivity in low voltage dc grids with non-unit protection schemes. It was experimentally shown that the current and current rate of change of circuit breakers in non-faulted regions of the grid can exceed their thresholds before the faulted circuit breakers can clear the fault. Furthermore, interrupted inductive currents temporarily commutate to healthy parts of the system, causing overcurrents. As a consequence of these two phenomena, undesired tripping can occur of circuit breakers in non-faulted parts of the system.
This paper proposes a decentralized plug-and-play protection scheme that ensures security and selectivity, without utilizing communication and with minimal knowledge of the system. The protection scheme delays fault propagation by introducing RC dampers at both ends of the solid-state circuit breaker, which then forms a second order filter for the fault. Furthermore, commutated inductive overcurrents are ignored by incorporating the lines’ worst time constant into a time-current characteristic. Additionally, design guidelines were provided for the proposed solid-state circuit breaker topology. Several experiments were carried out that showed that the proposed protection scheme provides secure and selective fault interruption for radial and meshed low voltage dc grids.
Although the proposed protection scheme provides an effective and robust solution, further research is still required. The effectiveness of the protection scheme for medium and high voltage grids must be investigated. Moreover, more research is required on solid-state protection devices, since they are still inefficient and expensive compared to their mechanical counterparts. Additionally, SSCBs have potential for providing additional functionality to the grid, with or without utilizing a communication infrastructure.