Direct Power Control of a Single Stage Current Source Inverter Grid-Tied PV System
Abstract
1. Introduction
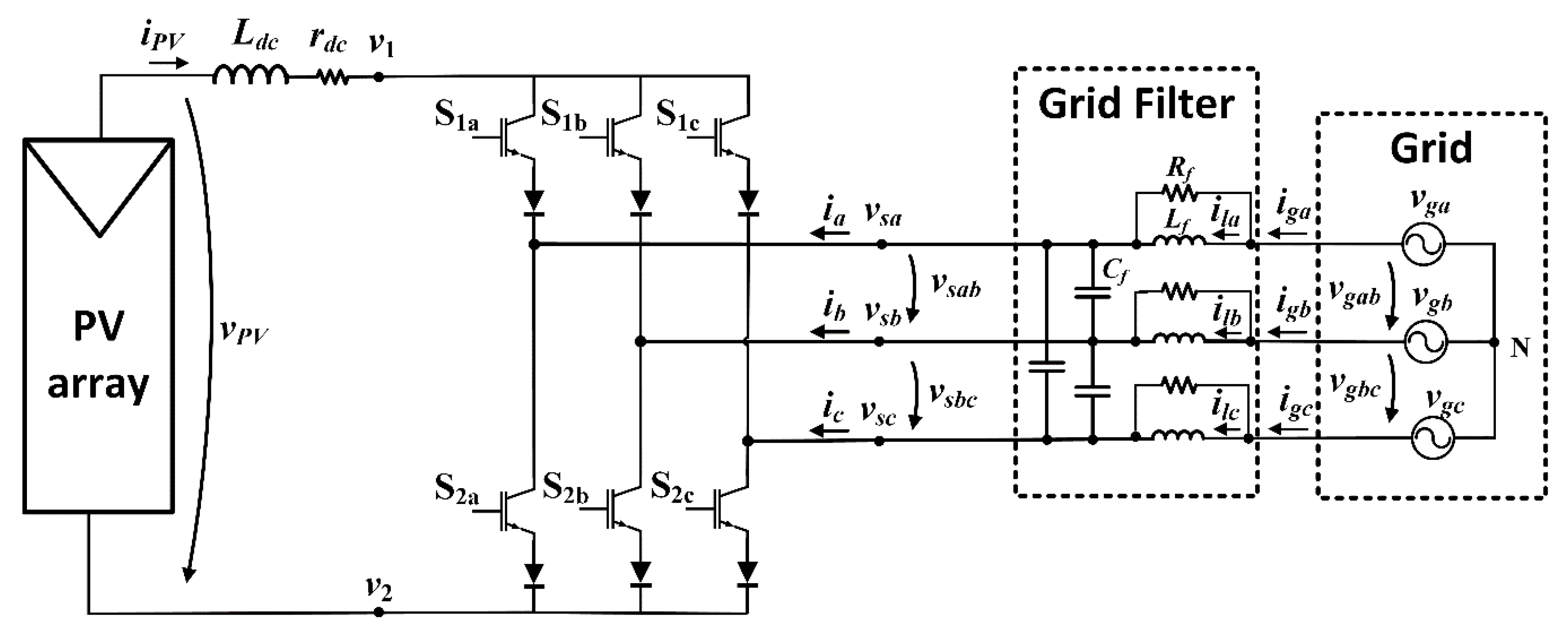
2. System Description
2.1. PV Array Model
2.2. Current Source Inverter Model
2.3. Equations of PV Power Dynamics
2.4. Equations of the Dynamics of Active and Reactive Power in the Connection to the Grid
3. Design of the Direct Power Predictive Controller
3.1. Prediction of the PV Power
3.2. Prediction of Active and Reactive Power in the Connection to the Grid
3.3. Cost Function and Selection of Swtiching Vector
4. Results
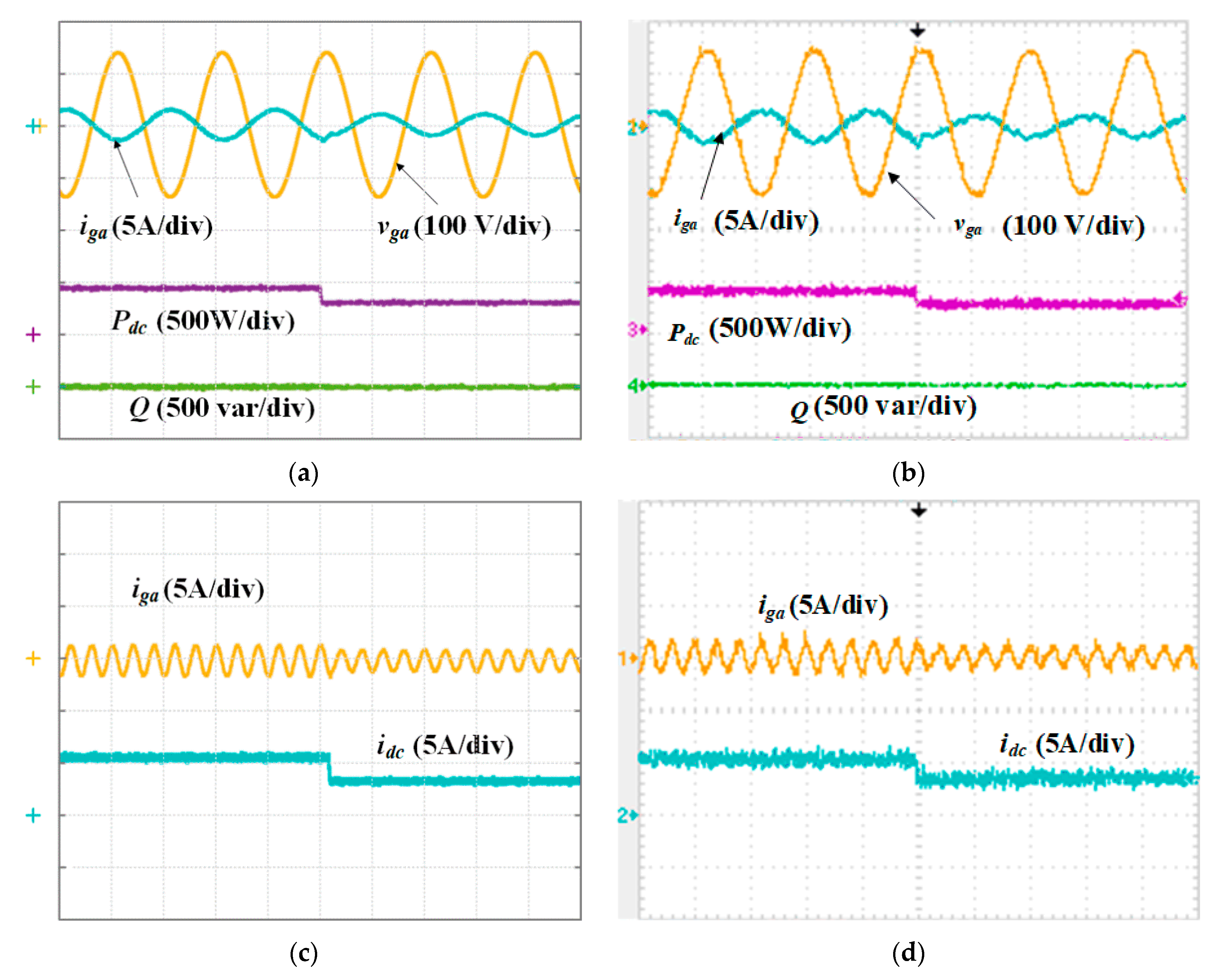
4.1. Response to a Step in Power
4.2. Active Power and Reactive Power Control Using DPPC
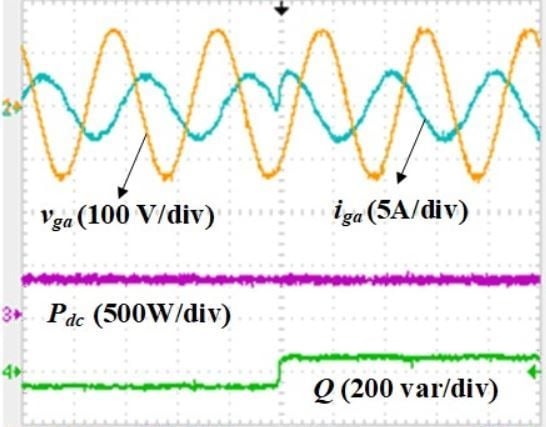
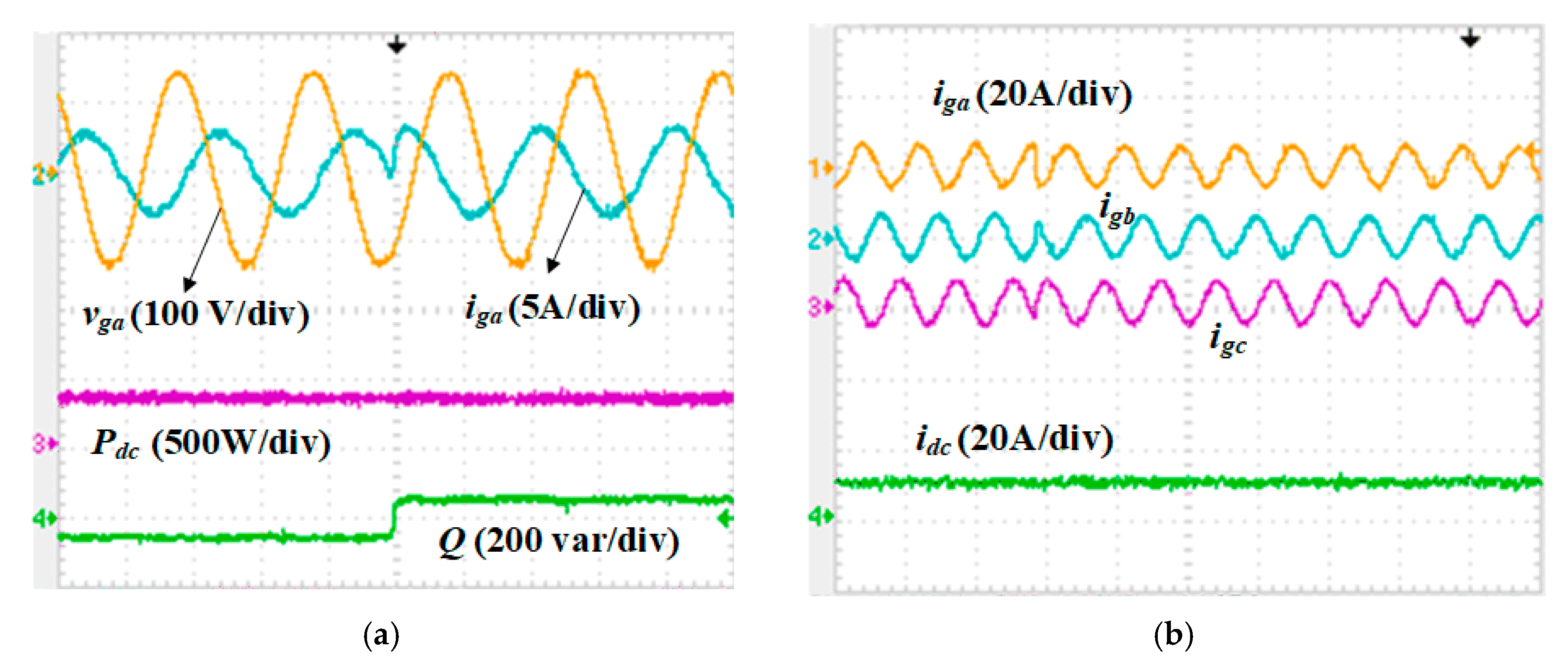
4.2.1. Step in the Reactive Power Q (Leading and Lagging)
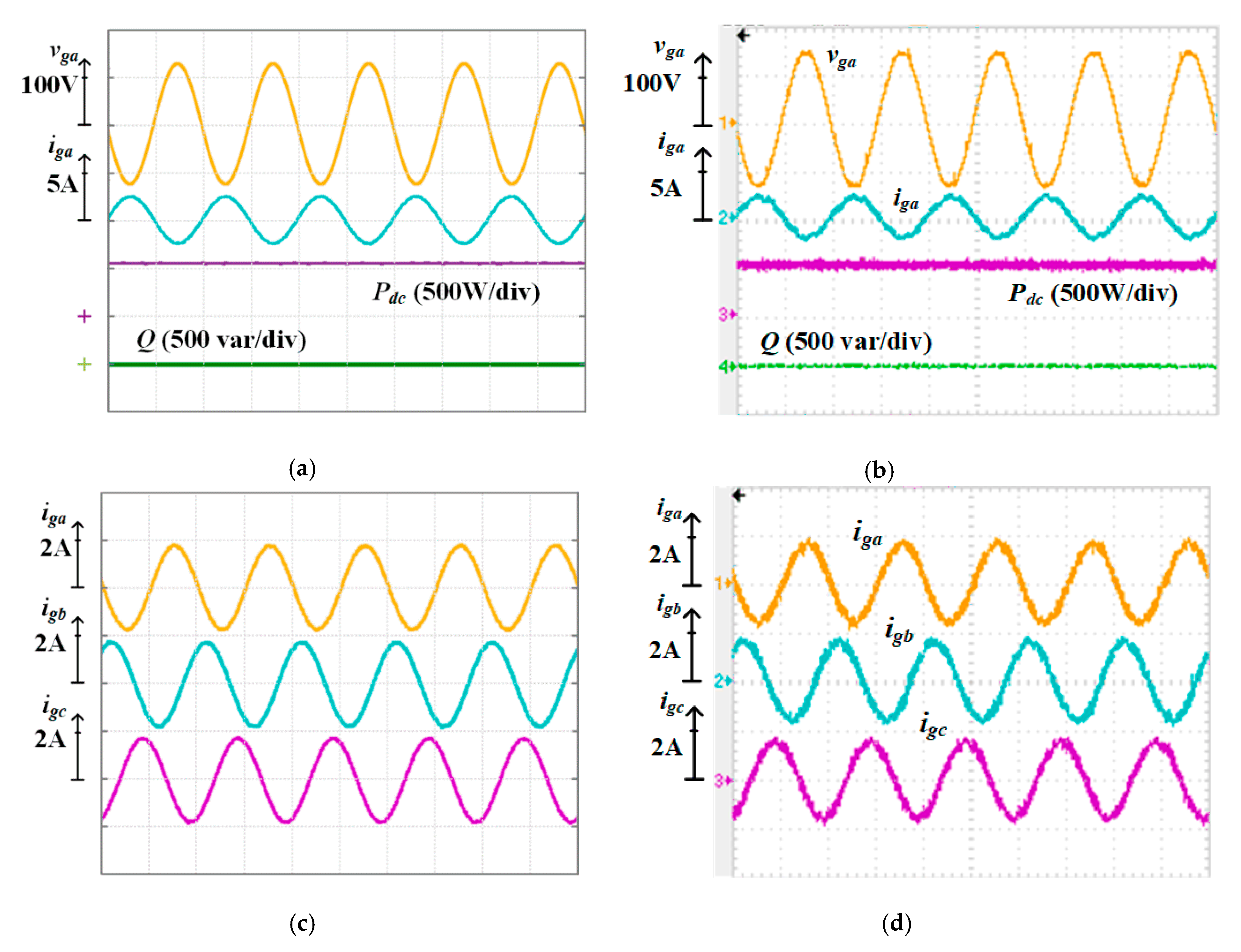
4.2.2. PV Power Profile Control
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Mancarella, P. Towards sustainable urban energy systems: High resolution modelling of electricity and heat demand profiles. In Proceedings of the 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, NSW, Australia, 28 September–1 October 2016; pp. 1–6. [Google Scholar]
- REN21. Connecting the Dots. Available online: http://www.ren21.net/ (accessed on 22 November 2018).
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Bae, Y.; Vu, T.; Kim, R. Implemental Control Strategy for Grid Stabilization of Grid-Connected PV System Based on German Grid Code in Symmetrical Low-to-Medium Voltage Network. IEEE Trans. Energy Convers. 2013, 28, 619–631. [Google Scholar] [CrossRef]
- Momeneh, A.; Castilla, M.; Miret, J.; Martí, P.; Velasco, M. Comparative study of reactive power control methods for photovoltaic inverters in low-voltage grids. IET Renew. Power Gener. 2016, 10, 310–318. [Google Scholar] [CrossRef]
- IEEE Standard 1547-2018. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; The Institute of Electrical and Electronics Engineers Standards Association: Piscataway, NJ, USA, 2018. [Google Scholar]
- Standard IEC 61000-3-2:2018. Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤16A per Phase); International Electrotechnical Comission: Geneva, Switzerland, 2018. [Google Scholar]
- IEEE Standard 519-2014. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Power and Energy Society; The Institute of Electrical and Electronics Engineers Standards Association: Piscataway, NJ, USA, 2014. [Google Scholar]
- Standard IEC 61727. Photovoltaic (PV) Systems—Characteristics of the Utility Interface; International Electrotechnical Comission: Geneva, Switzerland, 2004. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Requirements for PV. In Grid Converters for Photovoltaic and Wind Power Systems; John Wiley and Sons Ltd.: Chichester, UK, 2011; pp. 32–42. [Google Scholar]
- Al-Shetwi, A.Q.; Sujod, M.Z. Grid-connected photovoltaic power plants: A review of the recent integration requirements in modern grid codes. Int. J. Energy Res. 2018, 42, 1849–1865. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Pou, J.; Agelidis, V.G. Single- and two-stage inverter-based grid-connected photovoltaic power plants with ride-through capability under grid faults. IEEE Trans. Sustain. Energy 2015, 6, 1150–1159. [Google Scholar] [CrossRef]
- Liang, X. Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Meneses, D.; Blaabjerg, F.; García, Ó.; Cobos, J.A. Review and Comparison of Step-Up Transformerless Topologies for Photovoltaic AC-Module Application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef]
- Buticchi, G.; Barater, D.; Lorenzani, E.; Concari, C.; Franceschini, G. A Nine-Level Grid-Connected Converter Topology for Single-Phase Transformerless PV Systems. IEEE Trans. Ind. Electron. 2014, 61, 3951–3960. [Google Scholar] [CrossRef]
- Shayestegan, M. Overview of grid-connected two-stage transformer-less inverter design. J. Mod. Power Syst. Clean Energy 2018, 6, 642–655. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters—An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef]
- Bindra, A. Wide-Bandgap-Based Power Devices: Reshaping the power electronics landscape. IEEE Power Electron. Mag. 2015, 2, 42–47. [Google Scholar] [CrossRef]
- Costa, P.; Silva, J.F.; Pinto, S. Experimental evaluation of SiC MOSFET and GaN HEMT losses in inverter operation. In Proceedings of the IECON 2019, 45th Annual Conference of IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar] [CrossRef]
- Jain, S.; Agarwal, V. A Single-Stage Grid Connected Inverter Topology for Solar PV Systems with Maximum Power Point Tracking. IEEE Trans. Power Electron. 2007, 22, 1928–1940. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, Z.; Liu, J. A Single-Stage Three-Phase Grid-Connected Photovoltaic System with Modified MPPT Method and Reactive Power Compensation. IEEE Trans. Energy Convers. 2007, 22, 881–886. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F.; Simões, M.G.; Yang, Y. Power control flexibilities for grid-connected multi-functional photovoltaic inverters. IET Renew. Power Gener. 2016, 10, 504–513. [Google Scholar] [CrossRef]
- Dash, P.P.; Kazerani, M. Dynamic modeling and performance analysis of a grid-connected current-source inverter-based photovoltaic system. IEEE Trans. Sustain. Energy 2011, 2, 443–450. [Google Scholar] [CrossRef]
- Klumpner, C. A new single-stage current source inverter for photovoltaic and fuel cell applications using reverse blocking IGBTs. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1683–1689. [Google Scholar] [CrossRef]
- Umeda, H.; Yamada, Y.; Asanuma, K.; Kusama, F.; Kinoshita, Y.; Ueno, H.; Ishida, H.; Hatsuda, T.; Ueda, T. High power 3-phase to 3-phase matrix converter using dual-gate GaN bidirectional switches. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 894–897. [Google Scholar] [CrossRef]
- Geury, T.; Pinto, S.; Gyselinck, J. Current source inverter-based photovoltaic system with enhanced active filtering functionalities. IET Power Electron. 2015, 8, 2483–2491. [Google Scholar] [CrossRef]
- Geury, T.; Pinto, S.; Gyselinck, J. Assessment of Grid-Side Filters for Three-Phase Current-Source Inverter PV Systems. Int. Rev. Electr. Eng. 2016, 11, 567–578. [Google Scholar] [CrossRef][Green Version]
- Lorenzani, E.; Immovilli, F.; Migliazza, G.; Frigieri, M.; Bianchini, C.; Davoli, M. CSI7: A modified three-phase current-source inverter for modular photovoltaic applications. IEEE Trans. Ind. Electron. 2017, 64, 5449–5459. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.; Espinoza, J.; Zanchetta, P.; Abu-Rub, H.; Young, H.; Rojas, C. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Fundamentals of Model Predictive Control. In Model Predictive Control of Wind Energy Conversion Systems, 1st ed.; Wiley-IEEE Press: New York, NY, USA, 2016; pp. 128–130. [Google Scholar]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives, 1st ed.; Wiley-IEEE Press: New York, NY, USA, 2012. [Google Scholar]
- Barra, K.; Rahem, D. Predictive direct power control for photovoltaic grid connected system: An approach based on multilevel converters. Energy Convers. Manag. 2014, 78, 825–834. [Google Scholar] [CrossRef]
- Chaves, M.; Silva, J.F.; Pinto, S.F.; Margato, E.; Santana, J. A New Backward Euler Stabilized Optimum Controller for NPC Back-to-Back Five Level Converters. Energies 2017, 10, 735. [Google Scholar] [CrossRef]
- Gambôa, P.; Silva, J.F.; Pinto, S.F.; Margato, E. Input–Output Linearization and PI controllers for AC–AC matrix converter based Dynamic Voltage Restorers with Flywheel Energy Storage: A comparison. Electr. Power Syst. Res. 2019, 169, 214–228. [Google Scholar] [CrossRef]
- Feng, S.; Wei, C.; Lei, J. Reduction of Prediction Errors for Matrix Converter with Improved Model Predictive Control. Energies 2019, 12, 3029. [Google Scholar] [CrossRef]
- Youssef, E.; Pinto, S.; Amin, A.; Samahy, A. Multi-Terminal Matrix Converters as Enablers for Compact Battery Management Systems. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Masoum, M.; Dehbonei, H.; Fuchs, E. Theoretical and experimental analyses of photovoltaic systems with voltage and current-based maximum power point tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef]
- Wheeler, P.; Zhang, H.; Grant, D. A theoretical and practical consideration of optimised input filter design for a low loss Matrix Converter. In Proceedings of the 5th International Conference on Power Electronics and Variable-Speed Drives, London, UK, 26–28 October 1994; pp. 363–367. [Google Scholar] [CrossRef]
- Sahoo, A.; Basu, K.; Mohan, N. Systematic Input Filter Design of Matrix Converter by Analytical Estimation of RMS Current Ripple. IEEE Trans. Ind. Electron. 2015, 62, 132–143. [Google Scholar] [CrossRef]
- Sudubhi, B.; Pradhan, R. A Comparative Study on Maximum Power Point Tracking Technique for Photovoltaic Power Systems. IEEE Trans. Sustain. Energy 2013, 4, 89–98. [Google Scholar] [CrossRef]
- Pinto, S.; Silva, J. Sliding mode direct control of matrix converters. IET Elect. Power Appl. 2007, 1, 439–448. [Google Scholar] [CrossRef]







| Item | Value |
|---|---|
| Maximum Power, Pmax | 305 W |
| Open circuit voltage, voc | 64.2 V |
| Short circuit current, isc | 5.96 A |
| Voltage at Pmax, vmpp | 54.7 V |
| Current at Pmax, impp | 5.58 A |
| Parallel strings, np | 5 |
| Series-connected modules per string, ns | 1 |
| Vector | S1a | S1b | S1c | S2a | S2b | S2c | v12 | isa | isb | isc |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | vab | iPV | −iPV | 0 |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | −vab | −iPV | iPV | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 | vbc | 0 | iPV | −iPV |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | −vbc | 0 | −iPV | iPV |
| 5 | 0 | 0 | 1 | 1 | 0 | 0 | vca | −iPV | 0 | iPV |
| 6 | 1 | 0 | 0 | 0 | 0 | 1 | −vca | iPV | 0 | −iPV |
| 7 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Item | Value |
|---|---|
| Grid frequency (Hz) | 50 |
| Grid phase voltage, rms value (V) | 110 |
| Grid filter inductance (mH) | 4 |
| Grid side filter damping resistance (Ω) | 33 |
| Grid filter capacitance delta (μF) | 6 |
| DC link inductance (mH) | 12.5 |
| Sampling time (μs) | 20 |
| PV Power (W) | 600 |
| Grid Phase Voltage (V) | DC Voltage (V) | Pdc, ref (W) | Qref (var) |
|---|---|---|---|
| 110 | 70 | Step: 400 to 280 | 0 |
| Grid Phase Voltage (V) | DC Voltage (V) | Pdc, ref (W) | Qref (var) |
|---|---|---|---|
| 110 | 90 | 0 to 500 | Step: 0 to 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssef, E.; Costa, P.B.C.; Pinto, S.F.; Amin, A.; El Samahy, A.A. Direct Power Control of a Single Stage Current Source Inverter Grid-Tied PV System. Energies 2020, 13, 3165. https://doi.org/10.3390/en13123165
Youssef E, Costa PBC, Pinto SF, Amin A, El Samahy AA. Direct Power Control of a Single Stage Current Source Inverter Grid-Tied PV System. Energies. 2020; 13(12):3165. https://doi.org/10.3390/en13123165
Chicago/Turabian StyleYoussef, Erhab, Pedro B. C. Costa, Sonia F. Pinto, Amr Amin, and Adel A. El Samahy. 2020. "Direct Power Control of a Single Stage Current Source Inverter Grid-Tied PV System" Energies 13, no. 12: 3165. https://doi.org/10.3390/en13123165
APA StyleYoussef, E., Costa, P. B. C., Pinto, S. F., Amin, A., & El Samahy, A. A. (2020). Direct Power Control of a Single Stage Current Source Inverter Grid-Tied PV System. Energies, 13(12), 3165. https://doi.org/10.3390/en13123165