Analyzing Crude Oil Prices under the Impact of COVID-19 by Using LSTARGARCHLSTM
Abstract
1. Introduction
2. Related Work
3. Methodology
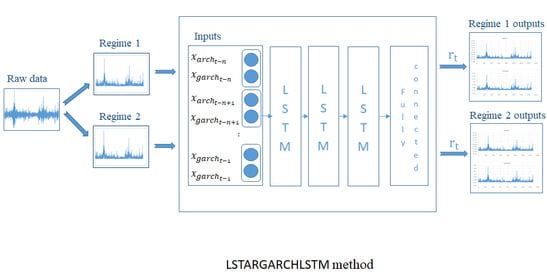
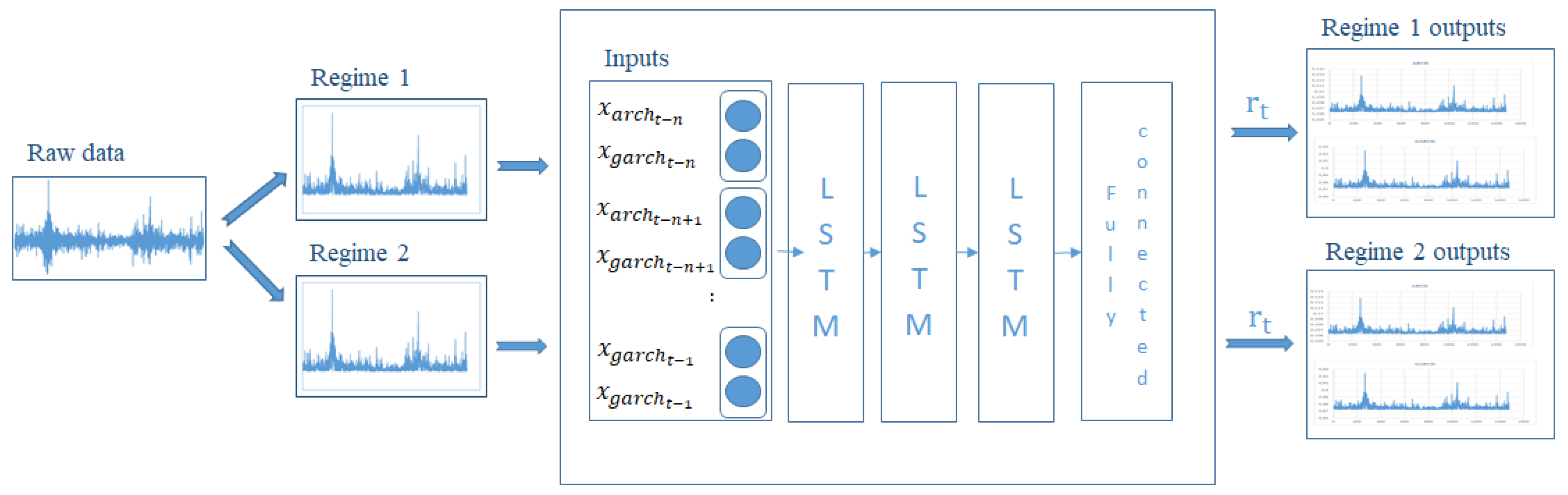
The Proposed Hybrid LSTARGARCHLSTM Model
4. Data and Results
4.1. Data
4.2. Results
- Firstly, some descriptive statistics were obtained. The Augmented Dickey-Fuller (ADF) unit root test [70,71] and Kapetanios, Shin, and Snell (KSS) unit root test [72] were applied. The ADF test is dependent upon a linear assumption that can cause the false results. Bigman et al. [73] showed that traditional unit root tests tends to produce “spurious regressions”. In this condition, for confirmation, we used the KSS test.
- Secondly, Tsay and Hsieh’s tests and the Brock–Dechert–Scheinkman (BDS) test were applied. These tests determined the presence of nonlinear structure, but they are not sufficient to determine the existence of chaotic behavior.
- Thirdly, SE and Le tests were applied. Le is a convenient means to decide on the presence of chaotic behavior.
- The LSTARGARCHLSTM method determines ARCH and GARCH effects. To evaluate the performance of our proposed method, we compared our proposed method with GARCHLSTM and traditional methods: GARCH and LSTARGARCH. For this purpose, GARCH and LSTARGARCH, and GARCHLSTM models were estimated and the most succesful model was determined.
- In the final step, the forecast accuracies of all of the models were determined.
4.2.1. Some Descriptive Statistics and Tsay and Hsieh’s Tests
4.2.2. BDS Test, Tsay Tests and Hsieh’s Coefficients Results
4.2.3. Lyapunov Exponent and Kolmogorov Entropy Tests
4.2.4. Results with the GARCH, LSTARGARCH, LSTARGARCHLSTM and GARCHLSTM Models
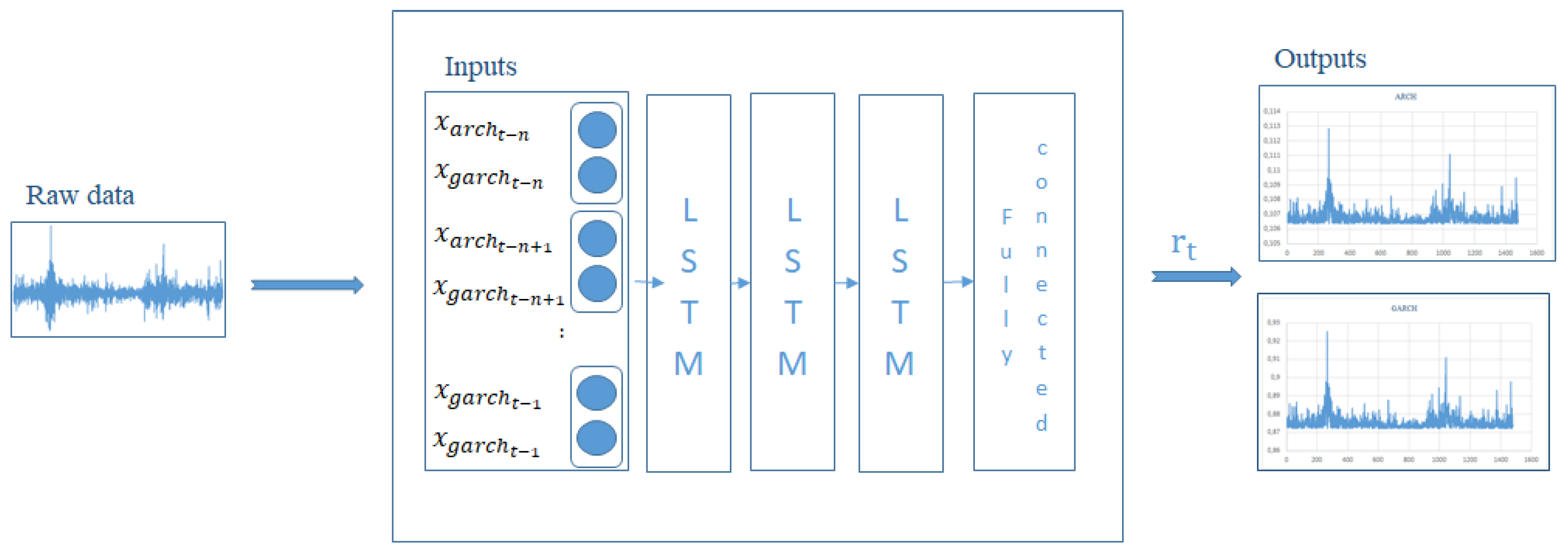
4.2.5. The Architecture of the GARCH–LSTM and LSTARGARCH–LSTM Models
4.2.6. The Results of the GARCHLSTM and LSTARGARCHLSTM Method
5. Forecast Results
5.1. In–Sample Forecast Results
5.2. Out-of-Sample Forecast Results
5.3. To Test for Forecast Accuracy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baldwin, R.; di Mauro, B.W. Mitigating the COVID Economic Crisis: Act Fast and Do Whatever; Baldwin, R., di Mauro, B.W., Eds.; CEPR Press: London, UK, 2020; pp. 1–24. [Google Scholar]
- Arezki, R.; Fan, R.Y.; Nguyen, H. Covid-19 and Oil Price Collapse: Coping with a Dual Shock in the Gulf Cooperation Council. ERF Policy Brief No. 52. April 2020. Available online: https://erf.org.eg/wp-content/uploads/2020/04/PB-52_Rabah_version3.pdf (accessed on 4 May 2020).
- Arezki, R.; Nguyen, H. Coping with a Dual Shock: COVID–19 and Oil Prices; World Bank: Washington, DC, USA, April 2020; Available online: https://www.worldbank.org/en/region/mena/brief/coping-with-a-dual-shock-coronavirus-covid-19-and-oil-prices (accessed on 4 May 2020).
- IEA. Oil Market Report—April (2020). Available online: https://www.iea.org/reports/oil–market–report–april–2020 (accessed on 4 May 2020).
- Kubursi, A. Oil Crash Explained: How Are Negative Oil Prices Even Possible? Available online: https://www.weforum.org/agenda/2020/04/negative–oil–prices–covid19/ (accessed on 4 May 2020).
- Soliman, M. COVID–19, the Oil Price War, and the Remaking of the Middle East. Available online: https://www.mei.edu/publications/covid–19–oil–price–war–and–remaking–middle–east (accessed on 4 May 2020).
- Bildirici, M.; Ersin, Ö.Ö. Forecasting oil prices: Smooth transition and neural network augmented GARCH family models. J. Pet. Sci. Eng. 2013, 109, 230–240. [Google Scholar] [CrossRef]
- Baldwin, R. The COVID–19 upheaval scenario: Inequality and pandemic make an explosive mix. VOX CEPR Policy Portal 2020. Available online: https://voxeu.org/article/inequality-and-pandemic-make-explosive-mix (accessed on 4 May 2020).
- Gourinchas, P.-O. Flattening the pandemic and recession curves. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever It Takes; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 31–40. [Google Scholar]
- Gopinath, G. Limiting the economic fallout of the coronavirus with large targeted policies. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 41–48. [Google Scholar]
- Blanchard, O. Italy, the ECB, and the need to avoid another euro crisis. In Peterson Institute for International Economics; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 49–50. [Google Scholar]
- Alesina, A.; Giavazzi, F. The EU must support the member at the centre of the COVID–19 crisis. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever It Takes; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 51–55. [Google Scholar]
- Galí, J. Helicopter money: The time is now. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 57–61. [Google Scholar]
- Galí, J. The effects of a money–financed fiscal stimulus. Working Paper 26249. 2019. Available online: https://www.nber.org/papers/w26249.pdf (accessed on 4 May 2020).
- Wyplosz, C. So far, so good: And now don’t be afraid of moral hazard. In Mitigating the COVID Economic Crisis: Act Fast and Do Whatever; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 25–30. [Google Scholar]
- Cecchetti, S.G.; Schoenholtz, K.L. Contagion: Bank runs and COVID-19. In Economics in the Time of COVID-19; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 77–81. [Google Scholar]
- Cochrane, J. Coronavirus Monetary Policy. Available online: https://seekingalpha.com/article/4329470–coronavirus–monetary–policy (accessed on 23 May 2020).
- Bénassy-Quéré, A.; Marimon, R.; Pisani-Ferry, J.; Reichlin, L.; Schoenmaker, D.; di Mauro, B.W. COVID–19: Europe needs a catastrophe relief plan|VOX, CEPR Policy Portal. In VOX, CEPR Policy Portal; Baldwin, R., di Mauro, B.W., Eds.; CEPR: London, UK, 2020; pp. 121–128. [Google Scholar]
- Barone-Adesi, G.; Bourgoin, F.; Giannopoulos, K. Don’t look back. Risk 1998, 11, 100–103. [Google Scholar]
- Adrangi, B.; Chatrath, A.; Dhanda, K.K.; Raffiee, K. Chaos in oil prices? Evidence from futures markets. Energy Econ. 2001, 23, 405–425. [Google Scholar] [CrossRef]
- Lahmiri, S. A study on chaos in crude oil markets before and after 2008 international financial crisis. Phys. A Stat. Mech. Its Appl. 2017, 466, 389–395. [Google Scholar] [CrossRef]
- Komijani, A.; Naderi, E.; Gandali Alikhani, N. A hybrid approach for forecasting of oil prices volatility. OPEC Energy Rev. 2014, 38, 323–340. [Google Scholar] [CrossRef]
- HE, L.-Y. Chaotic Structures in Brent & WTI Crude Oil Markets: Empirical Evidence. Int. J. Econ. Financ. 2011, 3, 242–249. [Google Scholar]
- Carnero, M.A.; Pena, D.; Ruiz, E. Effects of outliers on the identification and estimation of GARCH models. J. Time Ser. Anal. 2007, 28, 471–497. [Google Scholar] [CrossRef]
- Aggarwal, R.; Inclan, C.; Leal, R. Volatility in emerging stock markets. J. Financ. Quant. Anal. 1999, 34, 33–55. [Google Scholar] [CrossRef]
- Charles, A. Forecasting volatility with outliers in GARCH models. J. Forecast. 2008, 27, 551–565. [Google Scholar] [CrossRef]
- Ané, T.; Ureche-Rangau, L.; Gambet, J.-B.; Bouverot, J. Robust outlier detection for Asia—Pacific stock index returns. J. Int. Financ. Mark. Inst. Money 2008, 18, 326–343. [Google Scholar] [CrossRef]
- Charles, A.; Darné, O. Large shocks in the volatility of the Dow Jones Industrial Average index: 1928–2013. J. Bank. Financ. 2014, 43, 188–199. [Google Scholar] [CrossRef]
- Teräsvirta, T. Specification, estimation, and evaluation of smooth transition autoregressive models. J. Am. Stat. Assoc. 1994, 89, 208–218. [Google Scholar]
- Luukkonen, R.; Saikkonen, P.; Teräsvirta, T. Testing linearity against smooth transition autoregressive models. Biometrika 1988, 75, 491–499. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Teräsvirta, T. A simple nonlinear time series model with misleading linear properties. Econ. Lett. 1999, 62, 161–165. [Google Scholar] [CrossRef]
- González-Rivera, G. Smooth–transition GARCH models. Stud. Nonlinear Dyn. Econom. 1998, 3, 61–78. [Google Scholar] [CrossRef][Green Version]
- Hagerud, G. A Smooth Transition ARCH Model for Asset Returns. Available online: https://ideas.repec.org/p/hhs/hastef/0162.html (accessed on 29 April 2020).
- Dufrénot, G.; Marimoutou, V.; Peguin-Feissolle, A. LSTGARCH Effects in Stock Returns: The Case of US, UK and France. 2003. Available online: https://ideas.repec.org/p/hal/journl/halshs-00403739.html (accessed on 29 April 2020).
- Anderson, H.M.; Nam, K.; Vahid, F. Asymmetric nonlinear smooth transition GARCH models. In Nonlinear Time Series Analysis of Economic and Financial Data; Springer: Boston, MA, USA, 1999; pp. 191–207. [Google Scholar]
- Ané, T.; Ureche-Rangau, L. Stock market dynamics in a regime–switching asymmetric power GARCH model. Int. Rev. Financ. Anal. 2006, 15, 109–129. [Google Scholar] [CrossRef]
- Franses, P.H.; Neele, J.; van Dijk, D. Forecasting Volatility with Switching Persistence GARCH Models. 1998. Available online: https://ideas.repec.org/p/ems/eureir/1553.html (accessed on 4 May 2020).
- Lundbergh, S.; Terasvirta, T. Modelling Economic High–Frequency Time Series with STAR–STGARCH Models. Available online: https://www.econstor.eu/bitstream/10419/85508/1/99009.pdf (accessed on 4 May 2020).
- Lee, J.; Degennaro, R.P. Smooth transition ARCH models: Estimation and testing. Rev. Quant. Financ. Account. 2000, 15, 5–20. [Google Scholar] [CrossRef]
- Chan, F.; McAleer, M. Estimating smooth transition autoregressive models with GARCH errors in the presence of extreme observations and outliers. Appl. Financ. Econ. 2003, 13, 581–592. [Google Scholar] [CrossRef]
- Bildirici, M.; Ersin, Ö.Ö. Nonlinearity, volatility and fractional integration in daily oil prices: Smooth transition autoregressive ST–FI(AP)GARCH models. Rom. J. Econ. Forecast. 2014, 17, 108–135. [Google Scholar]
- Donaldson, R.G.; Kamstra, M. An artificial neural network–GARCH model for international stock return volatility. J. Empir. Financ. 1997, 4, 17–46. [Google Scholar] [CrossRef]
- Gonzalez Miranda, F.; Burgess, N. Modelling market volatilities: The neural network perspective. Eur. J. Financ. 1997, 3, 137–157. [Google Scholar] [CrossRef]
- Hamid, S.A.; Iqbal, Z. Using neural networks for forecasting volatility of S & P 500 Index futures prices. J. Bus. Res. 2004, 57, 1116–1125. [Google Scholar]
- Bildirici, M.; Ersin, Ö.Ö. Improving forecasts of GARCH family models with the artificial neural networks: An application to the daily returns in Istanbul Stock Exchange. Expert Syst. Appl. 2009, 36, 7355–7362. [Google Scholar] [CrossRef]
- Moshiri, S.; Foroutan, F. Forecasting nonlinear crude oil futures prices. Energy J. 2006, 27, 81–96. [Google Scholar] [CrossRef]
- Roh, T.H. Forecasting the volatility of stock price index. Expert Syst. Appl. 2007, 33, 916–922. [Google Scholar]
- Kaboudan, M.A. Compumetric forecasting of crude oil prices. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 283–287. [Google Scholar]
- Xie, W.; Yu, L.; Xu, S.; Wang, S. A new method for crude oil price forecasting based on support vector machines. In Proceedings of the International Conference on Computational Science, Reading, UK, 28–31 May 2006; pp. 444–451. [Google Scholar]
- Zhang, Z.; Hong, W.-C.; Li, J. Electric load forecasting by hybrid self–recurrent support vector regression model with variational mode decomposition and improved cuckoo search algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Kundra, H.; Sadawarti, H. Hybrid algorithm of cuckoo search and particle swarm optimization for natural terrain feature extraction. Res. J. Inf. Technol. 2015, 7, 58–69. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, L.; Wang, S.; Lai, K.K. Estimating the impact of extreme events on crude oil price: An EMD–based event analysis method. Energy Econ. 2009, 31, 768–778. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. Forecasting crude oil price with an EMD–based neural network ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Hernández, E. Volatility of main metals forecasted by a hybrid ANN–GARCH model with regressors. Expert Syst. Appl. 2017, 84, 290–300. [Google Scholar] [CrossRef]
- Bildirici, M.; Ersin, Ö. Forecasting volatility in oil prices with a class of nonlinear volatility models: Smooth transition RBF and MLP neural networks augmented GARCH approach. Pet. Sci. 2015, 12, 534–552. [Google Scholar] [CrossRef]
- Wex, F.; Widder, N.; Liebmann, M.; Neumann, D. Early warning of impending oil crises using the predictive power of online news stories. In Proceedings of the 2013 46th Hawaii International Conference on System Sciences, Wailea, Maui, HI, USA, 7–10 January 2013; pp. 1512–1521. [Google Scholar]
- Yu, L.; Wang, S.; Lai, K.K. A rough–set–refined text mining approach for crude oil market tendency forecasting. Int. J. Knowl. Syst. Sci. 2005, 2, 33–46. [Google Scholar]
- Zhao, Y.; Li, J.; Yu, L. A deep learning ensemble approach for crude oil price forecasting. Energy Econ. 2017, 66, 9–16. [Google Scholar] [CrossRef]
- Chen, Y.; He, K.; Tso, G.K.F. Forecasting crude oil prices: A deep learning based model. Procedia Comput. Sci. 2017, 122, 300–307. [Google Scholar] [CrossRef]
- Gupta, V.; Pandey, A. Crude Oil Price Prediction Using LSTM Networks. Int. J. Comput. Inf. Eng. 2018, 12, 226–230. [Google Scholar]
- Li, T.; Hu, Z.; Jia, Y.; Wu, J.; Zhou, Y. Forecasting crude oil prices using ensemble empirical mode decomposition and sparse Bayesian learning. Energies 2018, 11, 1882. [Google Scholar] [CrossRef]
- Huang, S.-C.; Wu, C.-F. Energy commodity price forecasting with deep multiple kernel learning. Energies 2018, 11, 3029. [Google Scholar] [CrossRef]
- Li, X.; Shang, W.; Wang, S. Text–based crude oil price forecasting: A deep learning approach. Int. J. Forecast. 2019, 35, 1548–1560. [Google Scholar] [CrossRef]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH–type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Franses, P.H.; Neele, J.; van Dijk, D. Modeling asymmetric volatility in weekly Dutch temperature data. Environ. Model. Softw. 2001, 16, 131–137. [Google Scholar] [CrossRef][Green Version]
- Terasvirta, T.; Anderson, H.M. Characterizing nonlinearities in business cycles using smooth transition autoregressive models. J. Appl. Econom. 1992, 7, S119–S136. [Google Scholar] [CrossRef]
- Chan, F.; McAleer, M. Maximum likelihood estimation of STAR and STAR-GARCH models: Theory and Monte Carlo evidence. J. Appl. Econom. 2002, 17, 509–534. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short–term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econom. J. Econom. Soc. 1981, 1057–1072. [Google Scholar] [CrossRef]
- Kapetanios, G.; Shin, Y.; Snell, A. Testing for a unit root in the nonlinear STAR framework. J. Econom. 2003, 112, 359–379. [Google Scholar] [CrossRef]
- Bigman, D.; Goldfarb, D.; Schechtman, E. Futures market efficiency and the time content of the information sets. J. Futures Mark. 1983, 3, 321–334. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- White, H. A heteroskedasticity–consistent covariance matrix estimator and a direct test for heteroskedasticity. Econom. J. Econom. Soc. 1980, 48, 817–838. [Google Scholar] [CrossRef]
- Brock, W.; Dechert, W.D.; Scheinkman, J. A test for independence based on the correlation dimension, University of Wisconsin. Econ. Work. Pap. 1996, 15, 197–235. [Google Scholar]
- Granger, C.W.J.; Teräsvirta, T. Modelling Nonlinear Economic Relationships; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Takala, K.; Virén, M. Testing Nonlinear Dynamics, Long Memory and Chaotic Behaviour with Macroeconomic Data. 1995. Available online: https://ideas.repec.org/p/bof/bofrdp/1995_009.html (accessed on 4 May 2020).
- Hsieh, D.A. Implications of Nonlinear Dynamics for Financial Risk Management. J. Financ. Quant. Anal. 1993, 28, 41–64. [Google Scholar] [CrossRef]
- Hsieh, D.A. Chaos and nonlinear dynamics: Application to financial markets. J. Financ. 1991, 46, 1839–1877. [Google Scholar] [CrossRef]
- Bildirici, M.; Sonustun, F.O. Chaotic structure of oil prices. Nonlinear Dyn. Psychol. Life Sci. 2019, 23, 377–394. [Google Scholar] [PubMed]
- Chao, A.; Shen, T.-J. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 2003, 10, 429–443. [Google Scholar] [CrossRef]
- Bildirici, M. The chaotic behavior among the oil prices, expectation of investors and stock returns: TAR–TR–GARCH copula and TAR–TR–TGARCH copula. Pet. Sci. 2019, 16, 217–228. [Google Scholar] [CrossRef]
- Davies, R.B. Hypothesis testing when a nuisance parameter is only present under the alternative. Biometrika 1987, 74, 33–43. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
| Lbopt | Ldopt | Lwopt | |
|---|---|---|---|
| Kurtosis | 17.583 | 21.69 | 18.763 |
| Skewness | −1.0417 | −1.5635 | −0.45 |
| JB | 346.64 | 282.65 | 208.5756 |
| ARCH effect | 17.89 | 27.67 | 19.25 |
| White | 14.36 | 13.73 | 10.88 |
| RESET | 13.58 | 10.72 | 2.18 |
| Unit Root Tests | |||
| - | Level | Level | Level |
| ADF | −56.86 | −15.069 | −68.44 |
| KSS | −54.25 | −11.38 | −53.58 |
| Decision | I(0) | I(0) | I(0) |
| Z Statistics | |||
|---|---|---|---|
| Dimension | Lbopt | Ldopt | Lwopt |
| 2 | 34.40350 | 35.9270 | 18.999077 |
| 3 | 35.62271 | 38.6123 | 22.72316 |
| 4 | 38.02877 | 41.3846 | 24.84834 |
| 5 | 41.58379 | 44.5027 | 26.97560 |
| 6 | 46.53435 | 49.7965 | 28.99879 |
| Hsieh’s Coefficients | Tsay’s Nonlinearity Test Statistic | |||||||
|---|---|---|---|---|---|---|---|---|
| rij are Hsich’s Third-Order Moment Coefficients for Lags i and j | Tsay’s Nonlinearity Test Statistic | |||||||
| Lbopt | Ldopt | Lwopt | Lbopt | Ldopt | Lwopt | |||
| r(1) | r(2) | r(1) | r(2) | r(1) | r(2) | 133.41 | 100.58 | 102.001 |
| 0.1 | −0.42 | −0.35 | 0.12 | −0.124 | 0.45 | - | - | - |
| Lyapunov Exponent Method | Shannon Entropy Method | ||||
|---|---|---|---|---|---|
| Lbopt | Ldopt | Lwopt | Lbopt | Ldopt | Lwopt |
| 0.9504 | 0.9071 | 0.8481 | 0.9617 | 0.983 | 0.9121 |
| Lwopt | Lbopt | Ldopt | |||||||
|---|---|---|---|---|---|---|---|---|---|
| - | GARCH | LSTARGARCH | GARCH | LSTARGARCH | GARCH | LSTARGARCH | |||
| - | Regime 1 | Regime 2 | Regime 1 | Regime 2 | Regime 1 | Regime 2 | |||
| Cst(M) | 0.0214 (2.13) (0.0) 1 | 00633 (3428) (00) 1 | 0116 (576) (00) 1 | 00215 (187) (00) 1 | 0015 (456) (00) 1 | 000520 (625) (00) 1 | 0.0754 (1.94) (0.0) 1 | 0.0004 (2.17) (0.0) 1 | 0.05377 (7.61) (0.0) 1 |
| Cst(V) | 0.255 (1.91) (0.0) 1 | 1109 (488) (00) 1 | 0287 (836) (00) 1 | 0312 (193) (00) 1 | 0338 (263) (00) 1 | 0089 (558) (00) 1 | 0.02905 (2.05) (0.0) 1 | 0.178 (1.93) (0.0) 1 | 0.205 (1.94) (0.0) 1 |
| ARCH | 0.19 (3.61) (0.0) 1 | 0128 (8689) (00) 1 | 0089 (1427) (00) 1 | 0189 (278) (00) 1 | 00287 (385) (00) 1 | 01052 (1246) (00) 1 | 0.19899 (2.67) (0.0) 1 | 0.201 (7.25) (0.0) 1 | 0.112 (2.27) (0.0) 1 |
| GARCH | 0.67 (4.78) (0.0) 1 | 0722 (686) (00) 1 | 0903 (516) (00) 1 | 0611 (1887) (00) 1 | 09401 (8136) (00) 1 | 08795 (1056) (00) 1 | 0.61922 (4.051) (0.0) 1 | 0.769 (2.105) (0.0) 1 | 0.872 (9.26) (0.0) 1 |
| LogL | 10536.28 | 271389 | 118421 | 316852 | 112345 | 388873 | |||
| AIC: | 10.353 | −3913 | 77224 | −33126 | 84167 | −44956 | |||
| SIC: | 10.042 | −389 | 77154 | −32997 | 84869 | −44836 | |||
| HQ: | 10.054 | −385 | 77199 | −33078 | 83940 | −44612 | |||
| ARCH (1–2): | 0.035 | 0097 | 0056 | 0042 | 0083 | 0064 | |||
| ARCH (1–5): | 0.039 | 0095 | 0058 | 0041 | 0078 | 0062 | |||
| Lbopt | Ldopt | Lwopt | ||||
|---|---|---|---|---|---|---|
| GARCHLSTM | LSTARGARCHLSTM | GARCHLSTM | LSTARGARCHLSTM | GARCHLSTM | LSTARGARCHLSTM | |
| Training rho 1 | 0.89 | 0.92 | 0.88 | 0.93 | 0.91 | 0.95 |
| Test rho | 0.88 | 0.90 | 0.87 | 0.92 | 0.90 | 0.91 |
| Training RMSE | 0.24 | 0.04 | 0.21 | 0.08 | 0.33 | 0.03 |
| Training MAE | 0.23 | 0.03 | 0.20 | 0.07 | 0.31 | 0.03 |
| Test RMSE | 0.22 | 0.022 | 0.1 | 0.07 | 0.29 | 0.06 |
| Test MAE | 0.21 | 0.022 | 0.09 | 0.06 | 0.289 | 0.059 |
| Lwopt | Lbopt | Ldopt | |||||||
|---|---|---|---|---|---|---|---|---|---|
| - | GARCH LSTM | LSTARGARCHLSTM | GARCH LSTM | LSTARGARCHLSTM | GARCH LSTM | LSTARGARCHLSTM | |||
| - | - | Regime 1 | Regime 2 | - | Regime 1 | Regime 2 | - | Regime 1 | Regime 2 |
| Cst(M) | 00618 (256) (00) 1 | 0986 (212) (00) 1 | 0651 (474) (00) 1 | 025 (281) (00) 1 | 0156 (276) (00) 1 | 0554 (288) (00) 1 | 0173 (262) (00) 1 | 0263 (281) (00) 1 | 0361 (453) (00) 1 |
| Cst(V) | 0985 (265) (00) 1 | 0431 (226) (00) 1 | 0562 (382) (00) 1 | 0861 (288) (00) 1 | 0297 (263) (00) 1 | 0441 (376) (00) 1 | 0565 (288) (00) 1 | 0428 (287) (00) 1 | 0397 (432) (00) 1 |
| ARCH | 0207 (316) (00) 1 | 0102 (977) (00) 1 | 0023 (229) (00) 1 | 0127 (458) (00) 1 | 0111 (803) (00) 1 | 0095 (297) (00) 1 | 0198 (448) (00) 1 | 0118 (675) (00) 1 | 0037 (236) (00) 1 |
| GARCH | 0721 (571) (00) 1 | 0881 (558) (00) 1 | 0962 (356) (00) 1 | 0811 (631) (00) 1 | 0878 (558) (00) 1 | 0901 (356) (00) 1 | 0781 (756) (00) 1 | 0844 (287) (00) 1 | 0942 (522) (00) 1 |
| LogL | 2849.2 | 2038.21 | 2669.3 | 1984.18 | 2986.2 | 1989.75 | |||
| AIC: | 2.981 | −1.413 | 2.661 | −1.513 | 2.875 | −1.897 | |||
| SIC: | 2.816 | −1.391 | 2.514 | −1.489 | 2.867 | −1.791 | |||
| HQ: | 2.807 | −1.388 | 2.507 | −1.417 | 2.821 | −1.745 | |||
| ARCH (1–2): | 0.123 | 0.089 | 0.107 | 0.076 | 0.109 | 0.081 | |||
| ARCH (1–5): | 0.124 | 0.090 | 0.114 | 0.071 | 0.112 | 0.082 | |||
| - | GARCH | GARCHLSTM | LSTARGARCH | LSTARGARCHLSTM | |
|---|---|---|---|---|---|
| lbopt | RMSE | 0.995 | 0.088 | 0.04 | 0.001 |
| MAE | 0.84 | 0.072 | 0.027 | 0.0009 | |
| ldopt | RMSE | 0.937 | 0.097 | 0.029 | 0.005 |
| MAE | 0.79 | 0.079 | 0.014 | 0.0039 | |
| lwopt | RMSE | 0.49 | 0.034 | 0.0291 | 0.006 |
| MAE | 0.35 | 0.022 | 0.0216 | 0.0055 |
| Lbopt | ||||||
|---|---|---|---|---|---|---|
| GARCH | LSTARGARCH | |||||
| - | T + 1 | T + 10 | T + 20 | T + 1 | T + 10 | T + 20 |
| RMSE | 0.5126 | 0.538 | 0.547 | 0.0107 | 0.0213 | 0.038 |
| MAE | 0.5028 | 0.536 | 0.51 | 0.0106 | 0.0209 | 0.0375 |
| GARCHLSTM | LSTARGARCHLSTM | |||||
| RMSE | 0.052 | 0.0459 | 0.01438 | 0.0031 | 0.0038 | 0.0051 |
| MAE | 0.049 | 0.0448 | 0.01399 | 0.0029 | 0.0036 | 0.0049 |
| ldopt | ||||||
| GARCH | LSTARGARCH | |||||
| RMSE | 0.5187 | 0.4896 | 0.626 | 0.01125 | 0.0308 | 0.0397 |
| MAE | 0.5098 | 0.4891 | 0.621 | 0.01117 | 0.0299 | 0.0394 |
| GARCHLSTM | LSTARGARCHLSTM | |||||
| RMSE | 0.059 | 0.051 | 0.0495 | 0.005 | 0.006 | 0.0068 |
| MAE | 0.058 | 0.0501 | 0.0471 | 0.0038 | 0.0043 | 0.0052 |
| lwopt | ||||||
| GARCH | LSTARGARCH | |||||
| RMSE | 0.4472 | 0.4526 | 0.5066 | 0.0131 | 0.0313 | 0.034 |
| MAE | 0.4463 | 0.4511 | 0.5012 | 0.0122 | 0.0310 | 0.032 |
| GARCHLSTM | LSTARGARCHLSTM | |||||
| RMSE | 0.041 | 0.039 | 0.0385 | 0.0022 | 0.0024 | 0.0025 |
| MAE | 0.040 | 0.037 | 0.0381 | 0.0021 | 0.0022 | 0.0024 |
| WS TEST | ||||||
|---|---|---|---|---|---|---|
| RMSEGARCH | RMSEGARCHLSTM | RMSELSTARGARCH | RMSELSTARGARCHLSTM | |||
| DM Test | RMSEGARCH | - | 0.00 | 0.00 | 0.00 | |
| lbopt | RMSEGARCHLSTM | 0.00 | - | 0.00 | 0.00 | |
| RMSELSTARGARCH | 0.00 | 0.00 | - | 0.00 | ||
| RMSELSTARGARCHLSTM | 0.00 | 0.00 | 0.00 | - | ||
| RMSEGARCH | - | 0.00 | 0.00 | 0.00 | ||
| ldopt | RMSEGARCHLSTM | 0.00 | - | 0.00 | 0.00 | |
| RMSELSTARGARCH | 0.00 | 0.00 | - | 0.00 | ||
| RMSELSTARGARCHLSTM | 0.00 | 0.00 | 0.00 | - | ||
| RMSEGARCH | - | 0.00 | 0.00 | 0.00 | ||
| lwopt | RMSEGARCHLSTM | 0.00 | - | 0.00 | 0.00 | |
| RMSELSTARGARCH | 0.00 | 0.00 | - | 0.00 | ||
| RMSELSTARGARCHLSTM | 0.00 | 0.00 | 0.00 | - | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bildirici, M.; Guler Bayazit, N.; Ucan, Y. Analyzing Crude Oil Prices under the Impact of COVID-19 by Using LSTARGARCHLSTM. Energies 2020, 13, 2980. https://doi.org/10.3390/en13112980
Bildirici M, Guler Bayazit N, Ucan Y. Analyzing Crude Oil Prices under the Impact of COVID-19 by Using LSTARGARCHLSTM. Energies. 2020; 13(11):2980. https://doi.org/10.3390/en13112980
Chicago/Turabian StyleBildirici, Melike, Nilgun Guler Bayazit, and Yasemen Ucan. 2020. "Analyzing Crude Oil Prices under the Impact of COVID-19 by Using LSTARGARCHLSTM" Energies 13, no. 11: 2980. https://doi.org/10.3390/en13112980
APA StyleBildirici, M., Guler Bayazit, N., & Ucan, Y. (2020). Analyzing Crude Oil Prices under the Impact of COVID-19 by Using LSTARGARCHLSTM. Energies, 13(11), 2980. https://doi.org/10.3390/en13112980