Design and Comparison of Resonant and Non-Resonant Single-Layer Microwave Heaters for Continuous Flow Microfluidics in Silicon-Glass Technology
Abstract
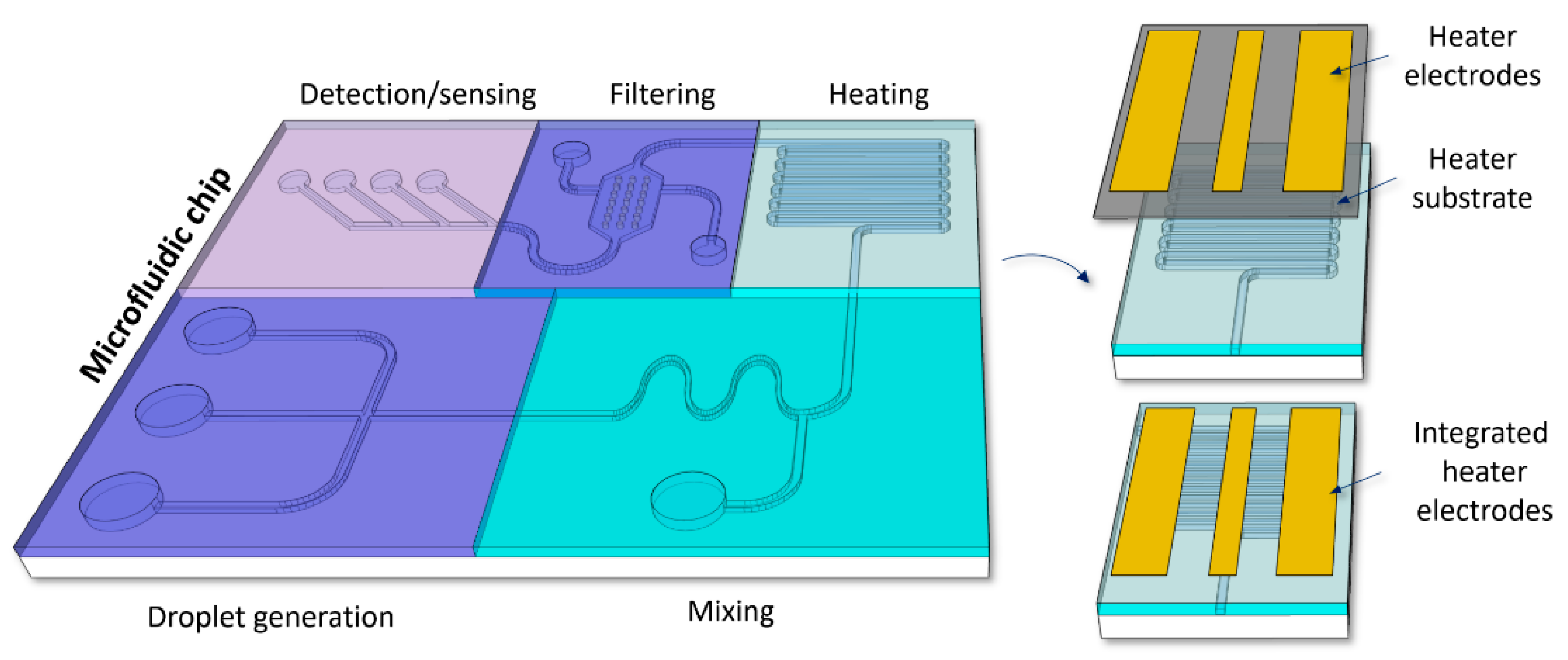
1. Introduction
2. Materials and Methods
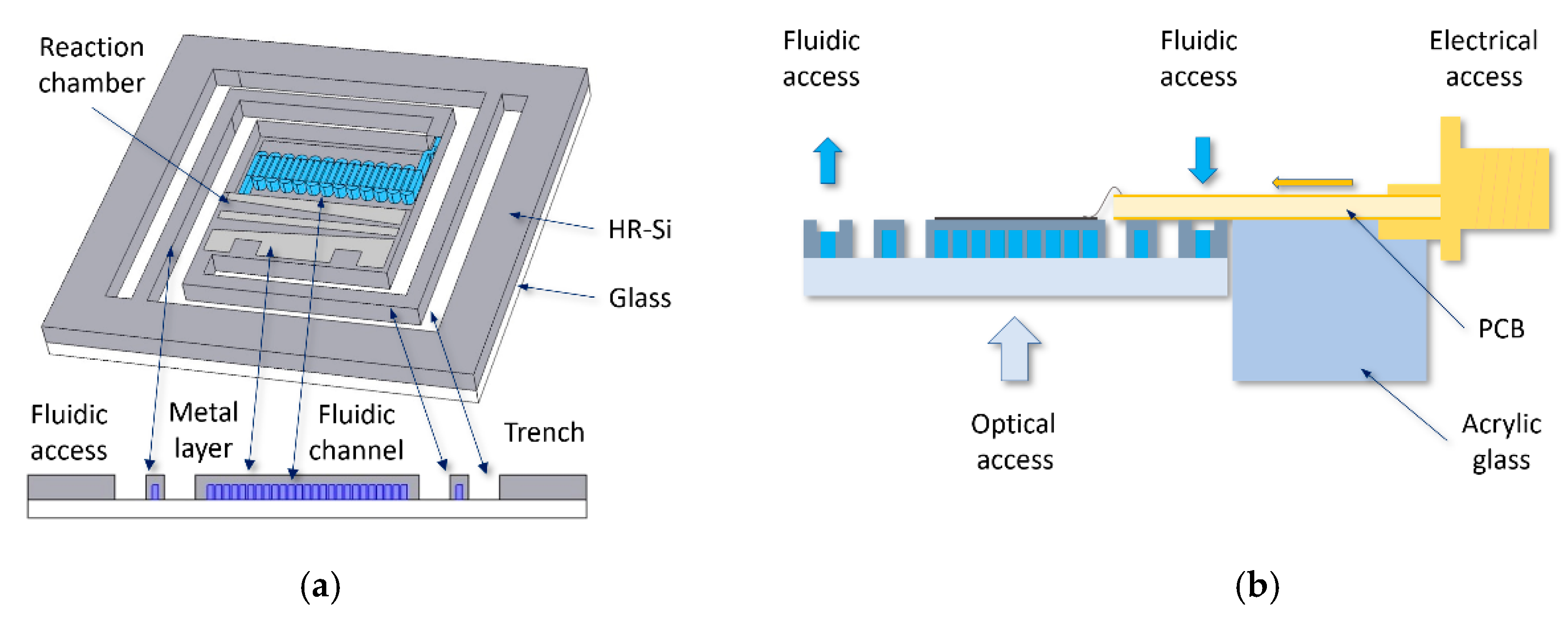
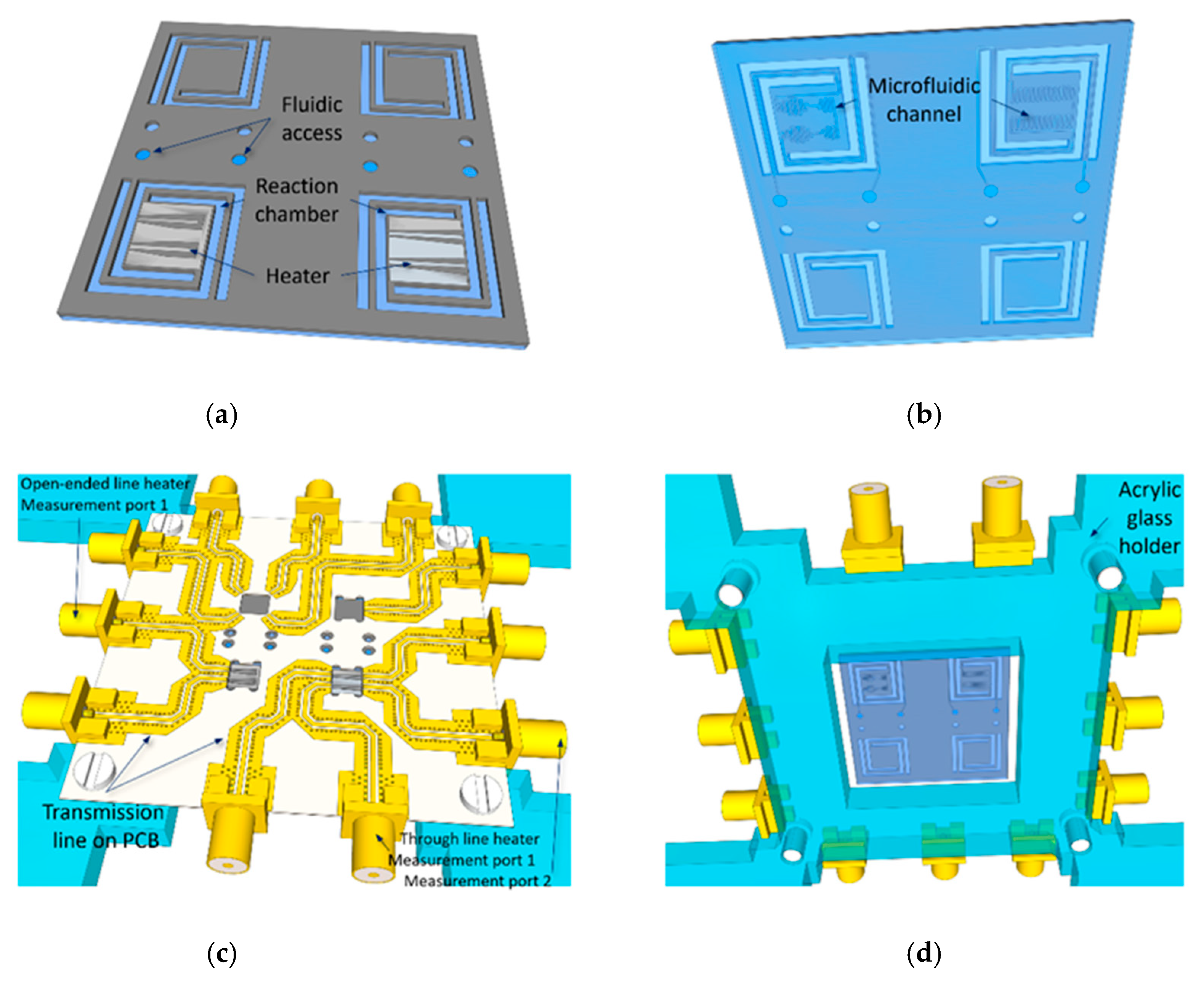
2.1. Device and System Fabrication and Integration
2.2. Heater Design and Integration
3. Results
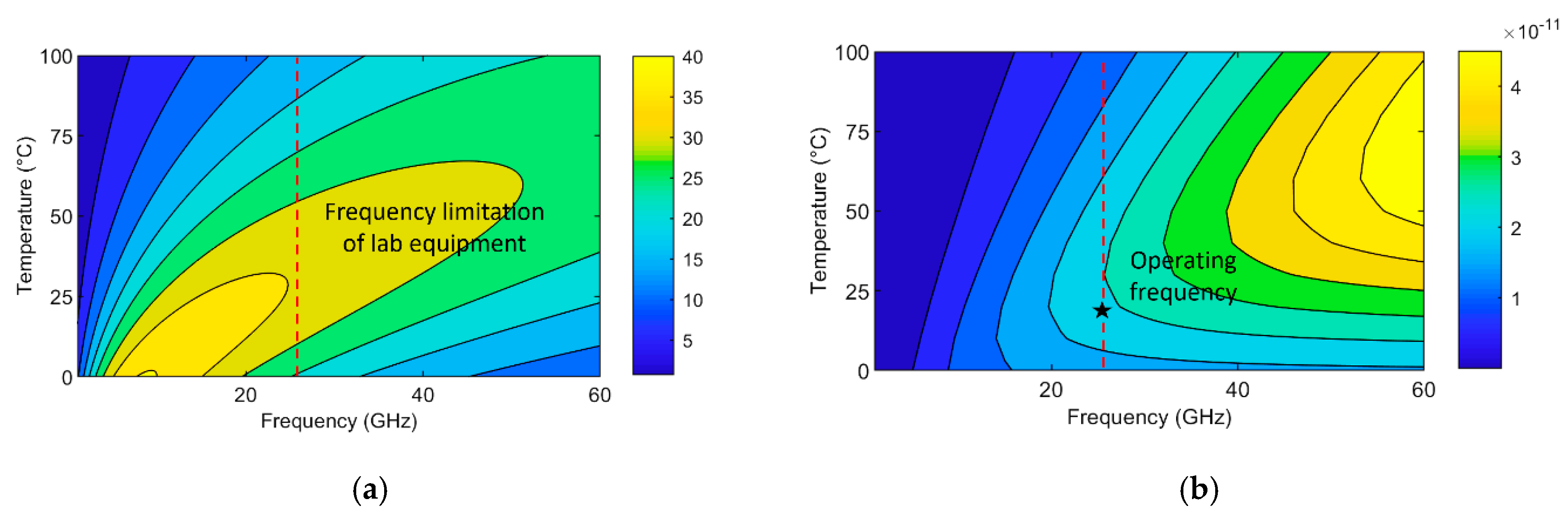
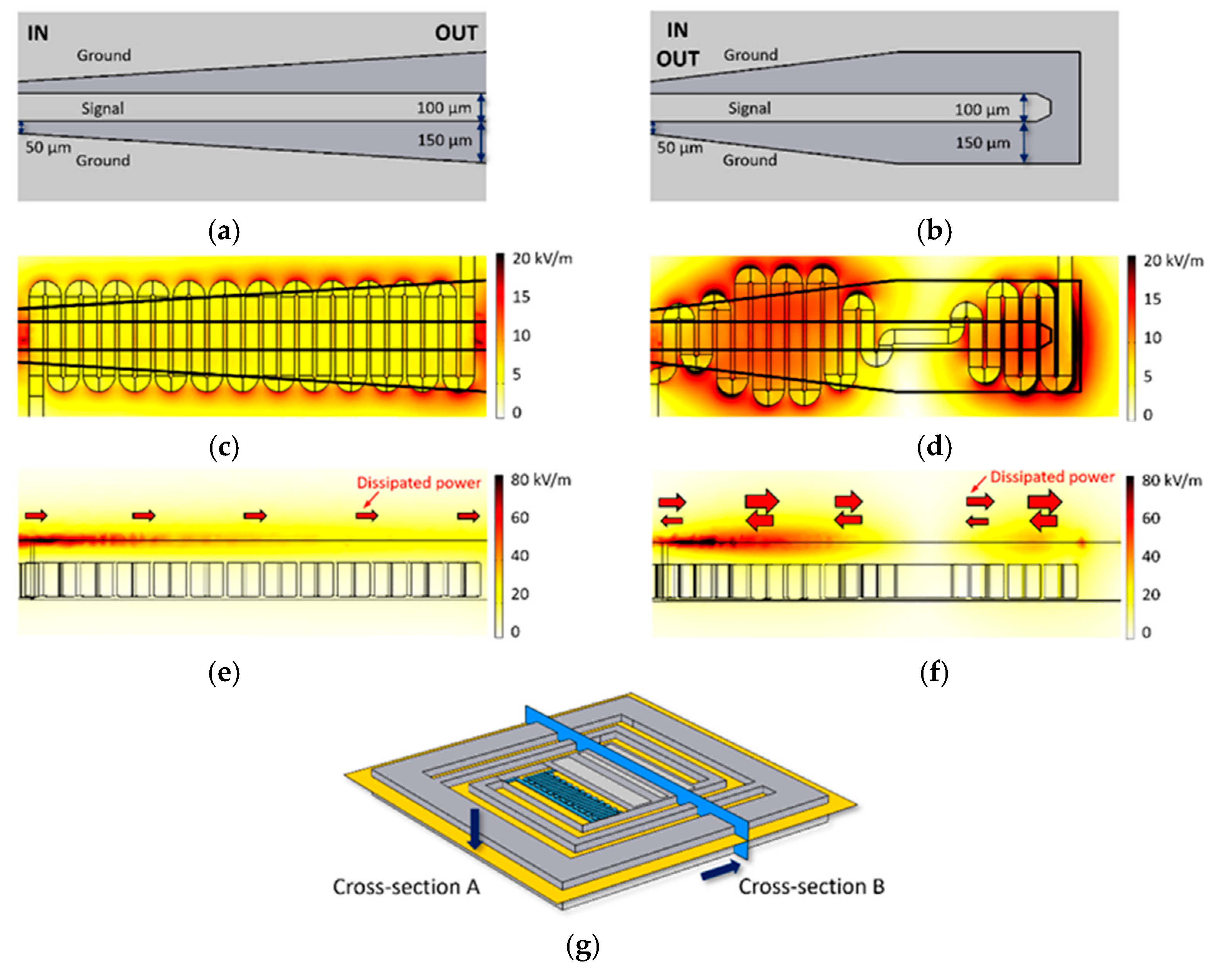
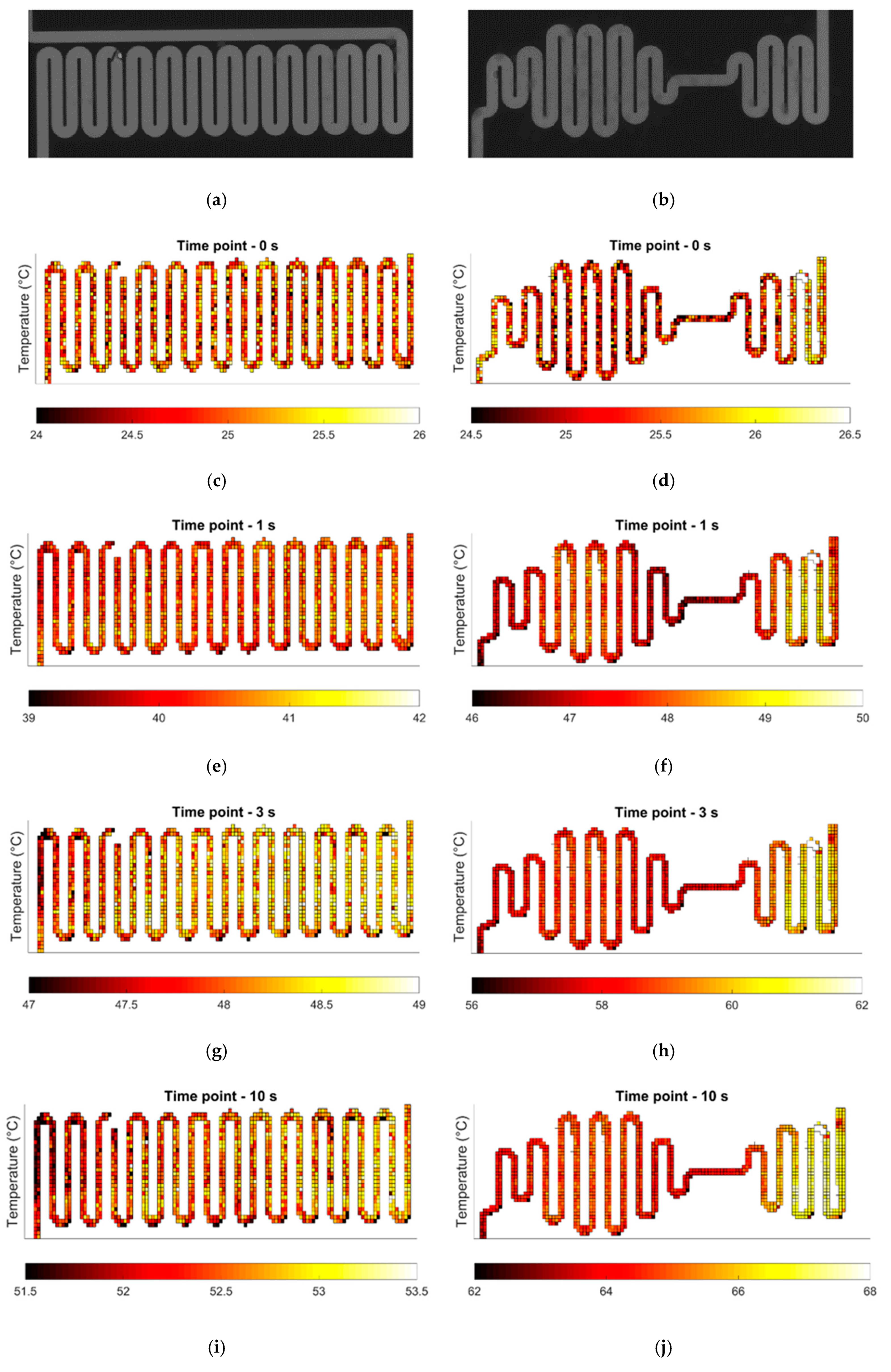
3.1. Heater Design
3.2. Platform Design
3.3. Microwave Measurements
3.4. Heating Experiments
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ward, K.; Hugh Fan, Z. Mixing in microfluidic devices and enhancement methods. J. Micromech. Microeng. 2015, 25, 094001. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.; Kim, S.; Lee, J.; Choi, J.; Kim, R.K.; Lee, S.J.; Sul, O.; Lee, S.B. Clogging-free microfluidics for continuous size-based separation of microparticles. Sci. Rep. 2016, 6, 26531. [Google Scholar] [CrossRef]
- Alves, P.U.; Vinhas, R.; Fernandes, A.R.; Birol, S.Z.; Trabzon, L.; Bernacka-Wojcik, I.; Igreja, R.; Lopes, P.; Baptista, P.V.; Águas, H.; et al. Multifunctional microfluidic chip for optical nanoprobe based RNA detection—Application to Chronic Myeloid Leukemia. Sci. Rep. 2018, 8, 381. [Google Scholar] [CrossRef]
- Curto, V.F.; Marchiori, B.; Hama, A.; Pappa, A.M.; Ferro, M.P.; Braendlein, M.; Rivnay, J.; Fiocchi, M.; Malliaras, G.G.; Ramuz, M.; et al. Organic transistor platform with integrated microfluidics for in-line multiparametric in vitro cell monitoring. Microsyst. Nanoeng. 2017, 3, 17028. [Google Scholar] [CrossRef]
- Bao, J.; Yan, S.; Markovic, T.; Ocket, I.; Kil, D.; Brancato, L.; Puers, L.; Nauwelaers, B. A 20-GHz microwave miniaturized ring resonator for nL microfluidic sensing applications. IEEE Sens. Lett. 2019, 3, 4500604. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, D.; Gu, C.; Qiu, Y.; Wan, H.; Wang, P. 3D microgroove electrical impedance sensing to examine 3D cell cultures for antineoplastic drug assessment. Microsyst. Nanoeng. 2020, 23, 6. [Google Scholar] [CrossRef]
- Miralles, V.; Huerre, A.; Malloggi, F.; Jullien, M.C. A review of heating and temperature control in microfluidic systems: Techniques and applications. Diagnostics 2013, 3, 33–67. [Google Scholar] [CrossRef] [PubMed]
- Markovic, T.; Bao, J.; Maenhout, G.; Ocket, I.; Nauwelaers, B. An interdigital capacitor for microwave heating at 25 GHz and wideband dielectric sensing of volumes in continuous microfluidics. Sensors 2019, 19, 715. [Google Scholar] [CrossRef]
- Abduljabar, A.A.; Choi, H.; Barrow, D.A.; Porch, A. Adaptive coupling of resonators for efficient microwave heating of microfluidics systems. IEEE Trans. Microw. Theory Tech. 2015, 63, 3681–3690. [Google Scholar] [CrossRef]
- Boybay, M.S.; Jiao, A.; Glawdel, T.; Ren, C.L. Microwave sensing and heating of individual droplets in microfluidic devices. Lab Chip 2013, 13, 3840–3846. [Google Scholar] [CrossRef]
- Issadore, D.; Humphry, K.J.; Brown, K.A.; Sandberg, L.; Weitz, D.A.; Westervelt, R.M. Microwave dielectric heating of drops in microfluidic devices. Lab Chip 2009, 9, 1701–1706. [Google Scholar] [CrossRef] [PubMed]
- Shah, J.J.; Sundaresan, S.G.; Geist, J.; Reyes, D.R.; Booth, J.C.; Rao, M.V.; Gaitan, M. Microwave dielectric heating of fluids in an integrated microfluidic device. J. Micromech. Microeng. 2007, 17, 2224–2230. [Google Scholar] [CrossRef]
- Marchiarullo, D.J.; Sklavounos, A.H.; Oh, K.; Poe, B.L.; Barker, N.S.; Landers, J.P. Low-power microwave-mediated heating for microchip-based PCR. Lab chip 2013, 13, 3417–3425. [Google Scholar] [CrossRef] [PubMed]
- Kempitiya, A.; Borca-Tasciuc, D.A.; Mohamed, H.S.; Hella, M.M. Localized microwave heating in microwells for parallel DNA amplification applications. Appl. Phys. Lett. 2009, 94, 064106. [Google Scholar] [CrossRef]
- Morgan, A.J.L.; Naylon, J.; Gooding, S.; John, C.; Squires, O.; Lees, J.; Barrow, D.A.; Porch, A. Efficient microwave heating of microfluidic systems. Sens. Actuators B Chem. 2013, 181, 904–909. [Google Scholar] [CrossRef]
- Shaw, K.J.; Docker, P.T.; Yelland, J.V.; Dyer, C.E.; Greenman, J.; Greenway, G.M.; Haswell, S.J. Rapid PCR amplification using a microfluidic device with integrated microwave heating and impingement cooling. Lab Chip 2010, 10, 1725–1728. [Google Scholar] [CrossRef]
- Markovic, T.; Liu, S.; Ocket, I.; Nauwelaers, B. A 20 GHz microwave heater for digital microfluidics. Int. J. Microw. Wirel. Technol. 2017, 9, 1591–1596. [Google Scholar] [CrossRef]
- Markovic, T.; Bao, J.; Ocket, I.; Kil, D.; Brancato, L.; Puers, R.; Nauwelaers, B. Uniplanar microwave heater for digital microfluidics. In Proceedings of the 2017 First IEEE MTT-S International Microwave Bio Conference (IMBioC), Gothenburg, Sweden, 15–17 May 2017. [Google Scholar]
- Majeed, B.; Jones, B.; Tezcan, D.S.; Tutunjyan, N.; Haspeslagh, L.; Peeters, S.; Fiorini, P.; de Beeck, M.O.; van Hoof, C.; Hiraoka, M.; et al. Silicon based system for single-nucleotide-polymorphism detection: Chip fabrication and thermal characterization of polymerase chain reaction. Jpn. J. Appl. Phys. 2012, 51, 04DL01. [Google Scholar] [CrossRef]
- Duffy, D.C.; McDonald, J.C.; Schueller, O.J.A.; Whitesides, G.M. Rapid prototyping of microfluidic systems in poly(dimethylsiloxane). Anal. Chem. 1998, 70, 4974–4984. [Google Scholar] [CrossRef]
- Bao, J.; Markovic, T.; Brancato, L.; Kil, D.; Ocket, I.; Puers, R.; Nauwelaers, B. Novel fabrication process for integration of microwave sensors in microfluidic channels. Micromachines 2020, 11, 320. [Google Scholar] [CrossRef]
- Markovic, T.; Ocket, I.; Jones, B.; Nauwelaers, B. Characterization of a novel microwave heater for continuous flow microfluidics fabricated on high-resistivity silicon. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016. [Google Scholar]
- Markovic, T.; Ocket, I.; Jones, B.; Nauwelaers, B. Contactless microwave heating of continuous flow microfluidics on silicon. In Proceedings of the 20th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Dublin, Ireland, 9–13 October 2016. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Liu, S.; Ocket, I.; Barmuta, P.; Markovic, T.; Lewandowski, A.; Schreurs, D.; Nauwelaers, B. Broadband dielectric spectroscopy calibration using calibration liquids with unknown permittivity. In Proceedings of the 84th ARFTG Microwave Measurement Conference, Boulder, CO, USA, 4–5 December 2014. [Google Scholar]
- Barmuta, P.; Bao, J.; Zhang, M.; Marković, T.; Nauwelaers, B.; Schreurs, D.; Ocket, I. Broadband electrical determination of liquid mixing ratios for microfluidics. In Proceedings of the 2019 European Microwave Conference in Central Europe (EuMCE), Prague, Czech Republic, 13–15 May 2019. [Google Scholar]
- Liu, S.; Orloff, N.D.; Little, C.A.; Zhao, W.; Booth, J.C.; Williams, D.F.; Nauwelaers, B. Hybrid characterization of nanolitre dielectric fluids in a single microfluidic channel up to 110 GHz. IEEE Trans. Microw. Theory Tech. 2017, 65, 5063–5073. [Google Scholar] [CrossRef]
- Ellison, W.J. Permittivity of pure water, at standard atmospheric pressure, over the frequency range 0–25 THz and the temperature range 0–100 °C. J. Phys. Ref. Data 2007, 36. [Google Scholar] [CrossRef]
- Markovic, T.; Jones, B.; Barmuta, P.; Ocket, I.; Nauwelaers, B. A transmission line based microwave heater at 25 GHz for continuous flow microfluidics fabricated on silicon. In Proceedings of the 2019 49th European Microwave Conference (EuMC), Paris, France, 1–3 October 2019. [Google Scholar]
- Shah, J.J.; Gaitan, M.; Geist, J. Generalized temperature measurement equations for Rhodamine B dye solution and its application to microfluidics. Anal. Chem. 2009, 81, 8260–8263. [Google Scholar] [CrossRef] [PubMed]

| Frequency 25 GHz | TLMH | OELMH | ||
|---|---|---|---|---|
| S11 | S21 | S11 | ||
| HR-Si die | Air | −17.74 | −0.93 | −0.92 |
| DI Water | −23.57 | −2.63 | −4.45 | |
| Integrated die and PCB | Air | −11.62 | −5.26 | −4.82 |
| Di Water | −10.39 | −8.55 | −16.92 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markovic, T.; Ocket, I.; Baric, A.; Nauwelaers, B. Design and Comparison of Resonant and Non-Resonant Single-Layer Microwave Heaters for Continuous Flow Microfluidics in Silicon-Glass Technology. Energies 2020, 13, 2635. https://doi.org/10.3390/en13102635
Markovic T, Ocket I, Baric A, Nauwelaers B. Design and Comparison of Resonant and Non-Resonant Single-Layer Microwave Heaters for Continuous Flow Microfluidics in Silicon-Glass Technology. Energies. 2020; 13(10):2635. https://doi.org/10.3390/en13102635
Chicago/Turabian StyleMarkovic, Tomislav, Ilja Ocket, Adrijan Baric, and Bart Nauwelaers. 2020. "Design and Comparison of Resonant and Non-Resonant Single-Layer Microwave Heaters for Continuous Flow Microfluidics in Silicon-Glass Technology" Energies 13, no. 10: 2635. https://doi.org/10.3390/en13102635
APA StyleMarkovic, T., Ocket, I., Baric, A., & Nauwelaers, B. (2020). Design and Comparison of Resonant and Non-Resonant Single-Layer Microwave Heaters for Continuous Flow Microfluidics in Silicon-Glass Technology. Energies, 13(10), 2635. https://doi.org/10.3390/en13102635





