Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison
Abstract
1. Introduction
2. Nonlinear Frequency-Domain Models
- Frequency Transfer Matrix;
- X-Parameters;
- Simplified Volterra models.
2.1. Frequency Transfer Matrix
Identification Procedure
2.2. X-Parameters
Identification Procedure
2.3. Simplified Volterra Model
Identification Procedure
3. Case Study: Diode Bridge Rectifier
4. Model Identification
4.1. Frequency Transfer Matrix
4.2. X-Parameters
4.3. Simplified Volterra Model
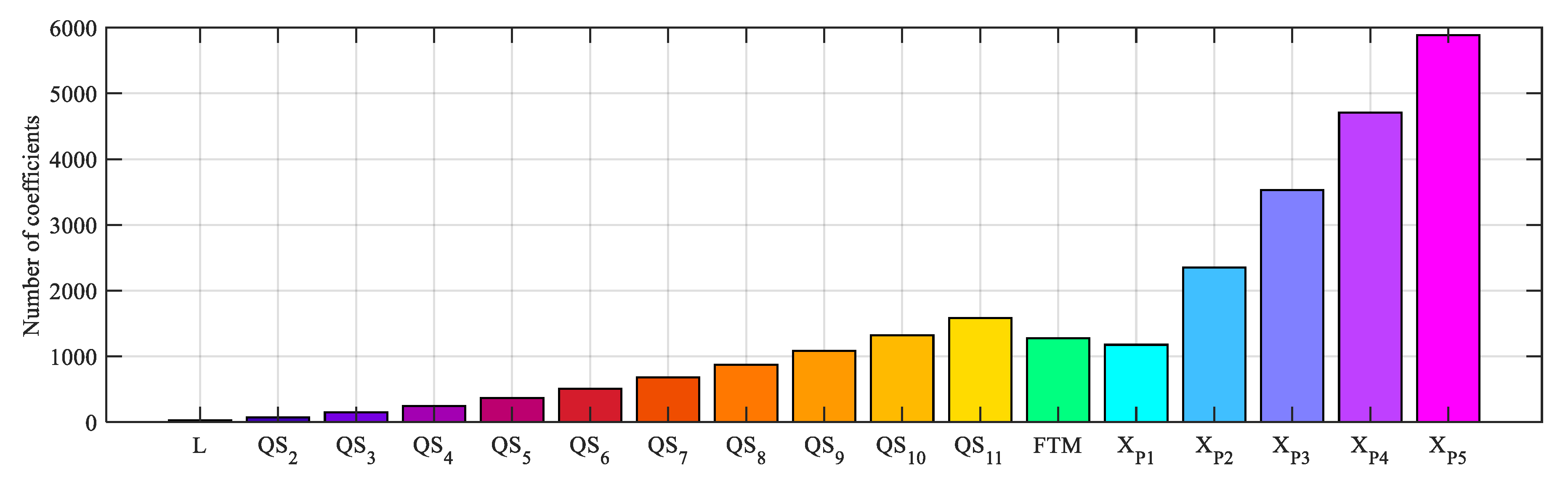
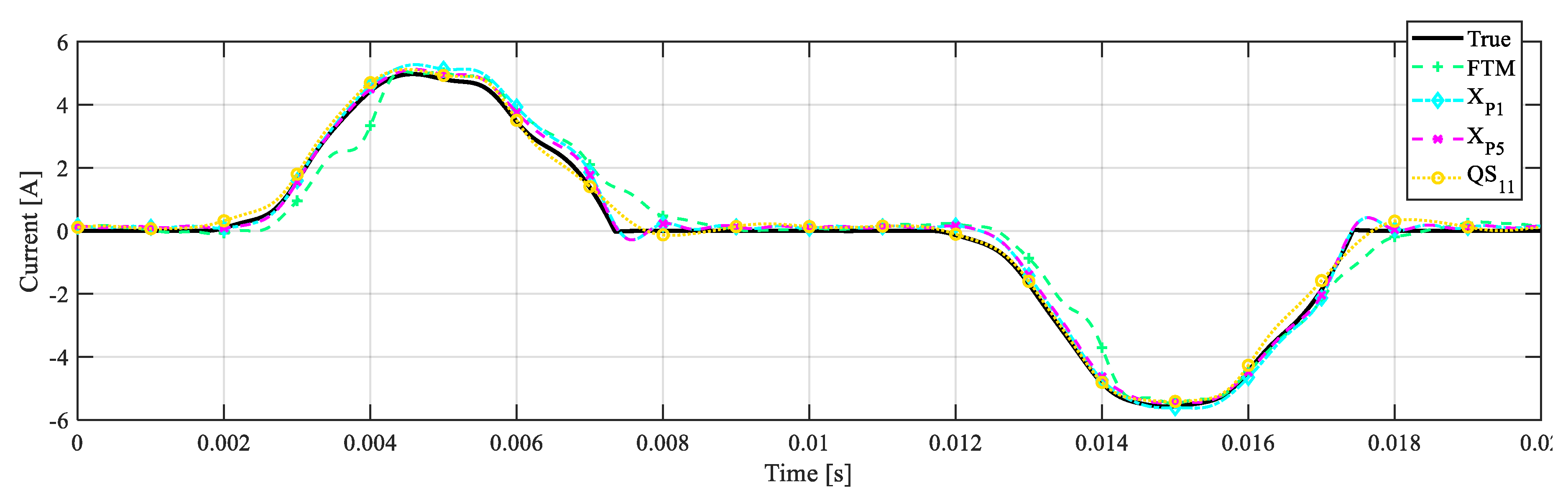
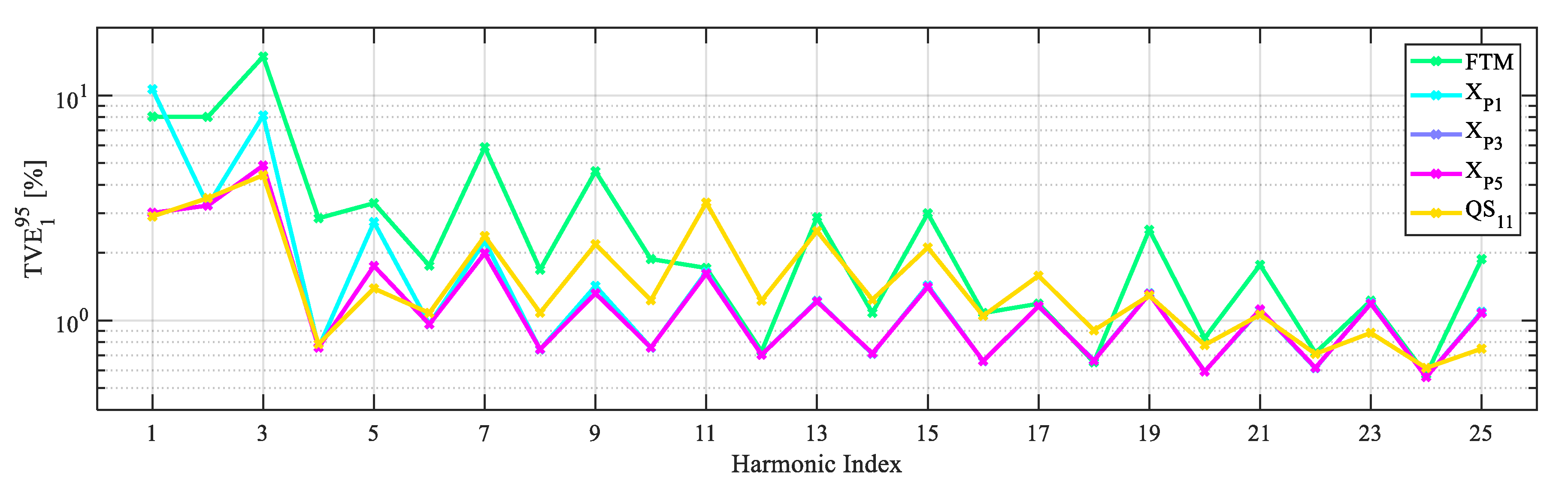
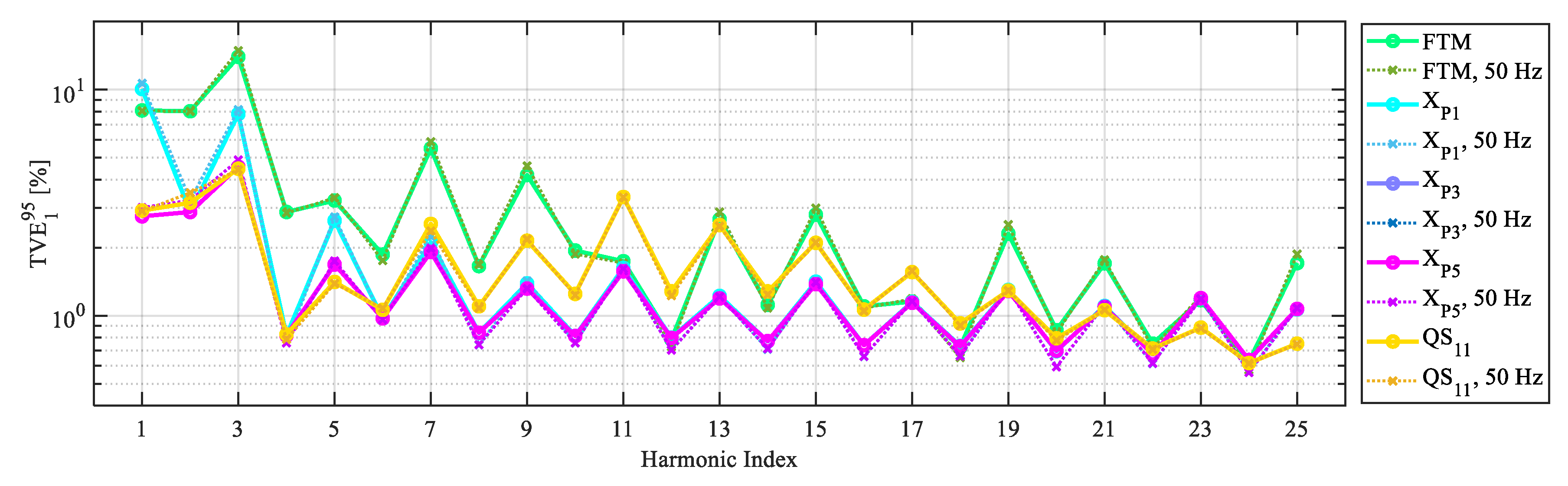
5. Model Comparison
5.1. Random Fundamental Amplitude
5.2. Random Fundamental Amplitude and Frequency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Misra, R.; Paudyal, S.; Ceylan, O.; Mandal, P. Harmonic Distortion Minimization in Power Grids with Wind and Electric Vehicles. Energies 2017, 10, 932. [Google Scholar] [CrossRef]
- Mastny, P.; Moravek, J.; Vojtek, M.; Drapela, J. Hybrid Photovoltaic Systems with Accumulation—Support for Electric Vehicle Charging. Energies 2017, 10, 834. [Google Scholar] [CrossRef]
- Arrillaga, J.; Smith, B.C.; Watson, N.R.; Wood, A.R. Power System Harmonic Analysis; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Acha, E.; Madrigal, M. Power System Harmonics: Computer Modelling and Analysis; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- IEEE Task Force on Harmonic Modeling and Simulation. Modeling and simulation of the propagation of harmonics in electric power systems Part I: Concepts, models, and simulation techniques. IEEE Trans. Power Deliv. 1996, 11, 452–464. [Google Scholar] [CrossRef]
- IEEE Task Force on Harmonic Modeling and Simulation. Modeling and simulation of the propagation of harmonics in electric power systems Part II: Sample systems and examples. IEEE Trans. Power Deliv. 1996, 11, 466–474. [Google Scholar] [CrossRef]
- IEEE Task Force on Harmonic Modeling and Simulation. Harmonic analysis in frequency and time domain. IEEE Trans. Power Deliv. 2013, 28, 1813–1821. [Google Scholar] [CrossRef]
- Kundert, K.S.; Sangiovanni-Vincentelli, A. Simulation of nonlinear circuits in the frequency domain. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1986, 5, 521–535. [Google Scholar] [CrossRef]
- Kundert, K.S.; Sorkin, G.B.; Sangiovanni-Vincentelli, A. Applying harmonic balance to almost-periodic circuits. IEEE Trans. Microw. Theory Tech. 1988, 36, 366–378. [Google Scholar] [CrossRef]
- Gilmore, R.J.; Steer, M.B. Nonlinear circuit analysis using the method of harmonic balance—A review of the art. Part I. Introductory concepts. Int. J. Microw. Millim.-Wave Comput.-Aided Eng. 1991, 1, 22–37. [Google Scholar] [CrossRef]
- Fauri, M. Harmonic modelling of non-linear load by means of crossed frequency admittance matrix. IEEE Trans. Power Syst. 1997, 12, 1632–1638. [Google Scholar] [CrossRef]
- Smith, B.C.; Watson, N.R.; Wood, A.R.; Arrillaga, J. Harmonic tensor linearisation of HVDC converters. IEEE Trans. Power Deliv. 1998, 13, 1244–1250. [Google Scholar] [CrossRef]
- Yong, J.; Chen, L.; Chen, S. Modeling of Home Appliances for Power Distribution System Harmonic Analysis. IEEE Trans. Power Deliv. 2010, 25, 3147–3155. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, J.; Wang, Q.; Wei, N. Measurement-Based Harmonic Modeling of an Electric Vehicle Charging Station Using a Three-Phase Uncontrolled Rectifier. IEEE Trans. Smart Grid 2015, 6, 1332–1340. [Google Scholar] [CrossRef]
- Yong, J.; Chen, L.; Nassif, A.B.; Xu, W. A Frequency-Domain Harmonic Model for Compact Fluorescent Lamps. IEEE Trans. Power Deliv. 2010, 25, 1182–1189. [Google Scholar] [CrossRef]
- Caicedo, J.E.; Romero, A.A.; Zini, H.C. Frequency domain modeling of nonlinear loads, considering harmonic interaction. In Proceedings of the 2017 IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Bogota, Colombia, 31 May–2 June 2017; pp. 1–6. [Google Scholar]
- Root, D.E.; Verspecht, J.; Horn, J.; Marcu, M. X-Parameters: Characterization, Modeling, and Design of Nonlinear RF and Microwave Components; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Baylis, C.; Marks, R.J.; Martin, J.; Miller, H.; Moldovan, M. Going Nonlinear. IEEE Microw. 2011, 12, 55–64. [Google Scholar] [CrossRef]
- Verspecht, J.; Williams, D.F.; Schreurs, D.; Remley, K.A.; McKinley, M.D. Linearization of large-signal scattering functions. IEEE Trans. Microw. Theory Tech. 2005, 53, 1369–1376. [Google Scholar] [CrossRef]
- Verspecht, J.; Root, D.E. Polyharmonic distortion modeling. IEEE Microw. 2006, 7, 44–57. [Google Scholar] [CrossRef]
- Verspecht, J. Describing Functions Can Better Model Hard Nonlinearities in the Frequency Domain Than the Volterra Theory. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, November 1995. [Google Scholar]
- Uhl, R.; Mirz, M.; Vandeplas, T.; Barford, L.; Monti, A. Non-linear behavioral X-Parameters model of single-phase rectifier in the frequency domain. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6292–6297. [Google Scholar]
- Mirz, M.; Uhl, R.; Vandeplas, T.; Barford, L.; Monti, A. Measurement-based parameter identification of non-linear polynomial frequency domain model of single-phase four diode bridge rectifier. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Faifer, M.; Ottoboni, R.; Prioli, M.; Toscani, S. Simplified Modeling and Identification of Nonlinear Systems Under Quasi-Sinusoidal Conditions. IEEE Trans. Instrum. Meas. 2016, 65, 1508–1515. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Prioli, M.; Toscani, S.; Zanoni, M. Definition of Simplified Frequency-Domain Volterra Models with Quasi-Sinusoidal Input. IEEE Trans. Circuits Syst. I 2018, 65, 1652–1663. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Behavioral Representation of a Bridge Rectifier Using Simplified Volterra Models. IEEE Trans. Instrum. Meas. 2019, 68, 1611–1618. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Modeling and identification of a bridge rectifier under quasi-sinusoidal conditions. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–5. [Google Scholar]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M.; Crotti, G.; Giordano, D.; Barbieri, L.; Gondola, M.; Mazza, P. Overcoming Frequency Response Measurements of Voltage Transformers: An Approach Based on Quasi-Sinusoidal Volterra Models. IEEE Trans. Instrum. Meas. 2018, 68, 2800–2807. [Google Scholar] [CrossRef]
- Collin, A.J.; Djokic, S.Z.; Drapela, J.; Langella, R.; Testa, A. Light Flicker and Power Factor Labels for Comparing LED Lamp Performance. IEEE Trans. Ind. Appl. 2019, 55, 7062–7070. [Google Scholar] [CrossRef]
- Femia, N.; di Capua, G.; Ohashi, R.A.P. Harmonic analysis of diode-bridge rectifiers in Wireless Power Transfer System. In Proceedings of the 2017 14th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Giardini Naxos, Italy, 12–15 June 2017; pp. 1–4. [Google Scholar]
- Voltage Characteristics of Electricity Supplied by Public Electricity Networks, Standard EN 50160; CENELEC: Brussels, Belgium, 2010.
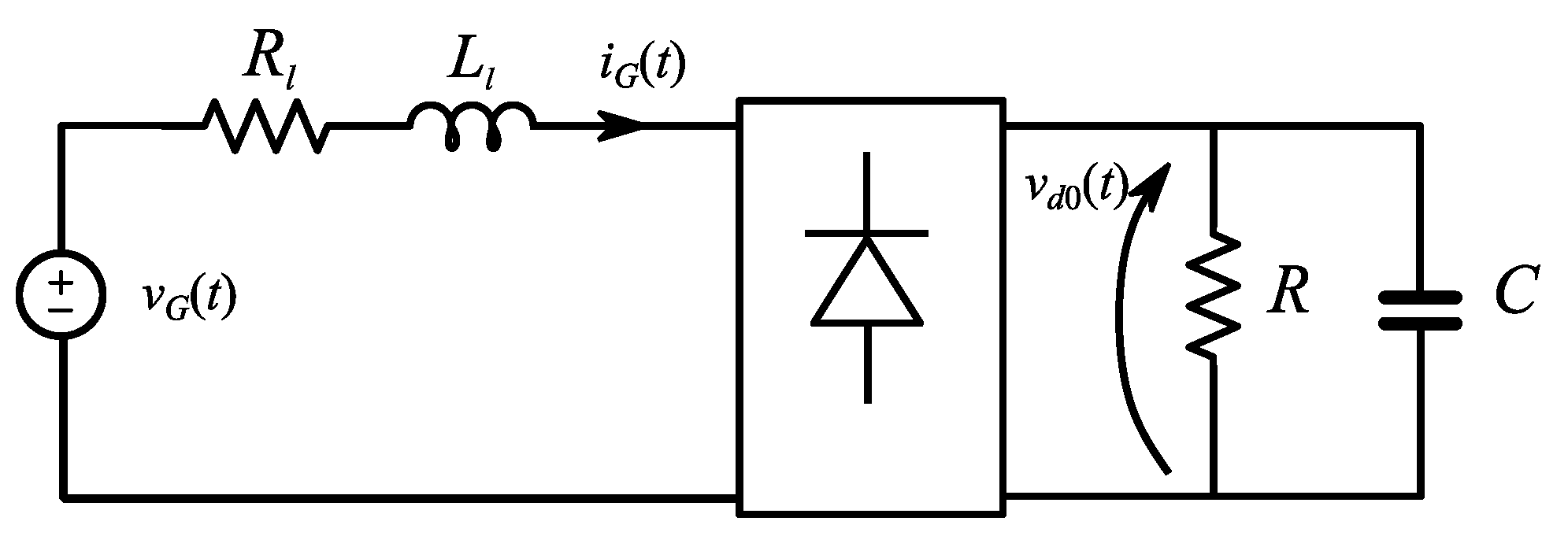
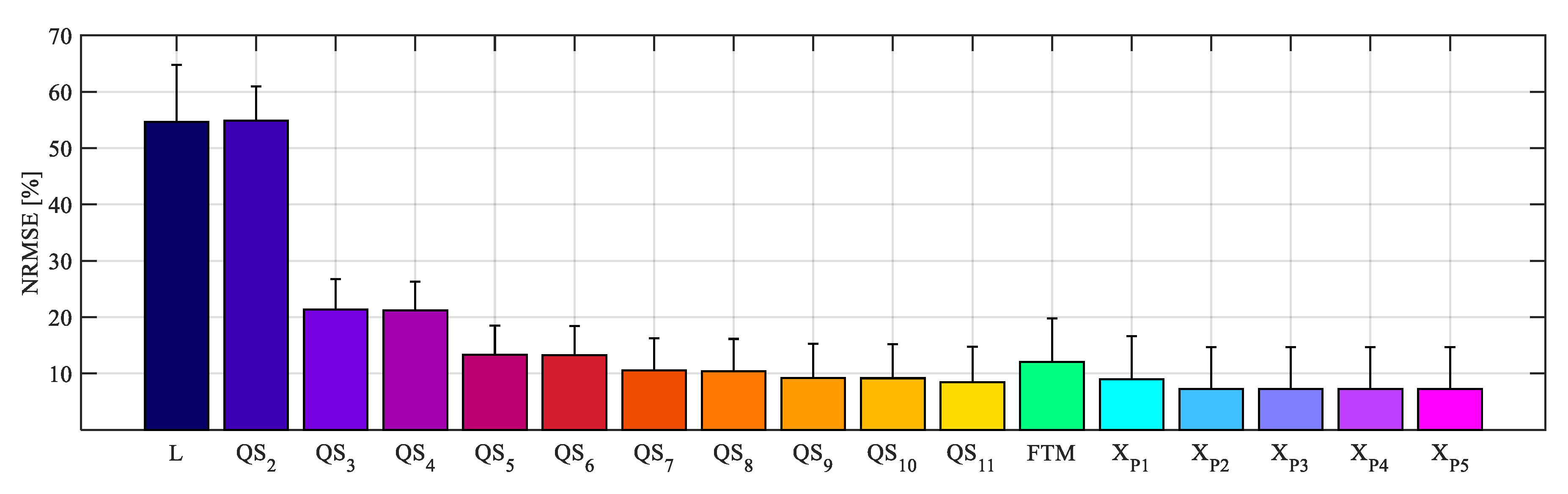
| VG,n (V) | Rl (Ω) | Ll (mH) | R (Ω) | C (mF) |
|---|---|---|---|---|
| 53 | 0.4 | 4 | 50 | 1.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison. Energies 2020, 13, 2609. https://doi.org/10.3390/en13102609
Faifer M, Laurano C, Ottoboni R, Toscani S, Zanoni M. Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison. Energies. 2020; 13(10):2609. https://doi.org/10.3390/en13102609
Chicago/Turabian StyleFaifer, Marco, Christian Laurano, Roberto Ottoboni, Sergio Toscani, and Michele Zanoni. 2020. "Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison" Energies 13, no. 10: 2609. https://doi.org/10.3390/en13102609
APA StyleFaifer, M., Laurano, C., Ottoboni, R., Toscani, S., & Zanoni, M. (2020). Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison. Energies, 13(10), 2609. https://doi.org/10.3390/en13102609









