Overview on Grid-Forming Inverter Control Methods
Abstract
1. Introduction
2. Terminology
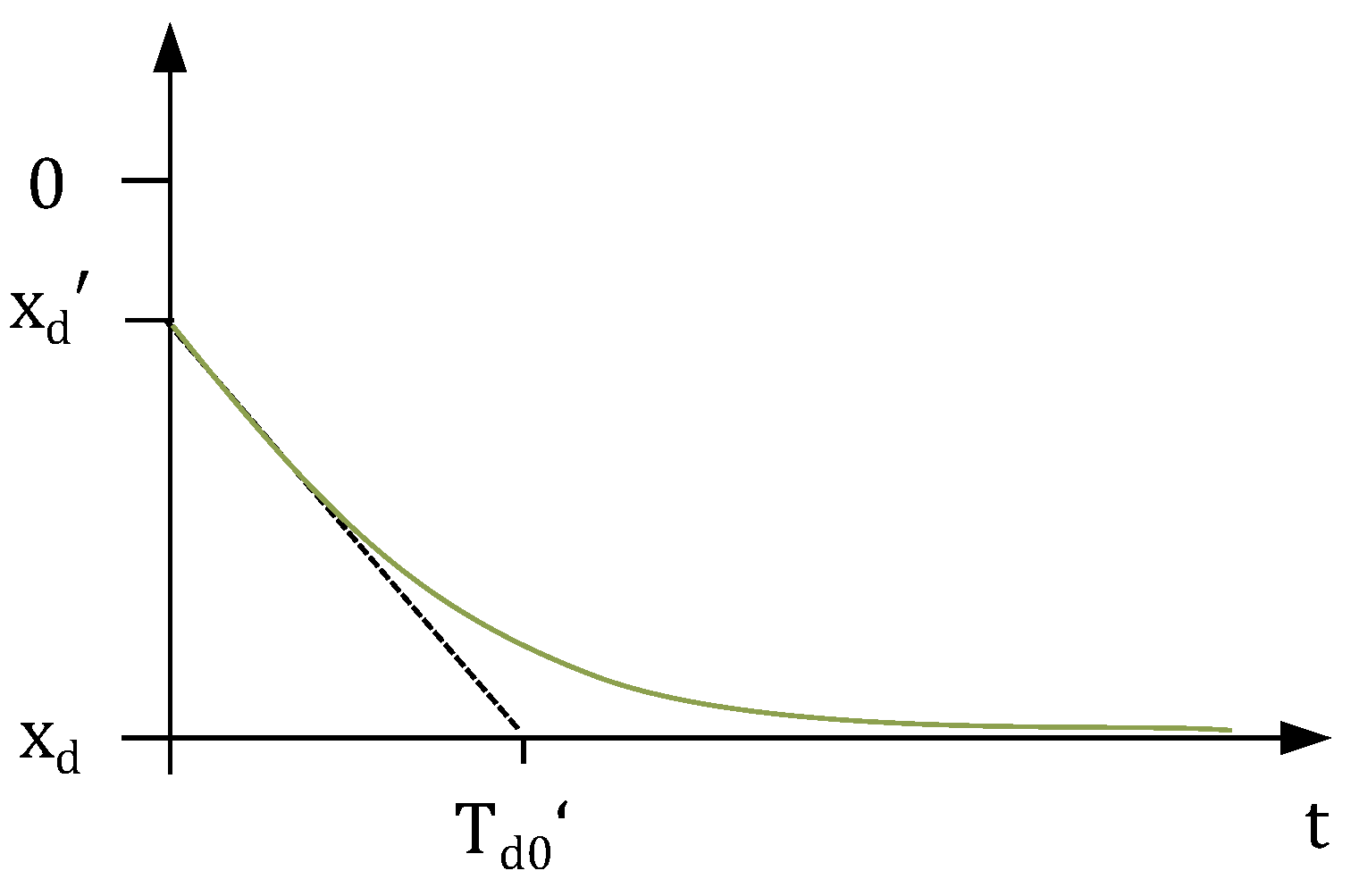
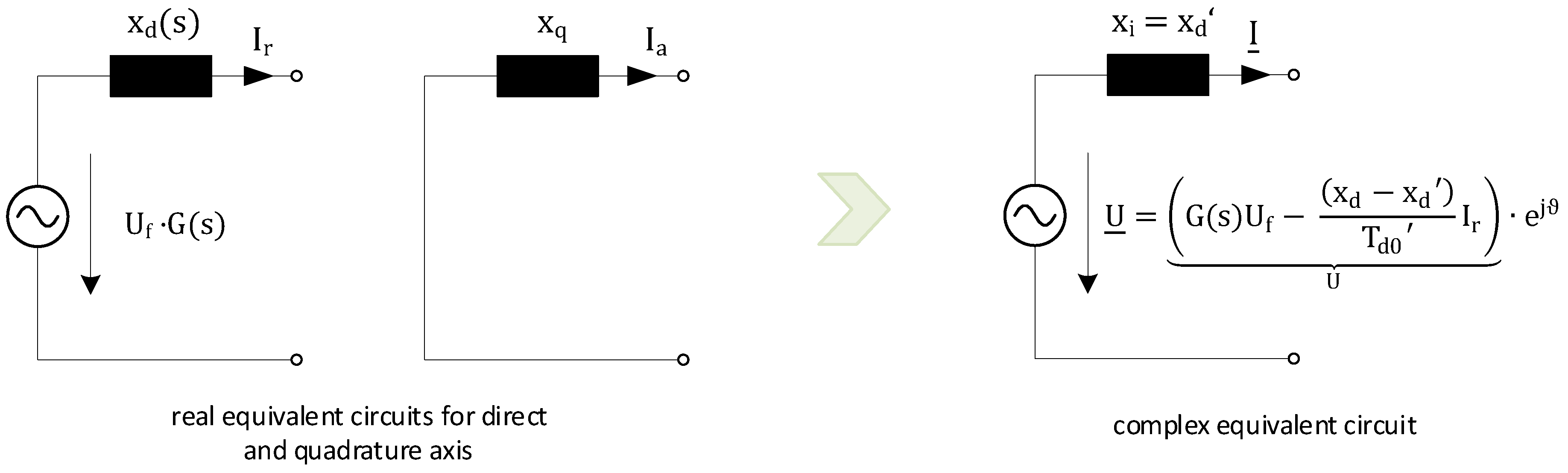
3. Functional Principle of Synchronous Machines
4. Grid-Forming Inverter Control Methods
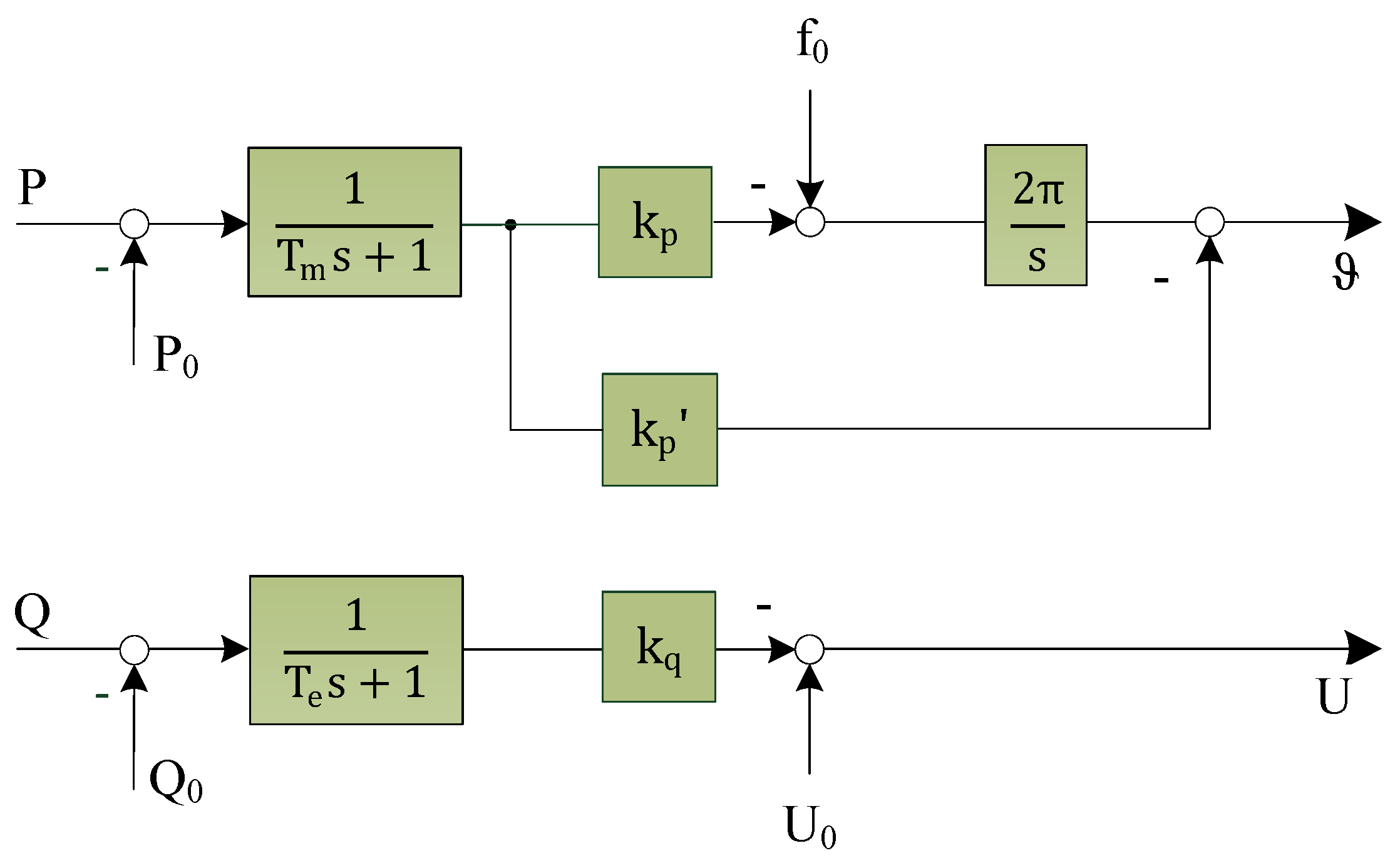
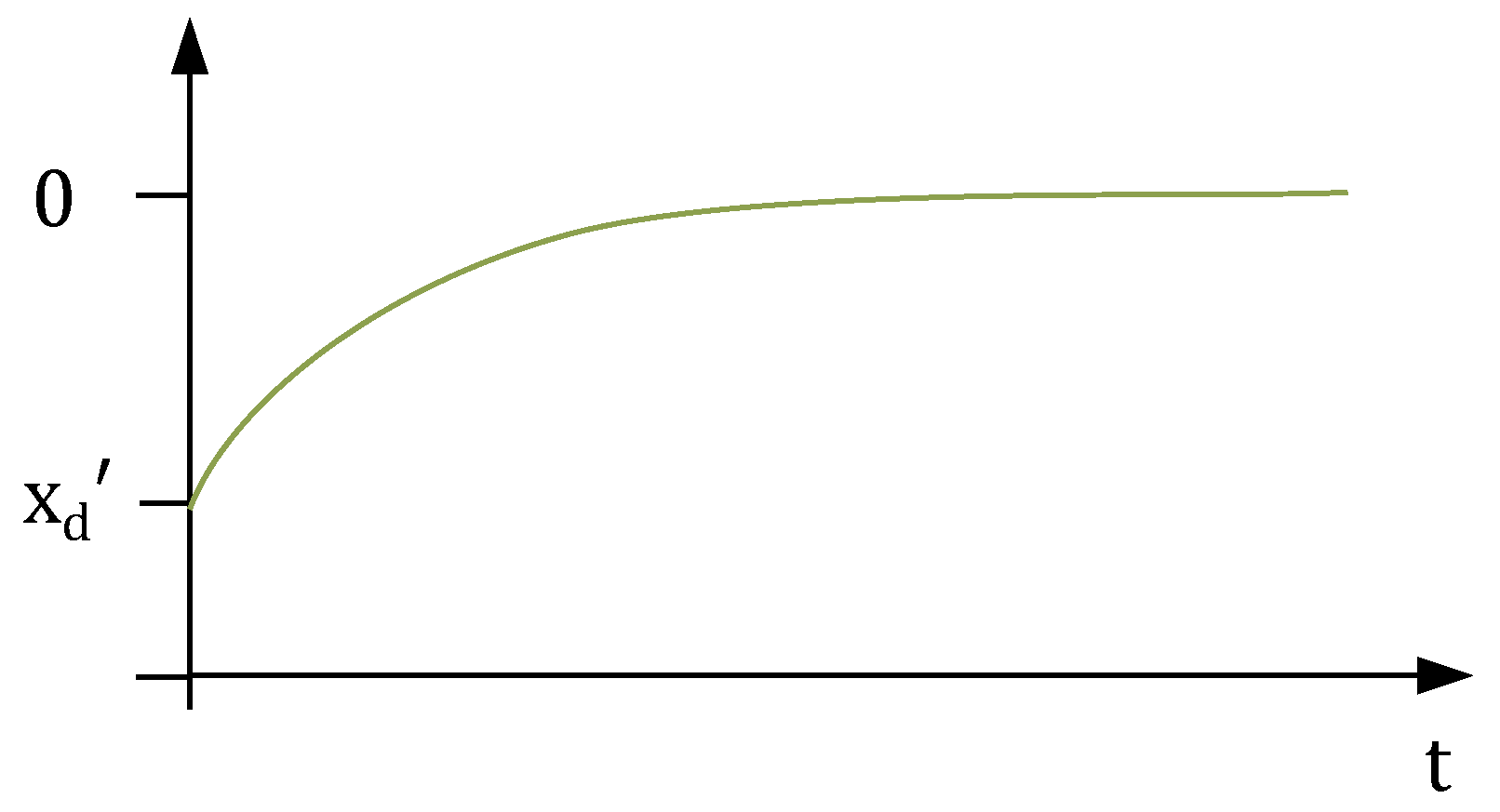
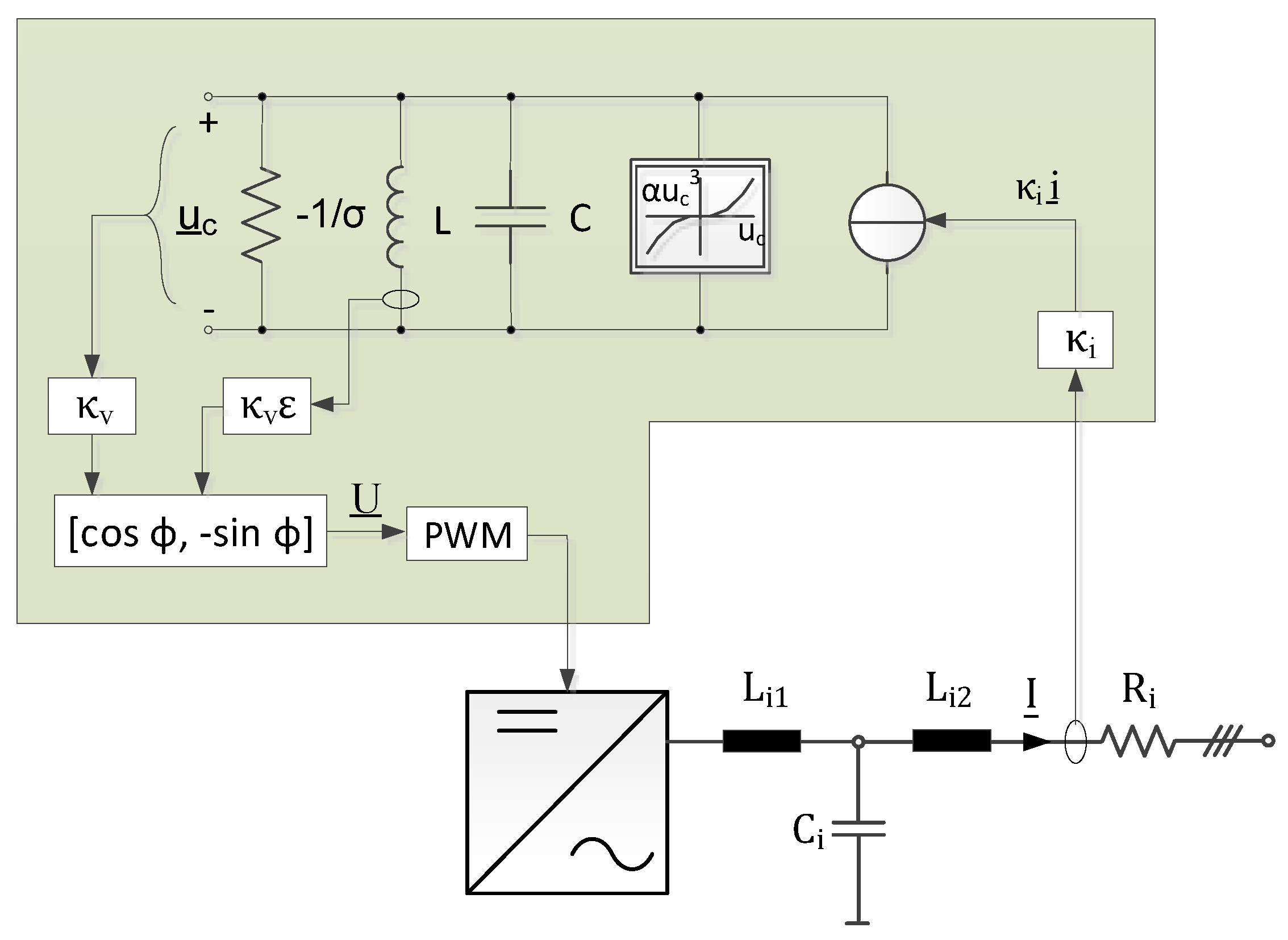
4.1. Droop-Based Grid-Forming Control Methods (e.g. Selfsync)
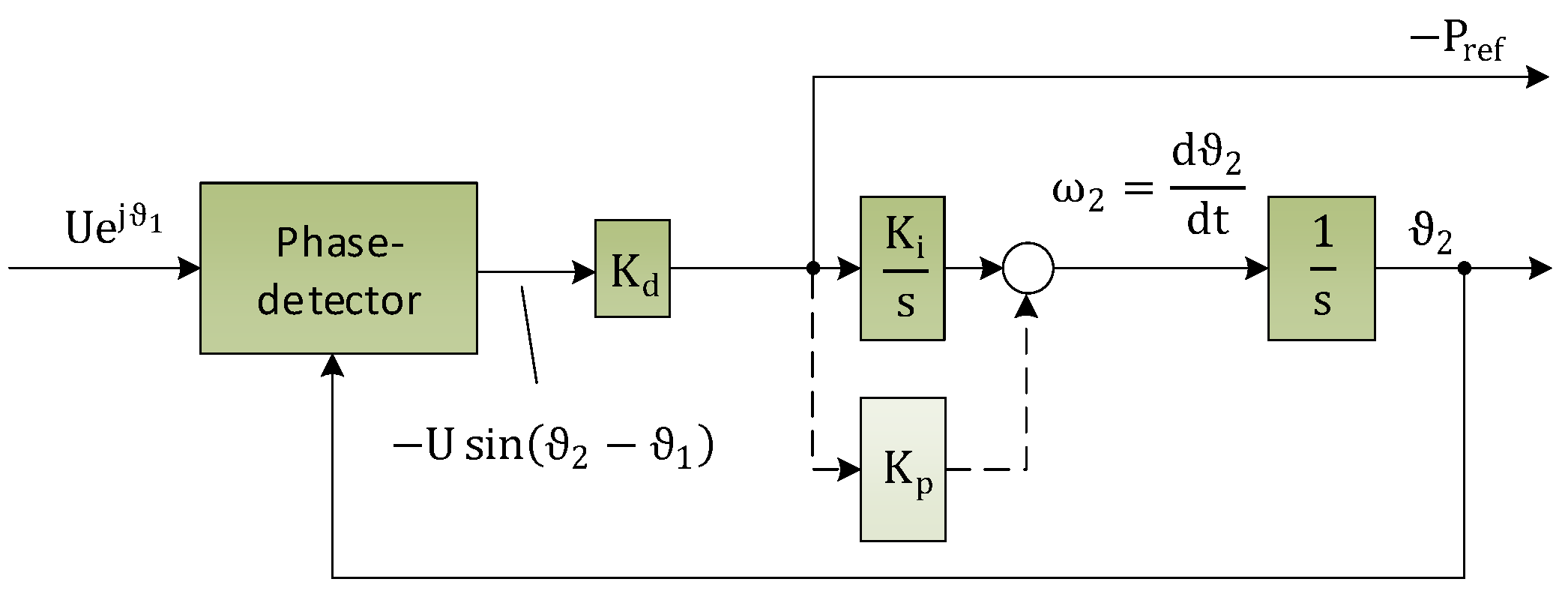
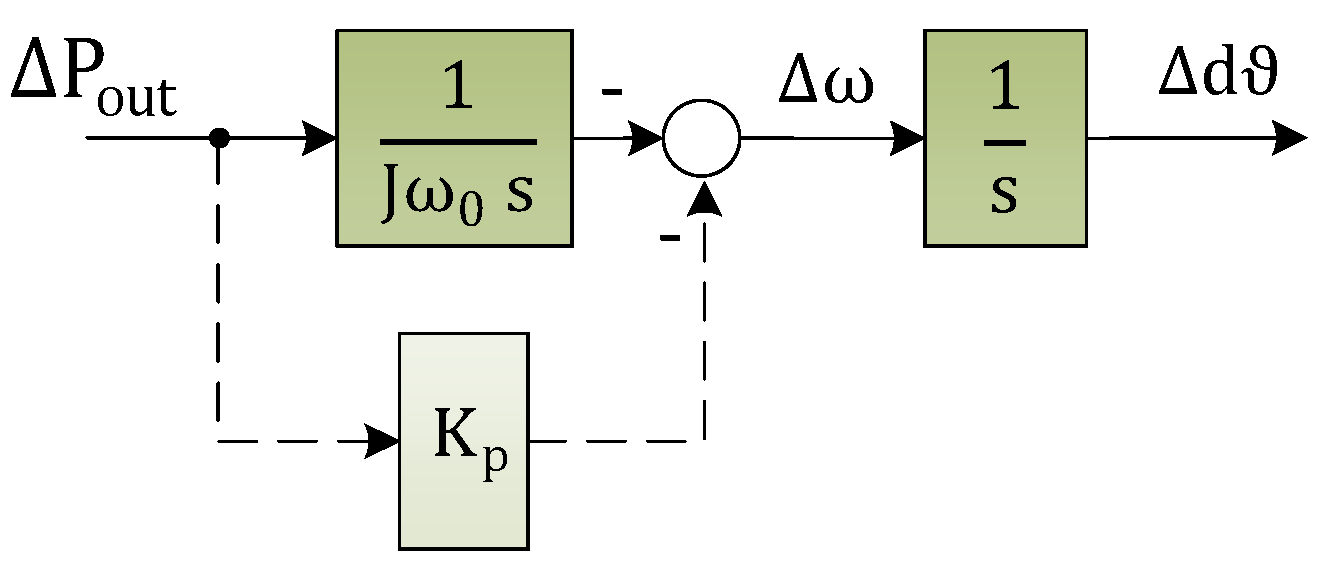
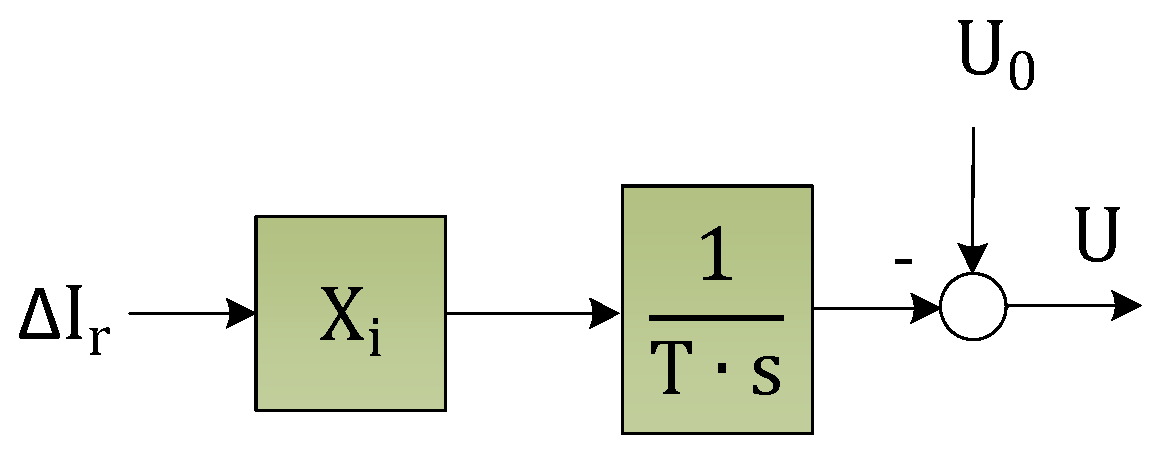
4.2. Power Synchronization Loop
4.3. Voltage Controlled Inverter (VCI)
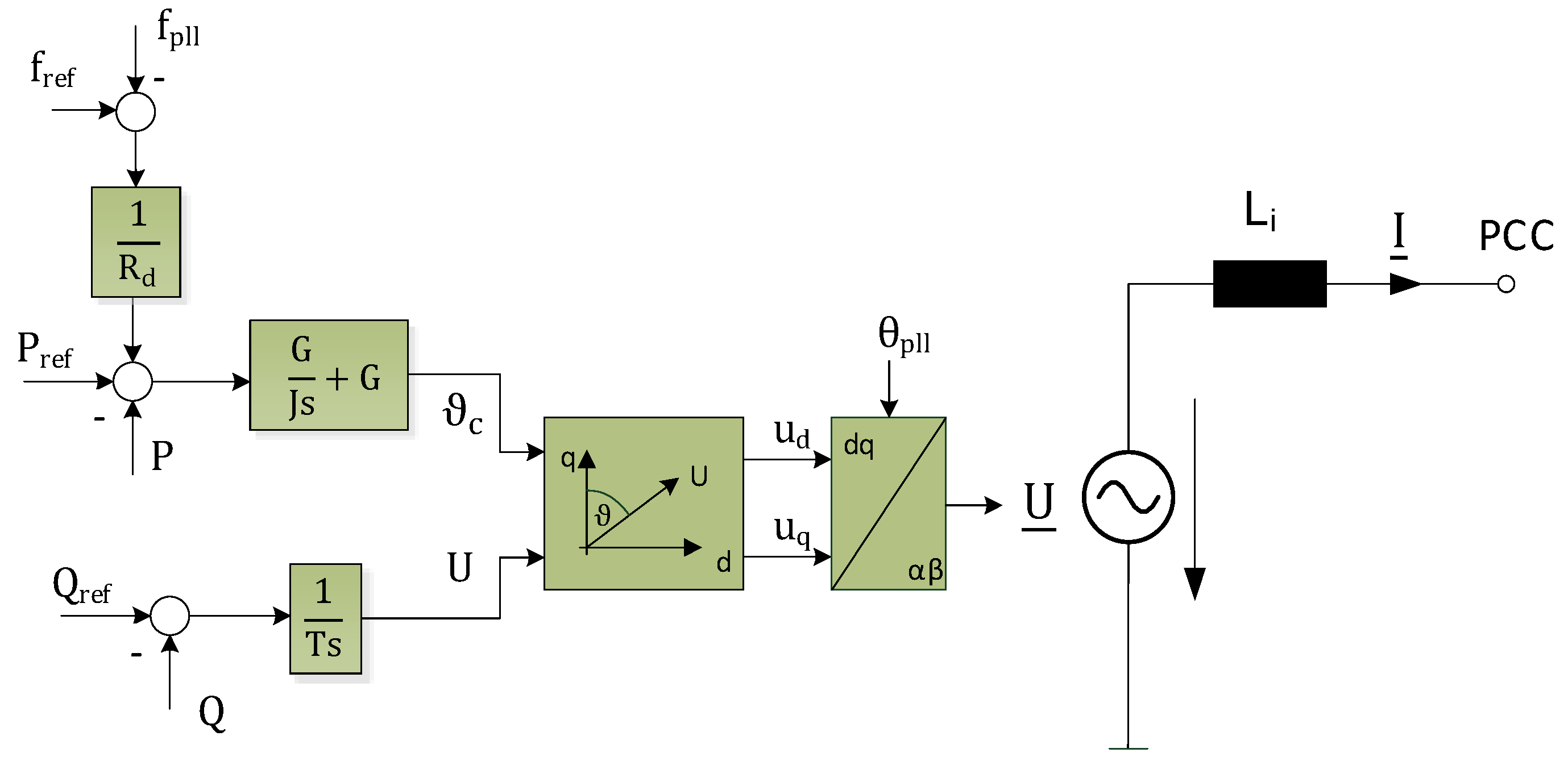
4.4. Virtual Synchronous Machine (VSM)
4.5. Virtual Oscillator Control (VOC)
4.6. Matching Control
4.7. PLL-Based Modified Current-Controlled Methods
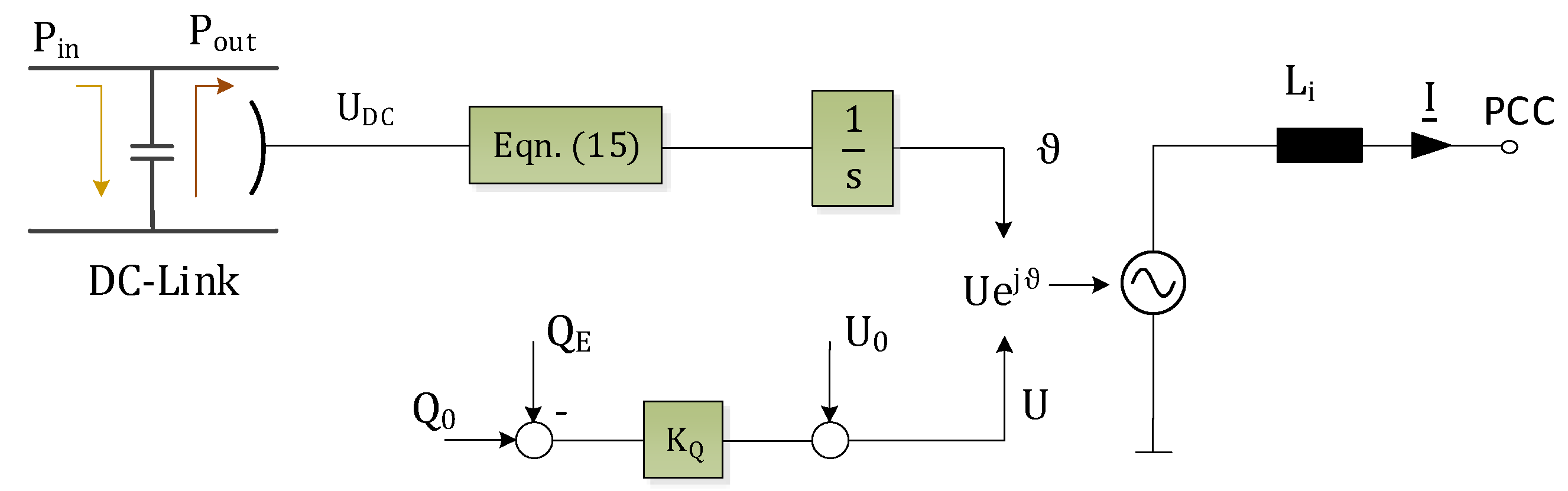
4.8. Direct Power Control (DPC)
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Engler, A.; Hardt, C.; Strauss, P.; Vandenbergh, M. Parallel Operation of Generators for Stand-Alone Single-Phase Hybrid Systems—First Implementation of a new control Technology. In Proceedings of the 17th European Photovoltaic Solar Energy Conference, München, Germany, 22–26 October 2001; WIP-Renewable Energies: Munich, Germany, 2001; pp. 2690–2693. [Google Scholar]
- Visscher, K.; de Haan, S.W.H. Virtual synchronous machines (VSG’s) for frequency stabilisation in future grids with a significant share of decentralized generation. In Proceedings of the CIRED Seminar 2008: SmartGrids for Distribution, Frankfurt, Germany, 23–24 June 2008; pp. 334–337. [Google Scholar]
- Engler, A.; Haas, O.; Kansteiner, B.; Raptis, F.; Sachau, J.; Zacharias, P. Control of Parallel Working Power Units in Expandable Grids. In Proceedings of the 14th European Photovoltaic Solar Energy Conference, Barcelona, Spain, 30 June–4 July 1997; Ossenbrink, H.A., Helm, P., Ehmann, H., Eds.; H.S. Stephens & Associates: Bedfort, UK, 1997; pp. 2029–2032. [Google Scholar]
- Anderson, P.M.; Fouad, A.-A.A. Power System Control and Stability, 2nd ed.; IEEE Press, Wiley-Interscience: Piscataway, NJ, USA, 2003; ISBN 9780471238621. [Google Scholar]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Milano, F. Power System Modelling and Scripting; Springer: Heidelberg, Germany, 2010; ISBN 3642136680. [Google Scholar]
- Weckesser, T.; Johannsson, H.; Ostergaard, J. Impact of model detail of synchronous machines on real-time transient stability assessment. In Proceedings of the 2013 IREP Symposium Bulk Power System Dynamics and Control—IX Optimization, Security and Control of Emerging Power Grid (IREP), Rethymnon, Crete, Greece, 25–30 August 2013; Voumas, C., Ed.; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Prabha, K. Power System Stability and Control, 1st ed.; McGraw-Hill: Hightstown, NJ, USA, 1994. [Google Scholar]
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2020; ISBN 9781119526346. [Google Scholar]
- Van Cutsem, T.; Βουρνάς, Κ. Voltage Stability of Electric Power Systems, 1st ed.; Springer Science + Business Media: Dordrecht, The Netherlands, 1998; ISBN 9780792381396. [Google Scholar]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability, updated ed.; Stipes Publishing L.L.C: Champaign, IL, USA, 2006; ISBN 9781588746733. [Google Scholar]
- Crastan, V.; Westermann, D. Elektrische Energieversorgung 3. Dynamik, Regelung und Stabilität, Versorgungsqualität, Netzplanung, Betriebsplanung und -Führung, Leit- und Informationstechnik, FACTS, HGÜ, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 3642201008. [Google Scholar]
- Crastan, V. Elektrische Energieversorgung 1. Netzelemente, Modellierung, Stationäres Verhalten, Bemessung, Schalt- und Schutztechnik, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 366245985X. [Google Scholar]
- Oeding, D.; Oswald, B.R. Elektrische Kraftwerke und Netze, 7th ed.; Springer: Heidelberg, Germany, 2011; ISBN 3642192459. [Google Scholar]
- Alberto, A. Arrangement of Parallel Static AC Power Sources Proportions. U.S. Patent 3864620A, 11 September 1973. [Google Scholar]
- Torres, L.A.B.; Hespanha, J.P.; Moehlis, J. Power supply synchronization without communication. In Proceedings of the 2012 IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Kawabata, T.; Higashino, S. Parallel operation of voltage source inverters. IEEE Trans. Ind. Appl. 1988, 24, 281–287. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- Tayab, U.B.; Roslan, M.A.B.; Hwai, L.J.; Kashif, M. A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- Engler, A. Device for Parallel Operation of Equal Range Single-Phase or Three-Phase Voltage Sources. EP1286444B1, 21 August 2001. [Google Scholar]
- Engler, A. Regelung von Batteriestromrichtern in Modularen und Erweiterbaren Inselnetzen. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2002. [Google Scholar]
- De Brabandere, K.; Bolsens, B.; van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A voltage and frequency droop control method for parallel inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Yajuan, G.; Weiyang, W.; Xiaoqiang, G.; Herong, G. An improved droop controller for grid-connected voltage source inverter in microgrid. In Proceedings of the 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Hefei, China, 16–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 823–828. [Google Scholar]
- Guerrero, J.M.; GarciadeVicuna, L.; Matas, J.; Castilla, M.; Miret, J. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems. IEEE Trans. Power Electron. 2004, 19, 1205–1213. [Google Scholar] [CrossRef]
- Yao, W.; Chen, M.; Matas, J.; Guerrero, J.M.; Qian, Z.-M. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing. IEEE Trans. Ind. Electron. 2011, 58, 576–588. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Chen, Z. An improved design of virtual output impedance loop for droop-controlled parallel three-phase voltage source inverters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2466–2473. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Zhang, L. Modeling and Control of VSC-HVDC Links Connected to Weak AC Systems. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2010. [Google Scholar]
- Remon, D.; Cantarellas, A.M.; Rakhshani, E.; Candela, I.; Rodriguez, P. An active power synchronization control loop for grid-connected converters. In Proceedings of the IEEE Power & Energy Society General Meeting, National Harbor, MD, USA, 27–31 July 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Laudahn, S.; Seidel, J.; Engel, B.; Bulo, T.; Premm, D. Substitution of synchronous generator based instantaneous frequency control utilizing inverter-coupled DER. In Proceedings of the 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Hesse, R.; Turschner, D.; Beck, H.-P. Micro grid stabilization using the Virtual Synchronous Machine (VISMA). In Proceedings of the International Conference on Renewable Energies and Power, Valencia, Spain, 15–17 April 2009. [Google Scholar]
- Glockler, C.; Duckwitz, D.; Welck, F. Virtual synchronous machine control with virtual resistor for enhanced short circuit capability. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the IEEE Grenoble PowerTech, Grenoble, France, 16–20 June 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- D’Arco, S.; Suul, J.A. Equivalence of Virtual Synchronous Machines and Frequency-Droops for Converter-Based MicroGrids. IEEE Trans. Smart Grid 2014, 5, 394–395. [Google Scholar] [CrossRef]
- Beck, H.-P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–6. [Google Scholar]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.-P. Investigation of the Virtual Synchronous Machine in the island mode. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; IEEE, Ed.; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Ebrahimi, M.; Khajehoddin, S.A.; Karimi-Ghartemani, M. An Improved Damping Method for Virtual Synchronous Machines. IEEE Trans. Sustain. Energy 2019, 10, 1491–1500. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. Adjusting Synchronverter Dynamic Response Speed via Damping Correction Loop. IEEE Trans. Energy Convers. 2017, 32, 608–619. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. A Virtual Synchronous Machine implementation for distributed control of power converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Sinha, M.; Dorfler, F.; Johnson, B.B.; Dhople, S.V. Uncovering droop control laws embedded within the nonlinear dynamics of Van der Pol oscillators. IEEE Trans. Control Netw. Syst. 2017, 4, 347–358. [Google Scholar] [CrossRef]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dorfler, F.; Dhople, S.V. Synthesizing virtual oscillators to control islanded inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Johnson, B.; Rodriguez, M.; Sinha, M.; Dhople, S. Comparison of virtual oscillator and droop control. In Proceedings of the IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–14 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Cvetkovic, I.; Boroyevich, D.; Burgos, R.; Li, C.; Mattavelli, P. Modeling and control of grid-connected voltage-source converters emulating isotropic and anisotropic synchronous machines. In Proceedings of the IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12–15 July 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Milano, F.; Dorfler, F.; Hug, G.; Hill, D.J.; Verbic, G. Foundations and challenges of low-inertia systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Huang, L.; Xin, H.; Wang, Z.; Wu, K.; Wang, H.; Hu, J.; Lu, C. A virtual synchronous control for voltage-source converters utilizing dynamics of DC-Link capacitor to realize self-synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1565–1577. [Google Scholar] [CrossRef]
- Jouini, T.; Arghir, C.; Dörfler, F. Grid-friendly matching of synchronous machines by tapping into the DC storage. IFAC-PapersOnLine 2016, 49, 192–197. [Google Scholar] [CrossRef]
- Lasseter, R.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Mo, O.; D’Arco, S.; Suul, J.A. Evaluation of Virtual Synchronous Machines with Dynamic or Quasi-Stationary Machine Models. IEEE Trans. Ind. Electron. 2017, 64, 5952–5962. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Effect of Using PLL-Based Grid-Forming Control on Active Power Dynamics Under Various SCR. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4799–4804. [Google Scholar]
- Duckwitz, D. Power System Inertia. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2019. [Google Scholar]
- Karapanos, V.; de Haan, S.; Zwetsloot, K. Real time simulation of a power system with VSG hardware in the loop. In Proceedings of the IECON 2011—37th Annual Conference of IEEE Industrial Electronics Society, Melbourne, Vic, Australia, 7–10 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3748–3754. [Google Scholar]
- Van Wesenbeeck, M.P.N.; de Haan, S.W.H.; Varela, P.; Visscher, K. Grid tied converter with virtual kinetic storage. In Proceedings of the IEEE Bucharest PowerTech (POWERTECH) 2009, Bucharest, Romania, 28 June–2 July 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Duckwitz, D. Performance of df/dt-based inertia control during emergency islanding. In Proceedings of the 15th Wind Integration Workshop, Vienna, Austria, 15–17 November 2016; Betancourt, U., Ackermann, T., Eds.; Energynautics GmbH: Darmstadt, Germany, 2016. [Google Scholar]
- Duckwitz, D.; Fischer, B. Modeling and design of df/dt -based inertia control for power converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1553–1564. [Google Scholar] [CrossRef]
- Laudahn, S. Dynamisches Verhalten von Wechselrichterbasierten Erzeugungsanlagen im Kontext Eines Sicheren und Stabilen Netzbetriebs. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2017. [Google Scholar]
- Erlich, I.; Korai, A. Study on the minimum share of conventional generation units required for stable operation of future converter-dominated grids. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Erlich, I.; Korai, A.; Neumann, T.; Koochack Zadeh, M.; Vogt, S.; Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. New control of wind turbines ensuring stable and secure operation following islanding of wind farms. IEEE Trans. Energy Convers. 2017, 32, 1263–1271. [Google Scholar] [CrossRef]
- Korai, A.W.; Erlich, I. Frequency dependent voltage control by DER units to improve power system frequency stability. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Winter, P.; Wrede, H. Impact of power converter control on transient stability of power systems. In Proceedings of the Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 20–21 September 2018; Schulz, D., Ed.; VDE Verlag GmbH: Berlin, Germany, 2018. [Google Scholar]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Wang, X.; Guerrero, J.M.; Blaabjerg, F.; Chen, Z. A Review of Power Electronics Based Microgrids. J. Power Electron. 2012, 12, 181–192. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtual-flux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Malinowski, M.; Jasinski, M.; Kazmierkowski, M.P. Simple Direct Power Control of Three-Phase PWM Rectifier Using Space-Vector Modulation (DPC-SVM). IEEE Trans. Ind. Electron. 2004, 51, 447–454. [Google Scholar] [CrossRef]
- Gui, Y.; Kim, C.; Chung, C.C.; Guerrero, J.M.; Guan, Y.; Vasquez, J.C. Improved Direct Power Control for Grid-Connected Voltage Source Converters. IEEE Trans. Ind. Electron. 2018, 65, 8041–8051. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Wu, H.; Blaabjerg, F. Voltage-Modulated Direct Power Control for a Weak Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Blaabjerg, F.; Pan, D. Control of Grid-Connected Voltage-Source Converters: The Relationship Between Direct-Power Control and Vector-Current Control. IEEE Ind. Electron. Mag. 2019, 13, 31–40. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Blaabjerg, F. Vector Current Control Derived from Direct Power Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 9224–9235. [Google Scholar] [CrossRef]
- Ndreko, M.; Rüberg, S.; Winter, W. Grid forming control for stable power systems with up to 100% inverter based generation: A paradigm scenario using the IEEE 118-Bus system. In Proceedings of the 17th Wind Integration Workshop, Stockholm, Sweden, 17–19 October 2018; Betancourt, U., Ackermann, T., Eds.; Energynautics GmbH: Darmstadt, Germany, 2018. [Google Scholar]

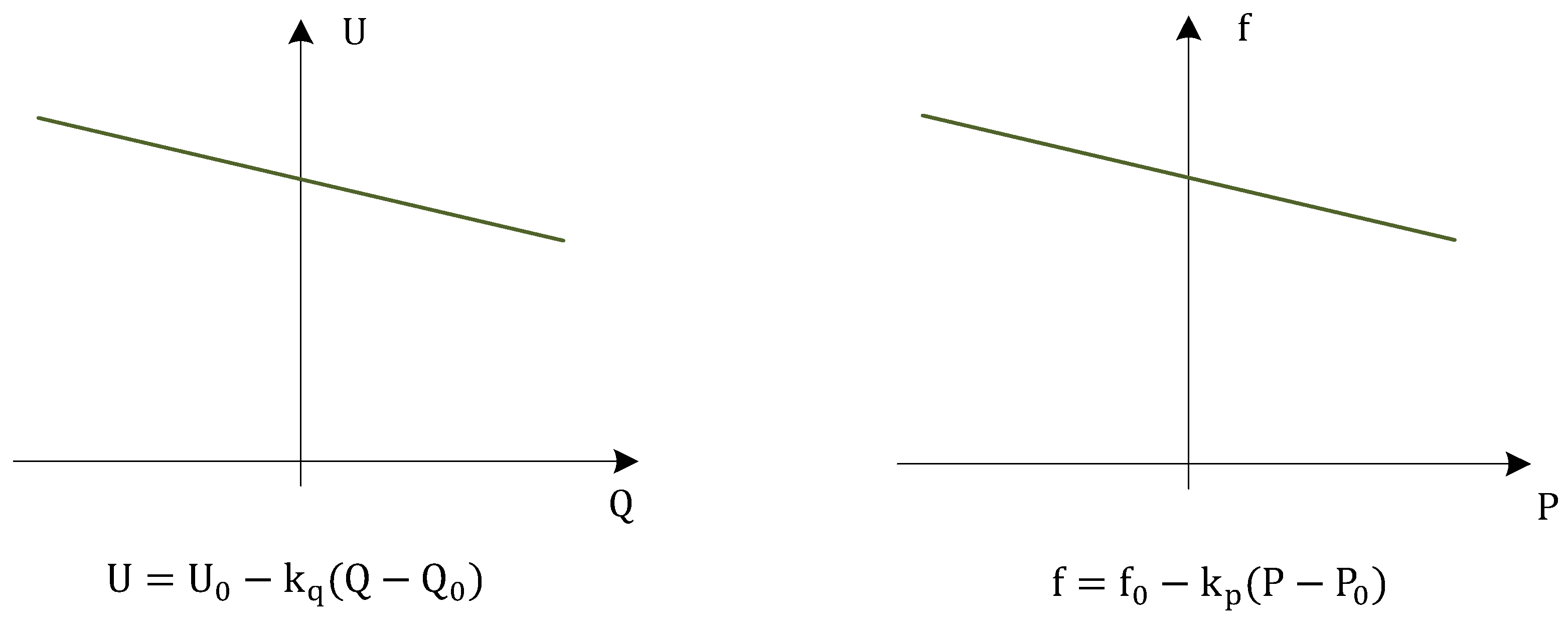

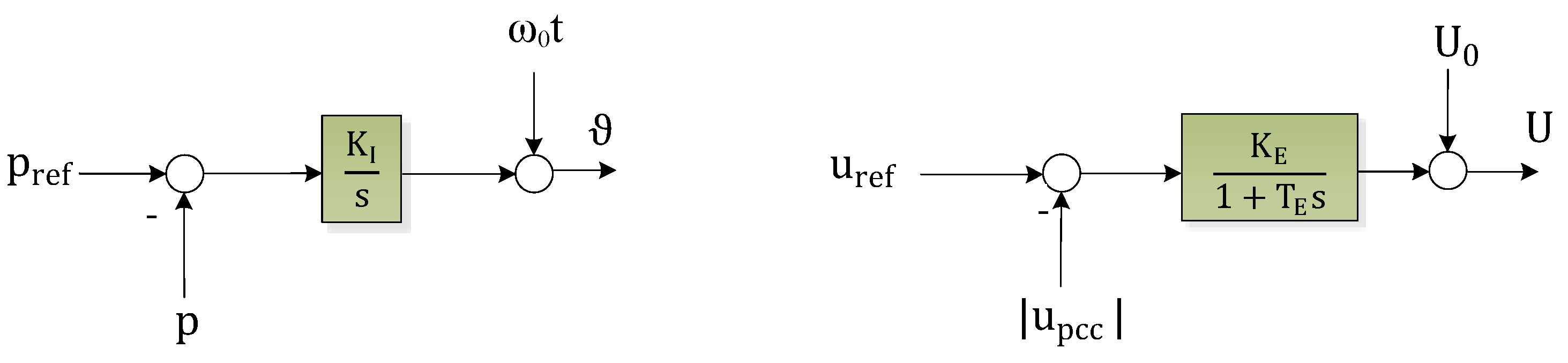
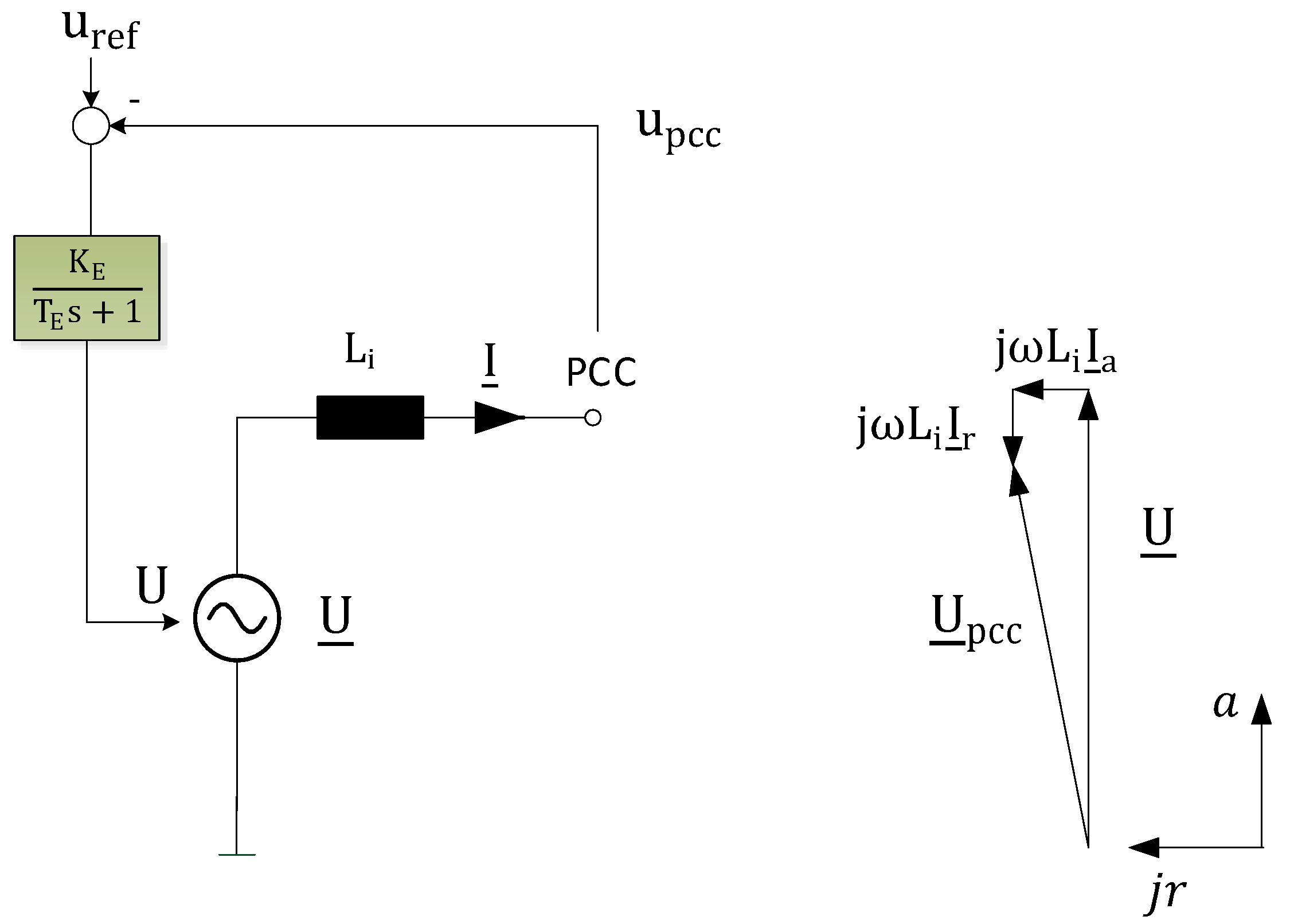
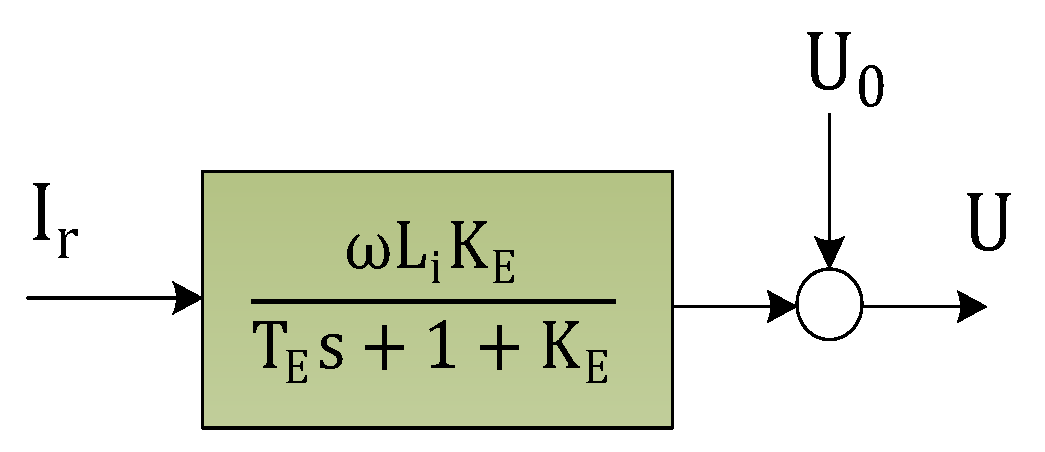
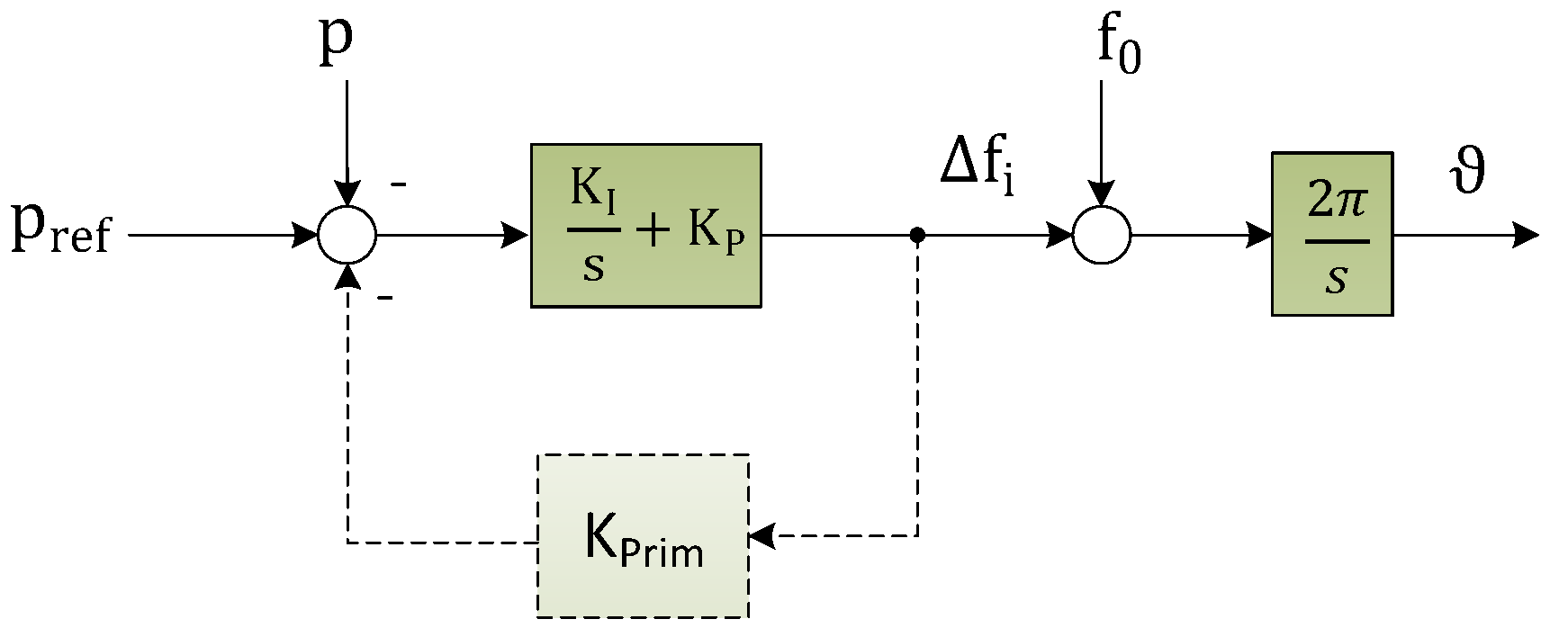



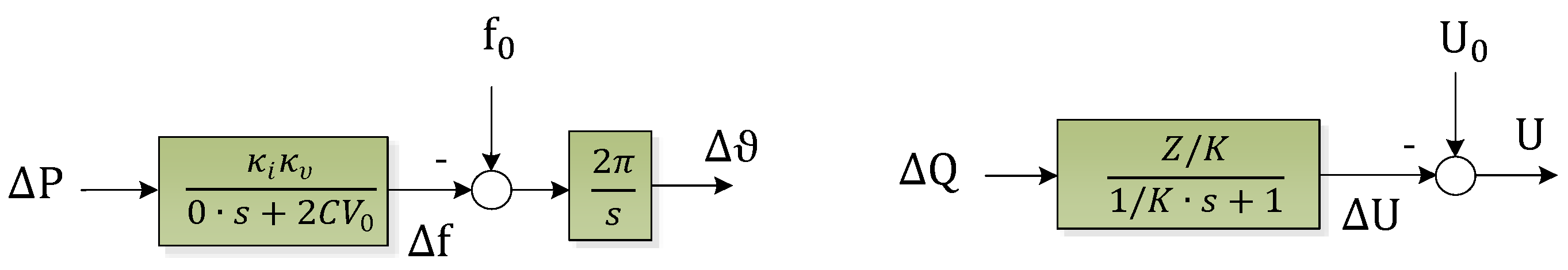

| Parameter | Value |
|---|---|
| Tm | kp·10 s |
| kp | 0.05 pu |
| Te | 1 s |
| kq | 0.1 pu |
| kp’ | 5 pu |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. https://doi.org/10.3390/en13102589
Unruh P, Nuschke M, Strauß P, Welck F. Overview on Grid-Forming Inverter Control Methods. Energies. 2020; 13(10):2589. https://doi.org/10.3390/en13102589
Chicago/Turabian StyleUnruh, Peter, Maria Nuschke, Philipp Strauß, and Friedrich Welck. 2020. "Overview on Grid-Forming Inverter Control Methods" Energies 13, no. 10: 2589. https://doi.org/10.3390/en13102589
APA StyleUnruh, P., Nuschke, M., Strauß, P., & Welck, F. (2020). Overview on Grid-Forming Inverter Control Methods. Energies, 13(10), 2589. https://doi.org/10.3390/en13102589





