Integration of Demand Response and Short-Term Forecasting for the Management of Prosumers’ Demand and Generation
Abstract
1. Introduction
- Firstly, short-term forecasting methods are used to predict hourly load and photovoltaic generation with a horizon of 24 h.
- Secondly, the predicted daily PV generation of the training dataset is grouped into homogeneous clusters according to their shape. Next, a representative PV curve is obtained for each cluster, and a discriminant analysis is developed to assign each predicted PV curve of the test dataset to a cluster.
- Finally, Demand Response strategies are applied to those days with a predicted PV curve in the suitable cluster (the one that provides more accurate predictions).
2. Materials and Methods
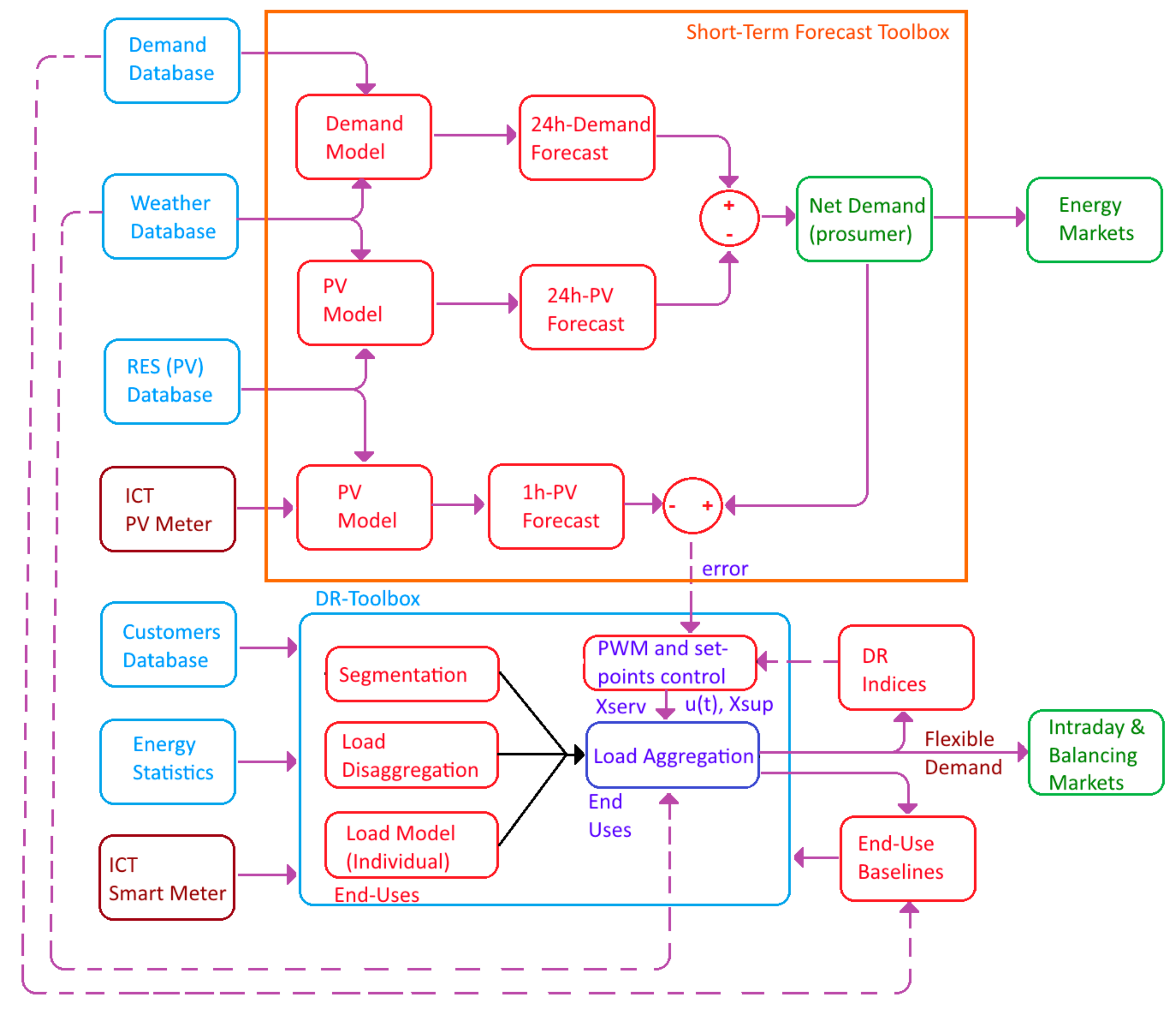
2.1. Methodology Overview
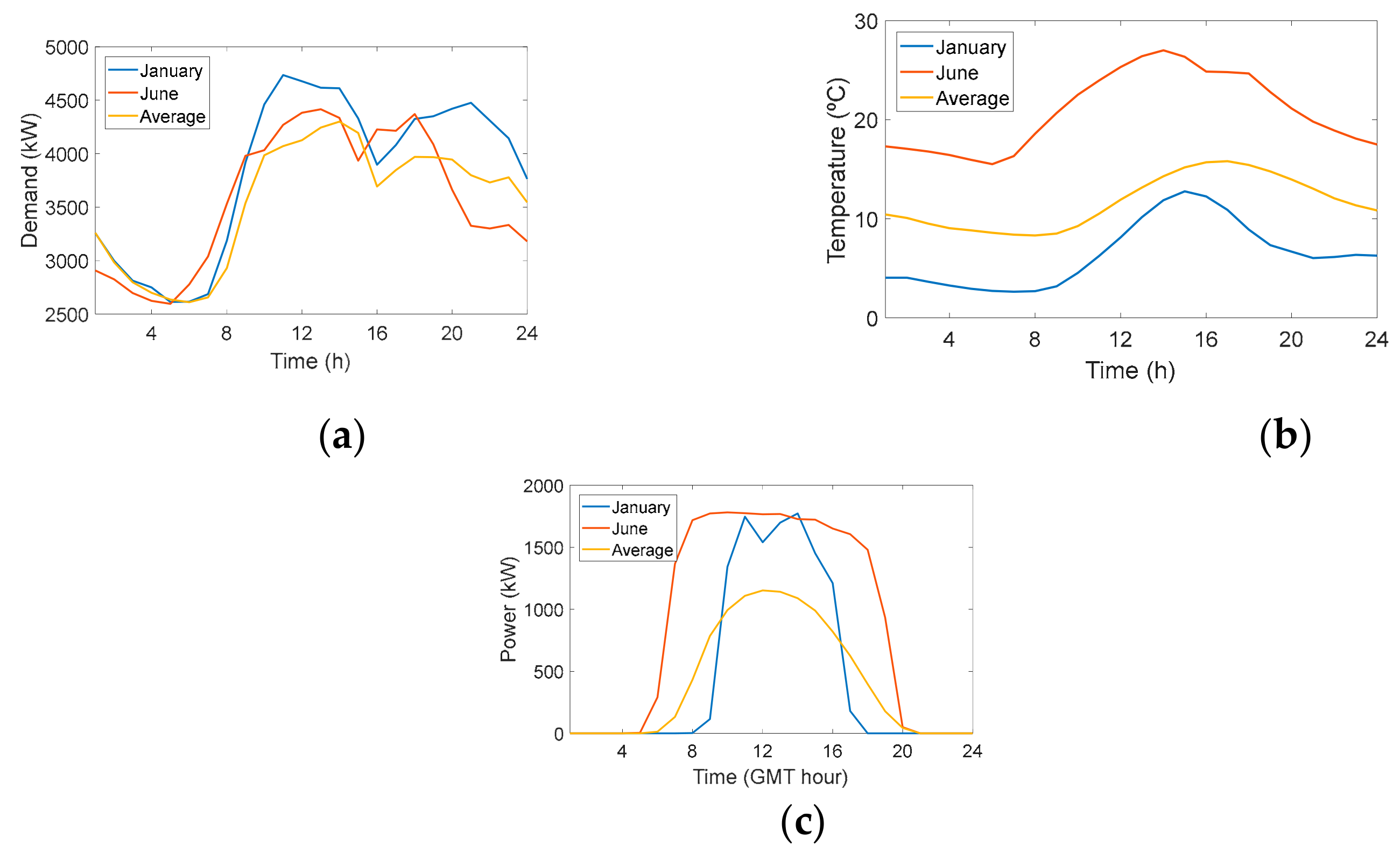
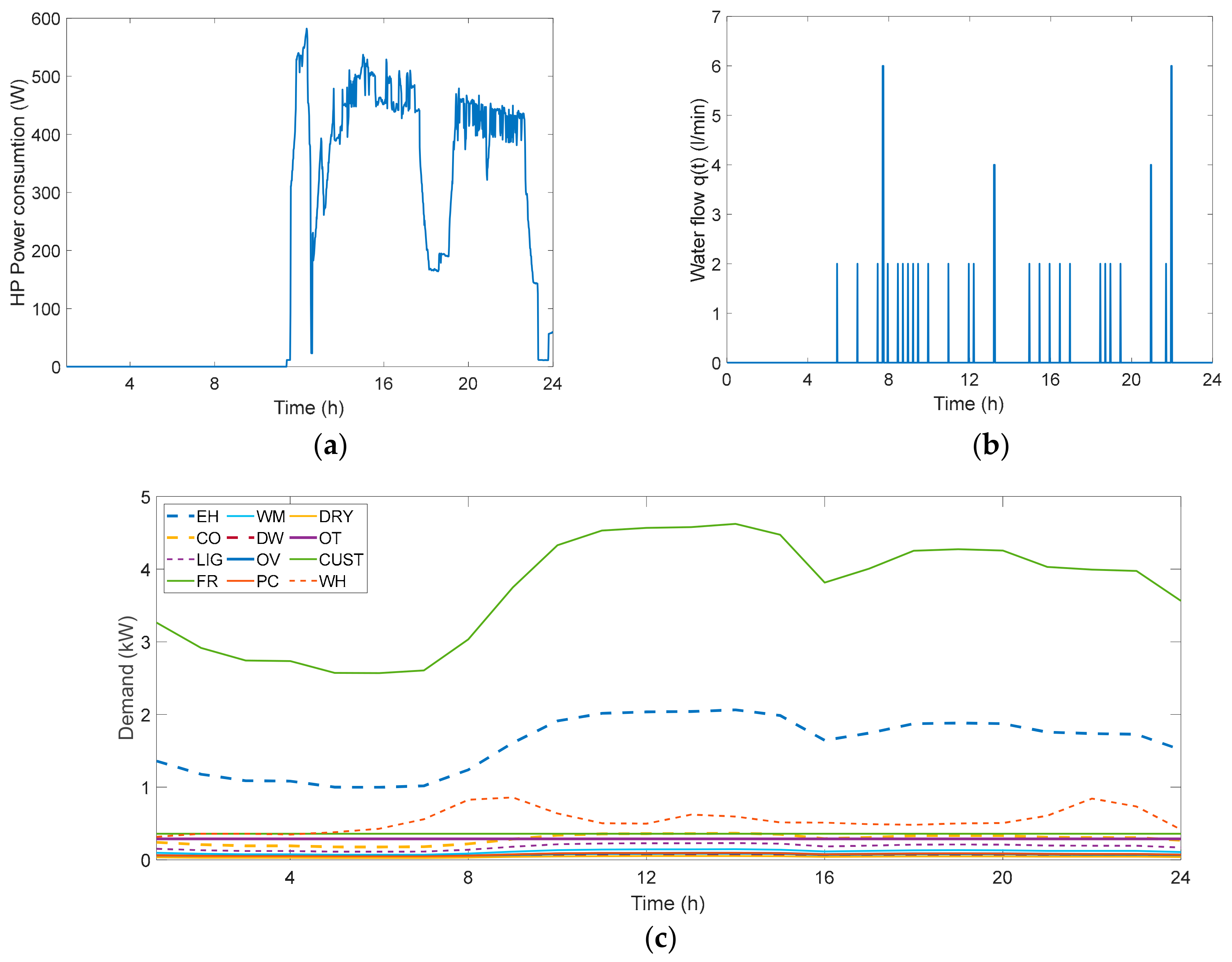
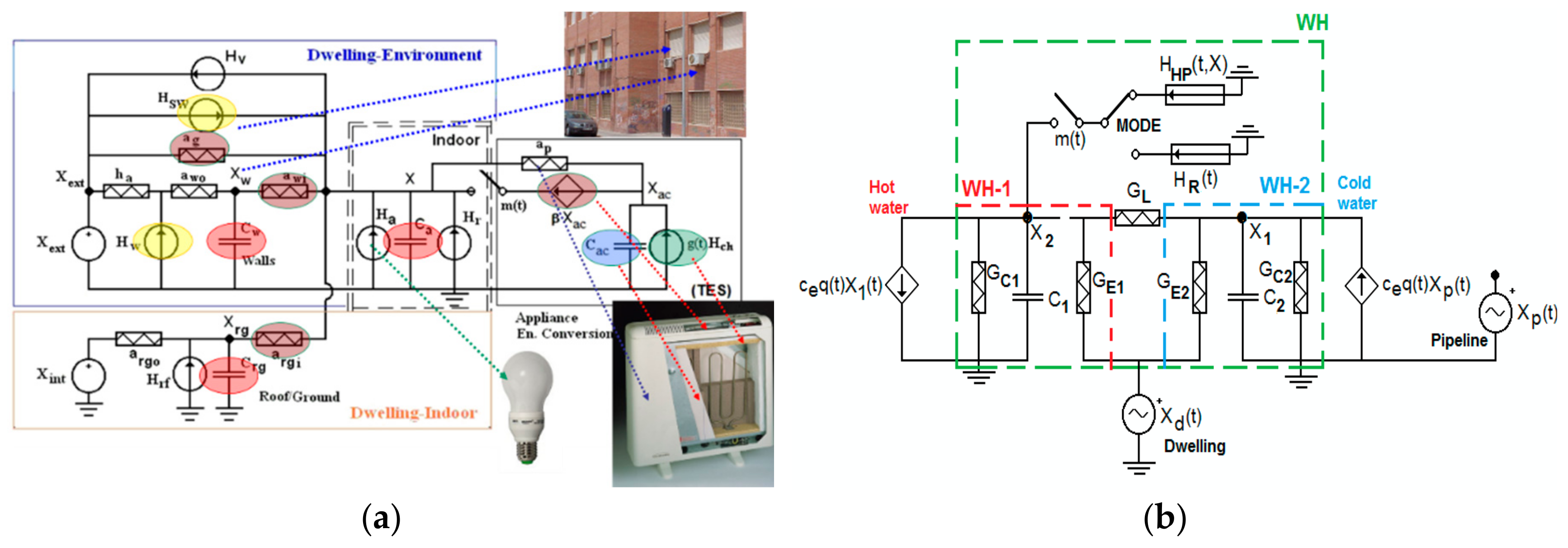
2.2. Characteristics of the Customers: Demand, Photovoltaic Generation, and End-Uses
2.3. Short-Term Forecasting Methods
2.3.1. Random Forest
2.3.2. Stochastic Gradient Boosting (SGB)
2.4. Time-Series Clustering
- Boundary conditions: w1 = (1; 1) and wk = (m; n), where k is the length of the warping path.
- Continuity: if wi = (a, b) then wi−1 = (a’, b’), where a − a’ ≤ 1 and b − b’ ≤ 1.
- Monotonicity: if wi = (a, b) then wi−1 = (a’, b’), where a − a’ ≥ 0 and b − b’ ≥ 0.
2.5. Demand Response Strategies
3. Results and Discussion
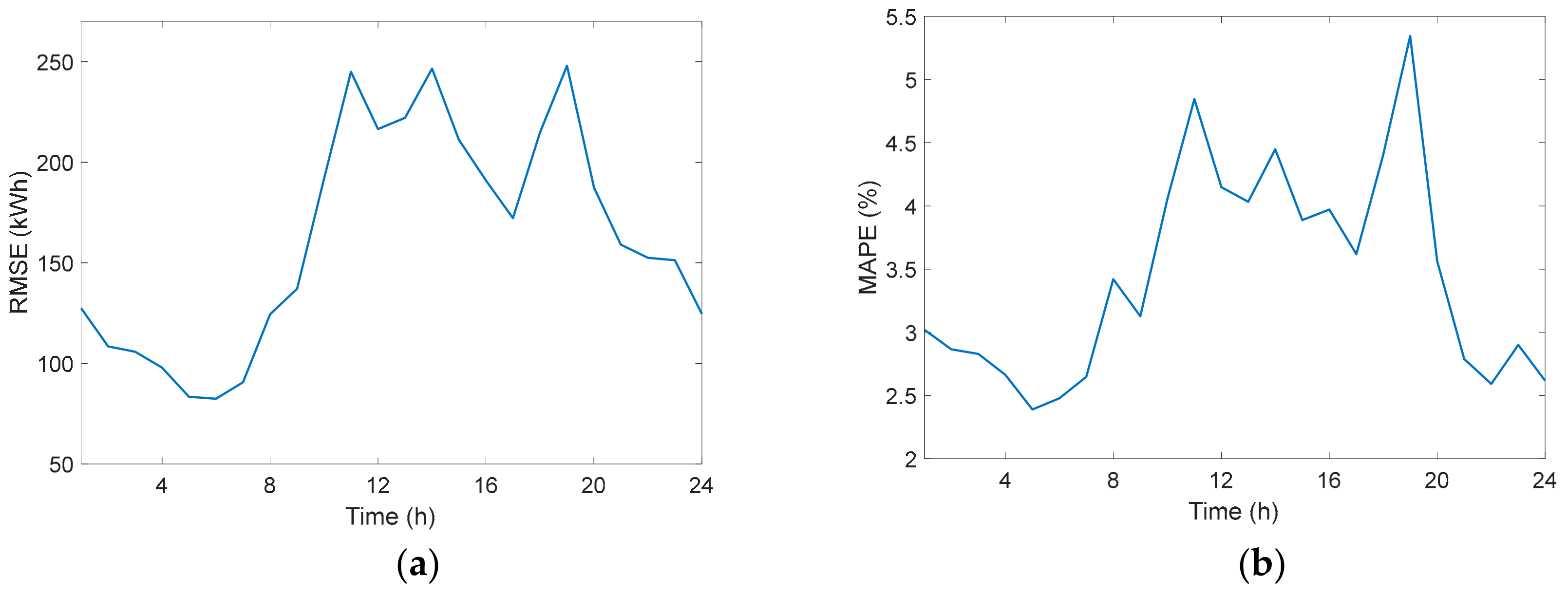
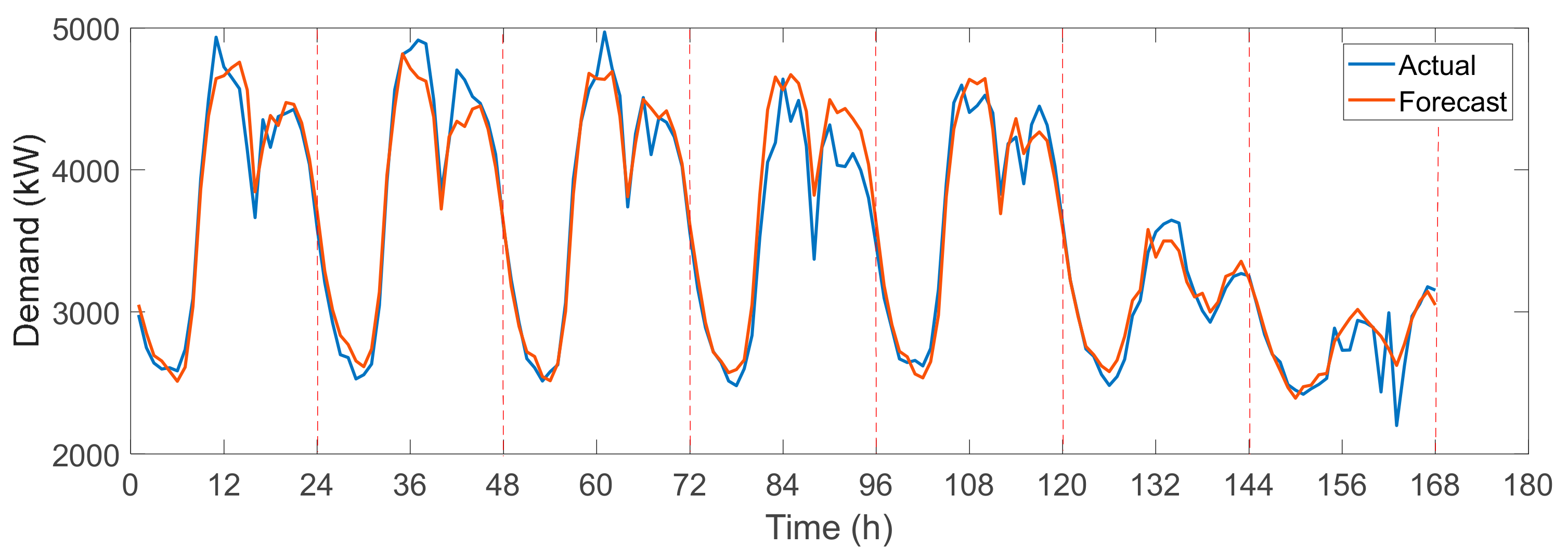
3.1. Prediction Results for the Electricity Consumption
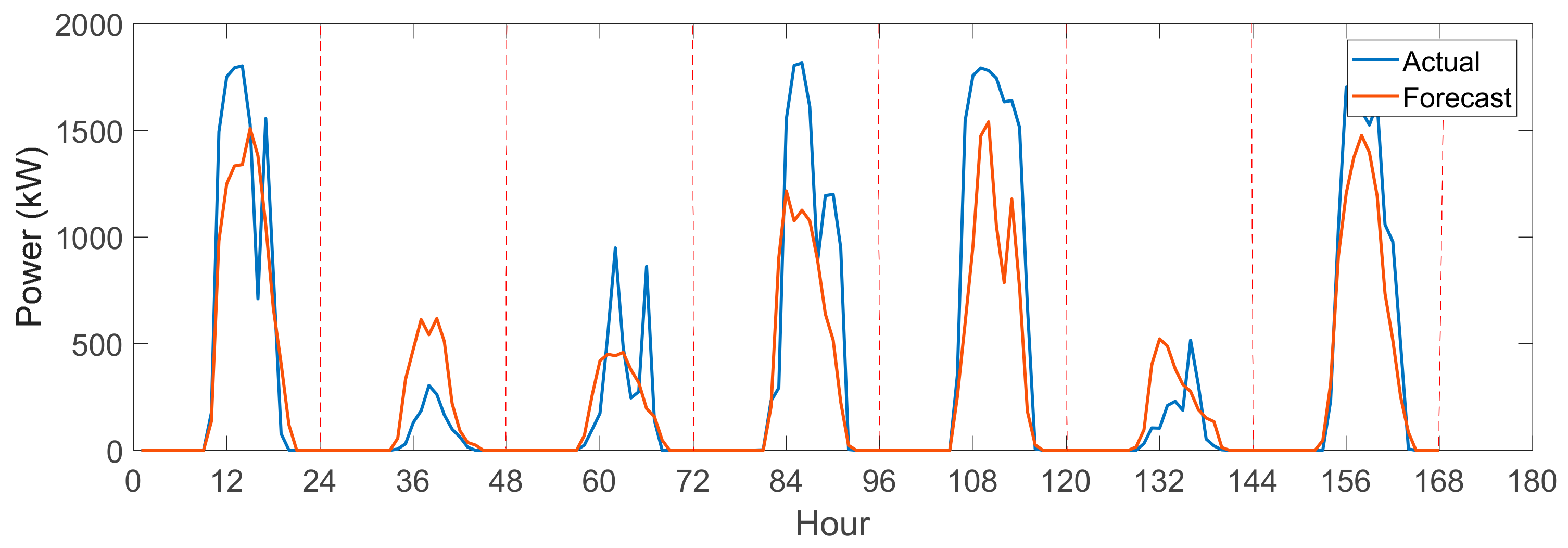
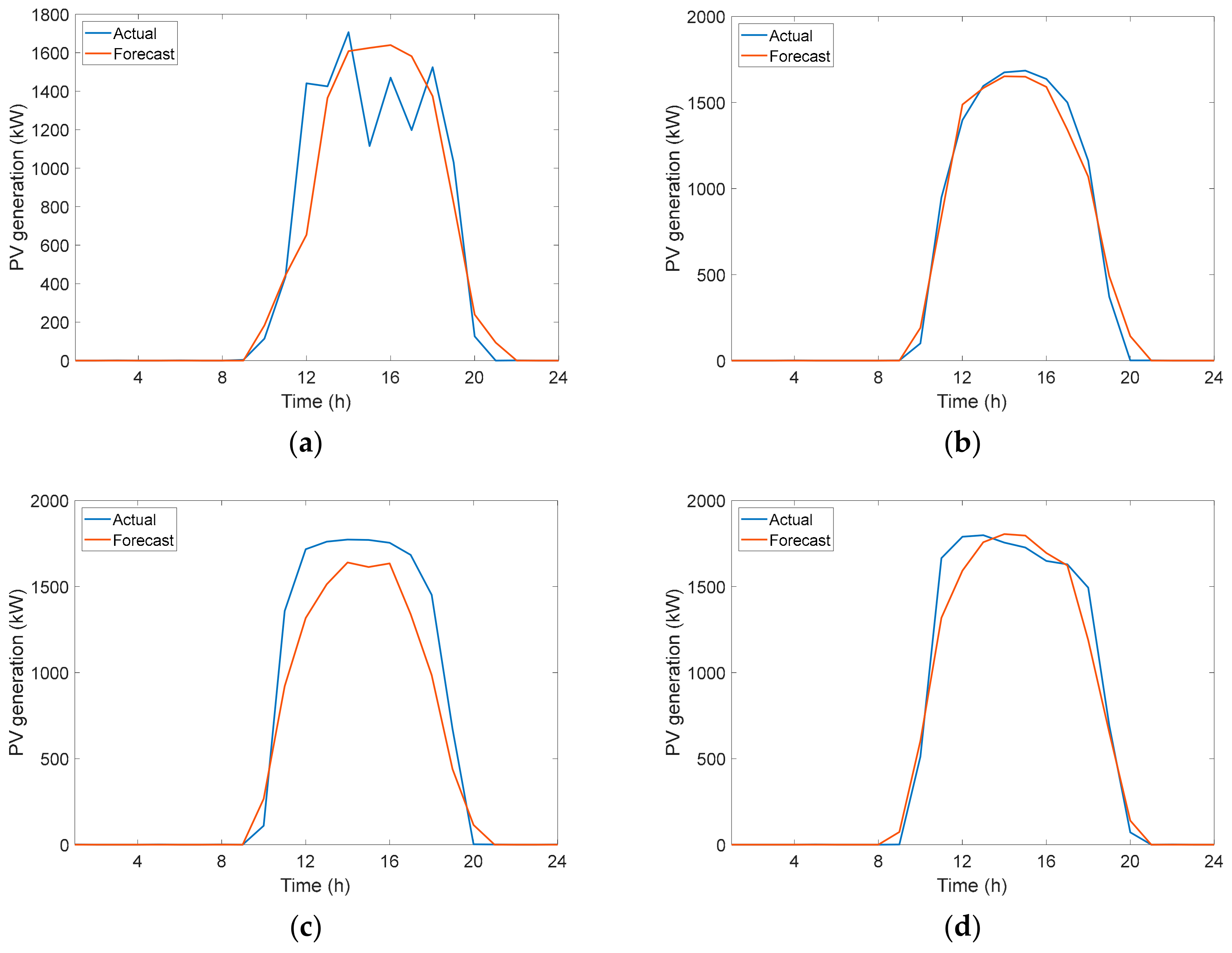
3.2. Prediction Results for the Photovoltaic Generation
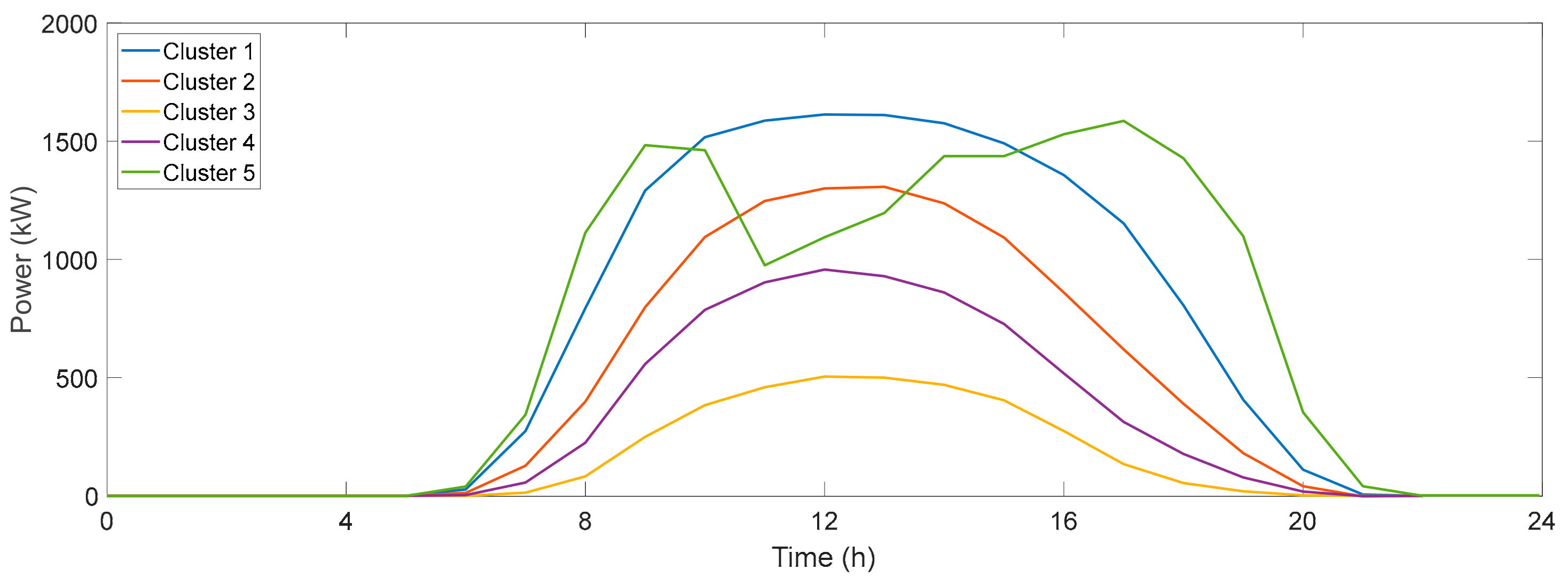
3.3. Classification Results of Photovoltaic Curves
3.4. Results for Demand Response Strategies
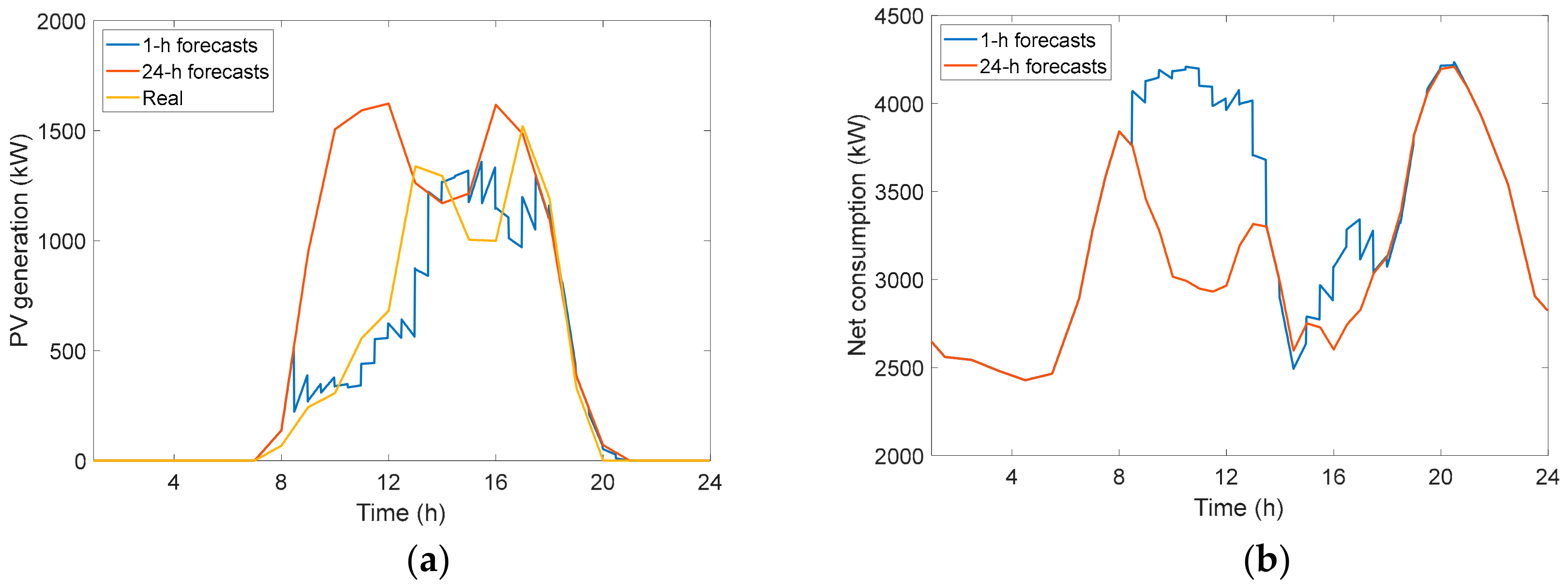
3.4.1. Very Short-Term PV Adjusted Forecasting
3.4.2. Balancing Net Demand through DR
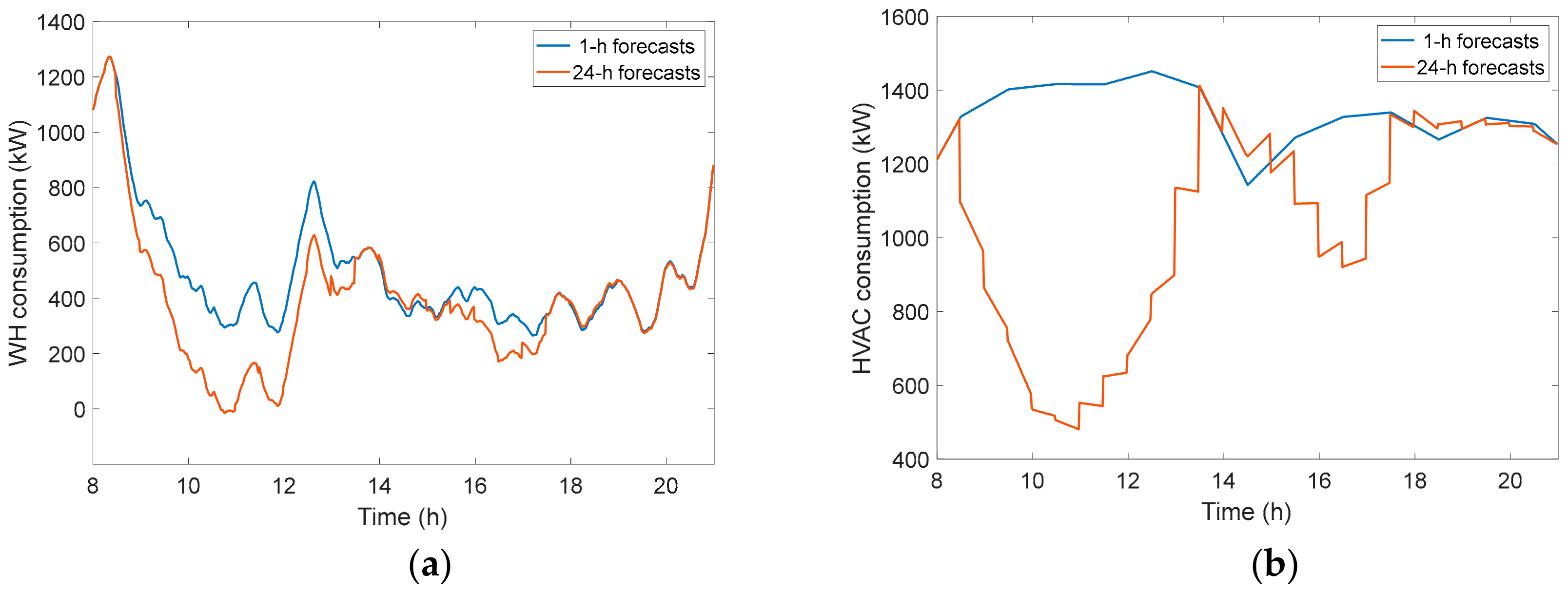
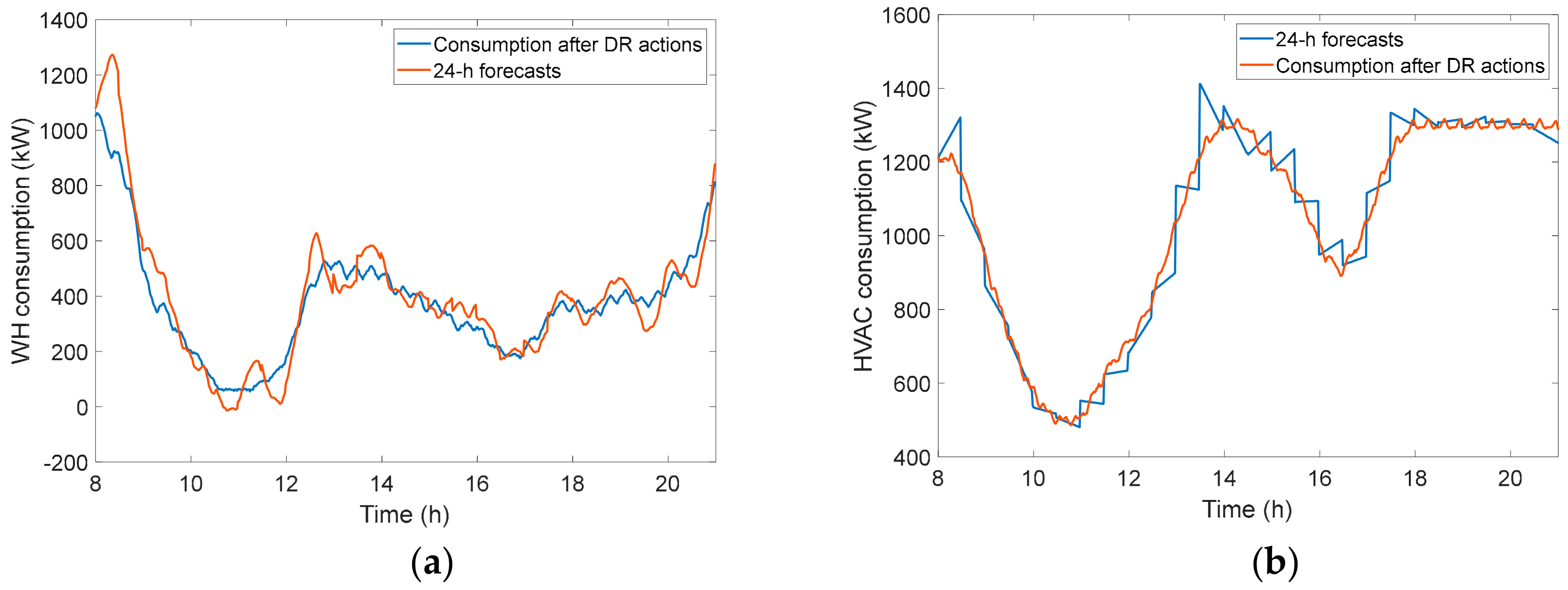
3.4.3. Analysis of DR Flexibility
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catalão, J.P.S. Electric Power Systems: Advanced Forecasting Techniques and Optimal Generation Scheduling; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Alfares, H.K.; Nazeeruddin, M. Electric load forecasting: Literature survey and classification of methods. Int. J. Syst. Sci. 2002, 33, 23–34. [Google Scholar] [CrossRef]
- Yang, H.T.; Huang, C.M.; Huang, C.L. Identification of ARMAX model for short term load forecasting: An evolutionary programming approach. IEEE Trans. Power Syst. 1996, 11, 403–408. [Google Scholar] [CrossRef]
- Taylor, J.W.; de Menezes, L.M.; McSharry, P.E. A comparison of univariate methods for forecasting electricity demand up to a day ahead. Int. J. Forecast. 2006, 22, 1–16. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Bruhns, A.; Deurveilher, G.; Roy, J.S. A non-linear regression model for mid-term load forecasting and improvements in seasonality. In Proceedings of the 15th Power Systems Computation Conference, Liege, Belgium, 22–26 August 2005. [Google Scholar]
- Charytoniuk, W.; Chen, M.S. Nonparametric regression based short-term load forecasting. IEEE Trans. Power Syst. 1998, 13, 725–730. [Google Scholar] [CrossRef]
- Li, K.; Su, H.; Chu, J. Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study. Energy Build. 2011, 43, 2893–2899. [Google Scholar] [CrossRef]
- Liao, G.C.; Tsao, T.P. Application of a fuzzy neural network combined with a chaos genetic algorithm and simulated annealing to short-term load forecasting. IEEE Trans. Evol. Comput. 2006, 10, 330–340. [Google Scholar] [CrossRef]
- Tso, G.K.F.; Yau, K.K.W. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, X.; Ma, C.; Wang, J. Research and application of a hybrid forecasting model based on data decomposition for electrical load forecasting. Energies 2016, 9, 1050. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-Term Load Forecasting with Deep Residual Networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef]
- Dudek, G. Short-term load forecasting using random forests. Adv. Intell. Syst. Comput. 2015, 323, 821–828. [Google Scholar] [CrossRef]
- Lin, Y.; Luo, H.; Wang, D.; Guo, H.; Zhu, K. An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting. Energies 2017, 10, 1186. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Y.M.; Li, D.; Tan, Z.; Zhou, J. Short term electricity load forecasting using a hybrid model. Energy 2018, 158, 774–781. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Shu, L. An ARMAX model for forecasting the power output of a grid connected photovoltaic system. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Su, Y.; Shu, L. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines. Appl. Energy 2016, 180, 392–401. [Google Scholar] [CrossRef]
- Abdullah, N.A.; Abd Rahim, N.; Gan, C.K.; Nor Adzman, N. Forecasting Solar Power Using Hybrid Firefly and Particle Swarm Optimization (HFPSO) for Optimizing the Parameters in a Wavelet Transform-Adaptive Neuro Fuzzy Inference System (WT-ANFIS). Appl. Sci. 2019, 9, 3214. [Google Scholar] [CrossRef]
- Chu, Y.; Urquhart, B.; Gohari, S.M.I.; Pedro, H.T.C.; Kleissl, J.; Coimbra, C.F.M. Short-term reforecasting of power output from a 48 MWe solar PV plant. Sol. Energy 2015, 112, 68–77. [Google Scholar] [CrossRef]
- Galicia, A.; Talavera-Llames, R.; Troncoso, A.; Koprinska, I.; Martínez-Álvarez, F. Multi-step forecasting for big data time series based on ensemble learning. Knowl. Based Syst. 2019, 163, 830–841. [Google Scholar] [CrossRef]
- Antonanzas, J.; Pozo-Vázquez, D.; Fernandez-Jimenez, L.A.; Martinez-de-Pison, F.J. The value of day-ahead forecasting for photovoltaics in the Spanish electricity market. Sol. Energy 2017, 158, 140–146. [Google Scholar] [CrossRef]
- Ferlito, S.; Adinolfi, G.; Graditi, G. Comparative analysis of data-driven methods online and offline trained to the forecasting of grid-connected photovoltaic plant production. Appl. Energy 2017, 205, 116–129. [Google Scholar] [CrossRef]
- Australian Energy Market Commission Integrating Distributed Energy Resources for the Grid of the Future. Economic Regulatory Framework Review. Available online: https://www.aemc.gov.au/sites/default/files/2019-09/Final report-ENERFR 2019-EPR0068.PDF (accessed on 6 November 2019).
- Sánchez Jiménez, M. Regulatory Proposal for deployment of flexibility. In Proceedings of the India SMART GRIDS Week, New Delhi, India, 8–10 March 2017; p. 15. [Google Scholar]
- EURELECTRIC Designing Fair and Equitable Market Rules for Demand Response Aggregation. Available online: http://www.eurelectric.org (accessed on 4 September 2019).
- Bemdt, D.J.; Clifford, J. Using Dynamic Time Warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Smart Energy Europe. SmartEn White Paper: A Vision for Smart and Active Buildings. Available online: https://www.smarten.eu/wp-content/uploads/2019/07/FINAL-smartEn-white-paper-Smart-Buildings.pdf (accessed on 6 November 2019).
- Zeifman, M.; Roth, K. Nonintrusive appliance load monitoring: Review and outlook. IEEE Trans. Consum. Electron. 2011, 57, 76–84. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission (FERC). Assessment of Demand Response and Advanced Metering: Staff Report. Available online: https://www.ferc.gov/legal/staff-reports/2016/DR-AM-Report2016.pdf (accessed on 14 June 2019).
- Gabaldón, A.; Molina, R.; Marín-Parra, A.; Valero-Verdú, S.; Álvarez, C. Residential end-uses disaggregation and demand response evaluation using integral transforms. J. Mod. Power Syst. Clean Energy 2017, 5, 91–104. [Google Scholar] [CrossRef]
- Jenssen, Å.; Borsche, T.; Wolst, J. Data Exchange in Electric Power Systems: European State of Play and Perspectives; THEMA Consulting: Oslo, Norway, 2017; ISBN 9788283680133. [Google Scholar]
- Residential Energy Consumption Survey (RECS)—Data—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/consumption/residential/data/2015/ (accessed on 6 November 2019).
- Bertoldi, P.; López Lorente, J.; Labanca, N. Energy Consumption and Energy Efficiency Trends in the EU-28 2000–2014; Publication Office of the European Commission: Luxembourg, 2016. [Google Scholar]
- IDAE Consumo por usos y Energías del Sector Residencial (2010–2017). Available online: https://www.idae.es/estudios-informes-y-estadisticas (accessed on 6 November 2019).
- García-Garre, A.; Gabaldón, A.; Álvarez-Bel, C.; Ruiz-Abellón, M.; Guillamón, A. Integration of Demand Response and Photovoltaic Resources in Residential Segments. Sustainability 2018, 10, 3030. [Google Scholar] [CrossRef]
- Ellegård, K.; Palm, J. Visualizing energy consumption activities as a tool for making everyday life more sustainable. Appl. Energy 2011, 88, 1920–1926. [Google Scholar] [CrossRef]
- Del Carmen Ruiz-Abellón, M.; Gabaldón, A.; Guillamón, A. Load forecasting for a campus university using ensemble methods based on regression trees. Energies 2018, 11, 2038. [Google Scholar] [CrossRef]
- Caret R Package. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 6 November 2019).
- Ben Taieb, S.; Hyndman, R.J. A gradient boosting approach to the Kaggle load forecasting competition. Int. J. Forecast. 2014, 30, 382–394. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Ran, R.; Che, Y.; Zhou, Y. A Short-Term Photovoltaic Power Prediction Model Based on the Gradient Boost Decision Tree. Appl. Sci. 2018, 8, 689. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Warren Liao, T. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Seyed Shirkhorshidi, A.; Ying Wah, T. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Montero, P.; Vilar, J.A. TSclust: An R package for time series clustering. J. Stat. Softw. 2014, 62, 1–43. [Google Scholar] [CrossRef]
- Dau, H.A.; Silva, D.F.; Petitjean, F.; Forestier, G.; Bagnall, A.; Mueen, A.; Keogh, E. Optimizing dynamic time warping’s window width for time series data mining applications. Data Min. Knowl. Discov. 2018, 32, 1074–1120. [Google Scholar] [CrossRef]
- Wilson, E.; Christensen, C. Heat Pump Water Heater Modeling in EnergyPlus. In Proceedings of the Building America Residential Energy Efficiency Stakeholder Meeting, Austin, TX, USA, 29 February–1 March 2012; pp. 1–36. [Google Scholar]
- Li, X.; Wen, J. Review of building energy modeling for control and operation. Renew. Sustain. Energy Rev. 2014, 37, 517–537. [Google Scholar] [CrossRef]
- Gabaldón, A.; Álvarez, C.; Ruiz-Abellón, M.; Guillamón, A.; Valero-Verdú, S.; Molina, R.; García-Garre, A. Integration of Methodologies for the Evaluation of Offer Curves in Energy and Capacity Markets through Energy Efficiency and Demand Response. Sustainability 2018, 10, 483. [Google Scholar] [CrossRef]
- Demand Response (DR) Web Page. Available online: http://www.demandresponse.eu/ (accessed on 14 June 2019).
- NYISO Emergency Demand Response Program Manual. Available online: https://www.nyiso.com/demand-response (accessed on 4 September 2019).
- NYISO Day-Ahead Demand Response Program Manual. Available online: http://online.fliphtml5.com/qzli/zqaf/#p=1 (accessed on 6 November 2019).
- PROLAN Ripple Control Receiver and Tone Frequency Receiver (HKV-RKV). Available online: https://www.prolan.hu/en/solutions/HKV-RKV (accessed on 6 November 2019).
- TenneT und Bayernwerk: Dezentrale Flexibilität aus Bayern für die Energiewende—TenneT. Available online: https://www.tennet.eu/de/news/news/tennet-und-bayernwerk-dezentrale-flexibilitaet-aus-bayern-fuer-die-energiewende/ (accessed on 6 November 2019).
- Wireless Smart Home and Home Automation | FIBARO. Available online: https://www.fibaro.com/en/ (accessed on 6 November 2019).
- Symcom. IP-Symcon Integrators. Automation Software. Available online: https://www.symcon.de/en/product/integrators/ (accessed on 6 November 2019).
- Samad, T.; Koch, E.; Stluka, P. Automated Demand Response for Smart Buildings and Microgrids: The State of the Practice and Research Challenges. Proc. IEEE 2016, 104, 726–744. [Google Scholar] [CrossRef]
- OpenADR Alliance. Available online: https://www.openadr.org/ (accessed on 2 December 2019).
- Universal Devices Web Page. Available online: https://www.universal-devices.com/ (accessed on 2 December 2019).
- Cui, T.; Carr, J.; Brissette, A.; Ragaini, E. Connecting the Last Mile: Demand Response in Smart Buildings. In Proceedings of the 8th International Conference on Sustainability in Energy and Buildings, SEB-16, Turin, Italy, 11–13 September 2016; Volume 111, pp. 720–729. [Google Scholar]
- Gabaldón, A.; Álvarez, C.; Moreno, J.I.; Matanza, J.; López, G.; Ruiz-Abellón, M.C.; Valero-Verdu, S. Evaluation of the performance of Aggregated Demand Response by the use of Load and Communication Technologies Models. In Proceedings of the EEDAL Conference, Irvine, CA, USA, 13–15 September 2017. [Google Scholar]
- Monitoring Analytics LLC. 2019 Quarterly State of the Market Report for PJM: January through September. Available online: https://www.monitoringanalytics.com/reports/PJM_State_of_the_Market/2019/2019q3-som-pjm.pdf (accessed on 2 December 2019).
- Steffes, P. The Path to Grid-Interactive Water Heating (GIWH), Opportunities & Challenges. Available online: https://www.peakload.org/assets/36thConf/PLMA Steffes Presentation 11-13-17.pdf (accessed on 6 November 2019).
- Lueken, R.; Hledik, R.; Chang, J. The Hidden Battery. Opportunities in Electric Water Heating. In Proceedings of the PLMA Grid Interactive Behind the Meter Storage Interest Group Meeting; The Brattle Group; NRECA; NRDC; PLMA: Boston, MA, USA, 2015. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3 (No. NCAR/TN-475+STR). Available online: https://opensky.ucar.edu/islandora/object/technotes%3A500/datastream/PDF/view (accessed on 6 November 2019).
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Lave, M.; Hayes, W.; Pohl, A.; Hansen, C.W. Evaluation of global horizontal irradiance to plane-of-array irradiance models at locations across the United States. IEEE J. Photovolt. 2015, 5, 597–606. [Google Scholar] [CrossRef]
- Sanz-Garcia, A.; Fernandez-Ceniceros, J.; Antonanzas-Torres, F.; Pernia-Espinoza, A.V.; Martinez-De-Pison, F.J. GA-PARSIMONY: A GA-SVR approach with feature selection and parameter optimization to obtain parsimonious solutions for predicting temperature settings in a continuous annealing furnace. Appl. Soft Comput. J. 2015, 35, 13–28. [Google Scholar] [CrossRef]
- ‘GAparsimony’ R Package. Available online: https://cran.r-project.org/web/packages/GAparsimony/GAparsimony.pdf (accessed on 13 November 2019).
- Lake, C. PJM Empirical Analysis of Demand Response Baseline Methods. Available online: https://www.pjm.com/-/media/markets-ops/demand-response/pjm-analysis-of-dr-baseline-methods-full-report.ashx?la=en (accessed on 4 September 2019).
- Gabaldon, A.; Valero-Verdu, S.; Garcia-Garre, A.; Senabre, C.; Alvarez-Bel, C.; Lopez, M.; Penalvo, E.; Sanchez, E.P. A physically-based model of heat pump water heaters for demand respose policies: Evaluation and testing. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies, Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
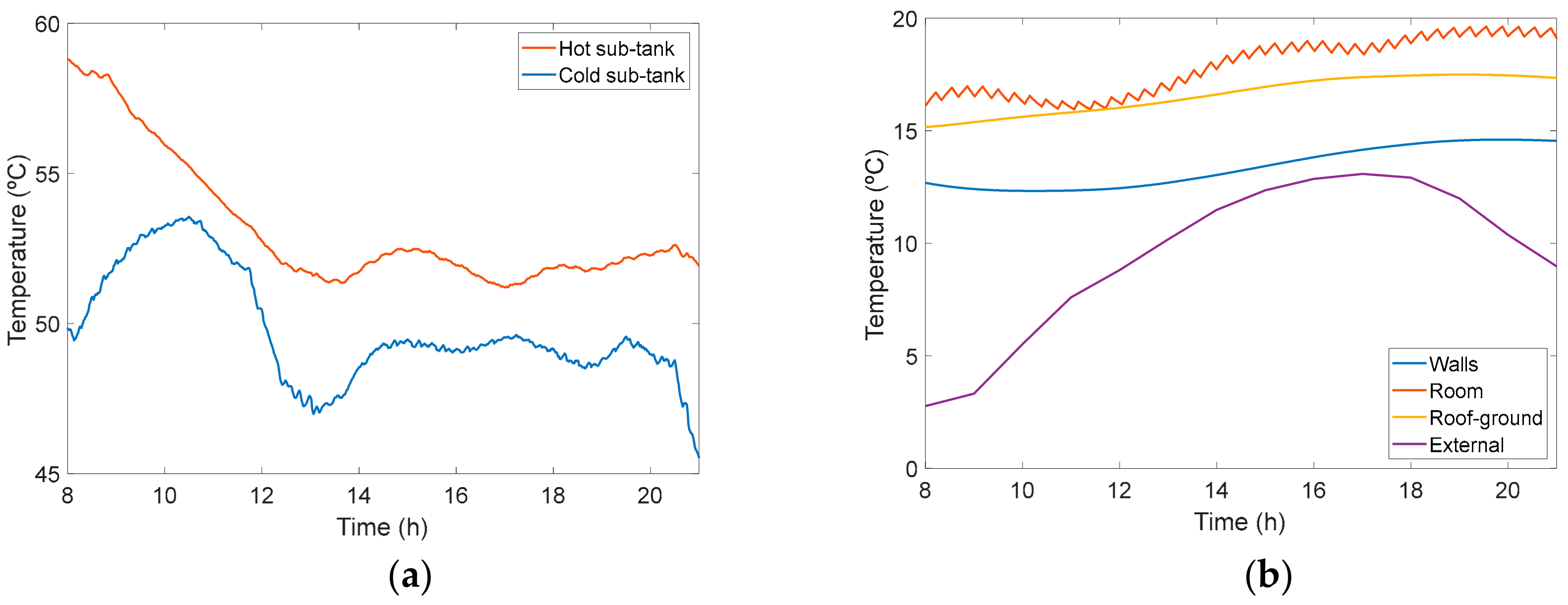
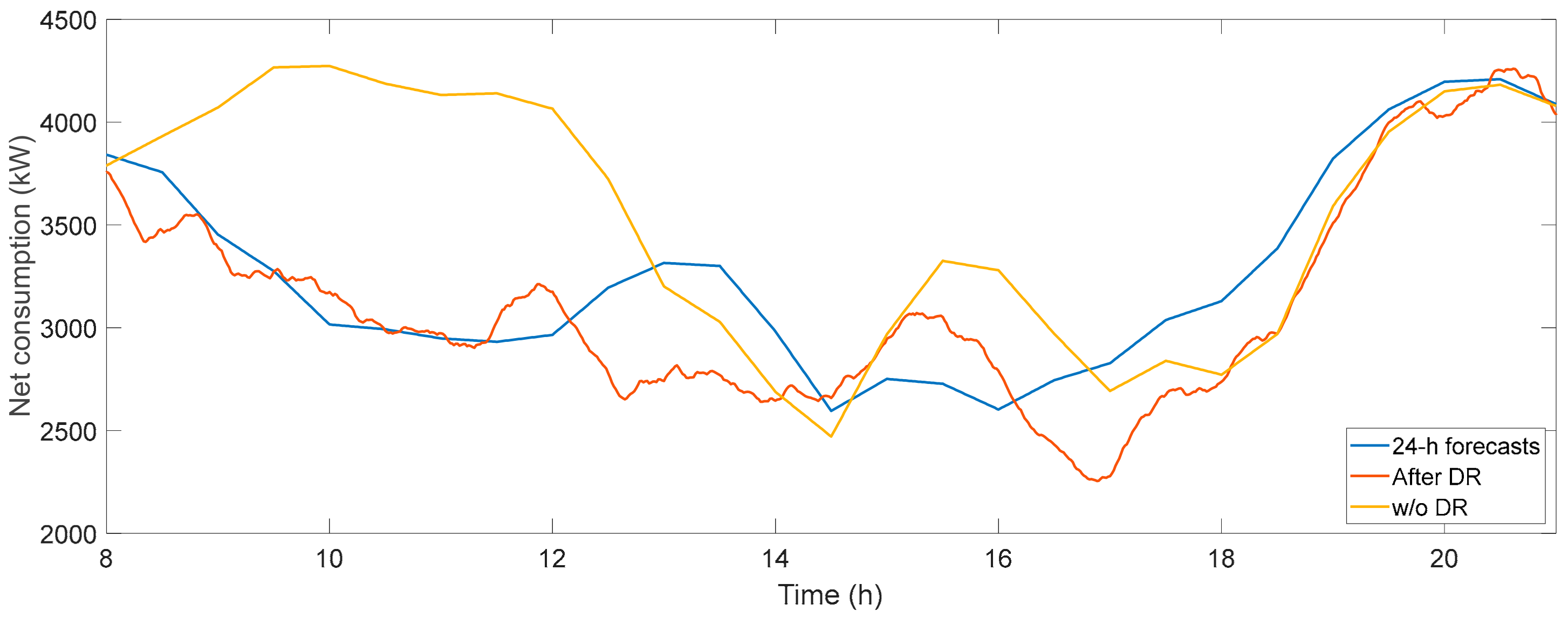
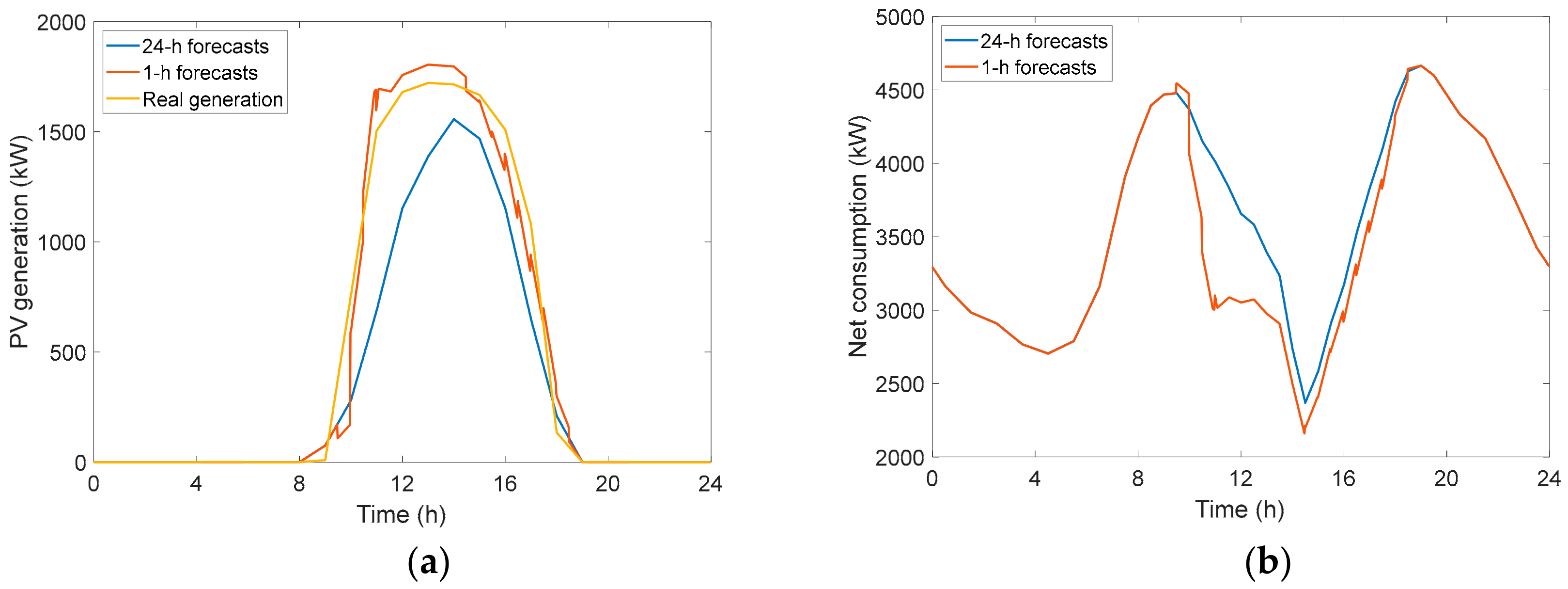
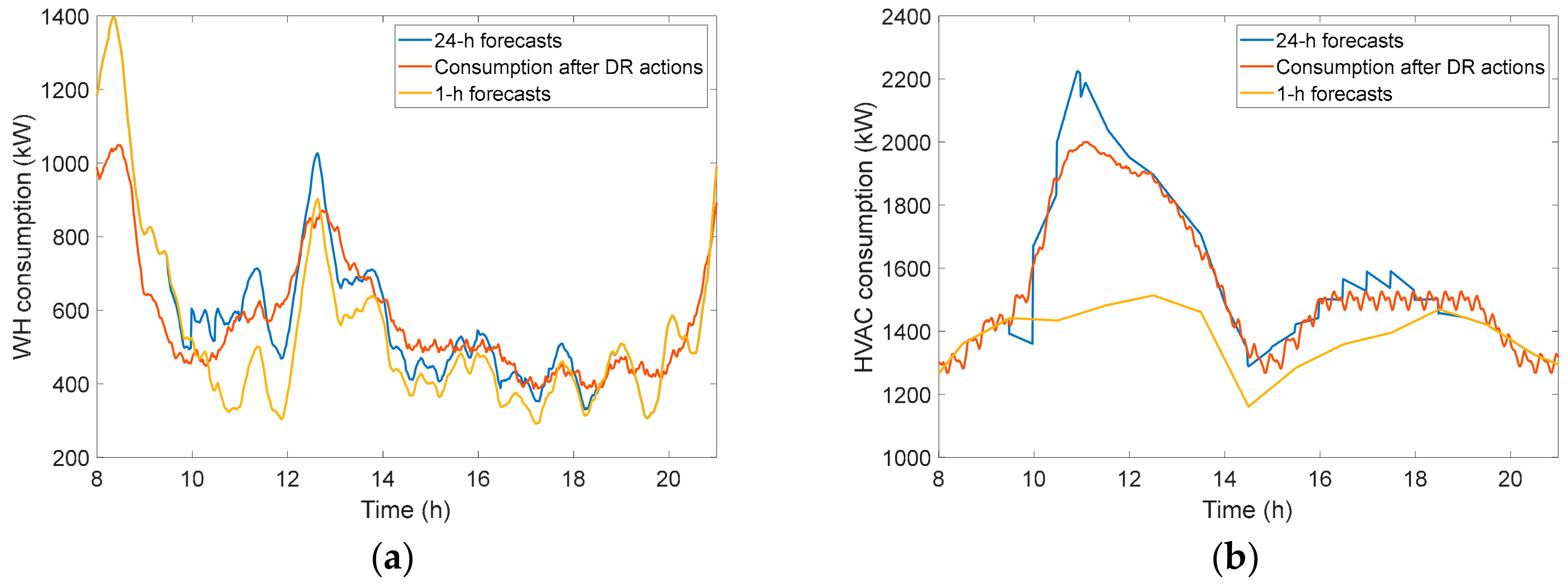
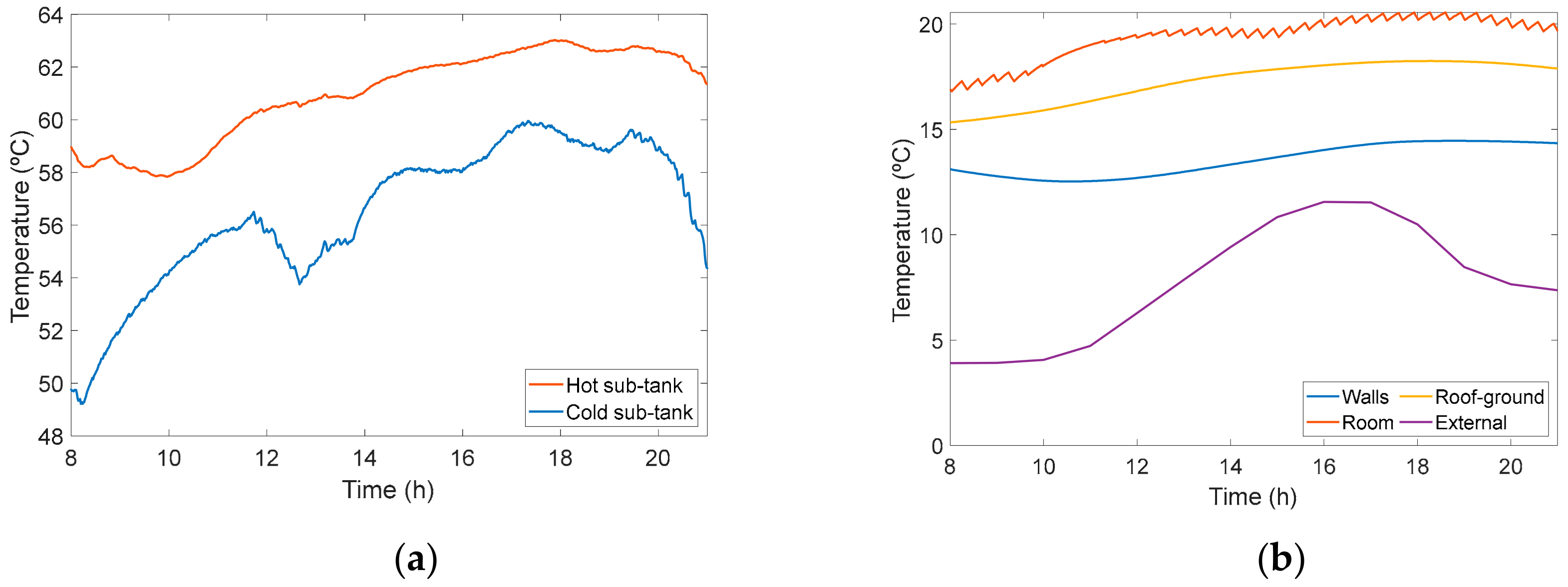
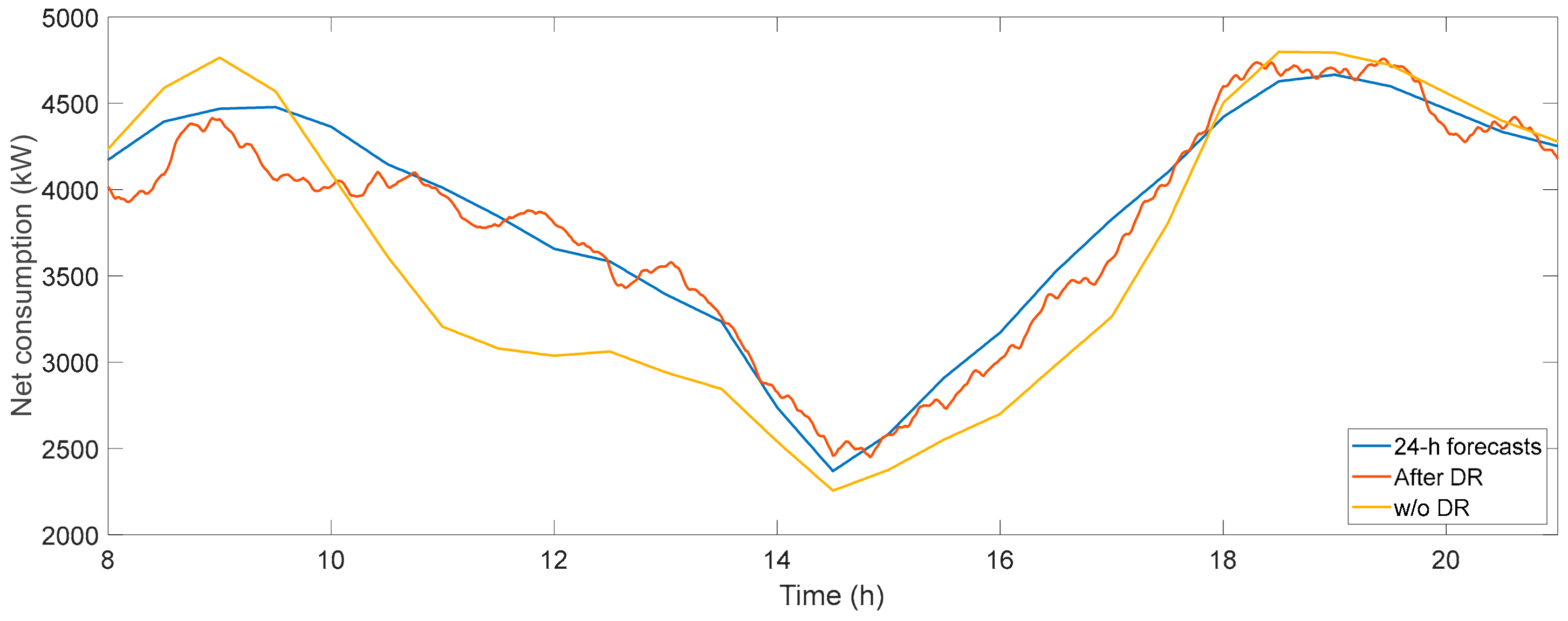
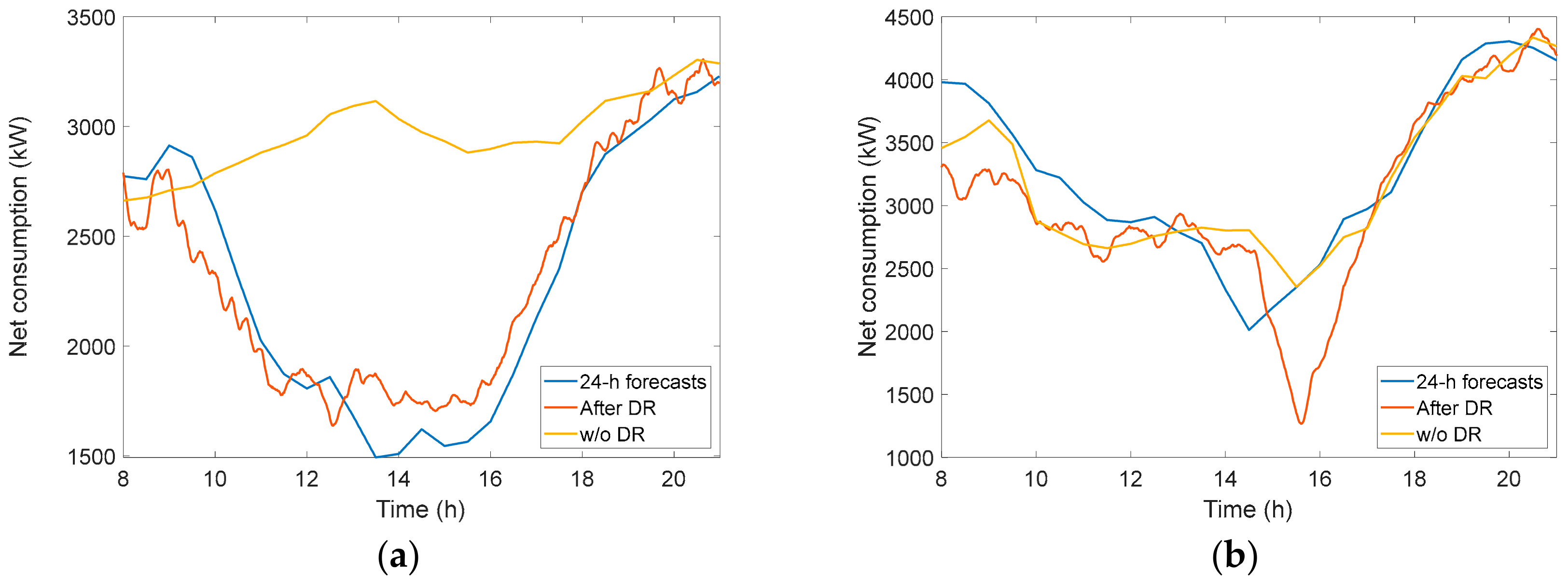
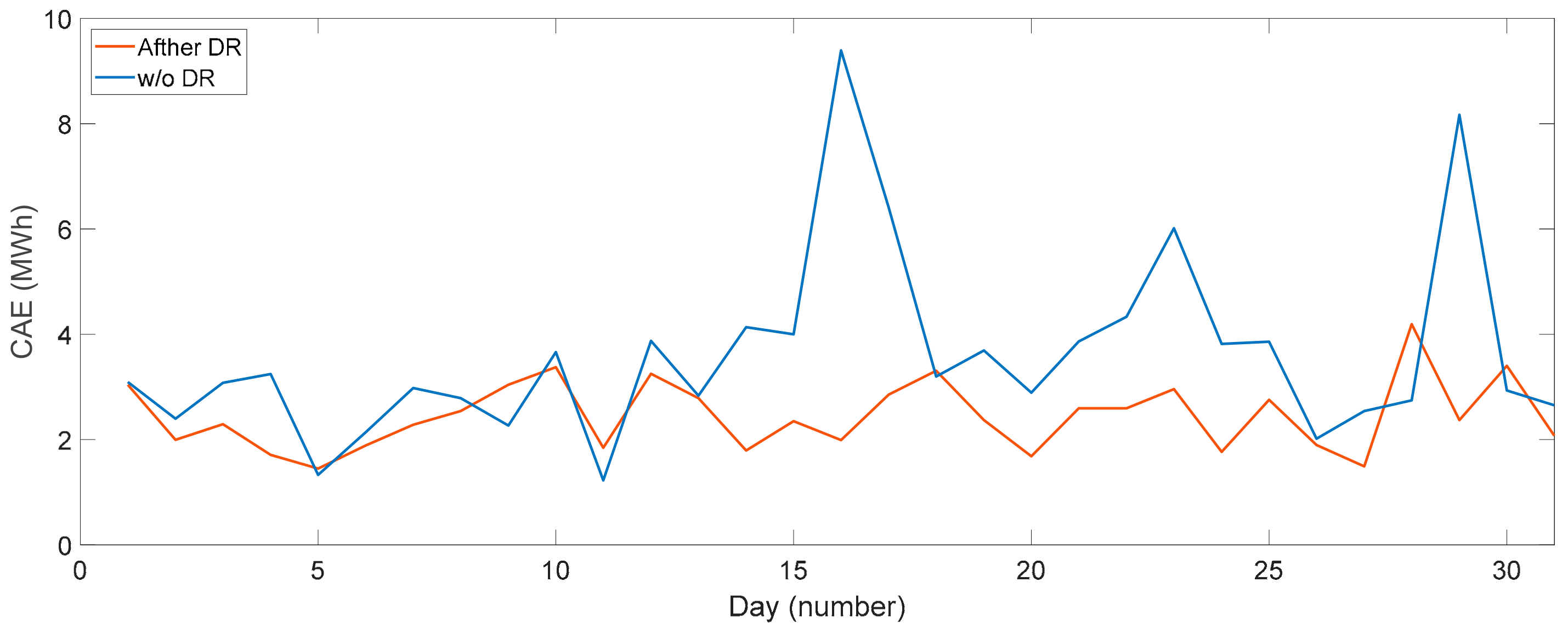
| Type of End-Use | USA (2015) All Fuels | USA (2015) Electricity | EU (2016) All Fuels | Spain (2014) All Fuels | Spain (2014) Electricity |
|---|---|---|---|---|---|
| Space Heating | 43 | 14.76 | 64.7 | 42.9 | 7.36 |
| Water Heater | 19 | 13.65 | 14.5 | 17.9 | 7.47 |
| Air Conditioning | 6.24 | 16.89 | 0.3 | 0.98 | 2.33 |
| Refrigerators | 4.75 | 7.02 | - | 7.94 | - |
| Other * | 29.8 | 47.67 | 20.5 | 39.22 | 82.84 |
| Predictors | Description |
|---|---|
| H2, H3, …H24 | Hourly dummy variables corresponding to the hour of the day |
| WH2, WH3, …WH7 | Hourly dummy variables corresponding to the day of the week |
| MH2, MH3, …, MH12 | Hourly dummy variables corresponding to the month of the year |
| FH1 | Hourly dummy variable corresponding to national, regional or local holidays |
| Temperature | Predicted hourly external temperature. |
| LOAD_lag_i | Hourly load lagged “i” hours, with i = 24, 48, …,168. |
| Measure | Regular Days | Special Days | All Days |
|---|---|---|---|
| Error_mean_train (kW) | 6.88 | −11.87 | 0.83 |
| Error_mean_test (kW) | 35.39 | −4.94 | 22.84 |
| Error_sd_train (kW) | 114.29 | 107.18 | 112.39 |
| Error_sd_test (kW) | 173.84 | 154.95 | 169.19 |
| Error_skewness_train | −0.16 | −0.19 | −0.15 |
| Error_skewness_test | 0.37 | 0.45 | 0.42 |
| Error_kurtosis_train | 10.93 | 8.48 | 10.21 |
| Error_kurtosis_test | 4.05 | 5.74 | 4.44 |
| RMSE_train (kW) | 114.49 | 107.83 | 112.39 |
| RMSE_test (kW) | 177.34 | 154.92 | 170.68 |
| R-squared_train | 0.98 | 0.94 | 0.98 |
| R-squared_test | 0.95 | 0.81 | 0.95 |
| MAPE_train | 2.05 | 2.45 | 2.18 |
| MAPE_test | 3.36 | 3.63 | 3.44 |
| Name | Description |
|---|---|
| swflx | Surface downwelling shortwave flux (W·m−2) |
| temp | Temperature at 2 m (Kelvin) |
| pres | Surface sea level pressure (hPa) |
| mod | Wind speed at 10 m (m/s) |
| dir | Wind direction at 10 m (degrees) |
| rh | Relative humidity at 2 m (per unit) |
| cft | Global cloud cover (per unit) |
| cfl | Cloud cover at low levels (per unit) |
| cfm | Cloud cover at medium levels (per unit) |
| cfh | Cloud cover at high levels (per unit) |
| prec | Accumulated rainfall in the hour (kg·m−2) |
| vis | Visibility (m) |
| clear | Clear-sky global horizontal irradiance (W·m−2) |
| aghi | Average global horizontal irradiance (W·m−2) |
| aip | Average irradiance on panel (W·m−2) |
| h1 | Cosine of the day fraction for the hour |
| h2 | Sine of the day fraction for the hour |
| Measure | Value |
|---|---|
| Error_mean_train (kW) | 4.96 |
| Error_mean_test (kW) | −19.52 |
| Error_sd_train (kW) | 308.60 |
| Error_sd_test (kW) | 362.12 |
| Error_skewness_train | −0.021 |
| Error_skewness_test | −0.173 |
| Error_kurtosis_train | 0.906 |
| Error_kurtosis_test | 0.994 |
| RMSE_train (kW) | 302.52 |
| RMSE_test (kW) | 350.34 |
| R-squared_train | 0.78 |
| R-squared_test | 0.70 |
| MAPE_train | 237.31 |
| MAPE_test | 310.06 |
| Day (Number) | Date (dd/mm) | Day (Number) | Date (dd/mm) | Day (Number) | Date (dd/mm) |
|---|---|---|---|---|---|
| 1 | 4 February | 11 | 10 March | 21 | 20 February |
| 2 | 5 February | 12 | 11 March | 22 | 20 March |
| 3 | 5 March | 13 | 12 February | 23 | 21 March |
| 4 | 6 February | 14 | 14 January | 24 | 22 March |
| 5 | 6 March | 15 | 14 February | 25 | 3 January |
| 6 | 7 February | 16 | 16 January | 26 | 23 March |
| 7 | 7 March | 17 | 18 February | 27 | 24 January |
| 8 | 8 February | 18 | 18 March | 28 | 25 February |
| 9 | 9 February | 19 | 19 March | 29 | 28 March |
| 10 | 10 February | 20 | 20 January | 30 | 29 March |
| 31 | 31 March |
| Day | MAPE (%) of PVF (24 h-Ahead Forecast) | MAPE (%) of PVBL (1 h-Ahead Forecast) |
|---|---|---|
| 1 | 12.5 | 7.7 |
| 2 | 13.9 | 9.1 |
| 4 | 18.6 | 8.7 |
| 5 | 4.8 | 5.6 |
| 14 | 28.2 | 11.1 |
| 16 | 128.1 | 30.6 |
| 17 | 39.2 | 11.9 |
| 20 | 22.9 | 5.8 |
| 23 | 52.6 | 21.7 |
| 26 | 9.7 | 9.9 |
| 28 | 8.2 | 6.7 |
| Energy 24-h (MWh) | Energy w/o DR (MWh) | Energy w/DR (MWh) | CAE 24 h-w/o DR (MWh) | CAE 24 h-w/DR (MWh) | Error w/o DR (%) | Error w/DR (%) | Max. ∆P w/o DR (kW) | Max. ∆P w/DR (kW) |
|---|---|---|---|---|---|---|---|---|
| 42.16 | 45.96 | 40.37 | 6.02 | 2.96 | 14.27 | 7.02 | 1256.93 | 579.32 |
| Energy 24-h (MWh) | Energy w/o DR (MWh) | Energy w/DR (MWh) | CAE 24 h-w/o DR (MWh) | CAE 24 h-w/DR (MWh) | Error w/o DR (%) | Error w/DR (%) | Max. ∆P w/o DR (kW) | Max. ∆P w/DR (kW) |
|---|---|---|---|---|---|---|---|---|
| 50.13 | 47.23 | 49.43 | 4.13 | 1.79 | 8.25 | 3.58 | 805.45 | 451.54 |
| Day | Energy 24-h (MWh) | Energy w/o DR (MWh) | Energy w/DR (MWh) | CAE 24 h-w/o DR (MWh) | CAE 24 h-w/DR (MWh) | Error w/o DR (%) | Error w/DR (%) | Max. ∆P w/o DR (kW) | Max. ∆P w/DR (kW) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 44.84 | 43.41 | 43.09 | 3.09 | 3.04 | 6.90 | 6.78 | 629.51 | 558.59 |
| 2 | 32.52 | 30.93 | 31.22 | 2.39 | 2.00 | 7.37 | 6.14 | 732.47 | 449.26 |
| 4 | 27.06 | 25.19 | 26.42 | 3.24 | 1.71 | 11.99 | 6.32 | 581.92 | 411.86 |
| 5 | 22.34 | 22.07 | 21.86 | 1.32 | 1.44 | 5.94 | 6.48 | 419.74 | 380.21 |
| 14 | 50.13 | 47.23 | 49.43 | 4.13 | 1.79 | 8.25 | 3.58 | 805.45 | 451.54 |
| 16 | 29.70 | 38.64 | 30.09 | 9.39 | 1.99 | 31.63 | 6.70 | 1622.69 | 472.04 |
| 17 | 47.15 | 41.59 | 45.25 | 6.40 | 2.85 | 13.58 | 6.05 | 1108.13 | 538.99 |
| 20 | 48.31 | 47.04 | 48.74 | 2.89 | 1.68 | 5.99 | 3.49 | 622.92 | 342.69 |
| 21 | 27.59 | 23.97 | 25.27 | 3.86 | 2.59 | 13.99 | 9.40 | 776.20 | 534.47 |
| 23 | 42.16 | 45.96 | 40.37 | 6.02 | 2.96 | 14.27 | 7.02 | 1256.93 | 579.32 |
| 26 | 41.01 | 42.38 | 42.08 | 2.01 | 1.90 | 4.92 | 4.63 | 487.96 | 572.66 |
| 28 | 41.97 | 41.25 | 39.32 | 2.75 | 4.19 | 6.55 | 9.99 | 792.76 | 1124.70 |
| Day | Balance Mileage (MWh) | Demand Mileage (MWh) | Mileage Ratio (%) | Symmetry Equation (12) | Performance Equation (13) |
|---|---|---|---|---|---|
| 1 | 2.64 | 5.54 | 47.5 | 0.95 | 0.27 |
| 2 | 2.62 | 4.52 | 57.5 | 1.59 | 0.34 |
| 4 | 2.86 | 4.06 | 70.17 | 4.24 | 0.05 |
| 5 | 1.52 | 3.92 | 38.89 | 0.83 | 1.89 |
| 14 | 3.12 | 5.72 | 54.50 | 7.06 | 0.047 |
| 16 | 3.06 | 4.12 | 74.20 | 0.008 | 0.036 |
| 17 | 4.32 | 5.34 | 80.9 | 17.92 | 0.064 |
| 20 | 1.66 | 5.54 | 28.9 | 5.24 | 0.268 |
| 23 | 4.14 | 5.28 | 78.13 | 0.038 | 0.073 |
| 26 | 1.88 | 5.16 | 36 | 0.953 | 0.467 |
| 28 | 2.08 | 5.22 | 39.8 | 0.224 | 2.34 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Abellón, M.C.; Fernández-Jiménez, L.A.; Guillamón, A.; Falces, A.; García-Garre, A.; Gabaldón, A. Integration of Demand Response and Short-Term Forecasting for the Management of Prosumers’ Demand and Generation. Energies 2020, 13, 11. https://doi.org/10.3390/en13010011
Ruiz-Abellón MC, Fernández-Jiménez LA, Guillamón A, Falces A, García-Garre A, Gabaldón A. Integration of Demand Response and Short-Term Forecasting for the Management of Prosumers’ Demand and Generation. Energies. 2020; 13(1):11. https://doi.org/10.3390/en13010011
Chicago/Turabian StyleRuiz-Abellón, María Carmen, Luis Alfredo Fernández-Jiménez, Antonio Guillamón, Alberto Falces, Ana García-Garre, and Antonio Gabaldón. 2020. "Integration of Demand Response and Short-Term Forecasting for the Management of Prosumers’ Demand and Generation" Energies 13, no. 1: 11. https://doi.org/10.3390/en13010011
APA StyleRuiz-Abellón, M. C., Fernández-Jiménez, L. A., Guillamón, A., Falces, A., García-Garre, A., & Gabaldón, A. (2020). Integration of Demand Response and Short-Term Forecasting for the Management of Prosumers’ Demand and Generation. Energies, 13(1), 11. https://doi.org/10.3390/en13010011





