1. Introduction
Power transformers represent one of the main parts of transmission and distribution systems [
1] and are ubiquitous in power electronics applications. Therefore, the analysis of power systems and of any power electronics circuit containing transformers, requires accurate transformer model [
2,
3].
Transformer modeling, i.e. the estimation of transformer equivalent circuit parameters, is an important subject in many studies (power systems, stability, modeling of power electronics converters etc.). It is necessary for transformer design, diagnostic purposes and service information [
4,
5]. Namely, equivalent circuit parameters characterize the behavior and performance of a transformer. Hence, estimation of transformer equivalent circuit parameters can provide significant information about the condition, performance and behavior of the machine, on one hand, and to its operation on grid, on the other.
Work on developing transformer model has been widely investigated. For that reason, a few different views on transformer parameters estimation can be found in the available literature [
6,
7,
8,
9,
10,
11,
12,
13,
14]. Some of them include transformer’s nonlinear behavior [
6,
7,
8], whereas others deal with traditional (Steinmetz) transformer equivalent circuit [
9,
10,
11,
12,
13,
14]. Since transformers and induction machines have similar equivalent circuit, some studies investigate parameter estimation of both induction machine and transformer [
15,
16]. This paper deals with parameter estimation of traditional (Steinmetz) equivalent circuit of single-phase transformer.
The equivalent circuit parameters of transformer can be determined based on its geometrical dimensions [
17,
18]. However, this approach is not useful for all transformers due to dimensional data unavailability, which is often case for old machines. On the other hand, these parameters can be determined from the standard test procedures, that are based on open-circuit and short-circuit tests, and hence cannot be used for transformers which are in operation [
1]. In addition, deviation of environmental and operational conditions (such as temperature change, change of air conditions, short circuits, overloading etc.) can cause variation of the equivalent circuit parameters [
16]. Single-phase transformer, considered in this paper, usually operates in a control system or in a measuring system. Therefore, the application of short-circuit and open-circuit tests require additional time for the tests realization and disconnection of the transformer from the power system, which is usually impossible to carry out.
Optimization techniques based on the evolutionary algorithms have become the most widely used methods in a large variety of optimization problems. The main advantage of the optimization techniques, based on the evolutionary algorithms is that the form of the cost (or goal) function can be defined arbitrary. This is reason why these techniques are also very popular for transformer parameters estimation [
9,
10,
11,
12,
13,
14,
15,
16]. They include Practical Swarm Optimization (PSO) [
9,
15,
16], Genetic Algorithm (GA) [
9,
13], Imperialist Competitive Algorithm (ICA) [
10], Gravitational Search Algorithm (GSA) [
10], Bacterial Foraging Algorithm (BFA) [
11,
12] and Artificial Bee Colony Algorithm (ABCA) [
14] and can be applied on transformer nameplate data or on the measured load data, without disconnection of the transformer from the power system. Let us briefly describe these techniques.
In [
9], PSO and GA are used for the estimation of transformer parameters from the nameplate data and the estimated parameters are compared to the corresponding ones obtained from the standard tests—open-circuit and short-circuit tests. Furthermore, the estimated values of the primary current, secondary current and secondary voltage have been compared to the corresponding ones obtained from the full load test. The usage of ICA and GSA for transformer parameters estimation is proposed in [
10] and compared to PSO and GA algorithms. In the optimization procedure in [
10], unknown parameters are obtained by using an objective function which takes into account the values of primary current, secondary current and secondary voltage at full load. However, the differences between the estimated and the measured values of the primary current, secondary current and secondary voltage values at full load in the previous studies (especially in [
9]) are significant.
The use of BFA for single-phase transformer parameter estimation based on the load data obtained from experiments is presented in [
11]. The estimated values of parameters and of values of primary current, secondary current and secondary voltage, have been compared to the results obtained from the short-circuit and open-circuit tests [
11]. However, in [
11] there are significant differences between the estimated and the measured output characteristics (primary current–load resistance, secondary current–load resistance and secondary voltage–load resistance). An ABCA-based transformer parameter estimation using values of currents and voltages at any known load (i.e. for one load value) is presented in [
14]. This approach is also characterized by obvious differences between the estimated and the measured values of the parameters and observed variables. Therefore, based on all results presented in [
9,
10,
11,
14], it can be concluded that there is a room for improvement by using other optimization techniques. This also indicates that different objective functions can be used for precise transformer parameter estimation. Finally, studies [
9,
10,
11,
14] lack any discussion about the impact of the objective function on the values of estimated parameters and parameter estimation by using all three possible procedures (standard tests, nameplate data and load data obtained from experiments) has not been performed on the same transformer.
In [
9,
10], the authors pay attention to the difference between estimated transformer parameters and the parameters obtained by using open-circuit and short-circuit tests. The parameters obtained by using the open-circuit and short-circuit tests do not guarantee an ideal matching between the measured and estimated (by using an equivalent circuit and in that manner calculated parameters value) output characteristics (for example: secondary current–load resistance characteristic) or an ideal matching between the measured and the estimated values of the primary current, secondary current and secondary voltage at full load. The unknown parameters of the transformer equivalent circuit need to be accurately estimated for the best possible matching between the measured and the estimated transformer output characteristics for all possible load values. For that reason, the objective function for parameters estimation presented in [
9,
10] contains primary current, secondary current and secondary voltage. In other papers, a different objective function can be found (see, for example, [
16]).
In this paper, the use of chaotic optimization approach (COA) for transformer parameter estimation by using the nameplate data and load data obtained from experiments will be presented. The effectiveness of the proposed technique will be evaluated through its application on different transformers (different with respect to machine power and voltage levels) found in the literature and in laboratory environment. COA has found application in various optimization techniques [
19,
20,
21]. In [
19], COA is successfully applied for parameter identification of Jiles-Atherton hysteresis model. Design of PID parameters for automatic voltage regulation of synchronous machine by using COA is presented in [
20]. In [
21], the usage of the chaotic beamforming adaptive algorithm for antenna array’s radiation pattern synthesis is presented. In addition, chaos is used to improve the existing heuristic optimization techniques [
22,
23]. COA systems prevent stuck in local minima, they are easy to implement, have short execution time and high precision [
24].
The paper is organized as follows.
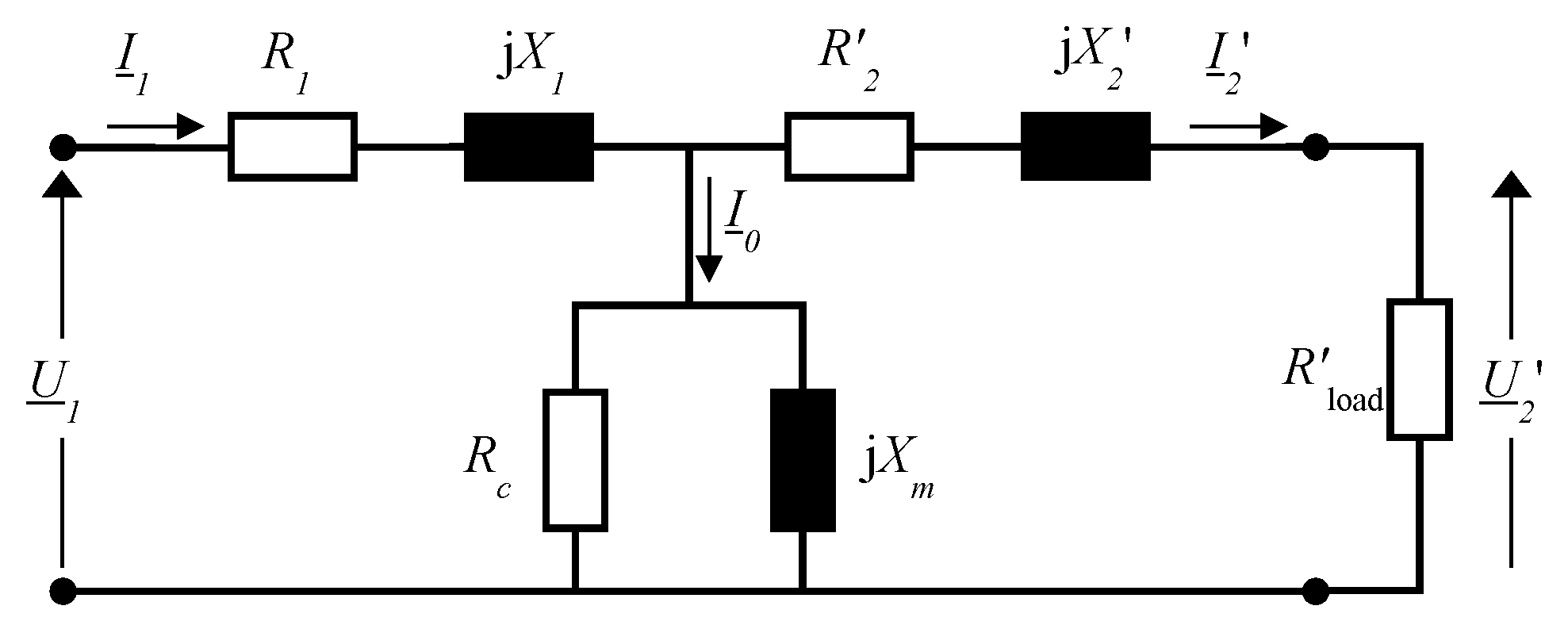
Section 2 provides a short description of the transformer equivalent circuit. COA is presented in
Section 3. The application of COA for parameter estimation of transformer equivalent circuit is presented in
Section 4. The experimental results and the COA-based estimation are presented in
Section 5.
Section 6 concludes the paper.
3. Chaotic Optimization Approach
Chaos is a form of an aperiodic long-term behavior that occurs under certain conditions in non-linear deterministic systems that exhibit a sensitive dependence on the initial conditions. It is about the steady state of dynamical systems described by ordinary differential equations or by iterative map. The behavior of the system depends on the value of its parameters. Parameter that can be changed is called the bifurcation parameter. Changing the bifurcation parameter leads to bifurcations i.e. qualitative changes in the state of the system. So, the system exhibits various forms of dynamic behavior, i.e., the trajectories can converge to the equilibrium point, the boundary circle or the chaotic attractor [
25,
26].
The characteristic property of chaotic dynamic systems is sensitive dependence on the initial conditions. If the evolution of such systems starts from two close points, after long enough time they will be arbitrarily far from each other. Time waveforms for the chaotic attractor are completely irregular and there is no repetition in any period of observation of the ultimate length. Although produced by deterministic equations, randomness in time-domain and long-term unpredictability in the state are present. The chaotic time waveform possesses a noise-like power spectrum.
One of the most famous chaotic systems is the Lorenz system [
26]. Meteorologist Edward Lorenz has accidentally discovered sensitive dependence on initial conditions while modeling the atmospheric convention. He describes this complex system with three equations, since then known as the three-dimensional Lorenz system:
with chaotic solutions for
σ = 10,
r = 28, and
b = 8/3. The chaotic signal
x(
t) from the Lorenz system is shown in
Figure 2a, and the corresponding chaotic attractor in the phase space (known as the butterfly attractor) is projected onto the
x-
y plane in
Figure 2b.
Chaotic behavior is also observed in iterative maps such as: Logistic map, Lozi map, Tent map and other [
26]. In this paper, the chaotic sequence was obtained using the well-known Logistic map [
26] given by
where
k represents the iteration number, and parameter
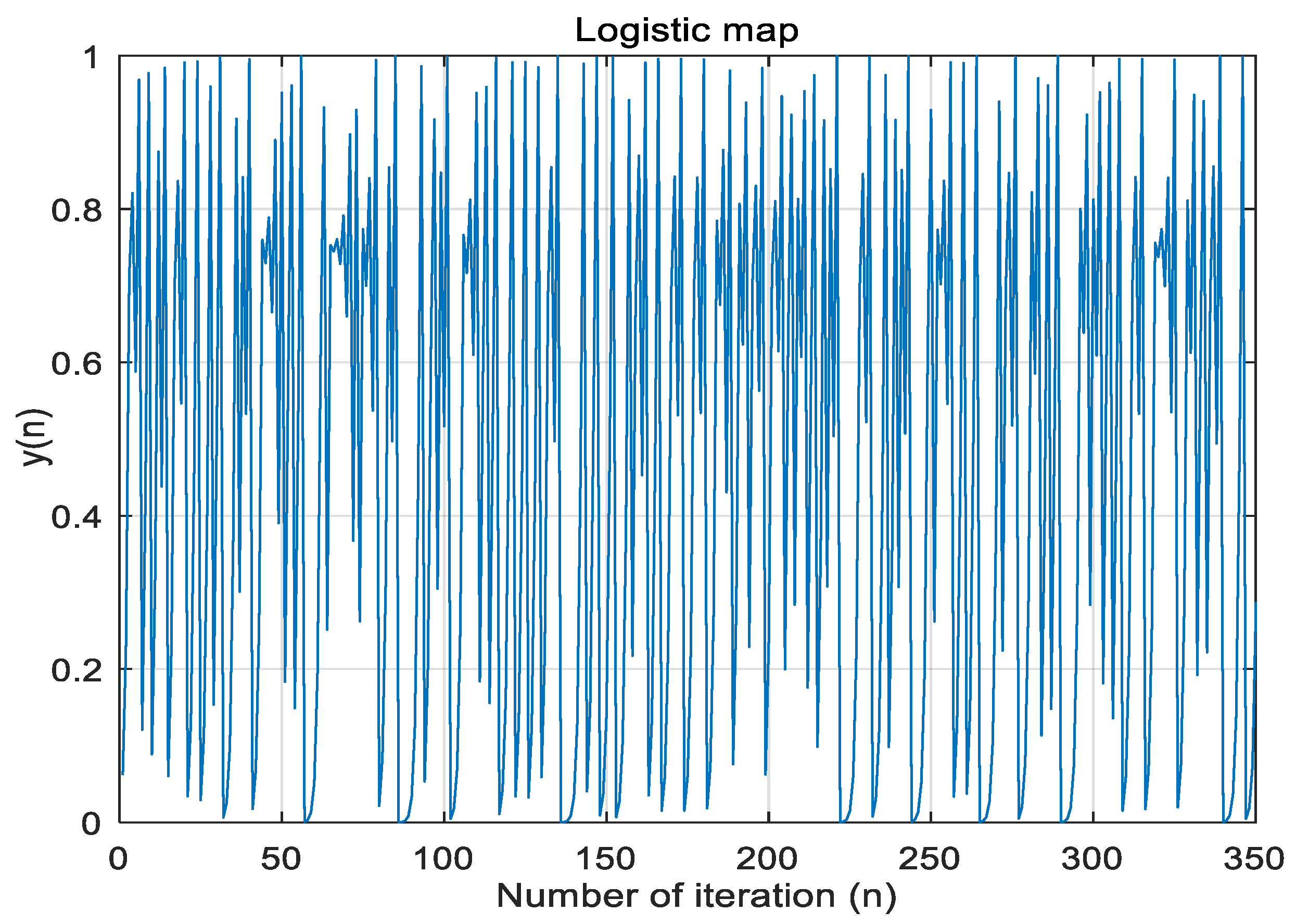
r = 4. The logistic equation models a process that exhibits initial exponential growth with a nonlinearity that ultimately stops the growth. Most of the common features of chaos are manifest in this simple example. The chaotic signal obtained by Logistic map is shown in
Figure 3. Details about chaotic systems can be found in [
25,
26].
The task of the chaotic optimization is to determine X which minimizes the fitness function F(X). The vector X = [x1,x2,…,xn] contains the variables , limited to the lower (Li) and upper (Ui) permitted value. In this paper, for estimation transformer equivalent circuit parameters, we adopt and .
COA is based on the chaotic search [
19,
21].
Table 1 presents the search procedure, composed of two stages: global and local search. In local search, parameter λ is a corrective factor in determining the size of the search area around X*. Larger λ allows searching in larger area and vice versa.
5. Experimental Results and Application of COA
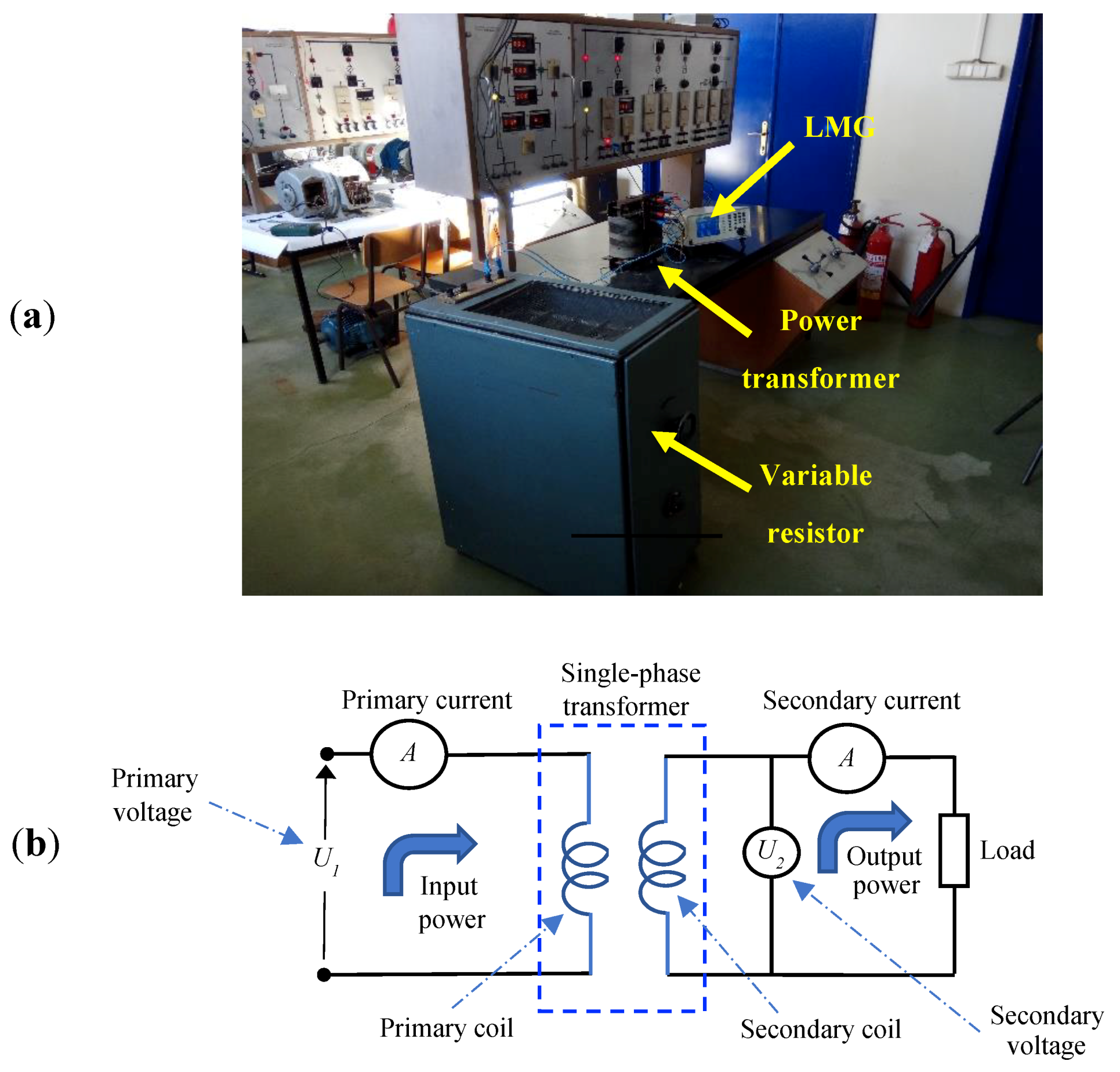
The experimental setup used for obtaining the data (primary current, secondary current, secondary voltage at full load, as well as primary current—load resistance, secondary current—load resistance, secondary voltage—load resistance, input power—load resistance and output power—load resistance characteristics) is composed of a one-phase transformer (KONCAR, 2 kVA, 220 V/110 V, 50 Hz) which supplies one variable resistor (maximum resistance 1000 Ω, and maximum current 25 A) (see
Figure 4a—Experimental setup and
Figure 4b—Electrical diagram of experimental setup). The variable resistor is used for transformer loading, i.e. it is used to vary the transformer load. All currents, voltages and powers were measured with power analyzer LMG (
Leistungsmessgerät).
Firstly, on this transformer we have performed standard open-circuit and short-circuit tests as described in [
1]. The transformer equivalent circuit parameters obtained by using results from open-circuit and short-circuit tests are presented in
Table 7. After that, we have performed full load test, in order to be able to apply the method [
9,
10], which requires results from full load test and transformer nameplate data. By using data obtained from full load test (measured values of primary current, secondary current and secondary voltage are 8.95 A, 17.55 A and 105.5 A, respectively), as well as by using COA, we have obtained transformer parameters by applying method [
9,
10]. The estimated values of transformer parameters are also presented in
Table 7.
Finally, by changing resistance of variable resistor, we have performed a set of experiments in order to obtain the transformer characteristics for different loads. All measured data for transformer loading are presented in
Table 8. In order to obtain transformer equivalent circuit parameters, except (13), we have also proposed the following objective functions:
and
In (13)–(15) the estimated values are calculated by using (3)–(7).
The estimated transformer parameters, for the three objective functions, by applying COA, are presented in
Table 7. The general conclusion is that all the applied methods yield close results. Therefore, it is expecting the good matching between measured and estimated output characteristics for all values of parameters (obtained by using open-circuit and short-circuit tests; obtained by using methods [
9,
10] and obtained by using COA and different objective functions).
The measured and calculated (for parameters given in
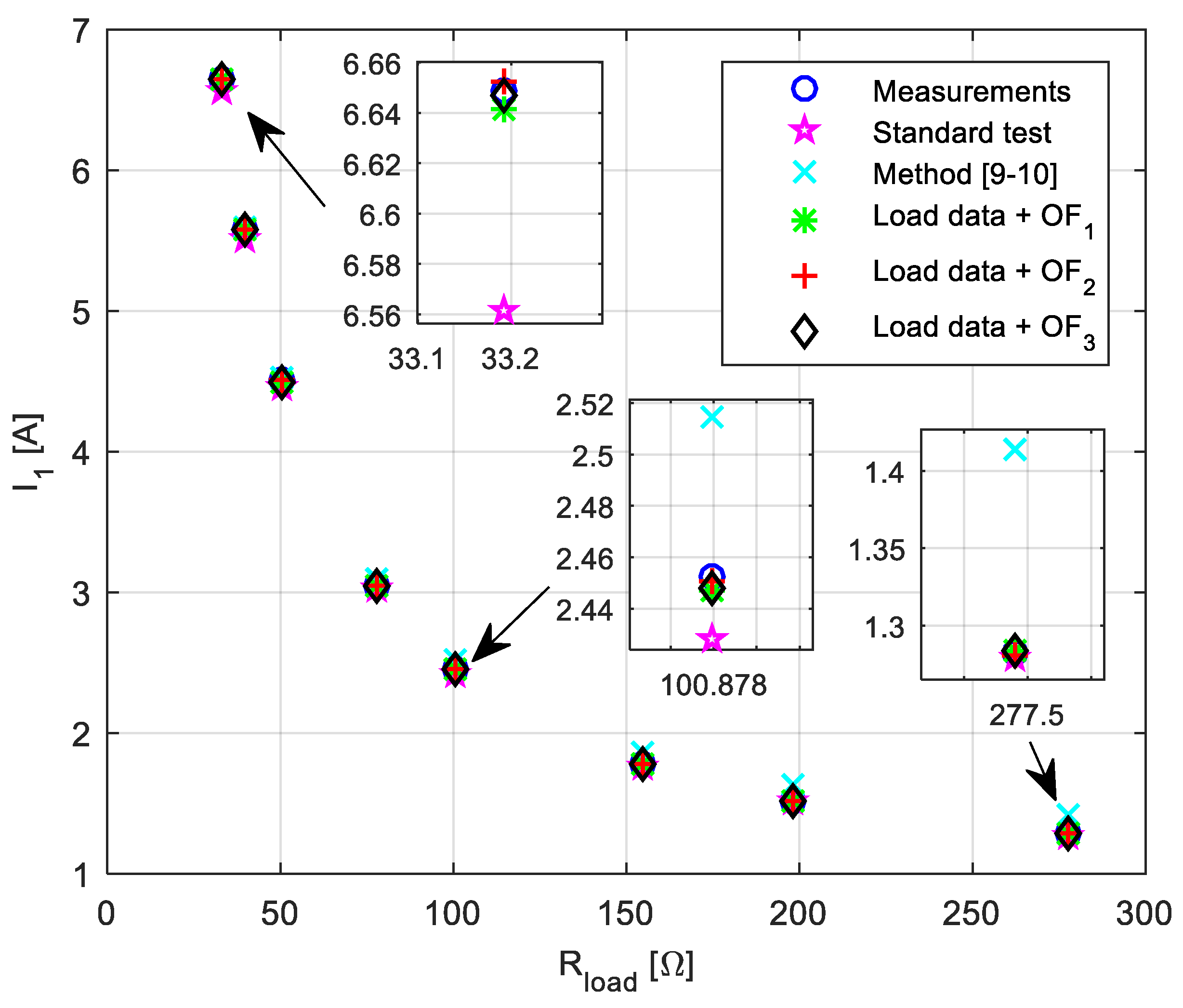
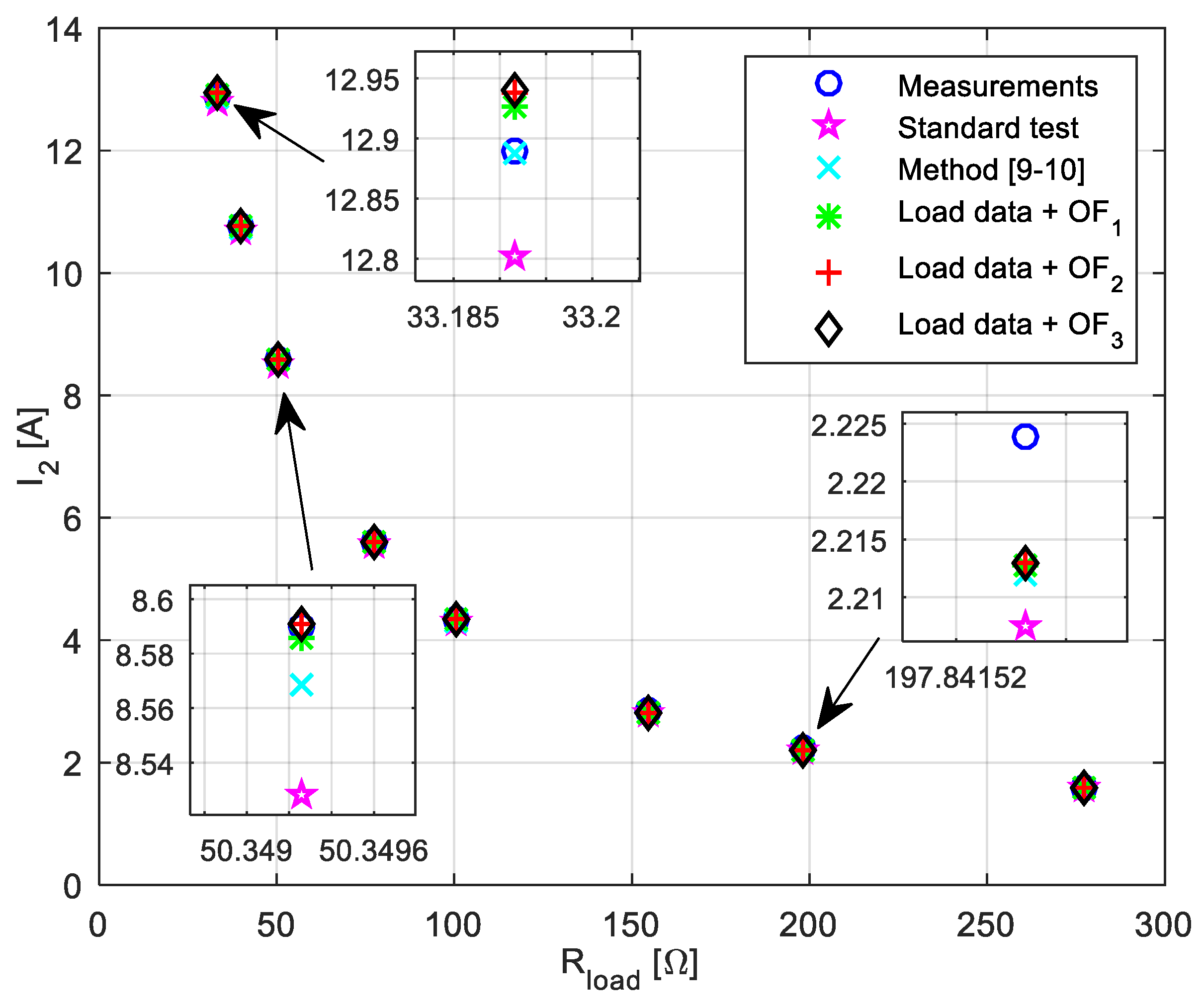
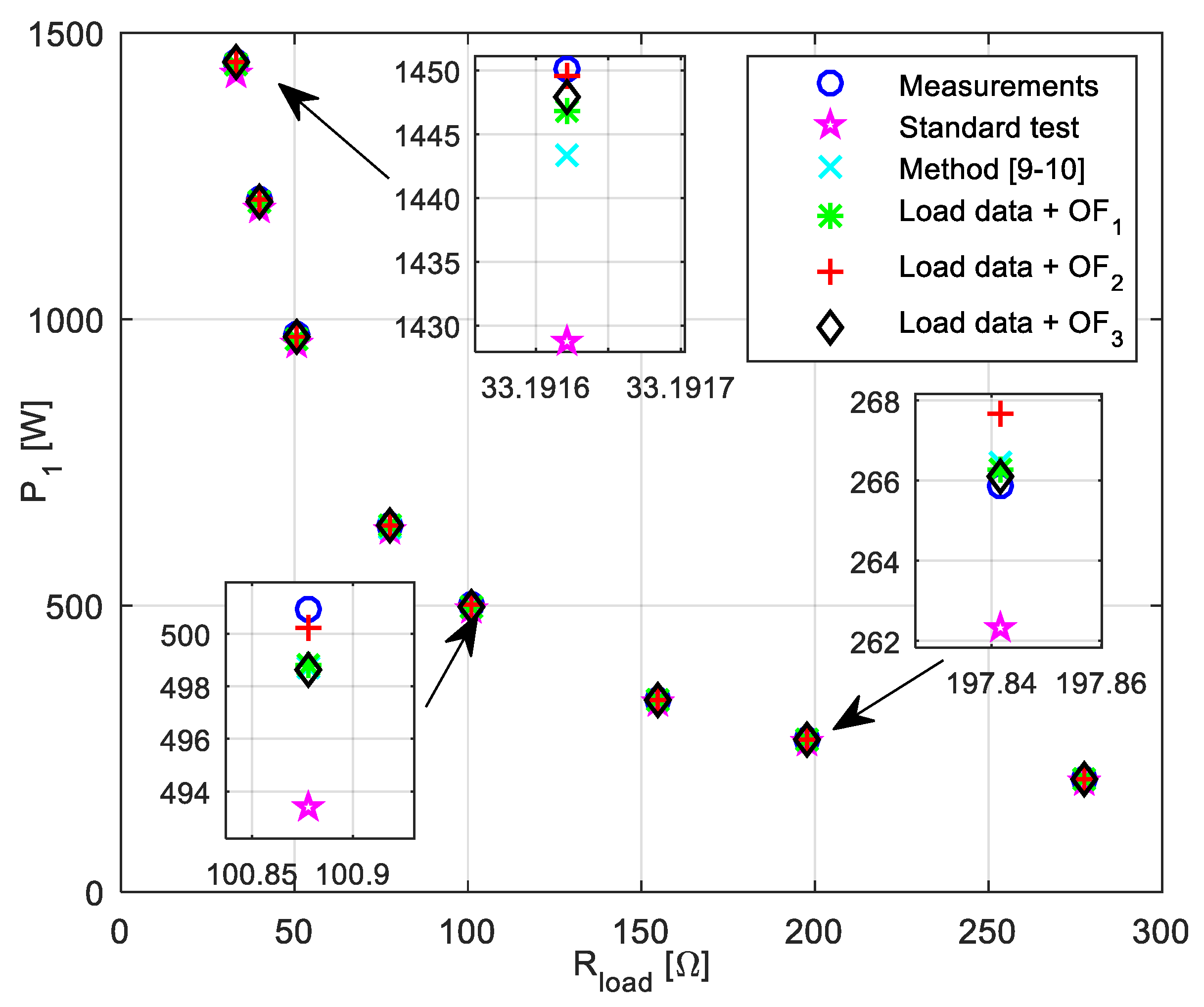
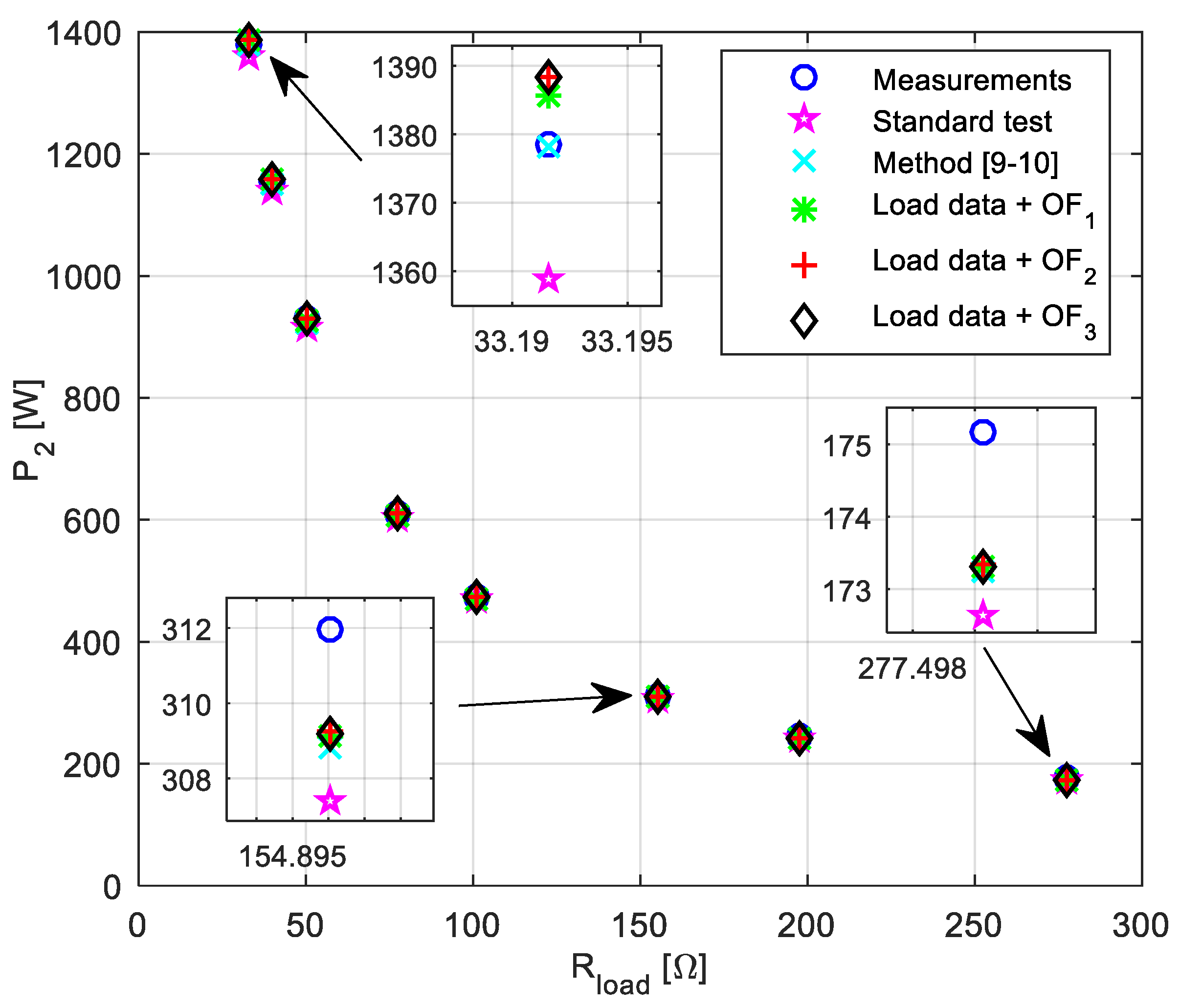
Table 7) primary current–load resistance, secondary current–load resistance, input power–load resistance and output power–load resistance characteristics are presented in
Figure 5,
Figure 6,
Figure 7 and
Figure 8, respectively. All presented characteristics are very close to each other (see zoomed parts in presented
Figure 5,
Figure 6,
Figure 7 and
Figure 8). However, using load data provides the best matching, whereas the worst matching is in the case of using parameters obtained from standard short-circuit and open-circuit tests.
By observing the presented results, it can be also concluded that [
9,
10] gives better result if the primary and secondary currents values are high (see
Figure 5 and
Figure 6). This is a consequence of the fact that this method is based on full load data (high value of current). However, for lower current values, there are certain deviations between the measured and estimated values.
On the other hand, parameters obtained by using load data and any of the proposed objective functions (13)–(15), in the whole load range, match the measured results very well (see for example
Figure 7 and
Figure 8). Therefore, for a precise estimation of the transformer equivalent circuit it is not needed to measure input (or output) active power or magnetizing current as proposed in [
16].
Therefore, it is once again shown that the estimation of single-phase transformer equivalent circuit parameters by using COA, based on the nameplate and load data obtained from the experiments, provides very accurate results with reference to the measurements. Furthermore, all these testing’s have confirmed the applicability of COA in transformer parameters estimation. Also, regardless of the type of the objective function (which combines different variables), COA can precisely estimate transformer equivalent circuit parameters.