Distributed Capacity Allocation of Shared Energy Storage Using Online Convex Optimization
Abstract
:1. Introduction
- The ES capacity allocation problem is formulated to be solvable in online convex optimization framework, in which capacity has to be allocated before user load profiles are disclosed.
- An online capacity allocation algorithm is developed, which does not require day-ahead load forecasting or estimating probability distribution functions of loads.
- A distributed implementation of the online algorithm is proposed, in which users do not need to send private load data to any other.
2. System Model and Problem Statement
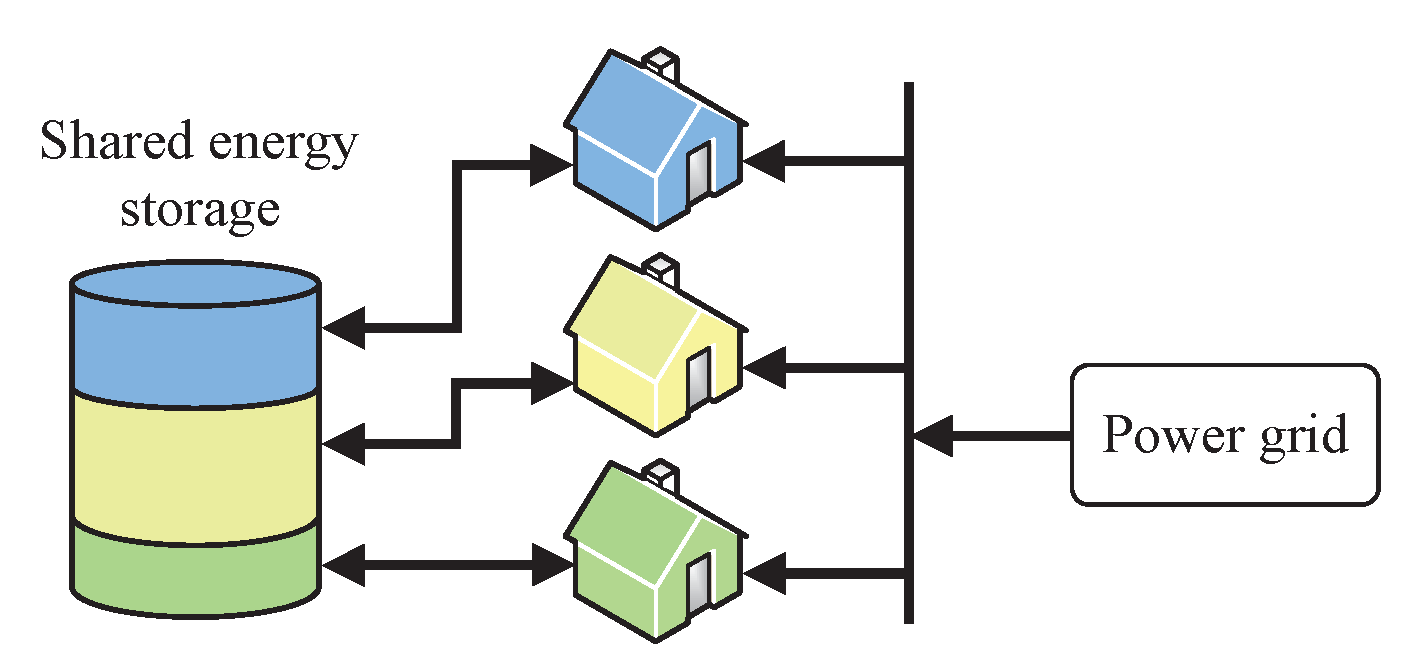
2.1. ES Sharing Model
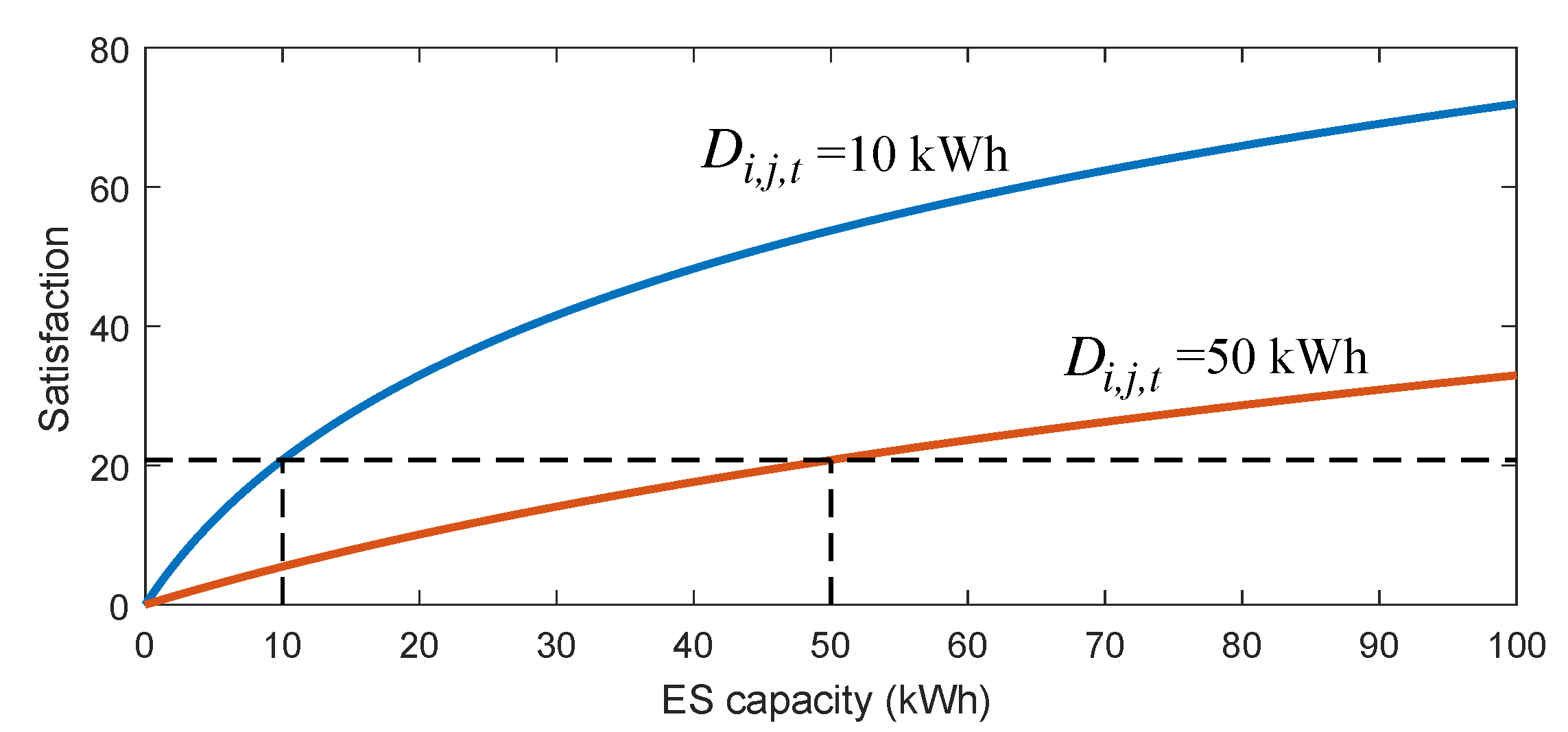
2.2. System Cost Minimization
3. Online Convex Optimization
3.1. Performance Metrics
3.2. Online Algorithm
| Algorithm 1: Online algorithm for solving P1 |
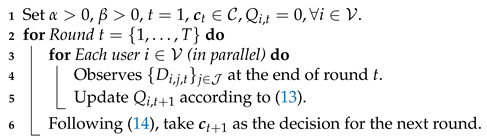 |
- There exists such that .
- Define . There exists such that .
- There exists such that .
- There exists such that .
- There exist and such that .
- If , then . If , then . Combining these two cases, we have .
- According to the definition of , we can derive that where the inequality is obtained from Cauchy-Schwarz inequality.
- , where the second inequality is also derived from Cauchy-Schwarz inequality.
- .
- There exists such that . Thus, the constant exists such that .
4. Distributed Implementation
4.1. Network Problem
4.2. ADMM Algorithm
| Algorithm 2: Distributed Algorithm for solving P3 |
 |
5. Numerical Result
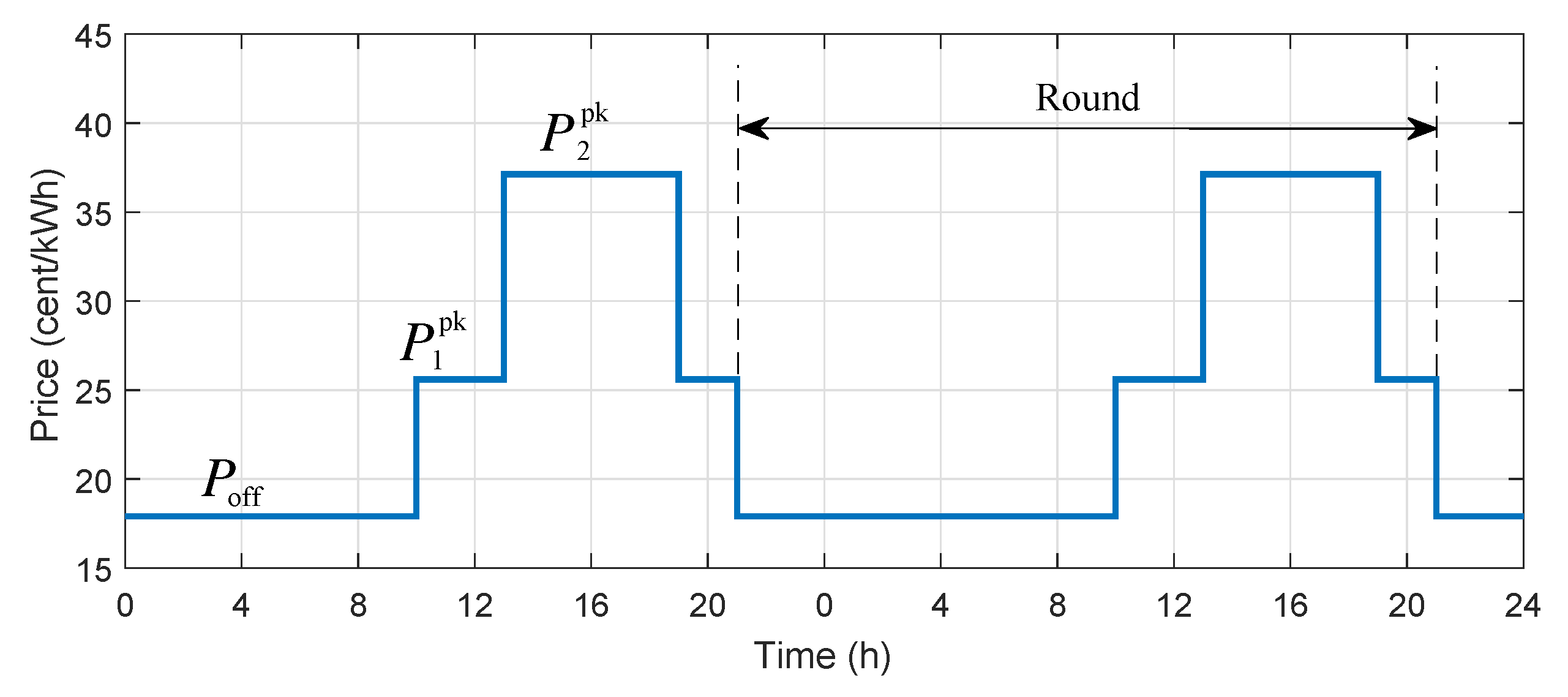
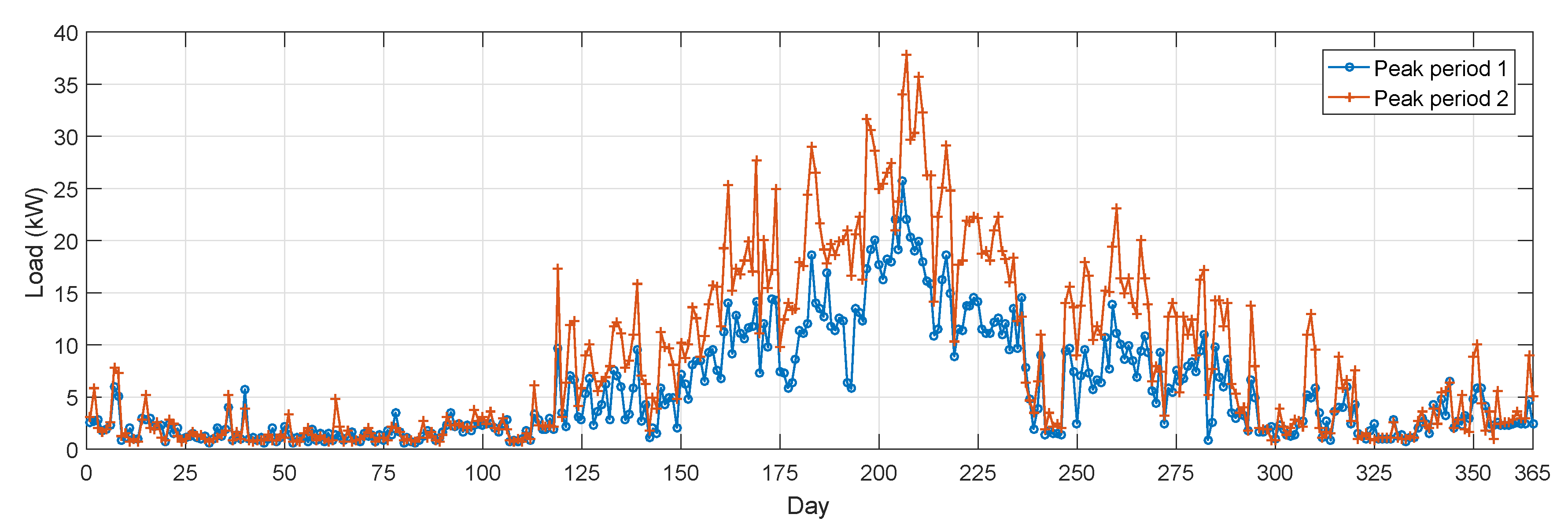
5.1. Simulation Setup
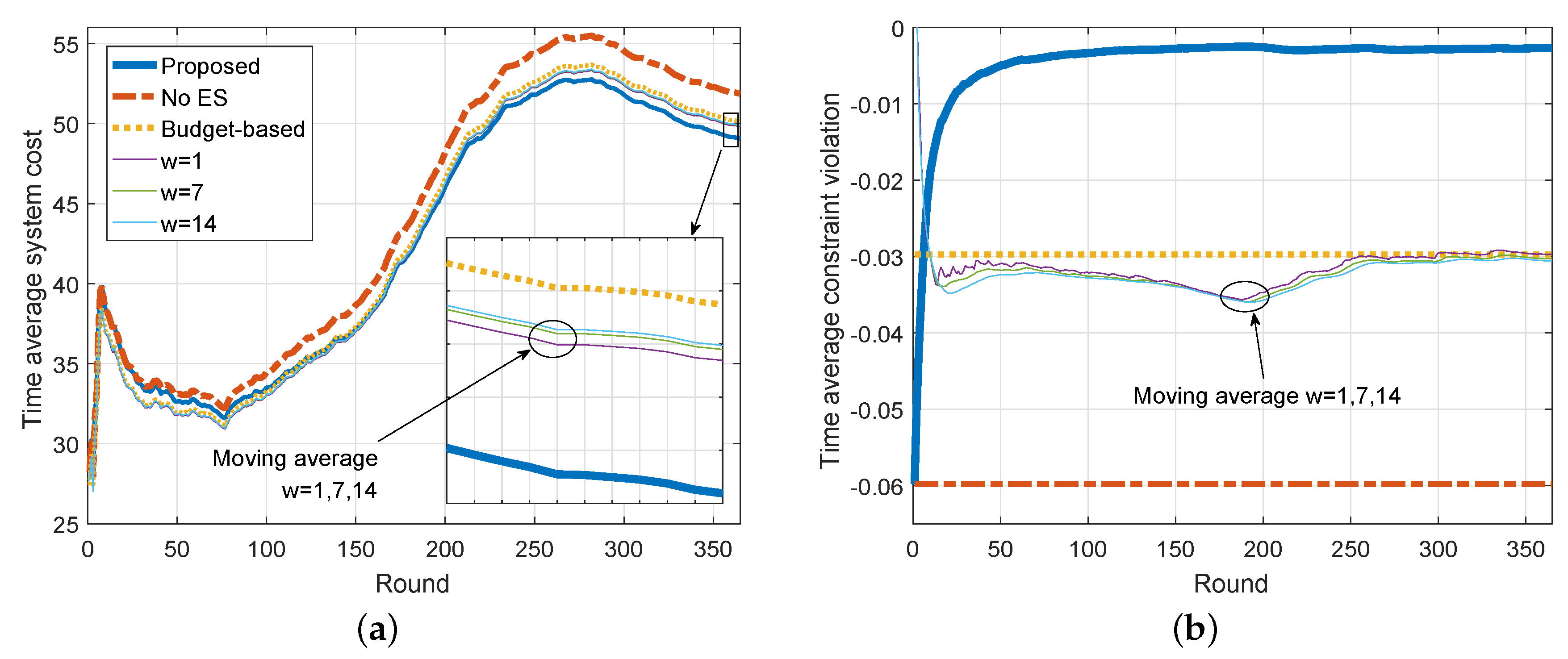
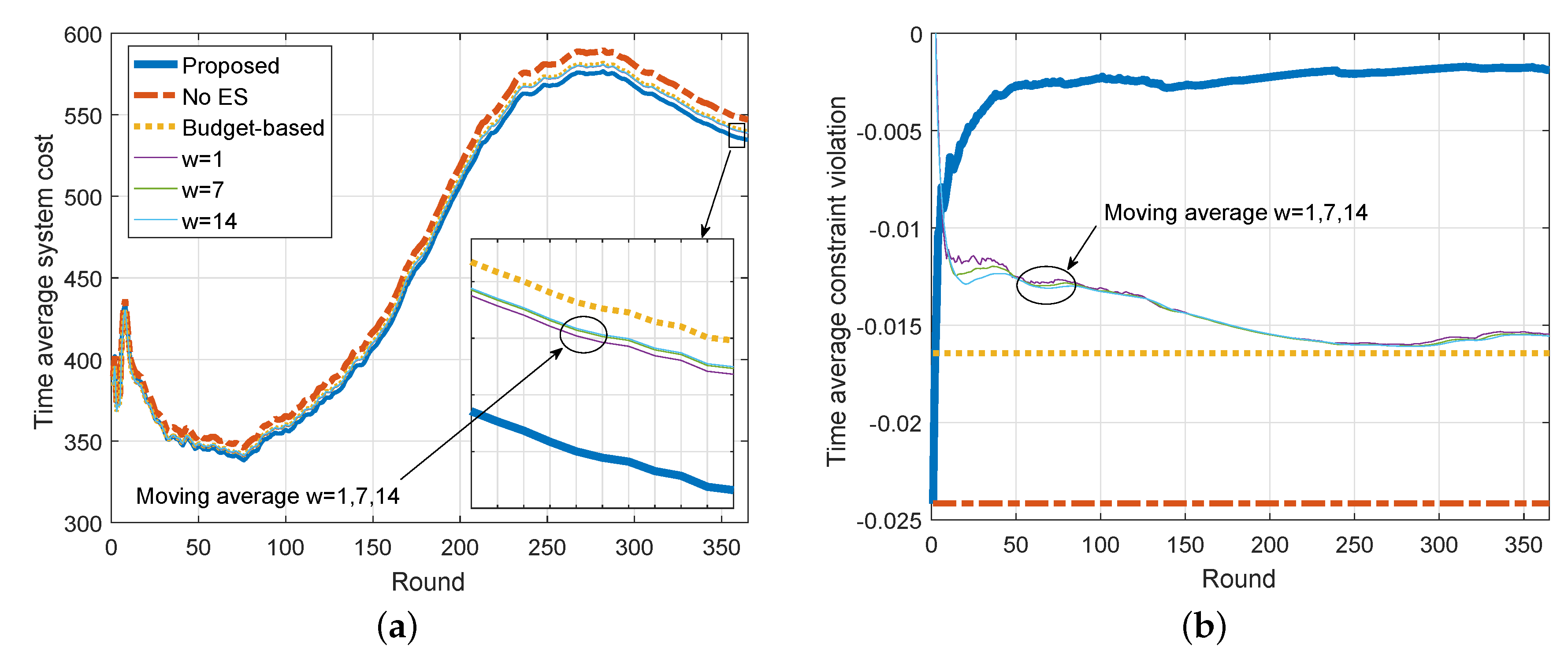
- No ES: In the case of no shared ES, users have to buy electricity from the grid to meet their immediate demands.
- Budget-based: This is a fixed ES capacity allocation approach based on users’ budgets. The amount of capacity allocated to user i for peak period j is given bywhere is the length of peak period j. Note that for each user i, we have which indicates that each user is budget-balanced.
- Moving Average: This is a time-variant ES capacity allocation approach based on moving average [35]. This approach is parameterized by a time window w. The allocation decision for round t will be determined based on the average peak loads from round to round .DefineThe amount of capacity allocated to user i for peak period j for round t is given byNote that users’ budgets are not considered in this approach, so budget balance may not be guaranteed.
5.2. ES Capacity Allocation Performance
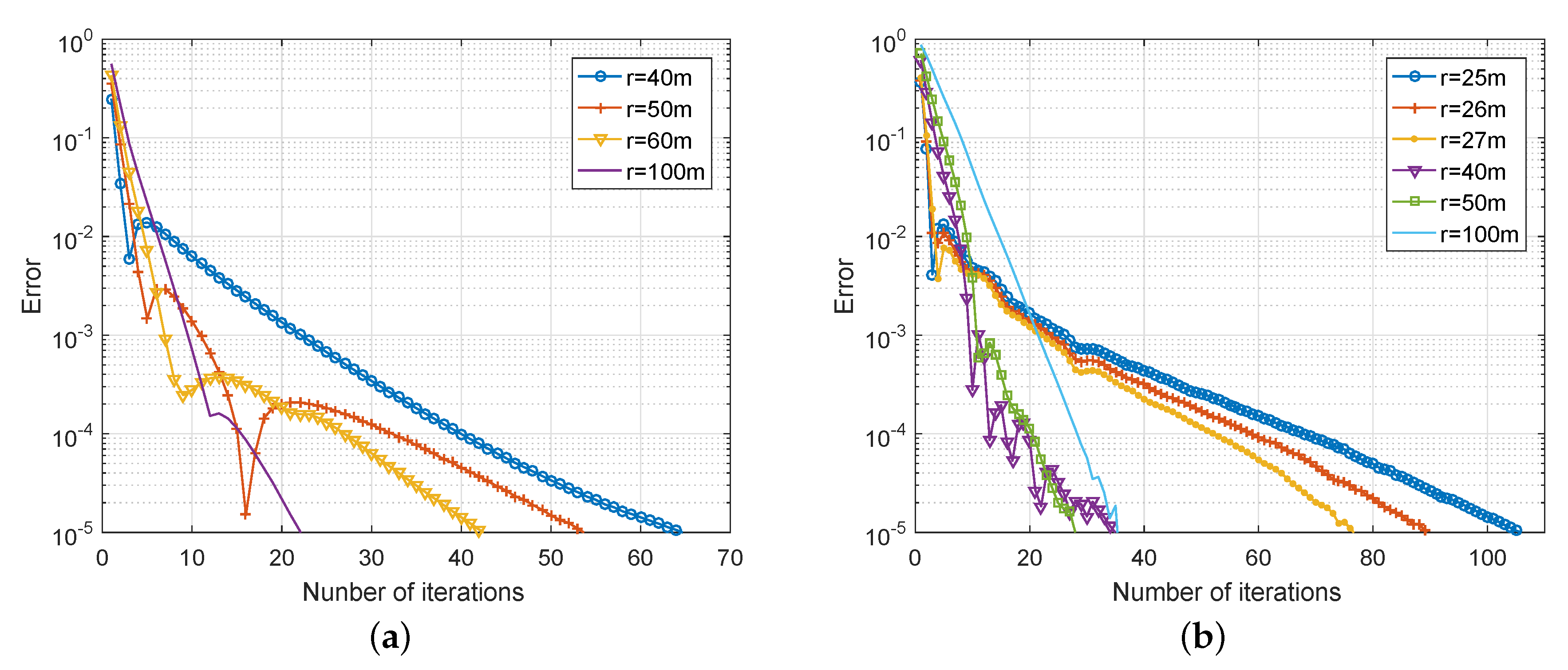
5.3. Convergence Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ES | Energy storage |
| TOU | Time of use |
| ADMM | Alternating direction method of multipliers |
| P2P | Peer-to-peer |
References
- NIST Framework and Roadmap for Smart Grid Interoperability Standards, Release 3.0. Available online: http://dx.doi.org/10.6028/NIST.SP.1108r3 (accessed on 20 December 2018).
- Liu, Y.; Yang, C.; Jiang, L.; Xie, S.; Zhang, Y. Intelligent edge computing for IoT-based energy management in smart cities. IEEE Netw. 2019, 33, 111–117. [Google Scholar] [CrossRef]
- Guo, Y.; Pan, M.; Fang, Y. Optimal power management of residential customers in the smart grid. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1593–1606. [Google Scholar] [CrossRef]
- Yang, C.; Lou, W.; Yao, J.; Xie, S. On charging scheduling optimization for a wirelessly charged electric bus system. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1814–1826. [Google Scholar] [CrossRef]
- Sun, S.; Dong, M.; Liang, B. Distributed real-time power balancing in renewable-integrated power grids with storage and flexible loads. IEEE Trans. Smart Grid 2016, 7, 2337–2349. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, R.; Xie, S.; Zhang, Y.; Yau, D.K.Y. On Stability and Robustness of Demand Response in V2G Mobile Energy Networks. IEEE Trans. Smart Grid 2018, 9, 3203–3212. [Google Scholar] [CrossRef]
- Li, N.; Hedman, K.W. Economic assessment of energy storage in systems with high levels of renewable resources. IEEE Trans. Sustain. Energy 2015, 6, 1103–1111. [Google Scholar] [CrossRef]
- Yang, C.; Yao, J.; Lou, W.; Xie, S. On demand response management performance optimization for microgrids under imperfect communication constraints. IEEE Internet Things J. 2017, 4, 881–893. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, C.; Li, F.; Bale, P.; Sun, H. Active demand response using shared energy storage for household energy management. IEEE Trans. Smart Grid 2013, 4, 1888–1897. [Google Scholar] [CrossRef]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The sharing economy for the electricity storage. IEEE Trans. Smart Grid 2018, 10, 556–567. [Google Scholar] [CrossRef]
- Rahbar, K.; Moghadam, M.R.V.; Panda, S.K.; Reindl, T. Shared energy storage management for renewable energy integration in smart grid. In Proceedings of the 2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Rahbar, K.; Moghadam, M.R.V.; Panda, S.K.; Reindl, T. Energy management for demand responsive users with shared energy storage system. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, NSW, Australia, 6–9 November 2016; pp. 290–295. [Google Scholar]
- Paridari, K.; Parisio, A.; Sandberg, H.; Johansson, K.H. Demand response for aggregated residential consumers with energy storage sharing. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 2024–2030. [Google Scholar]
- Zhao, D.; Wang, H.; Huang, J.; Lin, X. Pricing-based energy storage sharing and virtual capacity allocation. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Dimitrov, P.; Piroddi, L.; Prandini, M. Distributed allocation of a shared energy storage system in a microgrid. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3551–3556. [Google Scholar]
- Chakraborty, P.; Baeyens, E.; Poolla, K.; Khargonekar, P.P.; Varaiya, P. Sharing storage in a smart grid: A coalitional game approach. IEEE Trans. Smart Grid (Early Access) 2018. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S. Online learning and online convex optimization. Found. Trends Mach. Learn. 2012, 4, 107–194. [Google Scholar] [CrossRef]
- Yu, H.; Neely, M.J. A low complexity algorithm with regret and finite constraint violations for online convex optimization with long term constraints. arXiv 2016, arXiv:1604.02218. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Dataport. Available online: https://www.dataport.cloud/ (accessed on 15 December 2018).
- Pacific Gas & Electric - Tariffs. Available online: https://www.pge.com/tariffs/electric.shtml#RESELEC_TOU/ (accessed on 15 December 2018).
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable Demand Response Management in the Smart Grid: A Stackelberg Game Approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, X.; Qian, L.; Tsang, D.H.K.; Song, W.; Yu, L. Optimal pricing and energy scheduling for hybrid energy trading market in future smart grid. IEEE Trans. Ind. Inform. 2015, 11, 1585–1596. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S. Topology-aware vehicle-to-grid energy trading for active distribution systems. IEEE Trans. Smart Grid 2019, 10, 2137–2147. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S. Auction Mechanisms for Energy Trading in Multi-Energy Systems. IEEE Trans. Ind. Informat. 2018, 14, 1511–1521. [Google Scholar] [CrossRef]
- Tsai, S.; Tseng, Y.; Chang, T. Communication-efficient distributed demand response: A randomized ADMM approach. IEEE Trans. Smart Grid 2017, 8, 1085–1095. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, R.; Pan, M.; Zhang, Y.; Xie, S. SD-MAC: Spectrum database-driven MAC protocol for cognitive machine-to-machine networks. IEEE Trans. Veh. Technol. 2017, 66, 1456–1467. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Xie, S.; Chen, W.; Liu, K. Credit-based payments for fast computing resource trading in edge-assisted internet of things. IEEE Internet Things J. (Early Access) 2019. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Yang, C.; Liu, Y.; Chen, X.; Zhong, W.; Xie, S. Efficient mobility-aware task offloading for vehicular edge computing networks. IEEE Access 2019, 7, 26652–26664. [Google Scholar] [CrossRef]
- Zhong, W.; Yang, C.; Xie, K.; Xie, S.; Zhang, Y. ADMM-based distributed auction mechanism for energy hub scheduling in smart buildings. IEEE Access 2018, 6, 45635–45645. [Google Scholar] [CrossRef]
- Mateos, G.; Bazerque, J.A.; Giannakis, G.B. Distributed sparse linear regression. IEEE Trans. Signal Process. 2010, 58, 5262–5276. [Google Scholar] [CrossRef]
- Bertsekas, D.; Nedić, A.; Ozdaglar, A. Convex Analysis and Optimization; Athena Scientific Optimization and Computation Series; Athena Scientific: Belmont, MA, USA, 2003. [Google Scholar]
- Chang, T.; Hong, M.; Wang, X. Multi-agent distributed optimization via inexact consensus ADMM. IEEE Trans. Signal Process. 2015, 63, 482–497. [Google Scholar] [CrossRef]
- Hund, T.D.; Gonzalez, S.; Barrett, K. Grid-tied PV system energy smoothing. In Proceedings of the 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 2762–2766. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, K.; Zhong, W.; Li, W.; Zhu, Y. Distributed Capacity Allocation of Shared Energy Storage Using Online Convex Optimization. Energies 2019, 12, 1642. https://doi.org/10.3390/en12091642
Xie K, Zhong W, Li W, Zhu Y. Distributed Capacity Allocation of Shared Energy Storage Using Online Convex Optimization. Energies. 2019; 12(9):1642. https://doi.org/10.3390/en12091642
Chicago/Turabian StyleXie, Kan, Weifeng Zhong, Weijun Li, and Yinhao Zhu. 2019. "Distributed Capacity Allocation of Shared Energy Storage Using Online Convex Optimization" Energies 12, no. 9: 1642. https://doi.org/10.3390/en12091642
APA StyleXie, K., Zhong, W., Li, W., & Zhu, Y. (2019). Distributed Capacity Allocation of Shared Energy Storage Using Online Convex Optimization. Energies, 12(9), 1642. https://doi.org/10.3390/en12091642




