Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors
Abstract
1. Introduction
2. Methods
2.1. Mathematical Model
2.1.1. Governing Equations
2.1.2. Constitutive Equation for the Stress Tensor
“Under the term gels may be understood fluid-containing systems of various compositions (fluid-fluid, solid -fluid, fluid-solid), and various but usually colloidal, degrees of dispersion. The gels, which are formed from a fluid, are distinguished purely superficially by a change in the mechanics properties of the original system, namely by a transition into a state which has much in common with the solid state of aggregation: high viscosity, elasticity, proportional limit and yield stress.”
2.1.3. Expanded form of the Governing Equations
3. Experimental Setup
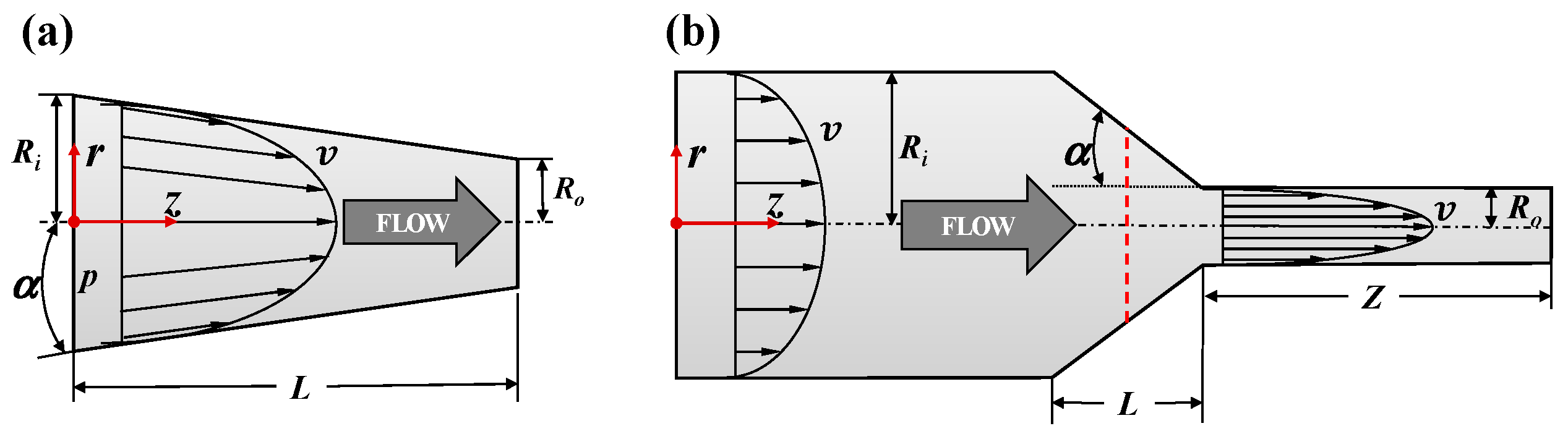
4. Problem Description
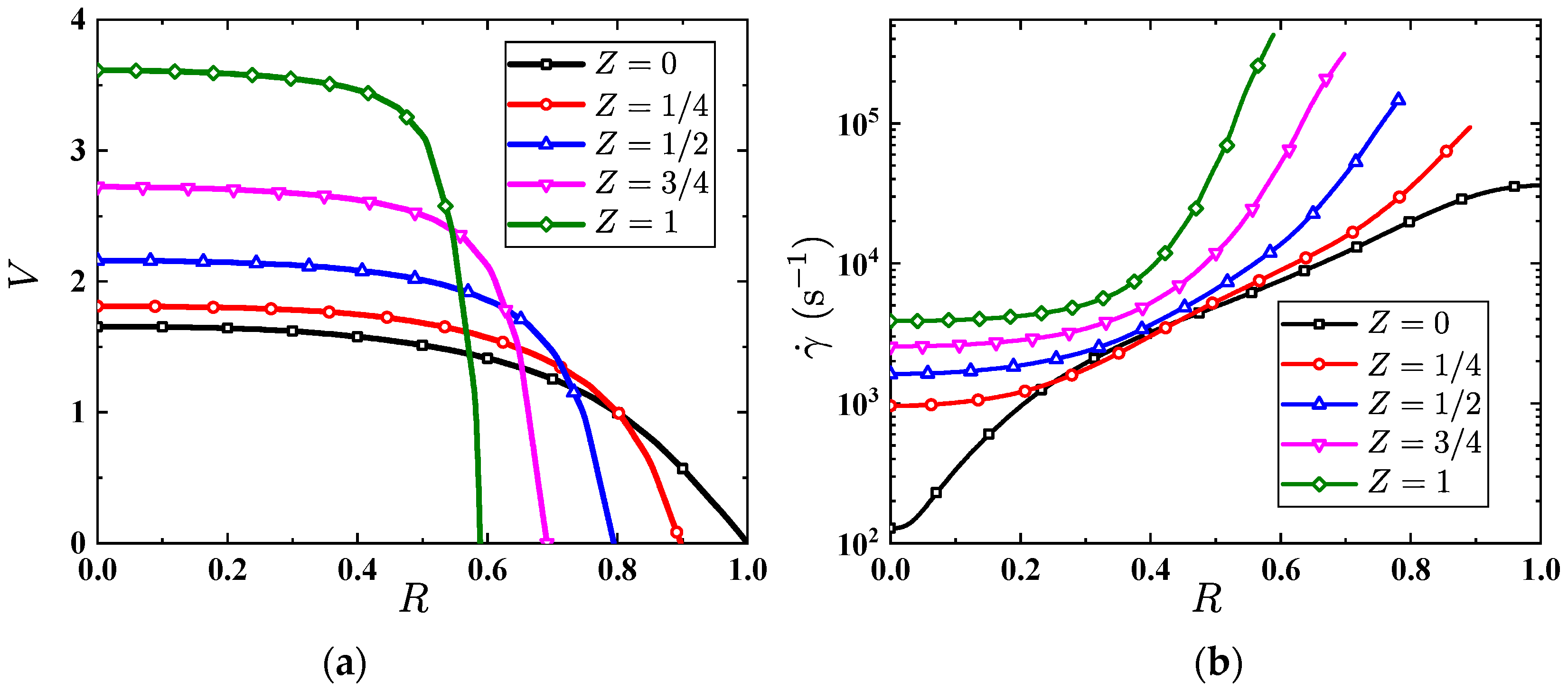
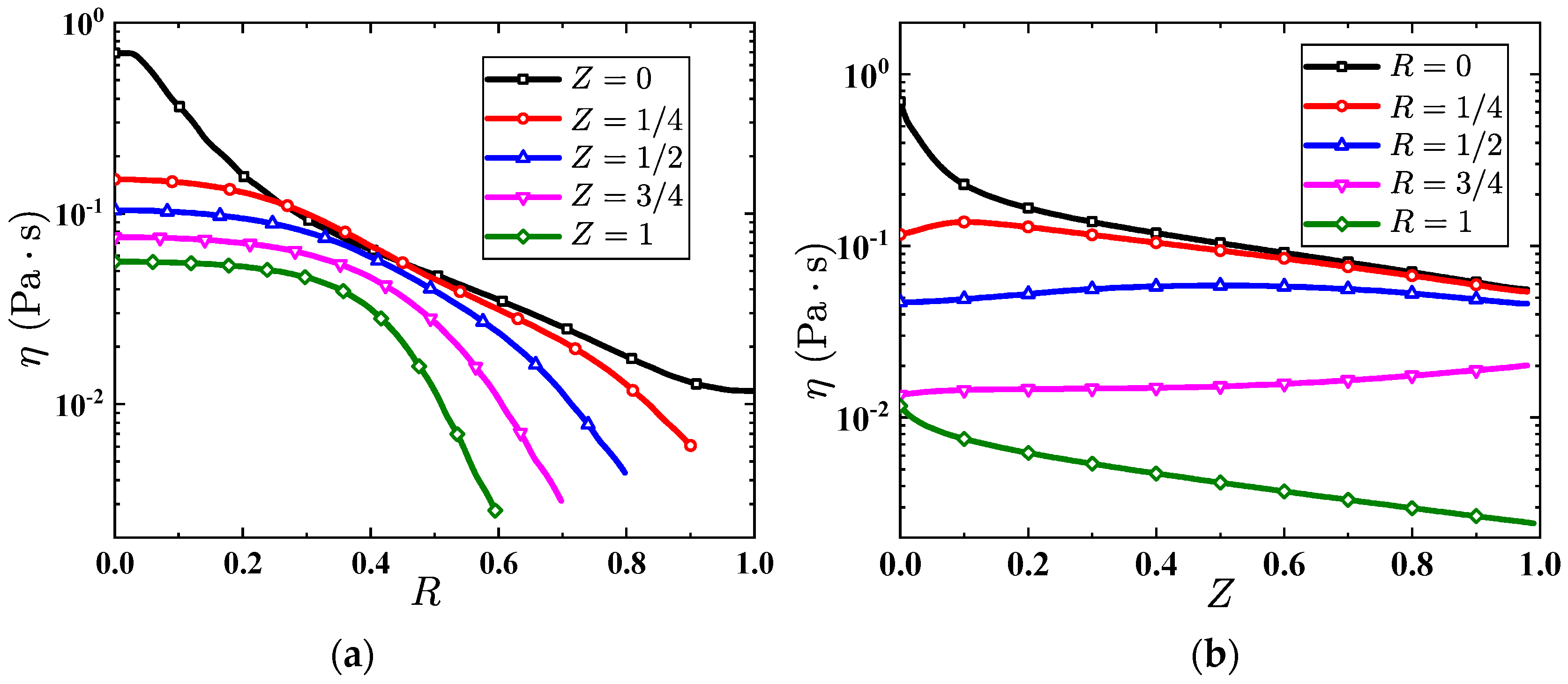
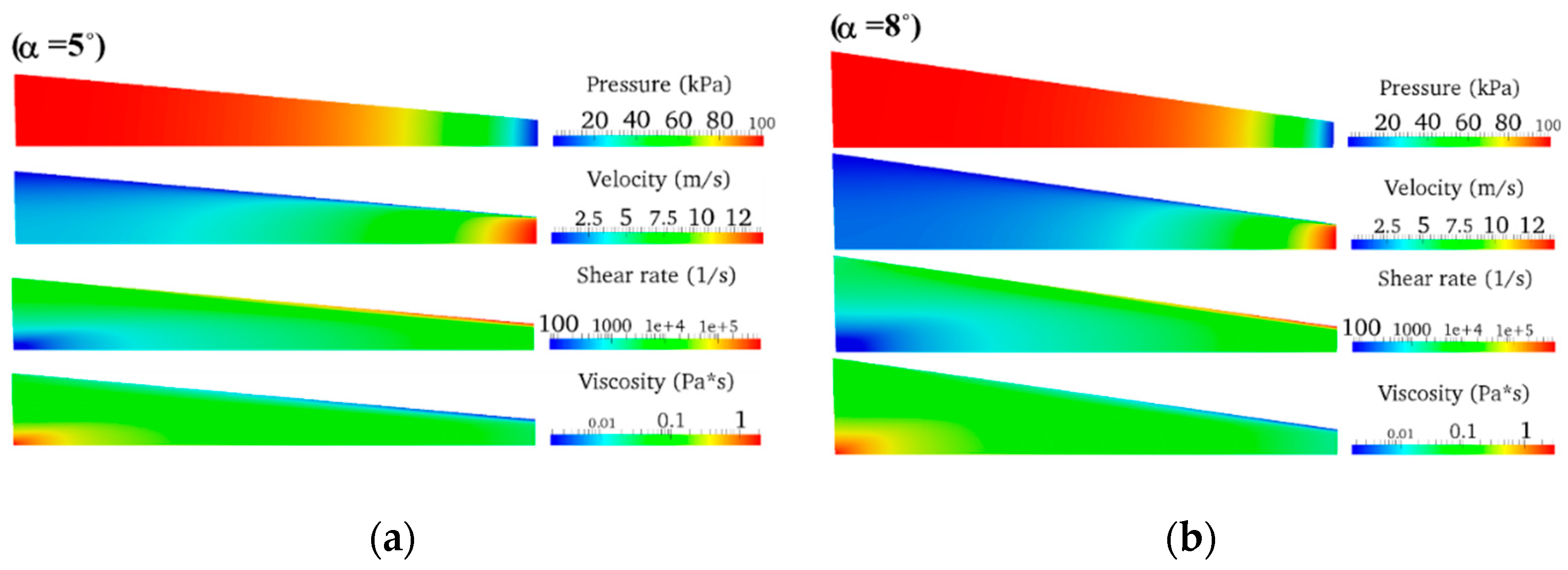
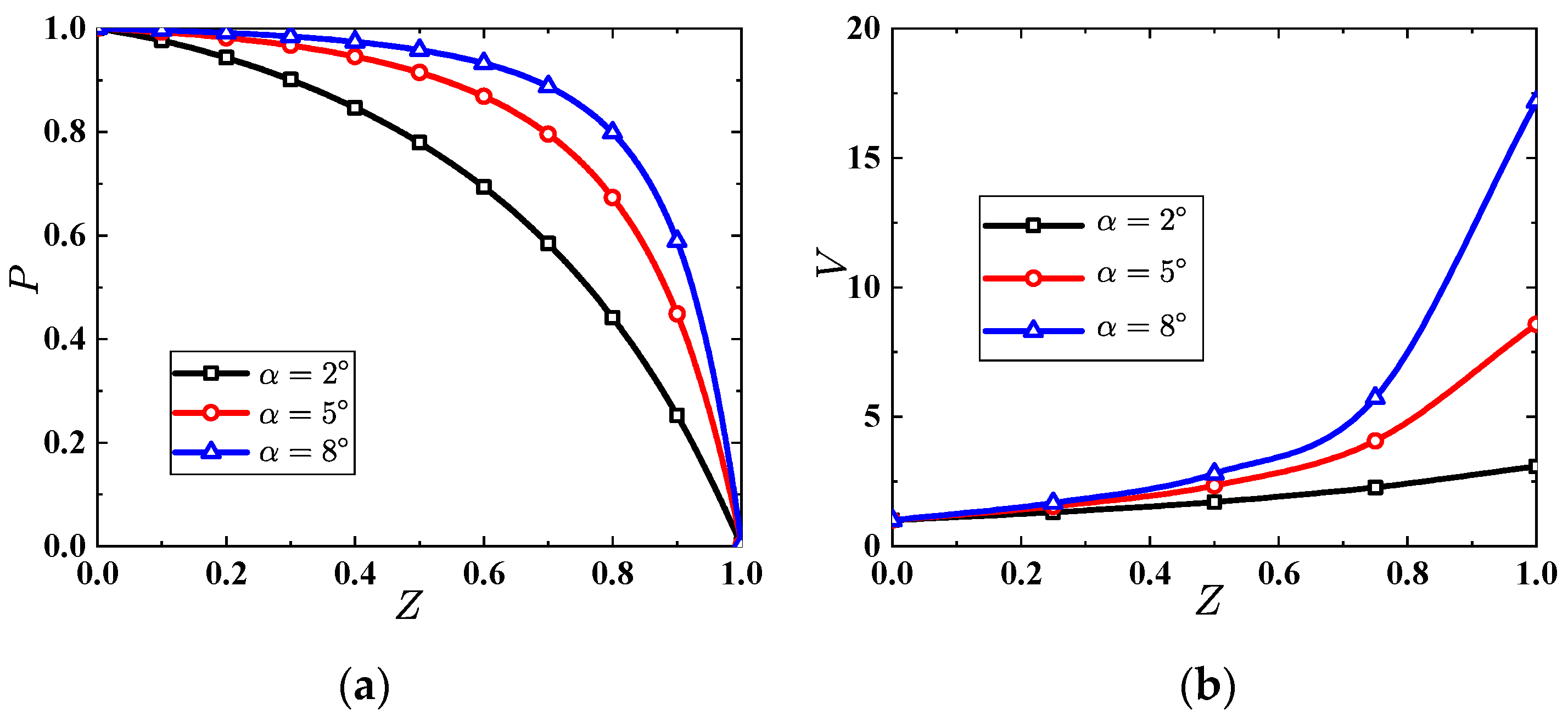
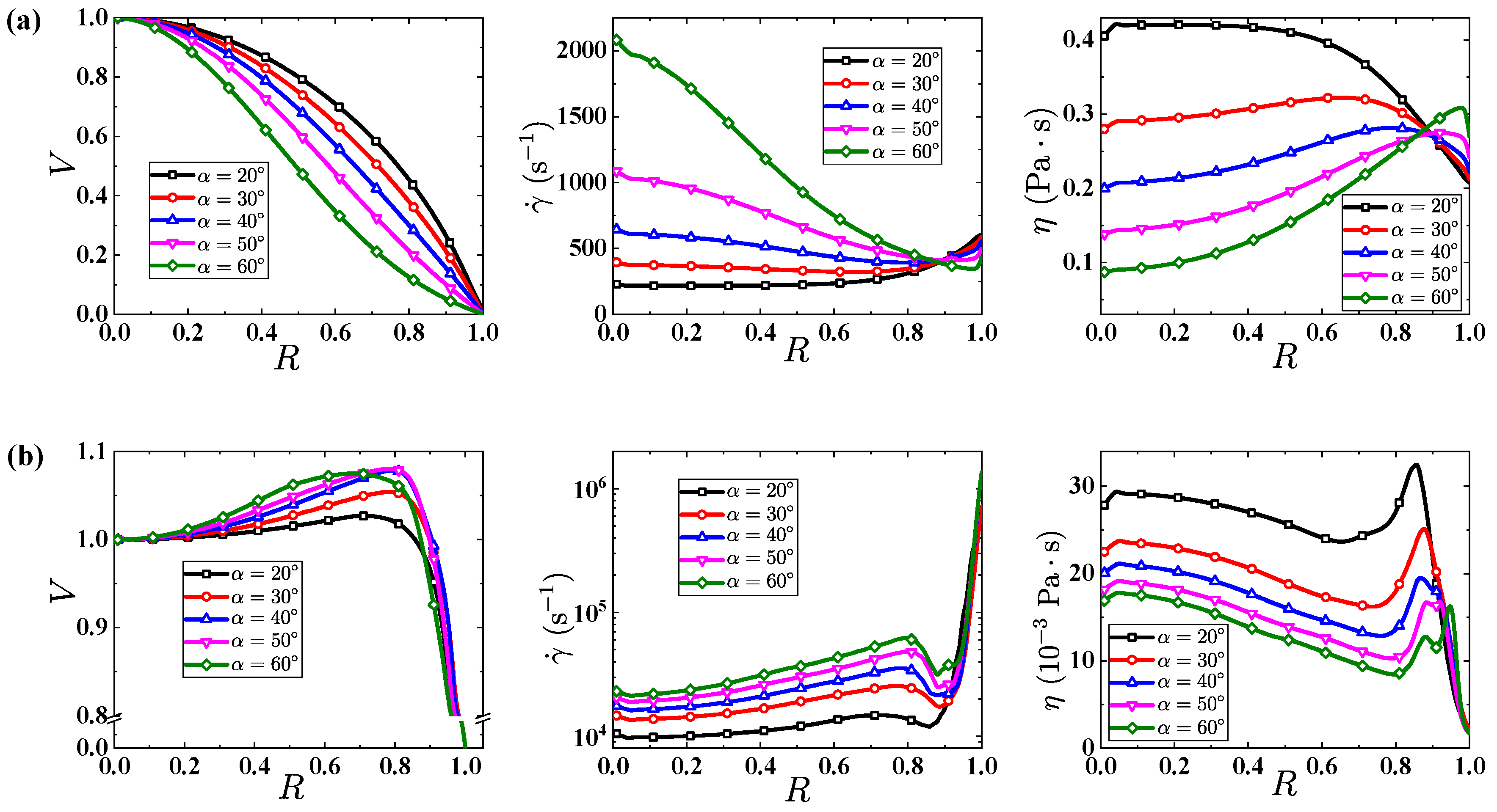
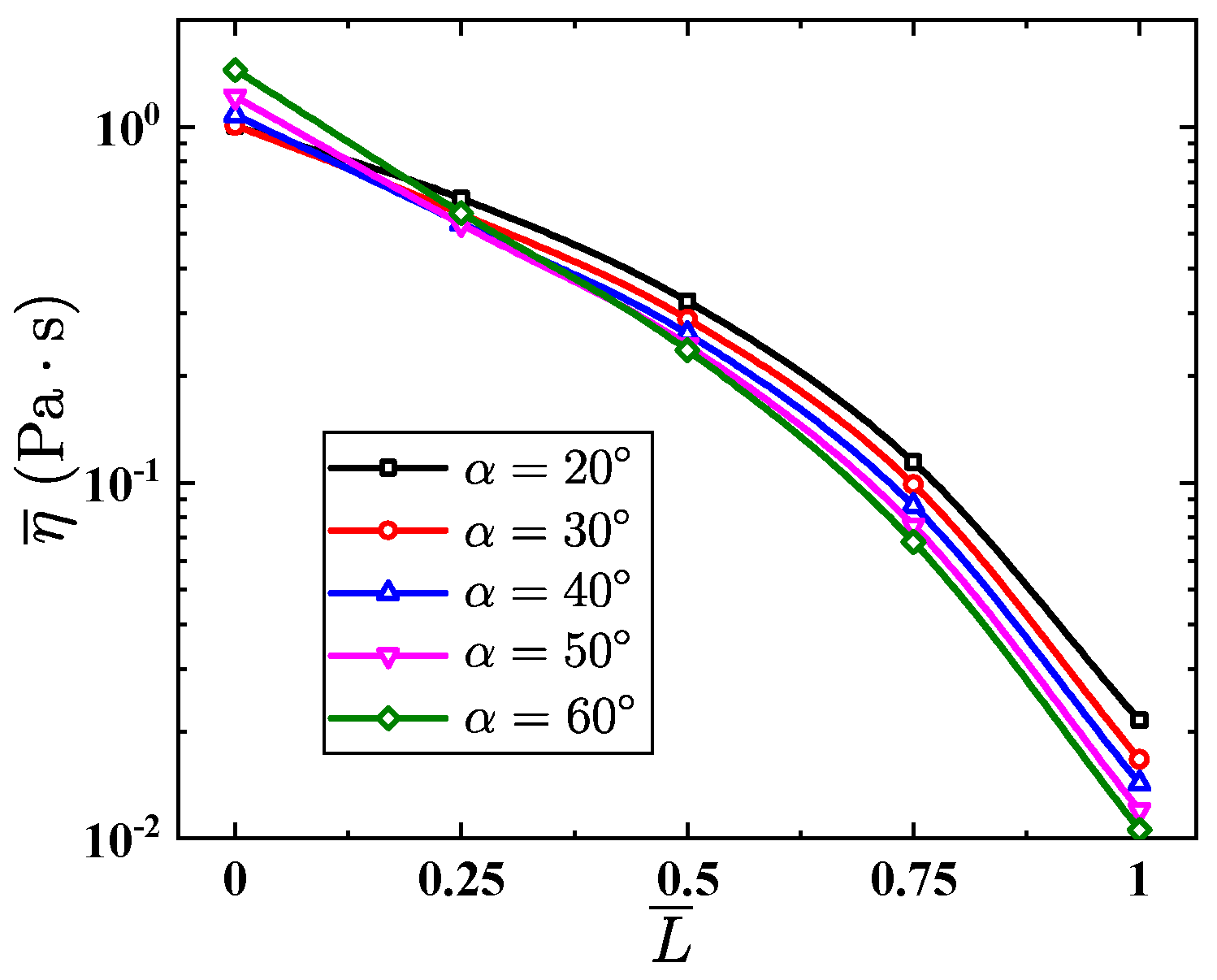
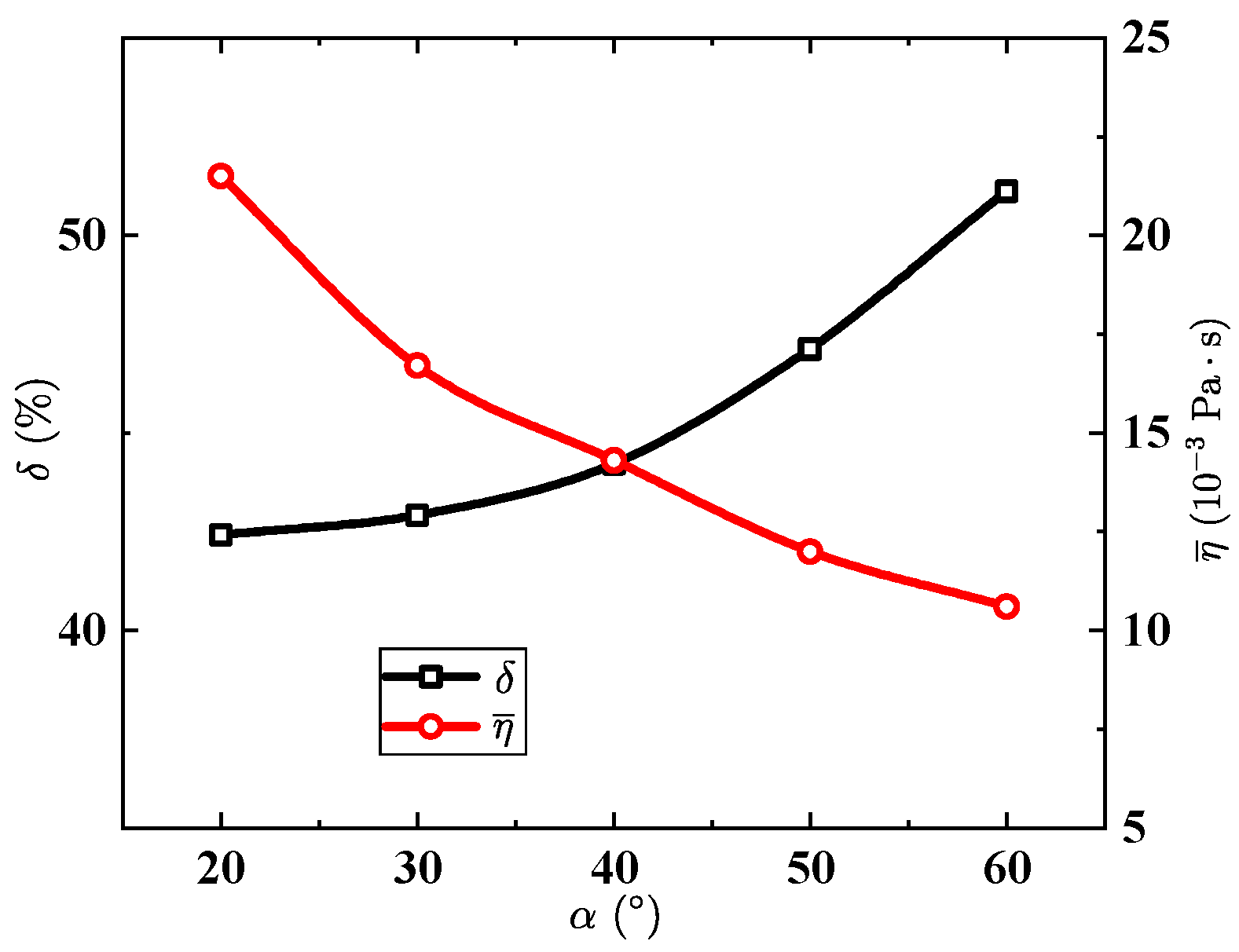
5. Results and Discussion
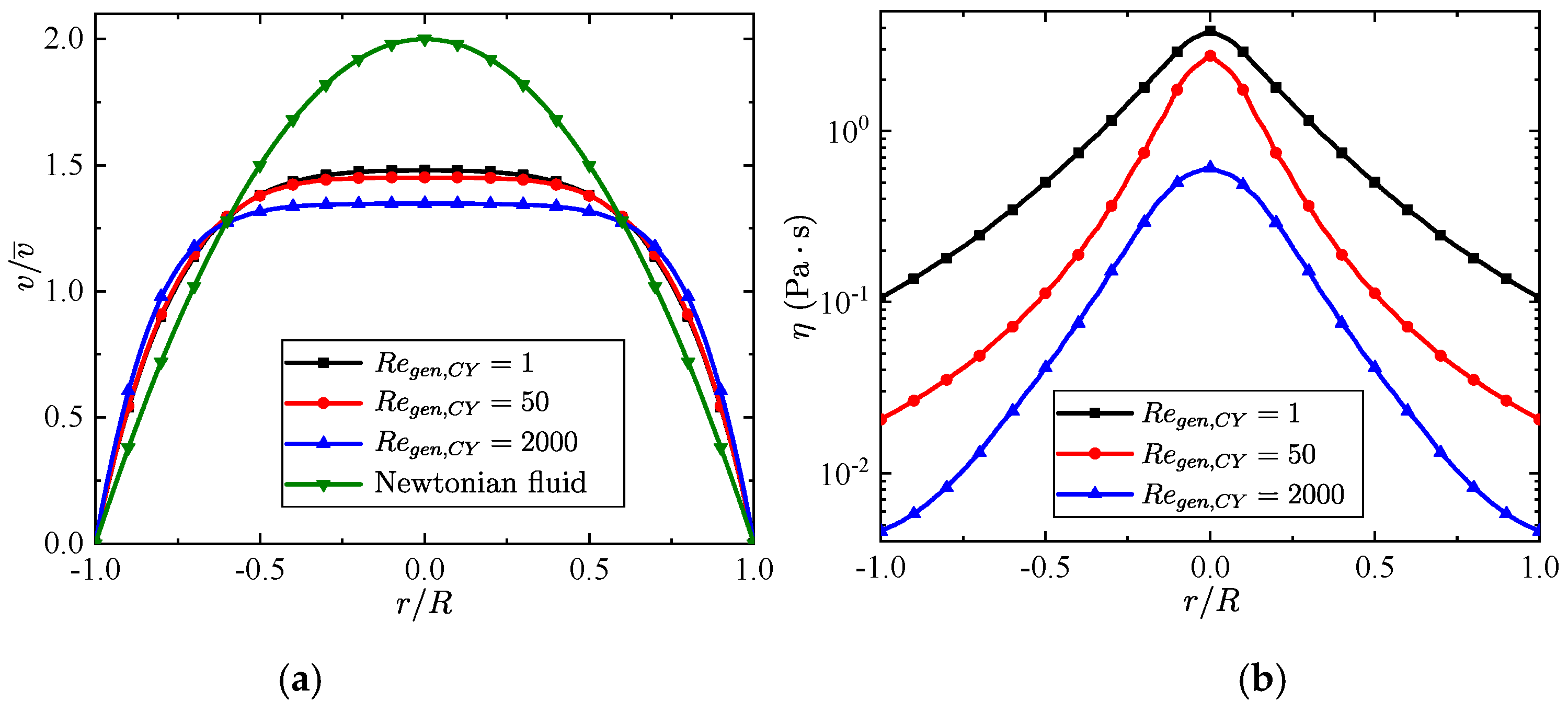
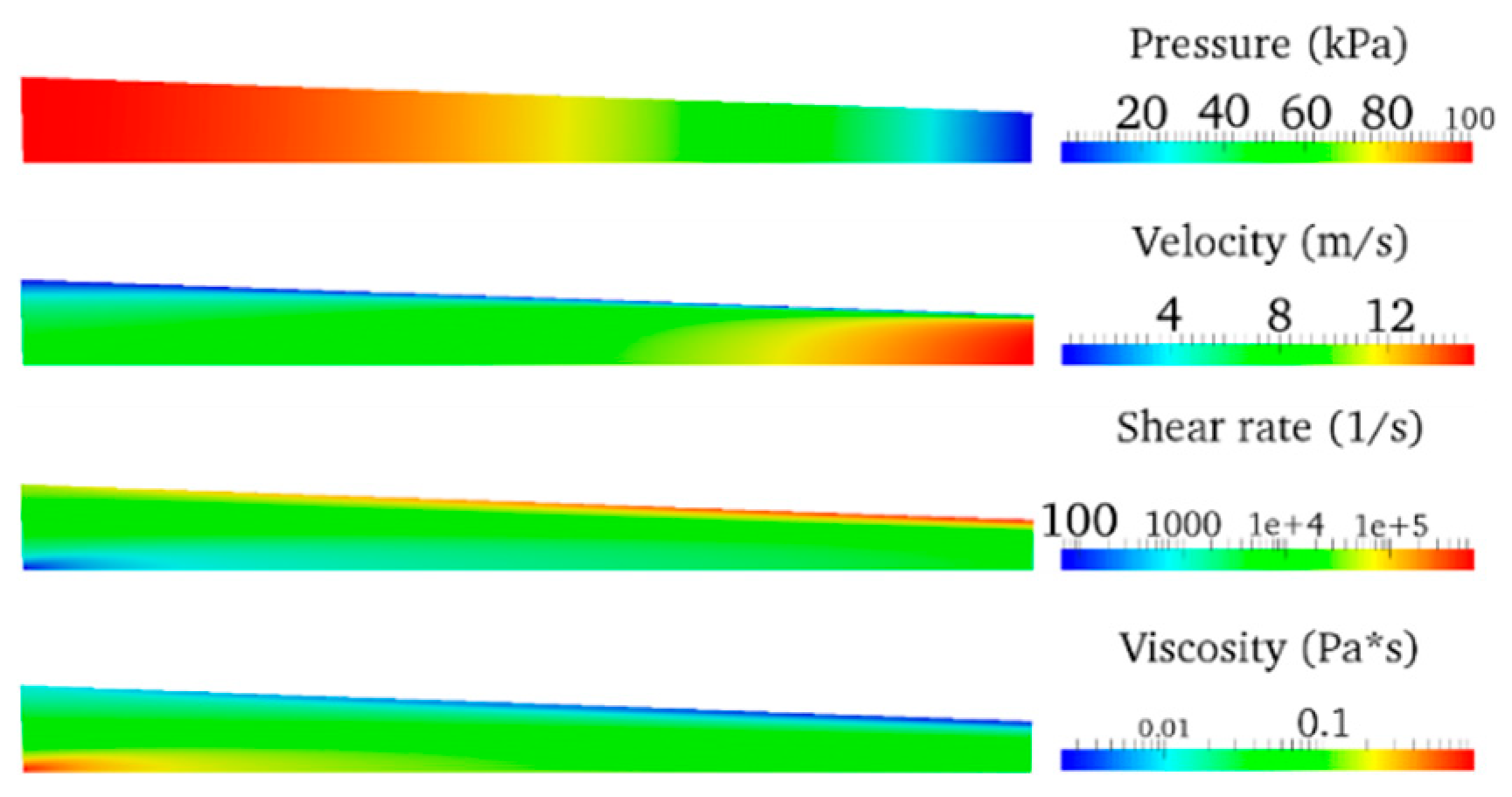
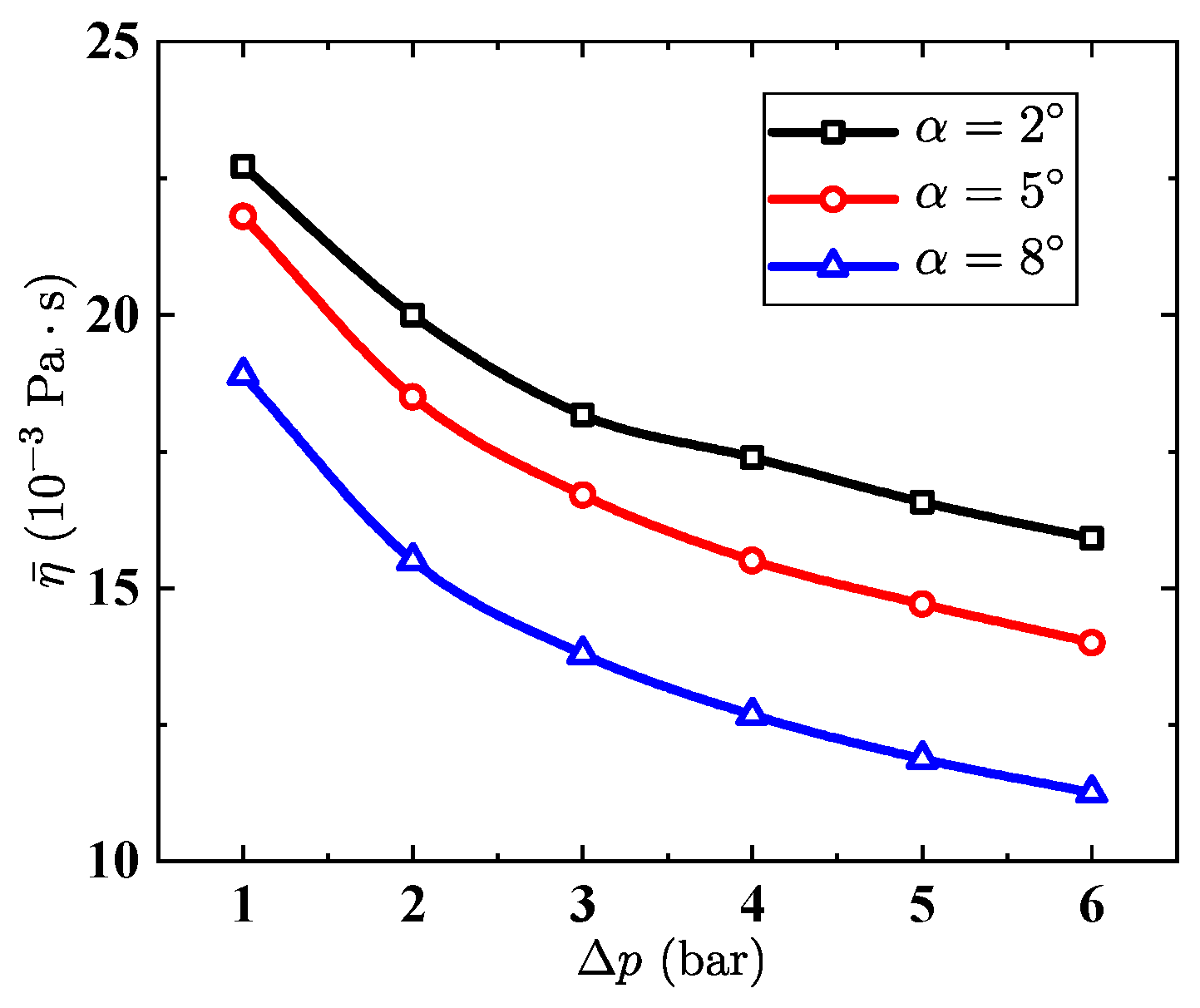
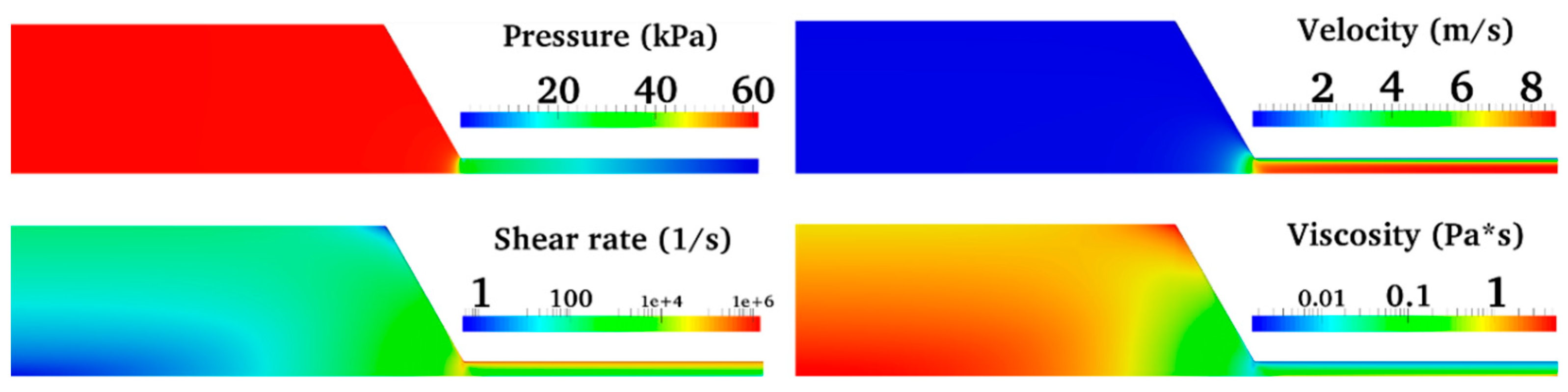
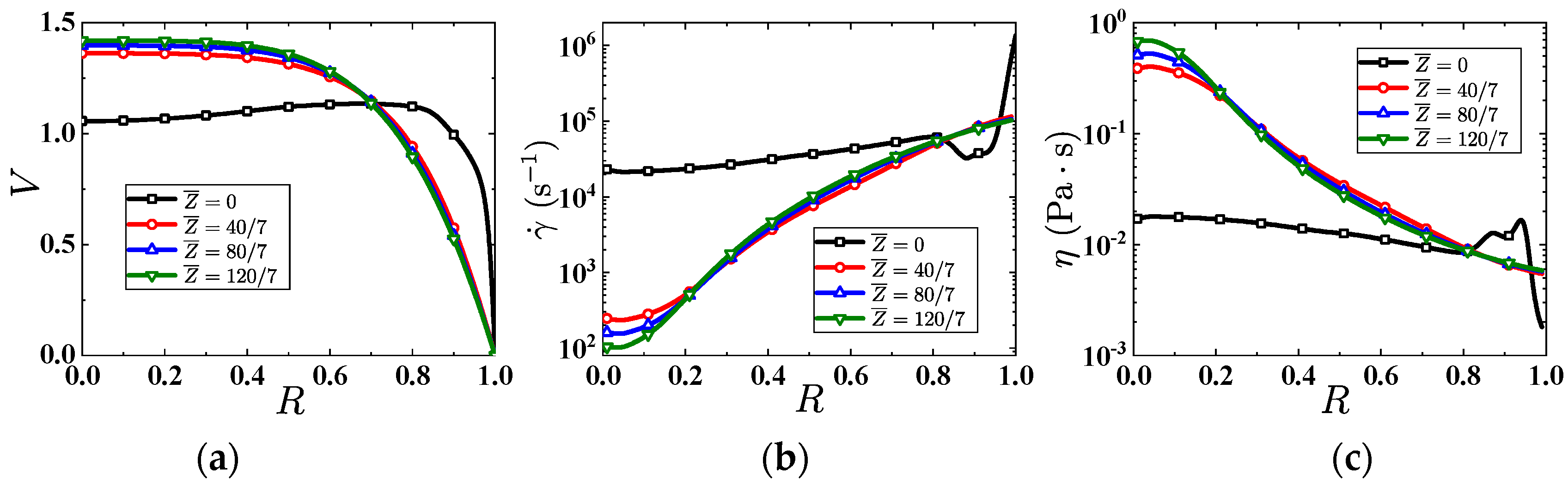
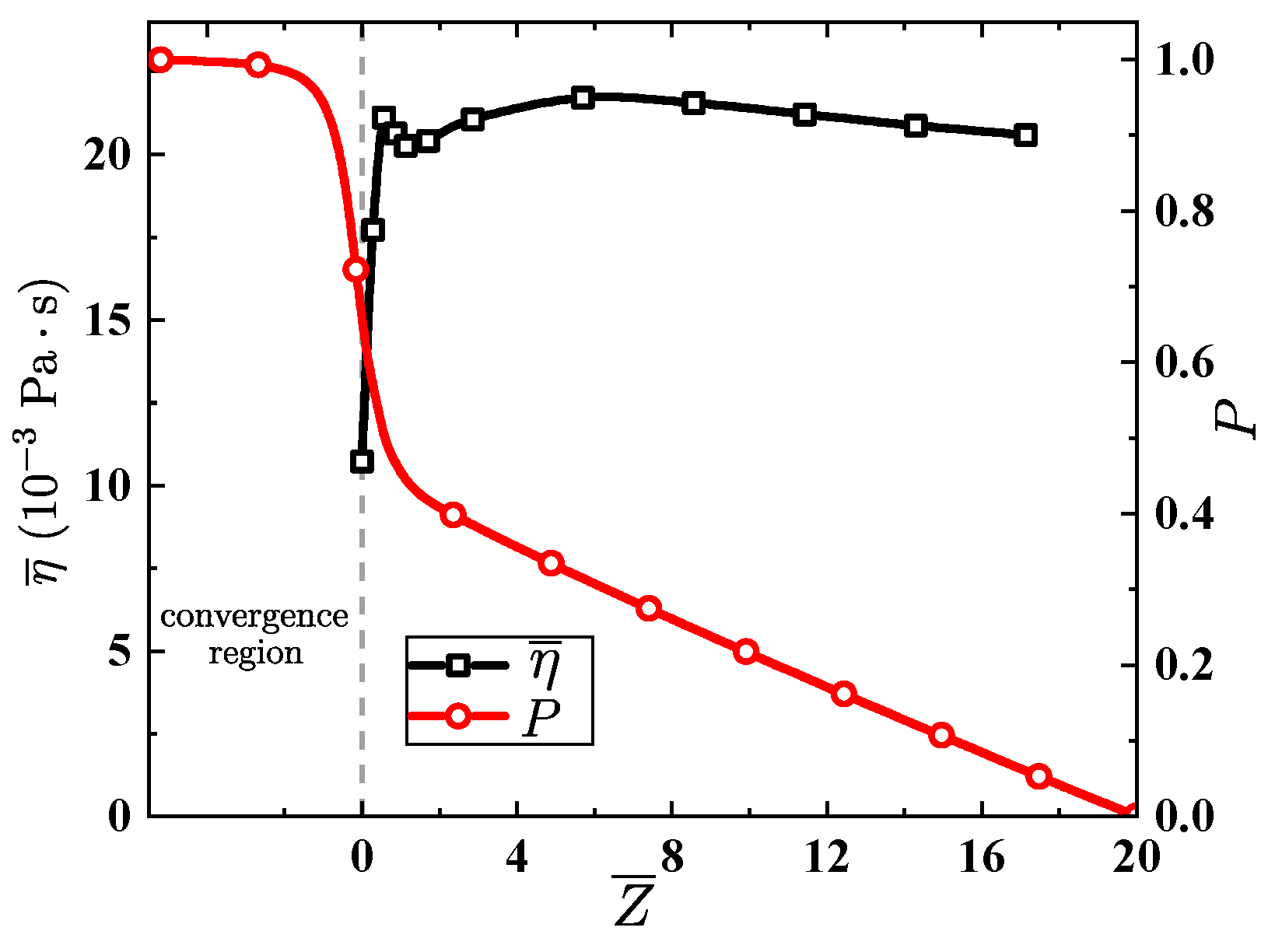
5.1. Converging Tube
5.2. Tapered Injectors
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ferry, J.D.; Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Natan, B.; Rahimi, S. The status of gel propellants in year 2000. Int. J. Energ. Mater. Chem. Propuls. 2009, 5, 172–194. [Google Scholar] [CrossRef]
- Arnold, R.; Anderson, W. Droplet burning of JP-8/Silica gels. In Proceedings of the 48th 2010 AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 1–12. [Google Scholar]
- Yang, L.J.; Fu, Q.F.; Qu, Y.Y.; Zhang, W.; Du, M.L.; Xu, B.R. Spray characteristics of gelled propellants in swirl injectors. Fuel 2012, 97, 253–261. [Google Scholar] [CrossRef]
- Nahamoni, G.; Natan, B.; Nahamoni, G.; Natan, B. Investigation of the combustion process of gel propellants. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; p. 2973. [Google Scholar]
- Ciezki, H.K.; Naumann, K.W.; Weiser, V. Status of Gel Propulsion in the Year 2010 with a Special View on the German Activities. In Proceedings of the 2010 Deutschen Luft-und Raumfahrtkongress, Hamburg, Germany, 31 Agust–2 September 2010. [Google Scholar]
- Ciezki, H.K.; Negri, M.; Weiser, V.; Naumann, K.W.; Program, P.T.; Program, T.; Grund, L.; Heterogenious, H.; Group, S.; Grund, L.; et al. Overview of the German Gel Propulsion Technology. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; pp. 1–16. [Google Scholar]
- Rahimi, S.; Hasan, D.; Peretz, A. Development of Laboratory-Scale Gel Propulsion Technology. J. Propuls. Power 2008, 20, 93–100. [Google Scholar] [CrossRef]
- Naumann, K.W.; Ramsel, J.; Pinto, P.C.; Niedermaier, H.; Thumann, A. Gelled Green Propellant Rocket Motor and Gas Generator Technology at Bayern-Chemie-Status and Applications for Space Systems. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3796. [Google Scholar]
- Kubal, T.; Arnold, R.; Pourpoint, T.; Campanella, O.; Anderson, W. Rheological Characterization of Hydroxypropylcellulose/Monomethylhydrazine and\r\nSilica/Red Fuming Nitric Acid Gels. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010; p. 7140. [Google Scholar]
- Mishra, D.P.; Patyal, A.; Padhwal, M. Effects of gellant concentration on the burning and flame structure of organic gel propellant droplets. Fuel 2011, 90, 1805–1810. [Google Scholar] [CrossRef]
- Gafni, G.; Kuznetsov, A.; Har-Lev, D.; Natan, B. Experimental Investigation of a Ramjet Combustor Using an Aluminized Gel Fuel. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; p. 3748. [Google Scholar]
- Matsibeker, E.; Natan, B. Numerical Solution of the Flowfield in an Aluminized Gel Fuel Ramjet. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint PropulsionConference, San Jose, CA, USA, 14–17 July 2013; p. 3976. [Google Scholar]
- Natan, B.; Haddad, A.; Arieli, R. Performance assessments of a boron containing gel fuel ramjet. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 1421. [Google Scholar]
- Wu, W.-T.; Yang, F.; Antaki, J.F.; Aubry, N.; Massoudi, M. Study of blood flow in several benchmark micro-channels using a two-fluid approach. Int. J. Eng. Sci. 2015, 95, 49–59. [Google Scholar] [CrossRef]
- Wu, W.-T.; Zhou, Z.-F.; Aubry, N.; Antaki, J.F.; Massoudi, M. Heat transfer and flow of a dense suspension between two cylinders. Int. J. Heat Mass Transf. 2017, 112, 597–606. [Google Scholar] [CrossRef]
- Yan, C.; Altunbas, A.; Yucel, T.; Nagarkar, R.P.; Schneider, J.P.; Pochan, D.J. Injectable solid hydrogel: Mechanism of shear-thinning and immediate recovery of injectable β-hairpin peptide hydrogels. Soft Matter 2010, 6, 5143–5156. [Google Scholar] [CrossRef] [PubMed]
- Yoon, C.; Heister, S.; Sojka, P.; Watson, C.; Xia, G.; Merkle, C. Injector Flow Characteristics for Gel Propellants. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Doi, M. Explanation for the 3.4-power law for viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Phys. Ed. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4 power law of viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Lett. Ed. 1981, 19, 265–273. [Google Scholar] [CrossRef]
- Krieger, I.M. Rheology of monodisperse latices. Adv. Colloid Interface Sci. 1972, 3, 111–136. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B. Numerical solution of the flow of power-law gel propellants in converging injectors. Propellants Explos. Pyrotech. 2000, 25, 203–212. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B.; Rahimi, S.; Natan, B. The injection process of gel fuels. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; p. 2972. [Google Scholar]
- Rahimi, S.; Natan, B. Flow of gel fuels in tapered injectors. J. Propuls. Power 2000, 16, 458–464. [Google Scholar] [CrossRef]
- Yoon, C.; Heister, S.D.; Xia, G.; Merkle, C.L. Numerical modeling of injection of shear-thinning gel propellants through plain-orifice atomizer. J. Propuls. Power 2011, 27, 944–954. [Google Scholar]
- Beg, O.A.; Motsa, S.S.; Islam, M.N.; Lockwood, M. Pseudo-spectral and variational iteration simulation of exothermically-reacting Rivlin-Ericksen viscoelastic flow and heat transfer in a rocket propulsion duct. Comput. Therm. Sci. Int. J. 2014, 6, 91–102. [Google Scholar] [CrossRef]
- Chernov, V.; Natan, B. Estimation of the rheological properties of a suspension in a gel fluid. AIAA J. 2013, 51, 998–1003. [Google Scholar] [CrossRef]
- Yoon, C.; Heister, S.D.; Campanella, O.H. Modeling gelled fluid flow with thixotropy and rheological hysteresis effects. Fuel 2014, 128, 467–475. [Google Scholar] [CrossRef]
- Von Kampen, J.; Madlener, K.; Ciezki, H.K. Characteristic Flow and Spray Properties of Gelled Fuels. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Yoon, C.; Heister, S.D.; Merkle, C.L.; Xia, G. Simulations of Plain-Orifice Injection of Gelled Propellants Under Manifold Crossflow Conditions. J. Propuls. Power 2012, 29, 136–146. [Google Scholar] [CrossRef]
- Wu, W.T.; Aubry, N.; Massoudi, M. Flow of granular materials modeled as a non-linear fluid. Mech. Res. Commun. 2013, 52, 62–68. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Massoudi, M. Heat transfer in complex fluids. In Two Phase Flow, Phase Change and Numerical Modeling; INTECH Open Access Publisher: Rijeka, Croatia, 2011. [Google Scholar]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Houwink, R. Elasticity, Plasticity and Structure of Matter, 2nd ed.; Harren Press: Washington, DC, USA, 1953. [Google Scholar]
- Roscoe, R. Suspensions, flow properties of disperse systems. In Flow Properties of Disperse Systems; North. Holl. Publ. Company: Amsterdam, The Netherlands, 1953. [Google Scholar]
- Arnold, R.; Anderson, W.; Santos, P.H.S.; deRidder, M.; Campanella, O.H. Comparison of Monomethylhydrazine/hydroxypropylcellulose and Hydrocarbon/silica Gels. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 422. [Google Scholar]
- Fiordilino, J.; Massoudi, M.; Vaidya, A. On the heat transfer and flow of a non-homogenous fluid. Appl. Math. Comput. 2014, 243, 184–196. [Google Scholar] [CrossRef]
- Wu, W.-T.; Aubry, N.; Antaki, J.F.; McKoy, M.L.; Massoudi, M. Heat Transfer in a Drilling Fluid with Geothermal Applications. Energies 2017, 10, 1349. [Google Scholar] [CrossRef]
- OpenCFD. OpenFOAM Programmer’s Guide Version 2.1.0; OpenCFD, Ed.; Free Software Foundation, Inc.: Boston, MA, USA, 2011. [Google Scholar]

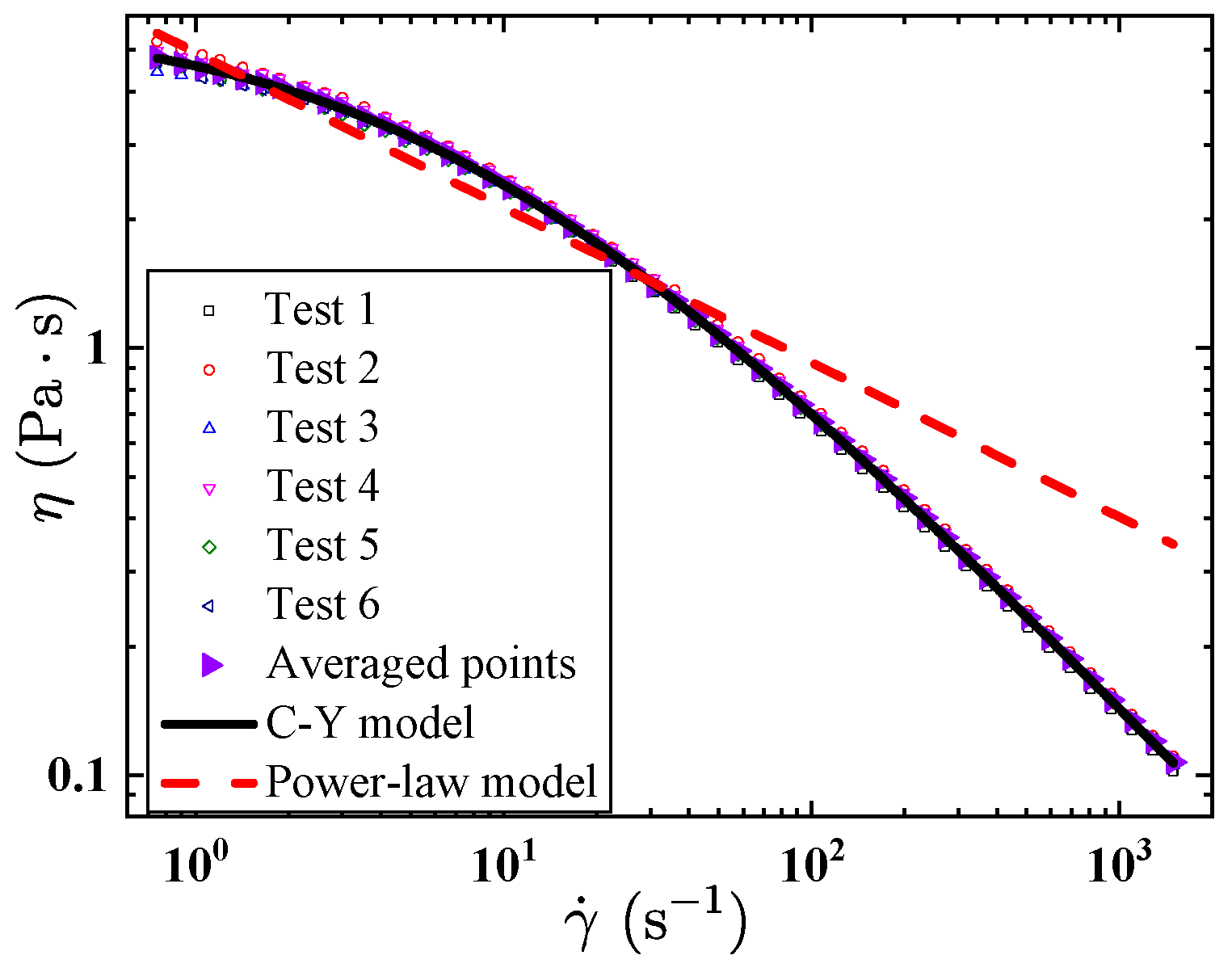

| Fluid Type (Weight-Based) | The Carreau-Yasuda Parameters | ||||
|---|---|---|---|---|---|
| η0, Pa·s | η∞, mPa·s | a | λ | n | |
| Water + 1.5%HPC | 5.882 | 0.895 | 0.692 | 0.149 | 0.267 |
| Geometries | Converging Tube | Tapered Injector |
|---|---|---|
| Convergence angle (, °) | 2, 5, 8 | 20, 30, 40, 50, 60 |
| Boundary Type | Converging Tube | |
| Pressure | Velocity | |
| Wall | Zero gradient | Fixed value (0) |
| Inlet | Fixed value | Zero gradient |
| Outlet | Fixed value | Zero gradient |
| Boundary type | Tapered injector | |
| Pressure | Velocity | |
| Wall | Zero gradient | Fixed value (0) |
| Inlet | Zero gradient | Fixed value |
| Outlet | Fixed value | Zero gradient |
| Label | Grid Number | Mean Velocity at Tube Exit (m/s) | Mean Apparent Viscosity at Tube Exit (Pa·s) |
|---|---|---|---|
| Grid A | 167,029 | 12.38545 | 0.024526 |
| Grid B | 384,569 | 12.42003 | 0.024528 |
| Grid C | 691,509 | 12.35038 | 0.024543 |
| Grid D | 1,087,849 | 12.41336 | 0.024582 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.-L.; Massoudi, M.; Liao, W.-H.; Feng, F.; Wu, W.-T. Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors. Energies 2019, 12, 1643. https://doi.org/10.3390/en12091643
Cao Q-L, Massoudi M, Liao W-H, Feng F, Wu W-T. Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors. Energies. 2019; 12(9):1643. https://doi.org/10.3390/en12091643
Chicago/Turabian StyleCao, Qin-Liu, Mehrdad Massoudi, Wen-He Liao, Feng Feng, and Wei-Tao Wu. 2019. "Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors" Energies 12, no. 9: 1643. https://doi.org/10.3390/en12091643
APA StyleCao, Q.-L., Massoudi, M., Liao, W.-H., Feng, F., & Wu, W.-T. (2019). Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors. Energies, 12(9), 1643. https://doi.org/10.3390/en12091643







