Dynamic Crack Initiation Toughness of Shale under Impact Loading
Abstract
:1. Introduction
2. Methods and Materials
2.1. Sample Preparation
2.2. Test System and Principle
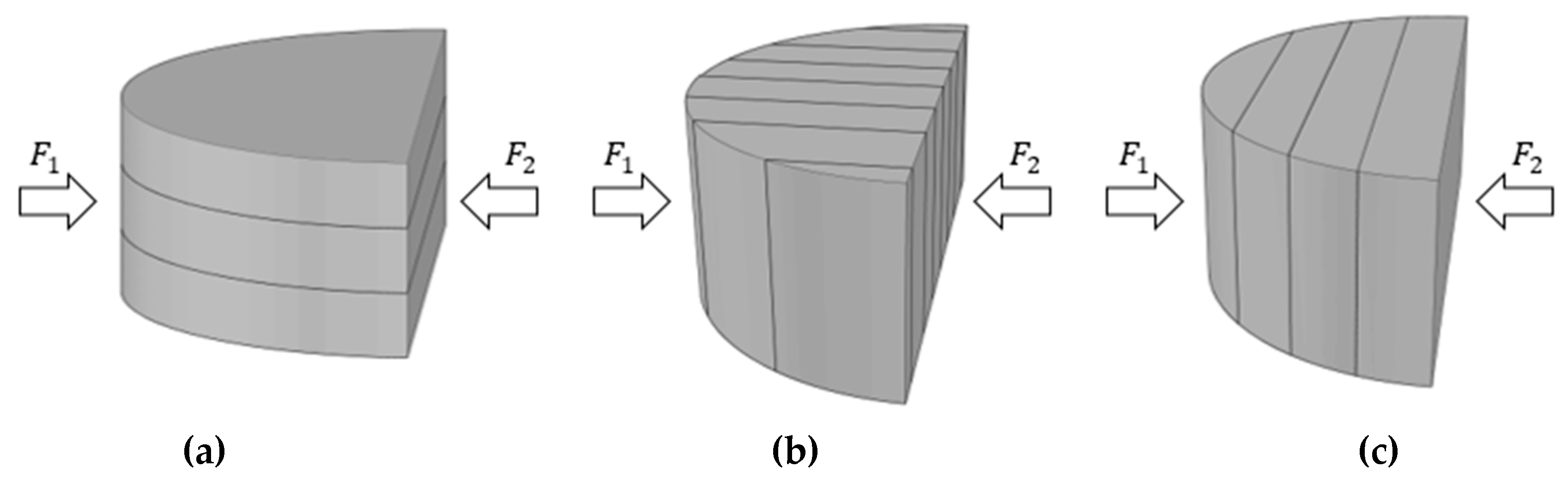
2.3. Loading Method
3. Results and Analysis
3.1. Effect of Bedding on Shale Crack Initiation Toughness
3.2. Shale Fracture Mode
4. Discussion
5. Conclusions
- We studied the influence of bedding plane on dynamic crack initiation toughness of shale. Under the condition of parallel bedding plane loading, the bedding plane had a significant influence on the shale cracking. The shale had the lowest crack initiation toughness under Crack-splitter loading. Compared with the bedding plane and perpendicular loading directions, the shale cracking mainly depended on the strength of the rock mass, so the dynamic crack initiation toughness had a high value.
- We analyzed the effect of the loading rate on shale dynamic crack initiation toughness under three loading modes. The Crack-arrester loading mode had the strongest loading rate correlation and Crack-splitter had the weakest.
- We analyzed the fracture modes of shale under different loading conditions. When loading was carried out using Crack-arrester, the bedding planes can change the crack expansion direction and consume the most energy. The Crack-splitter loading only required a small amount of energy to achieve effective crack expansion.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, Y.K.; Pietruszczak, S. Application of critical plane approach to the prediction of strength anisotropy in transversely isotropic rock masses. Int. J. Rock Mech. Min. Sci. 2008, 45, 513–523. [Google Scholar] [CrossRef]
- Zhao, W.R. Strength properties of anisotropic rock of an argillaceous siltstone. Chin. J. Geotech. Eng. 1984, 1, 32–37. [Google Scholar]
- Mao, H.J.; Yang, C.H. Study on influence of discontinuities on mechanical characters of slate. Chin. J. Rock Mech. Eng. 2005, 20, 53–58. [Google Scholar]
- Gao, C.Y.; Xu, J.; Li, Z.H.; Deng, J.H. Experimental study of anisotropically mechanical characteristics of sandy slate in Xuefeng Mountain Tunnel. Rock Soil Mech. 2011, 32, 1360–1364. [Google Scholar]
- Vernik, L.; Nur, A. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics 1992, 57, 727–735. [Google Scholar] [CrossRef]
- Kuila, U.; Dewhurst, D.N.; Siggins, A.F.; Raven, M.D. Stress anisotropy and velocity anisotropy in low porosity shale. Tectonophysics 2011, 503, 34–44. [Google Scholar] [CrossRef]
- Niandou, H.; Shao, J.F.; Henry, J.P.; Fourmaintraux, D. Laboratory investigation of the mechanical behaviour of Tournemire shale. Int. J. Rock Mech. Min. Sci. 1997, 34, 3–16. [Google Scholar] [CrossRef]
- Li, Q.H.; Chen, M.; Jin, Y. Experimental research on failure modes and mechanical behaviors of gas-bearing shale. Chin. J. Rock Mech. Eng. 2012, 31, 3763–3771. [Google Scholar]
- Hou, P.; Gao, F.; Yang, Y.G.; Zhang, Z.Z.; Gao, Y.N.; Zhang, X.X.; Zhang, J. Effect of bedding plane direction on acoustic emission characteristics of shale in Brazilian tests. Rock Soil Mech. 2016, 37, 1603–1612. [Google Scholar]
- Heng, S.; Yang, C.H.; Guo, Y.T.; Wang, C.Y.; Wang, L. Influence of bedding planes on hydraulic fracture propagation in shale formations. Chin. J. Rock Mech. Eng. 2015, 34, 228–237. [Google Scholar]
- Man, K.; Zhou, H.W. Research on dynamic fracture toughness and tensile strength of rock at different depths. Chin. J. Rock Mech. Eng. 2010, 29, 1657–1663. [Google Scholar]
- Ni, M.; Gou, X.P.; Wang, Q.Z. Test method for rock dynamic fracture toughness using single cleavage drilled compression specimen impacted by split Hopkinson pressure bar. Eng. Mech. 2013, 30, 365–372. [Google Scholar]
- Chen, R.; Xia, K.; Dai, F.; Lu, F.; Luo, S.N. Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing. Eng. Fract. Mech. 2009, 76, 1268–1276. [Google Scholar] [CrossRef]
- Dai, F.; Xia, K. Laboratory measurements of the rate dependence of the fracture toughness anisotropy of Barre granite. Int. J. Rock Mech. Min. Sci. 2013, 60, 57–65. [Google Scholar] [CrossRef]
- Goldsmith, W.; Sackman, J.L.; Ewert, C. Static and dynamic fracture strength of Barre granite. Int. J. Rock Mech. Min. Sci. 1976, 13, 303–309. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Xia, K.W.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.L.; Dai, F. Suggested method for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]
- Tang, C.A. Catastrophe in Rock Unstable Failure; China Coal Industry Publishing House: Beijing, China, 1991. [Google Scholar]
- Fan, T.Y. Dynamic Fracture Mechanics Principle and Its Application; Beijing Institute of Technology Press: Beijing, China, 2006. [Google Scholar]





| Diameter D/mm | Thickness B/mm | Pre-Crack Length a/mm | Pre-Crack Width /mm | Pre-Crack Tip Width/mm |
|---|---|---|---|---|
| 100 | 45 | 10 | 0.3 | 0.1 |
| Bar Diameter/mm | Incident Bar Length/mm | Transmission Bar Length/mm | Elastic Modulus/GPa | Poisson’s Ratio | Longitudinal Wave Velocity /(m/s) | |
|---|---|---|---|---|---|---|
| 75 | 3500 | 3500 | 7800 | 210 | 0.3 | 5190 |
| Test Sample Number | ||||
|---|---|---|---|---|
| 0.54 | -1 | 21.65 | 11.53 | 12.17 |
| -2 | 22.36 | 12.38 | ||
| -3 | 23.72 | 12.61 | ||
| 0.56 | -4 | 25.33 | 13.65 | 13.66 |
| -5 | 25.26 | 13.60 | ||
| -6 | 25.64 | 13.72 | ||
| 0.58 | -7 | 28.15 | 14.38 | 14.90 |
| -8 | 28.72 | 14.87 | ||
| -9 | 29.39 | 15.44 | ||
| 0.60 | -10 | 33.75 | 16.67 | 16.28 |
| -11 | 32.51 | 16.14 | ||
| -12 | 32.48 | 16.03 |
| Test Sample Number | ||||
|---|---|---|---|---|
| 0.54 | -1 | 20.50 | 10.13 | 9.87 |
| -2 | 20.11 | 9.87 | ||
| -3 | 19.51 | 9.60 | ||
| 0.56 | -4 | 23.41 | 11.23 | 11.31 |
| -5 | 23.06 | 11.14 | ||
| -6 | 24.56 | 11.56 | ||
| 0.58 | -7 | 27.20 | 12.00 | 11.99 |
| -8 | 27.40 | 12.08 | ||
| -9 | 26.71 | 11.89 | ||
| 0.60 | -10 | 30.60 | 12.57 | 12.80 |
| -11 | 30.12 | 12.24 | ||
| -12 | 31.07 | 13.58 |
| Test Sample Number | ||||
|---|---|---|---|---|
| 0.54 | -1 | 21.64 | 12.67 | 13.32 |
| -2 | 22.41 | 13.43 | ||
| -3 | 23.24 | 13.87 | ||
| 0.56 | -4 | 25.82 | 15.61 | 15.75 |
| -5 | 26.63 | 16.40 | ||
| -6 | 25.57 | 15.24 | ||
| 0.58 | -7 | 33.37 | 19.71 | 18.97 |
| -8 | 32.62 | 18.78 | ||
| -9 | 32.17 | 18.42 | ||
| 0.60 | -10 | 38.06 | 23.77 | 22.51 |
| -11 | 36.55 | 21.59 | ||
| -12 | 37.23 | 22.18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Li, X.; Bi, J.; Cheng, S. Dynamic Crack Initiation Toughness of Shale under Impact Loading. Energies 2019, 12, 1636. https://doi.org/10.3390/en12091636
Yang G, Li X, Bi J, Cheng S. Dynamic Crack Initiation Toughness of Shale under Impact Loading. Energies. 2019; 12(9):1636. https://doi.org/10.3390/en12091636
Chicago/Turabian StyleYang, Guoliang, Xuguang Li, Jingjiu Bi, and Shuaijie Cheng. 2019. "Dynamic Crack Initiation Toughness of Shale under Impact Loading" Energies 12, no. 9: 1636. https://doi.org/10.3390/en12091636
APA StyleYang, G., Li, X., Bi, J., & Cheng, S. (2019). Dynamic Crack Initiation Toughness of Shale under Impact Loading. Energies, 12(9), 1636. https://doi.org/10.3390/en12091636





