Virtual Organization Structure for Agent-Based Local Electricity Trading
Abstract
:1. Introduction
- A new virtual organization of agents’ structure in the distribution network.
- A novel iterative algorithm for energy trade between end-users and the DisCo in the power distribution system.
- The evaluation of energy trading scenarios through the proposed model.
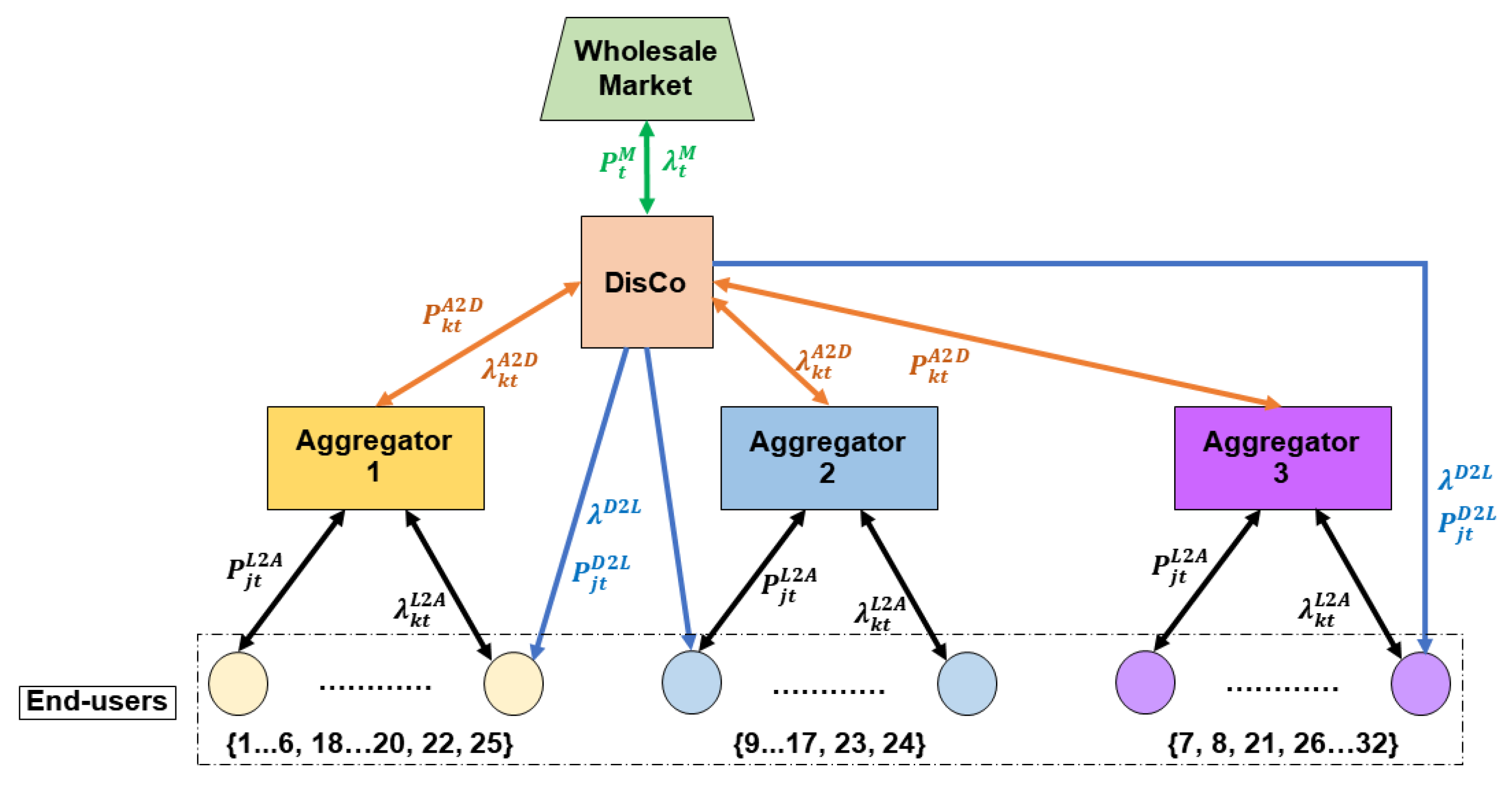
2. Virtual Organization of Agents in the Power Distribution Grid
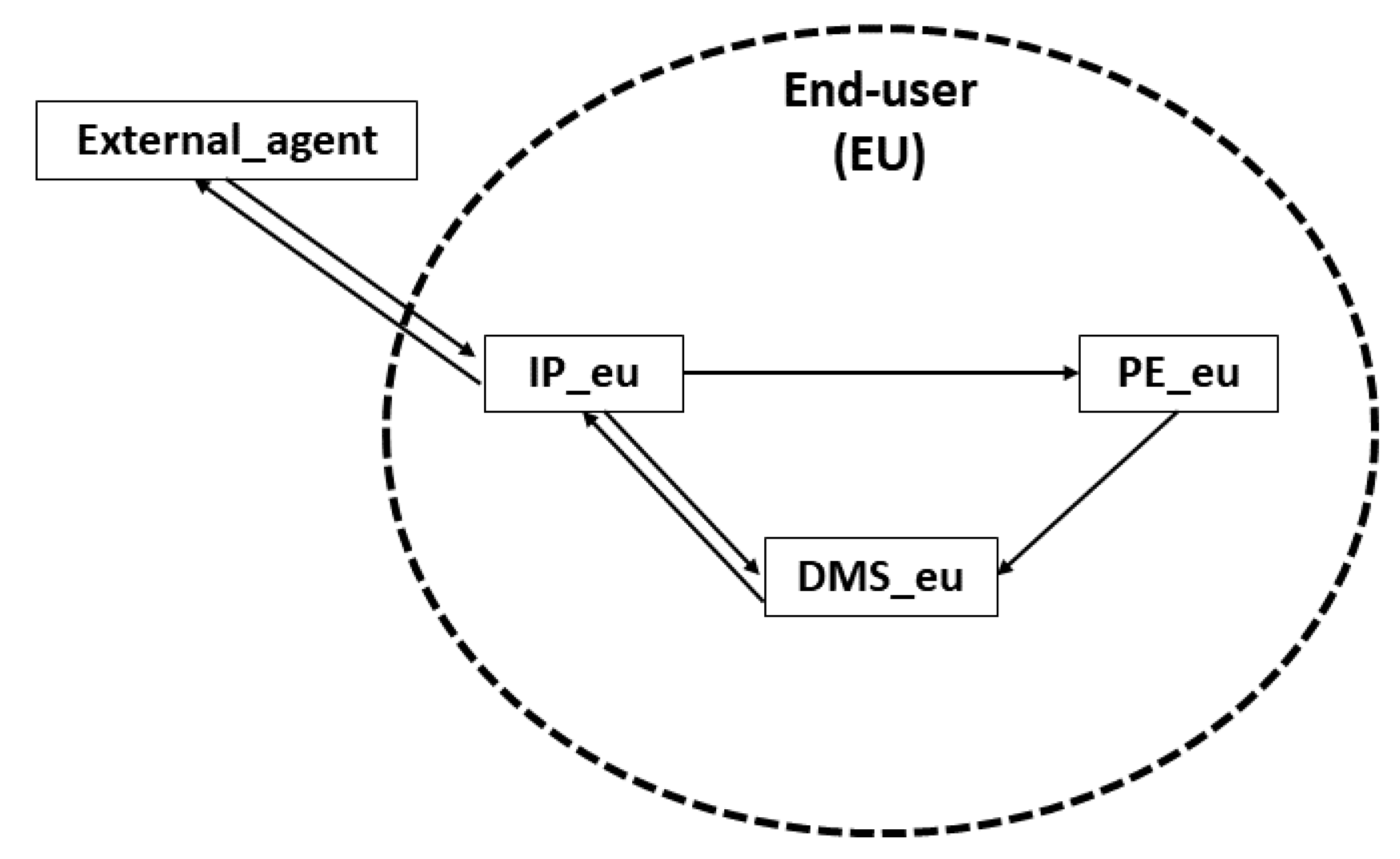
2.1. End-Users
- The Information Provider (IP) records information of all other agents, as well as the environmental conditions. Furthermore, the IP is responsible for sending/receiving information to/from the external agents that correspond to its organization, as shown in Figure 1.
- The Prediction Engine (PE) forecasts the uncertain variables (e.g., the energy generated from distributed energy resources, electrical consumption, electricity price, etc.) of end-users based on information provided by the IP. In this way, the values predicted by the PE are the inputs of the DMS.
- The Decision-Making System (DMS) is in charge of making optimum decisions for its corresponding organization (e.g., end-user, aggregator, and the DisCo). On the one hand, the inputs of the DMS are received from the IP and the PE. On the other hand, the outputs of the DMS are sent to the IP, which exchanges them with the external agents from the corresponding organization. Figure 1 shows interactions between agents in the end-user’s organization.
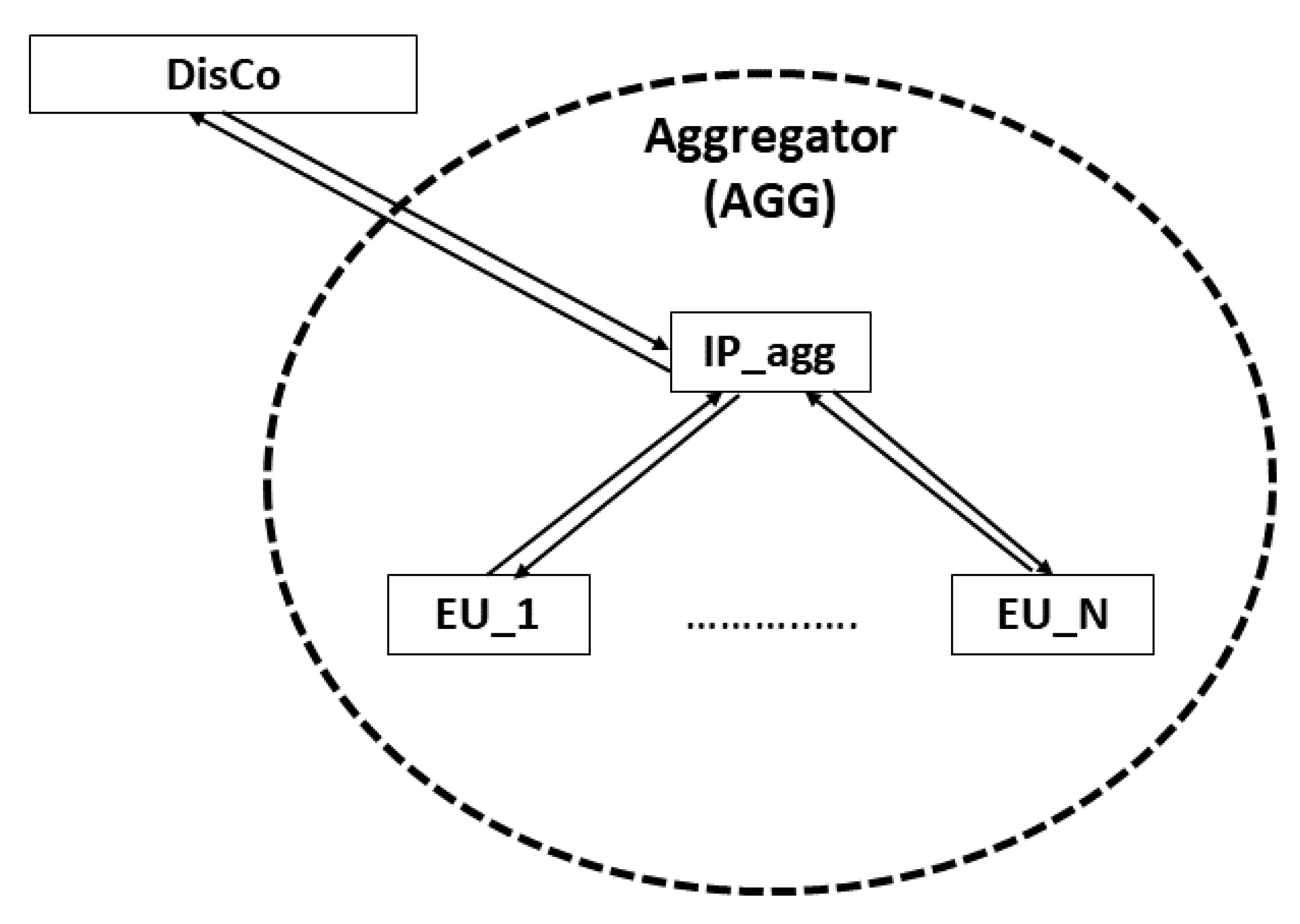
2.2. Aggregators
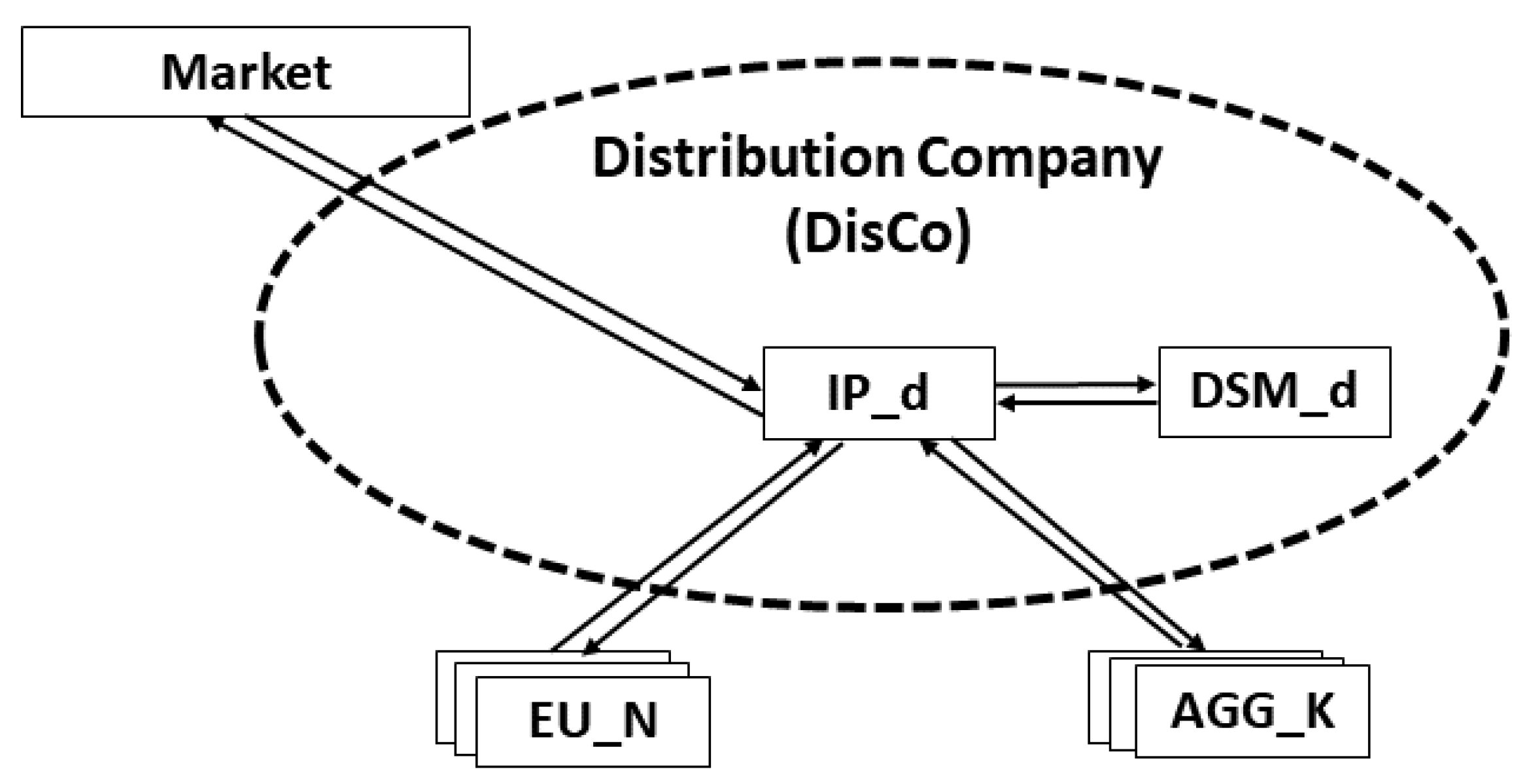
2.3. Distribution Company
3. Problem Formulation
3.1. Energy Trading Model
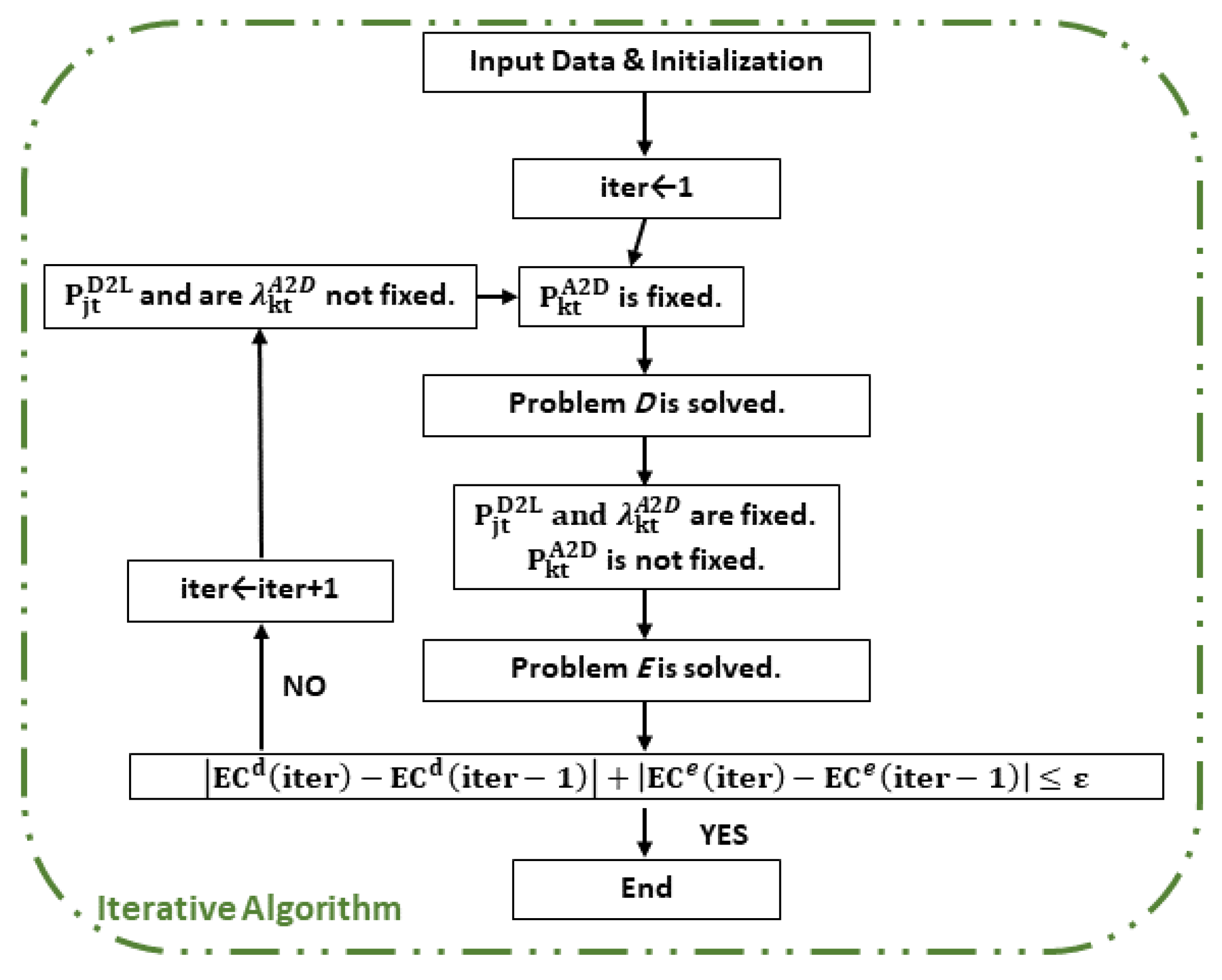
3.2. Proposed Iterative Algorithm
- End-users energy trading problem (Problem E):
- DSO’s problem (Problem D):
4. Simulation Results
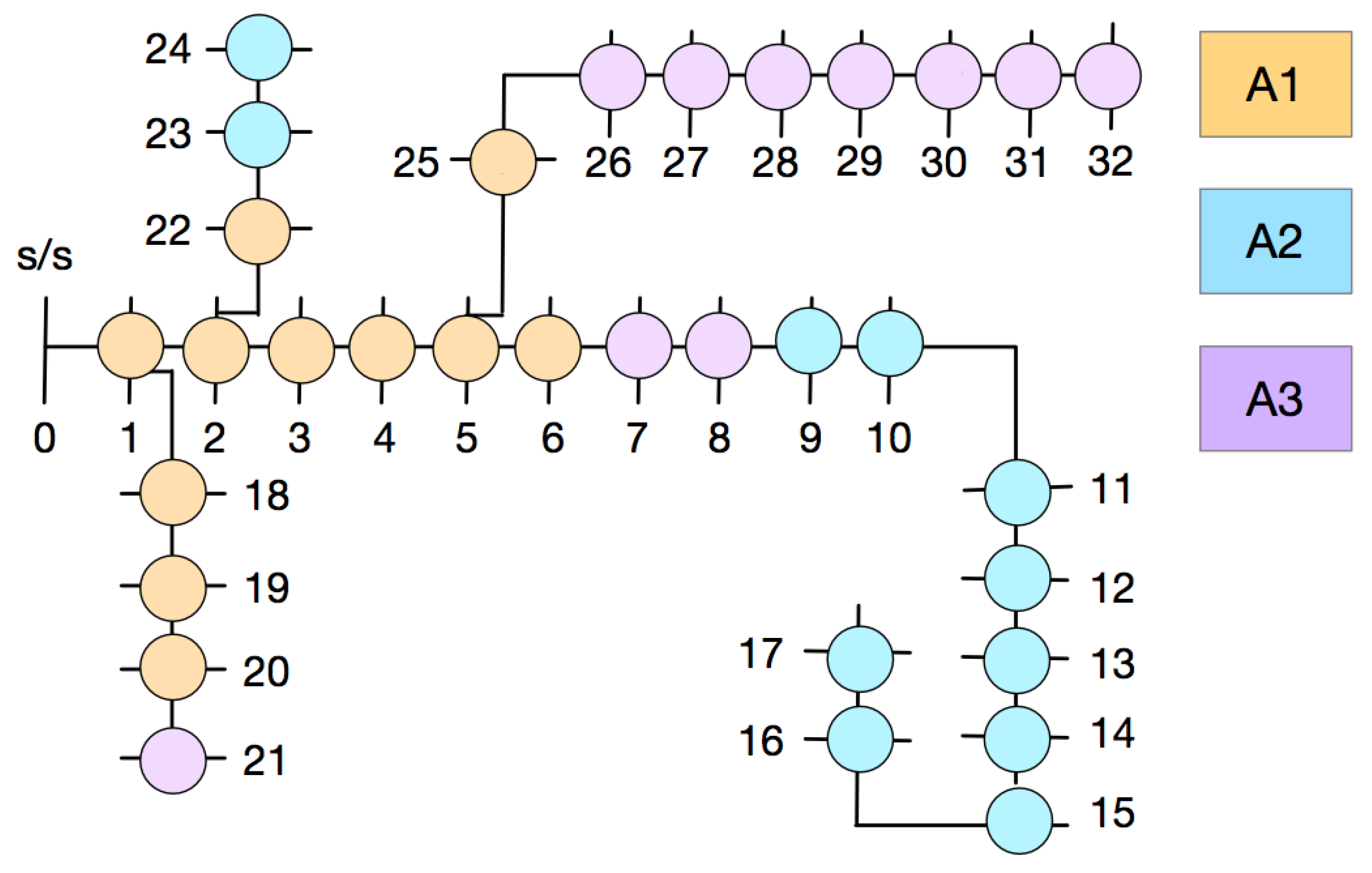
4.1. Case Study
4.2. Evaluation of the Proposed Iterative Algorithm
5. Conclusions
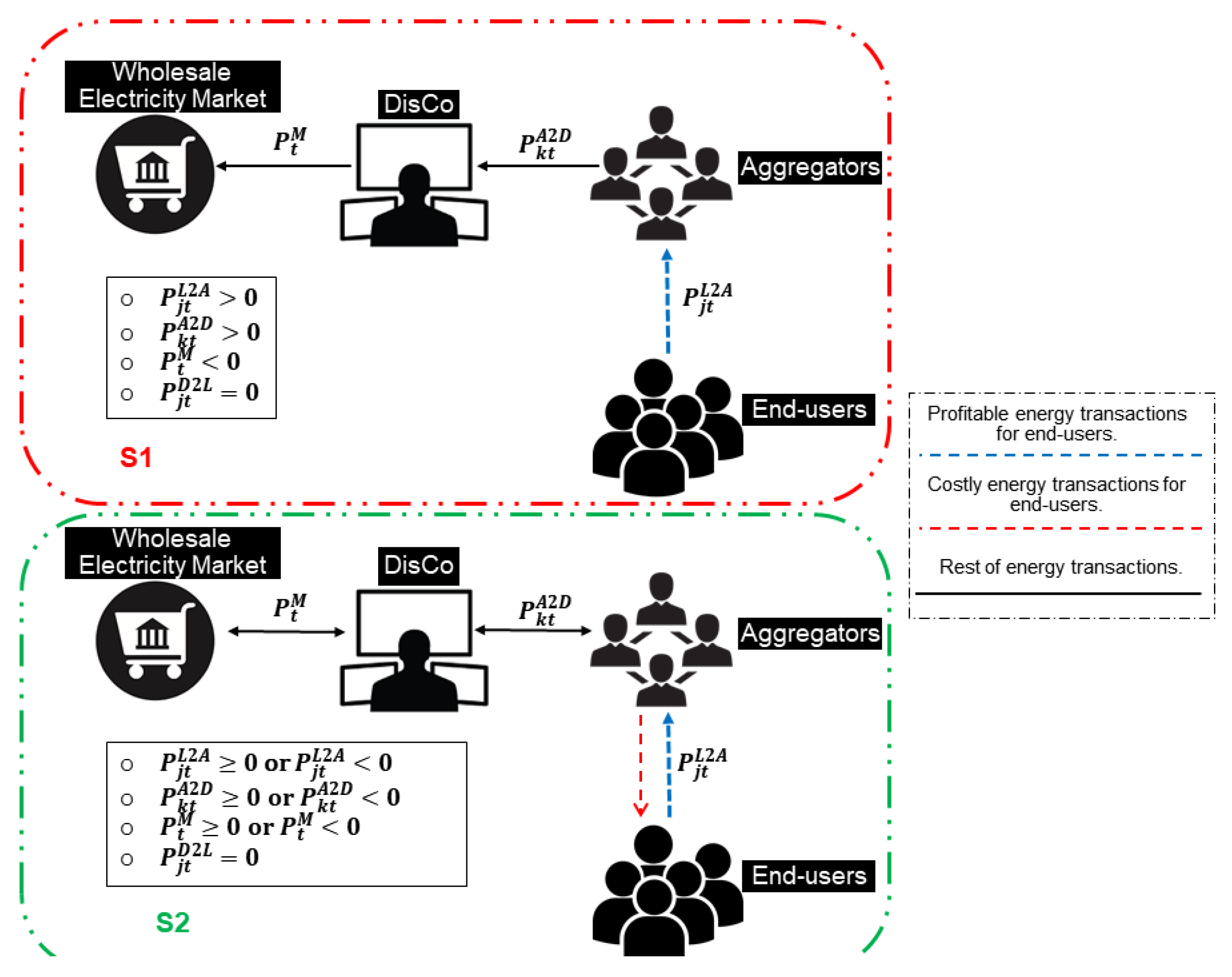
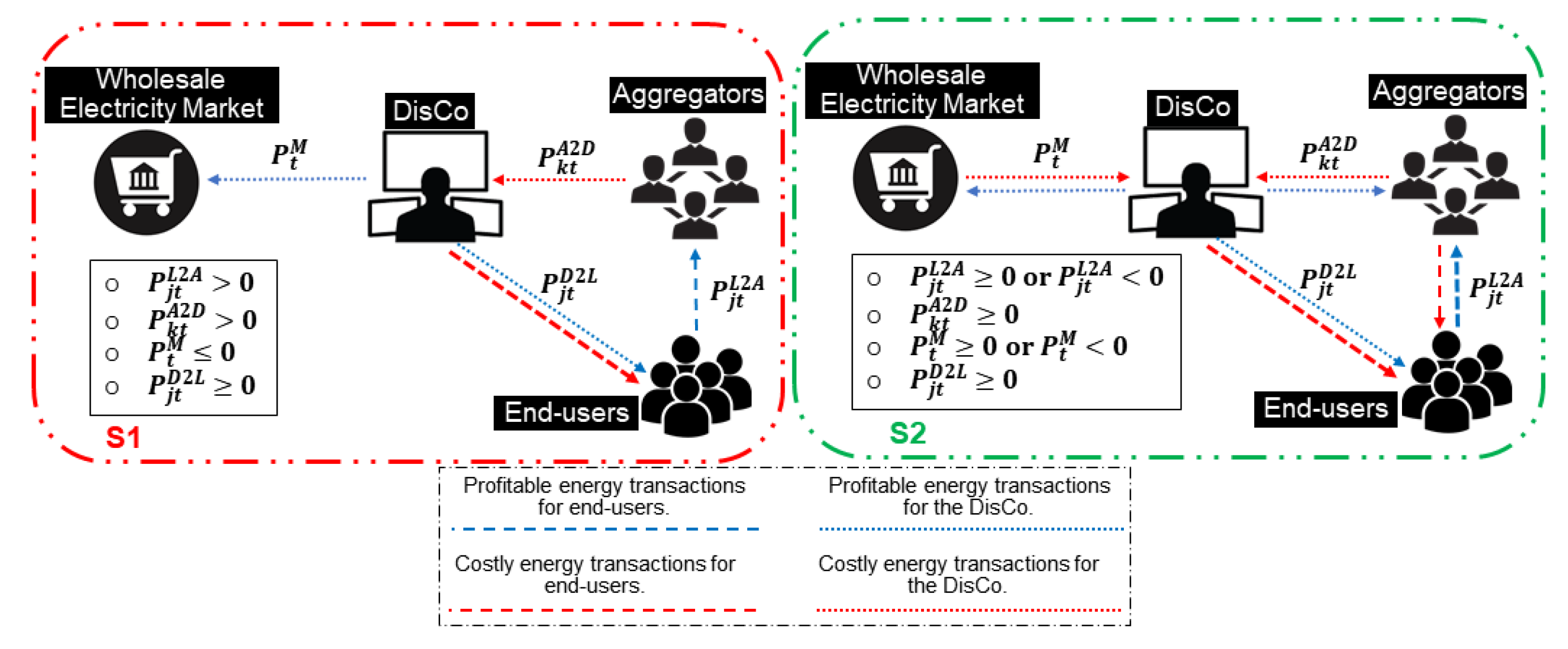
- If all end-users participate as interruptible loads in the distribution network, the energy trade was more profitable for all the agents.
- Our proposed algorithm was profitable for aggregators and the DisCo, who are policy makers in the power distribution system.
- The proposed algorithm was costly for all end-users in comparison with the decentralized approach (which is not practical in current power systems) to manage energy by end-users in the distribution network, because the DisCo is in charge of determining the amount of energy that can be traded between the DisCo and end-users.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sayadi, H.; Makrani, H.M.; Randive, O.; PD, S.M.; Rafatirad, S.; Homayoun, H. Customized machine learning-based hardware-assisted malware detection in embedded device. In Proceedings of the 17th IEEE International Conference On Trust, Security And Privacy in Computing And Communications (IEEE TrustCom-18), New York, NY, USA, 1–3 August 2018. [Google Scholar]
- Gazafroudi, A.S.; Prieto-Castrillo, F.; Pinto, T.; Corchado, J.M. Organization-Based Multi-Agent System of Local Electricity Market: Bottom-Up Approach. In Proceedings of the 15th International Conference on Practical Applications of Agents and Multi-Agent Systems (PAAMS), Porto, Portugal, 21–23 June 2017. [Google Scholar]
- Pratt, A.; Krishnamurthy, D.; Ruth, M.; Wu, H.; Lunacek, M.; Vaynshenk, P. Transactive Home Energy Management Systems. IEEE Electrif. Mag. 2016, 4, 8–14. [Google Scholar]
- Jokic, A.; van den Bosch, P.P.J.; Hermans, R.M. Distributed, Price-based Control Approach to Market-based Operation of Future Power Systems. In Proceedings of the 2009 6th International Conference on the European Energy Market, Leuven, Belgium, 27–29 May 2009. [Google Scholar]
- Sajjadi, S.M.; Mandal, P.; Tseng, T.L.; Velez-Reyes, M. Transactive energy market in distribution systems: A case study of energy trading between transactive nodes. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016. [Google Scholar]
- Shafie-khah, M.; Catalão, J.P.S. A Stochastic Multi-Layer Agent-Based Model to Study Electricity Market Participants Behavior. IEEE Trans. Power Syst. 2015, 30, 867–881. [Google Scholar]
- Nunna, H.K.; Srinivasan, D. Multiagent-Based Transactive Energy Framework for Distribution Systems With Smart Microgrids. IEEE Trans. Ind. Inform. 2017, 13, 2241–2250. [Google Scholar] [CrossRef]
- Warrington, J.; Mariéthoz, S.; Jones, C.N.; Morari, M. Predictive power dispatch through negotiated locational pricin. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010. [Google Scholar]
- Chai, B.; Chen, J.; Yang, Z.; Zhang, Y. Demand response management with multiple utility companies: A two-level game approach. IEEE Trans. Smart Grid 2014, 5, 722–731. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Hou, F.; Chow, M.-Y.; Chen, J. Distributed realtime demand response in multiseller-multibuyer smart distribution grid. IEEE Trans. Power Syst. 2015, 30, 2364–2374. [Google Scholar] [CrossRef]
- Disfani, V.R.; Fan, L.; Miao, Z. Distributed dc optimal power flow for radial networks through partial primal dual algorithm. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalão, J.P.S. A decentralized renewable generation management and demand response in power distribution networks. IEEE Trans. Sustain. Energy 2018. [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalão, J.P.S. A decentralized electricity market scheme enabling demand response deployment. IEEE Trans. Power Syst. 2018, 33, 4218–4227. [Google Scholar] [CrossRef]
- Mustafa, M.A.; Cleemput, S.; Abidin, A. A local electricity trading market: Security analysis. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Ljubljana, Slovenia, 9–12 October 2016. [Google Scholar]
- Park, S.; Lee, J.; Bae, S.; Hwang, G.; Choi, J.K. Contribution-Based Energy-Trading Mechanism in Microgrids for Future Smart Grid: A Game Theoretic Approach. IEEE Trans. Ind. Electron. 2016, 63, 4255–4265. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.; Wang, J.; Pinson, P.; Morales, J.M.; Ostergaard, J. Real-time procurement strategies of a proactive distribution company with aggregator-based demand response. IEEE Trans. Smart Grid 2016, 9, 766–776. [Google Scholar] [CrossRef]
- Prieto-Castrillo, F.; Gazafroudi, A.S.; Prieto, J.; Corchado, J.M. An Ising Spin-Based Model to Explore Efficient Flexibility in Distributed Power Systems. Complexity 2018, 2018, 5905932. [Google Scholar] [CrossRef]
- Gazafroudi, A.S.; Corchado, J.M.; Keane, A.; Soroudi, A. Decentralised flexibility management for EVs. IET Renew. Power Gener. 2019, 13, 952–960. [Google Scholar] [CrossRef]
- Gazafroudi, A.S.; Prieto-Castrillo, F.; Pinto, T.; Corchado, J.M. Energy Flexibility Management in Power Distribution Systems: Decentralized Approach. In Proceedings of the IEEE International Conference on Smart Energy Systems and Technologies (SEST), Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Mithulananthan, N.; Hung, Q.D.; Kwang, Y. Intelligent Network Integration of Distributed Renewable Generation; Springer International Publishing: Berlin, Germany, 2017. [Google Scholar]
| Time | ||||
|---|---|---|---|---|
| (h) | (€/kWh) | (€/kWh) | (€/kWh) | (€/kWh) |
| 1 | 0.05 | 0.08 | 0.06 | 0.13 |
| 2 | 0.05 | 0.08 | 0.07 | 0.12 |
| 3 | 0.05 | 0.09 | 0.07 | 0.15 |
| 4 | 0.04 | 0.07 | 0.05 | 0.11 |
| 5 | 0.11 | 0.18 | 0.15 | 0.30 |
| 6 | 0.12 | 0.20 | 0.16 | 0.32 |
| 7 | 0.13 | 0.22 | 0.17 | 0.35 |
| 8 | 0.15 | 0.24 | 0.19 | 0.40 |
| 9 | 0.16 | 0.25 | 0.20 | 0.42 |
| 10 | 0.24 | 0.41 | 0.33 | 0.66 |
| 11 | 0.26 | 0.42 | 0.36 | 0.71 |
| 12 | 0.28 | 0.43 | 0.37 | 0.74 |
| 13 | 0.25 | 0.40 | 0.32 | 0.69 |
| 14 | 0.18 | 0.26 | 0.21 | 0.50 |
| 15 | 0.15 | 0.24 | 0.20 | 0.41 |
| 16 | 0.14 | 0.22 | 0.18 | 0.40 |
| 17 | 0.15 | 0.25 | 0.19 | 0.42 |
| 18 | 0.20 | 0.36 | 0.30 | 0.60 |
| 19 | 0.21 | 0.36 | 0.29 | 0.65 |
| 20 | 0.22 | 0.41 | 0.30 | 0.67 |
| 21 | 0.24 | 0.42 | 0.33 | 0.70 |
| 22 | 0.12 | 0.22 | 0.16 | 0.35 |
| 23 | 0.11 | 0.19 | 0.15 | 0.28 |
| 24 | 0.06 | 0.09 | 0.07 | 0.15 |
| Expected Cost (Case) | ||
|---|---|---|
| (Case 1) (€) | −2394.438 | −714.291 |
| (Case 1) (€) | −239.444 | 733.548 |
| (Case 1) (€) | −2273.819 | −1461.078 |
| (Case 2) (€) | 159.767 | 1111.734 |
| (Case 2) (€) | −239.444 | −100.082 |
| (Case 2) (€) | −8607.231 | −5612.034 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokri Gazafroudi, A.; Prieto, J.; Corchado, J.M. Virtual Organization Structure for Agent-Based Local Electricity Trading. Energies 2019, 12, 1521. https://doi.org/10.3390/en12081521
Shokri Gazafroudi A, Prieto J, Corchado JM. Virtual Organization Structure for Agent-Based Local Electricity Trading. Energies. 2019; 12(8):1521. https://doi.org/10.3390/en12081521
Chicago/Turabian StyleShokri Gazafroudi, Amin, Javier Prieto, and Juan Manuel Corchado. 2019. "Virtual Organization Structure for Agent-Based Local Electricity Trading" Energies 12, no. 8: 1521. https://doi.org/10.3390/en12081521
APA StyleShokri Gazafroudi, A., Prieto, J., & Corchado, J. M. (2019). Virtual Organization Structure for Agent-Based Local Electricity Trading. Energies, 12(8), 1521. https://doi.org/10.3390/en12081521







