A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies
Abstract
:1. Introduction
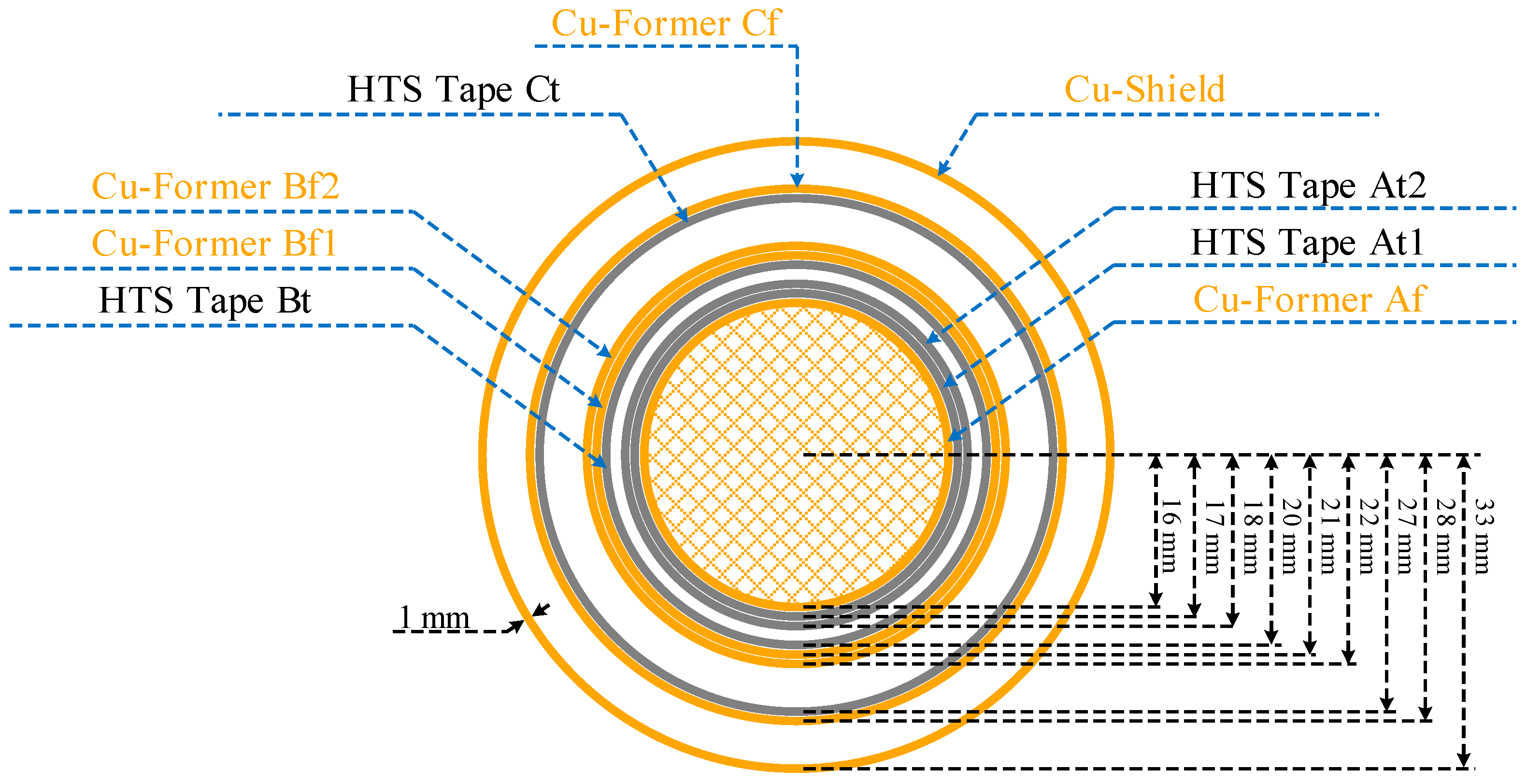
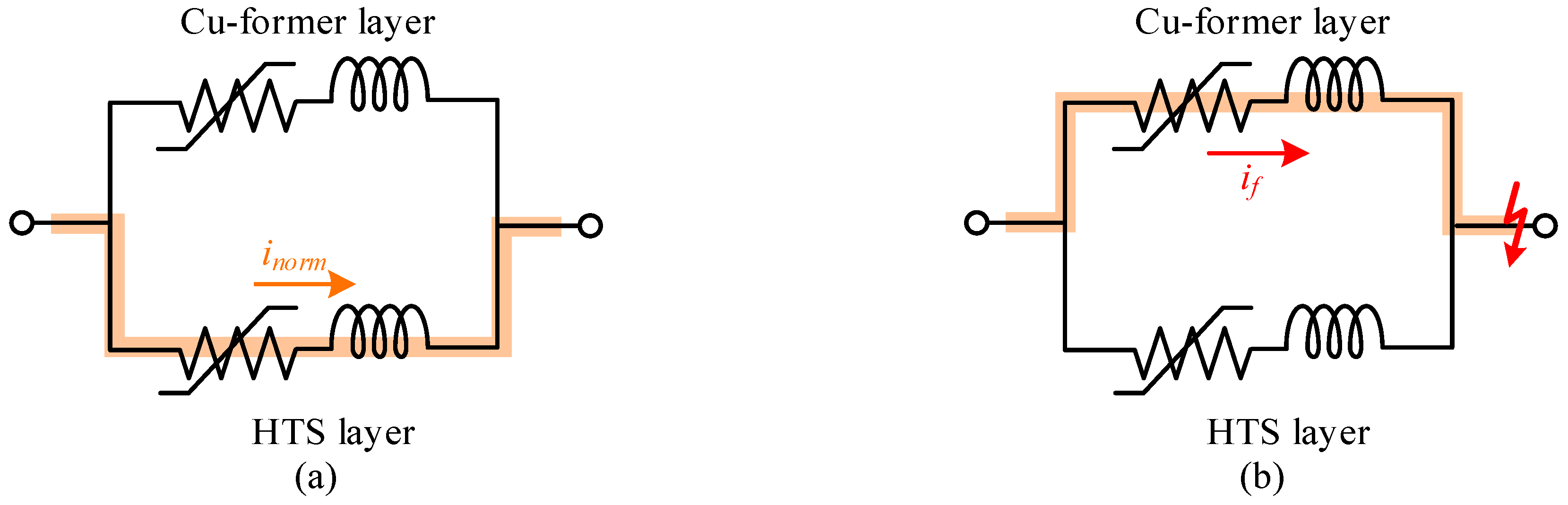
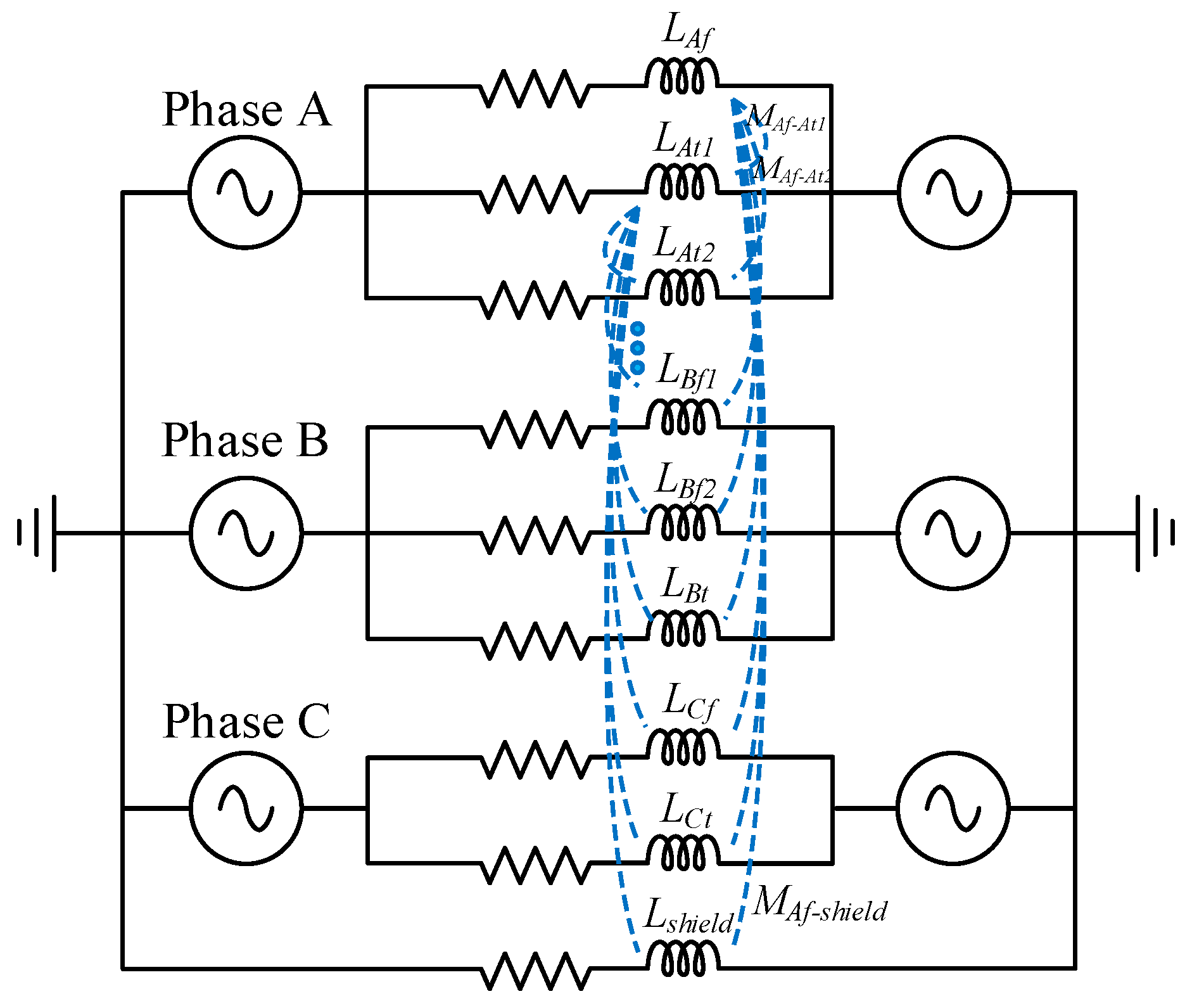
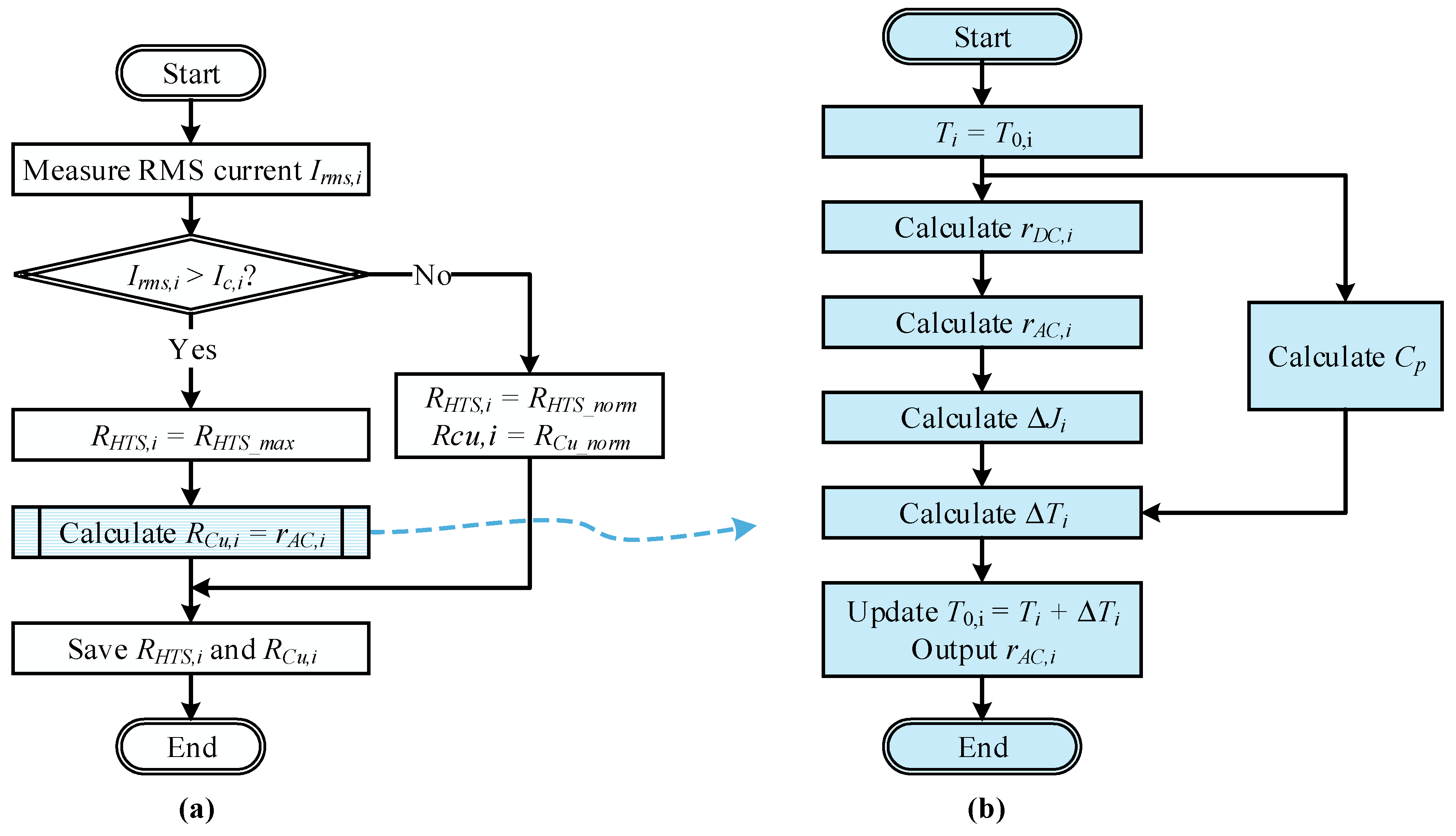
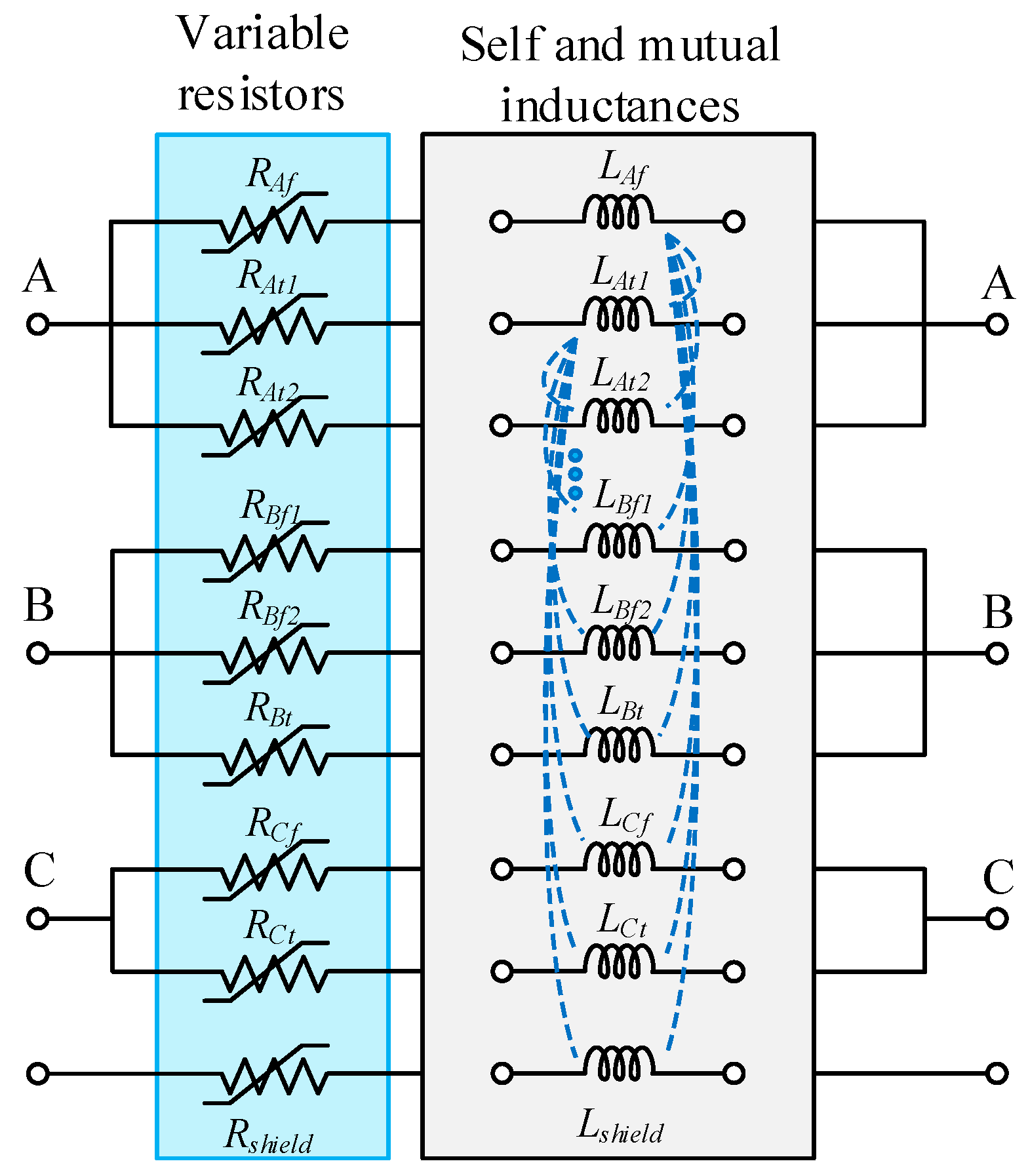
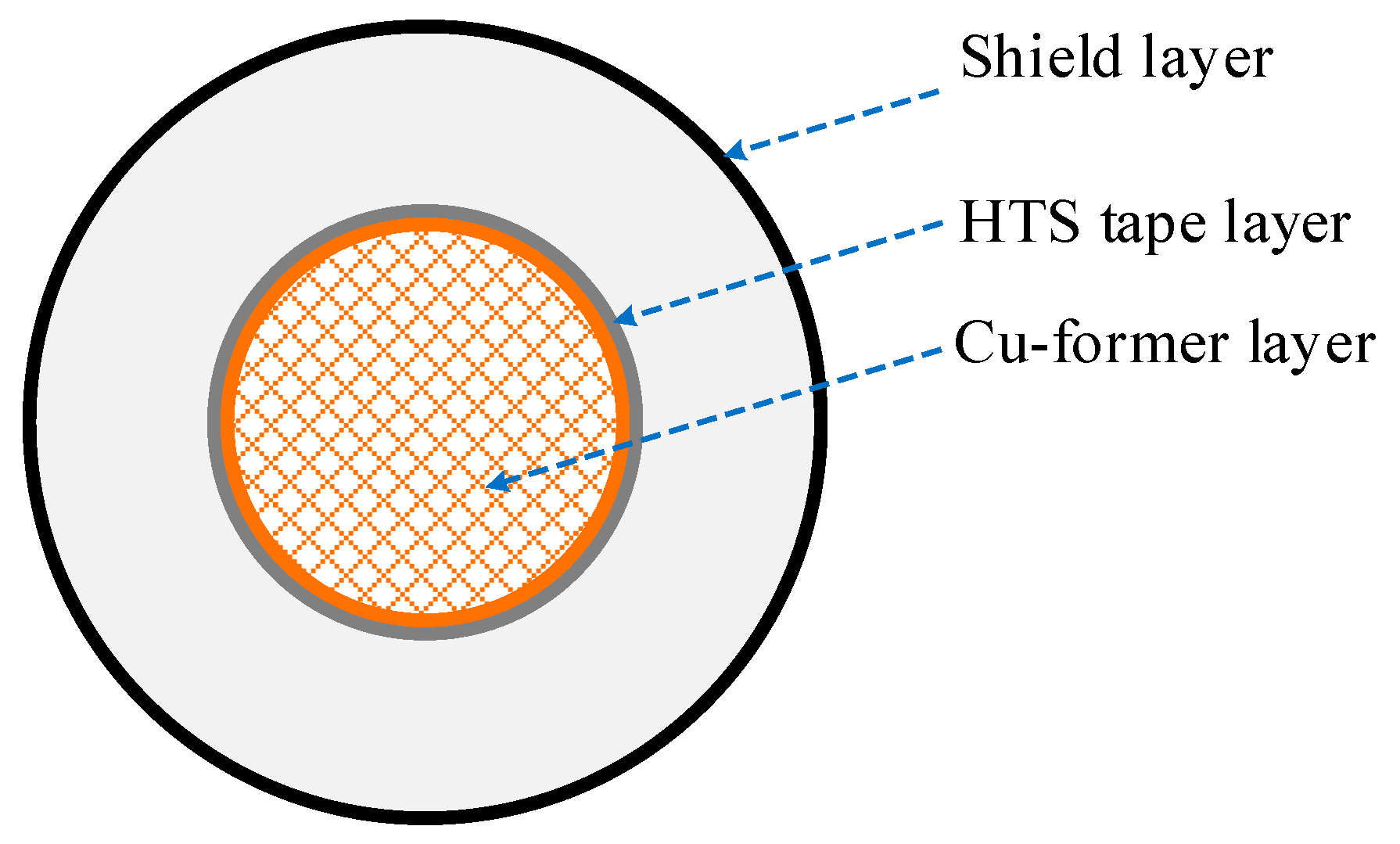
2. Cable Modeling in PSCAD/EMTDC
3. Simulation Results
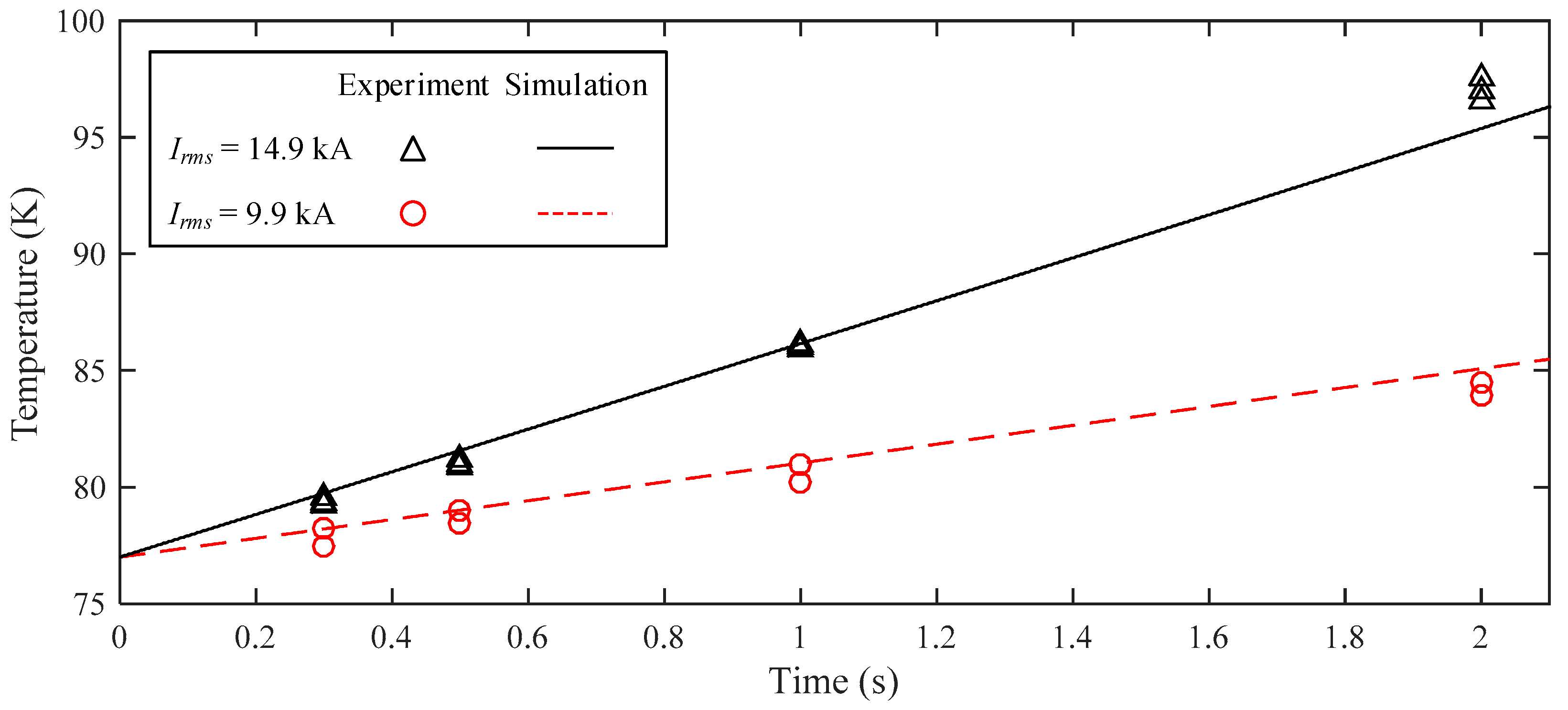
3.1. Validation of the High-Temperature Superconducting (HTS) Cable Model
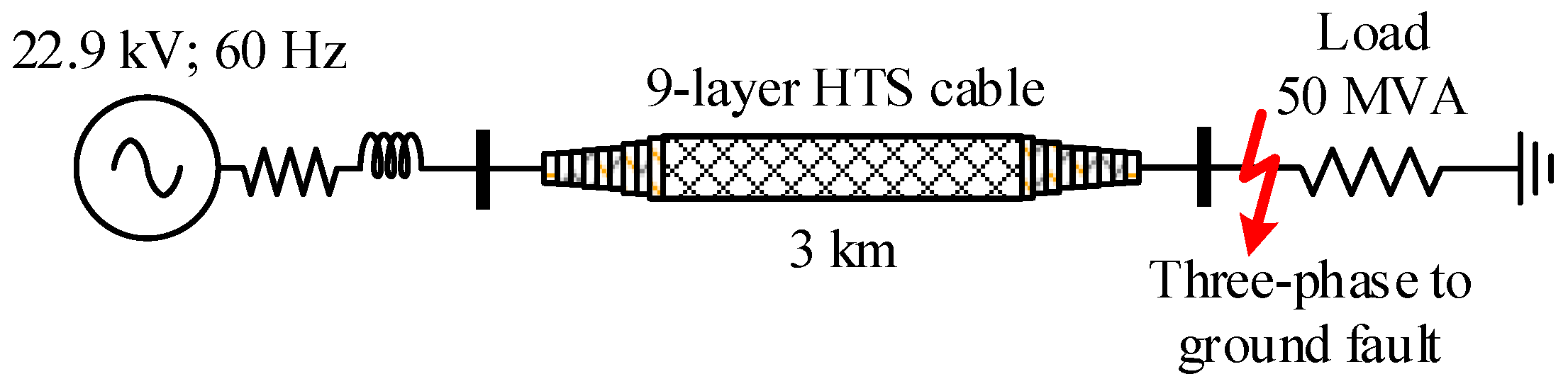
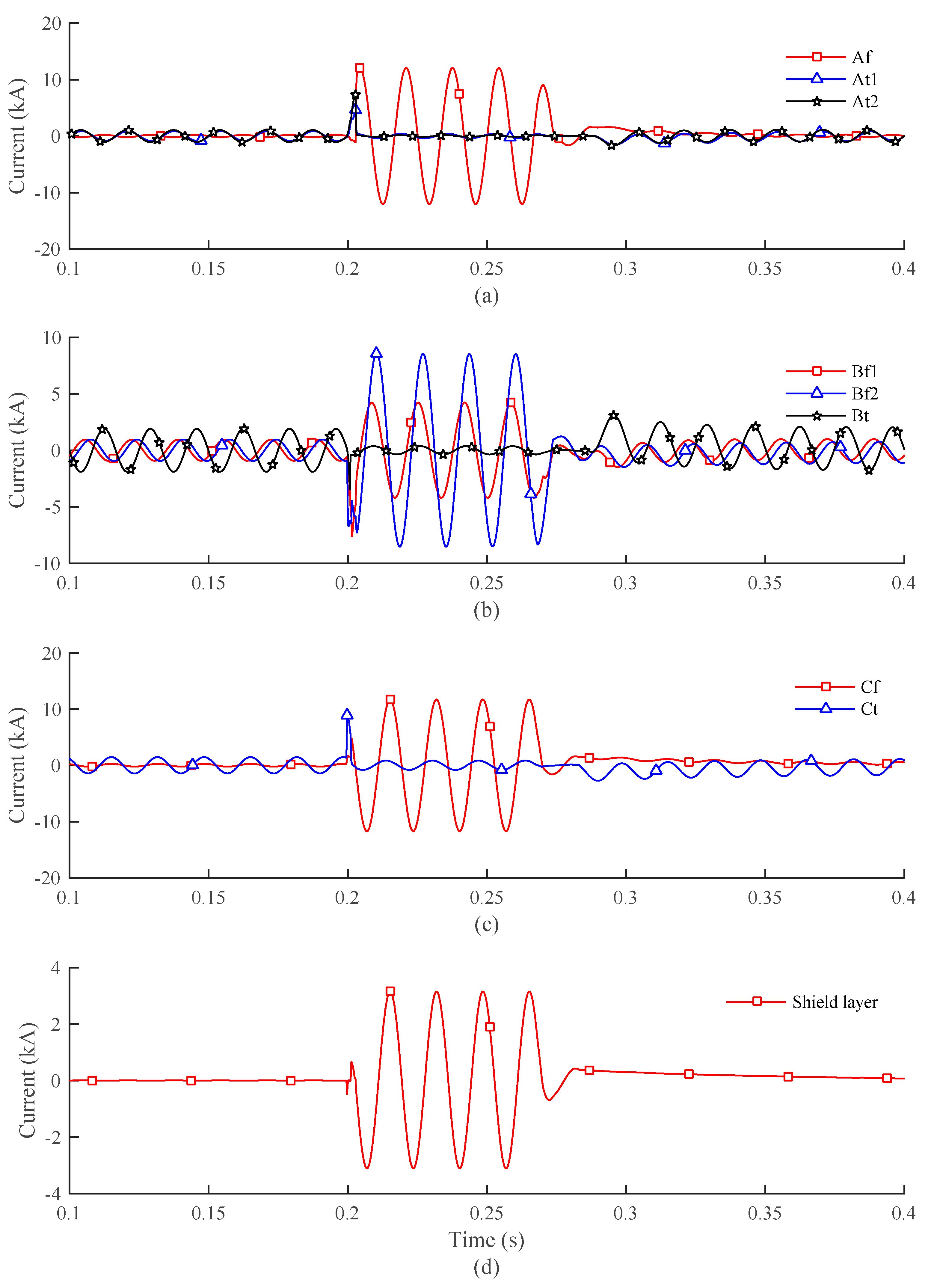
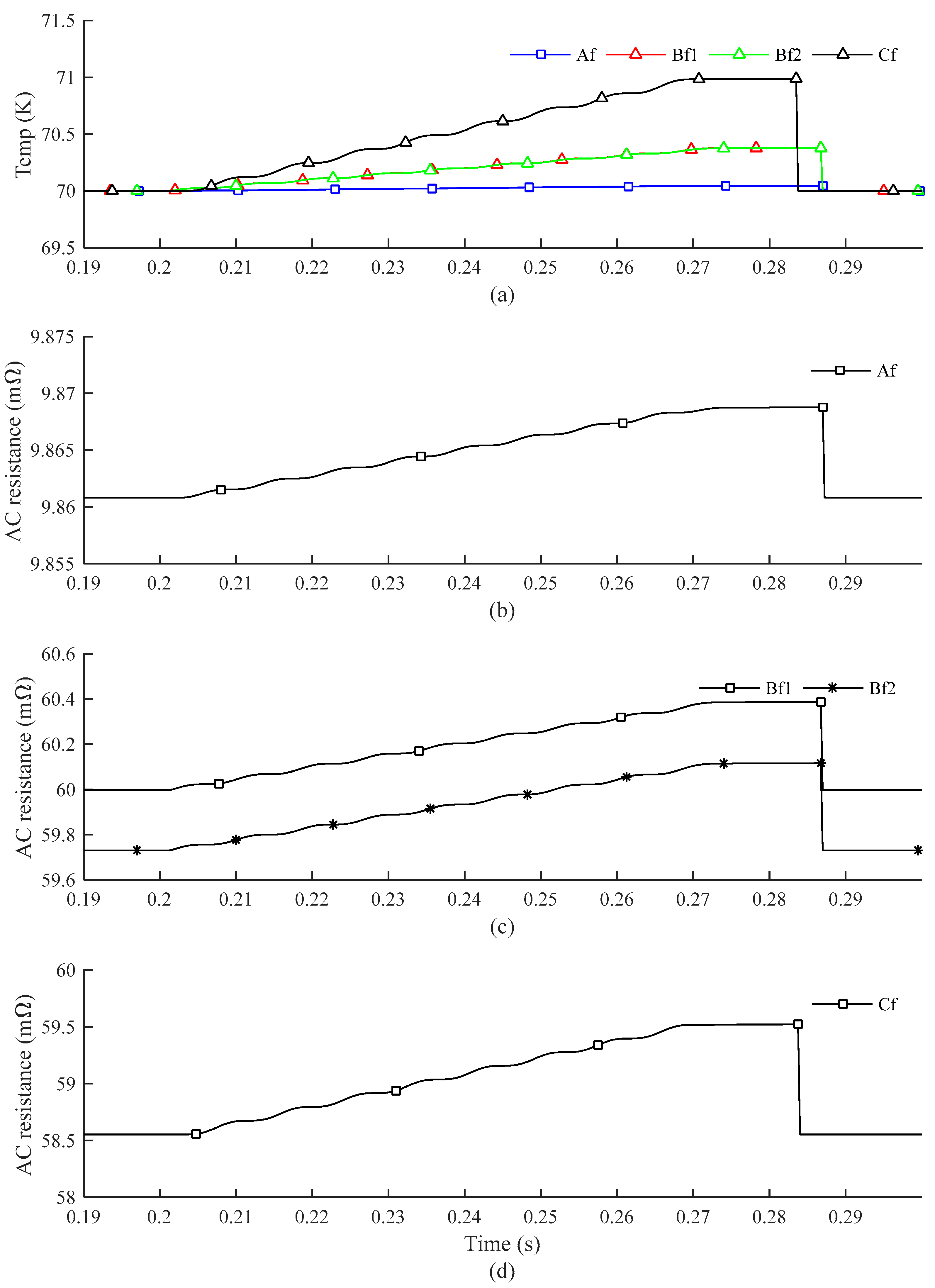
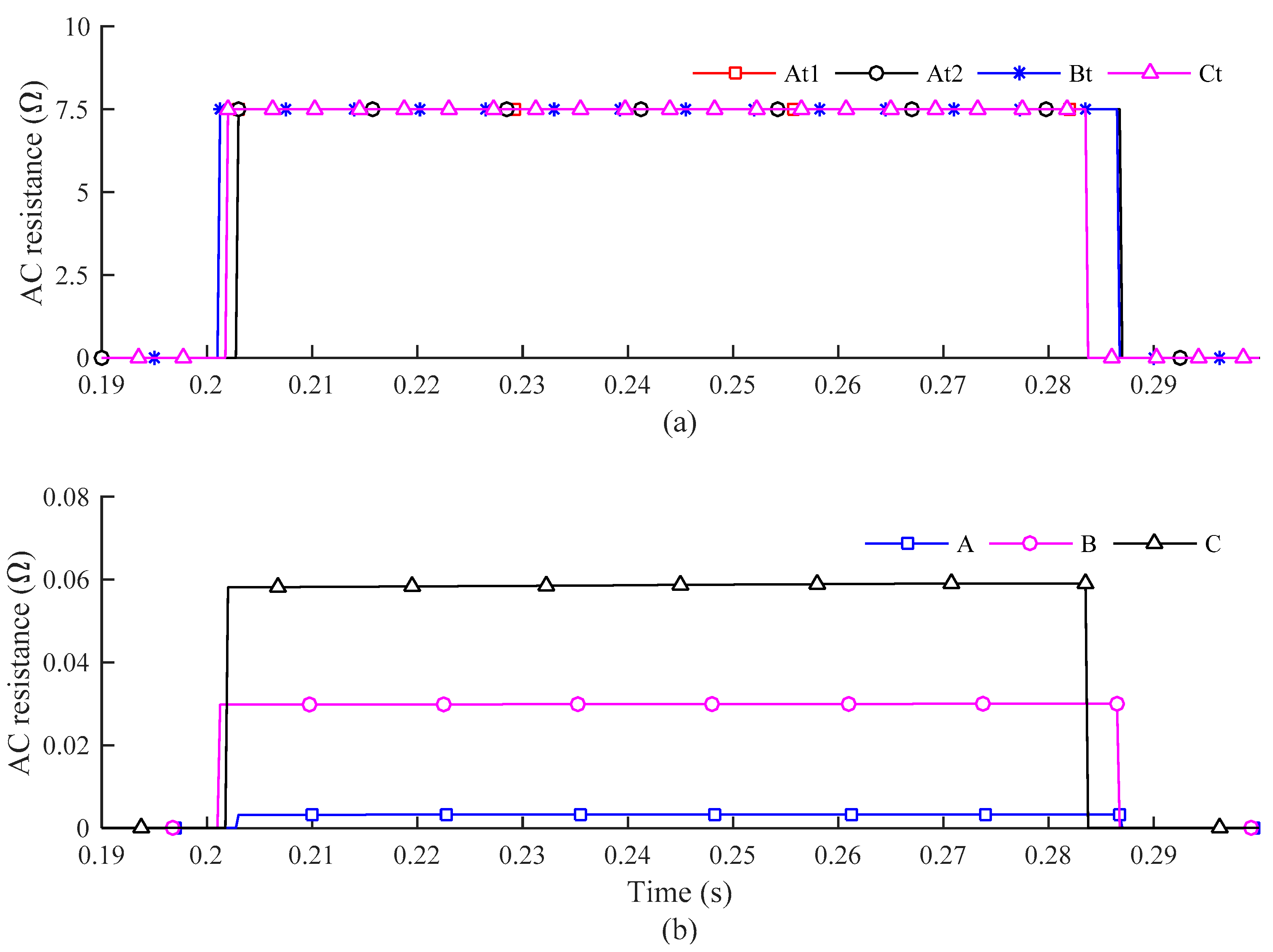
3.2. Performance of the Coaxial Multilayer HTS Cable Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kottonau, D.; de Sousa, W.T.B.; Bock, J.; Noe, M. Design comparisons of concentric three-phase HTS cables. IEEE Trans. Appl. Supercond. 2019, 29, 1. [Google Scholar] [CrossRef]
- Gholizad, B.; Ross, R.; Koopmans, G.; Mousavi Gargari, S.; Smit, J.J.; Ghaffarian Niasar, M.; Meijer, C.; Bucurenciu, A.M. Reliability considerations of electrical insulation systems in superconducting cables. Proc. IEEE Int. Conf. Prop. Appl. Dielectr. Mater. 2018, 2018, 194–197. [Google Scholar]
- McGuckin, P.; Burt, G. Overview and assessment of superconducting technologies for power grid applications. In Proceedings of the 53rd International Universities Power Engineering Conference UPEC, Glasgow, UK, 4–7 September 2018. [Google Scholar]
- Lee, S.J.; Park, M.; Yu, I.K.; Won, Y.; Kwak, Y.; Lee, C. Recent status and progress on HTS cables for AC and DC power transmission in Korea. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Youroukos, E. Economic Feasibility Study of ULMCS. Bachelor’s Thesis, National Technology University of Athens, Athens, Greece, 2007. [Google Scholar]
- Lee, C.; Kim, D.; Kim, S.; Won, D.Y.; Yang, H.S. Thermo-hydraulic analysis on long three-phase coaxial HTS power cable of several kilometers. IEEE Trans. Appl. Supercond. 2019, 8223, 1. [Google Scholar] [CrossRef]
- Samoilenkov, S.V.; Ivanov, S.S.; Lipa, D.; Balashov, N.N.; Altov, V.A.; Zheltov, V.V.; Sytnikov, V.E.; Degtyarenko, P.N.; Kopylov, S.I. Design versions of HTS three-phase cables with the minimized value of AC losses. J. Phys. Conf. Ser. 2018, 969, 012049. [Google Scholar]
- Yagi, M.; Fukushima, H.; Serizawa, M.; Mimura, T.; Nakano, T.; Mukoyama, S.; Takagi, T. Protection against ground faults for a 275-kV HTS cable: An experiment. IEEE Trans. Appl. Supercond. 2018, 28, 1–4. [Google Scholar]
- Bykovsky, N.; Uglietti, D.; Wesche, R.; Bruzzone, P. Damage investigations in the HTS cable prototype after the cycling test in EDIPO. IEEE Trans. Appl. Supercond. 2018, 28. [Google Scholar] [CrossRef]
- Fu, Y.; Tsukamoto, O.; Furuse, M. Copper stabilization of YBCO coated conductor for quench protection. IEEE Trans. Appl. Supercond. 2003, 13, 1780–1783. [Google Scholar] [CrossRef]
- Ishiyama, A.; Wang, X.; Ueda, H.; Yagi, M.; Mukoyama, S.; Kashima, N.; Nagaya, S.; Shiohara, Y. Over-current characteristics of superconducting model cable using YBCO coated conductors. Phys. C Supercond. Appl. 2008, 468, 2041–2045. [Google Scholar] [CrossRef]
- Yagi, M.; Mukoyama, S.; Hirano, H.; Amemiya, N.; Ishiyama, A.; Nagaya, S.; Kashima, N.; Shiohara, Y. Recent development of an HTS power cable using YBCO tapes. Phys. C Supercond. Appl. 2007, 463–465, 1154–1158. [Google Scholar] [CrossRef]
- Kim, S.H.; Seong, K.C.; Lee, C.Y.; Cho, J.W.; Jang, H.M.; Sim, K.D.; Kim, H.J.; Kim, J.H.; Bae, J.H. Design of HTS transmission cable with Cu stabilizer. IEEE Trans. Appl. Supercond. 2006, 16, 1622–1625. [Google Scholar]
- Grilli, F. Numerical modeling of HTS applications. IEEE Trans. Appl. Supercond. 2016, 26, 1–8. [Google Scholar] [CrossRef]
- Doukas, D.I.; Chrysochos, A.I.; Papadopoulos, T.A.; Labridis, D.P.; Harnefors, L.; Velotto, G. Coupled electro-thermal transient analysis of superconducting DC transmission systems using FDTD and VEM modeling. IEEE Trans. Appl. Supercond. 2017, 27, 1–8. [Google Scholar] [CrossRef]
- Fukui, S.; Ogawa, J.; Suzuki, N.; Oka, T.; Sato, T.; Tsukamoto, O.; Takao, T. Numerical analysis of AC loss characteristics of multi-layer HTS cable assembled by coated conductors. IEEE Trans. Appl. Supercond. 2009, 19, 1714–1717. [Google Scholar] [CrossRef]
- Fetisov, S.S.; Zubko, V.V.; Zanegin, S.Y.; Nosov, A.A.; Vysotsky, V.S. Numerical simulation and cold test of a compact 2G HTS power cable. IEEE Trans. Appl. Supercond. 2018, 28. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, J.; Li, H.; Qiu, M.; Li, Z.; Ding, K.; Wang, Y. Magnetic-thermal coupling analysis of the cold dielectric high temperature superconducting cable. IEEE Trans. Appl. Supercond. 2013, 23, 3–6. [Google Scholar]
- Conductor, Y.C.; Breschi, M.; Casali, M.; Cavallucci, L.; Marzi, G.D.; Tomassetti, G. Electrothermal analysis of a twisted stacked. IEEE Trans. Appl. Supercond. 2015, 25, 2–6. [Google Scholar]
- Su, R.; Shi, J.; Yan, S.; Li, P.; Wang, W.; Hu, Z.; Zhang, B.; Tang, Y.; Ren, L. Numerical model of HTS cable and its electric-thermal properties. IEEE Trans. Appl. Supercond. 2019, 29. [Google Scholar] [CrossRef]
- Yagi, M.; Masuda, T.; Hayakawa, N.; Hasegawa, T.; Mukoyama, S.; Maruyama, O.; Ohkuma, T.; Ashibe, Y.; Amemiya, N.; Ishiyama, A.; et al. Development of 66 kV and 275 kV Class REBCO HTS power cables. IEEE Trans. Appl. Supercond. 2012, 23, 5401405. [Google Scholar]
- Lee, S.R.; Lee, J.J.; Yoon, J.; Kang, Y.W.; Hur, J. Impact of 154-kV HTS cable to protection systems of the power grid in South Korea. IEEE Trans. Appl. Supercond. 2016, 26, 4–7. [Google Scholar] [CrossRef]
- Lee, S.; Yoon, J.; Lee, B.; Yang, B. Modeling of a 22.9 kV 50 MVA superconducting power cable based on PSCAD/EMTDC for application to the Icheon substation in Korea. Phys. C Supercond. Appl. 2011, 471, 1283–1289. [Google Scholar] [CrossRef]
- Bang, J.H.; Je, H.H.; Kim, J.H.; Sim, K.D.; Cho, J.; Yoon, J.Y.; Park, M.; Yu, I.K. Critical current, critical temperature and magnetic field based EMTDC model component for HTS power cable. IEEE Trans. Appl. Supercond. 2007, 17, 1726–1729. [Google Scholar] [CrossRef]
- Seokho, K.; A-Rong, K.; Ki-Deok, S.; Young-Jin, W.; Daewon, K.; Jun Kyoung, L.; In-Keun, Y.; Jin Geun, K.; Minwon, P.; Jeonwook, C. Development of a PSCAD/EMTDC model component for AC loss characteristic analysis of HTS power cable. IEEE Trans. Appl. Supercond. 2010, 20, 1284–1287. [Google Scholar]
- Seockho, K.; A-Rong, K.; Jeonwook, C.; Minwon, P.; Ki-Deok, S.; Jae-Ho, K.; Jeadeuk, L.; Jin Geun, K.; In-Keun, Y.; Jun Kyoung, L. HTS power cable model component development for PSCAD/EMTDC considering conducting and shield layers. IEEE Trans. Appl. Supercond. 2009, 19, 1785–1788. [Google Scholar]
- Ha, S.K.; Kim, S.K.; Kim, J.G.; Park, M.; Yu, I.K.; Lee, S.; Kim, J.H.; Sim, K. RTDS-based model component development of a tri-axial HTS power cable and transient characteristic analysis. J. Electr. Eng. Technol. 2015, 10, 2083–2088. [Google Scholar] [CrossRef]
- In-Keun, Y.; Minwon, P.; A-Rong, K.; Kideok, S.; Sung-Kyu, K.; Jin-Geun, K.; Sun-Kyoung, H.; Sangjin, L. Transient characteristic analysis of a tri-axial HTS power cable using PSCAD/EMTDC. IEEE Trans. Appl. Supercond. 2012, 23, 5400104. [Google Scholar]
- Magalhaes, A.P.C.; De Barros, M.T.C.; Lima, A.C.S. Earth return admittance effect on underground cable system modeling. IEEE Trans. Power Deliv. 2018, 33, 662–670. [Google Scholar] [CrossRef]
- Wikipedia Contributors Skin Effect. Available online: https://en.wikipedia.org/w/index.php?title=Skin_effect&oldid=865187719 (accessed on 11 February 2019).
- White, G.K.; Collocott, S.J. Heat capacity of reference materials: Cu and W. J. Phys. Chem. Ref. Data 1984, 13, 1251–1257. [Google Scholar] [CrossRef]
- Sim, K. Study on the Design and Transport Characteristics of 22.9 KV, 50 MVA HTS Power Cable. Doctoral Dissertation, Yonsei University, Seoul, Korea, 2011. [Google Scholar]
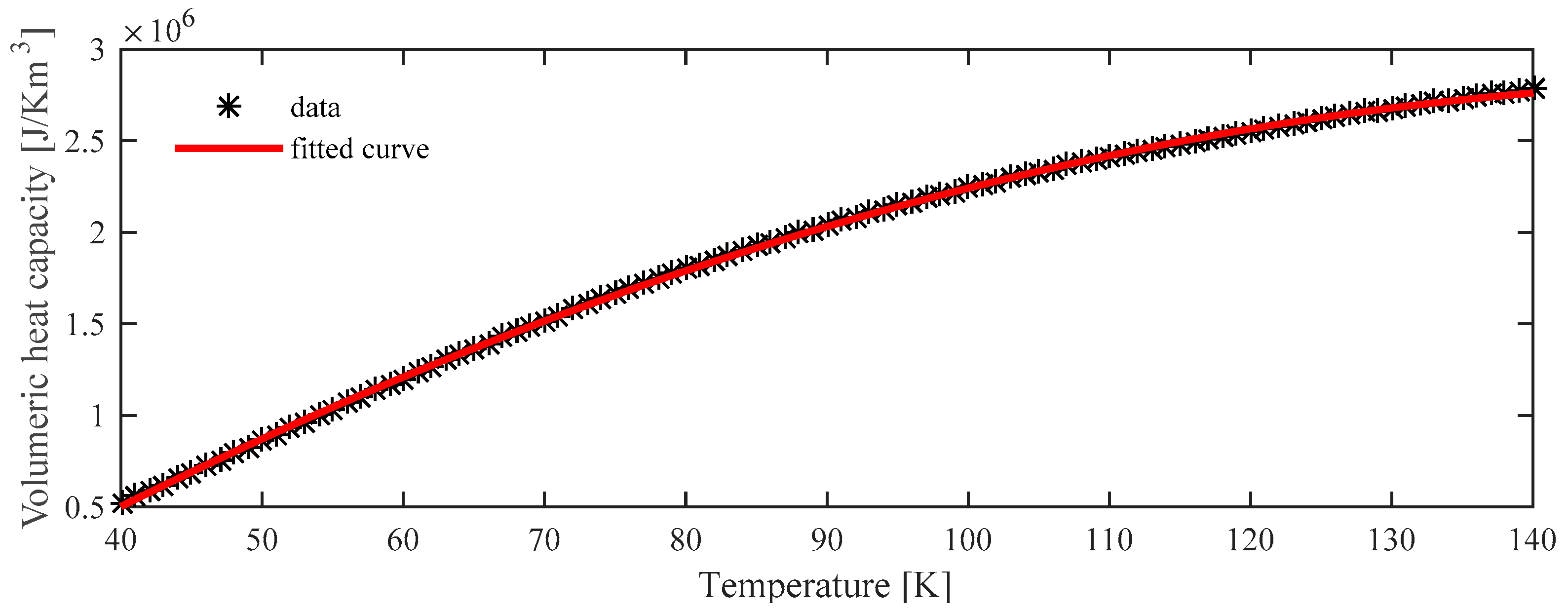
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| 4.89287 | −132.5425 | ||
| −57.51701 | 38.17399 | ||
| 238.2039 | −6.07962 | ||
| −345.4283 | 0.4118687 | ||
| 275.8975 |
| Parameter | Symbol | Value |
|---|---|---|
| Cable length | l | 3 km |
| Critical current | Ic | 3 kA |
| Resistance of HTS layer at normal state | RHTS_norm | 0.00000063 Ω/m |
| Resistance of HTS layer at transient state | RHTS_max | 2.5 mΩ/m |
| Winding pitches | Lp | 280 mm |
| Layer thickness | t | 1 mm |
| Former effective coefficient | k | 0.76 |
| Density of copper | DCu | 8900 kg/m3 |
| Relative permeability of copper | µr | 1 |
| Atomic mass of copper | µCu | 0.0635 kg/mol |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-T.; Lee, W.-G.; Lee, S.-J.; Park, M.; Kim, H.-M.; Won, D.; Yoo, J.; Yang, H.S. A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies. Energies 2019, 12, 1514. https://doi.org/10.3390/en12081514
Nguyen T-T, Lee W-G, Lee S-J, Park M, Kim H-M, Won D, Yoo J, Yang HS. A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies. Energies. 2019; 12(8):1514. https://doi.org/10.3390/en12081514
Chicago/Turabian StyleNguyen, Thai-Thanh, Woon-Gyu Lee, Seok-Ju Lee, Minwon Park, Hak-Man Kim, DuYean Won, Jaeun Yoo, and Hyung Suk Yang. 2019. "A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies" Energies 12, no. 8: 1514. https://doi.org/10.3390/en12081514
APA StyleNguyen, T.-T., Lee, W.-G., Lee, S.-J., Park, M., Kim, H.-M., Won, D., Yoo, J., & Yang, H. S. (2019). A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies. Energies, 12(8), 1514. https://doi.org/10.3390/en12081514






