Risk Based Maintenance in the Hydroelectric Power Plants
Abstract
:1. Introduction
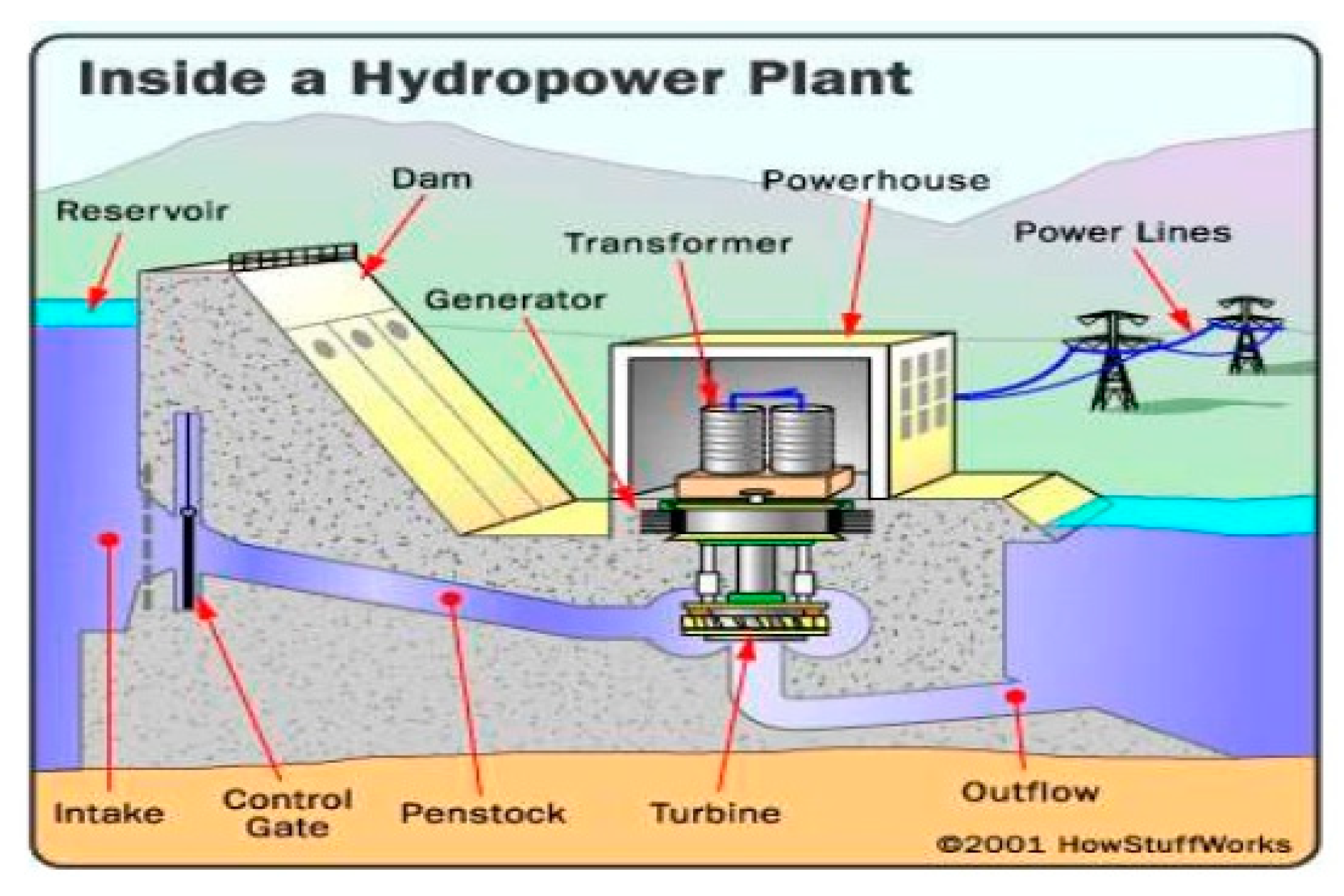
2. Operating and Maintenance Principles of Hydroelectric Power Facilities
- Corrective Maintenance Strategy: Repair and/or maintenance activities carried out in order for the machine/equipment to function in the design of the machine/equipment when it is unable to perform the expected task.
- Preventive Maintenance Strategy: Maintenance activities carried out within a timeline to ensure that the machine/equipment operates in uninterrupted and expected design specifications.
- Predictive Maintenance Strategy: It is the maintenance activities which include monitoring of the machine/equipment by using modern measurement and digital signal processing methods and taking necessary measures without failing according to the measurement results.
- Revision Maintenance Strategy: It is a maintenance strategy that requires periodic (8000 h or 5 years) of all critical equipment in the facility units, having a long time requirement (like 2 months) and stance of the central unit.
3. Studies in the Literature
4. Material and Method
4.1. AHP
4.2. TOPSIS
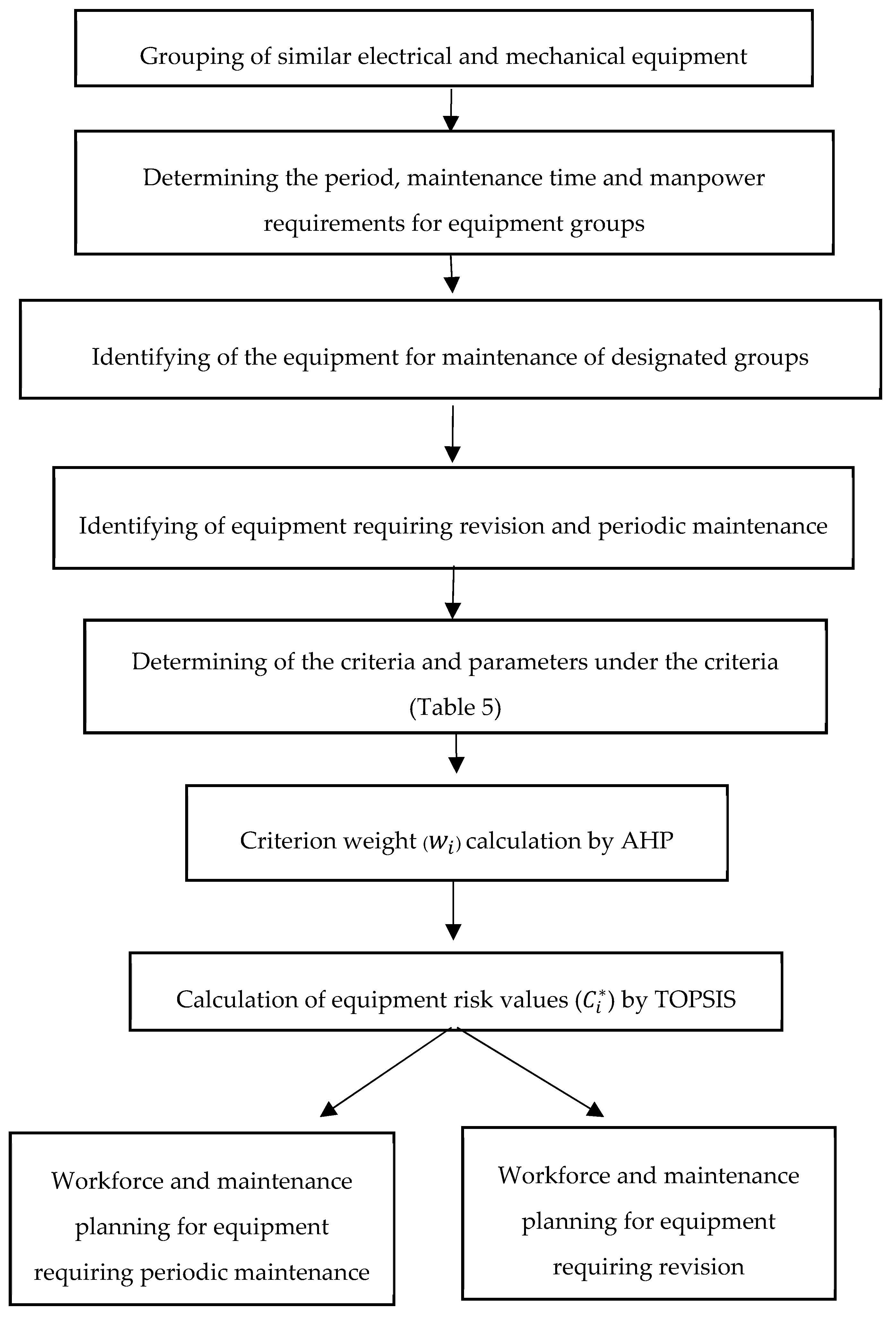
5. Case Study
5.1. Calculation of Risk Levels of Equipment in Terms of Facility
5.2. Revision and Periodic Maintenance Planning
5.2.1. Revision Maintenance Planning of Electrical Equipment
5.2.2. Revision Maintenance Planning of Mechanical Equipment
5.2.3. Periodic Maintenance Planning of Electrical Equipment
5.2.4. Periodic Maintenance Planning of Mechanical Equipment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Symbols and Acronyms
| Acronyms/Symbols | Explanation |
| AHP | Analytic Hierarchy Process |
| Am | Alternative m (mth equipment which is shown in Appendix B) |
| BDT | Boolean Decision Tree |
| C1 | Criteria 1 (Warehouse backup) |
| C2 | Criteria 2 (Maintenance pre-conditions) |
| C3 | Criteria 3 (Additional work requirement) |
| C4 | Criteria 4 (Failure period) |
| C5 | Criteria 5 (Possible consequences) |
| C6 | Criteria 6 (Availability of measuring equipment) |
| C7 | Criteria 7 (Static, dynamic or electrical property of equipment) |
| C8 | Criteria 8 (Fault shooting time) |
| C9 | Criteria 9 (Detectability of failure) |
| ELECTRE | Elimination and Choice Translating Reality English |
| FMEA | Failure Modes and Effects Analysis |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluation |
| S1 | Scenario 1 |
| S2 | Scenario 2 |
| S3 | Scenario 3 |
| WSM | Weighted Total Model |
| I&C | Instrumentation and Control |
| A | Comparison matrix (in AHP) |
| aij | Comparison matrix element (in AHP) |
| Bi | B column vectors (in AHP) |
| bij | B column vector element (in AHP) |
| Wi | Weight vector (in AHP) |
| wi | Weight vector element (in AHP) |
| D | D column vector (in AHP) |
| di | D column vector element (in AHP) |
| Ei | Base value vector (in AHP) |
| λ | Basic value (in AHP) |
| CI | Consistency index (in AHP) |
| RI | Random index (in AHP) |
| CR | Consistency ratio (in AHP) |
| Aij | Decision matrix (in TOPSIS) |
| aij | Decision matrix element (in TOPSIS) |
| Rij | Standard decision matrix (in TOPSIS) |
| rij | Standard decision matrix element (in TOPSIS) |
| Vij | Weighted standard decision matrix (in TOPSIS) |
| vij | Weighted standard decision matrix element (in TOPSIS) |
| A* | Ideal solution set (in TOPSIS) |
| A- | Negative ideal solution set (in TOPSIS) |
| v* | Ideal solution set element (in TOPSIS) |
| v- | Negative ideal solution set element (in TOPSIS) |
| Si* | Ideal solution (in TOPSIS) |
| Si- | Negative ideal solution (in TOPSIS) |
| Ci* | Closeness to ideal solution (in TOPSIS) |
Appendix A
| Criteria/Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1.000 | 0.200 | 2.000 | 1.000 | 0.111 | 1.000 | 1.000 | 2.000 | 1.000 |
| C2 | 5.000 | 1.000 | 9.000 | 4.000 | 0.200 | 4.000 | 5.000 | 9.000 | 5.000 |
| C3 | 0.500 | 0.111 | 1.000 | 0.333 | 0.111 | 0.500 | 0.500 | 1.000 | 1.000 |
| C4 | 1.000 | 0.250 | 3.000 | 1.000 | 0.143 | 1.000 | 1.000 | 3.000 | 1.000 |
| C5 | 9.000 | 5.000 | 9.000 | 7.000 | 1.000 | 7.000 | 8.000 | 9.000 | 3.000 |
| C6 | 1.000 | 0.250 | 2.000 | 1.000 | 0.143 | 1.000 | 1.000 | 2.000 | 1.000 |
| C7 | 1.000 | 0.200 | 2.000 | 1.000 | 0.125 | 1.000 | 1.000 | 2.000 | 1.000 |
| C8 | 0.500 | 0.111 | 1.000 | 0.333 | 0.111 | 0.500 | 0.500 | 1.000 | 0.500 |
| C9 | 1.000 | 0.200 | 1.000 | 1.000 | 0.333 | 1.000 | 1.000 | 2.000 | 1.000 |
Appendix B
| Alternative/Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 2 | 1 | 5 | 2 | 7 | 1 | 1 | 2 | 3 |
| A2 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A3 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A4 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A5 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A6 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A7 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A8 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A9 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A10 | 1 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A11 | 3 | 6 | 5 | 1 | 7 | 3 | 1 | 3 | 3 |
| A12 | 3 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A13 | 3 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A14 | 3 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A15 | 3 | 1 | 5 | 2 | 7 | 3 | 1 | 2 | 1 |
| A16 | 3 | 1 | 5 | 2 | 7 | 3 | 1 | 2 | 1 |
| A17 | 3 | 1 | 5 | 2 | 7 | 3 | 1 | 2 | 1 |
| A18 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A19 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A20 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A21 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A22 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A23 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A24 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A25 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A26 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A27 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A28 | 2 | 1 | 5 | 1 | 2 | 1 | 1 | 3 | 1 |
| A29 | 3 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
| A30 | 3 | 7 | 5 | 2 | 10 | 3 | 1 | 3 | 3 |
References
- Özcan, E.C.; Ünlüsoy, S.; Eren, T. A combined goal programming—AHP approach supported with TOPSIS for maintenance strategy selection in hydroelectric power plants. Renew. Sustain. Energy Rev. 2017, 78, 1410–1423. [Google Scholar] [CrossRef]
- Márquez, A.C. The Maintenance Management Framework: Models and Methods for Complex Systems Maintenance; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Özcan, E. Bakım Yönetim Sistemi: Kurulum ve İşletme Esasları; Elektrik Üretim, A.Ş., Ed.; Yayınları: Ankara, Turkey, 2016. [Google Scholar]
- YEGM. Yenilenebilir Enerji Kaynaklarından Elektrik Üreten Tesislerin Kurulu Güç Gelişimi. 2018. Available online: http://www.yegm.gov.tr/yenilenebilir.aspx (accessed on 18 April 2019).
- TEİAŞ. Aylık Elektrik İstatistikleri. 2018. Available online: https://www.teias.gov.tr/tr/elektrik-istatistikleri (accessed on 1 October 2018).
- Başeşme, H. Hidroelektrik Santrallar ve Hidroelektrik Santral Tesisleri; EÜAŞ Genel Müdürlüğü Hidrolik Santraller Dairesi Başkanlığı: Ankara, Turkey, 2003. [Google Scholar]
- Bonsor, K. Hydraulic Power Plant. HowStuffWorks. 2019. Available online: https://science.howstuffworks.com/environmental/energy/hydropower-plant1.htm) (accessed on 18 April 2019).
- Zhang, C.; Gao, W.; Guo, S.; Li, Y.; Yang, T. Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance. Renew. Energy 2017, 103, 606–612. [Google Scholar] [CrossRef]
- Alaswad, S.; Xiang, Y. A review on condition-based maintenance optimization models for stochastically deteriorating system. Reliab. Eng. Syst. Saf. 2017, 157, 54–63. [Google Scholar] [CrossRef]
- Khan, F.I.; Haddara, M.M. Risk-based maintenance (RBM): A quantitative approach for maintenance/inspection scheduling and planning. J. Loss Prev. Process Ind. 2003, 16, 561–573. [Google Scholar] [CrossRef]
- Krishnasamy, L.; Khan, F.; Haddara, M. Development of a risk-based maintenance (RBM) strategy for a power-generating plant. J. Loss Prev. Process Ind. 2005, 18, 69–81. [Google Scholar] [CrossRef]
- Doostparast, M.; Kolahan, F.; Doostparast, M. A reliability-based approach to optimize preventive maintenance scheduling for coherent systems. Reliab. Eng. Syst. Saf. 2014, 126, 98–106. [Google Scholar] [CrossRef]
- Kobbacy, K.A.H. Application of Artificial Intelligence in maintenance modelling and management. IFAC Proc. Vol. 2012, 45, 54–59. [Google Scholar] [CrossRef]
- Carlos, S.; Sanchez, A.; Martorell, S.; Villanueva, J. Advances in Engineering Software Particle Swarm Optimization of safety components and systems of nuclear power plants under uncertain maintenance planning. Adv. Eng. Softw. 2012, 50, 12–18. [Google Scholar] [CrossRef]
- Chalabi, N.; Dahane, M.; Beldjilali, B.; Neki, A. Computers & industrial engineering optimisation of preventive maintenance grouping strategy for multi-component series systems: Particle swarm based approach. Comput. Ind. Eng. 2016, 102, 440–451. [Google Scholar] [CrossRef]
- Upasani, K.; Bakshi, M.; Pandhare, V.; Kumar, B. Computers & industrial engineering. Comput. Ind. Eng. 2017, 108, 1–14. [Google Scholar] [CrossRef]
- Borgonovo, E.; Marseguerra, M.; Zio, E. A Monte Carlo methodological approach to plant availability modeling with maintenance, aging and obsolescence. Reliab. Eng. Syst. Saf. 2000, 67, 61–73. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E.; Podofillini, L. Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation. Reliab. Eng. Syst. Saf. 2002, 77, 151–165. [Google Scholar] [CrossRef]
- Arzaghi, E.; Mahdi, M.; Abbassi, R.; Garaniya, V. Risk-based maintenance planning of subsea pipelines through fatigue crack growth monitoring. Eng. Fail. Anal. 2017, 79, 928–939. [Google Scholar] [CrossRef]
- Lapa, C.M.F.; Pereira, C.M.N.A.; e Melo, P.F.F. Surveillance test policy optimization through genetic algorithms using non-periodic intervention frequencies and considering seasonal constraints. Reliab. Eng. Syst. Saf. 2003, 81, 103–109. [Google Scholar] [CrossRef]
- Levitin, G.; Lisnianski, A. Joint redundancy and maintenance optimization for multistate series—Parallel systems. Reliab. Eng. Syst. Saf. 1999, 64, 33–42. [Google Scholar] [CrossRef]
- Busacca, P.G.; Marseguerra, M.; Zio, E. Multiobjective optimization by genetic algorithms: Application to safety systems. Reliab. Eng. Syst. Saf. 2001, 72, 59–74. [Google Scholar] [CrossRef]
- Xia, X. Control problems in building energy retrofit and maintenance planning. Annu. Rev. Control 2017, 44, 78–88. [Google Scholar] [CrossRef]
- Gopalakrishnan, M.; Skoogh, A.; Laroque, C. Simulation-based planning of maintenance activities in the automotive industry. In Proceedings of the Winter Simulations Conference (WSC), Washington, DC, USA, 8–11 December 2013. [Google Scholar] [CrossRef]
- Ilangkumaran, M.; Kumanan, S. Selection of maintenance policy for textile industry using hybrid multi-criteria decision making approach. J. Manuf. Technol. Manag. 2009, 20, 1009–1022. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Maiti, J. Risk-based maintenance policy selection using AHP and goal programming. Saf. Sci. 2010, 48, 238–247. [Google Scholar] [CrossRef]
- Hu, H.; Cheng, G.; Li, Y.; Tang, Y. Risk-based maintenance strategy and its applications in a petrochemical reforming reaction system. J. Loss Prev. Process Ind. 2009, 22, 392–397. [Google Scholar] [CrossRef]
- Froger, A.; Gendreau, M.; Mendoza, J.E.; Pinson, É.; Rousseau, L. Maintenance scheduling in the electricity industry: A literature review. Eur. J. Oper. Res. 2016, 251, 695–706. [Google Scholar] [CrossRef]
- Yssaad, B.; Abene, A. Rational reliability centered maintenance optimization for power distribution systems. Int. J. Electr. Power Energy Syst. 2015, 73, 350–360. [Google Scholar] [CrossRef]
- Sheikhalishahi, M.; Azadeh, A.; Pintelon, L. Dynamic maintenance planning approach by considering grouping strategy and human factors. Process Saf. Environ. Prot. 2017, 107, 289–298. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.; Wu, X.; Zhai, J.; Shao, W.; Duan, Y. Multi-time Scales Coordination Scheduling of Wind Power Integrated System. In Proceedings of the IEEE PES Innovative Smart Grid Technologies ASIA (ISGT Asia 2012), Tianjin, China, 21–24 May 2012; pp. 1–4. [Google Scholar]
- Backlund, F.; Hannu, J. Can we make maintenance decisions on risk analysis results? J. Qual. Maint. Eng. 2002, 8, 77–91. [Google Scholar] [CrossRef]
- Harnly, J.A. Risk based prioritization of maintenance repair work. Process Saf. Prog. 1998, 17, 32–38. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Maiti, J. Risk-based maintenance—Techniques and applications. J. Hazard. Mater. 2007, 142, 653–661. [Google Scholar] [CrossRef]
- Chareonsuk, C.; Nagarur, N.; Tabucanon, M.T. A multicriteria approach to the selection of preventive maintenance intervals. Int. J. Prod. Econ. 1997, 49, 55–64. [Google Scholar] [CrossRef]
- Chybowski, L.; Gawdzińska, K. On the Present State-of-the-Art of a Component Importance Analysis for Complex Technical Systems. In New Advances in Information Systems and Technologies; Springer: Cham, Germany, 2016; pp. 691–700. [Google Scholar]
- Chybowski, L.; Gawdzińska, K. On the Possibilities of Applying the AHP Method to a Multi-Criteria Component Importance Analysis of Complex Technical Objects. In New Advances in Information Systems and Technologies; Springer: Cham, Germany, 2016; pp. 701–710. [Google Scholar]
- Dey, P.K. A risk-based model for inspection and maintenance of cross-country petroleum pipeline. J. Qual. Maint. Eng. 2001, 7, 25–43. [Google Scholar] [CrossRef]
- Moazami, D.; Behbahani, H.; Muniandy, R. Expert systems with applications pavement rehabilitation and maintenance prioritization of urban roads using fuzzy logic. Expert Syst. Appl. 2011, 38, 12869–12879. [Google Scholar] [CrossRef]
- Chybowski, L.; Twardochleb, M.; Wiśnicki, B. Multi-criteria decision making in components importance analysis applied to a complex marine system. NAŠE MORE 2016, 63, 264–270. [Google Scholar] [CrossRef]
- Dhanisetty, V.S.V.; Verhagen, W.J.C.; Curran, R.J. Multi-criteria weighted decision making for operational maintenance processes. J. Air Transp. Manag. 2018, 68, 152–164. [Google Scholar] [CrossRef]
- De Almeida, A.T. Multicriteria model for selection of preventive maintenance intervals. Qual. ad Relia. Eng. Int. 2012, 28, 585–593. [Google Scholar] [CrossRef]
- Certa, A.; Enea, M.; Lupo, T. ELECTRE III to dynamically support the decision maker about the periodic replacements configurations for a multi-component system. Decis. Support Syst. 2013, 55, 126–134. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Opudo, J.; Nyambenya, S. Comparison of fuzzy AHP and fuzzy TOPSIS for road pavement maintenance prioritization: Methodological exposition and case study. Adv. Civ. Eng. 2015. [Google Scholar] [CrossRef]
- Azadeh, A.; Nazari-Shirkouhi, S.; Hatami-Shirkouhi, L.; Ansarinejad, A. A unique fuzzy multi-criteria decision making: Computer simulation approach for productive operators’ assignment in cellular manufacturing systems with uncertainty and vagueness. Int. J. Adv. Manuf. Technol. 2011, 56, 329–343. [Google Scholar] [CrossRef]
- Seiti, H.; Hafezalkotob, A. Developing the R-TOPSIS methodology for risk-based preventive maintenance planning: A case study in rolling mill company. Comput. Ind. Eng. 2019, 128, 622–636. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytical Hierarchy Process. Encyclopedia Biostat. 2005. [Google Scholar] [CrossRef]
- Gür, Ş.; Hamurcu, M.; Eren, T. Ankara’da Monoray projelerinin analitik hiyerarşi prosesi ve 0-1 hedef programlama yöntemleri ile seçimi. Pamukkale Üniv. Mühendis. Bilim. Derg. 2017, 23, 437–443. [Google Scholar]
- Uçakcıoğlu, B.; Eren, T. Hava Savunma Sanayinde Yatırım Projelerinin Çok Ölçütlü Karar Verme ve Hedef Programlama ile Seçimi. J. Aviat. 2017, 1, 39–63. [Google Scholar] [CrossRef]
- Taş, M.; Özlemiş, Ş.N.; Hamurcu, M.; Eren, T. Ankara’da AHP ve PROMETHEE yaklaşımıyla monoray hat tipinin belirlenmesi. Ekon. İşletme Siyaset ve Uluslararası İlişkiler Derg. 2017, 3, 65–89. [Google Scholar]
- Özyörük, B.; Özcan, E.C. Analitik Hiyerarşi Sürecinin Tedarikçi Seçiminde Uygulanmasi: Otomotiv Sektöründen Bir Örnek. Süleyman Demirel Üniversitesi İktisadi ve İdari Bilim. Fakültesi Derg. 2008, 13, 133–144. [Google Scholar]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin, Germany, 1981; pp. 58–191. [Google Scholar]
- Taş, C.; Bedir, N.; Eren, T.; Alağaş, H.M.; Çetin, S. AHP-TOPSIS yöntemleri entegrasyonu ile poliklinik değerlendirilmesi: Ankara’da bir uygulama. Sağlık Yönetimi Derg. 2018, 2, 1–16. [Google Scholar]
- Özcan, E.C.; Ünlüsoy, S.; Eren, T. ANP ve Topsis yöntemleriyle Türkiye’de yenilenebilir enerji yatırım alternatiflerinin değerlendirilmesi. Selcuk Uni. J. Eng. 2017, 5, 204–219. [Google Scholar] [CrossRef]
- Arıbaş, M.; Özcan, U. Akademik Araştırma Projelerinin AHP ve TOPSIS Yöntemleri Kullanılarak Değerlendirilmesi. Politek. Derg. 2016, 19, 163–173. [Google Scholar]
- Albayrak, B. 2016 Yılı Bütçe Sunumu. Enerji ve Tabii kaynaklar Bakanlığı. Available online: https://docplayer.biz.tr/17246161-2016-yili-butce-sunumu-t-c-enerji-ve-tabii-kaynaklar-bakani-sayin-dr-berat-albayrak-in-2016-yili-butcesini-tbmm-genel-kurulu-na-sunus-metni.html (accessed on 18 April 2019).
| Importance Values | Value Definitions |
|---|---|
| 1 | Equally important |
| 3 | Partly more important |
| 5 | Much more important |
| 7 | Extremely more important |
| 9 | Certainly more important |
| 2, 4, 6, 8 | Intermediate values |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 | 12 | 13 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.41 | 1.45 | 1.49 | 1.51 | 1.48 | 1.56 |
| Equipment Group | Maintenance Period (min) | Labor Requirement (person) |
|---|---|---|
| Switching bus bar disconnectors | 480 | 3 |
| Generator | 3840 | 18 |
| Warning transformer | 3840 | 3 |
| 380 kV switchyard breaker | 480 | 4 |
| 380 kV switchyard current transformer | 120 | 2 |
| 380 kV switchyard voltage transformer | 120 | 2 |
| Main power transformer | 2400 | 8 |
| Internal transformer | 240 | 4 |
| Equipment Group | Maintenance Period (min) | Labor Requirement (person) |
|---|---|---|
| Adjusting blade | 17355 | 18 |
| Oil tank | 1120 | 16 |
| The butterfly valve | 1750 | 8 |
| Snail wheel | 360 | 8 |
| Turbine | 960 | 12 |
| Speed Regulator | 495 | 8 |
| Generator lower top guide bearing | 135 | 8 |
| Brake system | 600 | 4 |
| Cooling water structure | 720 | 6 |
| Suction pipe | 615 | 8 |
| Criteria | Criteria Parameters | Numerical Equivalents of the Parameters | |
|---|---|---|---|
| C1 | Warehouse backup | Never | 3 |
| Sometimes | 2 | ||
| All the time | 1 | ||
| C2 | Maintenance pre-conditions | Unit shutdown | 7 |
| Shutdown by situation | 6 | ||
| Shutdown by time | 5 | ||
| Maintenance without back up | 2 | ||
| Shutdown does not require | 1 | ||
| C3 | Additional work requirement | Required | 5 |
| Not required | 1 | ||
| C4 | Failure period | Monthly | 8 |
| Quarterly | 5 | ||
| Semi-annually | 3 | ||
| Annually | 2 | ||
| Long term | 1 | ||
| Unknown | 1 | ||
| C5 | Possible consequences | Unit shutdown | 10 |
| Problem in emergency situation | 9 | ||
| Load reduction | 8 | ||
| Running without back up | 7 | ||
| Equipment shutdown | 6 | ||
| Security problem | 6 | ||
| Deficient function | 2 | ||
| Damage in associated equipment | 2 | ||
| Problem in start | 1 | ||
| Fluid consumption increase | 1 | ||
| C6 | Availability of measuring equipment | Yes | 3 |
| No | 1 | ||
| C7 | Static, dynamic or electrical property of equipment | Mechanical-dynamic | 2 |
| Mechanical-static | 1 | ||
| Electrical | 1 | ||
| I and C | 1 | ||
| C8 | Fault shooting time | One week | 9 |
| More than one day | 3 | ||
| Unknown | 3 | ||
| 2–8 h | 2 | ||
| Less than 2 h | 1 | ||
| C9 | Detectability of failure | Difficult | 3 |
| Easy | 1 | ||
| Criteria | Weights | |
|---|---|---|
| C1 | Warehouse backup | 0.055 |
| C2 | Maintenance pre-conditions | 0.239 |
| C3 | Additional work requirement | 0.033 |
| C4 | Failure period | 0.065 |
| C5 | Possible consequences | 0.402 |
| C6 | Availability of measuring equipment | 0.058 |
| C7 | Static, dynamic or electrical property of equipment | 0.056 |
| C8 | Fault shooting time | 0.029 |
| C9 | Detectability of failure | 0.062 |
| Equipment Name | C* |
|---|---|
| 220 V DC accumulators | 27.11 |
| 380 kV switchyard current transformer l1 phase | 95.02 |
| 380 kV switchyard voltage transformer l3 phase | 95.02 |
| 380 kV switchyard circuit breaker l3 phase | 95.02 |
| 6.3 kV breakers | 78.69 |
| A bus bar separator l3 phase | 100.00 |
| Main hook quick load lifting brake motor | 7.02 |
| Drive-in drive motors | 7.02 |
| Pressure less oil tank cooling pump drive motor | 63.93 |
| SCENARIO DETAILS | ||||||
|---|---|---|---|---|---|---|
| Scenario No | # Equip. | Total Time Requirement (min) | Distributed Time Requirement to Team (min) | Net Duration (days) | Duration per Unit (days) | Priority Range of Equipment |
| S1 | 192 | 477,600 | 39,800 | 82.92 | 16.58 | 85.81–100 |
| S2 | 8 | 7200 | 600 | 1.25 | 0.25 | 9.05–9.05 |
| TOTAL | 200 | 484,800 | 40,400 | 84 | 17 | - |
| Scenario Details | ||||||
|---|---|---|---|---|---|---|
| Scenario No | # Equip. | Total Time Requirement (min) | Distributed Time Requirement to Team (min) | Net Duration (days) | Duration per Unit (days) | Priority Range of Equipment |
| S1 | 230 | 1,464,480 | 122,040 | 254.25 | 50.85 | 95.91–97.97 |
| S2 | 16 | 43,200 | 3600 | 7.50 | 1.50 | 35.08–35.12 |
| S3 | 32 | 59,040 | 4920 | 10.25 | 2.05 | 6.78–8.06 |
| TOTAL | 278 | 1,566,720 | 130,560 | 272 | 54 | - |
| Scenario Details | ||||||
|---|---|---|---|---|---|---|
| No | Period | # Equip. | Total Time Requirement (min) | Distributed Time Requirement to Team (min) | Net duration requirement (day) | Priority Range of Equipment |
| S1 | 1 Week | 24 | 74,880 | 6240 | 13.00 | 95.02–95.02 |
| 1 Month | 72 | 172,800 | 14,400 | 30.00 | 95.02–100 | |
| 6 Months | 3 | 4320 | 360 | 0.75 | 94.16–94.16 | |
| S2 | 6 Month | 49 | 70,560 | 5880 | 12.25 | 63.93–83.79 |
| 1 Year | 8 | 5760 | 480 | 1.00 | 78.69–78.69 | |
| S3 | 1 Month | 5 | 32,640 | 2720 | 5.67 | 27.11–27.35 |
| 6 Month | 40 | 53,760 | 4480 | 9.33 | 6.71–33.37 | |
| 1 Year | 111 | 40,080 | 3340 | 6.96 | 7.02–33.27 | |
| Total | 312 | 454,800 | 37,900 | 79 | - | |
| Scenario Details | ||||||
|---|---|---|---|---|---|---|
| No | Period | # Equip. | Total Time Requirement (min) | Distributed Time Requirement to Team (min) | Net Duration (days) | Priority Range of Equipment |
| S1 | 1 Month | 133 | 107,640 | 6728 | 14.02 | 95.91–97.97 |
| 3 Month | 184 | 71,920 | 4495 | 9.36 | 95.91–97.83 | |
| 6 Month | 49 | 6120 | 383 | 0.80 | 96.51–97.54 | |
| 1 Year | 8 | 1920 | 120 | 0.25 | 97.97–97.97 | |
| S2 | 1 Week | 30 | 101,520 | 6345 | 13.22 | 71.42–82.49 |
| 3 Month | 8 | 3840 | 240 | 0.50 | 75.63–75.63 | |
| 6 Month | 4 | 1440 | 90 | 0.19 | 71.42–82.49 | |
| 1 Year | 30 | 40,800 | 2550 | 5.31 | 71.42–82.49 | |
| 2 Year | 1 | 2880 | 180 | 0.38 | 82.64 | |
| S3 | 1 Month | 38 | 15,720 | 983 | 2.05 | 6.78–33.19 |
| 3 Month | 63 | 43,040 | 2690 | 5.60 | 5.86–26.40 | |
| 6 Month | 44 | 29,760 | 1860 | 3.88 | 5.37–10.52 | |
| 1 Year | 7 | 1300 | 81 | 0.17 | 5.86–32.26 | |
| 2 Year | 1 | 4500 | 281 | 0.59 | 26.32 | |
| Total | 565 | 432,400 | 27,025 | 56 | - | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özcan, E.; Yumuşak, R.; Eren, T. Risk Based Maintenance in the Hydroelectric Power Plants. Energies 2019, 12, 1502. https://doi.org/10.3390/en12081502
Özcan E, Yumuşak R, Eren T. Risk Based Maintenance in the Hydroelectric Power Plants. Energies. 2019; 12(8):1502. https://doi.org/10.3390/en12081502
Chicago/Turabian StyleÖzcan, Evrencan, Rabia Yumuşak, and Tamer Eren. 2019. "Risk Based Maintenance in the Hydroelectric Power Plants" Energies 12, no. 8: 1502. https://doi.org/10.3390/en12081502
APA StyleÖzcan, E., Yumuşak, R., & Eren, T. (2019). Risk Based Maintenance in the Hydroelectric Power Plants. Energies, 12(8), 1502. https://doi.org/10.3390/en12081502





