The Magnetic Field and Impedances in Three-Phase Rectangular Busbars with a Finite Length
Abstract
1. Introduction
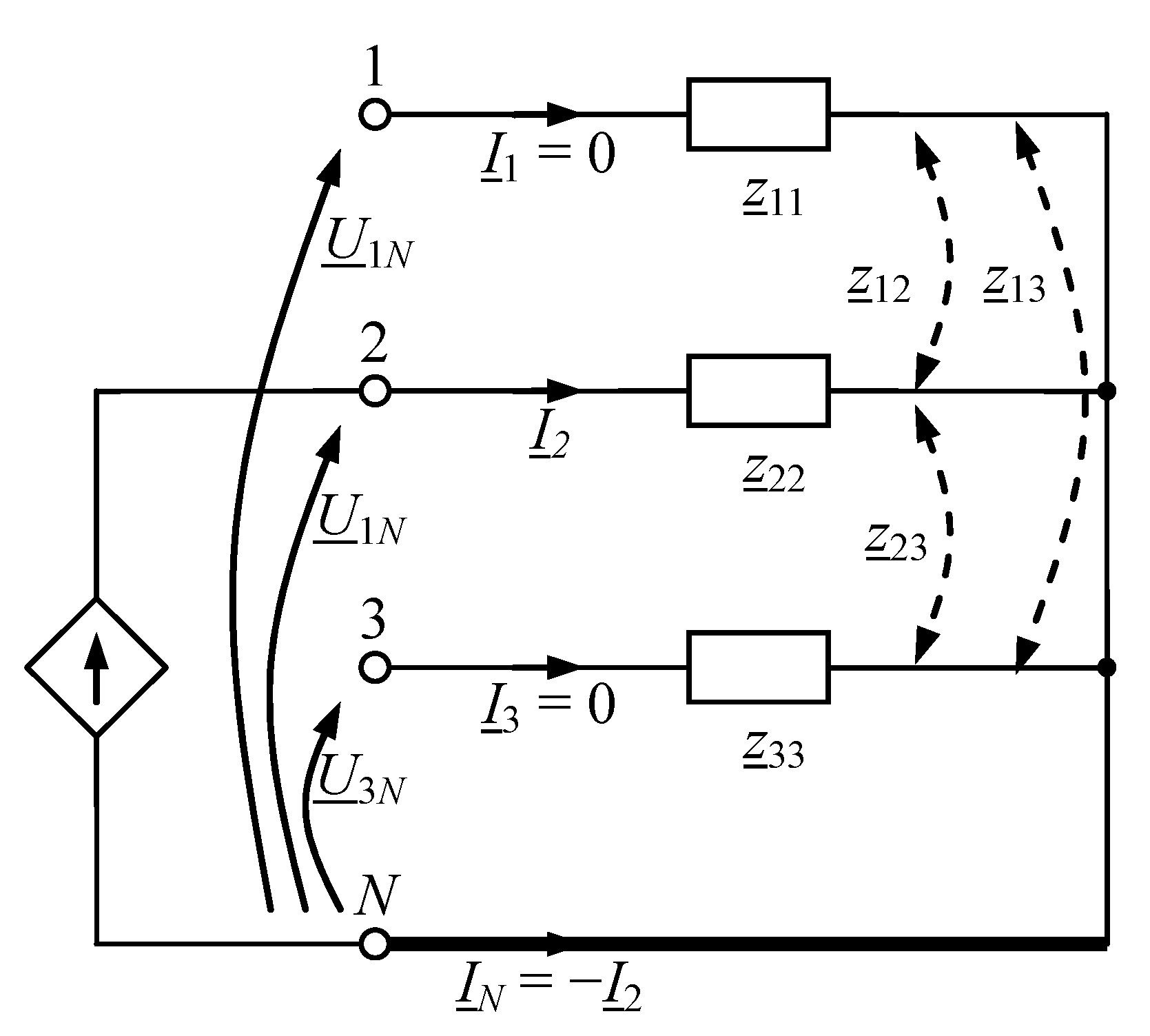
2. Impedances Rectangular Busbars with a Finite Length
2.1. Impedance—Analytic Equations
2.2. Impedances—Calculation Example
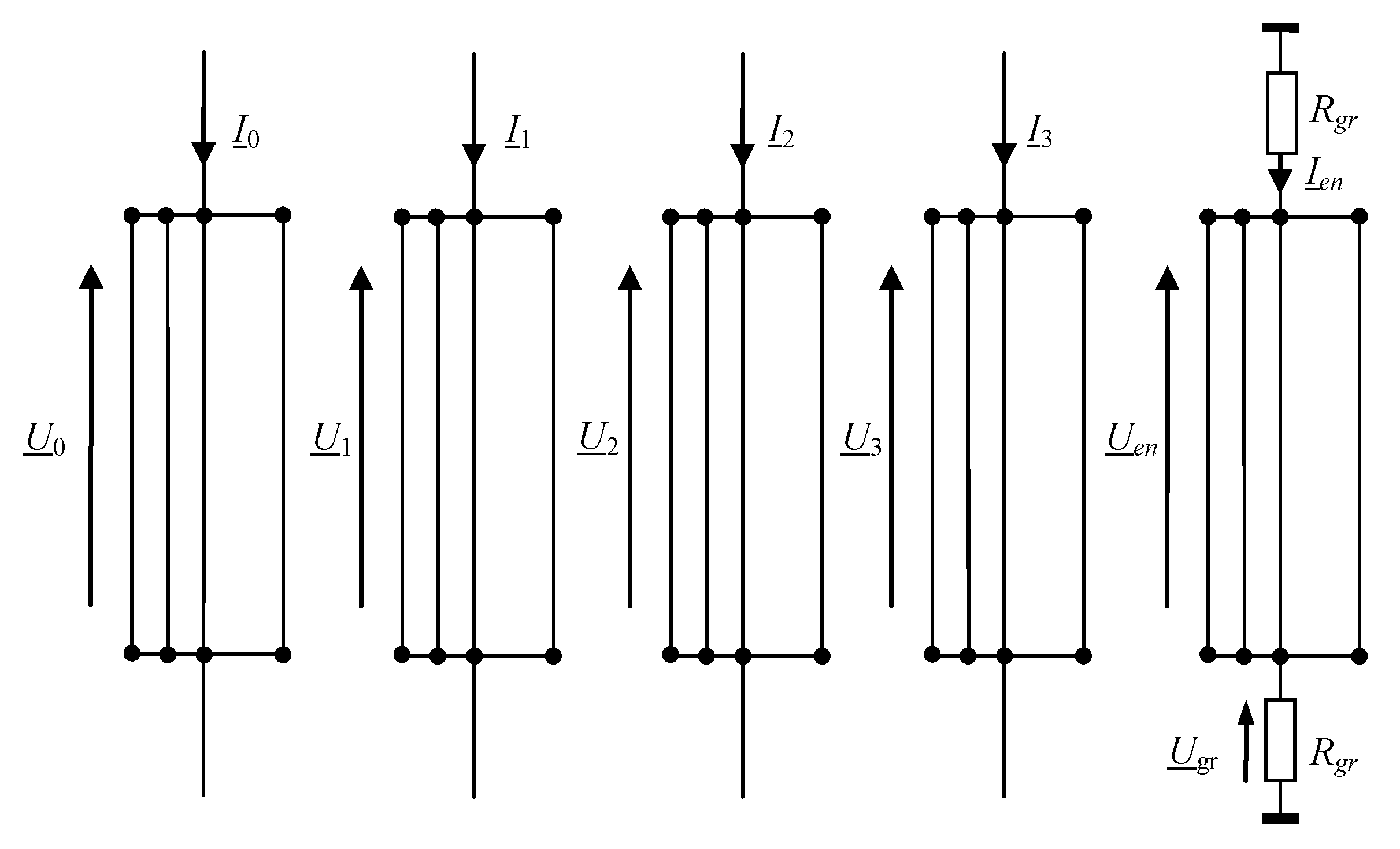
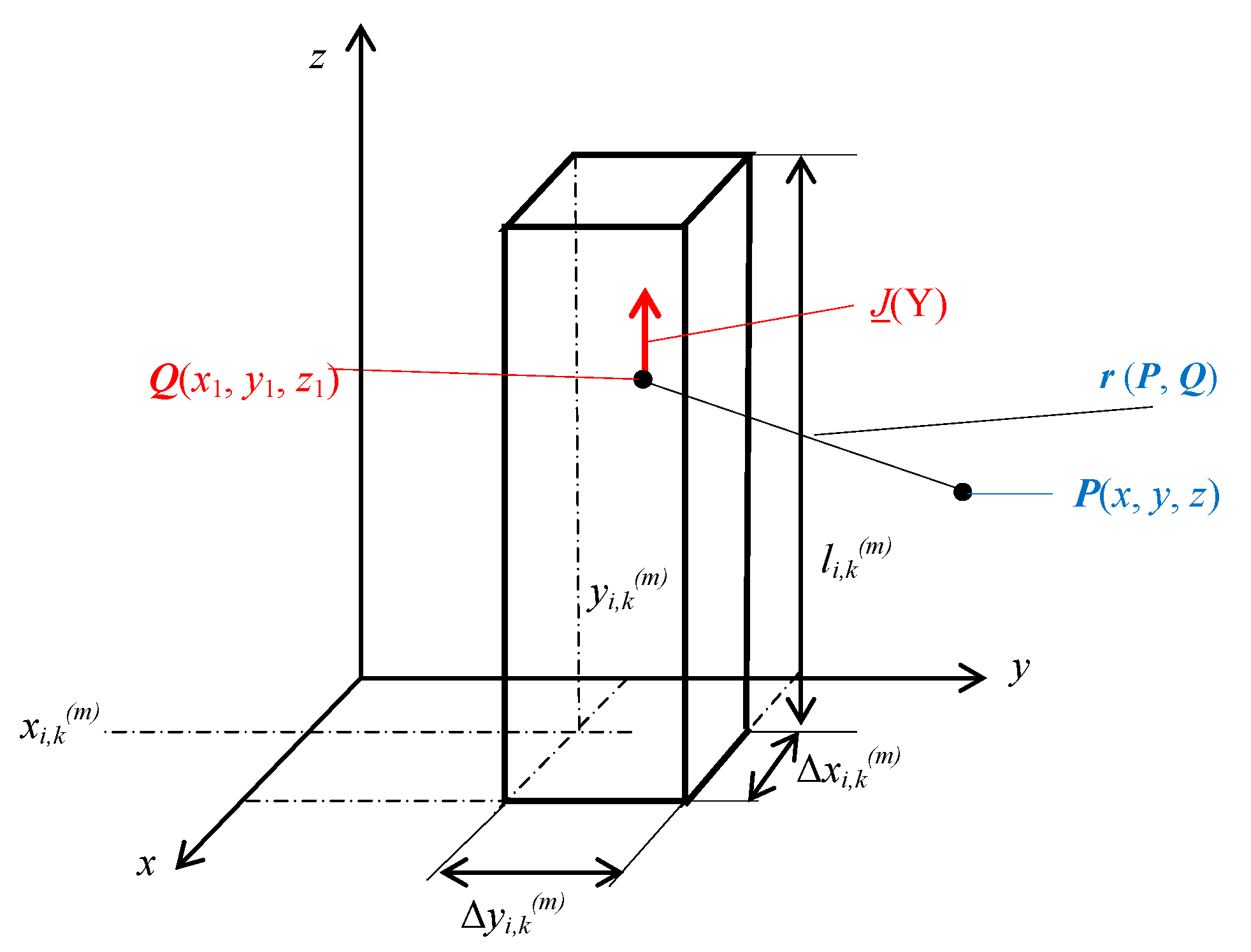
3. Magnetic Field of the Three-Phase Rectangular Busbars with a Finite Length
3.1. Current Densities at Rectangular Busducts
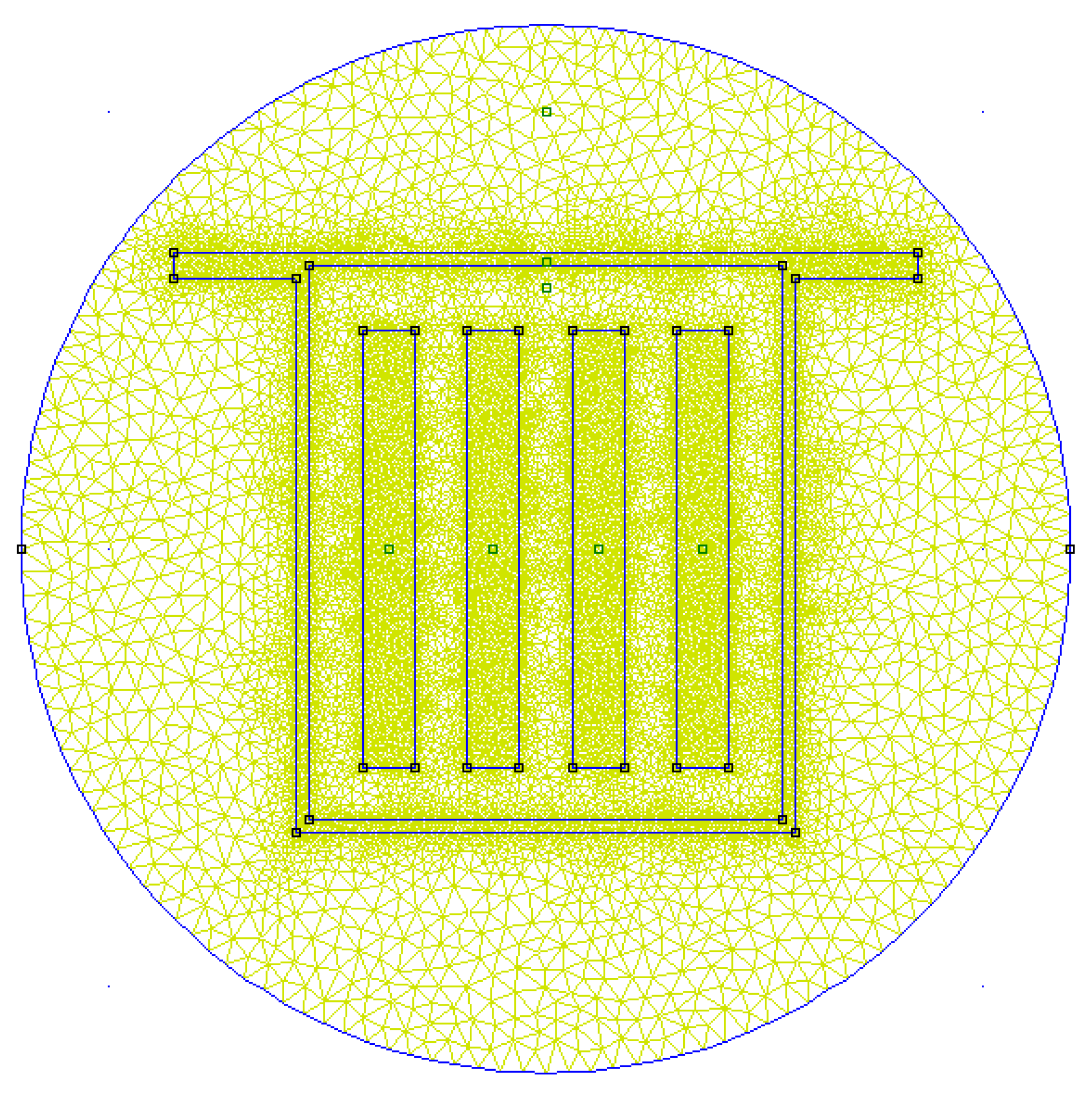
3.2. Magnetic Field of Rectangular Busducts
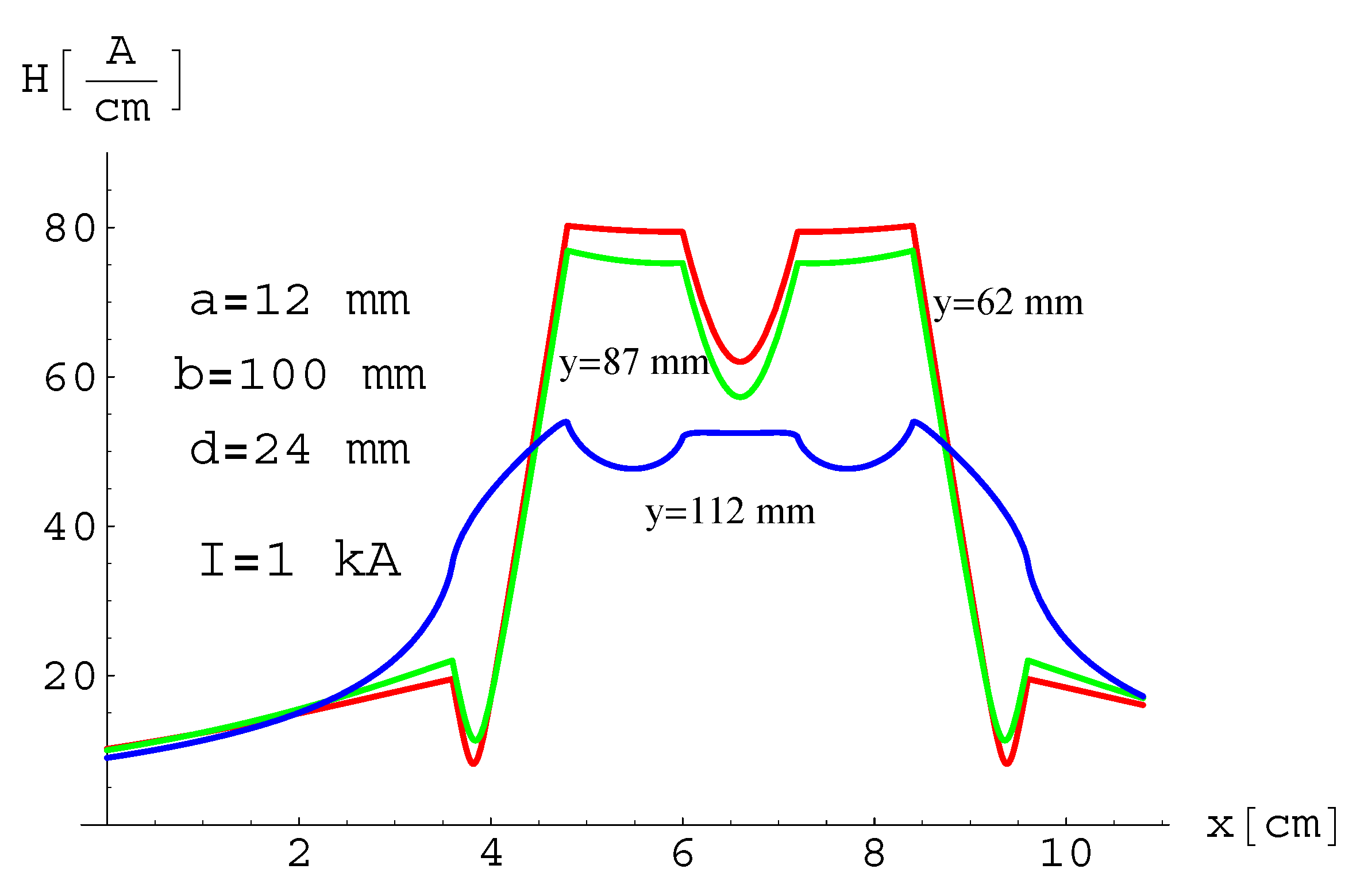
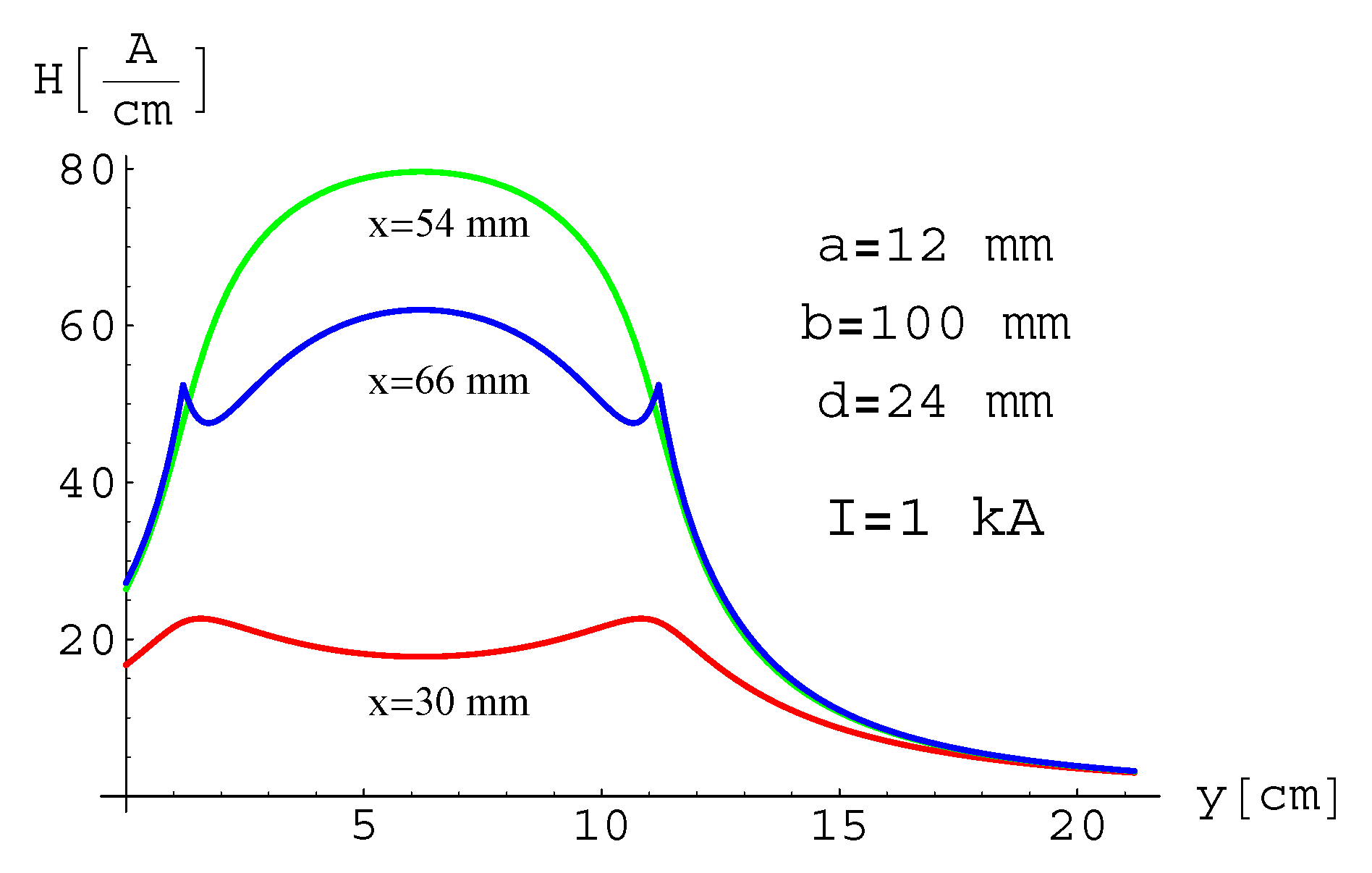
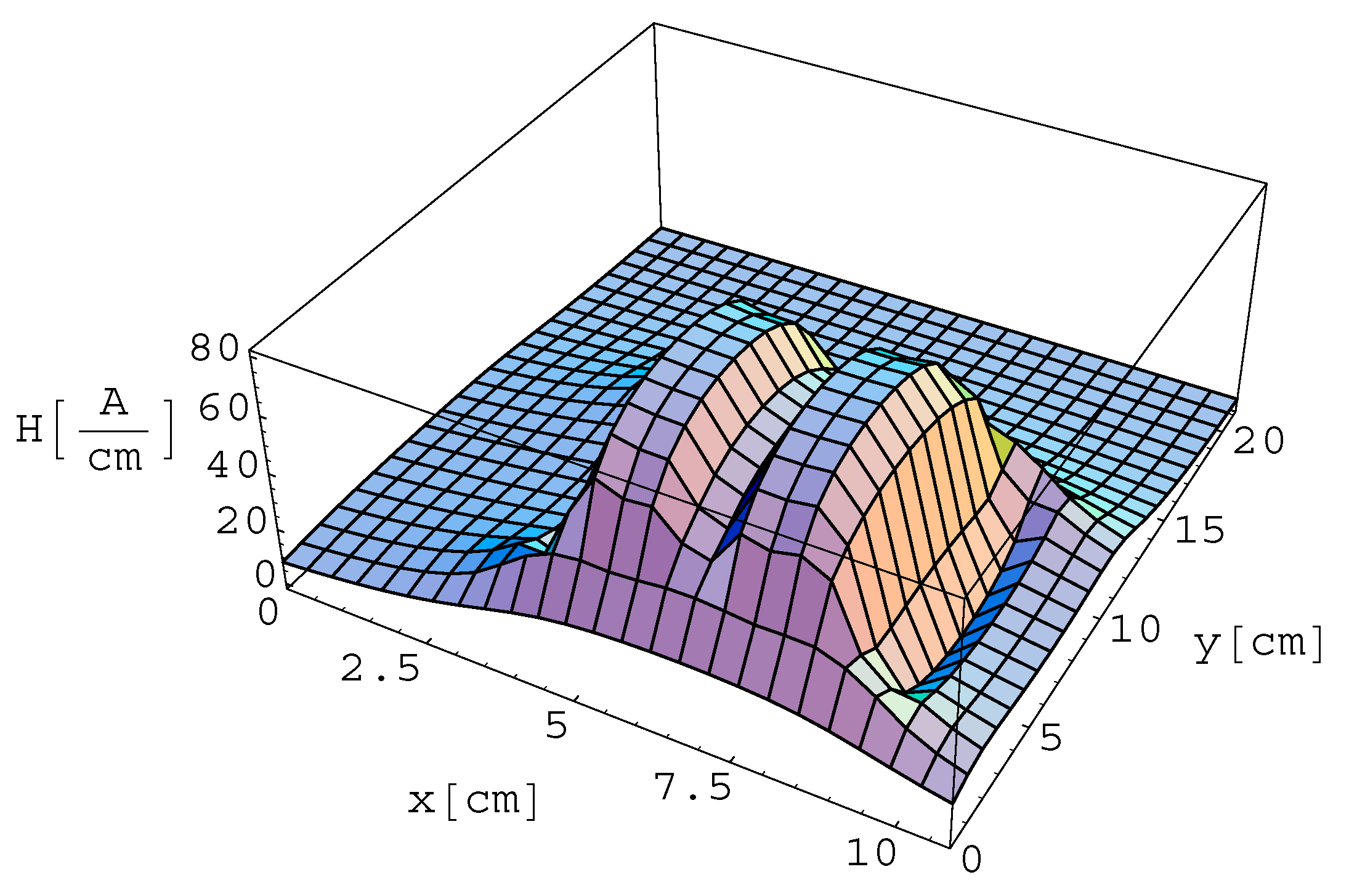
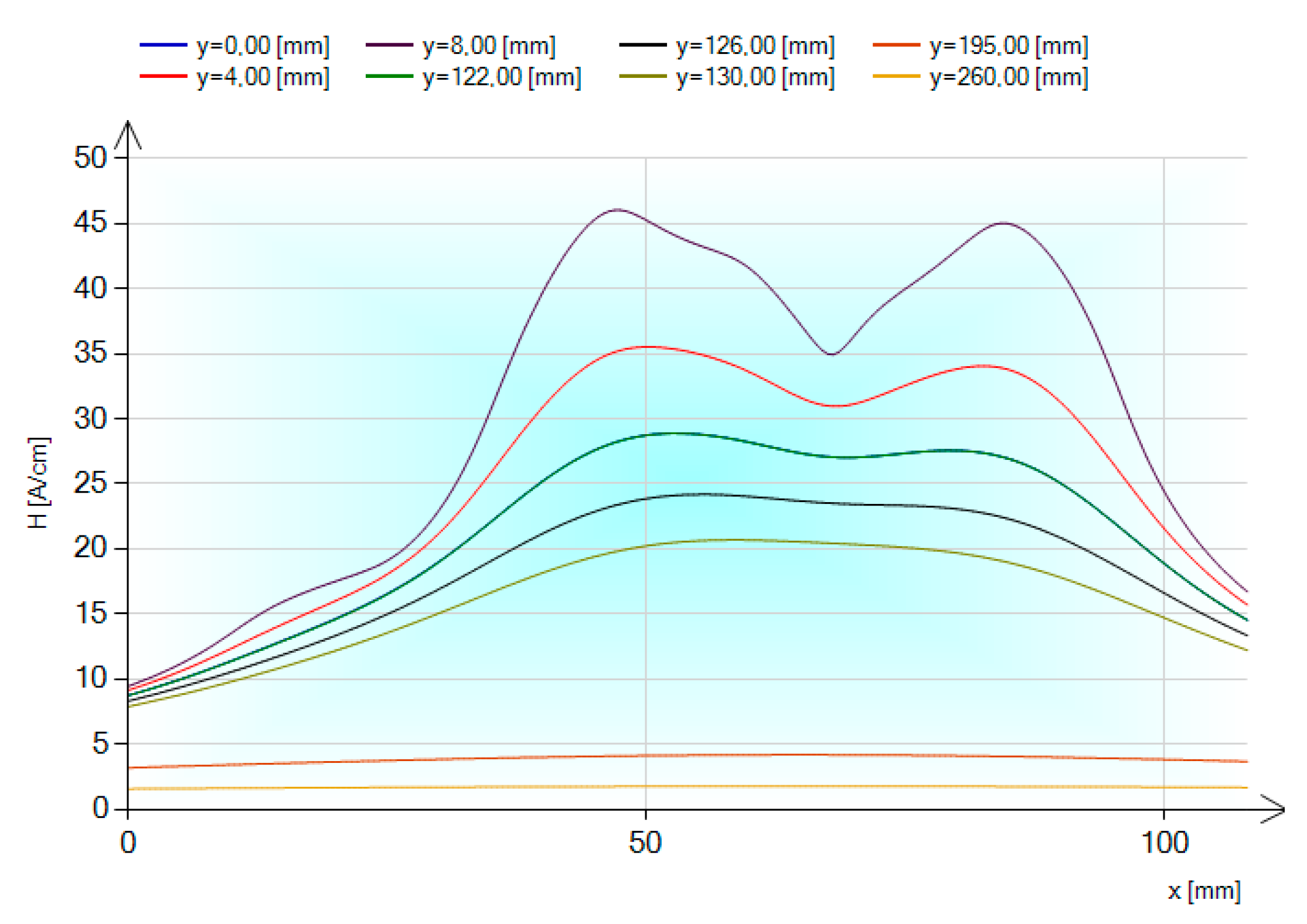
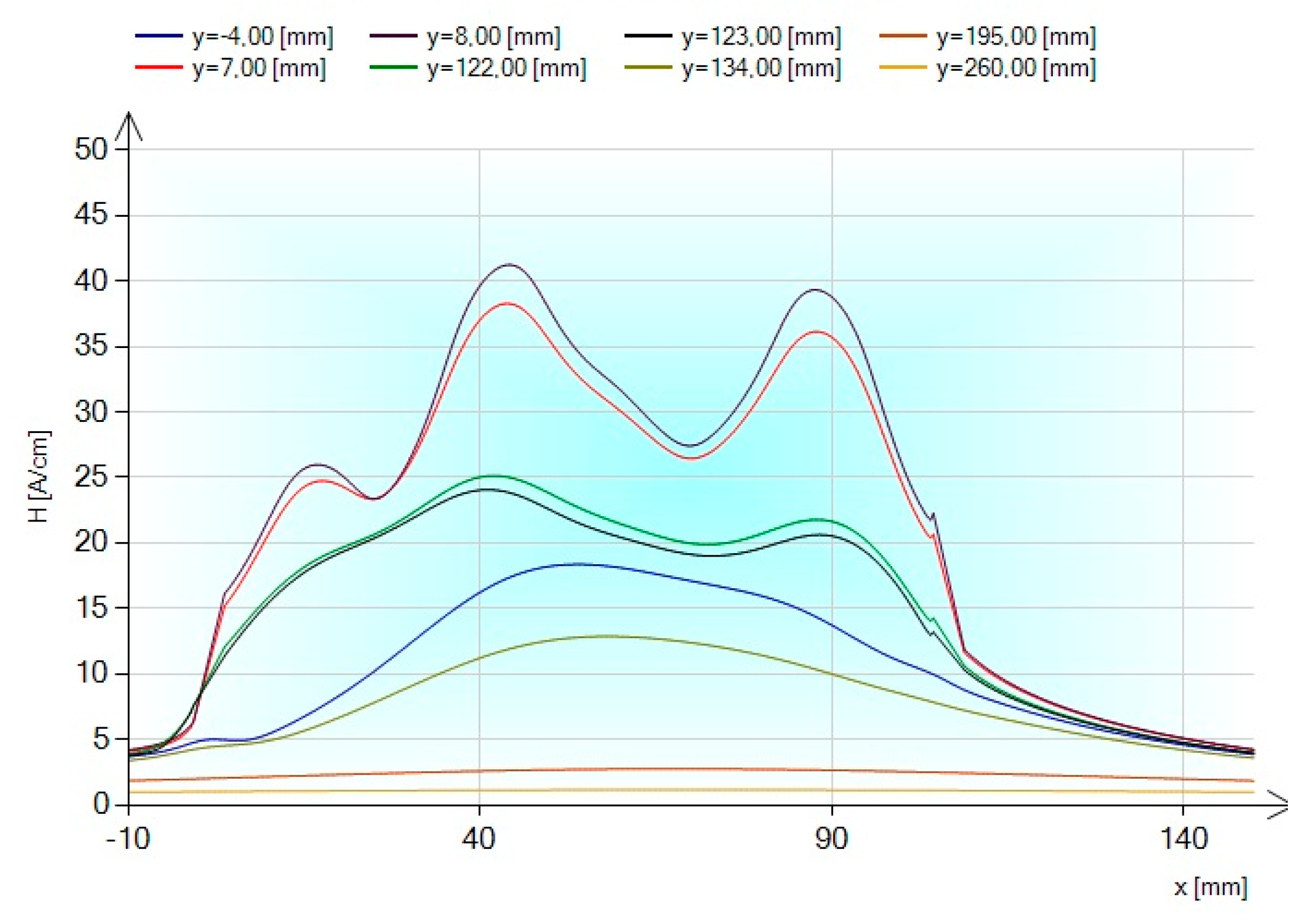
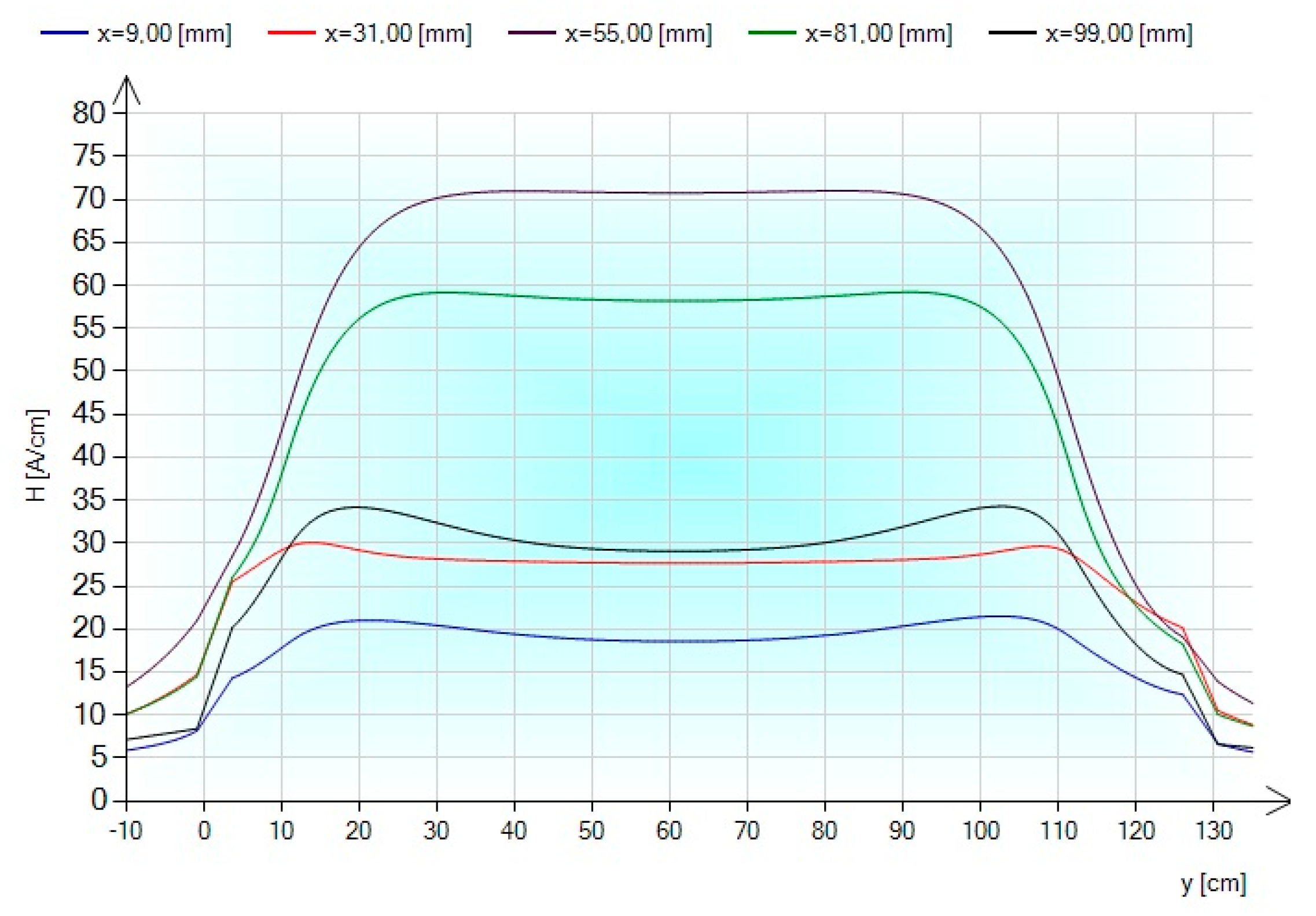
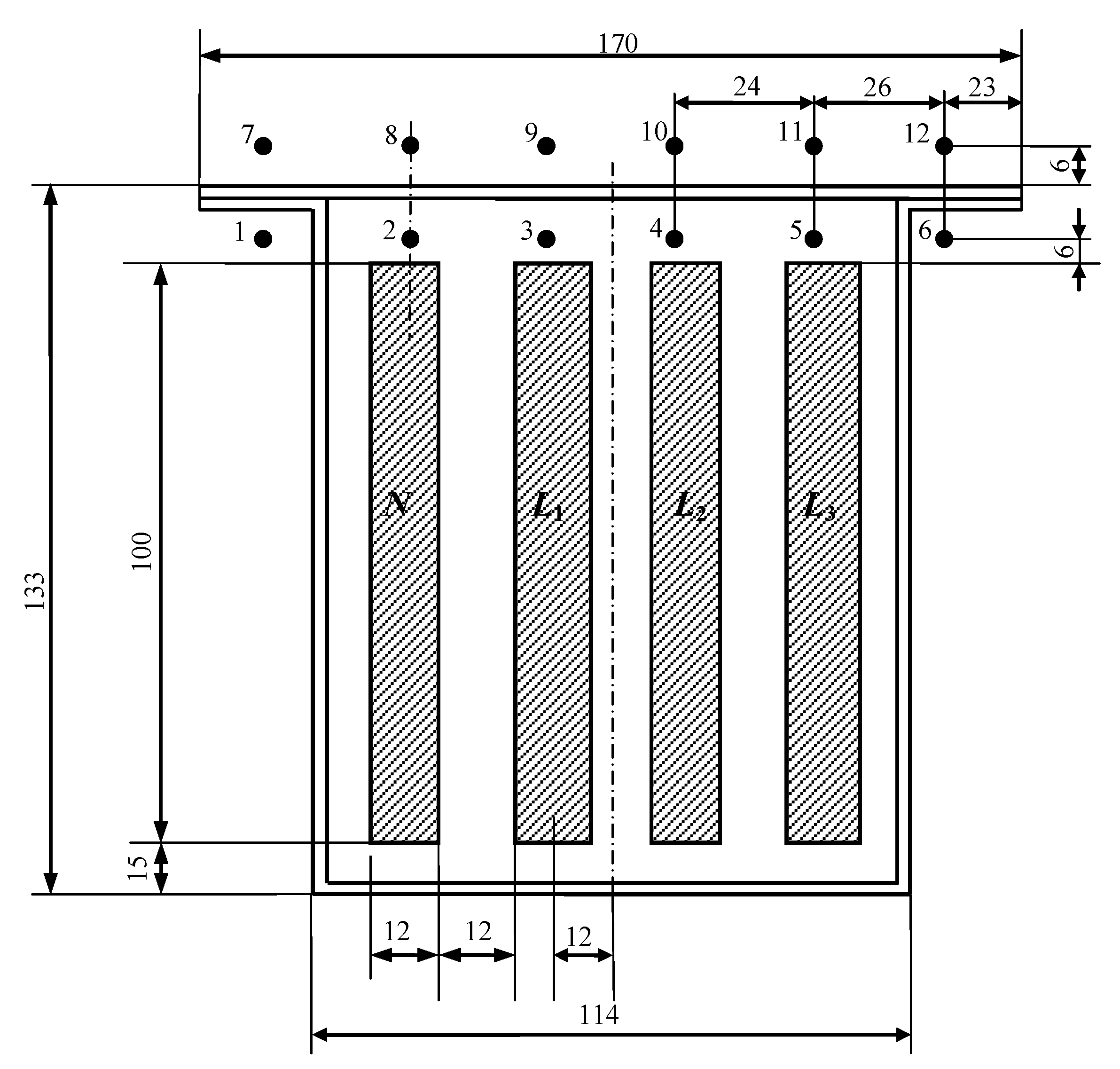
3.3. Magnetic Field—Measurement and Results
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kusiak, D.; Szczegielniak, T. Electromagnetic Calculations of Busbars; Series Monograph No. 326; Publisher Częstochowa University of Technology: Czestochowa, Poland, 2017; p. 177. (In Polish) [Google Scholar]
- Piątek, Z. Impedances of Tubular High Current Busducts; Polish Academy of Sciences: Warsaw, Poland, 2008. [Google Scholar]
- Kusiak, D.; Piątek, Z.; Szczegielniak, T.; Jabłoński, P. Calculations of the magnetic field of the 3-phase, 4-conductor line with rectangular busbar. Comput. Appl. Electr. Eng. 2016, 14, 25–38. (In Polish) [Google Scholar]
- Sarajčev, P.; Goić, R. Power loss computation in high-current generator busducts of rectangular cross-section. Electr. Power Compon. Syst. 2010, 38, 1469–1485. [Google Scholar]
- Holduct Ltd. Three-Phase Busduct; Poland. Available online: http://energetyka.holduct.com.pl (accessed on 12 March 2019).
- Rolicz, P. Skin effect in a system of two rectangular conductors carrying identical currents. Electr. Eng. 2000, 82, 285–290. [Google Scholar] [CrossRef]
- Capelli, F.; Riba, J.R. Analysis of formulas to calculate the AC inductance of different configurations of nonmagnetic circular conductors. Electr. Eng. 2017, 99, 827–837. [Google Scholar] [CrossRef]
- Cai, C.; Xuejun, P.; Yu, C.; Yong, K. Investigation, Evaluation and Optimization of Stray Inductance in Laminated Busbar. IEEE Trans. Power Electron. 2014, 29, 3679–3692. [Google Scholar]
- Riba, J.R.; Capelli, F. Calculation of the inductance of conductive nonmagnetic conductors by means of finite element method simulations. Int. J. Electr. Educ. 2018, 1–23. [Google Scholar] [CrossRef]
- Benato, R.; Dughiero, F.; Forzan, M.; Paolucci, A. Proximity effect and magnetic field calculation in GIL and in isolated phase busducts. IEEE Trans. Magn. 2002, 2, 781–784. [Google Scholar] [CrossRef]
- Piątek, Z. Self and mutual impedances of a finite length gas insulated transmission line (GIL). Electr. Power Syst. Res. 2007, 77, 191–203. [Google Scholar] [CrossRef]
- Piatek, Z.; Kusiak, D.; Szczegielniak, T. Electromagnetic Field and Impedances of High Current Busducts. In Proceedings of the International Symposium Modern Electric Power Systems (MEPS), Wroclaw, Poland, 20–22 September 2010. [Google Scholar]
- Lovrić, D.; Boras, V.; Vujević, S. Accuracy of approximate formulas for internal impedance of tubular cylindrical conductors for large parameters. Prog. Electromagn. Res. M 2011, 16, 171–184. [Google Scholar] [CrossRef]
- Fazljoo, S.A.; Besmi, M.R. A new method for calculation of impedance in various frequencies. In Proceedings of the 1st Power Electronic & Drive Systems & Technologies Conference(PEDSTC), Tehran, Iran, 17–18 February 2010; pp. 36–40. [Google Scholar]
- Goddard, K.F.; Roy, A.A.; Sykulski, J.K. Inductance and resistance calculations for a pair of rectangular conductor. IEE Proc. Sci. Meas. Technol. 2005, 152, 73–78. [Google Scholar] [CrossRef][Green Version]
- Xinglong, Z.; Baichao, C.; Yao, L.; Runhang, Z. Analytical Calculation of Mutual Inductance of Finite-Length Coaxial Helical Filaments and Tape Coils. Energies 2019, 12, 20. [Google Scholar]
- Aebischer, H.A.; Friedli, H. Analytical approximation for the inductance of circularly cylindrical two-wire transmission lines with proximity effect. Adv. Electromagn. 2018, 7, 25–34. [Google Scholar] [CrossRef]
- Piątek, Z.; Baron, B.; Jabłoński, P.; Kusiak, D.; Szczegielniak, T. Numerical method of computing impedances in shielded and unshielded three-phase rectangular busbar systems. Prog. Electromagn. Res. B 2013, 51, 135–156. [Google Scholar] [CrossRef]
- Sarajčev, P. Numerical analysis of the magnetic field of high-current busduct and GIL systems. Energies 2011, 4, 2196–2211. [Google Scholar] [CrossRef]
- Koch, H. Gas-Insulated Transmission Lines (GIL); John Wiley&Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Koch, H.; Benato, R.; Laußegger, M.; Köhler, M.; Leung, K.K.; Mirebeau, P.; Kindersberger, J.; Kunze, D.; di Mario, C.; Renaud, F.; et al. Application of long high capacity gas-insulated lines in structures. IEEE Trans. Power Deliv. 2007, 22, 619–626. [Google Scholar]
- Völcker, O.; Koch, H. Insulation co-ordination for gas-insulated transmission lines (GIL). IEEE Trans. Power Deliv. 2001, 16, 122–130. [Google Scholar] [CrossRef]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Numerical method of computing impedances of a three-phase busbar system of rectangular cross section. Prz. Elektrotech. 2013, 89, 150–154. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Exact closed form formula for mutual inductance of conductors of rectangular cross section. Prz. Elektrotech. 2013, 89, 61–64. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Inductance of along two-rectangular busbar single-phase line. Prz. Elektrotech. 2013, 89, 290–292. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Mutual inductance of two thin tapes with parallel widths. Prz. Elektrotech. 2013, 89, 281–283. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Mutual inductance of two thin tapes with perpendicular widths. Prz. Elektrotech. 2013, 89, 287–289. [Google Scholar]
- Szczegielniak, T.; Piątek, Z.; Kusiak, D.; Kusiak, D. Self and mutual impedances of rectangular bus-bars of finite length. Inform. Autom. Pomiary Gospod. Ochr. Śr. (IAPGOŚ) 2014, 4, 21–24. (In Polish) [Google Scholar]
- Piątek, Z.; Baron, B. Exact closed form formula for self inductance of conductor of rectangular cross section. Prog. Electromagn. Res. M 2012, 26, 225–236. [Google Scholar] [CrossRef]
- Piątek, Z.; Baron, B.; Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. A numerical method for current density determination in three-phase bus-bars of rectangular cross section. Prz. Elektrotech. 2013, 89, 294–298. [Google Scholar]
- Baron, B.; Piątek, Z.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Impedance of an isolated rectangular conductor. Prz. Elektrotech. 2013, 89, 278–280. [Google Scholar]
- Meeker, D.C. Finite Element Method Magnetics, Version 4.2. 25 October 2015. Available online: http://www.femm.info (accessed on 17 March 2019).
- Labridis, D.; Hatziathanassiou, V. Finite Element Computation of Field, Forces and Inductances in Underground SF6 Insulated Cables Using a Coupled Magneto-Thermal Formulation. IEEE Trans. Magn. 1994, 4, 1407–1415. [Google Scholar] [CrossRef]
- Krakowski, M. Theoretical Electrotechnics. Electromagnetic Field, 5th ed.; WN PWN: Warsaw, Poland, 1995. (In Polish) [Google Scholar]
- Piątek, Z.; Jabłoński, P. Basics of Electromagnetic Field Theory; WNT: Warszawa, Poland, 2010. (In Polish) [Google Scholar]
- Kazimierczuk, M.K. High-Frequency Magnetic Components; J Wiley&Sons: Chichester, UK, 2009. [Google Scholar]
- Gliński, H.; Grzymkowski, R.; Kapusta, A.; Słota, D. Mathematica 8; Wyd. Skalmierskiego: Gliwice, Poland, 2012. (In Polish) [Google Scholar]
- Broydé, F.; Clavelier, E.; Broydé, L. A direct current per-unit-length inductance matrix computation using modified partial inductance. In Proceedings of the CEM 2012 International Symposium on Electromagnetic Compatibility, Rouen, France, 25–27 April 2012. [Google Scholar]
- Paul, C.R. Inductance: Loop and Partial; J Wiley&Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Paul, C.R. Analysis of Multiconductor Transmission Lines; J Wiley&Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Clavel, E.; Roudet, J.; Foggia, A. Electrical modeling of transformer connecting bars. IEEE Trans. Magn. 2002, 38, 1378–1382. [Google Scholar] [CrossRef]
- Zhihua, Z.; Weiming, M. AC impedance of an isolated flat conductor. IEEE Trans. Electromagn. Compat. 2002, 44, 482–486. [Google Scholar] [CrossRef]
- Matsuki, M.; Matsushima, A. Improved numerical method for computing internal impedance of a rectangular conductor and discussions of its high frequency behavior. Prog. Electromagn. Res. M 2012, 23, 139–152. [Google Scholar] [CrossRef]
- Jabłoński, P.; Kusiak, D.; Szczegielniak, T.; Piątek, Z. Reduction of Impedance Matrices of Power Busducts. Prz. Elektrotech. 2016, 92, 49–52. [Google Scholar]
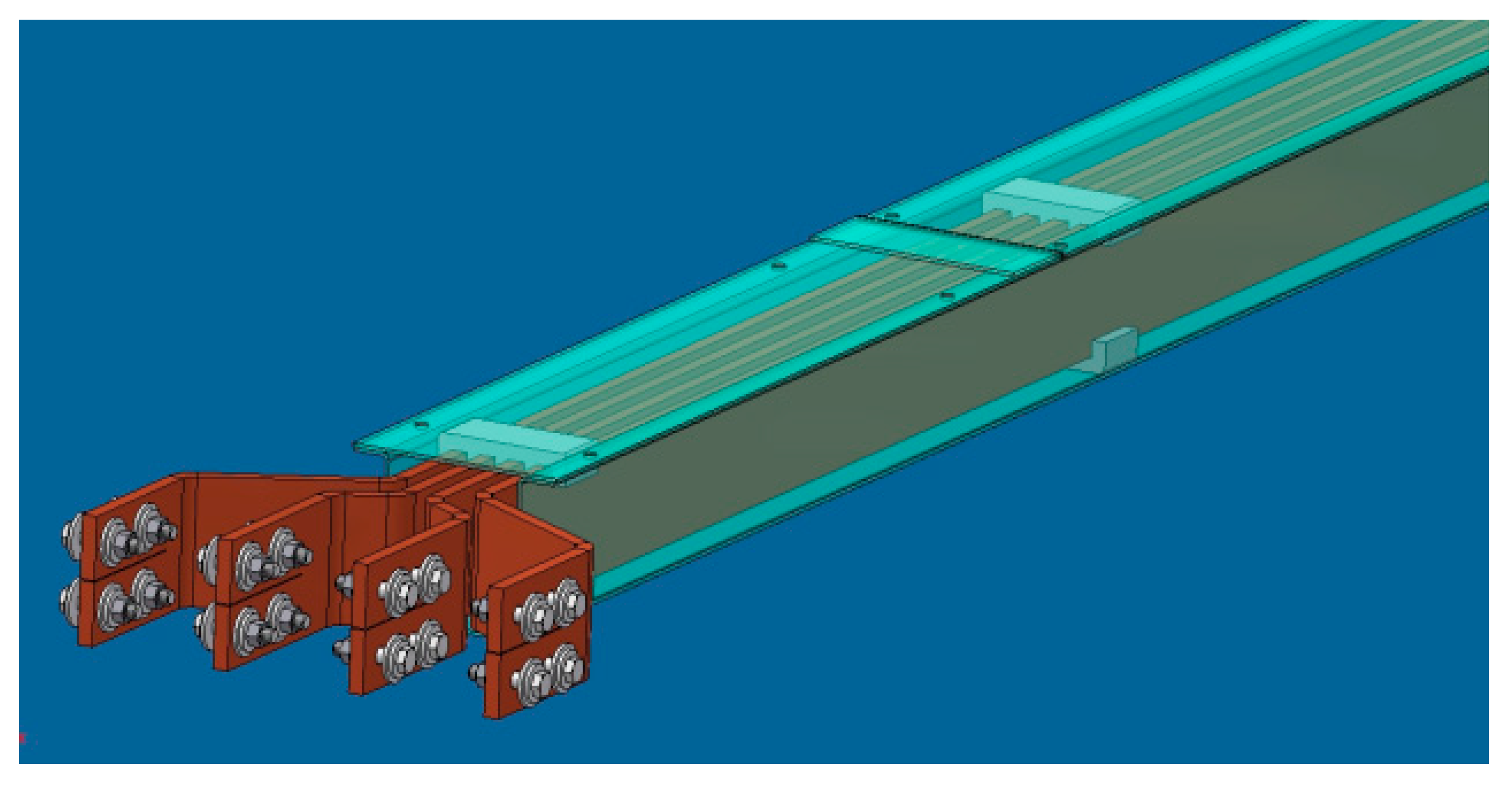
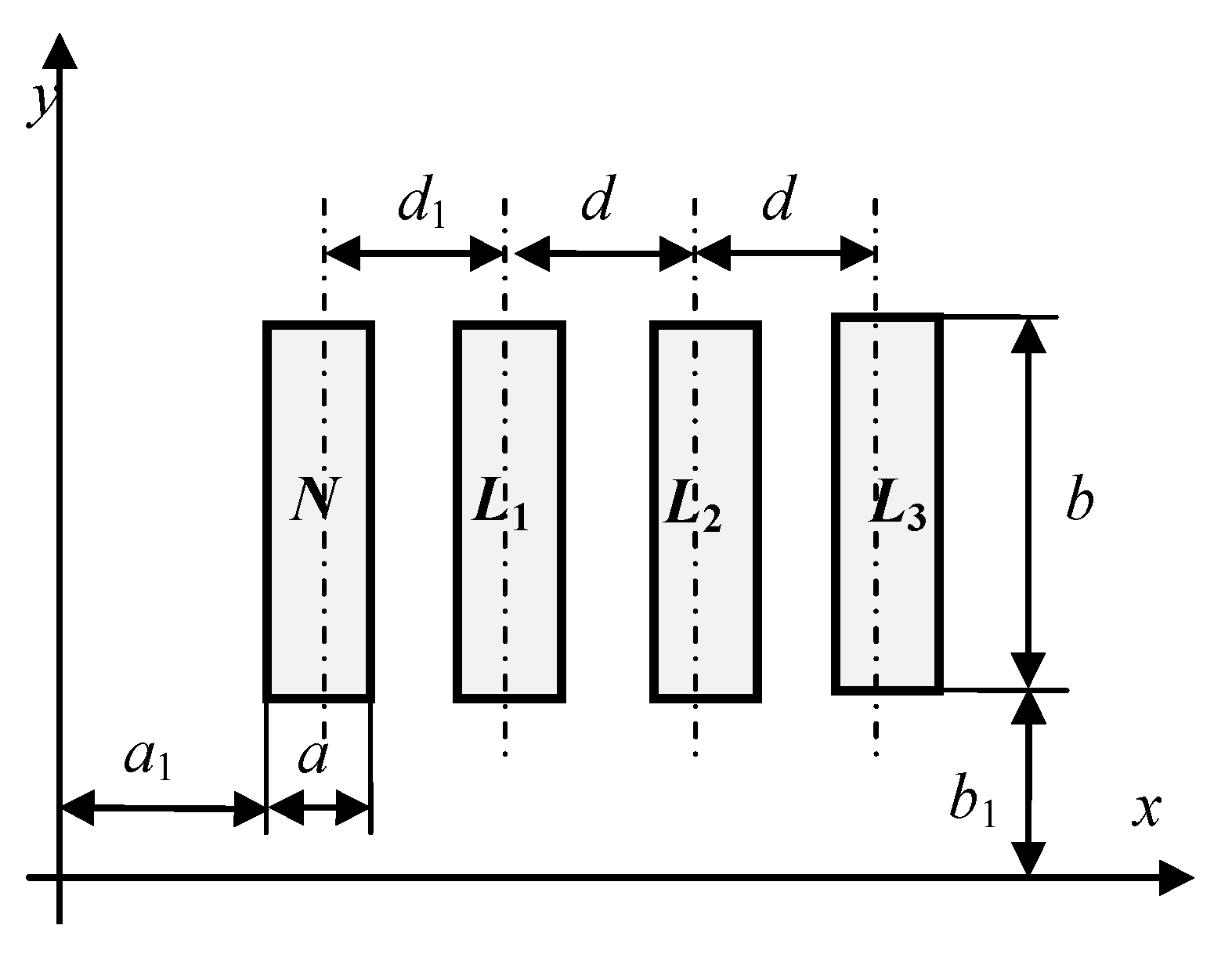
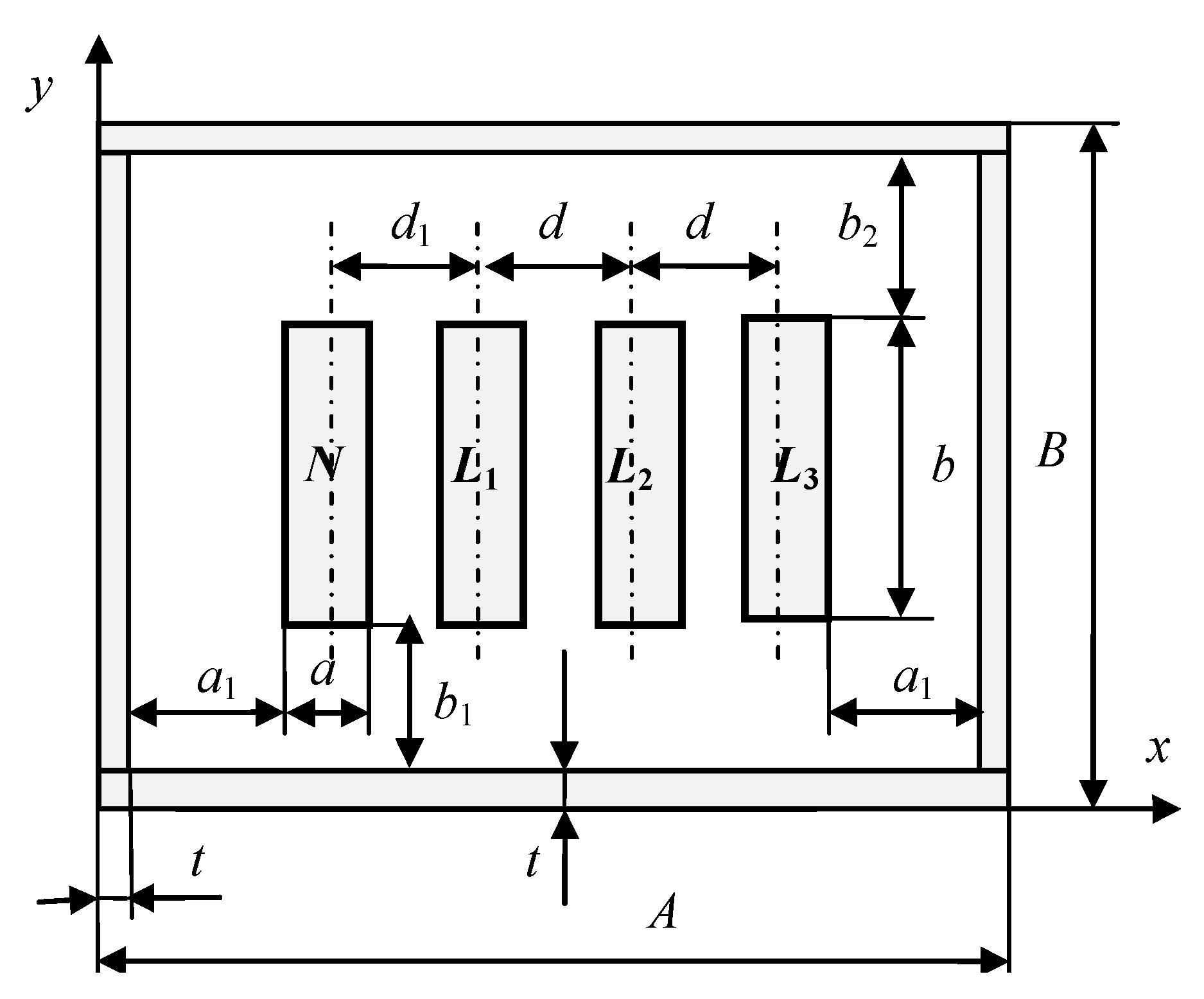
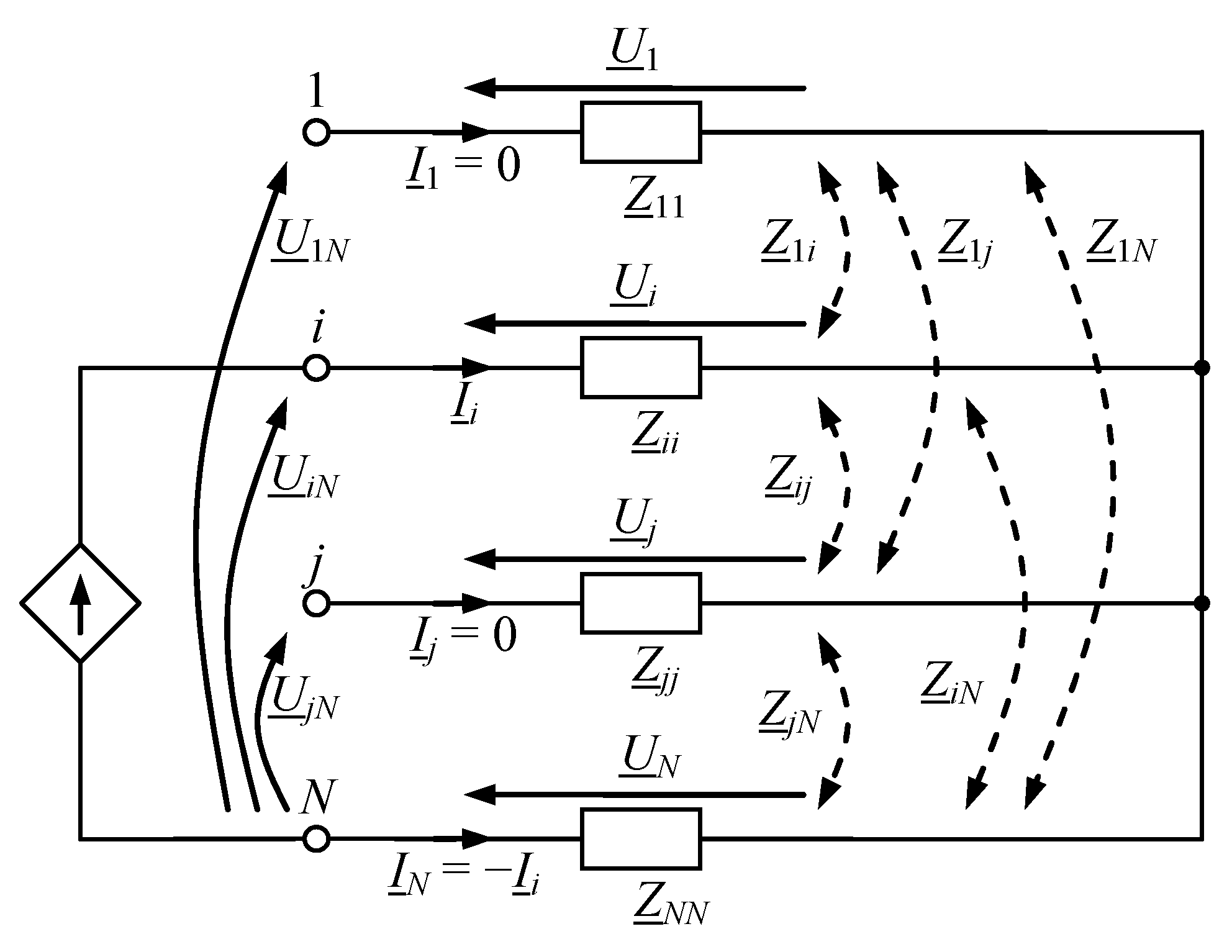


| Length l in m | Ni | s | Method | 1 (L1) | 2 (L2) | 3 (L3) | 4 (N) | ||
|---|---|---|---|---|---|---|---|---|---|
| Nj | u | ||||||||
| 1 | 1 (L1) | u | AM | 0.014 + j 0.214 | 0.000 + j 0.185 | 0.000 + j 0.161 | 0.000 + j 0.185 | ||
| IEM | 0.022 + j 0.202 | 0.005 + j 0.173 | 0.002 + j 0.149 | 0.004 + j 0.174 | |||||
| FEM | 0.021 + j 0.339 | 0.005 + j 0.339 | 0.002 + j 0.288 | 0.004 + j 0.312 | |||||
| s | IEM | 0.025 + j 0.199 | 0.006 + j 0.174 | 0.000 + j 0.153 | 0.008 + j 0.168 | ||||
| FEM | 0.023 + j 0.337 | 0.005 + j 0.312 | –0.005 + j 0.292 | 0.008 + j 0.306 | |||||
| 2 (L2) | u | AM | 0.000 + j 0.185 | 0.014 + j 0.214 | 0.000 + j 0.185 | 0.000 + j 0.161 | |||
| IEM | 0.005 + j 0.173 | 0.019 + j 0.202 | 0.004 + j 0.174 | 0.002 + j 0.149 | |||||
| FEM | 0.005 + j 0.339 | 0.021 + j 0.339 | 0.004 + j 0.313 | 0.002 + j 0.288 | |||||
| s | IEM | 0.006 + j 0.174 | 0.025 + j 0.199 | 0.008 + j 0.168 | 0.000 + j 0.153 | ||||
| FEM | 0.008 + j 0.306 | 0.024 + j 0.337 | 0.008 + j 0.306 | –0.005 + j 0.292 | |||||
| 3 (L3) | u | AM | 0.000 + j 0.161 | 0.000 + j 0.185 | 0.014 + j 0.214 | 0.000 + j 0.143 | |||
| IEM | 0.002 + j 0.149 | 0.004 + j 0.174 | 0.021 + j 0.203 | 0.000 + j 0.130 | |||||
| FEM | 0.002 + j 0.288 | 0.004 + j 0.174 | 0.021 + j 0.341 | –0.001 + j 0.270 | |||||
| s | IEM | 0.000 + j 0.153 | 0.008 + j 0.168 | 0.031 + j 0.187 | –0.007 + j 0.144 | ||||
| FEM | –0.005 + j 0.292 | 0.008 + j 0.306 | 0.032 + j 0.324 | –0.007 + j 0.283 | |||||
| 4 (N) | u | AM | 0.000 + j 0.185 | 0.000 + j 0.161 | 0.000 + j 0.143 | 0.014 + j 0.214 | |||
| IEM | 0.004 + j 0.174 | 0.002 + j 0.149 | 0.000 + j 0.130 | 0.021 + j 0.203 | |||||
| FEM | 0.004 + j 0.312 | 0.002 + j 0.288 | –0.001 + j 0.270 | 0.021 + j 0.341 | |||||
| s | IEM | 0.008 + j 0.168 | 0.000 + j 0.153 | –0.007 + j 0.144 | 0.031 + j 0.187 | ||||
| FEM | 0.008 + j 0.306 | –0.005 + j 0.292 | –0.007 + j 0.283 | 0.032 + j 0.324 | |||||
| 3.50 | 1 (L1) | u | AM | 0.053 + j 1.038 | 0.000 + j 0.935 | 0.000 + j 0.845 | 0.000 + j 0.935 | ||
| IEM | 0.075 + j 0.990 | 0.016 + j 0.891 | 0.006 + j 0.808 | 0.015 + j 0.892 | |||||
| FEM | 0.049 + j 0.749 | 0.017 + j 1.186 | 0.007 + j 1.008 | 0.014 + j 1.092 | |||||
| s | IEM | 0.086 + j 0.983 | 0.020 + j 0.894 | –0.002 + j 0.824 | 0.027 + j 0.876 | ||||
| FEM | 0.081 + j 1.179 | 0.017 + j 1.092 | –0.017 + j 1.022 | 0.028 + j 1.071 | |||||
| 2 (L2) | u | AM | 0.000 + j 0.935 | 0.053 + j 1.038 | 0.000 + j 0.935 | 0.000 + j 0.845 | |||
| IEM | 0.016 + j 0.891 | 0.075 + j 0.990 | 0.015 + j 0.893 | 0.006 + j 0.808 | |||||
| FEM | 0.017 + j 1.186 | 0.074 + j 1.186 | 0.014 + j 1.095 | 0.007 + j 1.008 | |||||
| s | IEM | 0.020 + j 0.894 | 0.086 + j 0.982 | 0.028 + j 0.875 | –0.002 + j 0.824 | ||||
| FEM | 0.017 + j 1.092 | 0.084 + j 1.179 | 0.028 + j 1.071 | –0.017 + j 1.022 | |||||
| 3 (L3) | u | AM | 0.000 + j 0.845 | 0.000 + j 0.935 | 0.053 + j 1.038 | 0.000 + j 0.778 | |||
| IEM | 0.006 + j 0.823 | 0.015 + j 0.893 | 0.073 + j 0.995 | 0.000 + j 0.745 | |||||
| FEM | 0.007 + j 1.008 | 0.014 + j 1.095 | 0.073 + j 1.193 | –0.003 + j 0.945 | |||||
| s | IEM | –0.002 + j 0.824 | 0.028 + j 0.875 | 0.107 + j 0.940 | –0.027 + j 0.792 | ||||
| FEM | –0.017 + j 1.022 | 0.028 + j 1.071 | 0.112 + j 1.134 | –0.024 + j 0.990 | |||||
| 4 (N) | u | AM | 0.000 + j 0.935 | 0.000 + j 0.845 | 0.000 + j 0.778 | 0.053 + j 1.038 | |||
| IEM | 0.015 + j 0.892 | 0.006 + j 0.808 | 0.000 + j 0.745 | 0.073 + j 1.012 | |||||
| FEM | 0.014 + j 1.092 | 0.007 + j 1.008 | –0.003 + j 0.945 | 0.073 + j 0.994 | |||||
| s | IEM | 0.027 + j 0.876 | –0.002 + j 0.824 | –0.027 + j 0.792 | 0.105 + j 0.942 | ||||
| FEM | 0.028 + j 1.071 | –0.017 + j 1.022 | –0.024 + j 0.990 | 0.112 + j 1.134 | |||||
| Length l in m | j | s | Methods | 1 (L1) | 2 (L2) | 3 (L3) | ||
|---|---|---|---|---|---|---|---|---|
| i | u | |||||||
| 3.50 | 1 (L1) | u | AM | 0.106 + j 0.206 | 0.053 + j 0.193 | 0.053 + j 0.170 | ||
| IEM | 0.117 + j 0.199 | 0.068 + j 0.184 | 0.064 + j 0.165 | |||||
| FEM | 0.118 + j 0.198 | 0.068 + j 0.183 | 0.064 + j 0.163 | |||||
| meas | 0.113 + j 0.208 | 0.058 + j 0.192 | 0.053 + j 0.172 | |||||
| s | IEM | 0.137 + j 0.173 | 0.100 + j 0.136 | 0.103 + j 0.098 | ||||
| FEM | 0.138 + j 0.172 | 0.102 + j 0.133 | 0.108 + j 0.094 | |||||
| meas | 0.131 + j 0.178 | 0.089 + j 0.144 | 0.095 + j 0.106 | |||||
| 2 (L2) | u | AM | 0.053 + j 0.193 | 0.106 + j 0.386 | 0.053 + j 0.350 | |||
| IEM | 0.068 + j 0.184 | 0.136 + j 0.368 | 0.081 + j 0.333 | |||||
| FEM | 0.068 + j 0.183 | 0.136 + j 0.365 | 0.081 + j 0.330 | |||||
| meas | 0.058 + j 0.192 | 0.117 + j 0.384 | 0.075 + j 0.342 | |||||
| s | IEM | 0.100 + j 0.136 | 0.196 + j 0.276 | 0.163 + j 0.201 | ||||
| FEM | 0.102 + j 0.133 | 0.200 + j 0.270 | 0.170 + j 0.193 | |||||
| meas | 0.090 + j 0.145 | 0.177 + j 0.296 | 0.148 + j 0.218 | |||||
| 3 (L3) | u | AM | 0.053 + j 0.170 | 0.053 + j 0.350 | 0.106 + j 0.520 | |||
| IEM | 0.064 + j 0.165 | 0.081 + j 0.333 | 0.145 + j 0.498 | |||||
| FEM | 0.064 + j 0.163 | 0.081 + j 0.330 | 0.145 + j 0.493 | |||||
| meas | 0.052 + j 0.172 | 0.074 + j 0.342 | 0.128 + j 0.513 | |||||
| s | IEM | 0.103 + j 0.098 | 0.163 + j 0.201 | 0.267 + j 0.299 | ||||
| FEM | 0.108 + j 0.094 | 0.170 + j 0.193 | 0.279 + j 0.287 | |||||
| meas | 0.095 + j 0.105 | 0.145 + j 0.218 | 0.243 + j 0.329 | |||||
| s | Method | Measurement Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| u | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| u | AM | 0.727 | 1.316 | 3.112 | 3.624 | 5.594 | 4.050 | 0.609 | 0.965 | 1.467 | 1.701 | 1.467 | 0.929 | |
| IEM | 0.550 | 1.450 | 3.150 | 3.250 | 4.560 | 4.250 | 0.600 | 1.200 | 1.250 | 1.850 | 1.200 | 0.950 | ||
| FEM | 1.036 | 2.118 | 4.778 | 5.537 | 4.966 | 1.818 | 0.873 | 1.439 | 2.206 | 2.547 | 2.238 | 1.357 | ||
| meas | 0.318 | 1.723 | 4.041 | 4.422 | 3.650 | 1.419 | 0.754 | 1.274 | 2.058 | 2.296 | 1.761 | 1.153 | ||
| s | IEM | 0.550 | 2.050 | 2.850 | 3.250 | 3.200 | 0.950 | 0.490 | 0.750 | 1.050 | 1.100 | 0.950 | 0.550 | |
| FEM | 1.180 | 2.823 | 4.725 | 4.313 | 4.464 | 1.890 | 0.626 | 0.908 | 1.183 | 1.468 | 1.406 | 0.807 | ||
| meas | 0.729 | 2.020 | 3.563 | 3.534 | 3.355 | 1.423 | 0.535 | 0.735 | 0.960 | 1.240 | 1.068 | 0.661 | ||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusiak, D. The Magnetic Field and Impedances in Three-Phase Rectangular Busbars with a Finite Length. Energies 2019, 12, 1419. https://doi.org/10.3390/en12081419
Kusiak D. The Magnetic Field and Impedances in Three-Phase Rectangular Busbars with a Finite Length. Energies. 2019; 12(8):1419. https://doi.org/10.3390/en12081419
Chicago/Turabian StyleKusiak, Dariusz. 2019. "The Magnetic Field and Impedances in Three-Phase Rectangular Busbars with a Finite Length" Energies 12, no. 8: 1419. https://doi.org/10.3390/en12081419
APA StyleKusiak, D. (2019). The Magnetic Field and Impedances in Three-Phase Rectangular Busbars with a Finite Length. Energies, 12(8), 1419. https://doi.org/10.3390/en12081419





