3D Imaging of Geothermal Faults from a Vertical DAS Fiber at Brady Hot Spring, NV USA
Abstract
1. Introduction
2. Materials and Methods
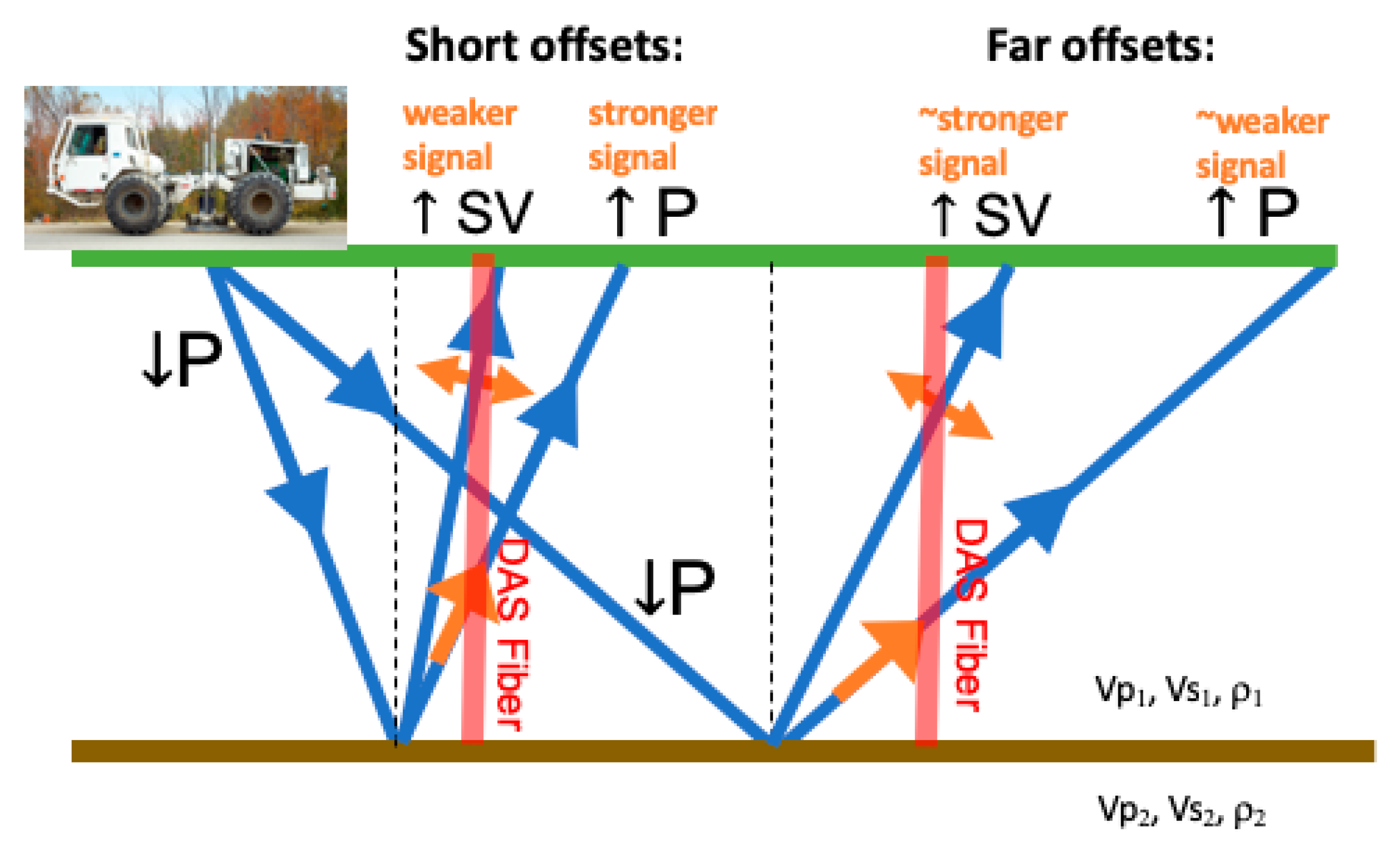
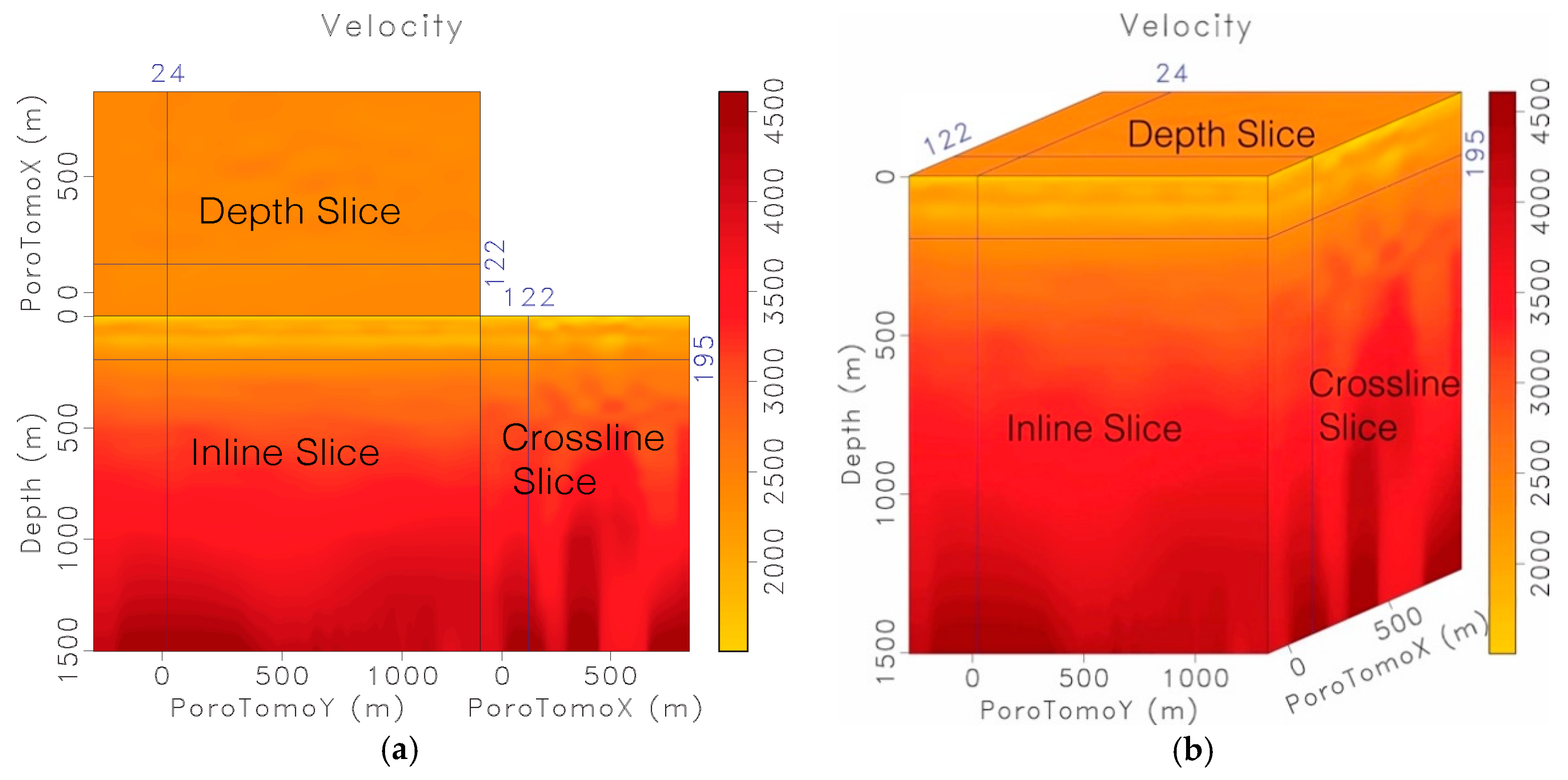
2.1. The Data: Distributed Acoustic Sensing at Brady
2.2. Seismic Imaging with Reverse Time Migration
2.3. Synthetic Data Generation with a Born Modeling Approach
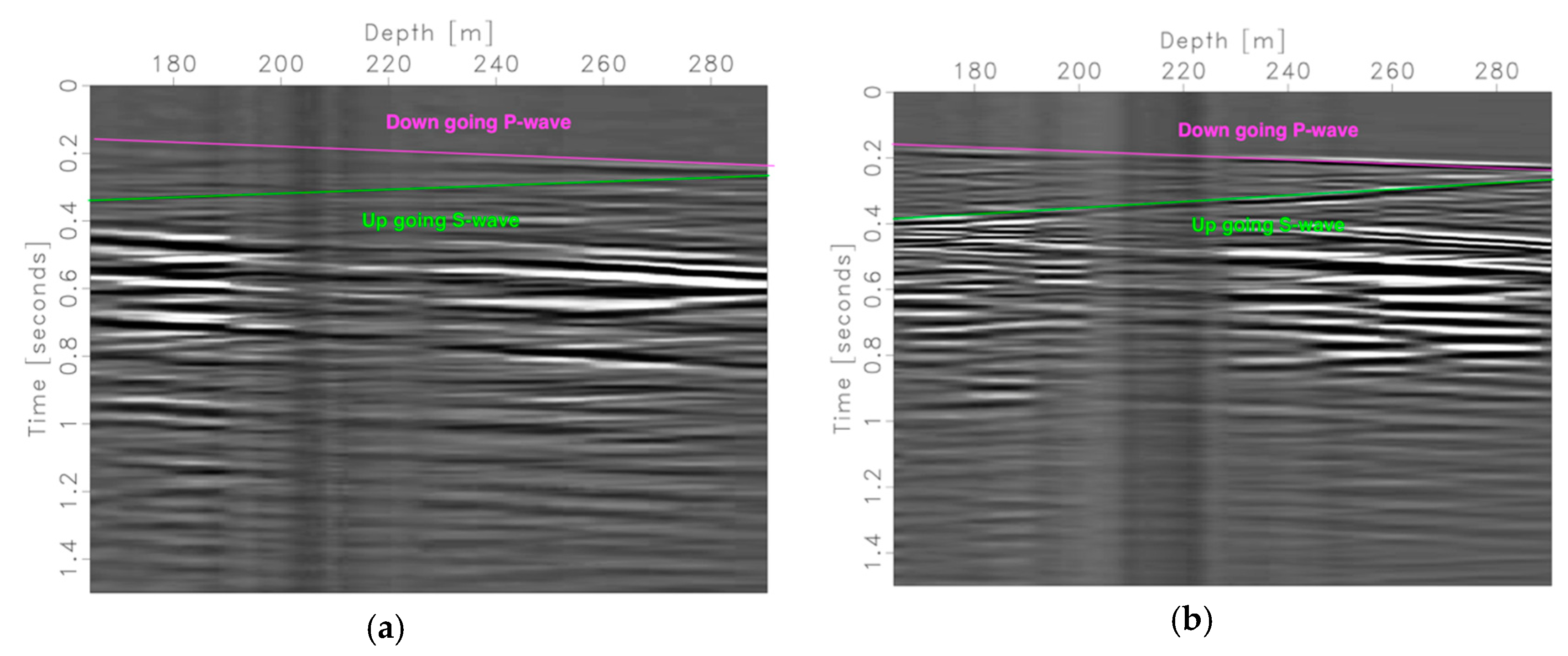
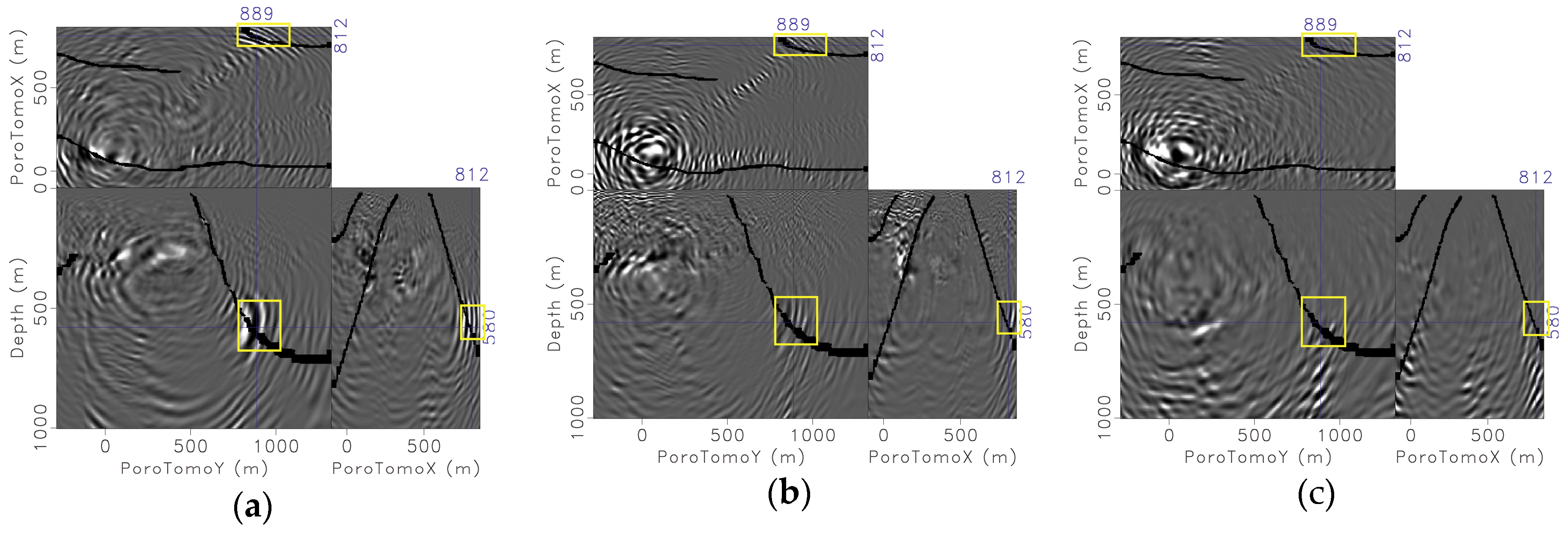
3. Imaging Results of PP and PS Waves with RTM
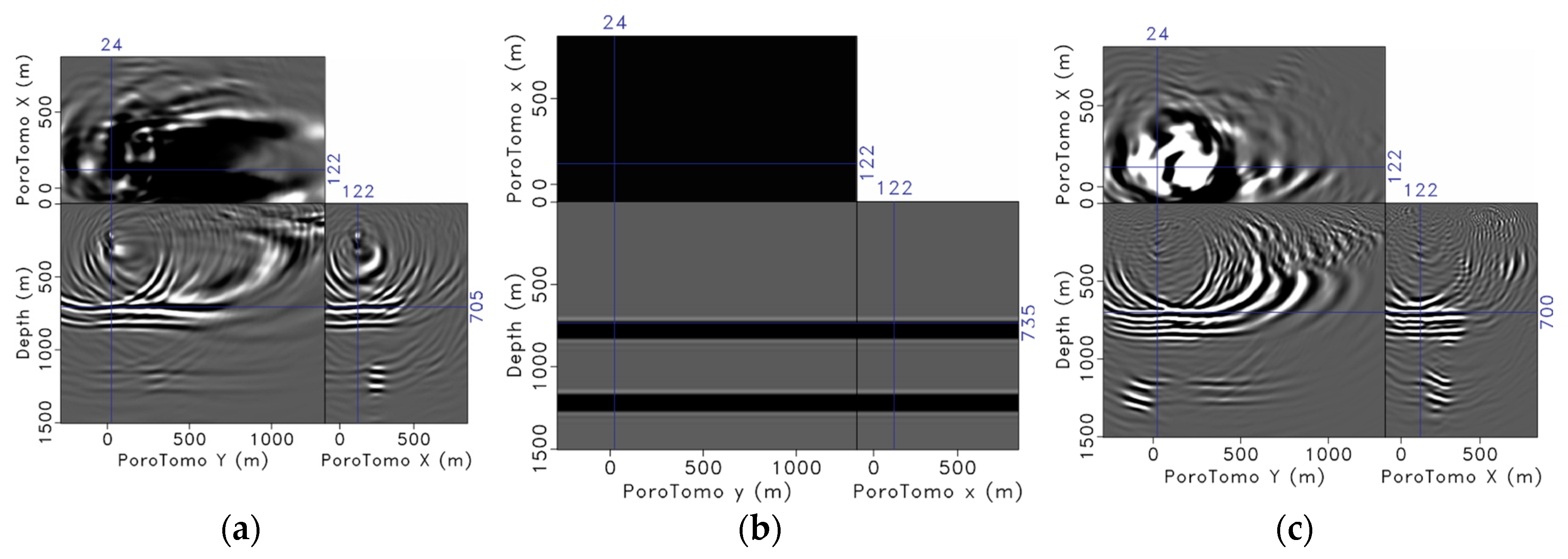
3.1. Estimating Illumination Volume: Four Horizontal Reflectors
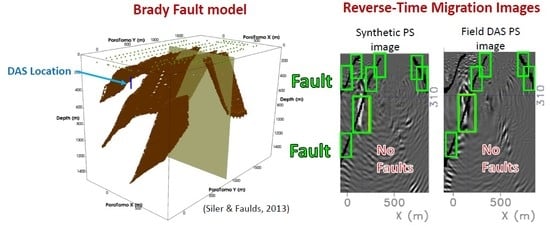
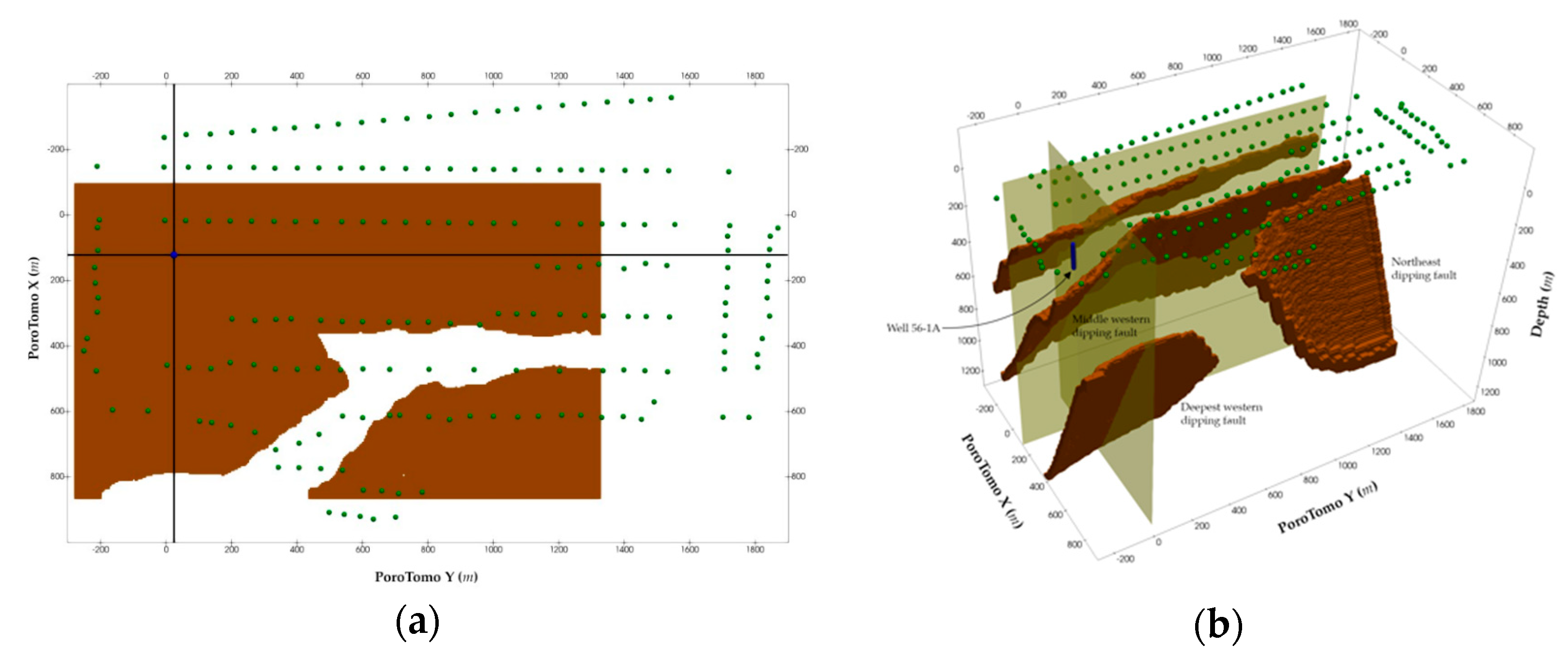
3.2. Comparison of Imaging with Brady DAS Observations and Data Generated with Siler and Faulds Fault Model
- Wr = Synthetic receiver wavefield generated using the Siler & Faulds fault model as reflectors
- Wr = DAS data from Brady collected in March 2016
- Wr = Pure random (white) noise
- The deepest northwest dipping fault
- The middle northwest dipping fault
- The eastern-dipping fault.
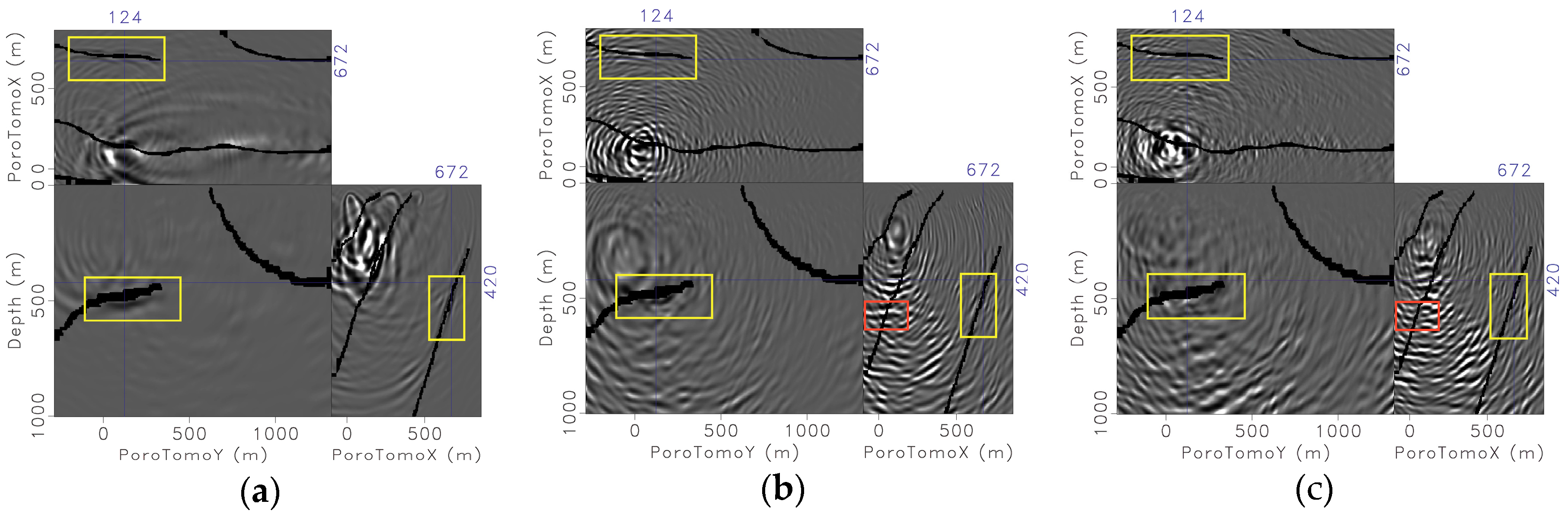
3.2.1. Deepest Northwestern Dipping Fault
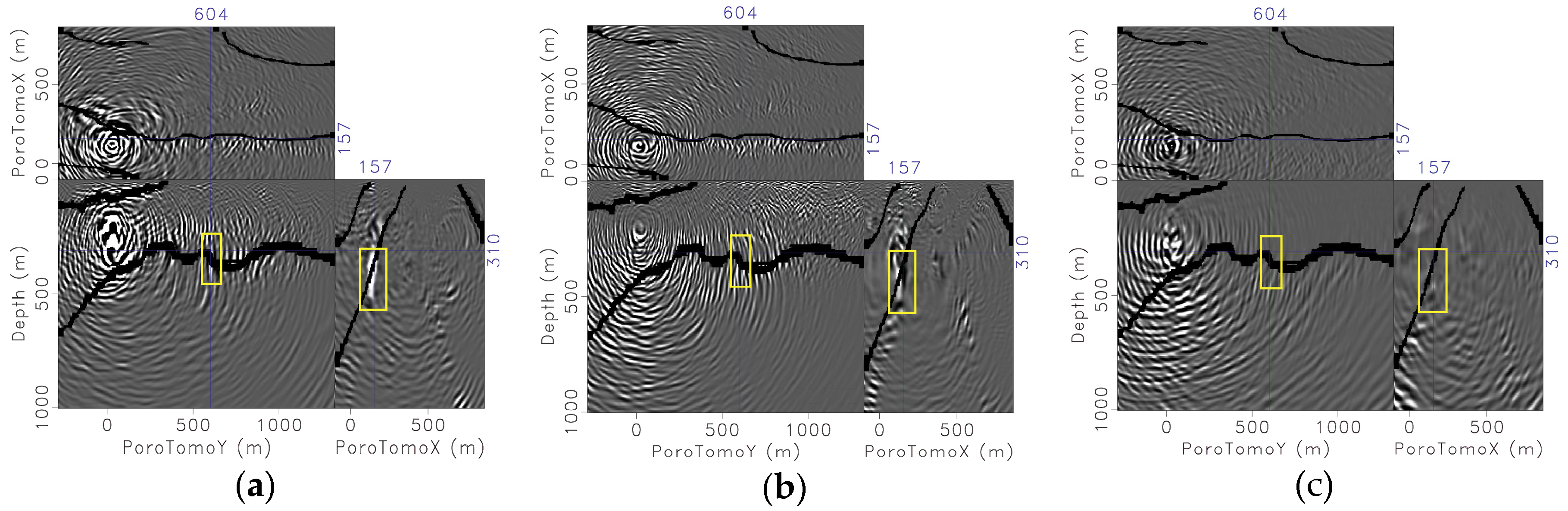
3.2.2. Middle Northwestern-Dipping Fault
3.2.3. Far Eastern-Dipping Fault
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mondol, N. Seismic Exploration. In Petroleum Geoscience: From Sedimentary Environments to Rock Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; p. 508. [Google Scholar]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1995. [Google Scholar]
- Allaby, M. (Ed.) A Dictionary of Geology and Earth Sciences; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Gritto, R.; Daley, T.M.; Majer, E.L. Seismic Mapping of the Subsudace Structure at the Ryepatch Geothermal Reservoir; DOEEEGTP (USDOE Office of Energy Efficiency and Renewable Energy Geothermal Tech Pgm): Berkeley, CA, USA, 2000. [Google Scholar]
- Melosh, G.; Cumming, W.; Casteel, J.; Niggemann, K.; Fairbank, B. Seismic Reflection Data and Conceptual Models for Geothermal Development in Nevada. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–29 April 2010; pp. 25–29. [Google Scholar]
- Huang, L.; Gao, K.; Huang, Y.; Cladouhos, T.T. Anisotropic Seismic Imaging and Inversion for Subsurface Characterization at the Blue Mountain Geothermal Field in Nevada. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018; pp. 1–10. [Google Scholar]
- Folsom, M.; Lopeman, J.; Perkin, D.; Sophy, M. Imaging Shallow Outflow Alteration to Locate Productive Faults in Ormat’s Brady’s and Desert Peak Fields Using CSAMT. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018; pp. 1–11. [Google Scholar]
- Coolbaugh, M.F.; Sladek, C.; Kratt, C.; Edmondo, G. Digital mapping of structurally controlled geothermal features with GPS units and pocket computers. Geotherm. Resour. Counc. Trans. 2004, 28, 321–325. [Google Scholar]
- Faulds, J.E.; Coolbaugh, M.F.; Benoit, D.; Oppliger, G.; Perkins, M.; Moeck, I.; Drakos, P. Structural Controls of Geothermal Activity in the Northern Hot Springs Mountains, Western Nevada: The Tale of Three Geothermal Systems (Brady’s, Desert Peak, and Desert Queen). Geotherm. Resour. Counc. Trans. 2010, 34, 675–683. [Google Scholar]
- Siler, D.L.; Faulds, J.E. Three-Dimensional Geothermal Fairway Mapping: Examples from the Western Great Basin, USA. GRC Trans. 2013, 37, 327–332. [Google Scholar]
- Feigl, K.L.; Lancelle, C.; Lim, D.D.; Parker, L.; Reinisch, E.C.; Ali, S.T.; Fratta, D.; Thurber, C.H.; Wang, H.F.; Robertson, M.; et al. Overview and Preliminary Results from the PoroTomo project at Brady Hot Springs, Nevada: Poroelastic Tomography by Adjoint Inverse Modeling of Data from Seismology, Geodesy, and Hydrology. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 13–15 February 2017; pp. 1–15. [Google Scholar]
- Ali, S.T.; Akerley, J.; Baluyut, E.C.; Davatzes, N.C.; Lopeman, J.; Moore, J. Geodetic Measurements and Numerical Models of Deformation: Examples from Geothermal Fields in the Western United States. In Proceedings of the 41st Stanford Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016. [Google Scholar]
- Queen, J.H.; Daley, T.M.; Majer, E.L.; Nihei, K.T.; Siler, D.L.; Faulds, J.E. Surface Reflection Seismic and Vertical Seismic Profile at Brady’s Hot Springs, NV, USA. In Proceedings of the 41st Stanford Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016. [Google Scholar]
- Feigl, K.; Team, P. Overview and Preliminary Results from the PoroTomo project at Brady Hot Springs, Nevada: Poroelastic Tomography by Adjoint Inverse Modeling of Data from Seismology, Geodesy, and Hydrology. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
- Dean, T.; Cuny, T.; Hartog, A.H. The effect of gauge length on axially incident P-waves measured using fibre optic distributed vibration sensing. Geophys. Prospect. 2017, 65, 184–193. [Google Scholar] [CrossRef]
- Hornman, J.C. Field trial of seismic recording using distributed acoustic sensing with broadside sensitive fibre-optic cables. Geophys. Prospect. 2017, 65, 35–46. [Google Scholar] [CrossRef]
- Lumens, P.G.E. Fibre-Optic Sensing for Application in Oil and Gas Wells. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2014. [Google Scholar]
- Mateeva, A.; Lopez, J.; Potters, H.; Mestayer, J.; Cox, B.; Kiyashchenko, D.; Wills, P.; Grandi, S.; Hornman, K.; Kuvshinov, B.; et al. Distributed acoustic sensing for reservoir monitoring with vertical seismic profiling. Geophys. Prospect. 2014, 62, 679–692. [Google Scholar] [CrossRef]
- Daley, T.M.; Miller, D.E.; Dodds, K.; Cook, P.; Freifeld, B.M. Field testing of modular borehole monitoring with simultaneous distributed acoustic sensing and geophone vertical seismic profiles at Citronelle, Alabama. Geophys. Prospect. 2016, 64, 1318–1334. [Google Scholar] [CrossRef]
- Raterman, K.T.; Farrell, H.E.; Mora, O.S.; Janssen, A.L.; Gomez, G.A.; Busetti, S.; Mcewen, J.; Davidson, M.; Friehauf, K.; Rutherford, J.; et al. Sampling a Stimulated Rock Volume: An Eagle Ford Example. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; pp. 24–26. [Google Scholar]
- Michlmayr, G.; Chalari, A.; Clarke, A.; Or, D. Fiber-optic high-resolution acoustic emission (AE) monitoring of slope failure. Landslides 2017, 14, 1139–1146. [Google Scholar] [CrossRef]
- Daley, T.; Freifeld, B.; Ajo-Franklin, J.; Dou, S.; Shulakova, V.; Kashikar, S.; Miller, D.E.; Goetz, J. Field testing of fiber-optic distribued acoustic sensing (DAS) for subsurface seismic monitoring. Lead. Edge 2013, 32, 699–706. [Google Scholar] [CrossRef]
- Claerbout, J. Toward a unified theory of reflector mapping. Geophysics 1971, 36, 467–481. [Google Scholar] [CrossRef]
- Yang, T.; Shragge, J.; Sava, P. Illumination compensation for image-domain wavefield tomography. Geophysics 2013, 78, U65–U76. [Google Scholar] [CrossRef][Green Version]
- Claerbout, J. Introduction to Seplib and SEP utility software. Stanf. Explor. Proj. 1991, 413, 436. [Google Scholar]
- Miller, D.E.; Coleman, T. DAS and DTS at BradyHot Springs: Observations about Coupling and Coupled Interpretations. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
- Woodward, M.J. Wave-equation tomography. Geophysics 1992, 57, 15–26. [Google Scholar] [CrossRef]
- Matzel, E.; Zeng, X.; Thurber, C.; Luo, Y.; Morency, C. Seismic Interferometry Using the Dense Array at the Brady Geothermal Field. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 13–15 February 2017; pp. 3–6. [Google Scholar]
- Thurber, C.; Zeng, X.; Parker, L.; Lord, N.; Fratta, D.; Wang, H.; Matzel, E.M.; Robertson, M.; Feigl, K.L.; PoroTomo Team. Active-Source Seismic Tomography at Bradys Geothermal Field, Nevada, with Dense Nodal and Fiber-Optic Seismic Arrays. Seismol. Res. Lett. 2018, 89, 1629–1640. [Google Scholar]
- Hokstad, K. Multicomponent Kirchhoff migration. Geophysics 2002, 65, 861–873. [Google Scholar] [CrossRef]
- Rickett, J.; Sava, P.C. Offset and angle-domain common image-point gathers for shot-profile migration. Geophysics 2002, 67, 883–889. [Google Scholar] [CrossRef]
- Jreij, S.; Trainor-Guitton, W.; Simmons, J. Improving Point-Sensor Image Resolution with Distributed Acoustic Sensing at Brady’s Enhanced Geothermal System. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
- Allegar, N.; Herrmann, F.J.; Mosher, C.C. Introduction to this special section: Impact of compressive sensing on seismic data acquisition and processing. Lead. Edge 2017, 36, 622–708. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Martin, E.R.; Dreger, D.S.; Freifeld, B.; Cole, S.; James, S.R.; Biondi, B.L.; Ajo-Franklin, J.B. Fiber-Optic Network Observations of Earthquake Wavefields. Geophys. Res. Lett. 2017, 44, 11792–11799. [Google Scholar] [CrossRef]
- Munn, J.D.; Coleman, T.I.; Parker, B.L.; Mondanos, M.J.; Chalari, A. Novel cable coupling technique for improved shallow distributed acoustic sensor VSPs. J. Appl. Geophys. 2017, 138, 72–79. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trainor-Guitton, W.; Guitton, A.; Jreij, S.; Powers, H.; Sullivan, B. 3D Imaging of Geothermal Faults from a Vertical DAS Fiber at Brady Hot Spring, NV USA. Energies 2019, 12, 1401. https://doi.org/10.3390/en12071401
Trainor-Guitton W, Guitton A, Jreij S, Powers H, Sullivan B. 3D Imaging of Geothermal Faults from a Vertical DAS Fiber at Brady Hot Spring, NV USA. Energies. 2019; 12(7):1401. https://doi.org/10.3390/en12071401
Chicago/Turabian StyleTrainor-Guitton, Whitney, Antoine Guitton, Samir Jreij, Hayden Powers, and Bane Sullivan. 2019. "3D Imaging of Geothermal Faults from a Vertical DAS Fiber at Brady Hot Spring, NV USA" Energies 12, no. 7: 1401. https://doi.org/10.3390/en12071401
APA StyleTrainor-Guitton, W., Guitton, A., Jreij, S., Powers, H., & Sullivan, B. (2019). 3D Imaging of Geothermal Faults from a Vertical DAS Fiber at Brady Hot Spring, NV USA. Energies, 12(7), 1401. https://doi.org/10.3390/en12071401