Distributed Economic Power Dispatch and Bus Voltage Control for Droop-Controlled DC Microgrids
Abstract
1. Introduction
2. Problem Formulation
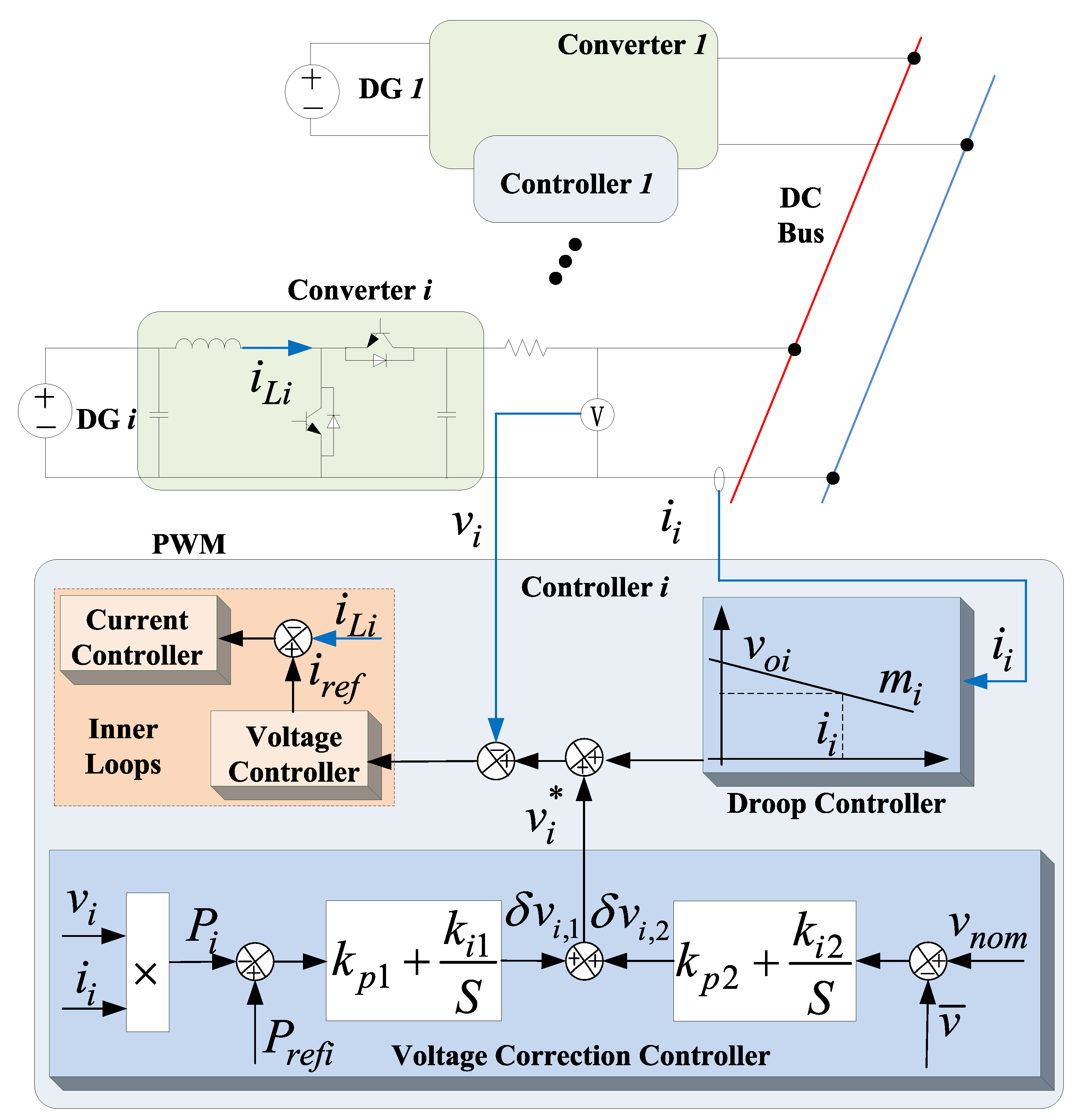
2.1. Conventional Droop Control Method in DC Microgrids
2.2. Proposed Optimal Bus Voltage Control
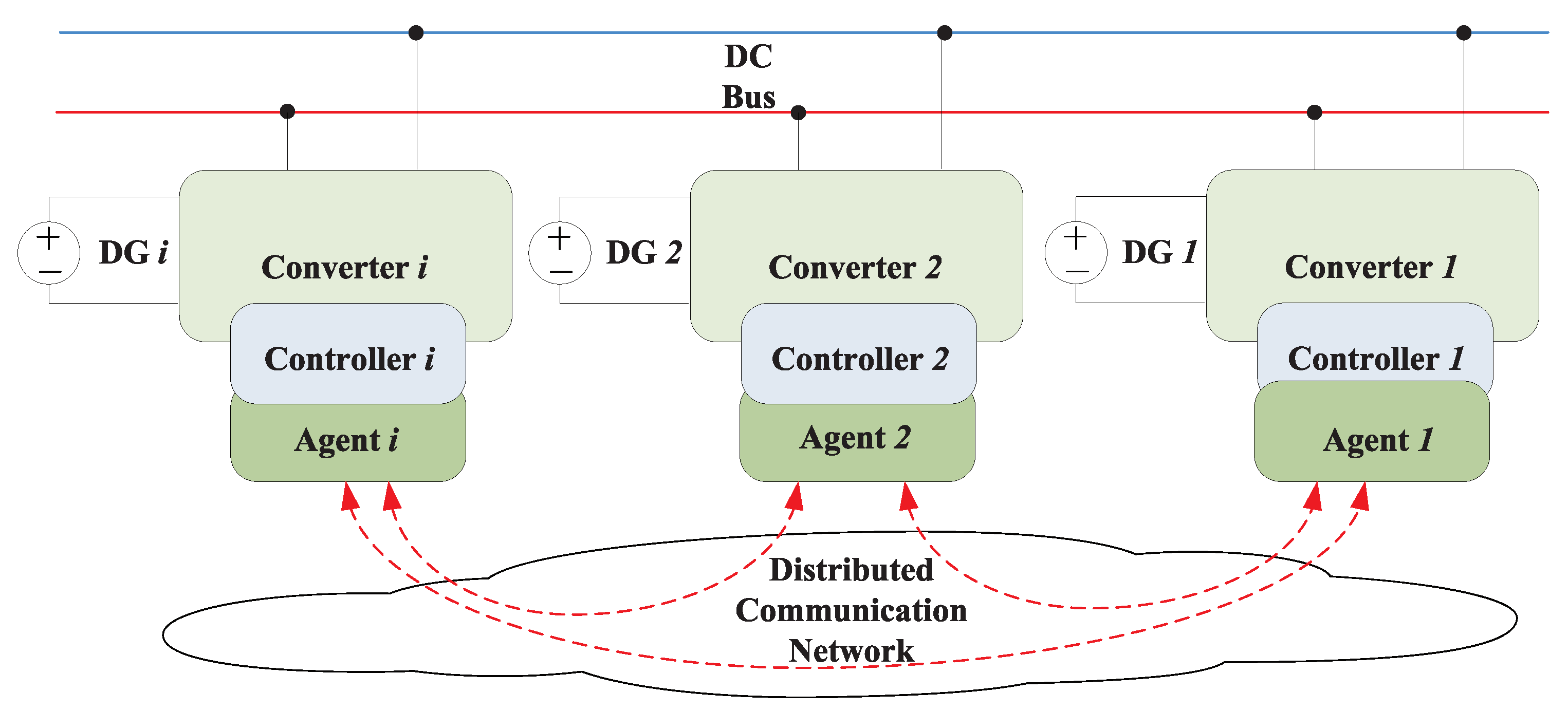
3. Distributed Consensus-Based EPD and ABVO Algorithms
3.1. Graph Theory Review
3.2. Distributed Consensus Algorithm
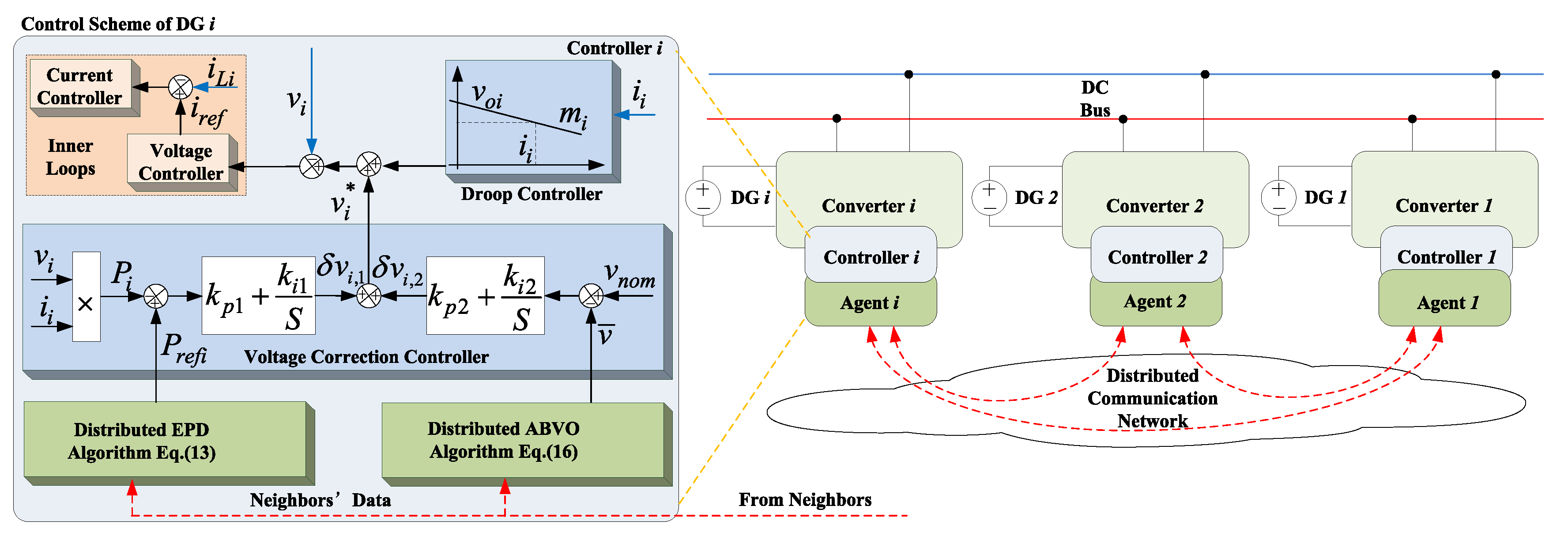
3.3. Distributed Consensus-Based EPD Algorithm
3.4. Distributed Consensus-Based ABVO Algorithm
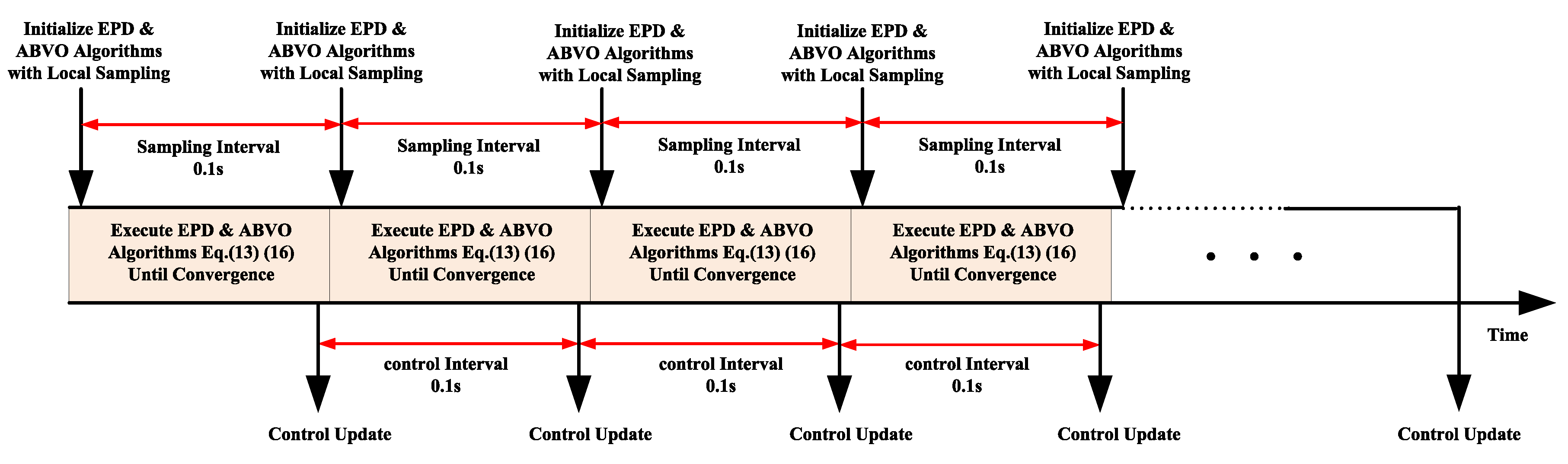
3.5. Algorithm Implementation
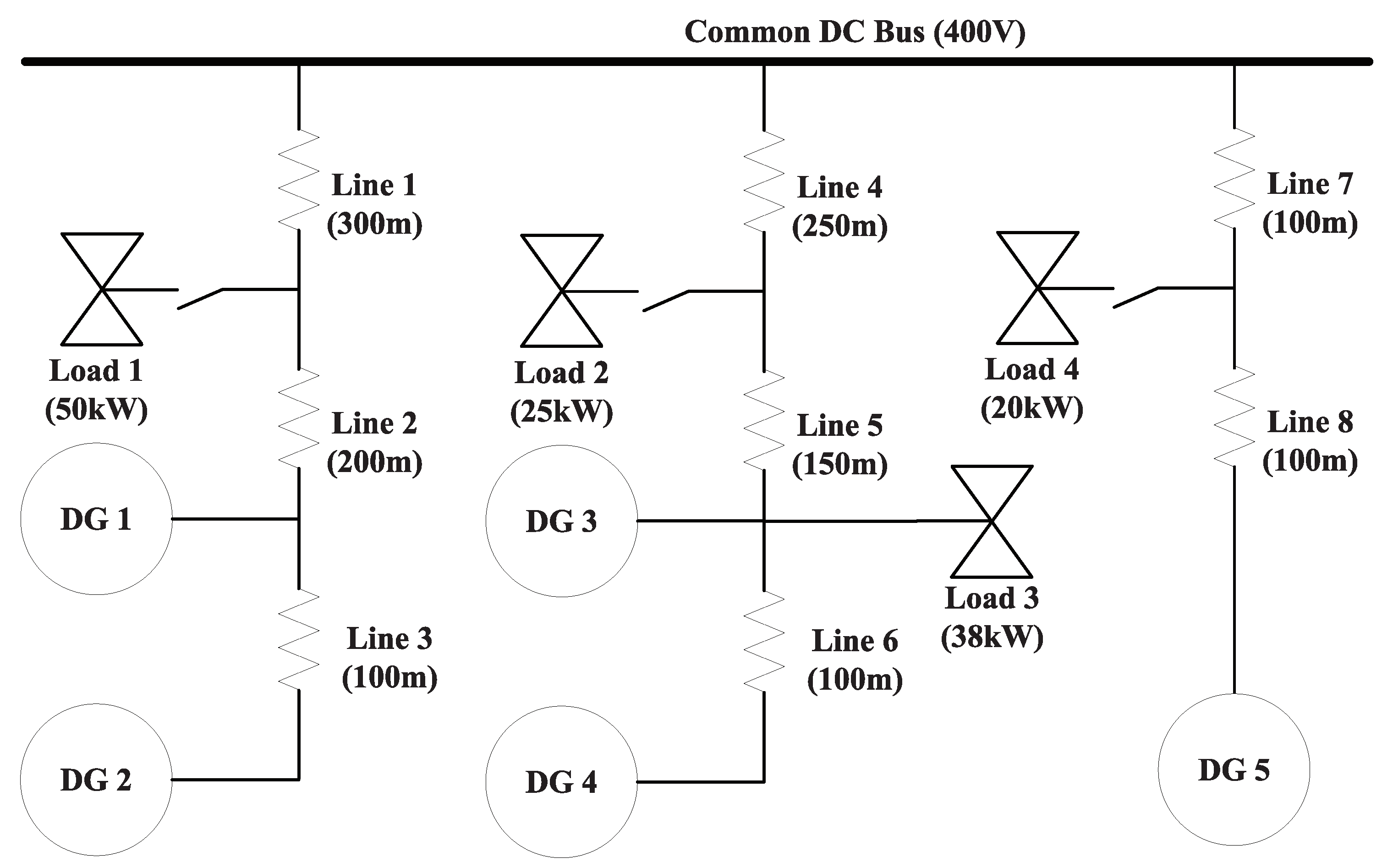
4. Simulation Studies
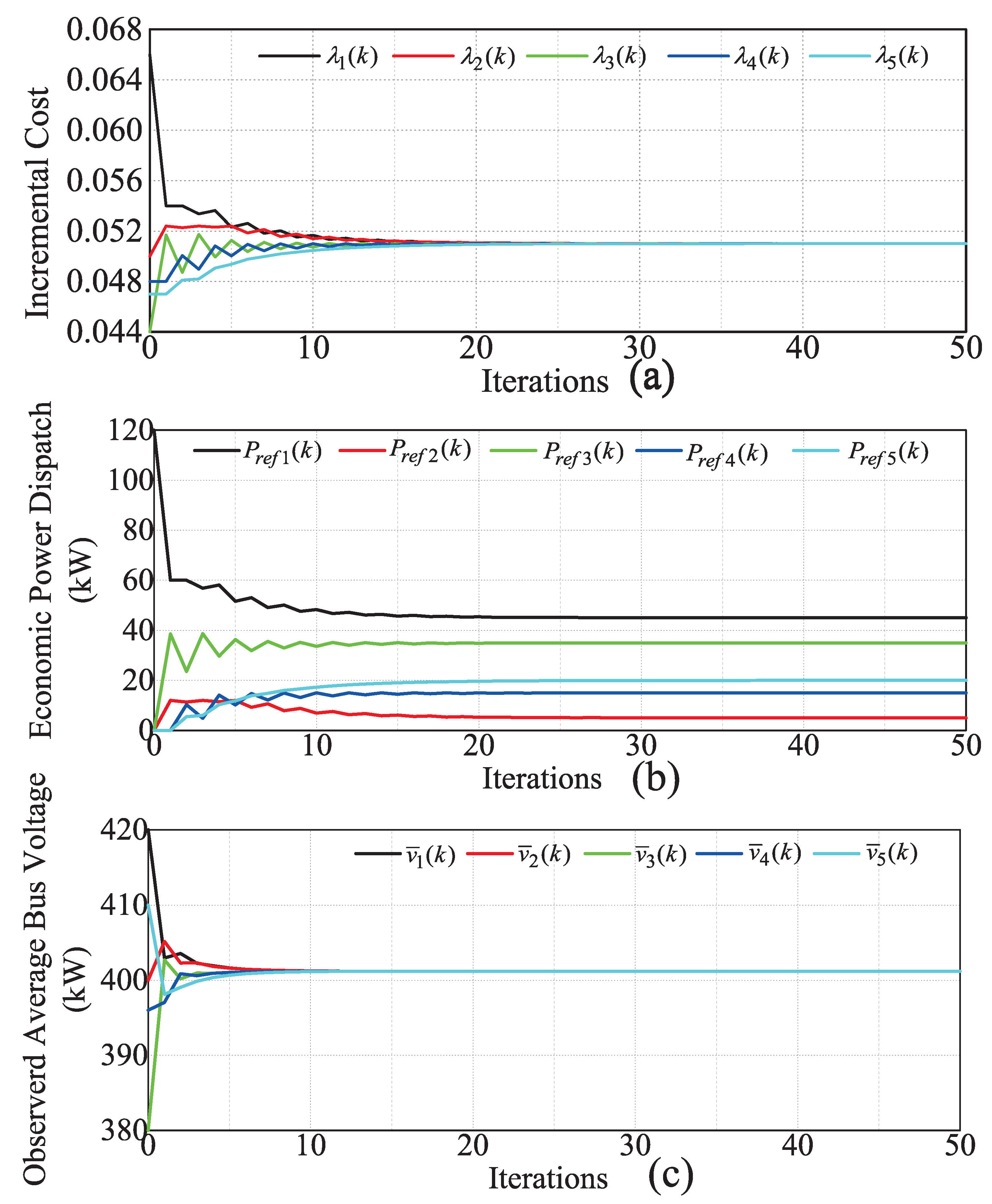
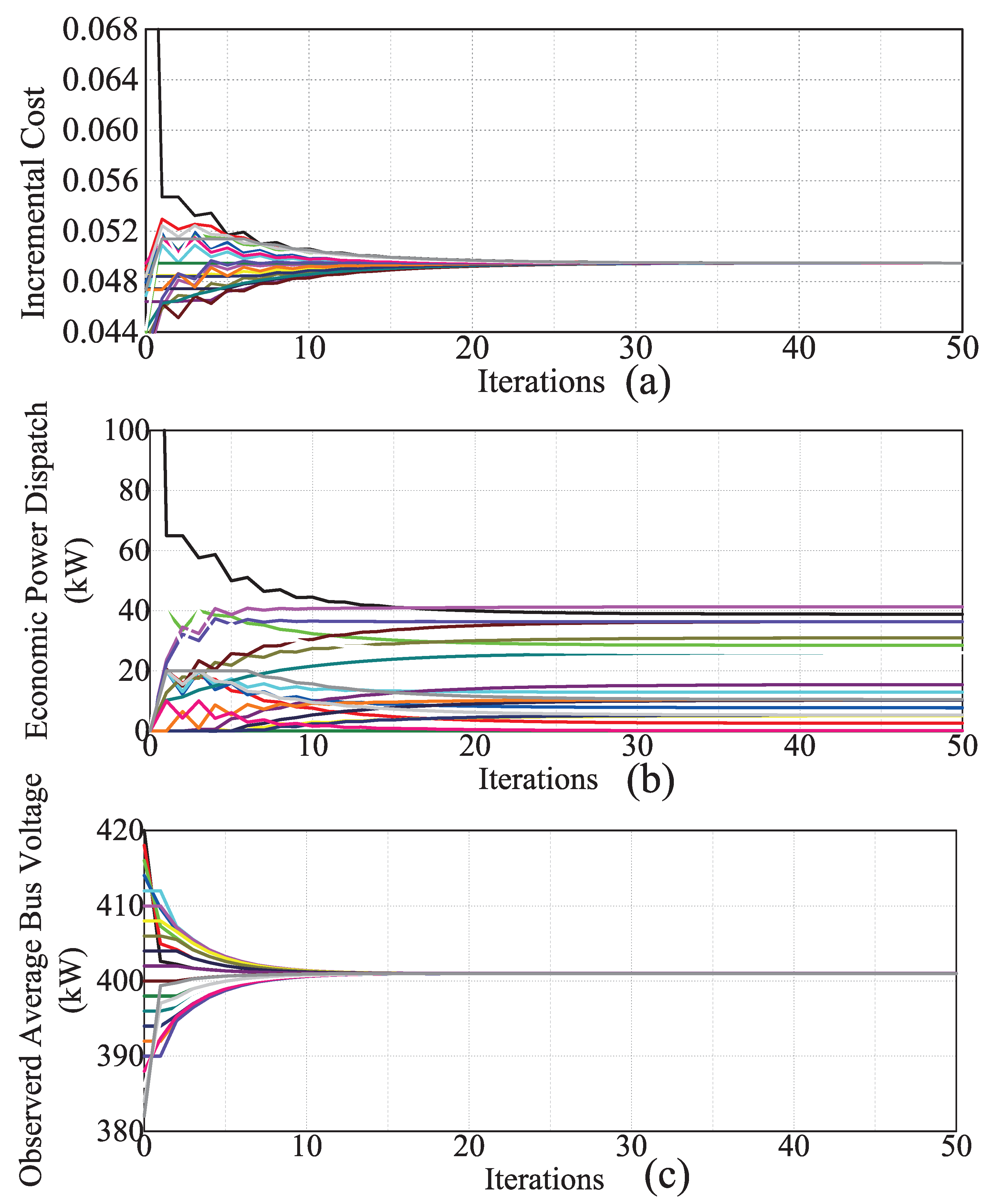
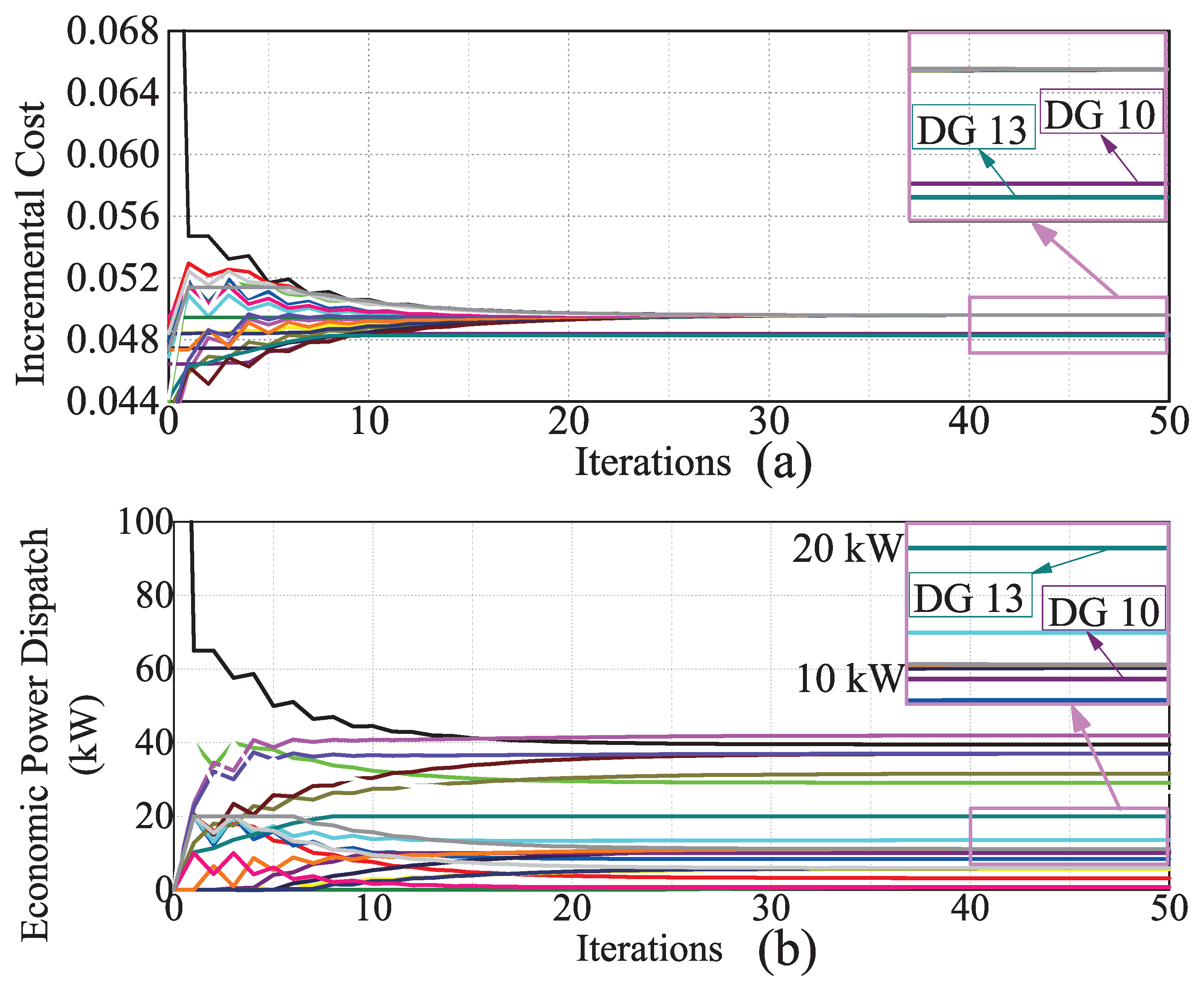
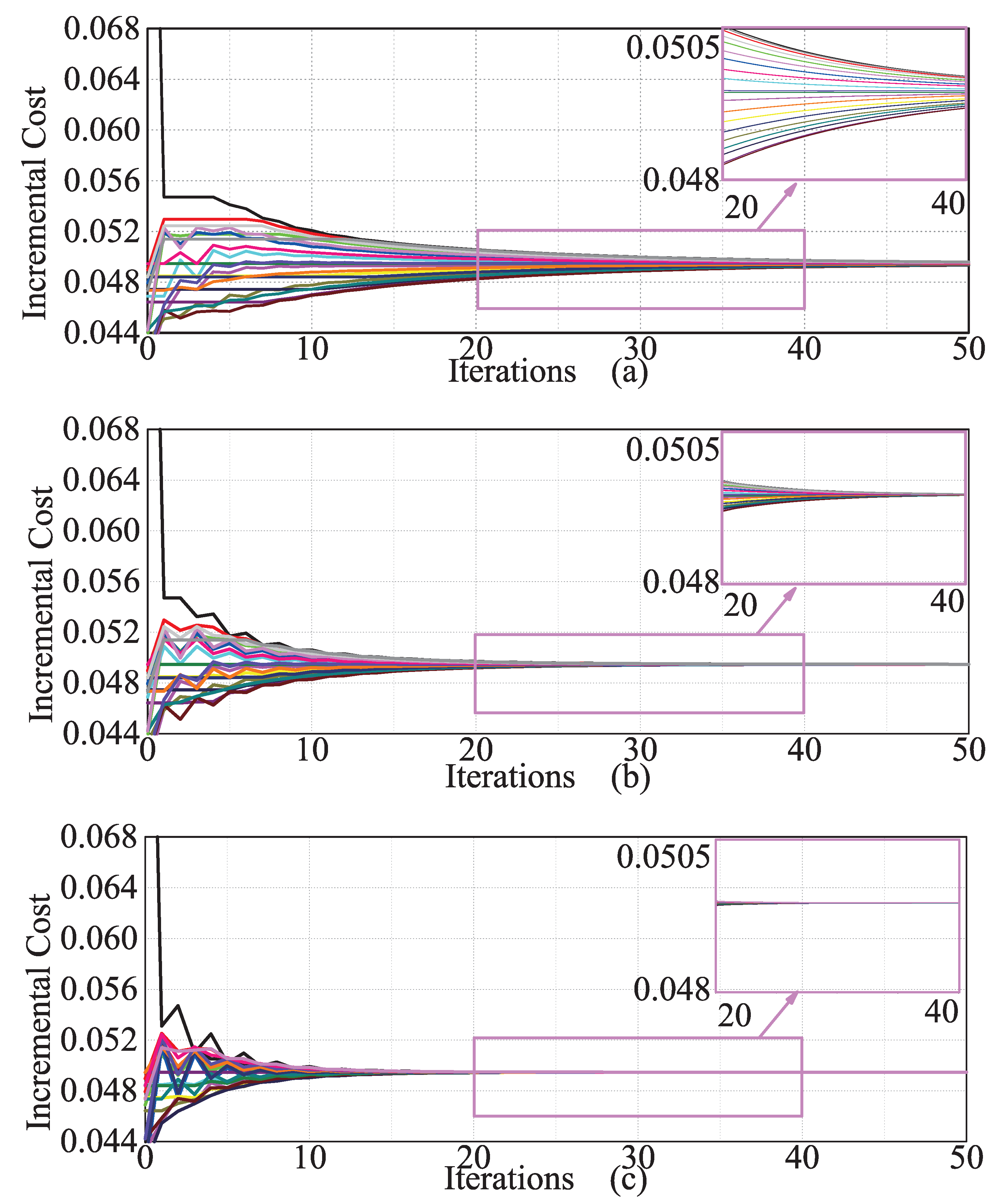
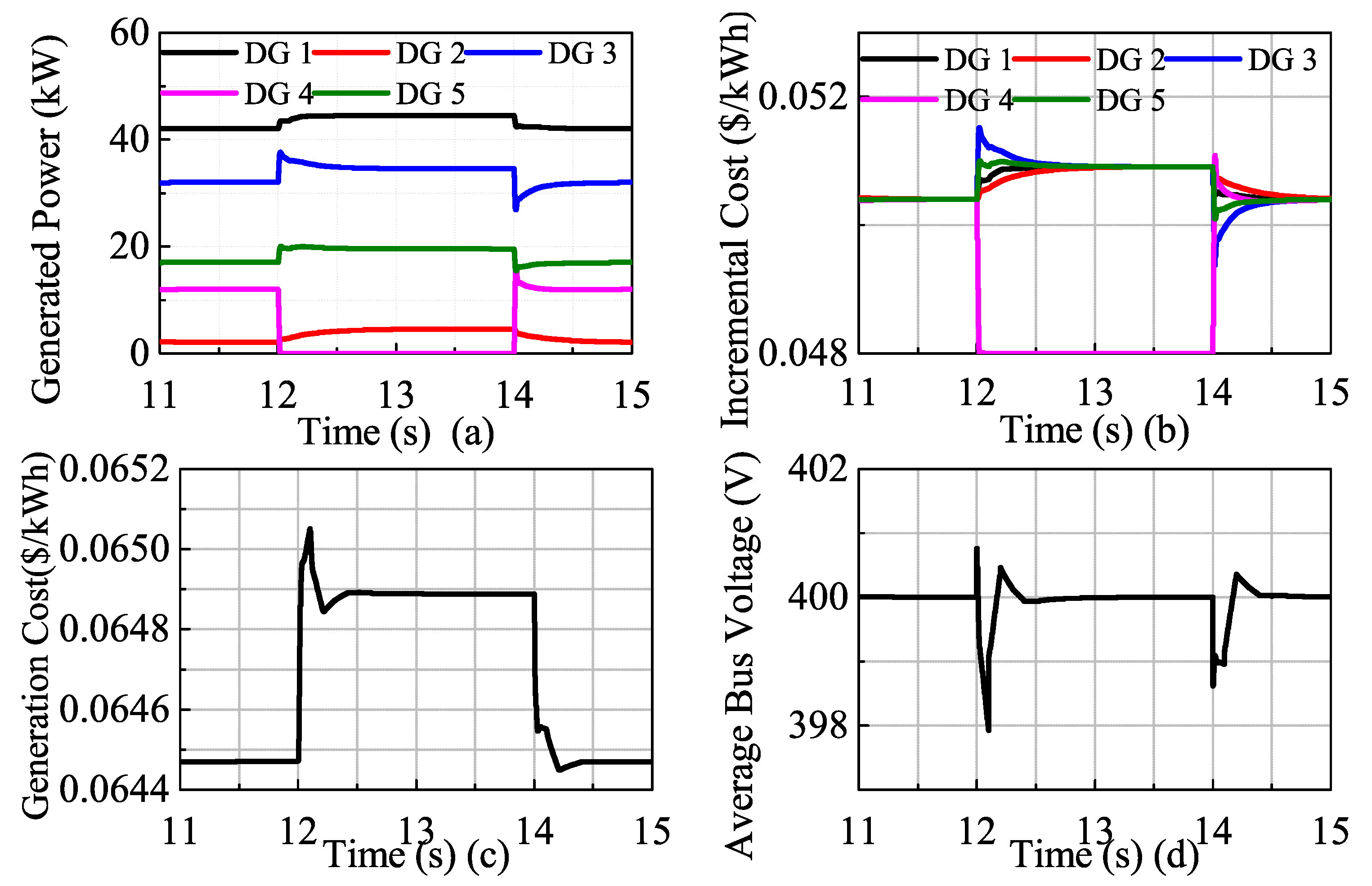
4.1. Algorithm Convergence Test
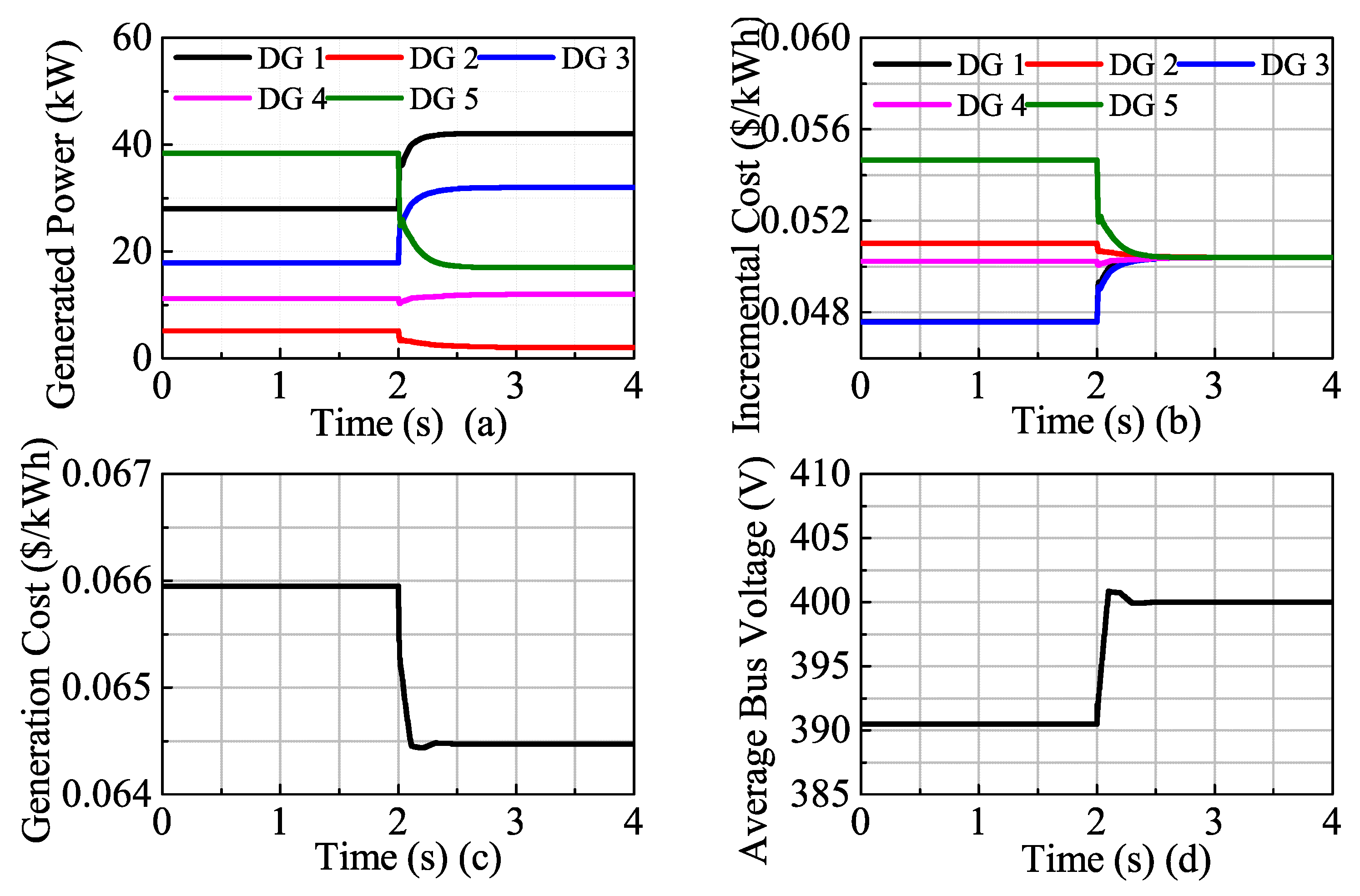
4.2. Performance Comparison with and without the Proposed Algorithm
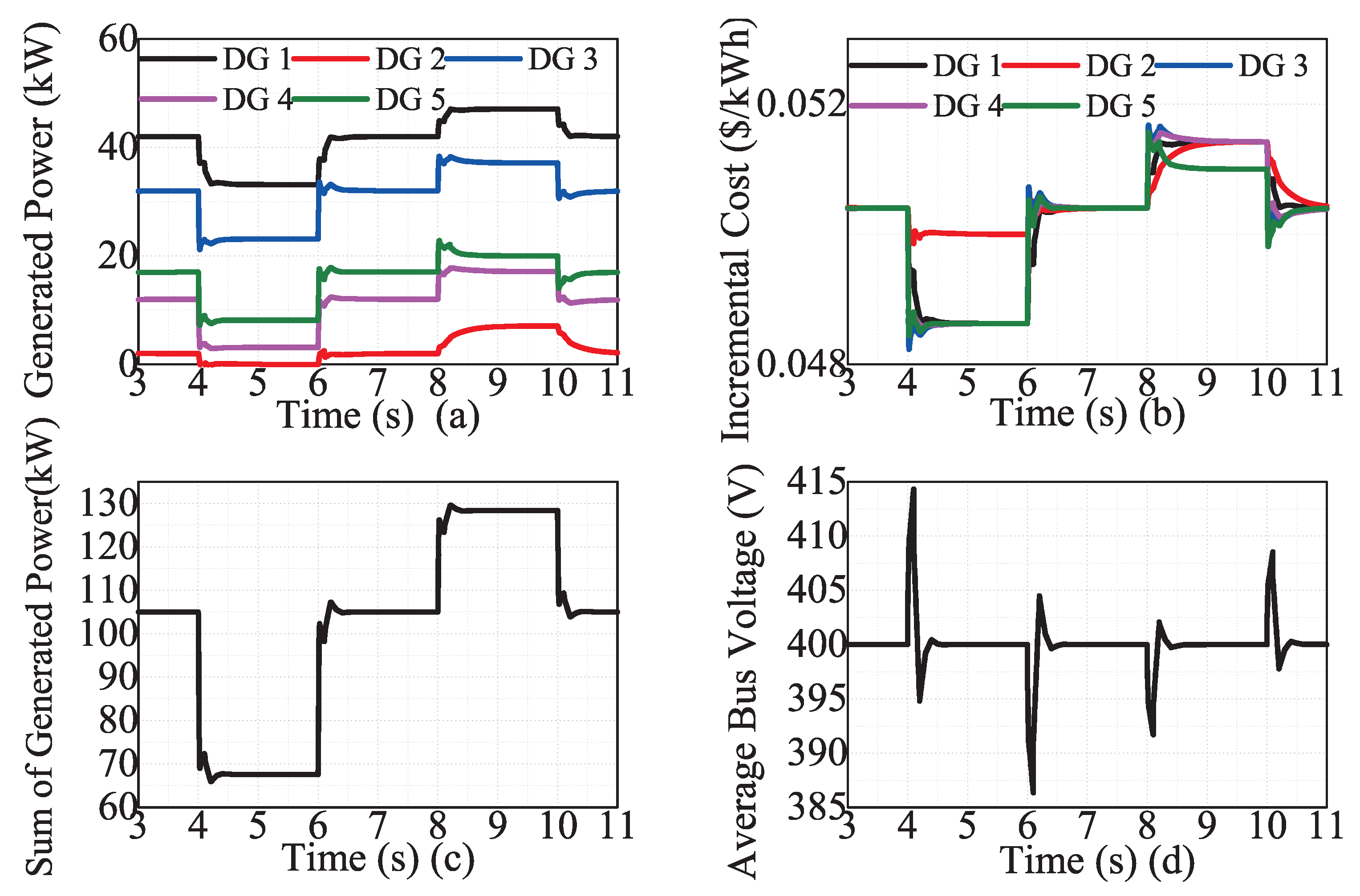
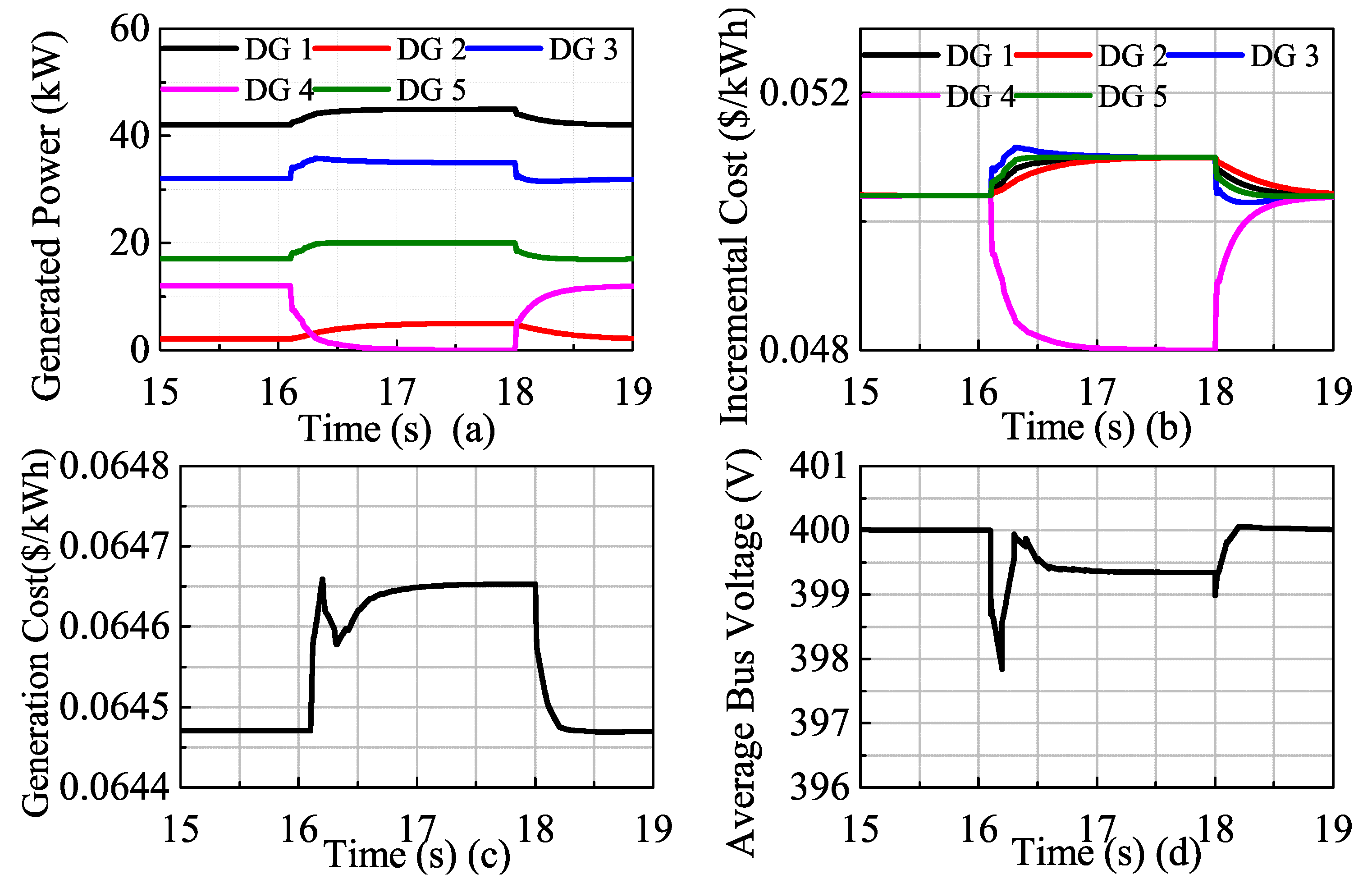
4.3. Time-Varying Load Demand Test
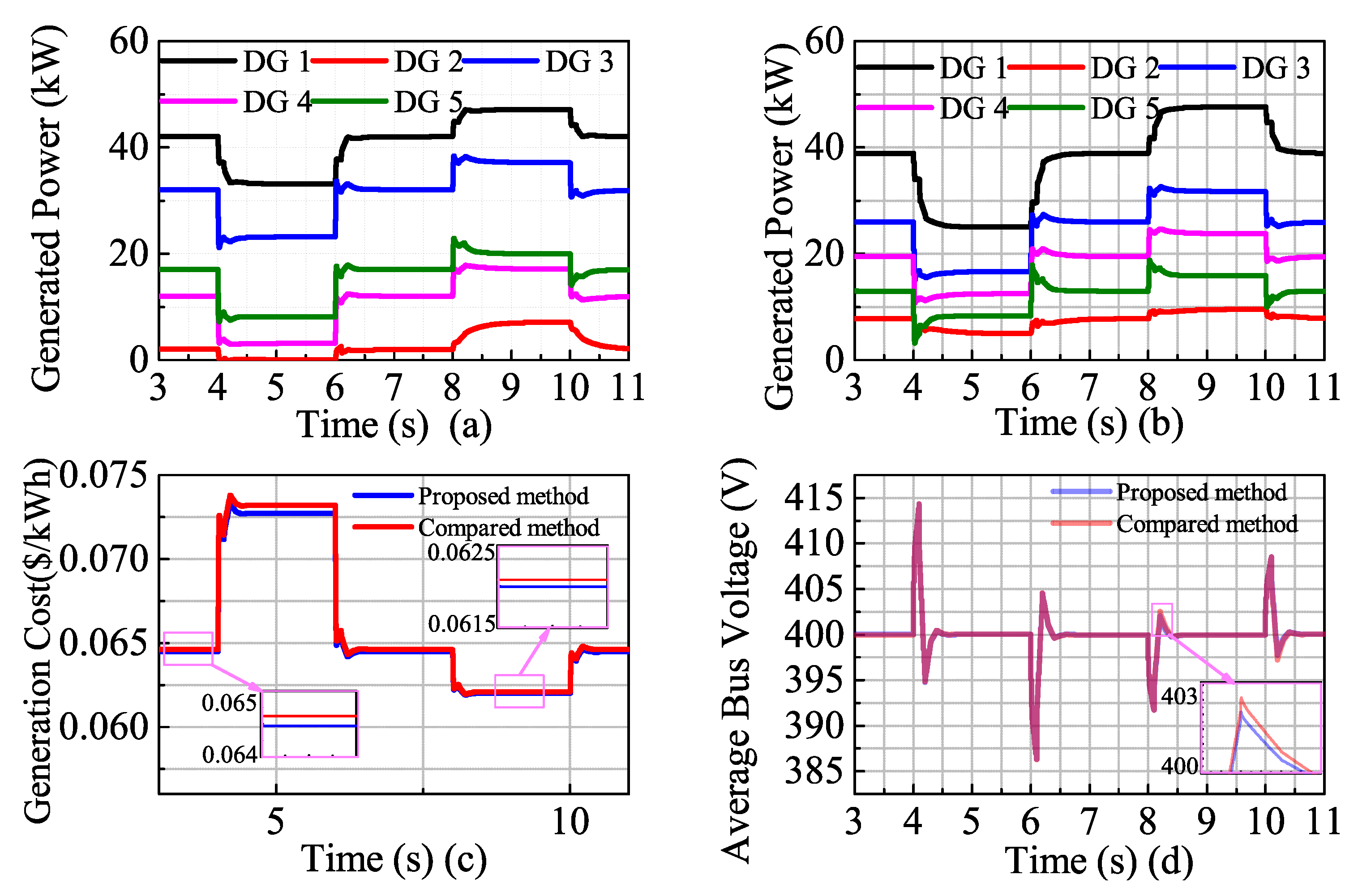
4.4. Performance Comparison with a Distributed Cooperative Control Strategy
4.5. Algorithm Robustness Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, R.; Meng, L.; Ferrari-Trecate, G.; Coelho, E.A.A.; Vasquez, J.C.; Guerrero, J.M. Containment and Consensus-Based Distributed Coordination Control to Achieve Bounded Voltage and Precise Reactive Power Sharing in Islanded AC Microgrids. IEEE Trans. Ind. Appl. 2017, 53, 5187–5199. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. Hybrid AC/DC microgrid planning. Energy 2017, 118, 37–46. [Google Scholar] [CrossRef]
- Vu, T.V.; Perkins, D.; Diaz, F.; Gonsoulin, D.; Edrington, C.S.; El-Mezyani, T. Robust adaptive droop control for DC microgrids. Electr. Power Syst. Res. 2017, 146, 95–106. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed Cooperative Control of DC Microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Cook, M.D.; Parker, G.G.; Robinett, R.D.; Weaver, W.W. Decentralized Mode-Adaptive Guidance and Control for DC Microgrid. IEEE Trans. Power Deliv. 2017, 32, 263–271. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. AC Versus DC Microgrid Planning. IEEE Trans. Smart Grid 2017, 8, 296–304. [Google Scholar] [CrossRef]
- Balog, R.S.; Weaver, W.W.; Krein, P.T. The Load as an Energy Asset in a Distributed DC SmartGrid Architecture. IEEE Trans. Smart Grid 2012, 3, 253–260. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, D.; Jin, C.; Koh, L.H.; Choo, F.H.; Wang, P.; Tang, Y. Droop control of a bipolar DC microgrid for load sharing and voltage balancing. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 795–799. [Google Scholar]
- Zhang, Y.; Li, Y.W. Energy Management Strategy for Supercapacitor in Droop-Controlled DC Microgrid Using Virtual Impedance. IEEE Trans. Power Electron. 2017, 32, 2704–2716. [Google Scholar] [CrossRef]
- Yang, N.; Paire, D.; Gao, F.; Miraoui, A. Compensation of droop control in DC microgrid with multiple distributed generators. In Cyber-Physical-Social Systems and Constructs in Electric Power Engineering; Suryanarayanan, S., Roche, R., Hansen, T., Eds.; The Institution of Engineering and Technology: London, UK, 2016; pp. 253–289. [Google Scholar]
- Khorsandi, A.; Ashourloo, M.; Mokhtari, H.; Iravani, R. Automatic droop control for a low voltage DC microgrid. IET Gener. Transm. Distrib. 2016, 10, 41–47. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An Improved Droop Control Method for DC Microgrids Based on Low Bandwidth Communication With DC Bus Voltage Restoration and Enhanced Current Sharing Accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids-A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Salomonsson, D.; Soder, L.; Sannino, A. An Adaptive Control System for a DC Microgrid for Data Centers. IEEE Trans. Ind. Appl. 2008, 44, 1910–1917. [Google Scholar] [CrossRef]
- Kakigano, H.; Miura, Y.; Ise, T. Distribution Voltage Control for DC Microgrids Using Fuzzy Control and Gain-Scheduling Technique. IEEE Trans. Power Electron. 2013, 28, 2246–2258. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Liu, W. Distributed Dynamic Programming-Based Approach for Economic Dispatch in Smart Grids. IEEE Trans. Ind. Inf. 2015, 11, 166–175. [Google Scholar] [CrossRef]
- Hu, J.; Duan, J.; Ma, H.; Chow, M.Y. Distributed Adaptive Droop Control for Optimal Power Dispatch in DC Microgrid. IEEE Trans. Ind. Electron. 2018, 65, 778–789. [Google Scholar] [CrossRef]
- Li, Q.; Gao, D.W.; Zhang, H.; Wu, Z.; Wang, F.Y. Consensus-Based Distributed Economic Dispatch Control Method in Power Systems. IEEE Trans. Smart Grid 2017, 10, 941–954. [Google Scholar] [CrossRef]
- Hu, J.; Chen, M.Z.Q.; Cao, J.; Guerrero, J.M. Coordinated Active Power Dispatch for a Microgrid via Distributed Lambda Iteration. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 250–261. [Google Scholar] [CrossRef]
- Mudumbai, R.; Dasgupta, S.; Cho, B.B. Distributed Control for Optimal Economic Dispatch of a Network of Heterogeneous Power Generators. IEEE Trans. Power Syst. 2012, 27, 1750–1760. [Google Scholar] [CrossRef]
- Zhang, Z.; Chow, M.Y. Convergence Analysis of the Incremental Cost Consensus Algorithm Under Different Communication Network Topologies in a Smart Grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, Y.; Liu, W.; Ranade, S.J.; Luo, Y. Distributed Optimal Active Power Dispatch Under Constraints for Smart Grids. IEEE Trans. Ind. Electron. 2017, 64, 5084–5094. [Google Scholar] [CrossRef]
- Khorsandi, A.; Ashourloo, M.; Mokhtari, H. A Decentralized Control Method for a Low-Voltage DC Microgrid. IEEE Trans. Energy Conv. 2014, 29, 793–801. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, H. MAS based distributed automatic generation control for cyber-physical microgrid system. IEEE/CAA J. Autom. Sin. 2016, 3, 78–89. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W. Novel Multiagent Based Load Restoration Algorithm for Microgrids. IEEE Trans. Smart Grid 2011, 2, 152–161. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, H.; Li, S. Analysis of Multi-Agent-Based Adaptive Droop-Controlled AC Microgrids with PSCAD: Modeling and Simulation. J. Power Electron. 2015, 15, 455–468. [Google Scholar] [CrossRef]
- Yang, Z.; Xiang, J.; Li, Y. Distributed Consensus Based Supply-Demand Balance Algorithm for Economic Dispatch Problem in a Smart Grid With Switching Graph. IEEE Trans. Ind. Electron. 2017, 64, 1600–1610. [Google Scholar] [CrossRef]
- Li, L.M.; Lu, K.D.; Zeng, G.Q.; Wu, L.; Chen, M.R. A novel real-coded population-based extremal optimization algorithm with polynomial mutation: A non-parametric statistical study on continuous optimization problems. Neurocomputing 2016, 174, 577–587. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S.; Xu, J.X. Consensus Based Approach for Economic Dispatch Problem in a Smart Grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Chen, J.; Song, Y.D. Hierarchical Decentralized Optimization Architecture for Economic Dispatch: A New Approach for Large-Scale Power System. IEEE Trans. Ind. Inf. 2018, 14, 523–534. [Google Scholar] [CrossRef]
- Xing, H.; Mou, Y.; Fu, M.; Lin, Z. Distributed Bisection Method for Economic Power Dispatch in Smart Grid. IEEE Trans. Power Syst. 2015, 30, 3024–3035. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, W.; Zang, C.; Liu, L. Multiagent System-Based Integrated Solution for Topology Identification and State Estimation. IEEE Trans. Ind. Inf. 2017, 13, 714–724. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Gu, W.; Xu, Y.; Li, Z. Optimal Distributed Control for Secondary Frequency and Voltage Regulation in an Islanded Microgrid. IEEE Trans. Ind. Inf. 2019, 15, 225–235. [Google Scholar] [CrossRef]
- Meng, W.; Wang, X.; Liu, S. Distributed Load Sharing of an Inverter-Based Microgrid With Reduced Communication. IEEE Trans. Smart Grid 2018, 9, 1354–1364. [Google Scholar] [CrossRef]
- Xu, Y. Robust Finite-Time Control for Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Ind. Inf. 2017, 13, 2717–2725. [Google Scholar] [CrossRef]
- Savaghebi, M.; Jalilian, A.; Vasquez, J.C.; Guerrero, J.M. Autonomous Voltage Unbalance Compensation in an Islanded Droop-Controlled Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 1390–1402. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Bosnjak, D.; Harris, B. Investigation and Active Damping of Multiple Resonances in a Parallel-Inverter-Based Microgrid. IEEE Trans. Power Electron. 2013, 28, 234–246. [Google Scholar] [CrossRef]
- Jayawarna, N.; Barnes, M. Study Of A Microgrid With Vehicle-To-Grid Sources During Network Contingencies. Intell. Autom. Soft Comput. 2010, 16, 289–302. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Zheng, Y. Constrained population extremal optimization-based robust load frequency control of multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2019, 105, 249–271. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Du, W. Design of PID controller based on a self-adaptive state-space predictive functional control using extremal optimization method. J. Frankl. Inst. Eng. Appl. Math. 2018, 355, 2197–2220. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Chen, J.; Dai, Y.X.; Li, L.M.; Zheng, C.W.; Chen, M.R. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 2015, 160, 173–184. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, S.; Bian, J. Control of a Grid-Forming Inverter Based on Sliding-Mode and Mixed H2/H∞ Control. IEEE Trans. Ind. Electron. 2017, 64, 3862–3872. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. Control of Single-Phase Grid-Connected Converters WithLCLFilters Using Recurrent Neural Network and Conventional Control Methods. IEEE Trans. Power Electron. 2016, 31, 5354–5364. [Google Scholar] [CrossRef]
| DG and Agent Index | Neighboring Agents | V/A | Range kW | |||
|---|---|---|---|---|---|---|
| 1 | 2,3 | 0.0001 | 0.042 | 0.25 | 0.1533 | [0, 60] |
| 2 | 1,4 | 0.0001 | 0.05 | 0.42 | 0.7667 | [0, 12] |
| 3 | 1,4,5 | 0.0001 | 0.044 | 0.35 | 0.2410 | [0, 40] |
| 4 | 2,3,5 | 0.0001 | 0.048 | 0.45 | 0.3213 | [0, 30] |
| 5 | 3,4 | 0.0001 | 0.047 | 0.33 | 0.0640 | [0, 20] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Li, Z.; Liang, J.; Gao, J.; Si, J.; Li, S. Distributed Economic Power Dispatch and Bus Voltage Control for Droop-Controlled DC Microgrids. Energies 2019, 12, 1400. https://doi.org/10.3390/en12071400
Cheng Z, Li Z, Liang J, Gao J, Si J, Li S. Distributed Economic Power Dispatch and Bus Voltage Control for Droop-Controlled DC Microgrids. Energies. 2019; 12(7):1400. https://doi.org/10.3390/en12071400
Chicago/Turabian StyleCheng, Zhiping, Zhongwen Li, Jing Liang, Jinfeng Gao, Jikai Si, and Shuhui Li. 2019. "Distributed Economic Power Dispatch and Bus Voltage Control for Droop-Controlled DC Microgrids" Energies 12, no. 7: 1400. https://doi.org/10.3390/en12071400
APA StyleCheng, Z., Li, Z., Liang, J., Gao, J., Si, J., & Li, S. (2019). Distributed Economic Power Dispatch and Bus Voltage Control for Droop-Controlled DC Microgrids. Energies, 12(7), 1400. https://doi.org/10.3390/en12071400






