Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range †
Abstract
:1. Introduction
2. Driving Cycle Data Preprocessing
2.1. Delivery Vehicle Fleet Description and Driving Data Collection
2.2. Preprocessing of Driving Cycles to Serve as Neural Network Inputs
3. Generating Energy Demand Data
3.1. Modeling of Delivery EREV
3.2. Simulation Results of Delivery EREV
4. Modeling of Energy Demand
4.1. Response Surface Modeling Approach
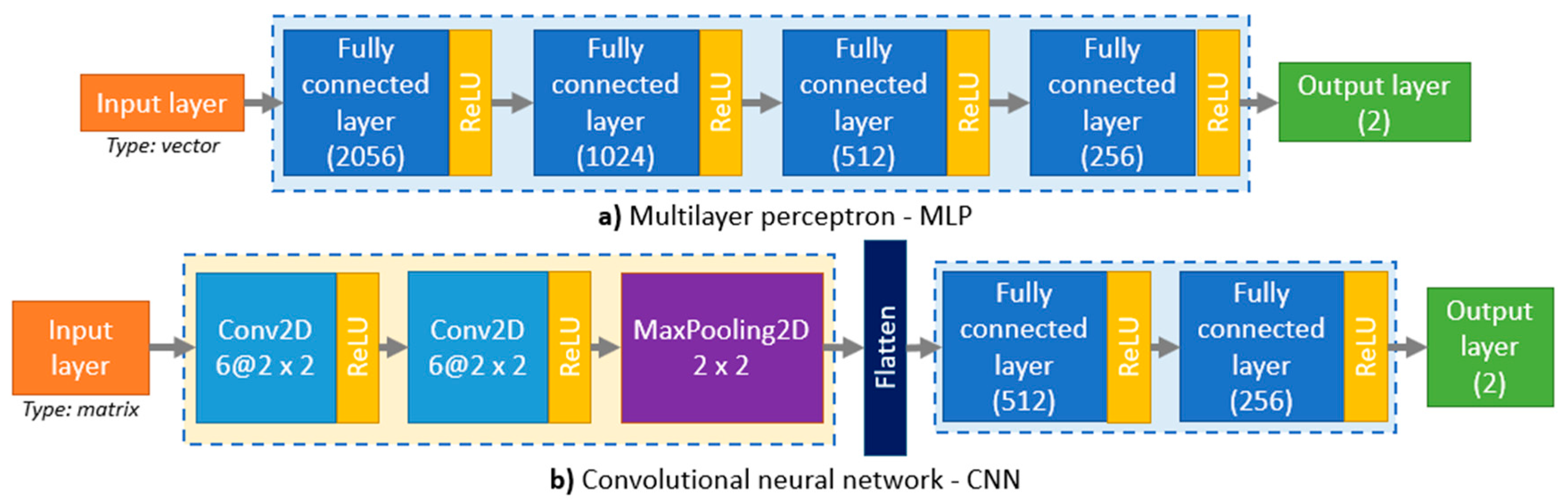
4.2. Neural Network Modeling Approach
4.2.1. Energy Demand Modeling
4.2.2. All-Electric Range Modeling
5. Analysis of Modeling Results
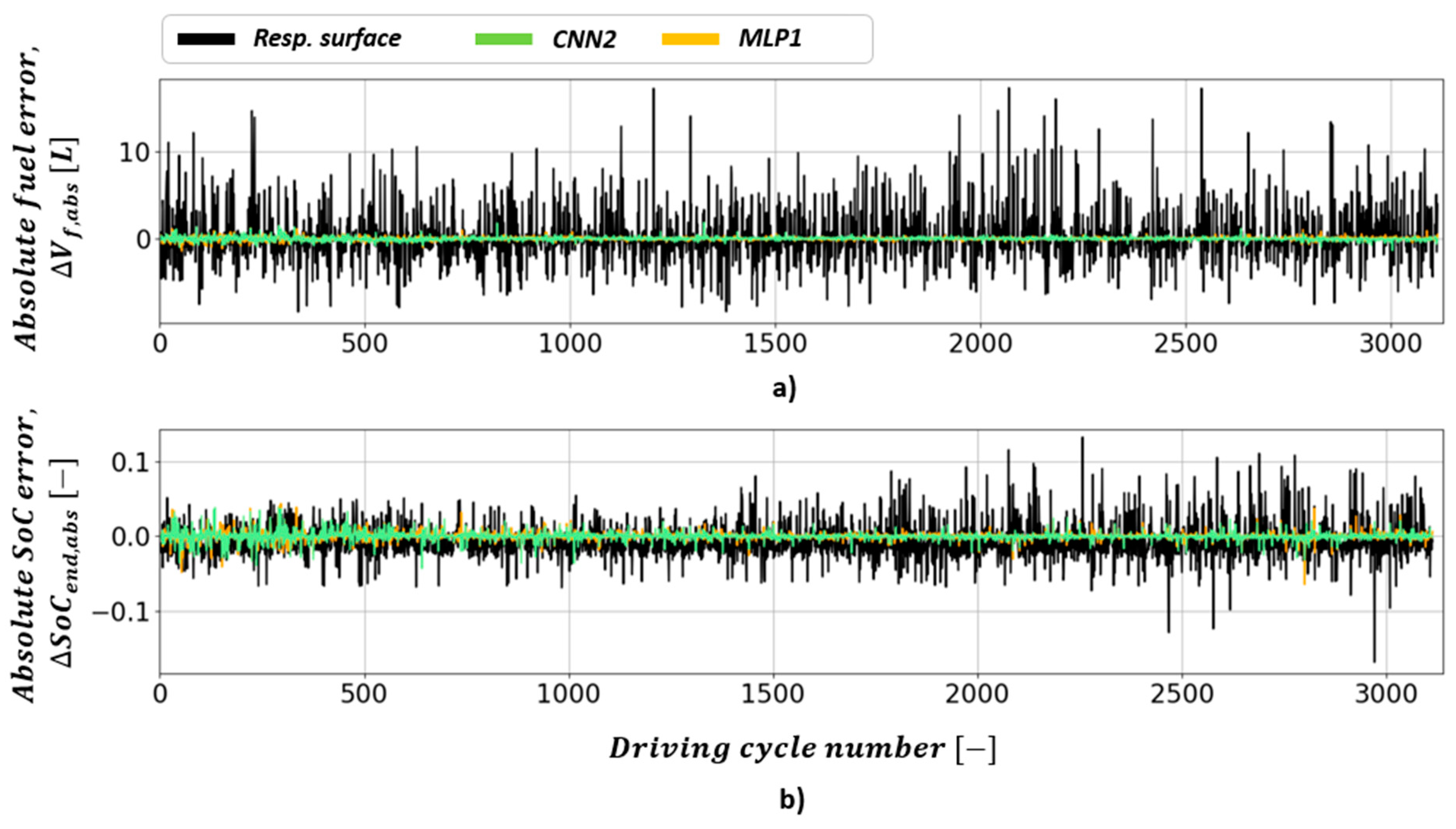
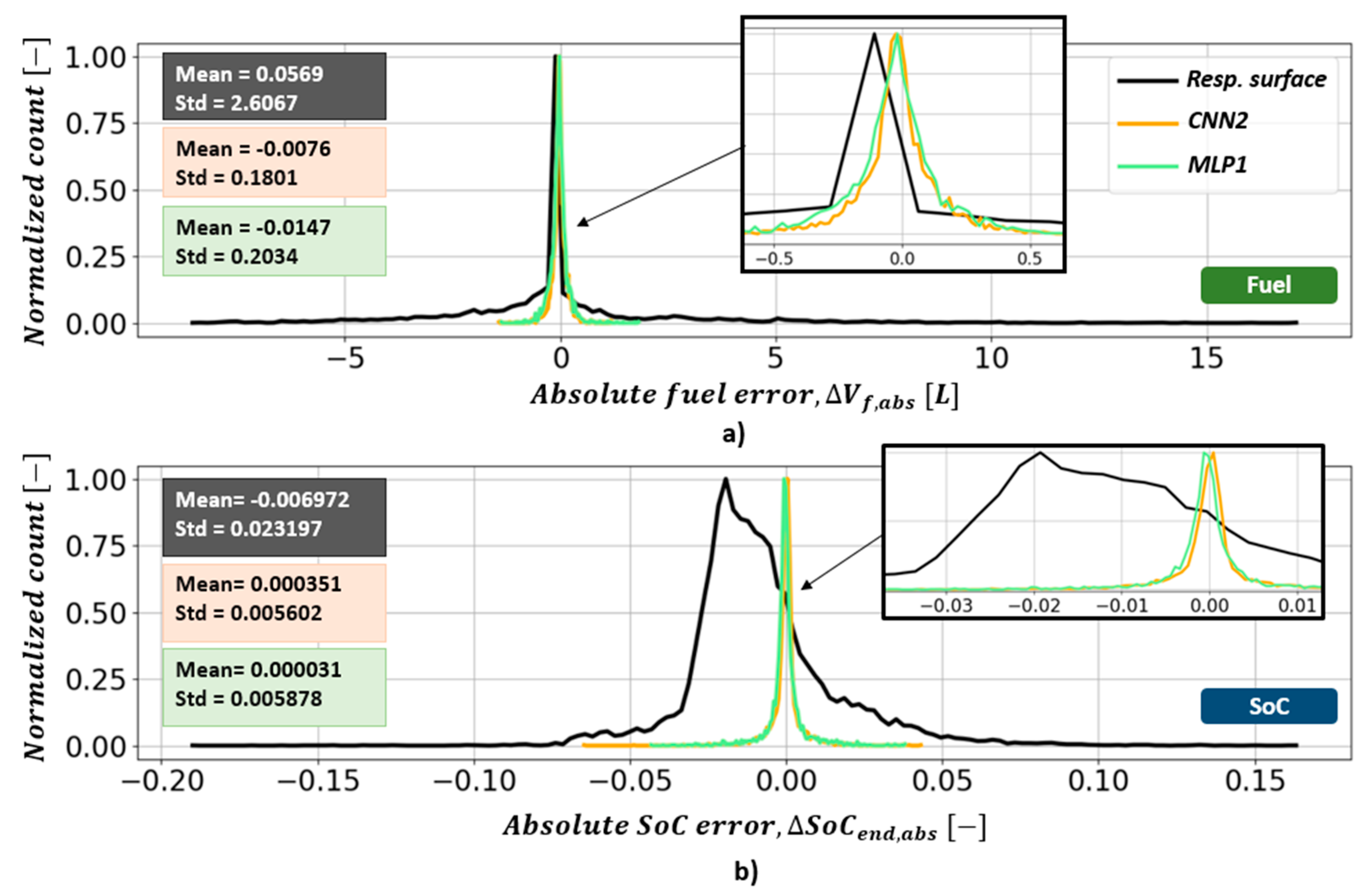
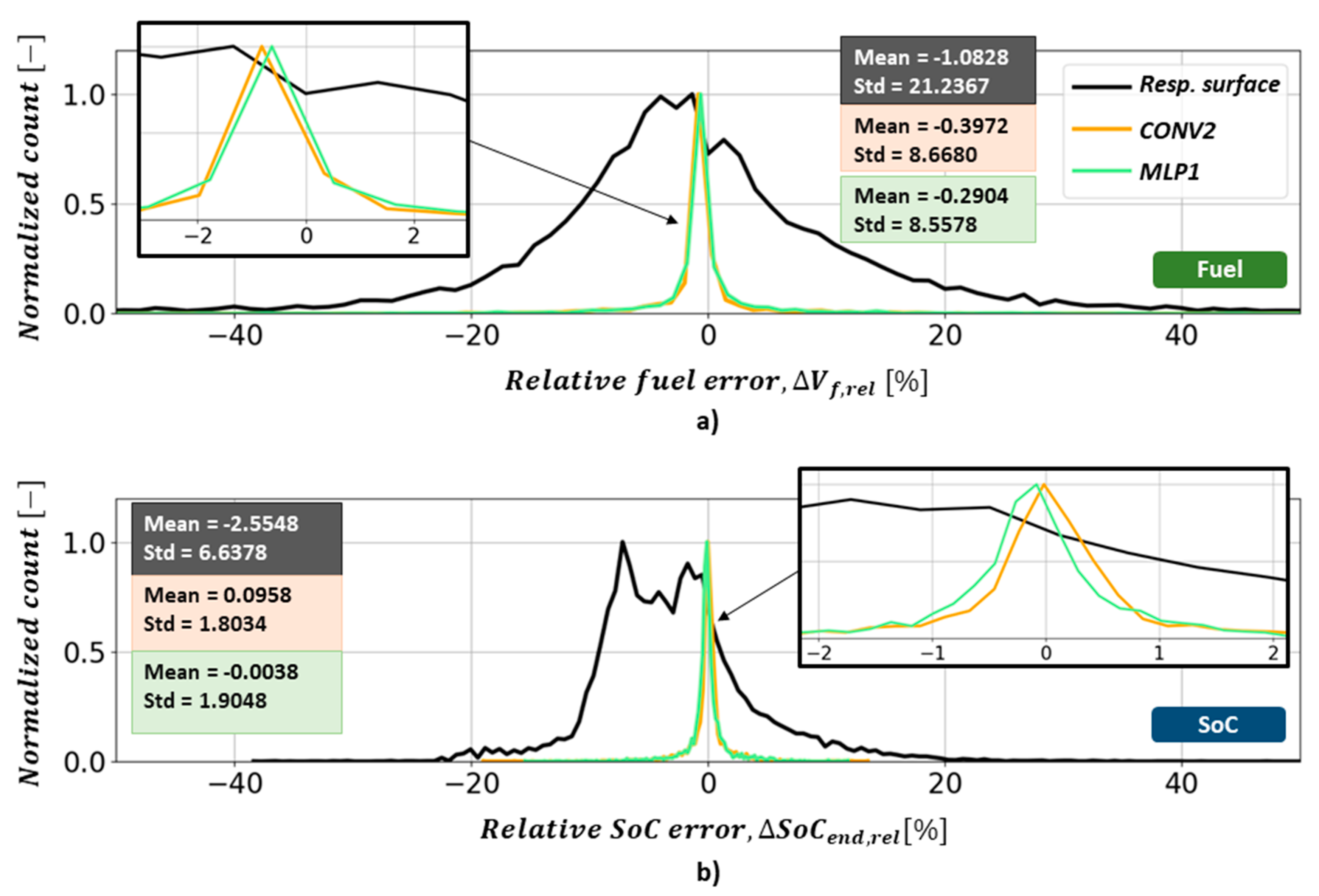
5.1. Energy Demand Prediction
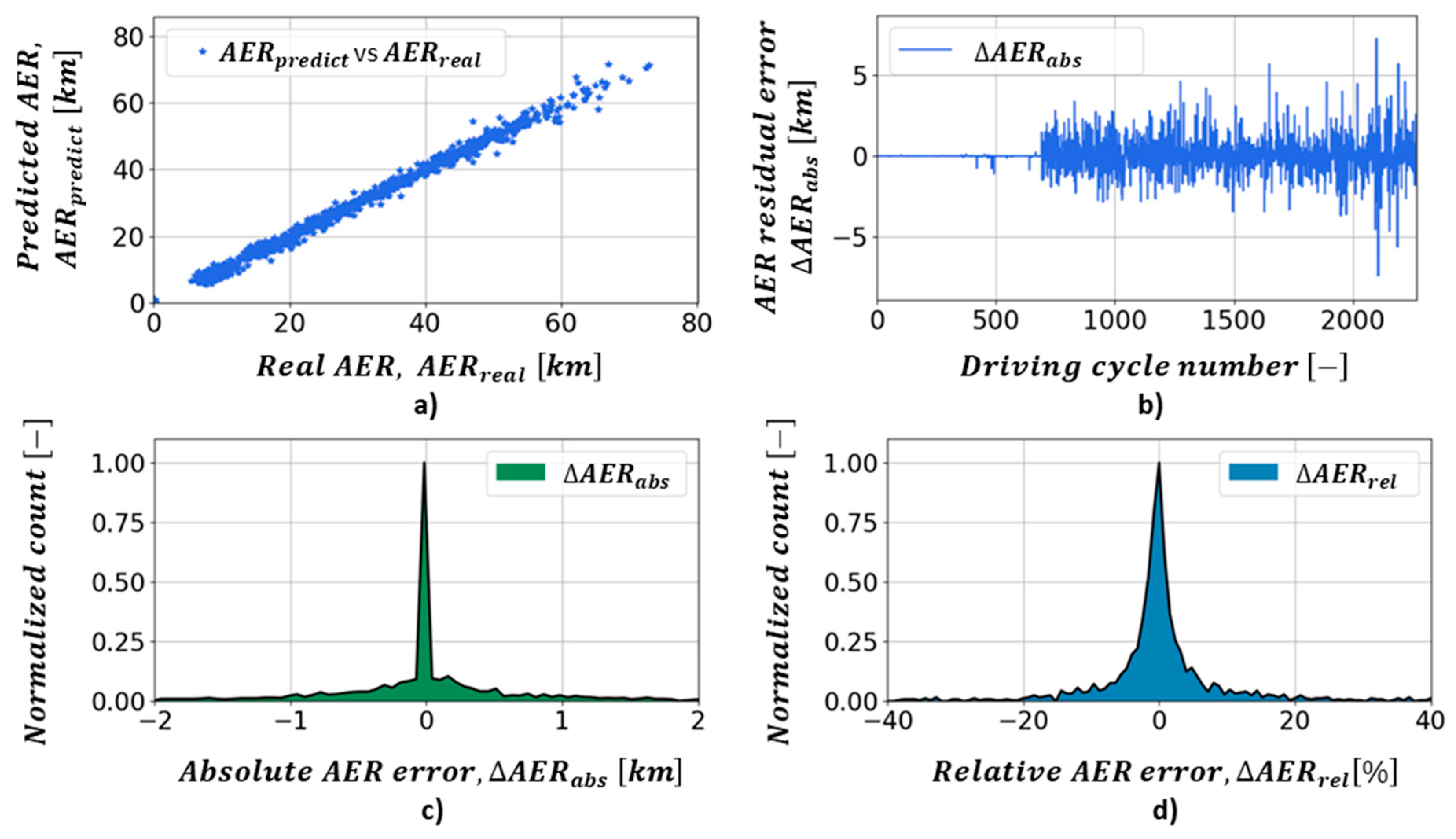
5.2. All-Electric Range (AER) Prediction
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Suhail Hussain, S.M.; Ustun, T.S.; Nsonga, P.; Ali, I. IEEE 1609 WAVE and IEC 61850 Standard Communication Based Integrated EV Charging Management in Smart Grids. IEEE Trans. Veh. Technol. 2018, 67, 7690–7697. [Google Scholar] [CrossRef]
- De Cauwer, C.; Verbeke, W.; Coosemans, T.; Faid, S.; Van Mierlo, J. A Data-Driven Method for Energy Consumption Prediction and Energy-Efficient Routing of Electric Vehicles in Real-World Conditions. Energies 2017, 10, 608. [Google Scholar] [CrossRef]
- Nageshrao, S.P.; Jacob, J.; Wilkins, S. Charging cost optimization for EV buses using neural network based energy predictor. IFAC-Pap. 2017, 50, 5947–5952. [Google Scholar] [CrossRef]
- Škugor, B.; Deur, J. Synthetic Driving Cycles-based Modelling of Extended Range Electric Vehicle Fleet Energy Demand. In Proceedings of the 30th International Electric Vehicle Symposium & Exhibition, Stuttgart, Germany, 9–11 October 2017. [Google Scholar]
- Lee, T.K.; Filipi, Z.S. Response surface modelling approach for the assessment of the PHEV impact on the grid. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar]
- Škugor, B.; Deur, J. Delivery vehicle fleet data collection, analysis, and naturalistic driving cycle synthesis. Int. J. Innov. Sustain. Dev. 2016, 10, 19–33. [Google Scholar] [CrossRef]
- Lee, T.K.; Filipi, Z.S. Synthesis of real-world driving cycles using stochastic process and statistical methodology. Int. J. Veh. Des. 2011, 56, 43–62. [Google Scholar] [CrossRef]
- Brand, C.; Anable, J.; Morton, C. Lifestyle, efficiency and limits: Modelling transport energy and emissions using a socio-technical approach. Energy Effic. 2019, 12, 187–207. [Google Scholar] [CrossRef]
- Geem, Z.W. Transport energy demand modeling of South Korea using artificial neural network. Energy Policy 2011, 39, 4644–4650. [Google Scholar] [CrossRef]
- Murat, Y.S.; Halim, C. Use of artificial neural networks for transport energy demand modelling. Energy Policy 2006, 34, 3165–3172. [Google Scholar] [CrossRef]
- Teng, G.; Xiao, J.; He, Y.; Zheng, T.; He, C. Use of group method of data handling for transport energy demand modelling. Energy Sci. Eng. 2017, 5, 302–317. [Google Scholar] [CrossRef]
- Shankar, R.; Marco, J. Method for estimating the energy consumption of electric vehicles and plug-in hybrid electric vehicles under real-world driving conditions. IET Intell. Transp. Syst. 2013, 7, 138–150. [Google Scholar] [CrossRef]
- Zeng, T.; Zhang, C.; Hu, M.; Chen, Y.; Yuan, C.; Chen, J.; Zhou, A. Modelling and predicting energy consumption of a range extender fuel cell hybrid vehicle. Energy 2018, 165, 187–197. [Google Scholar] [CrossRef]
- Delogu, M.; Del Pero, F.; Pierini, M. Lightweight Design Solutions in the Automotive Field: Environmental Modelling Based on Fuel Reduction Value Applied to Diesel Turbocharged Vehicles. Sustainability 2016, 8, 1167. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Neural Networks. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- A Medium Corporation. Available online: https://medium.com/@siddharthdas_32104/cnns-architectures-lenet-alexnet-vgg-googlenet-resnet-and-more-666091488df5 (accessed on 21 May 2018).
- Tian, Y.; Pei, K.; Jana, S.; Ray, B. DeepTest: Automated Testing of Deep-Neural-Network-driven Autonomous Cars. In Proceedings of the 40th International Conference on Software Engineering, Gothenburg, Sweden, 27 May–3 June 2018; pp. 303–314. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the 15th IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Lemieux, J.; Ma, Y. Vehicle Speed Prediction Using Deep Learning. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference, Montreal, QC, Canada, 19–22 October 2015. [Google Scholar]
- Jia, Y.; Wu, J.; Du, Y. Traffic speed prediction using deep learning method. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1217–1222. [Google Scholar]
- Song, C.; Lee, H.; Kang, C.; Lee, W.; Kim, Y.B.; Cha, S.W. Traffic speed prediction under weekday using convolutional neural networks concepts. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium, Redondo Beach, CA, USA, 11–14 June 2017; pp. 1293–1298. [Google Scholar]
- Park, J.; Chen, Z.; Kiliaris, L.; Kuang, M.L.; Masrur, M.A.; Phillips, A.M.; Murphey, Y.L. Intelligent vehicle power control based on machine learning of optimal control parameters and prediction of road type and traffic congestion. IEEE Trans. Veh. Technol. 2009, 58, 4741–4756. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.W.; Yang, X.; Zhou, Y.; Ye, K.; Wang, G. A comparison study on electric vehicle growth forecasting based on grey system theory and NAR neural network. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications, Sydney, Australia, 6–9 November 2016. [Google Scholar]
- He, H.; Yan, M.; Sun, C.; Peng, J.; Li, M.; Jia, H. Predictive air-conditioner control for electric buses with passenger amount variation forecast. Appl. Energy 2018, 227, 249–261. [Google Scholar] [CrossRef]
- Lopez, K.L.; Gagne, C.; Gardner, M. Demand-Side Management using Deep Learning for Smart Charging of Electric Vehicles. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Morsalin, S.; Mahmud, K.; Town, G. Electric vehicle charge scheduling using an artificial neural network. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia, Melbourne, VIC, Australia, 28 November–1 December 2016. [Google Scholar]
- Zhou, F.; Wang, L.; Lin, H.; Lv, Z. High accuracy state-of-charge online estimation of EV/HEV lithium batteries based on Adaptive Wavelet Neural Network. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013. [Google Scholar]
- Tian, H.; Ouyang, B. Estimation of EV battery SOC based on KF dynamic neural network with GA. In Proceedings of the 2018 Chinese Control and Decision Conference, Shenyang, China, 9–11 June 2018. [Google Scholar]
- Affanni, A.; Bellini, A.; Concari, C.; Franceschini, G.; Lorenzani, E.; Tassoni, C. EV battery state of charge: Neural network based estimation. In Proceedings of the IEEE International Electric Machines and Drives Conference, Madison, WI, USA, 1–4 June 2013. [Google Scholar]
- Cipek, M.; Škugor, B.; Deur, J. Comparative Analysis of Conventional and Electric Delivery Vehicles Based on Realistic Driving Cycles. In Proceedings of the European Electric Vehicle Congress, Brussels, Belgium, 2–5 December 2014. [Google Scholar]
- Škugor, B.; Cipek, M.; Deur, J. Control Variables Optimization and Feedback Control Strategy Design for the Blended Operating Regime of an Extended Range Electric Vehicle. SAE Int. J. Altern. Powertrains 2014, 3, 52–162. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; pp. 198–201. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 22 May 2018).
- Tensorflow. Available online: https://www.tensorflow.org (accessed on 22 May 2018).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimisation. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
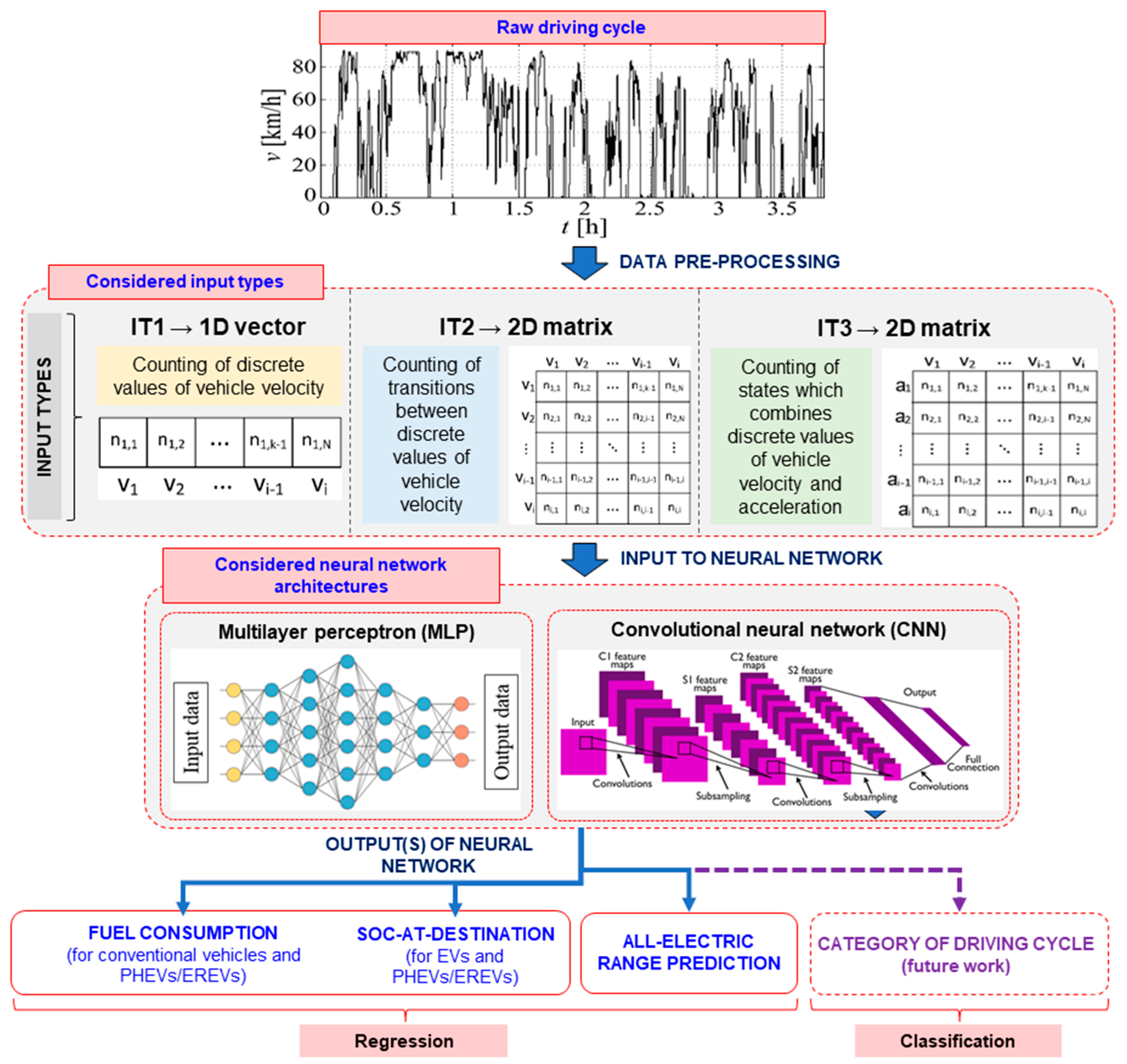
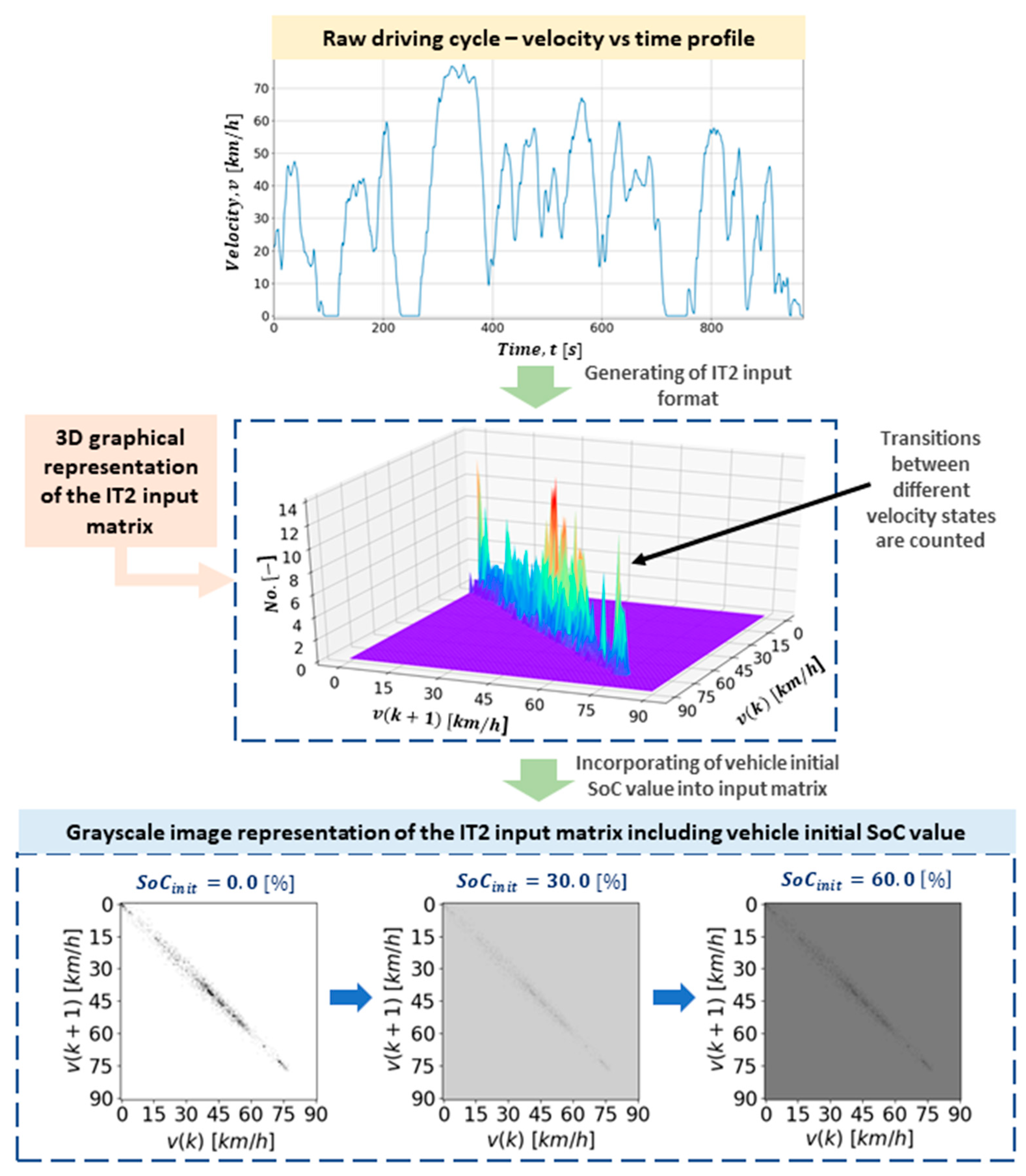
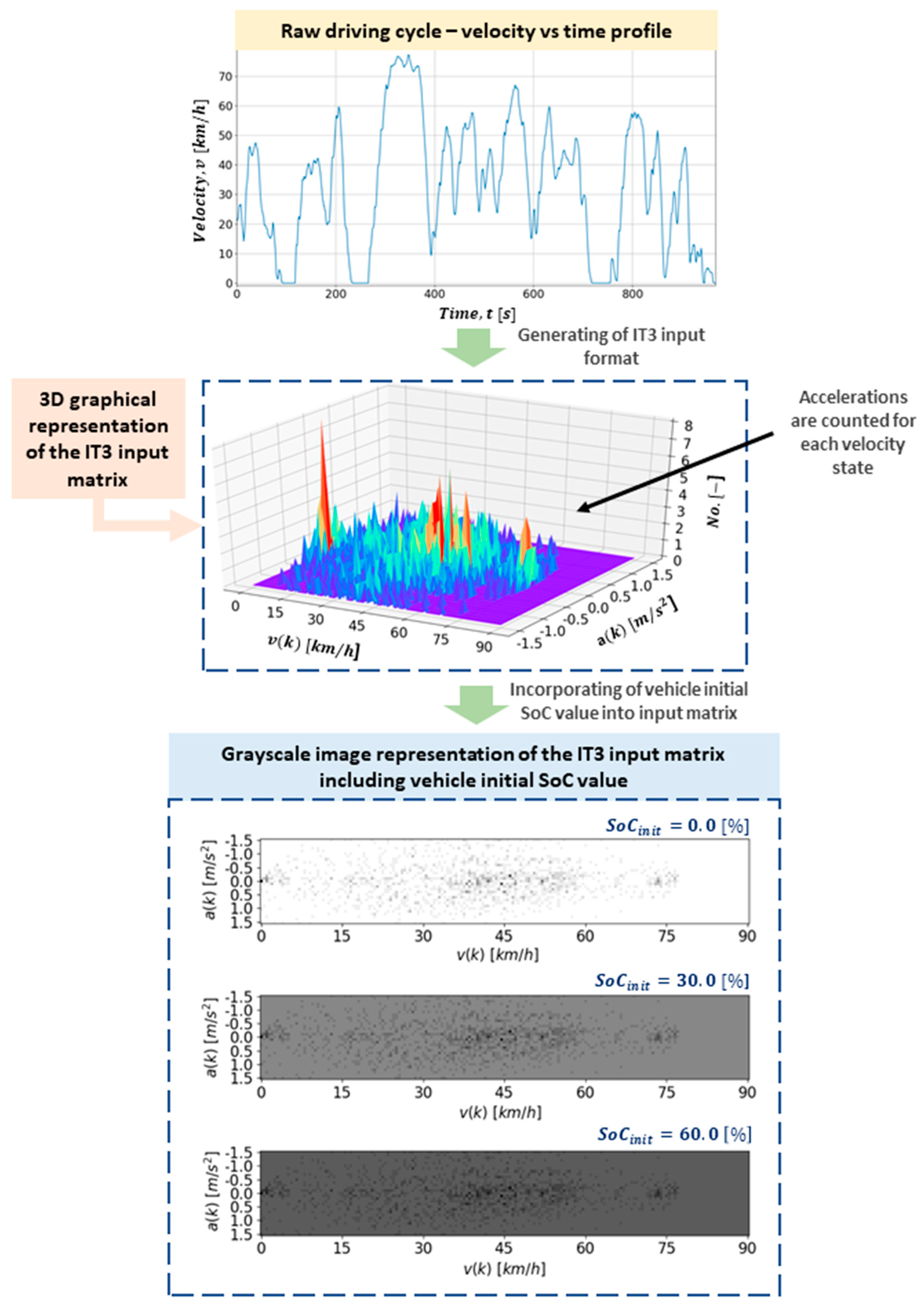
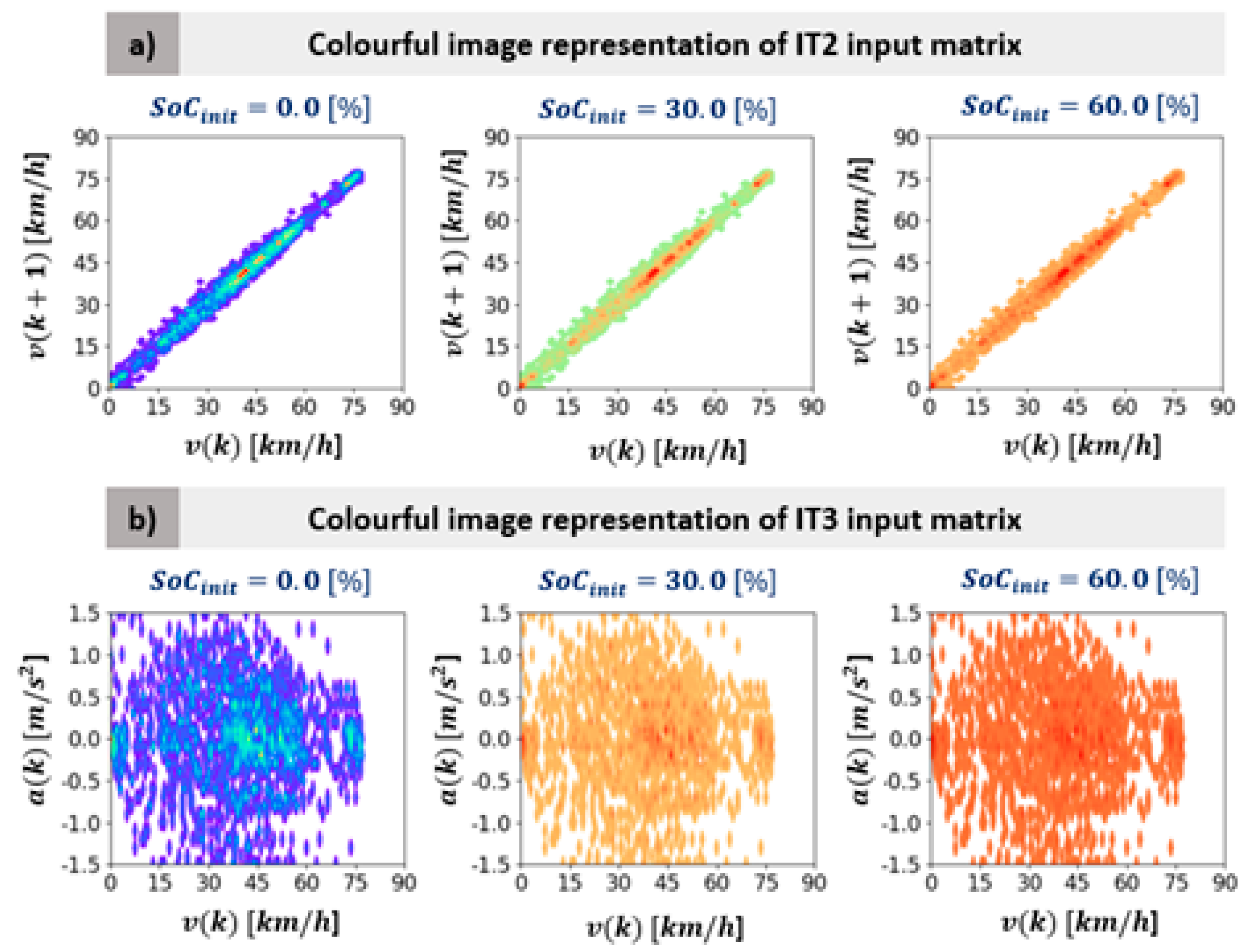
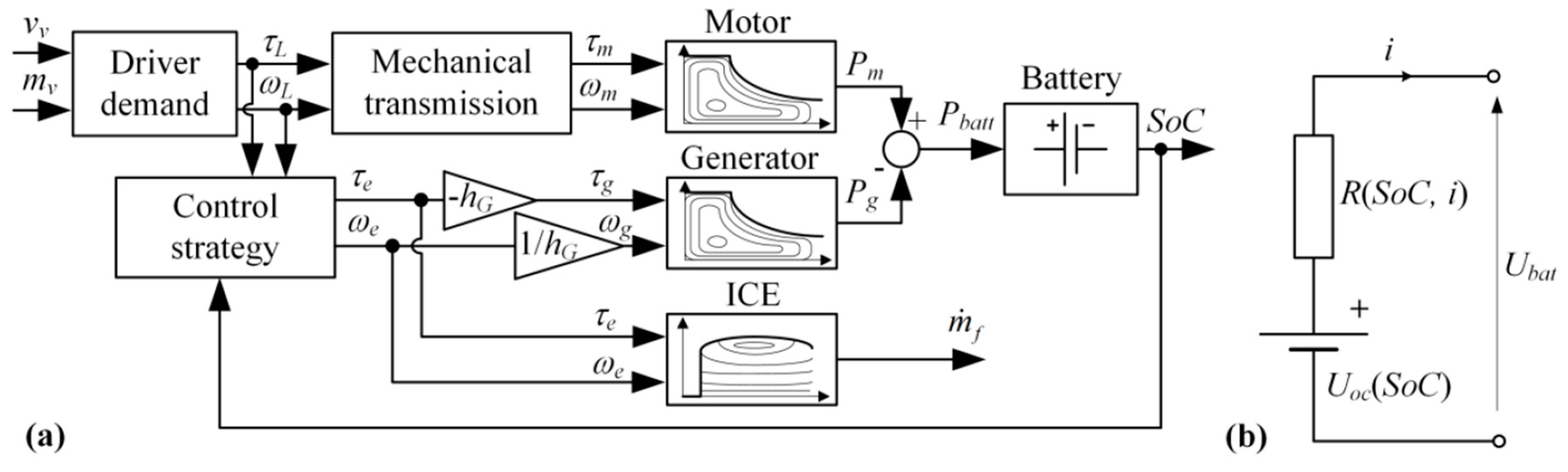
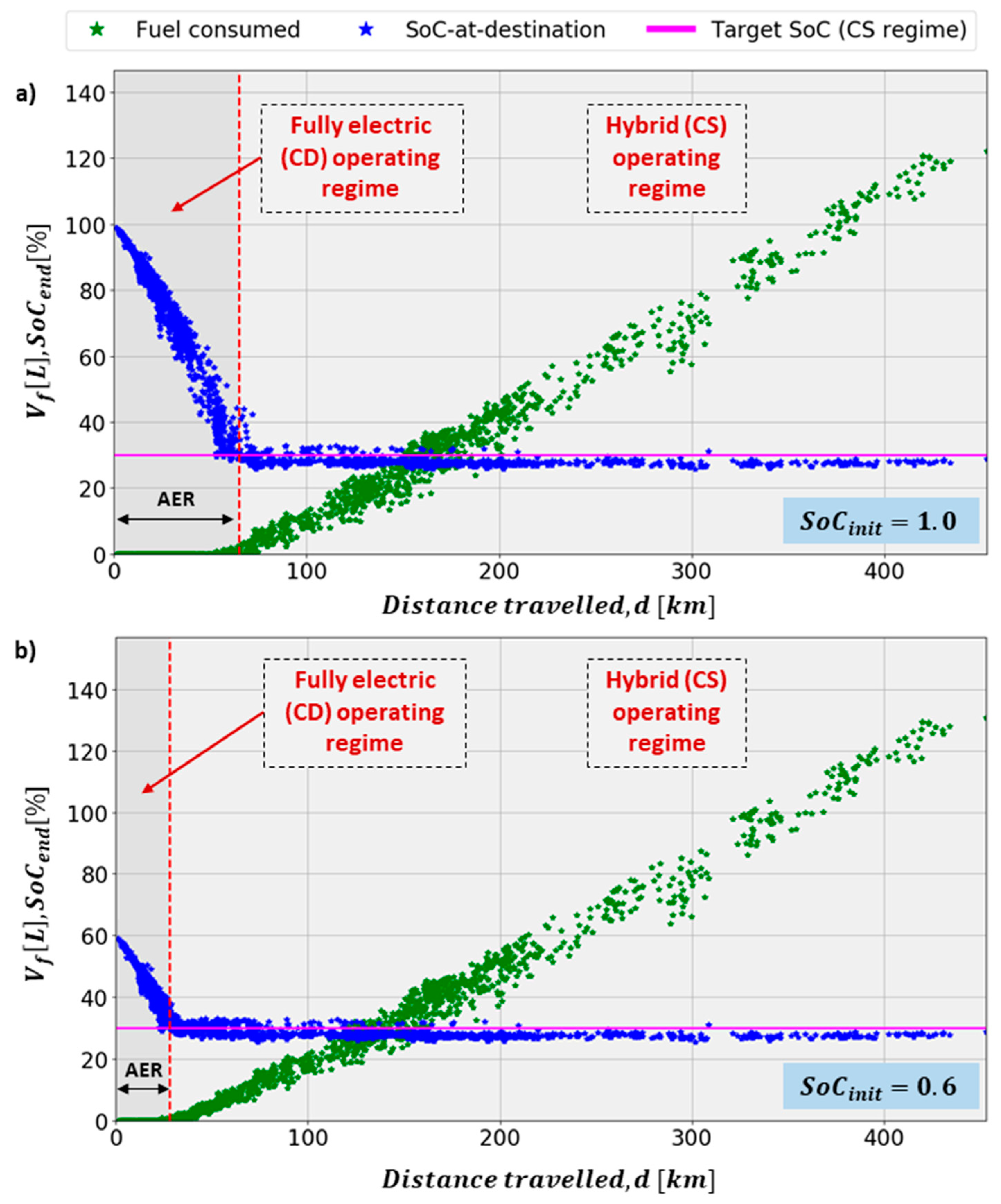
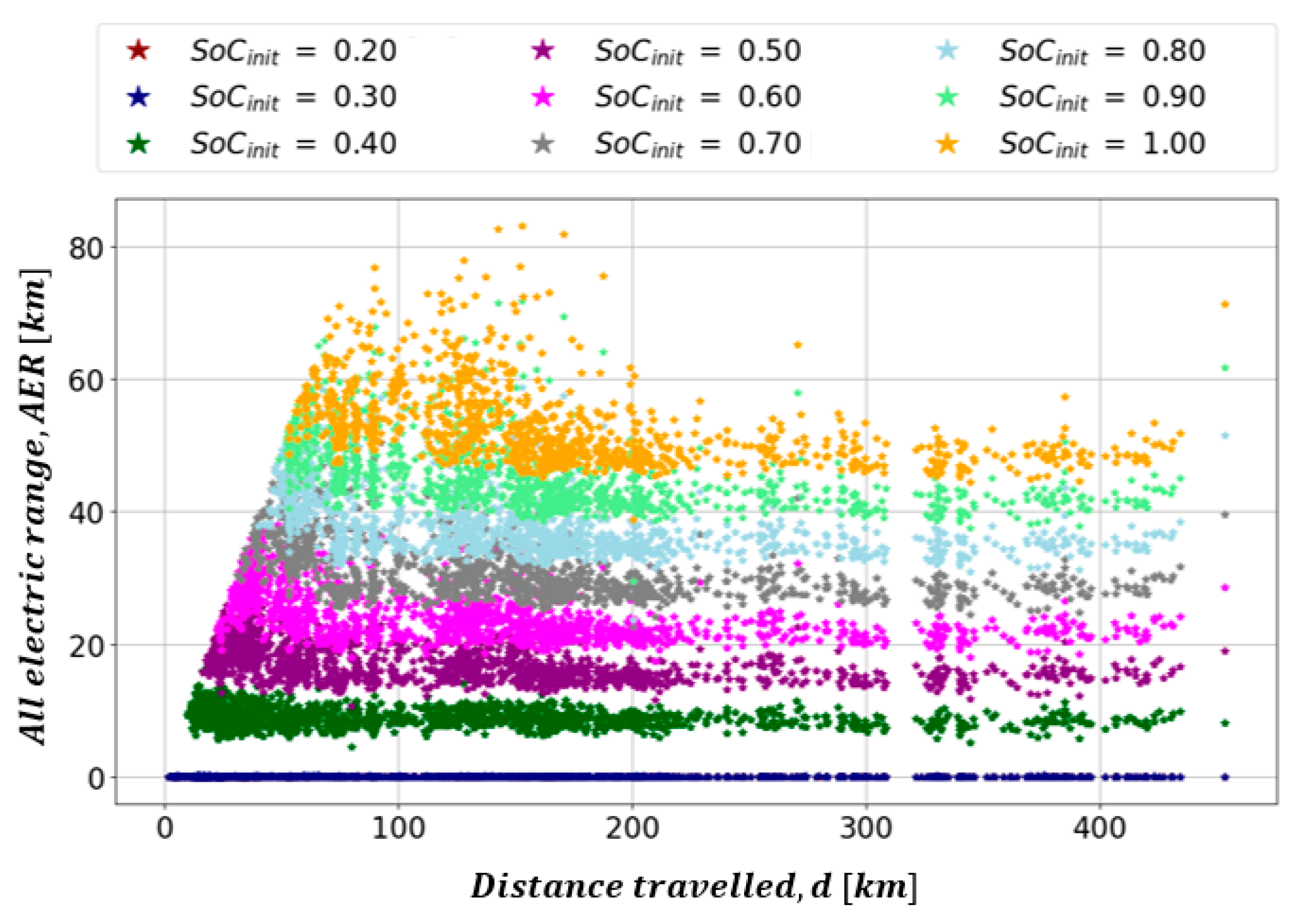
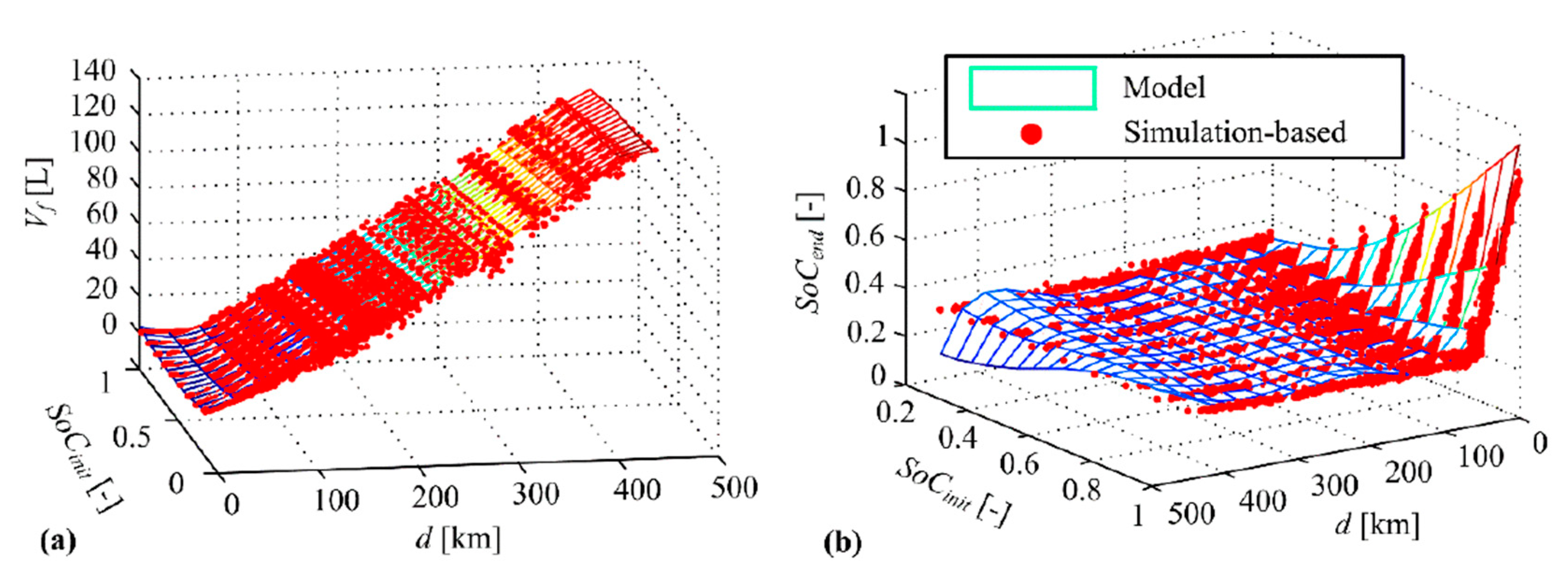
| Label | Type | Dimension | Velocity [km/h] | Acceleration [m/s2] | Incorporating of Initial SoC Value | ||
|---|---|---|---|---|---|---|---|
| Range | Resolution | Range | Resolution | ||||
| IT1 | Vector | 1 × 182 | [0, 90] | 0.5 | / | / | append |
| IT2 | Matrix | 91 × 91 | [0, 90] | 1.0 | / | / | addition |
| IT3 | Matrix | 31 × 182 | [0, 90] | 0.5 | [−1.5, 1.5] | 0.1 | addition |
| Model Label | Input Label | Input Dim. | Training Time [h] | Evaluation Time [ms] | Training Score | Testing Score | Trainable Params |
|---|---|---|---|---|---|---|---|
| MLP1 | IT1 * | 182 | 2.596 | 9.345 | 0.01329 | 0.19356 | 3,139,258 |
| MLP2 | IT3 * | 5612 | 17.846 | 11.128 | 0.01006 | 0.49081 | 14,303,338 |
| MLP3 | IT2 * | 8282 | 21.751 | 10.514 | 0.00922 | 0.30432 | 19,792,858 |
| CNN1 | IT2 | 91 × 91 | 9.967 | 4.500 | 0.05745 | 0.25890 | 6,079,926 |
| CNN2 | IT3 | 91 × 31 | 7.594 | 3.413 | 0.00531 | 0.17379 | 3,960,246 |
| Model Label | Min | Median | Mean | Max | Std | CFI 95% |
|---|---|---|---|---|---|---|
| MLP1 | −4.3172 | −0.0032 | 0.0031 | 3.8625 | 0.5878 | [−1.173, 1.179] |
| MLP2 | −4.2536 | −0.0223 | 0.0412 | 13.3202 | 0.9547 | [−1.868, 1.950] |
| MLP3 | −4.4600 | 0.0389 | 0.0551 | 10.2145 | 0.7504 | [−1.446, 1.556] |
| CNN1 | −6.0190 | −0.0038 | −0.0156 | 5.0332 | 0.6698 | [−1.356, 1.324] |
| CNN2 | −6.4613 | 0.0498 | 0.0351 | 4.3829 | 0.5602 | [−1.085, 1.155] |
| Resp. surface * | −18.9968 | −1.0147 | −0.6972 | 16.5657 | 2.3197 | [−5.337, 3.942] |
| Model Label | Min | Median | Mean | Max | Std | CFI 95% |
|---|---|---|---|---|---|---|
| MLP1 | −1.3655 | −0.0138 | −0.0147 | 1.8408 | 0.2034 | [−0.422, 0.392] |
| MLP2 | −1.0489 | 0.0043 | 0.0161 | 3.5083 | 0.2612 | [−0.506, 0.538] |
| MLP3 | −1.2630 | 0.0307 | 0.0341 | 2.7904 | 0.2035 | [−0.373, 0.441] |
| CNN1 | −2.7871 | 0.0301 | 0.0259 | 2.9722 | 0.2613 | [−0.497, 0.549] |
| CNN2 | −1.4150 | −0.0099 | −0.0076 | 1.1924 | 0.1801 | [−0.368, 0.352] |
| Resp. surface * | −8.5247 | 0.0000 | 0.0569 | 17.2393 | 2.6067 | [−5.157, 5.270] |
| Min | Median | Mean | Max | Std | CFI 95% |
|---|---|---|---|---|---|
| −7.40366 | 0.00096 | 0.04049 | 7.25466 | 0.91674 | [−1.793, 1.874] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Topić, J.; Škugor, B.; Deur, J. Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range. Energies 2019, 12, 1396. https://doi.org/10.3390/en12071396
Topić J, Škugor B, Deur J. Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range. Energies. 2019; 12(7):1396. https://doi.org/10.3390/en12071396
Chicago/Turabian StyleTopić, Jakov, Branimir Škugor, and Joško Deur. 2019. "Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range" Energies 12, no. 7: 1396. https://doi.org/10.3390/en12071396
APA StyleTopić, J., Škugor, B., & Deur, J. (2019). Neural Network-Based Modeling of Electric Vehicle Energy Demand and All Electric Range. Energies, 12(7), 1396. https://doi.org/10.3390/en12071396





