A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids
Abstract
:1. Introduction
2. Problem Formulation
- the active power losses:where and are the total active power generated and absorbed on the network;
- the average voltage deviation:where and are the current and the desired voltage at the node q respectively, and N is the number of nodes;
- the maximum voltage deviation:
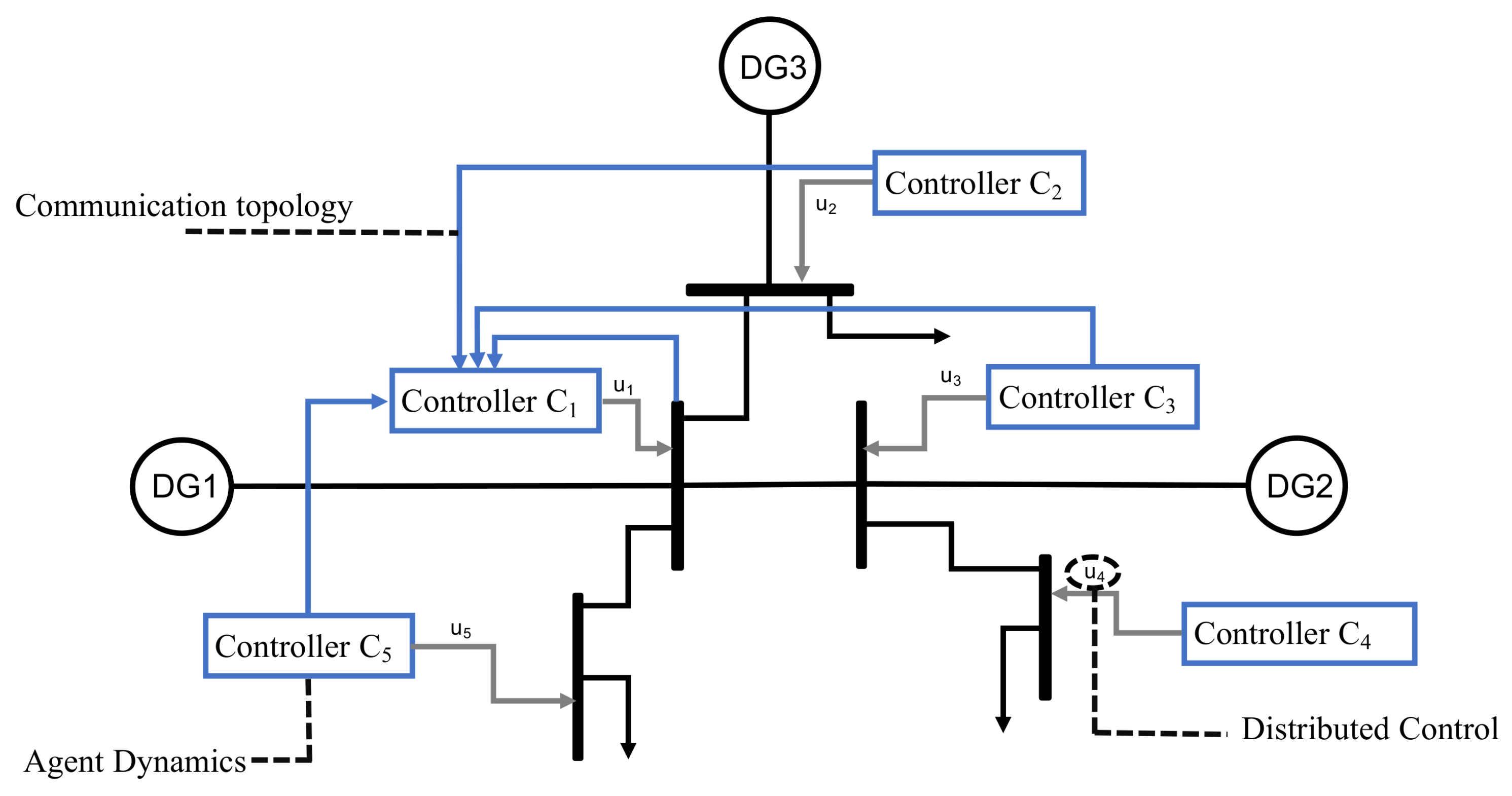
3. A Decentralized Solution of the Optimal Voltage Regulation Problem
- a set of sensors measuring the available set of local electrical variables (i.e., voltage magnitude, active and reactive bus power);
- a dynamical system, whose state is initialized by sensor measurements and evolves interactively with the states of nearby controllers, according to a properly designed distributed control strategy;
- a communication interface, carrying the interaction among controllers by transmitting the state of the dynamical system and receiving the state transmitted by the other nodes.
3.1. Agent Dynamics
3.2. Communication Topology
3.3. Control Design
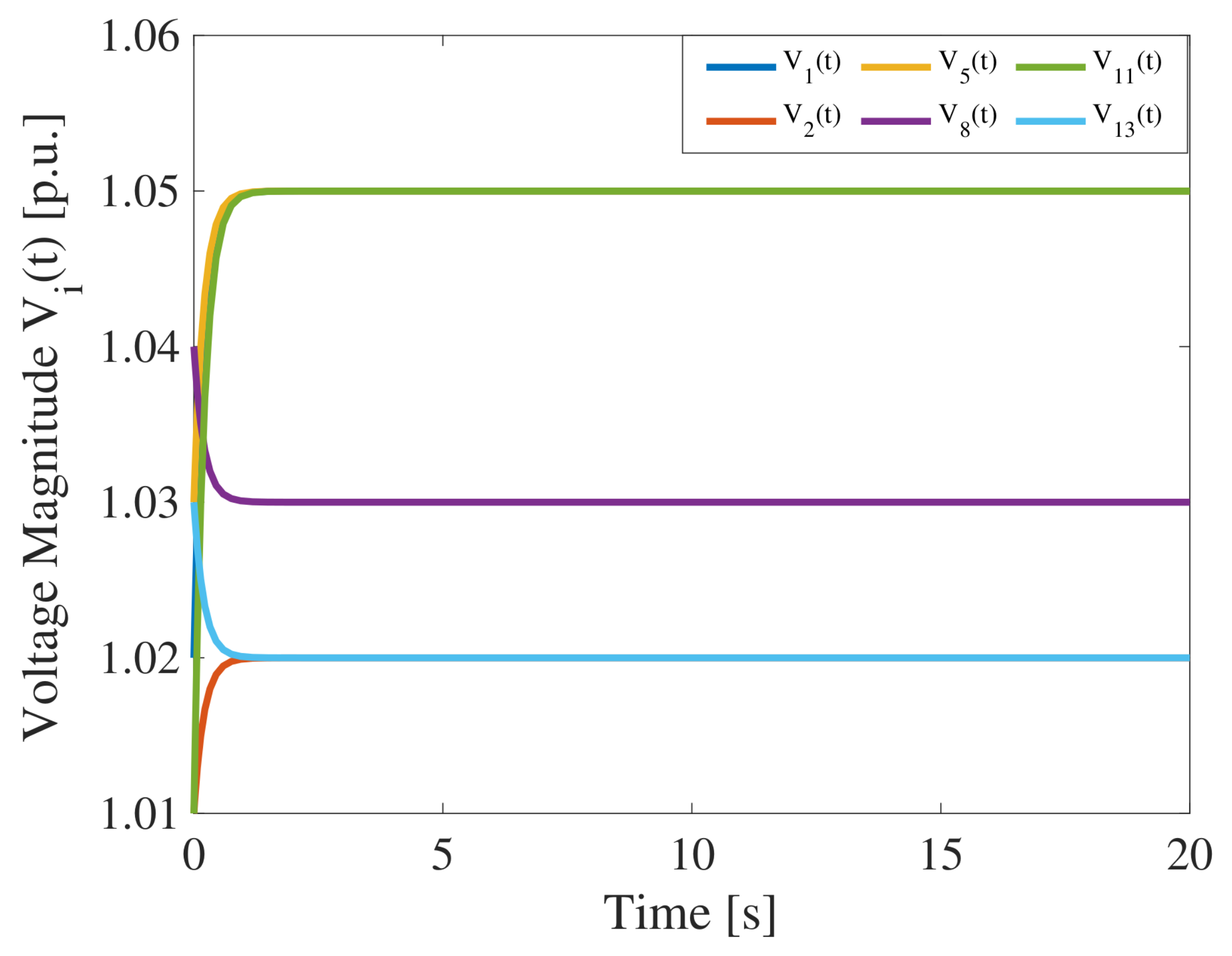
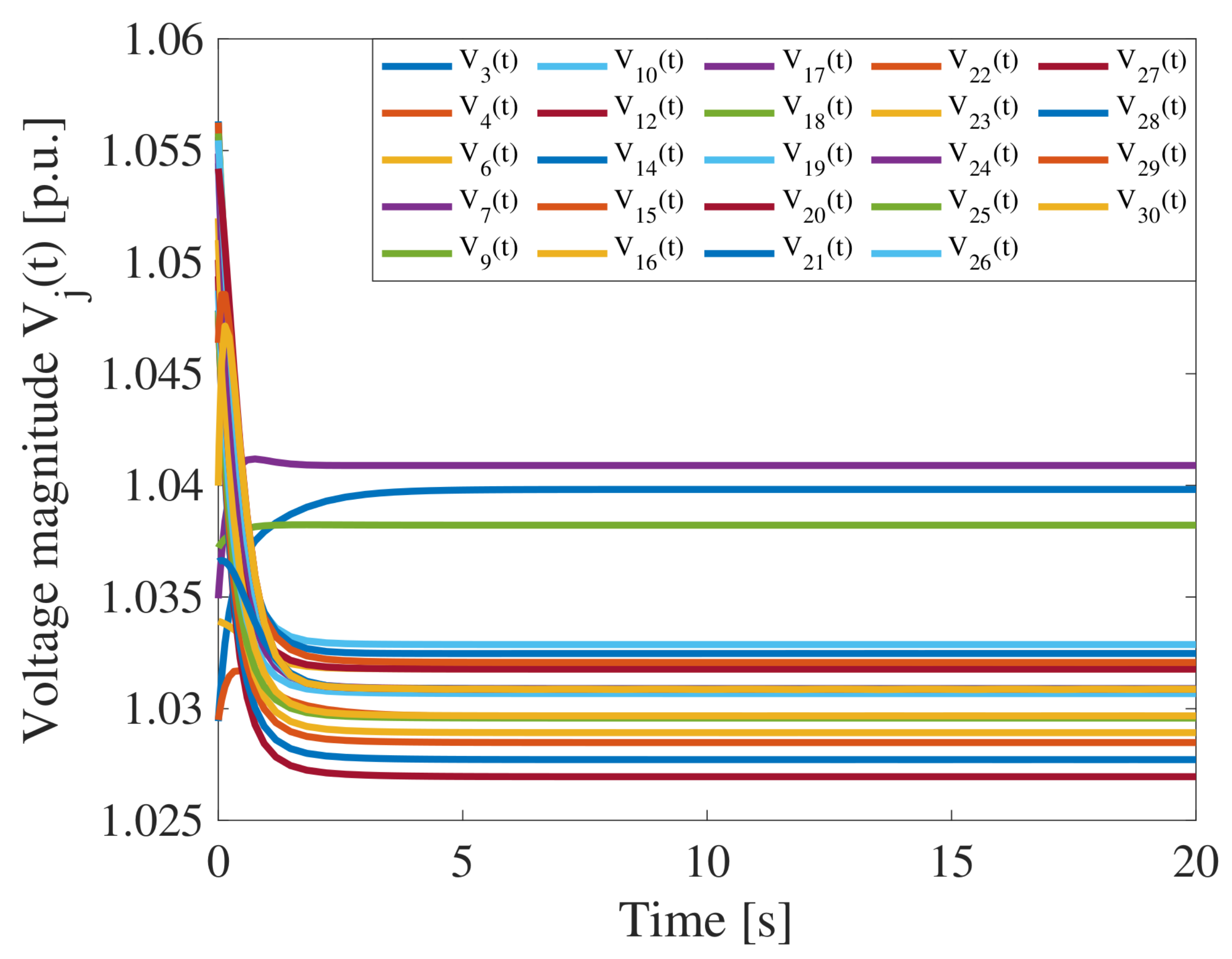
- designing the control strategy in (9), leveraging local electric information, to opportunely manage the voltage magnitude of the bus i so to reach and maintain the desired reference voltage value , i.e.,, being the voltage magnitude of the i-th electrical node;
- designing the distributed control input in (8), leveraging both local and neighboring electrical information, to opportunely manage the reactive power of the bus j, hence updating its voltage magnitude until it converges to the common reference behavior imposed by generators within the SG, i.e.,being the voltage magnitude of the i-th generation bus and the voltage magnitude of the neighboring nodes (, with ).
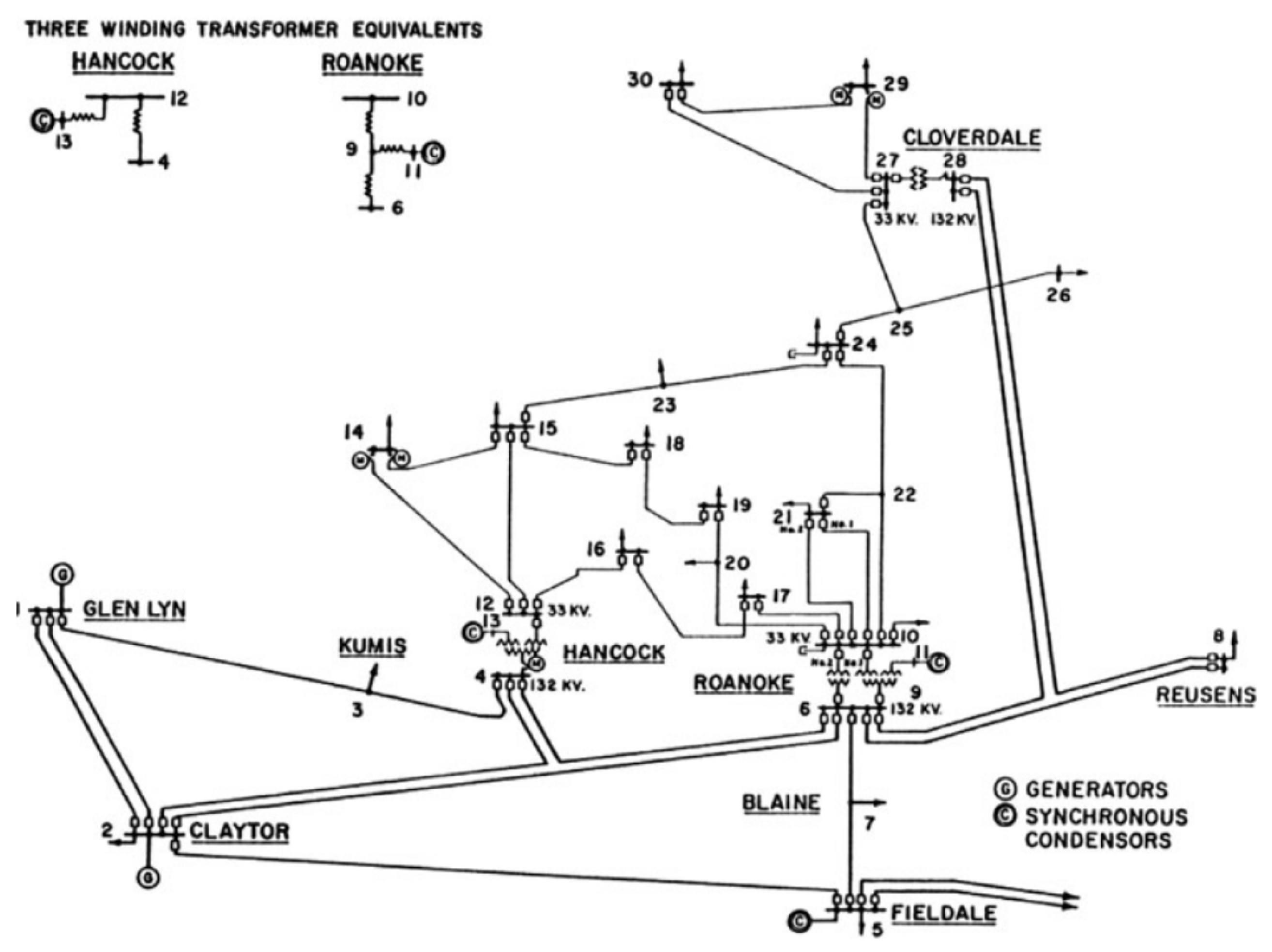
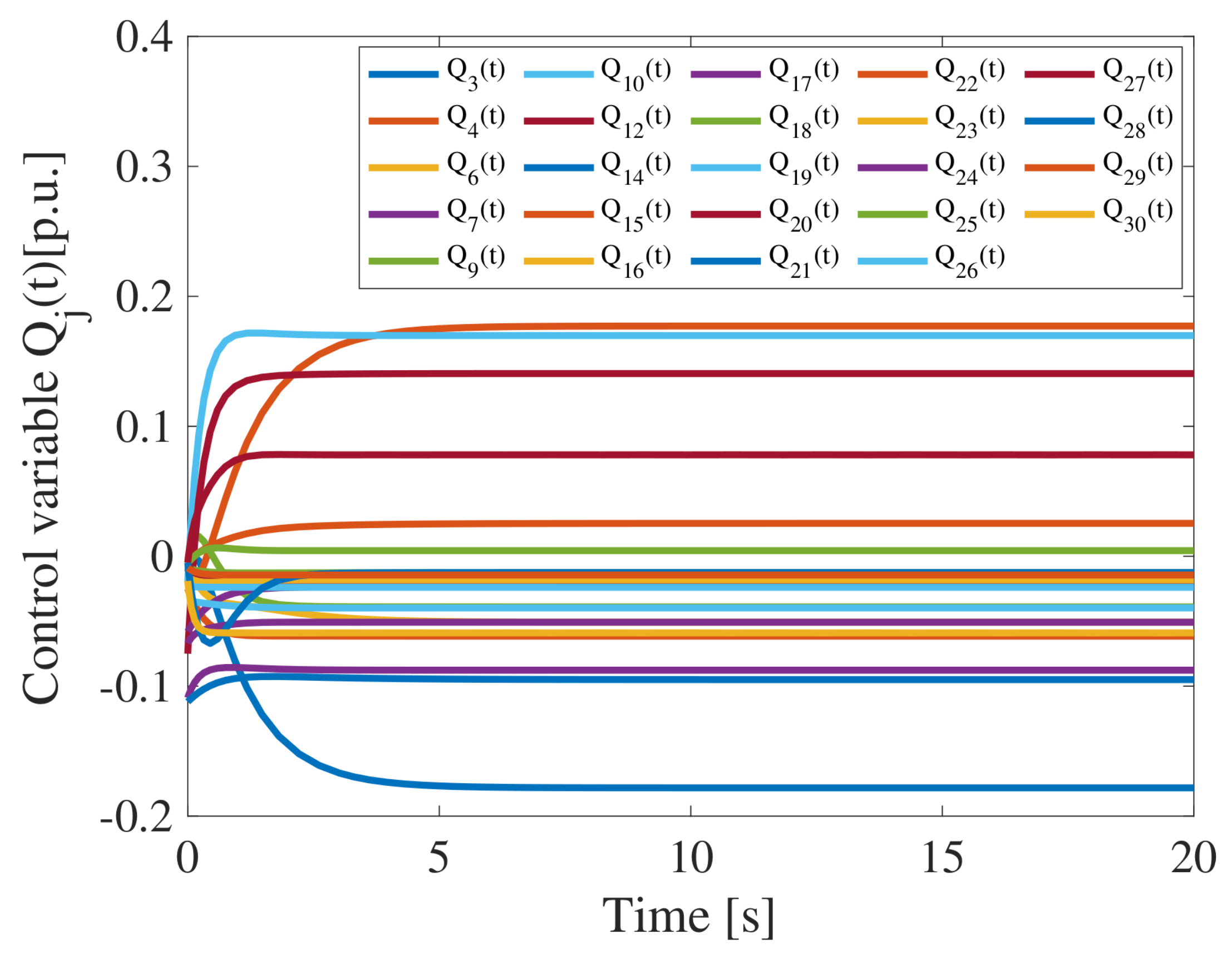
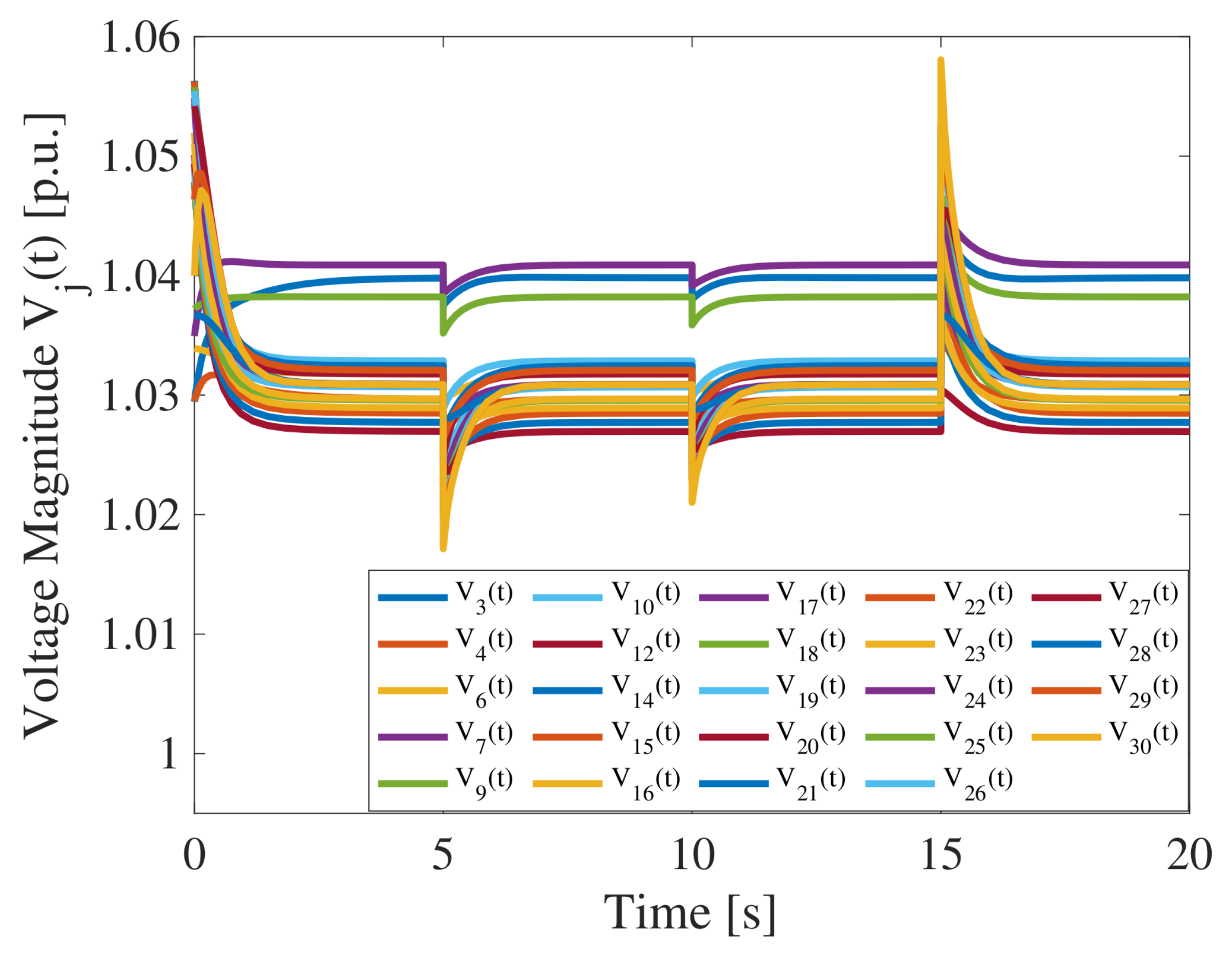
4. Case Study
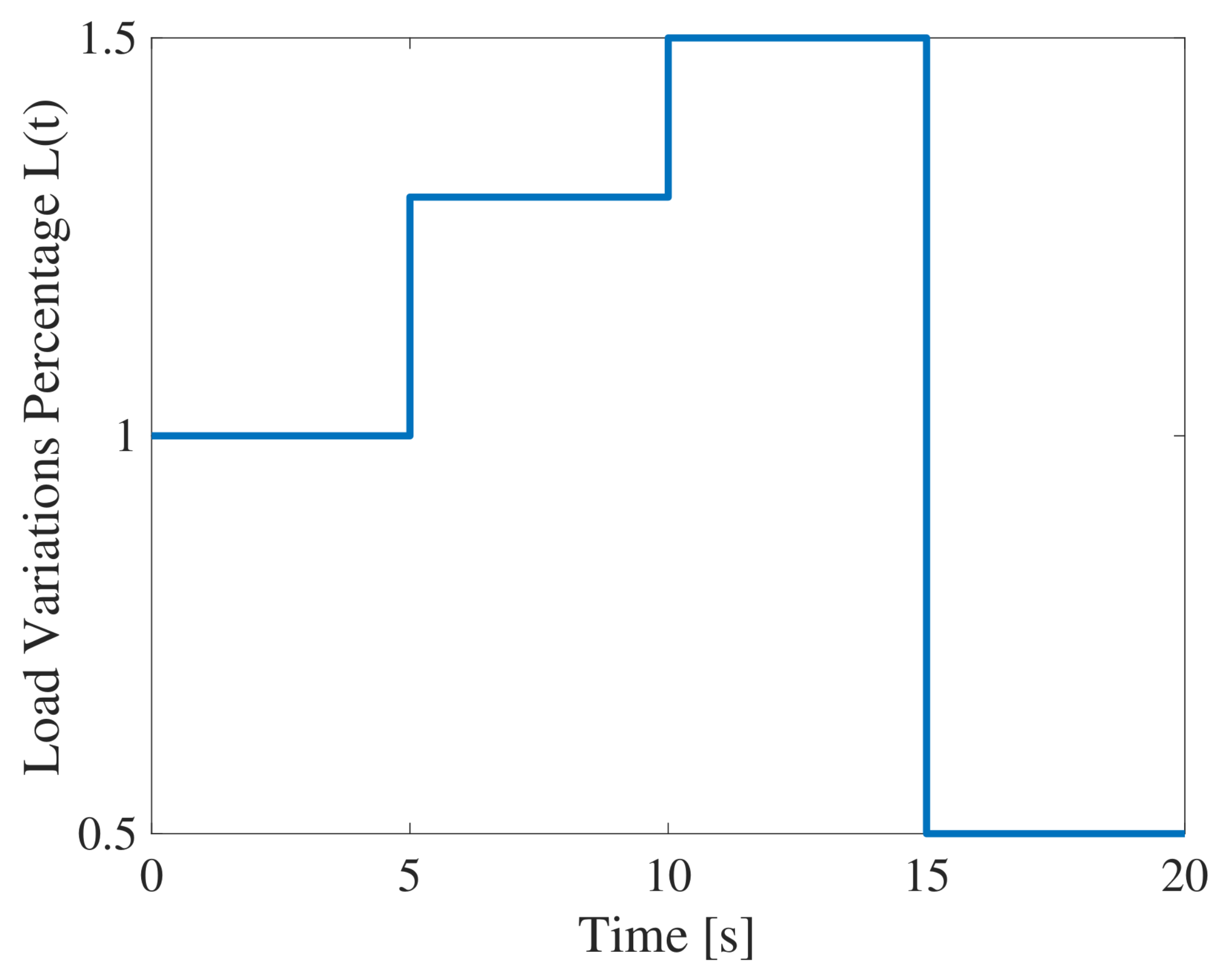
Robustness to Variable Load
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cossent, R.; Gómez, T.; Olmos, L. Large-scale integration of renewable and distributed generation of electricity in Spain: Current situation and future needs. Energy Policy 2011, 39, 8078–8087. [Google Scholar] [CrossRef]
- Liu, Y.; Bebic, J.; Kroposki, B.; De Bedout, J.; Ren, W. Distribution system voltage performance analysis for high-penetration PV. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–8. [Google Scholar]
- Rahman, M.M.; Arefi, A.; Shafiullah, G.; Hettiwatte, S. A new approach to voltage management in unbalanced low voltage networks using demand response and OLTC considering consumer preference. Int. J. Electr. Power Energy Syst. 2018, 99, 11–27. [Google Scholar] [CrossRef]
- Walling, R.; Saint, R.; Dugan, R.C.; Burke, J.; Kojovic, L.A. Summary of distributed resources impact on power delivery systems. IEEE Trans. Power Deliv. 2008, 23, 1636–1644. [Google Scholar] [CrossRef]
- Jamal, T.; Urmee, T.; Calais, M.; Shafiullah, G.; Carter, C. Technical challenges of PV deployment into remote Australian electricity networks: A review. Renew. Sustain. Energy Rev. 2017, 77, 1309–1325. [Google Scholar] [CrossRef]
- Kenneth, A.P.; Folly, K. Voltage rise issue with high penetration of grid connected PV. IFAC Proc. Vol. 2014, 47, 4959–4966. [Google Scholar] [CrossRef]
- Karimi, M.; Mokhlis, H.; Naidu, K.; Uddin, S.; Bakar, A. Photovoltaic penetration issues and impacts in distribution network—A review. Renew. Sustain. Energy Rev. 2016, 53, 594–605. [Google Scholar] [CrossRef]
- Stetz, T.; Marten, F.; Braun, M. Improved low voltage grid-integration of photovoltaic systems in Germany. IEEE Trans. Sustain. Energy 2013, 4, 534–542. [Google Scholar] [CrossRef]
- Varma, R.K.; Rangarajan, S.S.; Axente, I.; Sharma, V. Novel application of a PV solar plant as STATCOM during night and day in a distribution utility network. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–8. [Google Scholar]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Molina-García, Á.; Mastromauro, R.A.; García-Sánchez, T.; Pugliese, S.; Liserre, M.; Stasi, S. Reactive power flow control for PV inverters voltage support in LV distribution networks. IEEE Trans. Smart Grid 2017, 8, 447–456. [Google Scholar] [CrossRef]
- Perera, B.K.; Ciufo, P.; Perera, S. Point of common coupling (PCC) voltage control of a grid-connected solar photovoltaic (PV) system. In Proceedings of the IECON 2013 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7475–7480. [Google Scholar]
- Raju, L.; Milton, R.; Mahadevan, S. Multi agent systems based distributed control and automation of micro-grid using MACSimJX. In Proceedings of the 2016 10th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 7–8 January 2016; pp. 1–6. [Google Scholar]
- Fallahzadeh-Abarghouei, H.; Nayeripour, M.; Waffenschmidt, E.; Hasanvand, S. A new decentralized voltage control method of smart grid via distributed generations. In Proceedings of the 2016 International Energy and Sustainability Conference (IESC), Cologne, Germany, 30 June–1 July 2016; pp. 1–6. [Google Scholar]
- Higgins, N.; Vyatkin, V.; Nair, N.; Schwarz, K. Intelligent decentralised power distribution automation with IEC 61850, IEC 61499 and holonic control. IEEE Trans. Syst. Mach. Cybern. C 2010, 40, 1–12. [Google Scholar]
- Demirok, E.; Gonzalez, P.C.; Frederiksen, K.H.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovolt. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Local control of reactive power by distributed photovoltaic generators. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 79–84. [Google Scholar]
- Demirok, E.; Sera, D.; Rodriguez, P.; Teodorescu, R. Enhanced local grid voltage support method for high penetration of distributed generators. In Proceedings of the IECON 2011 37th Annual Conference of the IEEE Industrial Electronics Society, Hungary, Budapest, 26–30 August 2011; pp. 2481–2485. [Google Scholar]
- Martí, P.; Velasco, M.; Fuertes, J.M.; Camacho, A.; Miret, J.; Castilla, M. Distributed reactive power control methods to avoid voltage rise in grid-connected photovoltaic power generation systems. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar]
- Tanaka, K.; Oshiro, M.; Toma, S.; Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C.H. Decentralised control of voltage in distribution systems by distributed generators. IET Gen. Transm. Distrib. 2010, 4, 1251–1260. [Google Scholar] [CrossRef]
- Toma, S.; Senjyu, T.; Miyazato, Y.; Yona, A.; Funabashi, T.; Saber, A.Y.; Kim, C.H. Optimal coordinated voltage control in distribution system. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Shalwala, R.; Bleijs, J. Voltage control scheme using Fuzzy Logic for residential area networks with PV generators in Saudi Arabia. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–6. [Google Scholar]
- Gupta, N.; Garg, R.; Kumar, P. Asymmetrical Fuzzy logic control to PV Module Connected micro-grid. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–19 December 2015; pp. 1–6. [Google Scholar]
- Loia, V.; Vaccaro, A. A decentralized architecture for voltage regulation in smart grids. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1679–1684. [Google Scholar]
- Loia, V.; Vaccaro, A.; Vaisakh, K. A self-organizing architecture based on cooperative fuzzy agents for smart grid voltage control. IEEE Trans. Ind. Inf. 2013, 9, 1415–1422. [Google Scholar] [CrossRef]
- Hojo, M.; Hatano, H.; Fuwa, Y. Voltage rise suppression by reactive power control with cooperating photovoltaic generation systems. In Electricity Distribution-Part; IET: Stevenage, UK, 2009; Volume 2. [Google Scholar]
- Wang, X.; Wang, C.; Xu, T.; Guo, L.; Fan, S.; Wei, Z. Decentralised voltage control with built-in incentives for participants in distribution networks. IET Gen. Transm. Distrib. 2018, 12, 790–797. [Google Scholar] [CrossRef]
- Zhang, Z.; Ochoa, L.F.; Valverde, G. A novel voltage sensitivity approach for the decentralized control of DG plants. IEEE Trans. Power Syst. 2018, 33, 1566–1576. [Google Scholar] [CrossRef]
- Liu, H.J.; Shi, W.; Zhu, H. Decentralized dynamic optimization for power network voltage control. IEEE Trans. Signal Inf. Proc. Netw. 2017, 3, 568–579. [Google Scholar] [CrossRef]
- Lin, W.; Bitar, E. Decentralized stochastic control of distributed energy resources. IEEE Trans. Power Syst. 2018, 33, 888–900. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.E.; Kouveliotis-Lysikatos, I.N.; Georgilakis, P.S.; Hatziargyriou, N.D. Distributed and decentralized voltage control of smart distribution networks: Models, methods, and future research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Petrillo, A.; Salvi, A.; Santini, S.; Valente, A.S. Adaptive synchronization of linear multi-agent systems with time-varying multiple delays. J. Frankl. Inst. 2017, 354, 8586–8605. [Google Scholar] [CrossRef]
- Petrillo, A.; Pescapé, A.; Santini, S. A collaborative approach for improving the security of vehicular scenarios: The case of platooning. Comput. Commun. 2018, 122, 59–75. [Google Scholar] [CrossRef]
- Petrillo, A.; Salvi, A.; Santini, S.; Valente, A.S. Adaptive multi-agents synchronization for collaborative driving of autonomous vehicles with multiple communication delays. Trans. Res. C Emerg. Technol. 2018, 86, 372–392. [Google Scholar] [CrossRef]
- Di Vaio, M.; Fiengo, G.; Petrillo, A.; Salvi, A.; Santini, S.; Tufo, M. Cooperative shock waves mitigation in mixed traffic flow environment. IEEE Trans. Intell. Trans. Syst. 2019, 99, 1–15. [Google Scholar] [CrossRef]
- Dorfler, F.; Bullo, F. Synchronization and transient stability in power networks and nonuniform Kuramoto oscillators. SIAM J. Control Optim. 2012, 50, 1616–1642. [Google Scholar] [CrossRef]
- Zheng, J.; Jamalipour, A. Wireless Sensor Networks: A Networking Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Loia, V.; Furno, D.; Vaccaro, A. Decentralised smart grids monitoring by swarm-based semantic sensor data analysis. Int. J. Syst. Control Commun. 2013, 5, 1–14. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- He, D.; Shi, D.; Sharma, R. Consensus-based distributed cooperative control for microgrid voltage regulation and reactive power sharing. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Shahidehpour, M.; Wang, Y. Communication and Control in Electric Power Systems: Applications of Parallel and Distributed Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]

| Initial Conditions | |
| Voltage magnitude | |
| of generation bus i [] | |
| Reactive power | |
| of capacitor bank bus | ; |
| j [] | |
| Control Gains | |
| Control gains | i = 1, 2, 5, 8, 11, 13 |
| Control gains | |
| Control gains |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreotti, A.; Petrillo, A.; Santini, S.; Vaccaro, A.; Villacci, D. A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids. Energies 2019, 12, 1386. https://doi.org/10.3390/en12071386
Andreotti A, Petrillo A, Santini S, Vaccaro A, Villacci D. A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids. Energies. 2019; 12(7):1386. https://doi.org/10.3390/en12071386
Chicago/Turabian StyleAndreotti, Amedeo, Alberto Petrillo, Stefania Santini, Alfredo Vaccaro, and Domenico Villacci. 2019. "A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids" Energies 12, no. 7: 1386. https://doi.org/10.3390/en12071386
APA StyleAndreotti, A., Petrillo, A., Santini, S., Vaccaro, A., & Villacci, D. (2019). A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids. Energies, 12(7), 1386. https://doi.org/10.3390/en12071386








