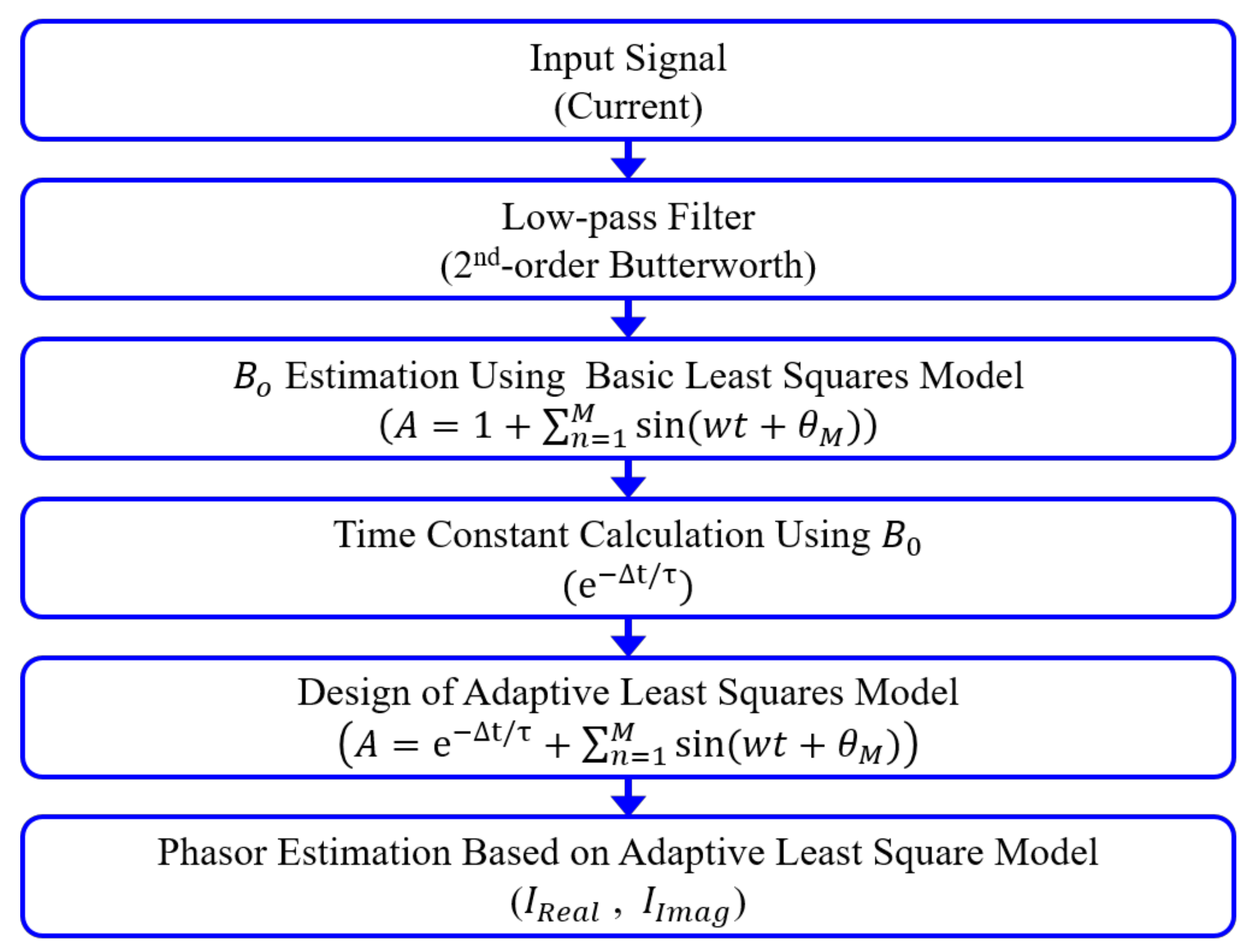
1. Introduction
Accurate phasor estimation of current and voltage signals is very important for the protection and control of a power system. When a power system fault occurs, the current signal may include noise components such as an exponentially decaying DC offset and high-frequency due to traveling waves in addition to the fundamental frequency component. This noise degrades phasor estimation performance. The high-frequency components generated by a traveling wave may be both harmonic and non-harmonic. The most commonly used discrete Fourier transform (DFT) and least squares method (LSM) for phasor estimation can eliminate harmonic components. However, non-harmonic components are not completely removed using these phasor estimation methods and must be removed because they can cause errors in the phasor estimation result. The frequency band of the high-frequency components generated by a traveling wave is determined by the length of a power system’s transmission line [
1]. Therefore, the cut-off frequency of the low-pass filter used for a power system’s protection relay should be chosen to be lower than the lowest frequency of high-frequency components generated by the traveling wave, thus suppressing the phasor estimation error caused by non-harmonic components generated by the traveling wave.
The exponentially decaying DC offset component contained in the fault current signal is not removed during the phasor estimation process and the filtering process by the low-pass filter, since the DC offset component is a non-periodic signal and its frequency spectrum includes all frequencies. Therefore, the DC offset component should be carefully taken into consideration in calculating the phasor of the fundamental frequency component.
Many techniques have been proposed for estimating the phasor of the correct fundamental frequency component without the adverse effect of the exponentially decaying DC offset component of the fault current signal. These can be classified into three main groups.
In the first group, the exponentially decaying DC offset component contained in the fault current signal is first filtered out and the phasor of the fundamental frequency component is estimated from the filtered signal using a DFT. In [
2], a digital mimic filter is proposed to suppress the DC offset component in a fault current signal. The digital mimic filter can completely remove the DC offset component only when the actual time constant of the fault current signal’s DC offset component is the same as the mimic filter’s time constant. In [
3], a Kalman filter is proposed to eliminate the DC offset component, only when the time constant of the DC offset component is the same as that modeled in a state transition matrix. In [
4], an algorithm that uses the average value of the fault current signal for one cycle is proposed. In [
5,
6], algorithms that use the integral value of the fault current signal during one cycle are proposed. These algorithms [
4,
5,
6] cannot completely eliminate the DC offset component if its time constant is small.
The second group uses a DFT to estimate the phasor of the fundamental frequency component and then calculate and remove the error due to the DC offset component in the DFT’s estimated phasor value. In [
7,
8,
9,
10,
11], the error due to the DC offset component in the DFT’s estimated phasor value is calculated and eliminated by using three successive estimated phasor values. However, these methods take one cycle plus two additional samples to estimate the correct phasor and are susceptible to high frequency noise. In [
12], the error due to the DC offset component in the DFT’s estimated phasor value is calculated and eliminated using the output of another DFT filter tuned at the n-th harmonic component. However, the performance of this algorithm is highly affected by random noise. In [
13], a partial summation algorithm is proposed to eliminate the error due to the DC offset component in the DFT’s estimated phasor value. However, if the DC offset component has a small time constant, this algorithm cannot completely eliminate the error due to the DC offset component in the DFT’s estimated phasor value. In [
14,
15,
16], the error due to the DC offset component in the DFT’s estimated phasor value is calculated and eliminated using the outputs of the even- and odd-sample-set DFTs. In [
17], the samples used for the DFT computation are split into four groups. The DFT then obtains an estimated phasor value from each of the four groups. Then, the parameters of the DC offset component are obtained from the four phasor results. In [
18], the error due to the DC offset component in the DFT’s estimated phasor value is calculated and eliminated by combining the DFT outputs from even and odd sample-sets obtained for a one cycle data window decimated by two and by four. In [
19,
20], algorithms using an average value over one cycle are proposed to estimate the error due to the DC offset component in the DFT’s estimated phasor value. However, these methods [
14,
15,
16,
17,
18,
19,
20] are disadvantageous because the high frequency noise components are amplified by the subtraction process that calculates the error due to the DC offset component.
The third group uses the least squares methods. These methods find a coefficient that minimizes the error between the input signal and the predefined signal. Therefore, the predefined signal must be selected appropriately. As in the techniques of the first two groups, it is necessary to consider both the harmonic components and the exponentially decaying DC offset component to achieve an accurate phasor estimate. In [
21,
22,
23,
24,
25,
26], the DC offset component is approximated to the first two or three terms of its Taylor series expansion. However, as in the first group of techniques, these methods cannot accurately approximate the DC offset component when the time constant of the DC offset component is small, so the estimated phasor of the fundamental frequency component will include the error due to the DC offset component.
In this paper, we propose an adaptive phasor estimation method based on a least squares method. This method estimates the time constant of the exponentially decaying DC offset component contained in a fault current signal and then redesigns the least squares model using the estimated time constant. This approach estimates the phasor of the fundamental frequency component without the influence of the DC offset component. We tested the performance of the proposed algorithm by running it against computer-generated signals and EMTP simulation signals. To evaluate the algorithm’s performance, we compared the results produced by the proposed algorithm to the results obtained from the conventional DFT, the even/odd DFT [
14], the modified DFT [
10], and the conventional LSM [
21].
3. Case Studies
We evaluated the proposed algorithm’s performance using computer-generated signals and EMTP-simulation signals. We compared these test results to those of the conventional DFT, the even/odd DFT [
14], the modified DFT [
10] and the conventional LSM [
21].
To evaluate the accuracy of the proposed algorithm, we calculated the phasor estimation error to be:
where, the reference RMS value is the RMS value at 10 cycles after the fault.
In all cases, the sampling frequency was set to 7680 Hz (i.e., 128 sample per cycle in a 60 Hz System). The input signal was pre-processed by a second-order Butterworth low-pass filter with a gain of 0.1 at a stop-band cut-off frequency of 750 Hz in order to remove high-frequency noises and prevent aliasing errors. Although the sampling frequency of the algorithm is 7680 Hz, the high-frequency noise that is higher than 750 Hz must be rejected by a preprocessing filter because the frequency band generated by a traveling wave in the assumed 100 km transmission line is 750~1500 Hz [
1].
In the conventional least squares method, the model matrix is designed to include harmonic and exponentially decaying DC offset components. The harmonic components are included up to the 12th order and the exponentially decaying DC offset is derived from the first two terms of the Taylor series expansion in Equation (3). The data window length of the conventional least squares method is one cycle. In the proposed algorithm, the model matrix of the basic least square is designed to include the harmonic and constant components. The harmonic components are included up to the 12th order. The data window length of the proposed algorithm is one cycle.
3.1. Computer-Generated Signals
We evaluated the proposed algorithm’s performance with computer-generated signals consisting of sinusoidal and exponentially decaying DC offset components. We investigated the algorithm’s sensitivity to DC offset variation by running the tests with two different time constants (0.5/ and 5/).
Case 1. Test for basic signals—the test signal was:
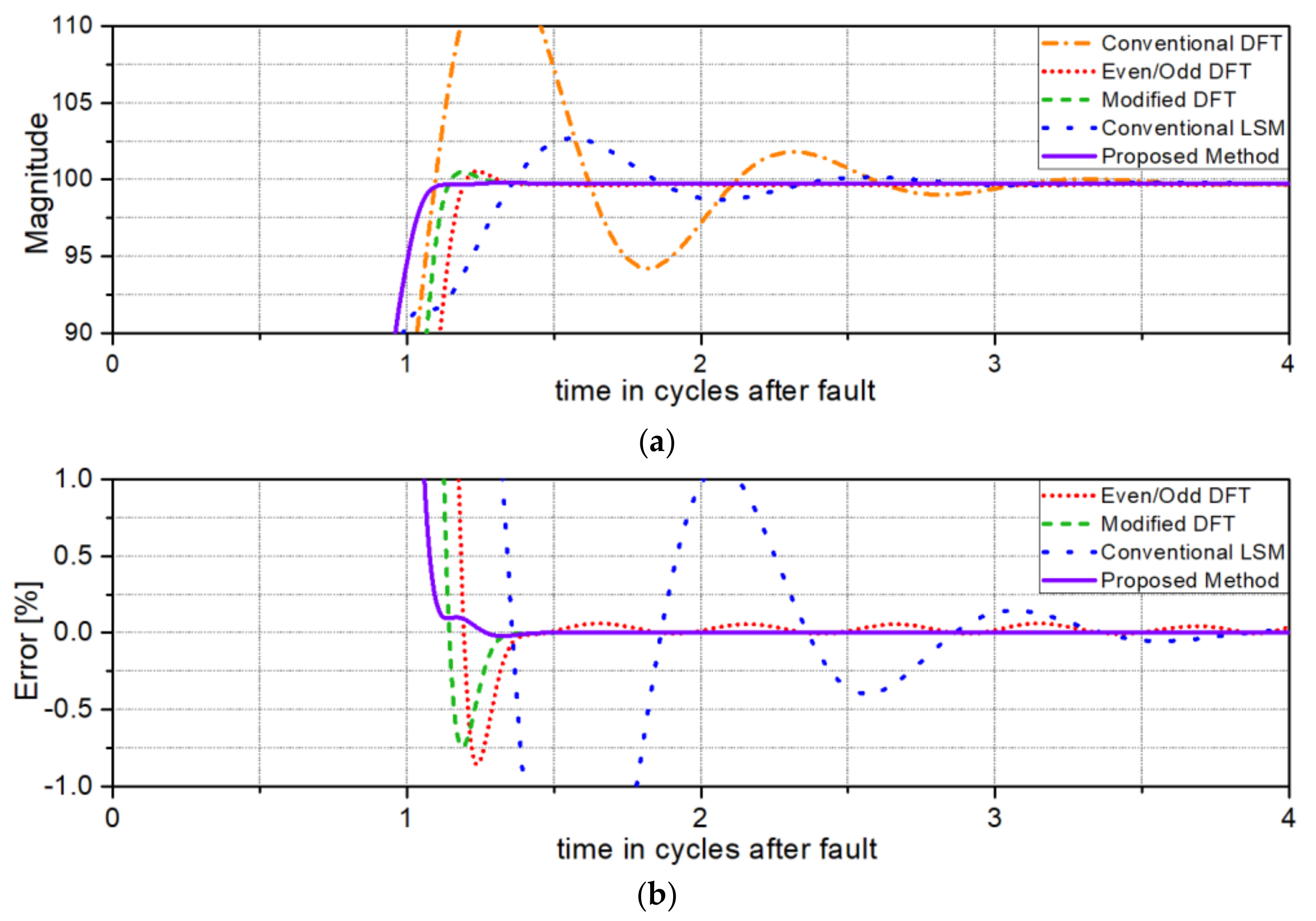
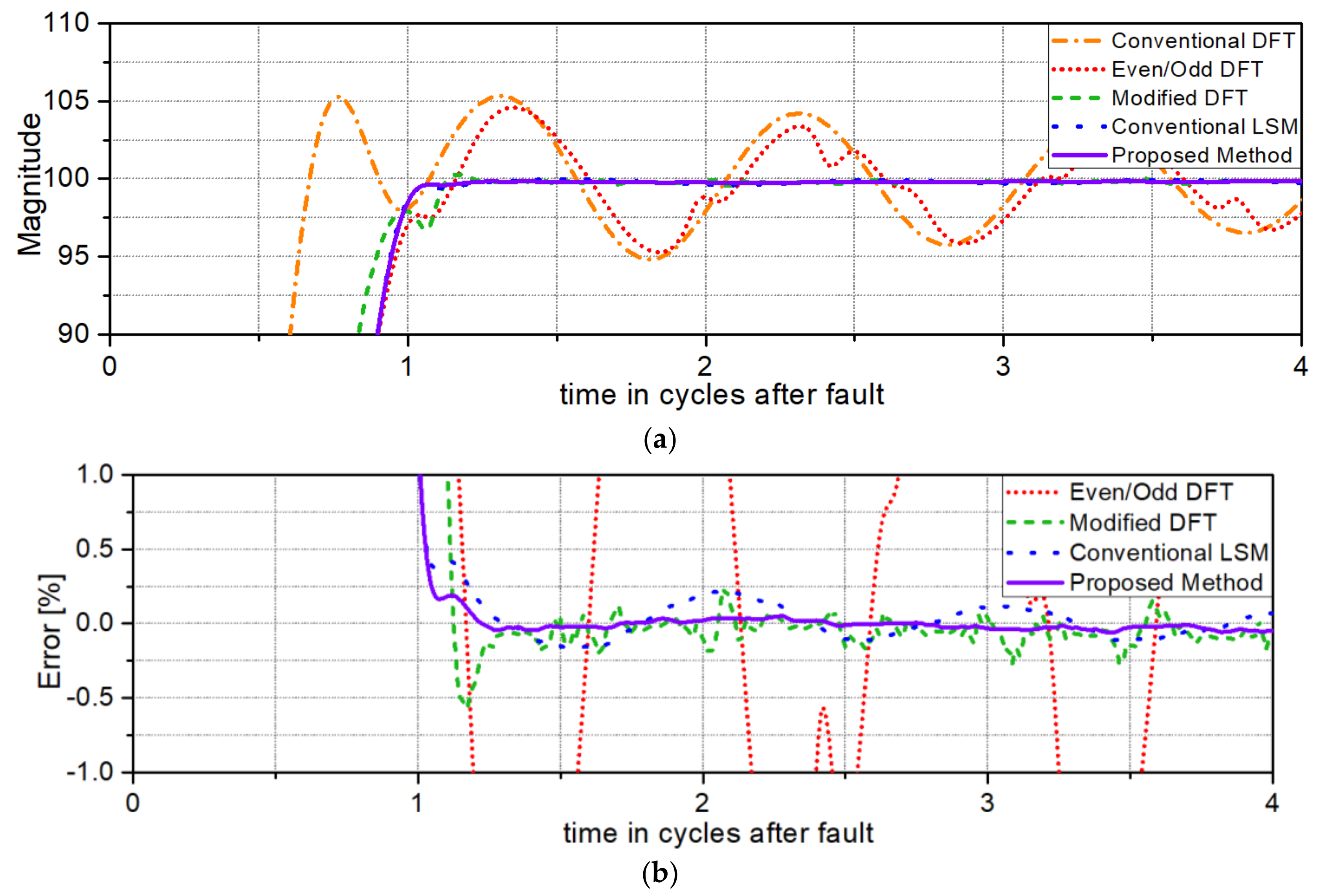
Figure 2 shows the test results for a time constant of 0.5/
. As shown in
Figure 2a, the result of the conventional DFT shows the largest transient overshoot and the largest oscillatory response. In
Figure 2b, the proposed algorithm is seen to more accurately remove the adverse influence of the exponentially decaying DC offset than the other methods.
Figure 3 shows the test results for a time constant of 5/
. These results show the same performance advantage demonstrated in
Figure 2 for a time constant of 0.5/
.
Case 2. Test for Random Noise: In this case, the focus is on the noise immunity of the proposed algorithm. Gaussian white noise is added to the signal of Case 1. The signal-to-noise ratio (SNR) is set to 40 dB. The test signal used in this case is:
Figure 4 and
Figure 5 show the robustness of the proposed algorithm in the presence of Gaussian white noise.
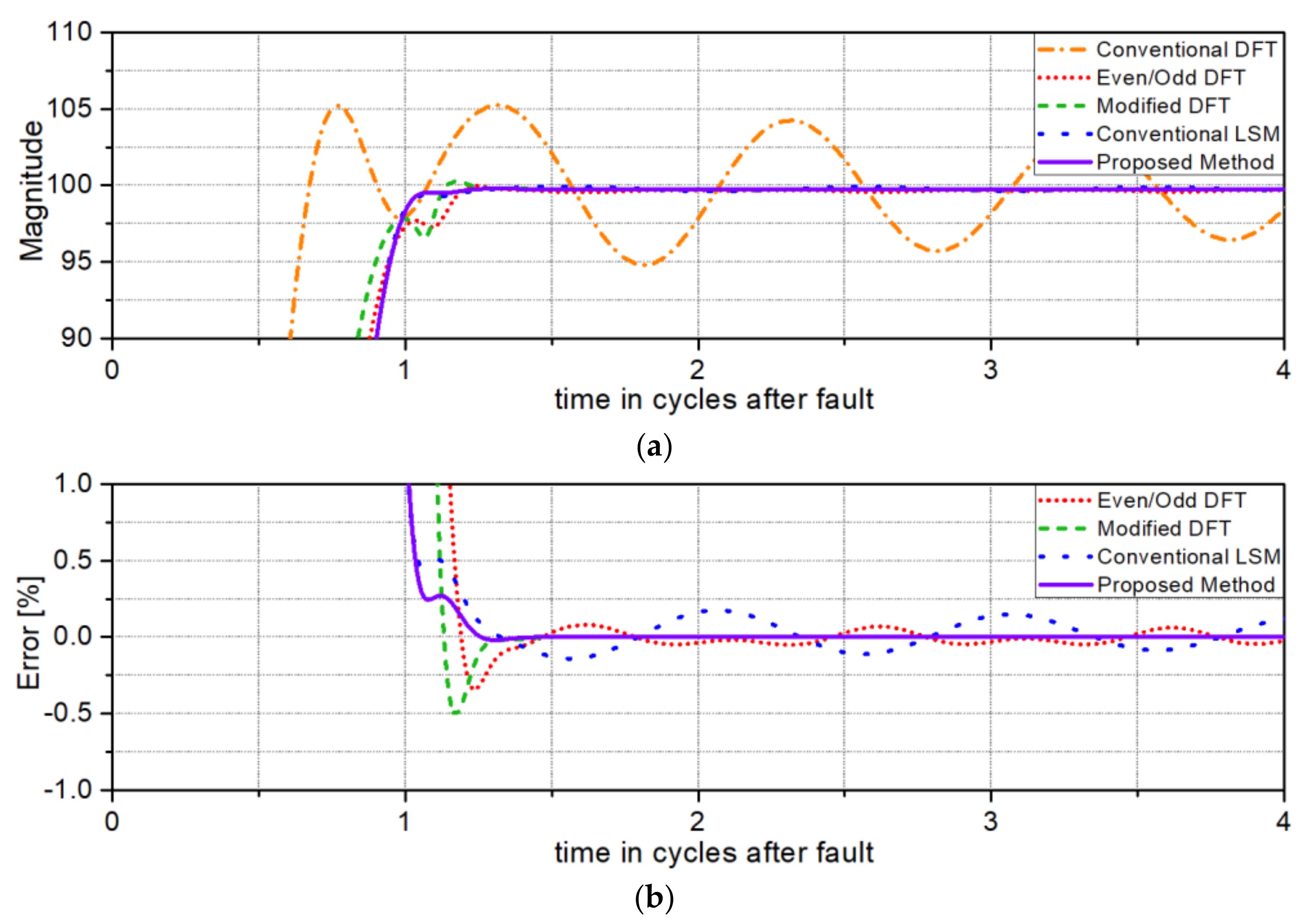
Figure 4 shows the test results for a time constant of 0.5/
.
As seen in
Figure 4a, the result of the conventional DFT and the even/odd DFT show a very large transient overshoot and a very large oscillatory response. In
Figure 4b, the proposed algorithm be seen to more accurately remove the adverse influence of the exponentially decaying DC offset than the other methods. Since the even/odd DFT and the modified DFT intrinsically use difference equations, an error occurs if a signal contains Gaussian white noise.
Figure 5 shows the test results for a time constant of 5/
. As in the previous results for time constant 0.5/
, the results for this time constant demonstrate that the proposed algorithm can more accurately remove the adverse influence of the exponentially decaying DC offset than the other methods.
The test results for the proposed algorithm show stable and superior results over the other methods, even when the signal contains Gaussian white noise.
3.2. EMTP Simulation Signals
The model system for the simulations is evaluated for a-g faults on a 154 kV, 100 km overhead transmission line with sources at both ends, as shown in
Figure 6. The transmission line parameters used in the simulations are given in
Table 1.
The equivalent source parameters used in the simulation are given
Table 2. The fault current signals are generated by the EMTP.
The magnitude and time constant of the exponentially decaying DC offset component varies depending on fault conditions such as fault location, fault resistance, and fault inception angle.
Figure 7,
Figure 8 and
Figure 9 show the estimated RMS values and percent error of the fault current. The magnitude and time constant of the DC offset components depend on the fault distance from the relaying point to the fault point, so the performance of the proposed algorithm is evaluated by changing fault distance. A fault inception angle of 0° was used to maximize the magnitude of the DC offset component.
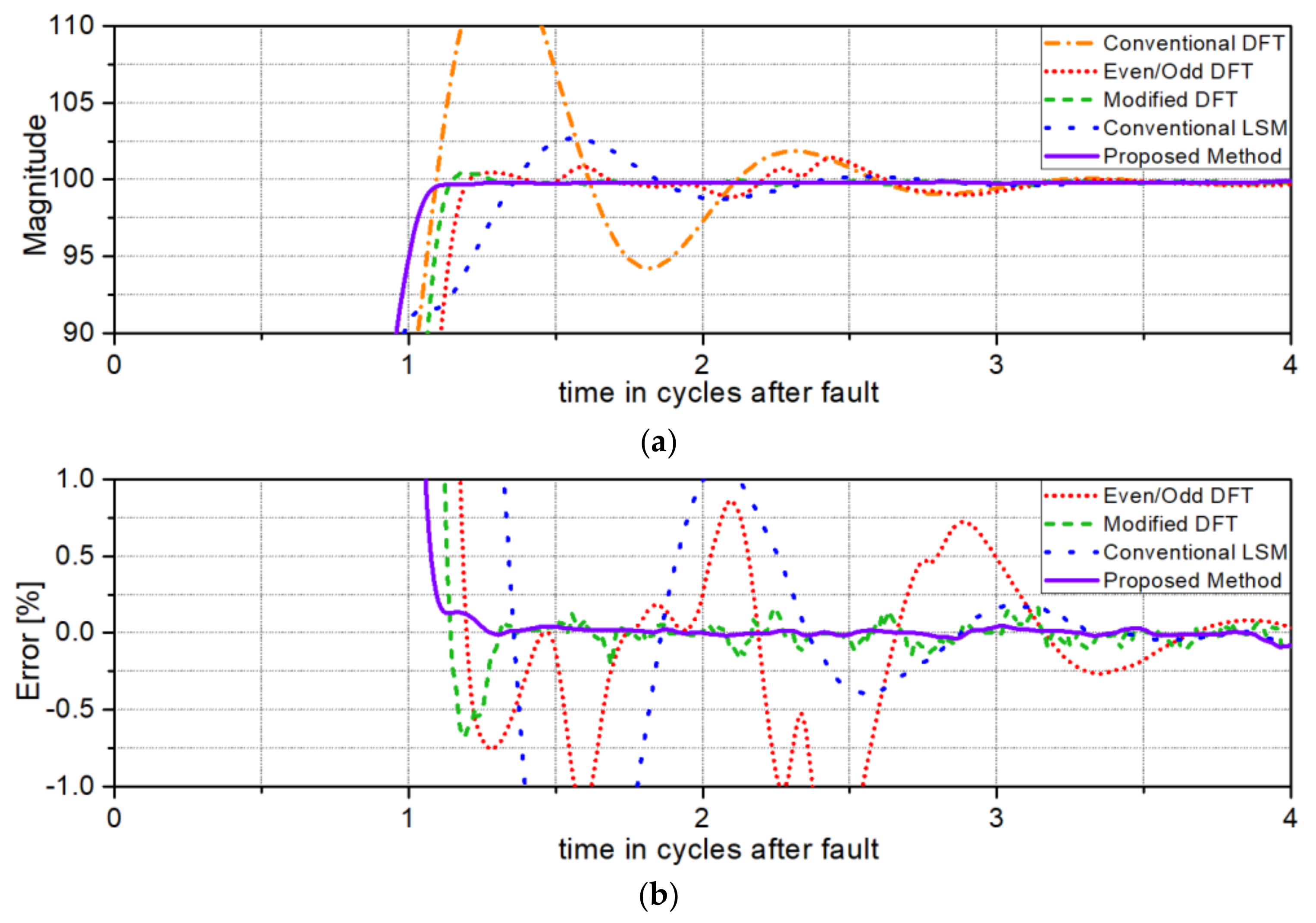
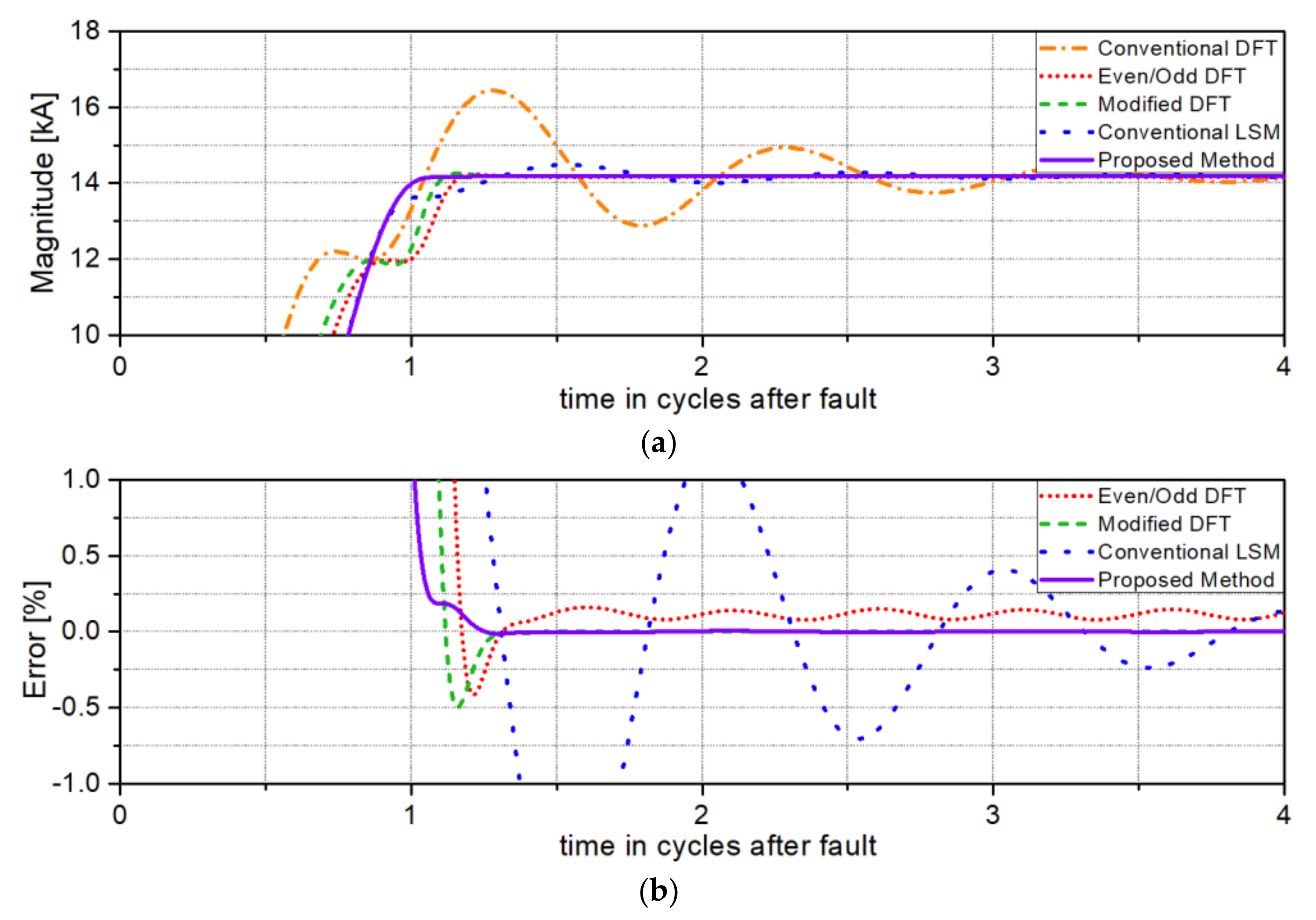
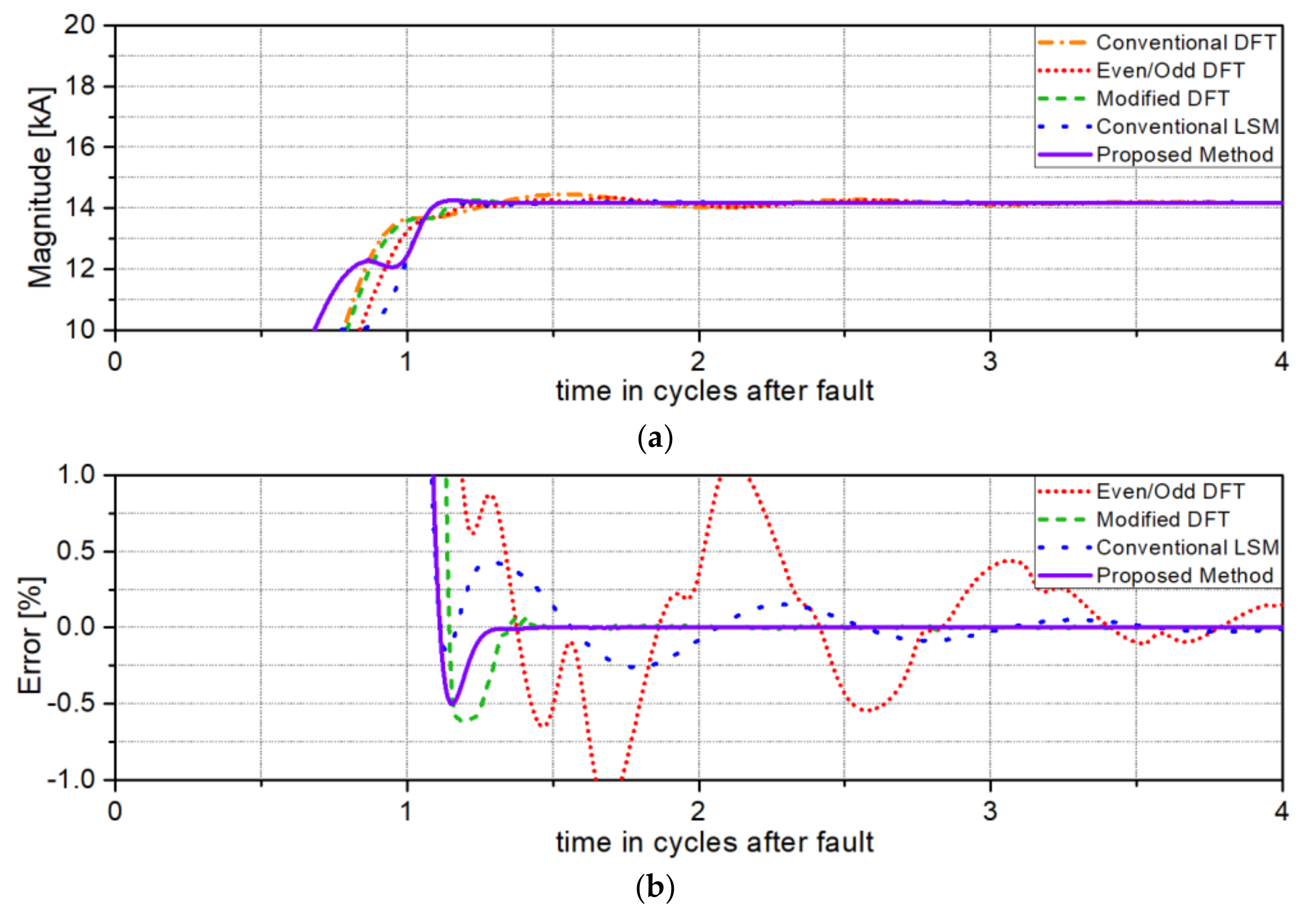
Figure 7 shows the test results for a solid single-phase to ground fault at 10% of the total line length from the relaying point. As seen in
Figure 7, the proposed algorithm accurately removes the adverse influence of the exponentially decaying DC offset more accurately than the conventional DFT, the even/odd DFT, and the conventional LSM, and also converges faster than the modified DFT.
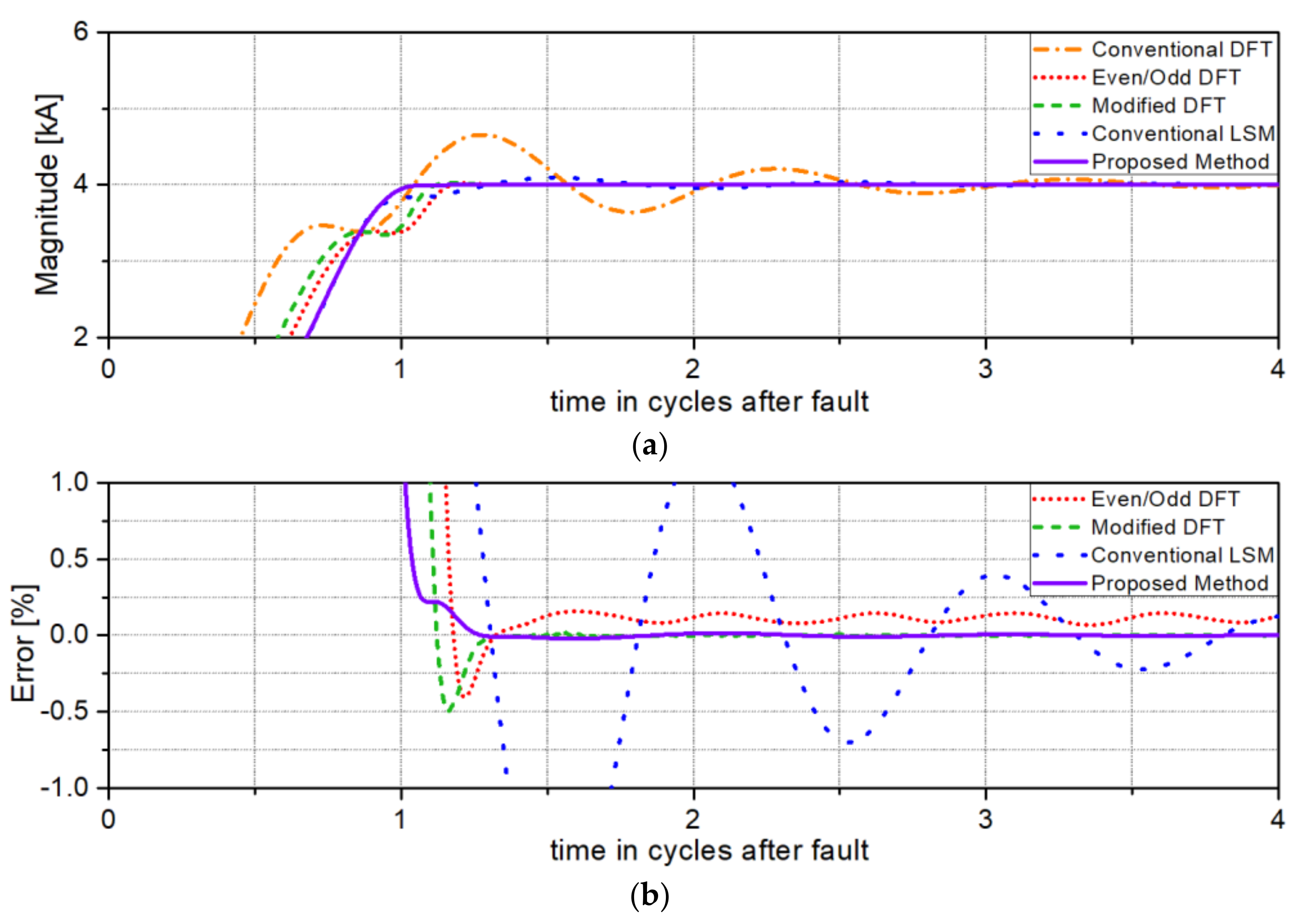
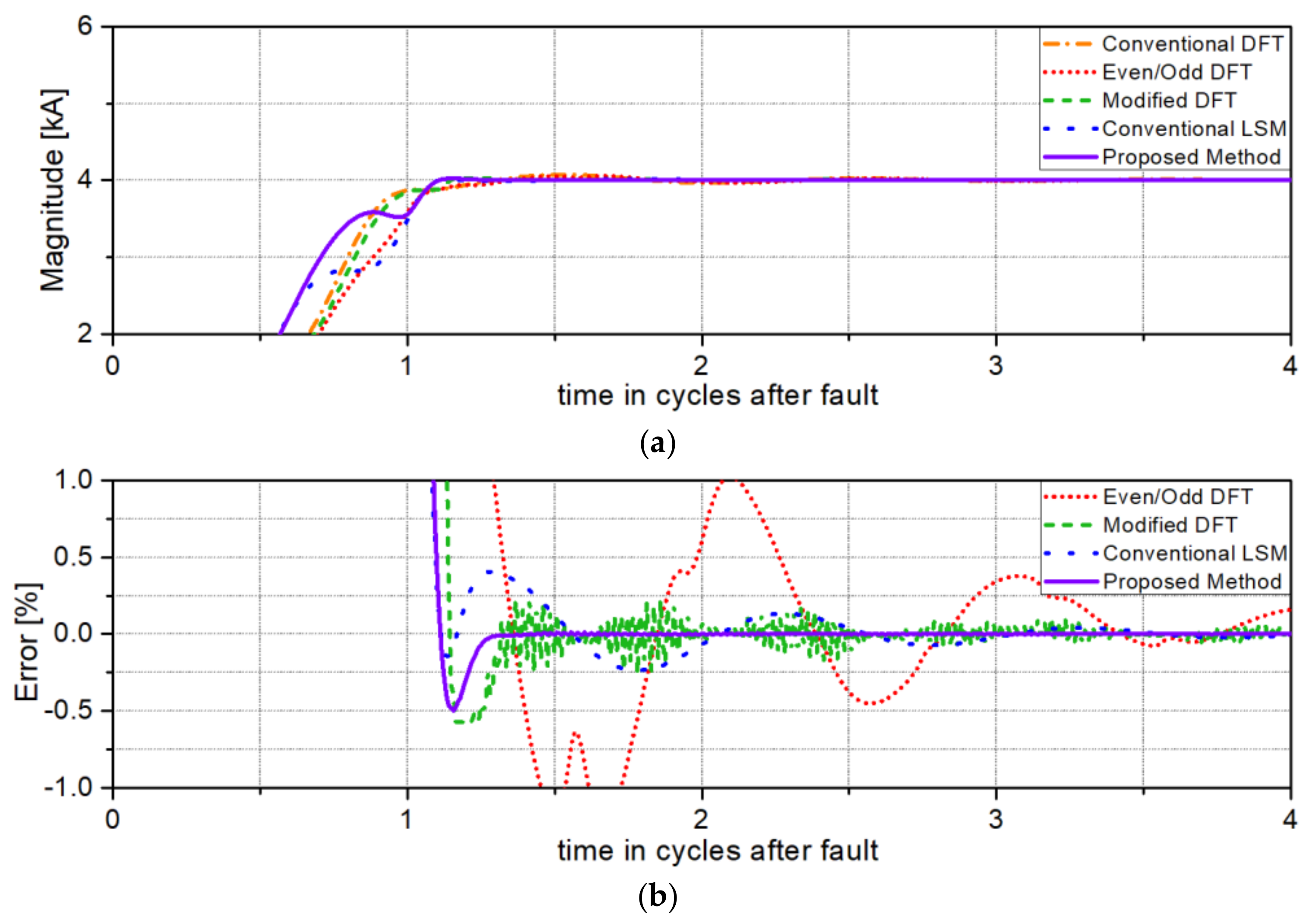
Figure 8 shows the test results for solid single-phase to ground faults at 50% of the total line length from the relaying point. These results show the same performance advantage demonstrated in
Figure 7 for the 10% distance.
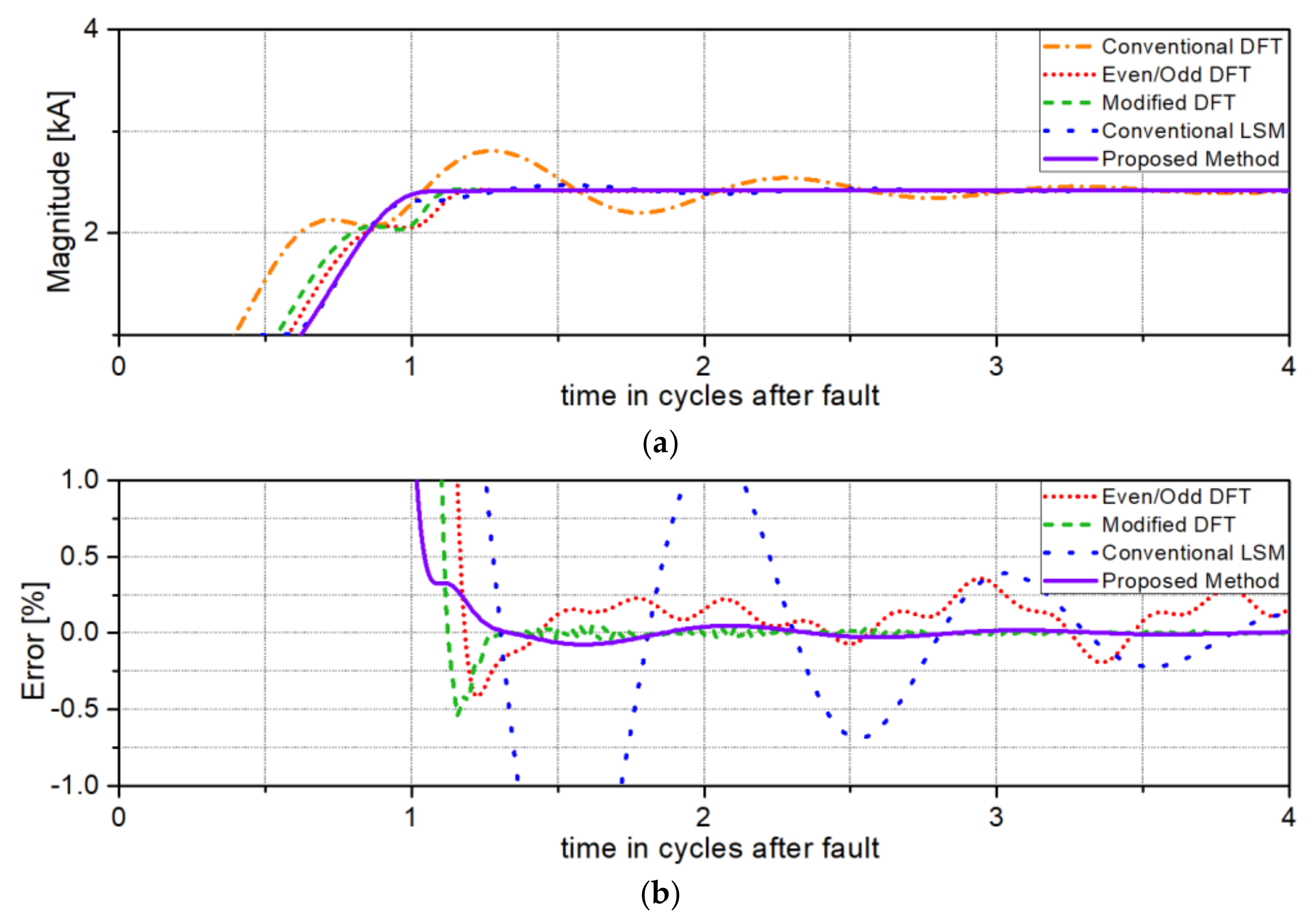
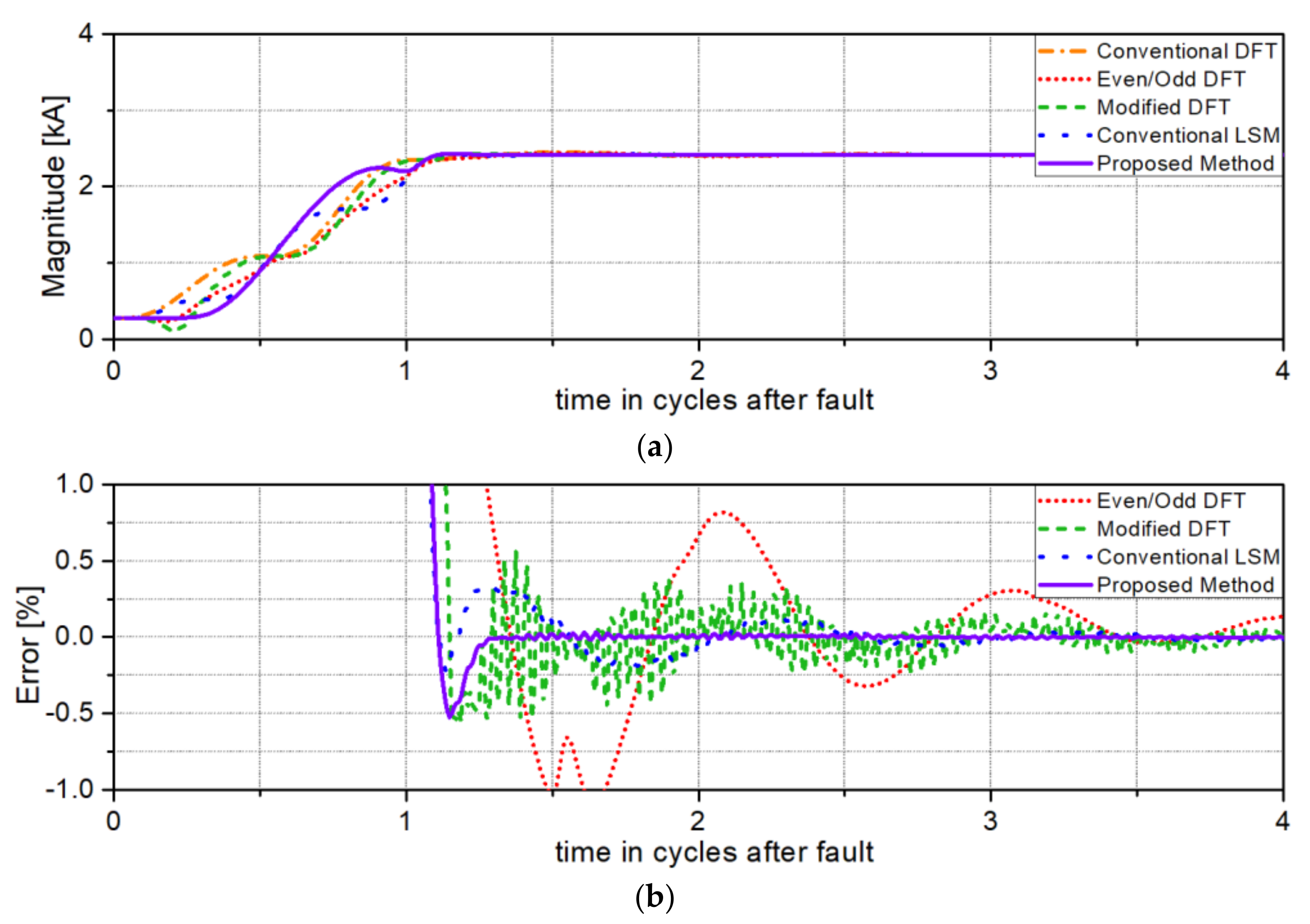
Figure 9 shows the test results for solid single-phase to ground faults at 90% of the total line length from the relaying point. These results show the same performance advantages demonstrated in
Figure 7 and
Figure 8 for their respective distances.
The magnitude and frequency band of the high-frequency components varies depending on fault conditions such as fault location, fault resistance, and fault inception angle.
Figure 10,
Figure 11 and
Figure 12 show the estimated RMS values and percent error of the fault current. The magnitude and frequency band of the high-frequency components depend on the fault distance from the relaying point to the fault point; thus, as in the tests of
Figure 7,
Figure 8 and
Figure 9, the performance of the proposed algorithm is evaluated by changing fault distance. A fault inception angle of 90° was used to maximize the magnitude of the high-frequency component.
Figure 10 shows the test results for a solid single-phase to ground fault at 10% of the total line length from the relaying point. As shown in
Figure 10b, the proposed algorithm can more accurately estimate the phasor of the fundamental frequency component than the conventional DFT, the modified DFT, the even/odd DFT, and the conventional LSM.
Figure 11 shows the test results for a solid single-phase to ground fault at 50% of the total line length from the relaying point. These results show the same performance advantages demonstrated in
Figure 10 for the 10% distance.
Figure 12 shows the test results for a solid single-phase to ground fault at 90% of the total line length from the relaying point. These results show the same performance advantages demonstrated in
Figure 10 and
Figure 11 for their respective distances.
The EMTP test results show that, the proposed algorithm can both remove the exponentially decaying DC offset and accurately estimate the phasor of the fundamental frequency component when the signal contains high-frequency noise components.