Abstract
Machine learning (ML) models have been widely used in the modeling, design and prediction in energy systems. During the past two decades, there has been a dramatic increase in the advancement and application of various types of ML models for energy systems. This paper presents the state of the art of ML models used in energy systems along with a novel taxonomy of models and applications. Through a novel methodology, ML models are identified and further classified according to the ML modeling technique, energy type, and application area. Furthermore, a comprehensive review of the literature leads to an assessment and performance evaluation of the ML models and their applications, and a discussion of the major challenges and opportunities for prospective research. This paper further concludes that there is an outstanding rise in the accuracy, robustness, precision and generalization ability of the ML models in energy systems using hybrid ML models. Hybridization is reported to be effective in the advancement of prediction models, particularly for renewable energy systems, e.g., solar energy, wind energy, and biofuels. Moreover, the energy demand prediction using hybrid models of ML have highly contributed to the energy efficiency and therefore energy governance and sustainability.
Keywords:
energy systems; machine learning; artificial neural networks (ANN); support vector machines (SVM); neuro-fuzzy; ANFIS; wavelet neural network (WNN); big data; decision tree (DT); ensemble; hybrid models; deep learning; blockchain; renewable energy systems; energy informatics; internet of things (IoT); smart sensors; remote sensing; prediction; forecasting; energy demand 1. Introduction
An energy system is a group of organized elements designed for the purpose of generation, control and/or transformation of energy [1,2]. Energy systems may incorporate combinations of mechanical, chemical, thermal, and electromagnetical components, covering a wide range of energy categories including renewables and alternatives [3,4,5]. The advancement of energy systems is facing critical decision-making tasks to satisfy numerous demanding and contradictory objectives considering functional performance, efficiency, financial burden, environmental impact, etc. [6].
The growing utilization of data collectors in energy systems has resulted in a massive amount of data accumulated. Smart sensors are now extensively used in energy production and energy consumption [7,8,9]. Such big data has created a vast number of opportunities and challenges for informed decision-making [10,11]. ML models have contributed to the implementation of big data technologies in various applications [12,13,14,15,16]. Since prediction methods based on ML models simplify the extraction of functional dependencies from observations, such data-driven models have gained popularity in the energy realm [17,18,19]. Today, ML models in energy systems are essential for predictive modeling of production, consumption, and demand analysis due to their accuracy, efficacy and speed [20,21]. ML models also provide an understanding on energy system functionality in the context of complex human interactions [22,23]. The use of ML models for conventional energy systems, along with alternative and renewable energy systems, has been promising [24,25]. Due to the popularity of the field, many review papers have emerged that present insight into present applications and future challenges and opportunities [26]. However, the existing review papers either survey the applications of a single ML model, e.g., ANNs [17], or cover only one energy domain, e.g., solar radiation forecasting [24]. Consequently, the advancements of ML models and their progress in various energy systems have not yet been addressed in the literature. Therefore, a comprehensive review of essential ML models is the main objective of this paper. Consequently, the contribution of this paper is to present the state of the art of ML models in energy systems and discuss their likely future trends.
The rest of this paper is organized as follows. In Section 2 the methodology of the research is presented. In the section three state of the art of ML models in energy systems is presented with an initial analysis of the database search. The ML models are categorized and the original papers with high relevance have been reviewed. Each subsection contains a brief discussions and outlook on the results related to each subject. Section 3 also includes an overview of recently emerged hybrid ML models. Section 4 focuses on the latest advancement of hybrid ML models in the highly demanding application areas e.g., solar, wind, and demand energy systems. Finally, in Section 4, an overall discussion and conclusions are presented.
2. Methodology of Survey
The purpose of the research methodology is to identify, classify and review the notable ML and DL models used in energy systems. In our comprehensive review, using the Thomson Reuters Web-of-Science and Elsevier Scopus for implementation of the search queries would ensure that any paper in the database would meet the essential quality measures, originality, high impact, and high h-index. Furthermore, to present an in-depth review and understanding of each modeling technique and its progress, we aimed at having four different categories for the models used in energy systems, i.e., single ML models, hybrid models, ensemble models, and DL.
Figure 1 demonstrates the methodology of this review. In step 1 of the methodology the initial database of the relevant articles is identified based on the search queries of: “energy system” and “machine learning” or “neural network” or “support vector” or “ANFIS” or “WNN” or “DT” or “MLP” or “ELM” or “ensemble” or “deep learning.” However, for every ML method, we applied a new search query to suit that search well. These queries will identify the relevant articles, yet the queries are uncertain whether the ML model belongs to either ensemble or hybrids. Also, some articles in the initial database might not be relevant at all. For instance, a hybrid or ensemble model of ML may include single model(s). For that reason, steps 2 and 3 of the methodology are designed in such a way to classify the ML models into the right categories for the review. In step 4 the models are classified into the four categories and arranged in separate tables to be reviewed individually.
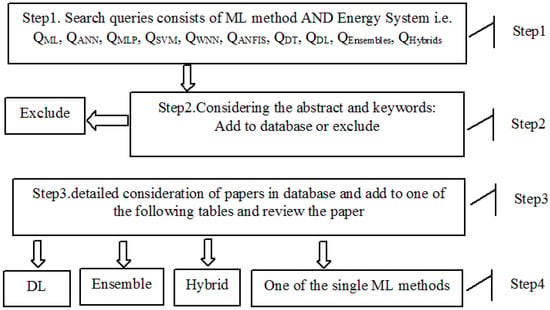
Figure 1.
Methodology of research.
The database includes 2601 relevant documents. During step two of the methodology the number of relevant documents drops to 240. In step three the documents are reduced to 70 original papers to be reviewed in this paper. Analyzing the initial database shows a great increase in the number of articles using ML models. Figure 2 and Figure 3 demonstrate the growth in the number of papers during the past two decades on energy systems that utilized ML and different subject areas using ML in energy systems, respectively. The increase in the number of documents in energy systems has also been due to the implementation of smart grid systems and the IoT. During the past decade, novel ML models including deep learning, ensembles, and hybrids have emerged in energy systems. Through introducing novel ML models to energy systems, the increasing number of papers represents a huge experimental effort to explore new opportunities.
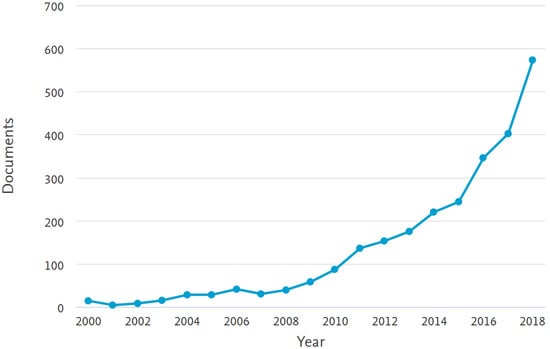
Figure 2.
The growth in the number of articles during the past two decades.
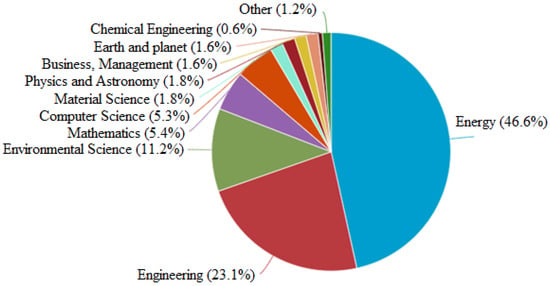
Figure 3.
Subject areas of ML in energy systems.
The initial consideration of the database of identified articles shows an exponential increase in the quantity of the literature on the use of ML in various energy systems (see Figure 2). Considering the application areas of the database, ML models have been extensively used in diverse applications of energy systems, especially for predicting electrical energy and renewable energies demand and consumption. The continued growth of literature can also confirm the great potential of ML models in energy systems.
3. State of the Art of ML Models in Energy Systems
The methodology identifies 10 major ML models frequently used in energy systems, i.e., ANN, MLP, ELM, SVM, WNN, ANFIS, decision trees, deep learning, ensembles, and advanced hybrid ML models. The notable manuscripts are accordingly categorized into the relevant groups and further reviewed in this section. Note that, in the presented taxonomy, deep learning as an emerging modeling technique has been categorized under the ML models. Furthermore, it is worth mentioning that WNN and ANFIS are of a hybrid nature. However, the category of “advanced hybrid ML models” includes only recently developed algorithms.
In this section the accuracy of the ML model is further evaluated. Since different ML models are available, choosing and demonstrating the superiority of the models requires comparing their performance. Hence, some comparative performance parameters are required. The most popular comparative performance parameters are the root mean square error (RMSE) and correlation coefficient (r), which are used to indicate the error and precision of the models [27,28]; Equations (1) and (2) represent these parameters.
where xti represents the target value, xpi represents the predicted value, and n is the number of data points.
3.1. ANN
Artificial neural networks are frameworks for different machine learning algorithms to process complex data inputs. ANNs can be utilized for several purposes such as forecasting, regression and curve fitting. An artificial neural network fundamental unit is a neuron that utilizes a transfer function for the output formulation. The main advantage of ANN models is their lower complexity for multiple-variable problems. Table 1 demonstrates some critical papers in this field. Instead of complicated rules, ANN can learn patterns of crucial information within an intricate information domain [4]. Also, due to the noise-immune and fault-tolerant characteristics of ANNs, they can be successfully used for inherently noisy data from energy systems.

Table 1.
Notable ANN models used in energy systems.
Abbas et al. (2018) [29] used genetic algorithms to optimize the generation capacities of renewable energy systems integrated with storage systems. This study evaluated the economic feasibility of the introduction of energy storage systems to the electric grid. The artificial neural network was used to validate the predicted load model. The uncertainties related to the renewable energy systems were dealt with using a chance-constrained model. Then, the problem was solved by genetic algorithms. The robustness of the proposed model was verified by its application to a case in western China. Figure 4 reports the results of the proposed method in comparison with the base case in terms of total expenditure (billion $), fuel cost (billion $), clean energy contribution (%), the average cost of electricity (cents $/kWh), and CO2 emissions (million Tons). Based on Figure 4, the use of clean energy nearly doubled, which led to a reduction in CO2 emissions from about 109 million tons to 38 million tons. Therefore the proposed case has an effective role compared with the base case.
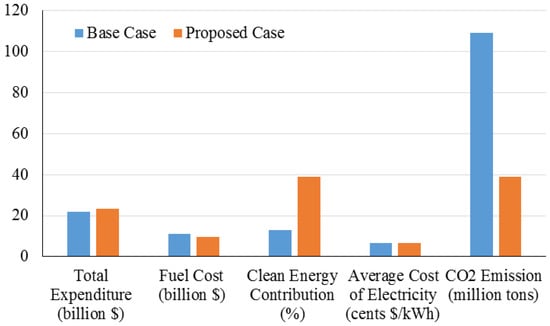
Figure 4.
Results for study by Abbas et al. (2018). Reproduced from [29], Elsevier: 2018.
Anwar et al. (2017) [30] presented a novel strategy for generation scheduling and power smoothing for a hybrid system of marine current and wind turbines. In this study, innovative strategies were proposed to mitigate wind intermittency effects. Contrary to the randomness of wind, marine currents are highly predictable. The presented methodologies incorporate an optimal strategy for sizing for this hybrid system. Bootstrapped artificial neural networks were developed to predict intervals for wind speed—speeds of marine currents modeled utilizing the Harmonic Analysis Method. The results of the model show the robustness of the presented methodology, which can be used to successfully decrease power fluctuations, make considerable cost savings, and ensure reliable dispatch scheduling for power generation. Boukelia et al. (2017) [31] used an ANN-based approach to assess a parabolic trough solar power plant. In this study, an ANN model was developed to predict the levelized electricity cost of two parabolic trough solar thermal power plants coupled with a fuel backup system and thermal energy storage. The techno-economic study was performed comparing molten salt and thermic oil usage to optimize thermal plants’ hourly and annual performance.
Chatziagorakis et al. (2016) [32] studied the control of hybrid renewable energy systems, using recurrent neural networks to forecast weather conditions. A forecasting model using a recurrent neural network for prediction of hourly and daily solar radiation and wind speed was presented. The results of the simulation indicated that a recurrent neural network was capable of delivering acceptable future estimation to evaluate the available renewable energy safely.
Gallagher et al. (2018) [33] studied the suitability of machine learning for the optimization of uncertainty in energy savings measurement and verification. In this paper, the new use of machine learning algorithms for energy savings in industrial buildings was studied. The applied machine learning techniques consisted of k-nearest neighbors, support vector machines, artificial neural networks, decision trees, and bi-variable and multi-variable ordinary least squares regression. The model’s prediction performances were validated to optimize model parameters. The results demonstrated that models based on ML algorithms were more precise than conventional methods. Results of RMSE have been presented in Figure 5.
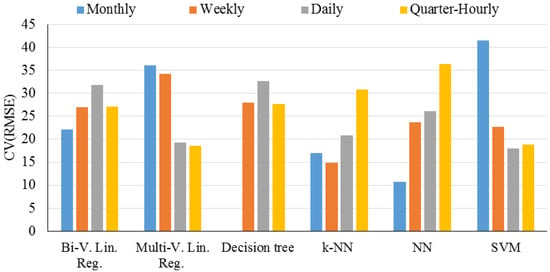
Figure 5.
RMSE values for study by Gallagher et al. (2018). Reproduced from [33], Elsevier: 2018.
3.2. MLP
MLP is an advanced version of ANN for engineering applications and energy systems; it is considered a feed-forward neural network and uses a supervised and back-propagation learning method for training purposes [34,35,36]. This is a simple and popular method for the modeling and prediction of a process, and, in many cases, it is considered as the control model. Table 2 demonstrates some important papers in this field.

Table 2.
Notable MLP models used in energy systems.
Ahmed et al. (2015) [37] performed a study on forecasting hourly solar irradiation for New Zealand. In this paper, the ability to provide 24-h-ahead hourly global solar irradiation forecasts was assessed utilizing several methods, especially incorporating autoregressive recurrent neural networks. Hourly time series were used for training and testing the forecasting methods. MLP, NARX, ARMA, and persistence methods were compared using RMSE. Figure 6 presents the related results. Based on the results, the NARX method with the lowest value of RMSE presented a precision about 49%, 22%, and 52% higher than that of the MLP, ARMA, and Persistence methods, respectively.
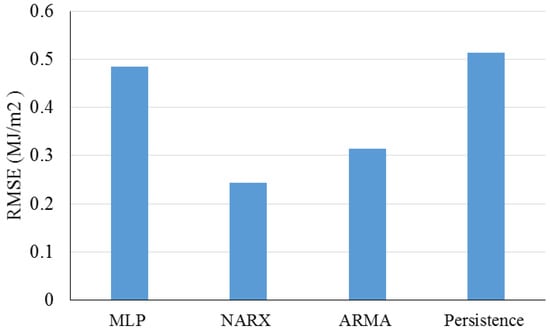
Figure 6.
RMSE values for study by Ahmed et al. (2015). Reproduced from [37], Elsevier: 2015.
Chahkoutahi et al. (2017) [38] introduced a seasonal optimal hybrid model to forecast the electricity load. In this study, a direct optimum parallel hybrid model was presented using multi-layer perceptron neural network, Seasonal Autoregressive Integrated Moving Average, and Adaptive Network-based Fuzzy Inference System to forecast the electricity load. The main reason for using this model was to utilize these models’ advantages for modeling complex systems. The validation of the presented model implies that it was more accurate than its components. Figure 7 presents the results of the proposed DOPH method against SARIMA, MLP, ANFIS, DE-based, and GA-based models. The output of each method was compared with target values using RMSE. Based on the results, the proposed method could improve the prediction capability by 51.4%, 33.18%, 31.10%, 16.44%, and 12.8%, compared with the SARIMA, MLP, ANFIS, DE-based, and GA-based models, respectively, in the test stage.
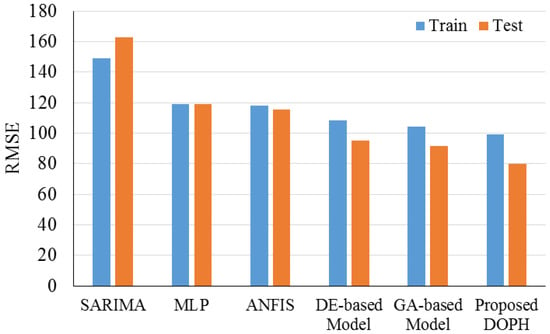
Figure 7.
RMSE values for study by Chahkoutahi and Khashei (2017). Reproduced from [38], Elsevier 2017.
Kazem et al. (2013) [39] designed and installed a photovoltaic system for electricity production. The output of the system was measured for one year. The photovoltaic system output was simulated and predicted by self-organizing feature maps, feed-forward networks, support vector machines, and multi-layer perceptron. Ambient temperature and solar radiation data were these model’s inputs, and the PV array current and current were the outputs. The outputs of each model were compared with the target values using RMSE factor. The results have been presented in Figure 8. Based on the results, the SOFM generates the lowest RMSE value compared to the MLP model, GFF model, and SVM model. Therefore the SOFM model is suitable for this purpose.
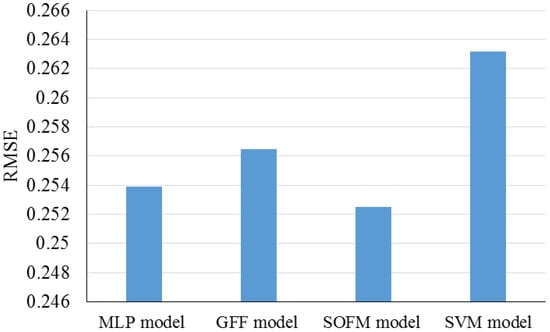
Figure 8.
RMSE values for study by Kazem and Yousif (2013). Reproduced from [39], Elsevier: 2013.
Loutfi et al. (2017) [40] presented an analysis of the design of solar energy systems. In this study, a comparison between multilayer perceptron and neural autoregressive with exogenous inputs was presented. The proposed model has excellent ability to produce hourly solar radiation forecasts for cheaper data such as relative humidity and temperature. The results of the best model are presented in Table 3 for the developed model. The study proposes the NARX method in conjunction with the MLP method. As is clear from Table 3, the proposed method has the best prediction capability with reference to nRMSE and correlation coefficient values.

Table 3.
Results of evaluations of models by Loutfi et al. (2017). Reproduced from [40], Elsevier: 2017.
Shimray et al. (2017) [41] performed a study on the installation of hydropower plant sites ranking using a Multi-layer Perceptron Neural Network. In this paper, a model was developed for decision makers to rank potential power plant sites based on water quality, air quality, energy delivery cost, natural hazard, ecological impact, and project duration. The case in this paper was ranking several potential plant sites in India.
3.3. ELM and Other Advanced ANNs
In order to find an advanced version of ANNs, the keywords of the search here were extreme learning machine, Feed-forward neural networks, Back-propagation neural networks, functional neural network, Feedforward, and back propagation. The ELM has a high speed of learning and the proper ability of generalization. Table 4 lists some important papers in this field.

Table 4.
Notable ELM models used in energy systems.
Arat and Arslan (2017) [42] presented an optimum design for a geothermal heat pump for a district heating system. Three different back propagation learning algorithms was used. These algorithms were Pola–Ribiere Conjugate Gradient, Levenberg-Marquardt, and Scaled Conjugate Gradient. The presented ELM model was composed of two stages. The second stage of the ELM structure was composed of three levels of ANN models in this proposed model. The results of this study showed that the values obtained from ANN were very close to the analytical data. Figure 9 demonstrates the correlation coefficient values, and Table 5 presents the RMSE values for each parameter separately.
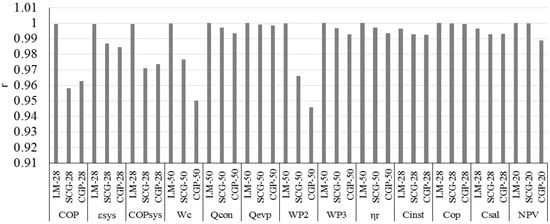
Figure 9.
r values of study of Arat and Arslan (2017). Reproduced from [42], Elsevier: 2017.

Table 5.
RMSE values of the study of Arat and Arslan (2017). Reproduced from [42], Elsevier: 2017.
Bagnasco et al. (2015) presented a study of power consumption forecasting (load forecasting model) in hospitals. The presented artificial neural network utilizing a backpropagation training algorithm can take loads, time of the day, data concerning the type of day (e.g., weekday/holiday) and weather data. The proposed forecast algorithm can be easily integrated into the Building Management Systems real-time monitoring system. Case A includes no weather data, and Case B includes day-ahead temperature data. RMSE values have been presented in Figure 10.
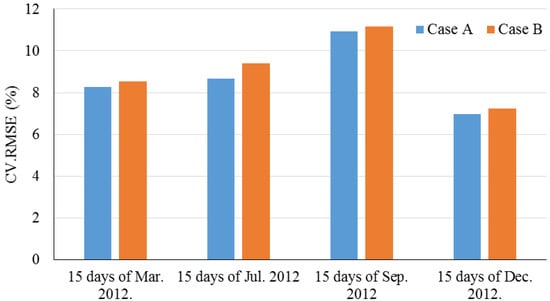
Figure 10.
RMSE values for study by Bagnasco et al. (2015). Reproduced from [43], Elsevier: 2015.
Li et al. (2018) [44] presented a multi-clustered echo state network model to directly forecast PV electricity generation. Measured and estimated PV electricity generation data characteristic such as stationarity (or non-stationarity), seasonality and complexity analysis were investigated through data mining approaches. The simulation results showed that the presented multi-clustered echo state network model can accurately forecast photovoltaic power output one hour ahead. The one-day forecast has 91–98% correlation coefficient for cloudy days and 99% for sunny days. Figure 11 presents the correlation coefficient values for the study based on day and method.
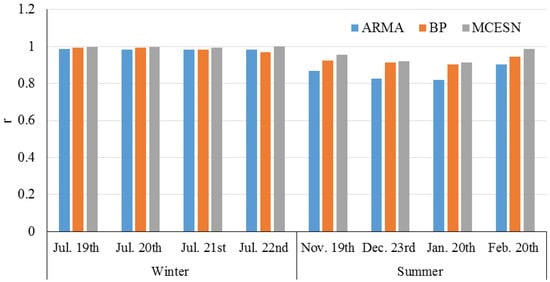
Figure 11.
Correlation coefficient values for the study by Li et al. (2018). Reproduced from [44], Elsevier: 2018.
Premalatha and Valan Arasu (2016) [45] utilized ANN models to predict global solar radiation. The main purpose of this study was to develop an ANN model for accurate prediction of solar radiation. Two different ANN models based on four algorithms were considered in this paper. The last 10 years of meteorological data were collected from five different sites in India to train the models. The criteria for determining best ANN algorithm were a minimum mean absolute error, root mean square error, and maximum linear correlation coefficient of 3.028, 3.646, and 0.927, respectively.
Yaïci and Entchev (2014) [46] utilized artificial neural networks to predict the performance of a solar thermal energy system. This system was used for space heating and domestic hot water—two different variants of the back-propagation learning algorithm (scaled conjugate gradient algorithms and the Levenberg-Marquardt). The presented model was applied for predicting several performance parameters of the system such as the temperature stratification of the preheat tank, the derived solar fractions, the solar collectors’ heat input to the heat exchanger, and auxiliary propane-fired tank heat input. This methodology can be used for condition monitoring and fault detection of a solar thermal energy system.
3.4. SVM
SVMs are machine learning algorithms built on statistical learning theory for structural risk minimization. In pattern recognition, classification, and analysis of regression, SVMs outperform other methodologies. The significant range of SVM applications in the field of load forecasting is due to its ability to make generalizations. Also, local minima lead to no problems in SVM. Table 6 presents some important papers in this field.

Table 6.
Notable SVM models used in energy systems.
Arabloo et al. (2015) [47] introduced a novel methodology for the optimization of the oxygen-steam ratio in the gasification process of coal. A methodology utilizing support vector machine algorithm was presented for estimation of proper steam-oxygen ratio to balance the heat requirement and released heat in the coal gasification process. A comparison of experimental data and predicted values showed the precision of the predictive model that can be used for commercial implications in the coal gasification process. Arikan et al. (2013) [48] performed a study to classify power quality disturbances utilizing support vector machines. In this paper, five kinds of power quality disturbances and pure sine was utilizing support vector machines that were based on wavelets. The proposed method performance was validated utilizing synthetic data derived from the mathematical model and real-time measurements. Support vector machines, artificial neural network, and the same future vector and data Bayes classifier were compared. It was observed that support vector machines gave the best results both for synthetic data and in real time.
Ma et al. (2017) [49] developed a soft sensor (a field-support vector regression) to upgrade the estimation accuracy of solar irradiance levels from photovoltaic electrical parameters. The soft sensor collected its input data into several groups based on ambient temperature. The introduced soft sensor can be implanted in a photovoltaic module, a current sensor, or a thermometer. It was validated by experimental prototype and simulations utilizing measured outdoor conditions. Figure 12 presents the RMSE values for the study.
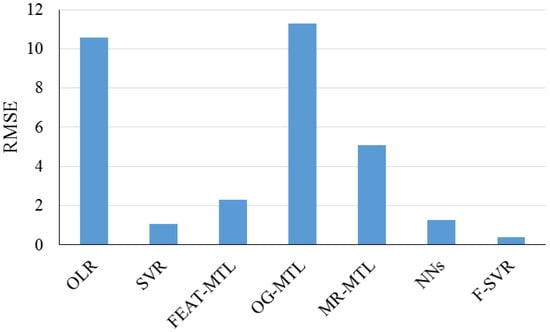
Figure 12.
RMSE values of the study of Ma et al. (2018). Reproduced from [49], Elsevier: 2018.
Özdemir et al. (2016) [50] used Support Vector Machine for harmonic distortion estimation. The power distribution network was studied, and the predicted results were compared with the quantified real data. The presented approach was compared with the artificial neural network and linear regression methods. The validation of the predicted results demonstrated that Support Vector Machine is robust for total harmonic distortion in the power network. Pinto et al. (2016) [51] developed a multi-agent system for modeling competitive electricity markets. This study proposed applying support vector machines to lay out decision support for electricity market players. The presented model was coupled with an Adaptive Learning Strategic Bidding System to be used as a decision support system. This methodology was validated and then compared with the artificial neural network. The results were encouraging: a robust price forecast for electricity market was obtained quickly.
3.5. WNN
WNN takes the benefits of both the theory of wavelets and neural networks and combines them. This method contains an FFNN with one hidden layer. One of the missions of WNNs is to estimate the function of a process or a trend or computing. A WNN can train the structure of a function using a series of data and generate or compute an expected output value for a given input value [52]. WNN has several advantages over other neural networks. WNN needs a smaller training amount than the MLP method, and has fast convergence. Table 7 presents some important papers in this field.

Table 7.
Notable WNN models used in energy systems.
Doucoure et al. (2016) [53] developed a prediction methodology for renewable energy sources to promote the use of renewable energy isolated and grid-connected power systems. The presented method was based on artificial neural networks and wavelet decomposition. The predictability of every component of the input data utilizing the Hurst coefficient was analyzed in this study. To ensure the predictability of the information, some components with low predictability potential were eliminated to reduce the computational algorithm complexity. Figure 13 presents the RMSE values for the study in three terms, with all data components, without random data and persistence data related to the proposed method.
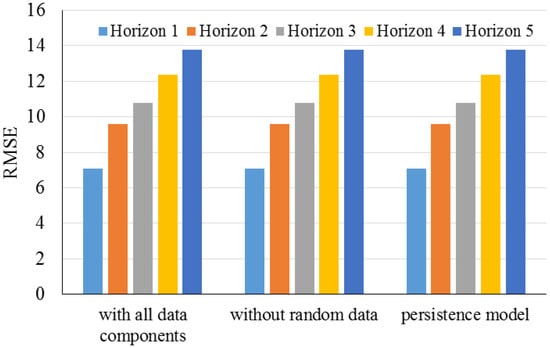
Figure 13.
RMSE values for study by Doucoure et al. (2016). Reproduced from [53], Elsevier: 2016.
Gu et al. (2018) [54] studied heat load prediction utilizing different prediction models such as extreme learning machine, wavelet neural network, support vector machine, back propagation neural network optimized using a genetic algorithm, and wavelet neural network. Historical loads and indoor temperature were assumed to be influential. The support vector machine demonstrated smaller errors compared to the three other neural network algorithms. Figure 14 presents the values of RMSE and correlation coefficient for the study.
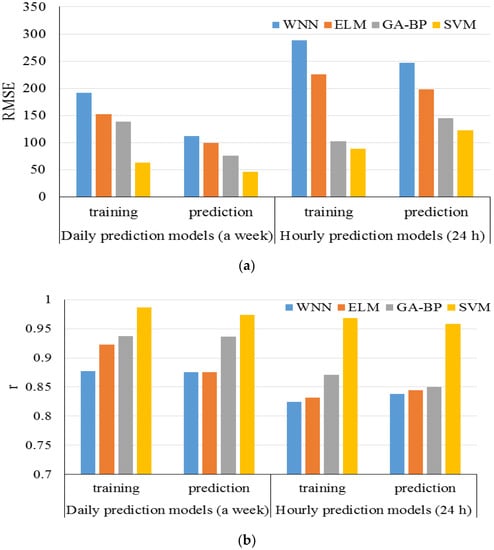
Figure 14.
RMSE and r values for study by Gu et al. (2018). Reproduced from [54], Elsevier: 2018.
He et al. (2018) [55] proposed a hybrid forecasting model which was composed of three modules: data clustering, data preprocessing and forecasting modules. The decomposing technique was used to decrease the noise influence within the raw data series to achieve a more stable sequence to extract traits from the original data. A similar fluctuation pattern was selected for the training database in the forecasting module to improve the forecasting accuracy. The experimental data demonstrate that the presented model outperforms other discussed forecasting models in the paper. Figure 15 presents the RMSE values in cases of non-season and season datasets.
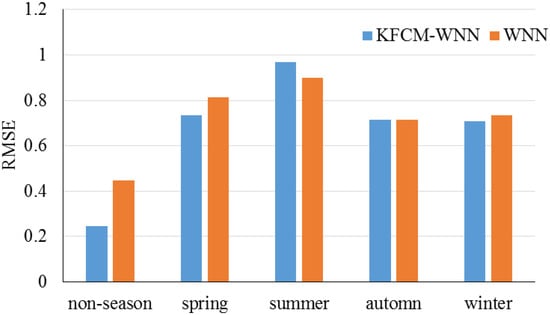
Figure 15.
RMSE values for study by He et al. (2018). Reproduced from [55], Elsevier: 2018.
Qin et al. (2018) [56] introduced online energy management control of hybrid electric vehicles based on NDP to optimize battery state of charge and fuel economy at the same time. In the proposed NDP method, the action network was a conventional wavelet neural network, and the critic network was a multi-resolution wavelet neural network. The action network was constructed on the Morlet function, and the critic network was stem from the Meyer wavelet function. Based on results, the NDP EMS have a high capability the same as the NDP in online applications. Based on comparisons, the RBFNN-based NDP EMS supports the efficiency of the CWNN and MRWNN.
Sarshar et al. (2017) [57] presented an adaptive probabilistic concept of the confidence interval for addressing randomness of wind speed. To increase forecasting accuracy, wavelet decomposition was utilized for time series of wind power, and the results were used in the artificial neural network. Then predicted wind power dependable levels adaptive probabilistic concept of confidence interval were calculated. An energy storage system was used to decrease the impact of forecasting errors on the micro-grid and to increase planning flexibility. Finally, the presented algorithm was validated with a typical micro-grid case study. The results indicated that the presented adaptive probabilistic concept of confidence interval worked well and demonstrated the superiority of WNN to ANN.
3.6. ANFIS
ANFIS is a modeling method that employs an artificial neural network based on the Takagi–Sugeno fuzzy inference system. This technique benefits from the capabilities of both fuzzy logic and neural network. ANFIS is a method with five main layers. This method is considered as an early form of the hybrid ML method [28]. Table 8 presents some important papers in this field.

Table 8.
Notable ANFIS models used in energy systems.
Abdulwahid and Wang (2018) [58] introduced a novel protection method for preventing reverse power flow developed on neuro-fuzzy networks for utilization in the smart grid. This study presented an upgraded protection device using a newly developed intelligent decision support system (IDSS). The presented IDSS was a decision system support system that coupled the robust specification for fuzzy inference systems and neural networks. The proposed methodology can monitor extreme environmental conditions.
Bassam et al. (2017) [59] developed an adaptive neuro-fuzzy inference to estimate the temperature of photovoltaic systems. Experimental measurements for the learning process were comprised of six environmental variables, namely wind velocity, temperature, wind direction, irradiance, atmospheric pressure, and relative humidity and PV power output as an operational variable, which were used for training parameters. The model was validated with experimental data from a photovoltaic system with a high value for fitness correlation parameter. The results of the model show that the presented methodology was a reliable tool for modules’ temperature estimation using environmental variables. Figure 16 presents the RMSE (a) and correlation coefficient (b) values for the study. This comparison is in line with choosing the best type of membership function for ANFIS. As is clear from Figure 16, a Gbell membership function with a low RMSE and a high correlation coefficient value has the highest accuracy compared with the other types.
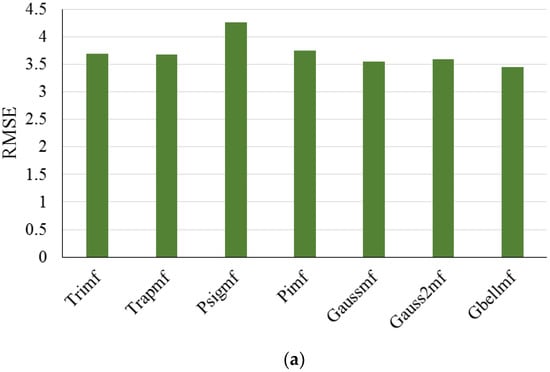
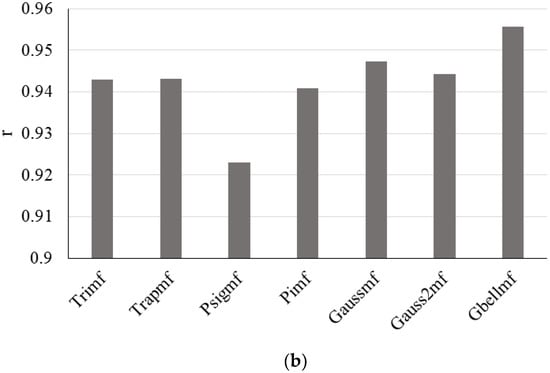
Figure 16.
(a) RMSE and (b) correlation coefficient values for study by Bassam et al. (2017). Reproduced from [59], Elsevier: 2017.
Kampouropoulos et al. (2018) [60] introduced a novel approach for multi-carrier energy systems’ energy optimization. In this study, an adaptive neuro-fuzzy inference system was applied to forecast the power demand of a factory, and a genetic algorithm was used to model its energy flow. The objective of the optimization algorithm was to fulfill the power demand of the factory to reduce optimization criteria. The proposed method was validated at SEAT.
Mohammadi et al. (2016) [61] presented a method to identify the essential parameters for forecasting global solar radiation utilizing an ANFIS selection procedure. In this study, a methodology based on ANFIS was applied to identify the most related parameters for daily prediction of global solar radiation. Three different cities were considered as case studies. Nine parameters of extraterrestrial radiation, sea level pressure, relative humidity, water vapor pressure, minimum, average and maximum air temperatures, maximum possible sunshine duration, and sunshine duration were considered for selection in ANFIS process. The results indicated that the optimal sets of inputs were different for different case studies. This study demonstrated the significance of the selection of input parameters for predicting daily global solar radiation. Figure 17 indicates the value of RMSE in terms of two and three inputs. Based on the results, three inputs provide better prediction performance compared with that for the two inputs.
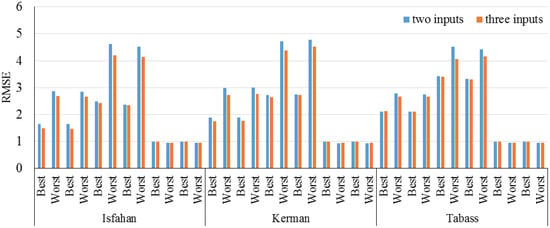
Figure 17.
RMSE values for study by Mohammadi et al. (2016). Reproduced from [61], Elsevier: 2016.
Sajjadi et al. (2016) [62] performed a sensitivity analysis using catalyzed-transesterification as a renewable energy production system [63] by an ANFIS-based methodology. Influential parameters on transesterification yield should be analyzed and predicted. ANFIS was applied in this paper to select the most critical parameters based on operational variables. Experimental results were used to extract training data for an adaptive neuro-fuzzy inference system network. The robustness of the presented method was verified by the simulation results.
3.7. Decision Trees
The decision tree method is used to approximate discrete-valued target functions that the learned function is illustrated by a decision tree. These methods are among the most powerful inductive inference algorithms and are successfully used in many different energy systems. Table 9 presents some important papers in this field.

Table 9.
Notable decision trees models used in energy systems.
Aguado et al. (2018) [64] introduced a methodology for railway electric energy systems optimal operation considering PV panels and wind turbines as renewable energy sources, hybrid electric energy storage systems, and regenerative braking capabilities. The uncertainties related to renewable energies were considered through a scenario tree methodology. All the compliments were coupled into a multi-period optimal power flow problem. Results were reported for different cases for different operation modes.
Costa et al. (2016) [65] presented a security dispatch method based on decision trees, which can be applied to coupled natural gas and electric power networks against contingencies that may cause interruptions. Preventive measures to the optimal gas production and electric energy generation were performed based on boundaries of controllable variables and security regions determined by decision trees. The decision tree’s rules give details of the security regions were tractable constraints and were included in the optimization procedures of gas production and power generation rescheduling. Kamali et al. (2017) [66] presented a novel two-stage method to predict the risk of a blackout in an electric power network. Firstly, electric islands’ boundaries were determined to utilize a mixed integer nonlinear programming method that optimized the cost of load curtailment and power generation re-dispatch. Secondly, a data-mining method was completed to forecast the risk of an electric island separation from the rest of the network. Several scenarios such as island and non-island situations were analyzed and then used by the decision tree classification method to forecast a possible blackout.
Moutis et al. (2016) [67] presented a novel tool for utilization of decision trees for planning storage systems in microgrids and controlling energy resources to balance energy for planned community microgrids. The presented methodology was validated by sensitivity analysis for several case studies. A test implementation was introduced for the utilization of distributed controller hardware to run the algorithm of energy balancing in real-time. Ottesen et al. (2016) [68] used decision tree for energy balancing and planning for planned community microgrids. The goal of this paper was to minimize the total cost by trading in an electricity market and considering grid tariffs costs, imbalance penalization and fuels use. The flexibility properties of the energy systems in the buildings of prosumers was modeled bidding rules and handling the interrelations between hours were considered. Uncertain parameters’ information structure was captured through scenario trees. Therefore, a two-stage stochastic mixed-integer linear program was applied for bidding decisions and scheduling.
3.8. Deep Learning
Deep learning aims at modeling the hierarchical characterization behind data prediction patterns through stacking multi-layer information processing modules. Increasing computing power and increasing data size resulted in the popularity of deep learning. Table 10 presents some important papers in this field.

Table 10.
Notable deep learning models used in energy systems.
Chemali et al. (2018) [69] introduced a machine learning methodology for state of charge (SOC) estimation in Li-ion batteries utilizing deep neural networks. In this study, a new approach utilizing deep neural networks was presented for estimating battery SOC. Training data were generated in the laboratory by applying drive cycle loads for different ambient temperatures to a Li-ion battery. As a result, the battery can be exposed to variable dynamics. The ability of deep neural networks to encode dependencies into the network weights in real time was demonstrated. Coelho et al. (2017) [70] presented a deep learning model for Graphics Processing Unit for time series forecasting. A new parallel methodology for time series learning was designed. The presented methodology was applied in a hybrid metaheuristic model for mini/microgrid forecasting problem (household electricity demand). Calculated results demonstrated that the presented graphics processing unit learning methodology was a robust deep learning tool to be used in smart sensors. Kim et al. (2017) [71] presented a nonintrusive load monitoring method based on advanced deep learning. In this study, an energy disaggregation utilizing advanced deep learning and long short-term memory recurrent neural network model was proposed. Then, a new signature to upgrade the proposed model classification performance in multistate appliance case was designated. It was demonstrated that the combination between novel signature and advanced deep learning could be a robust solution for improving load identification performance.
Mocanu et al. (2016) [72] introduced two novel models, namely Factored Conditional Restricted Boltzmann Machine and Conditional Restricted Boltzmann Machine, for prediction of energy consumption time series. The models were evaluated by four years of one-minute electric consumption data gathered from a residential building. The results demonstrated that Factored Conditional Restricted Boltzmann Machine outperformed ANN, SVM, RNN, and CRBM. In this study, predictions were performed in various scenarios. RMSE and correlation coefficient were employed to compare the results to choose the best model. Figure 18 presents the RMSE (a) and correlation coefficient (b) values in case of prediction for a year with a weekly resolution.
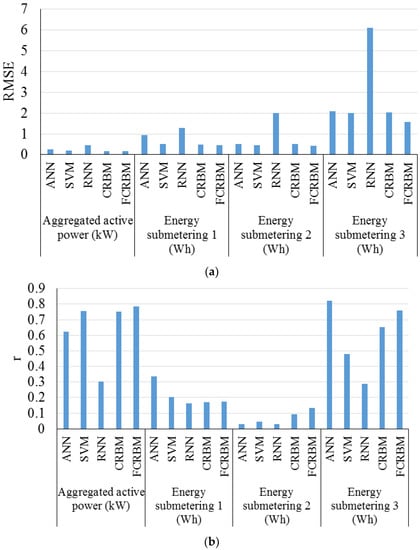
Figure 18.
(a) RMSE and (b) correlation coefficient values for study by Mocanu et al. (2016). Reproduced from [72], Elsevier: 2016.
Wang et al. (2017) [73] introduced a new method for photovoltaic electricity forecasting utilizing wavelet transform and deep convolutional neural network. The deep convolutional neural network was used to extract invariant structures and the nonlinear features exhibited in each frequency. Numerical results demonstrated that the introduced methods could improve the accuracy of forecasting for various seasons and different prediction horizons. Figure 19 presents the average RMSE values in two scenarios, 45- and 75-min-ahead PV power forecasting.
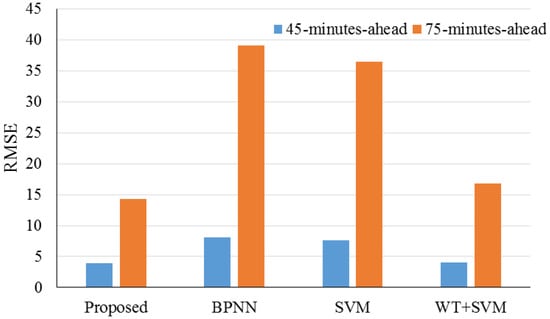
Figure 19.
RMSE values for the study by Wang et al. (2017). Reproduced from [73], Elsevier: 2017.
3.9. Ensemble Methods
Ensemble methods employ multiple learning algorithms in machine learning and statistics, in order to reach the best modeling performance compared any other single learning algorithms. In statistical mechanics, the ensemble method contains only a concrete finite set of alternative models but allows for a flexible architecture to exist among alternative models [74]. Table 11 presents some important papers in this field.

Table 11.
Notable ensemble models used in energy systems.
Burger and Moura (2015) [75] worked on the generalization of electricity demand forecasting by formulating an ensemble learning method to perform model validation. By learning from data streams of electricity demand, this method needed little information about energy end use, which made it desirable for real utilization.
Changfeng et al. (2017) used ensemble empirical mode decomposition (EEMD) and multiclass relevance vector machine for diagnosis of faults of self-validating air data sensing system. The EEMD working principle was highlighted for distinct faults features extraction. The multiclass relevance vector machine was utilized for fault diagnosis in a self-validating air data sensing system. By the failure mode analysis and prototype design of the self-validating air data sensing system, an experimental system was designed to verify the execution of the presented methodology.
Fu (2018) [76] presented an ensemble approach for forecasting of the cooling load of the air-conditioning system. The presented approach was used for deterministic forecasting of the cooling load with high precision. In this approach a deep belief network, empirical mode decomposition, and the ensemble technique were utilized. The data series of the original cooling load was decomposed into several components. The ensemble method was used to mitigate the influence of uncertainties, such as data noise and model uncertainty, on forecasting precision. Figure 20 presents the RMSE values of the study for each season by the employed models.
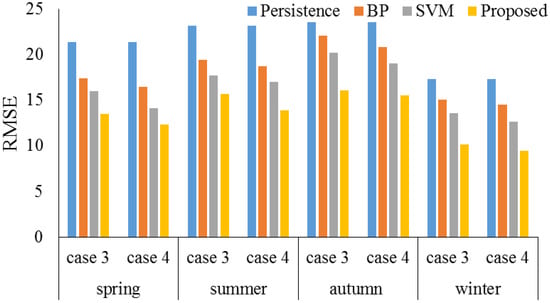
Figure 20.
RMSE values for study by Fu (2018). Reproduced from [76], Elsevier: 2018.
Gjoreski et al. (2015) [77] utilized the ensemble method for estimation of human energy expenditure. In this paper, a multiple contest ensemble method was presented to extract multiple features from the sensor data. Every feature was utilized as a context for building multiple regression models and applying other features as training data. The models related to the feature values in the evaluated sample were assembled regression models ensemble to estimate the energy expenditure of the user. Figure 21 presents the RMSE values of the study for each activity by the employed models.
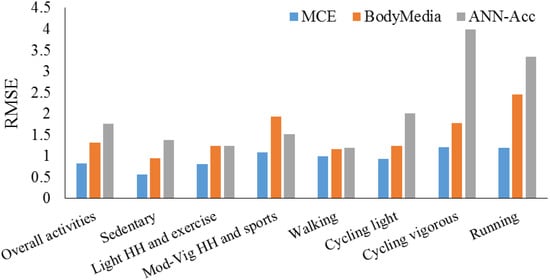
Figure 21.
RMSE values for study by Gjoreski et al. (2015). Reproduced from [77], Elsevier: 2015.
Hasan and Twala (2016) [78] presented an ensemble technique to monitor and predict the underground water dam level. Six different classifier methods were applied for this goal. The paper introduced a new method to select the most appropriate classifiers to construct the most accurate ensemble. This methodology was based on the determination of the amount of mutual information between pairs of classifiers and was utilized to find the optimum number of classifiers to build the most precise ensemble.
3.10. Hybrid ML Models
Hybrid models benefit from multiple ML methods and/or other soft computing and artificial intelligence methods. Data preprocessing and optimization tools have now become common to produce high-accuracy hybrid models for improved prediction capabilities. In these models, usually, one part is for prediction or acts as an estimator, and the other part acts as an optimizer. These models are mainly employed when there is a need for an accurate estimation. ANFIS and WNN are among the early generation of hybrid models [36,79]. Table 12 presents some important papers in this field.

Table 12.
Notable papers of hybrid models in energy systems.
Deng et al. (2018) [80] presented a hybrid short-term load-predicting model optimized by switching delayed particle swarm optimization. In this study, this method was proposed based on switching delayed particle swarm optimization, extreme learning machine with different kernels and empirical mode decomposition. At the first stage, the load database history was decomposed into independent intrinsic mode functions, and the intrinsic mode function sample entropy values were computed. The intrinsic mode function was categorized into three groups. Then the extreme learning machine was applied to predict the three groups. Lastly, the prediction results were gathered to achieve the final prediction result. The experimental results showed that the presented perdition model was robust. Figure 22 presents the RMSE values of the study for each load by the employed models. In this figure, L1, L2, and L3 are user-load datasets for three micro-grids located in Beijing, Yanqing, Guangdong Province, Dong’ao Island, and Xinjiang, Turpan, respectively.
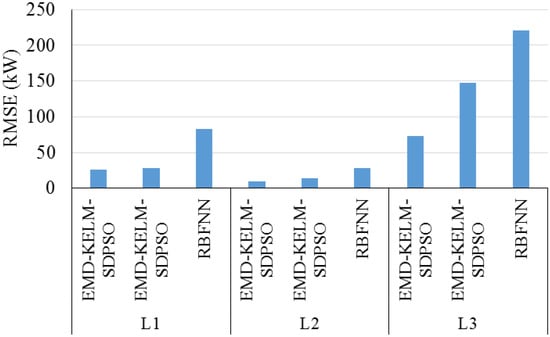
Figure 22.
RMSE values for study by Deng et al. (2018). Reproduced from [80], Elsevier: 2018.
Dou et al. (2016) [81] presented energy management strategies for a microgrid by utilizing a renewable energy source and load prediction. An energy management system based on a two-level multi-agent was built. Then, in the upper-level EMA, strategies of the energy management were constructed by using a PSO method based on renewable energy sources and load probabilistic forecasting. Ensemble empirical mode decomposition coupled with sparse Bayesian learning was used for forecasting of the lower-level renewable energy source and load agents. Simulation results examined the validity of the proposed method.
Peng et al. (2016) [82] introduced a method to hybridize differential empirical mode decomposition and quantum particle swarm optimization algorithm with support vector regression in electric load forecasting. The differential empirical mode decomposition method was applied for decomposing the electric load to several parts related to high frequencies and an approximate part related to low frequencies. The quantum particle swarm optimization algorithm was utilized for optimizing the parameters of support vector regression. The validation of the method demonstrated that it could provide forecasting with good precision and interpretability. Qu et al. (2016) [83] introduced a hybrid model for wind speed forecasting based on fruit fly optimization algorithm and ensemble empirical mode decomposition. The original data of wind speed was divided into a set of signal components using ensemble empirical mode decomposition. Then, the fruit fly optimization algorithm was used to optimize parameters of prediction artificial intelligence models. The final prediction values were acquired by reconstructing the refined series. The empirical results demonstrate that the presented hybrid model was better than some of the existing forecasting models. Figure 23 presents the RMSE values of the study by the employed models.
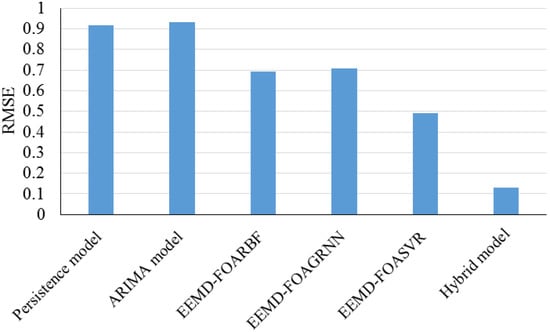
Figure 23.
RMSE values for study by Qu et al. (2016). Reproduced from [83], Elsevier: 2016.
Yang et al. (2017) [84] presented a hybrid model for electricity price forecasting utilizing ARMA, wavelet transform, and KELM methods. SAPSO was applied for searching the optimal kernel parameters. After the test of the wavelet decomposition components, the ARMA model was used to predict stationary series. SAPSO-KELM model. The proposed method performance is validated utilizing electricity price data from several cities. The real data demonstrated that the presented method was more accurate than individual methods. Figure 24 presents the RMSE values of the study for each season by the employed models.
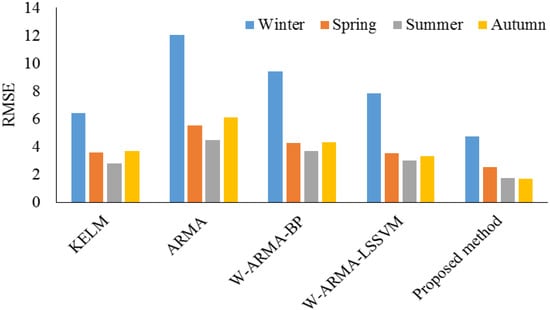
Figure 24.
RMSE values for the study by Yang et al. (2017). Reproduced from [84], Elsevier: 2017.
Renewable energy systems such as wind and solar are site-dependent and highly difficult to predict [7,87,88]. The prediction model using hybrid ML models effectively contributes to increased solar energy production [89]. The economic and environmental aspects of solar photovoltaic as a renewable energy source have caused a significant rise in the number of PV panels in recent years. The high level of computational power and data has empowered ML models for more precise predictions. Due to the significance of prediction in solar photovoltaic power output for decision makers in the energy industry, ML models are employed extensively. Table 13 lists some critical papers in this field.

Table 13.
Notable hybrid ML models in solar energy systems.
David et al. (2016) [90] evaluated performances of a combination of ARMA and GARCH models in econometrics to establish solar irradiance probabilistic forecasts. A testing procedure has been utilized to evaluate probabilistic forecasts and point forecasts. The results are presented in Table 14 and Figure 25.

Table 14.
Results related to the study by David et al. (2016). Reproduced from [90], Elsevier 2016.
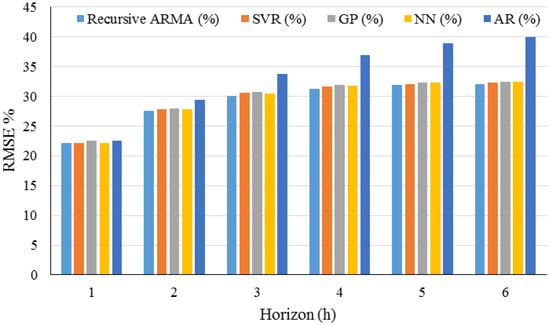
Figure 25.
RMSE values for study by David et al. (2016). Reproduced from [90], Elsevier: 2016.
As is clear from Table 14 and Figure 25, Recursive ARMA has a low value for RMSE compared with other models. Therefore it can be claimed that the presented model can carry out point forecasts as accurately as other models established on machine learning techniques, and the accuracy of the proposed model is same as the other machine learning techniques for both point and probabilistic forecasts.
Feng et al. (2017) [91] incorporated GRNN, RF, ELM, and optimized back propagation GANN to estimate daily Hd for two stations in northern China. All presented artificial models were compared with the empirical model (Table 15 and Figure 26).

Table 15.
Results related to the study by Feng et al. (2017). Reproduced from [91], Elsevier: 2017.
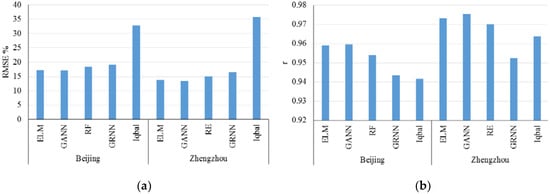
Figure 26.
(a) RMSE and (b) r values for study by Feng et al. (2017). Reproduced from [91], Elsevier: 2017.
Based on Figure 26 and Table 15, the GANN model presents the best accuracy due to its lowest RMSE and highest r values compared with those for others for both Beijing and Zhengzhou stations.
Hassan et al. (2017) [92] presented ensemble models for solar radiation modeling. Gradient boosting, RF and bagging were developed to estimate radiation in hourly and daily time scales. These novel ensemble models were developed to generate synthetic radiation data to be utilized to simulate the performance of solar energy systems with different configurations. Figure 27 presents the results of the study in detail. In this study, D1 is a daily model with day number, sunshine fraction as inputs and horizontal global irradiation as the output of the model. D2 is a daily model with global clearness index, day number as inputs and a diffuse fraction as the output of the model. D3 is a daily model with global clearness index, day number as inputs, and normal clearness index as the output of the model. H1 is an hourly model with horizontal global irradiation, sunshine time, day number as inputs, and horizontal global irradiance as the output of the model. H2 is an hourly model with global clearness index, sunshine fraction, day number as inputs, and a diffuse fraction as the output of the model. H3 is the hourly model with global clearness index, sunshine time, day number as inputs, and normal clearness index as the output of the model.
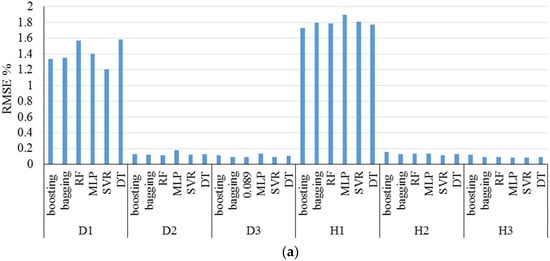
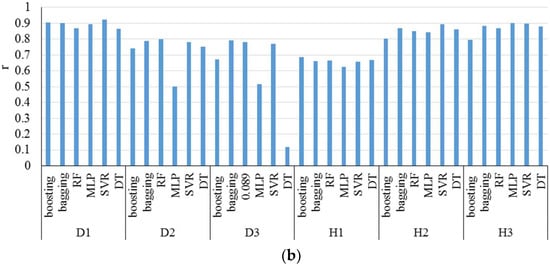
Figure 27.
(a) RMSE and (b) r values for study by Hassan et al. (2017). Reproduced from [92], Elsevier: 2017.
Based on Figure 27, generally, SVR has the best prediction ability compared with the other techniques because it has a high correlation coefficient and a low average RMSE compared with the other models employed by Hassan et al. [14]. Salcedo-Sanz et al. (2018) [93] integrated the CRO with the ELM model in their study. The presented algorithm was applied in two stages. An ELM algorithm was used for the feature selection process, and solar radiation was estimated using the optimally screened variables by the CRO-ELM model (Figure 28).
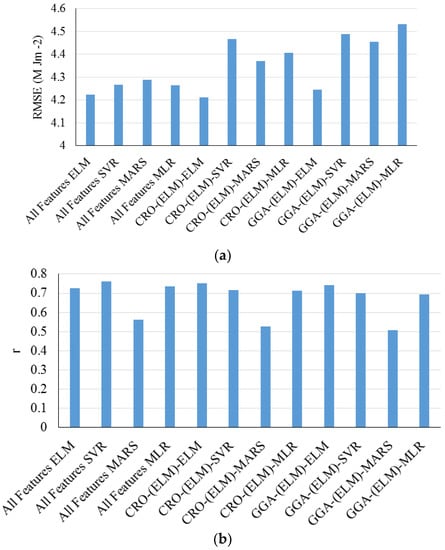
Figure 28.
(a) RMSE and (b) r values for study by Salcedo-Sanz et al. (2018). Reproduced from [93], Elsevier: 2018.
Based on Figure 28, the hybrid CRO-(ELM)-ELM model has the highest accuracy compared with that for hybrid CRO-(ELM)-MLR, CRO-(ELM)-MARS, and CRO-(ELM)-SVR and the GGA models. Generally, the CRO-based hybrid system is carefully screened through a wrapper-based modeling system. The hybrid CRO-(ELM)-ELM model presents clearer advantages compared with the alternative machine learning approaches.
Salcedo-Sanz et al. (2017) [94] studied the prediction of global solar radiation at a given point incorporating a multilayer perceptron trained with extreme learning machines. A coral reefs optimization algorithm with species was used to reduce the number of significant predictive variables. Based on the results (Figure 28), the proposed model (CRO-SP) has been tested by Toledo (Spain) data. The average best result of RMSE was equal to 69.19 (W/m2), which led to higher accuracy of predictions compared with other machine learning techniques. This claim is evident in Figure 29, which presents the average values of RMSE for the four developed techniques.
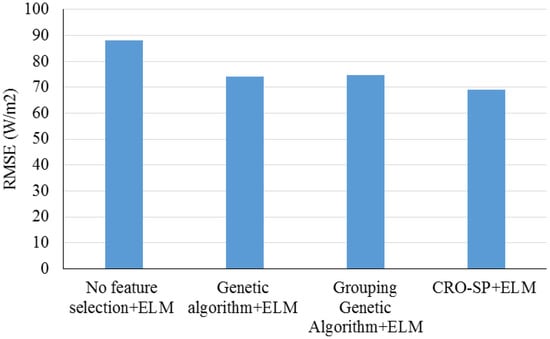
Figure 29.
RMSE values for study by Salcedo-Sanz et al. (2017). Reproduced from [94], Elsevier: 2017.
Touati et al. (2017) [95] predicted output power from photovoltaic panels under different atmospheric conditions. This study’s goal was to investigate photovoltaic performance in the harsh environmental conditions of Qatar. The ML model was used to relate various environmental factors such as irradiance, PV surface temperature, wind speed, temperature, relative humidity, dust, and cumulative dust to power production. Figure 30 presents the results of the analysis with correlation coefficient.
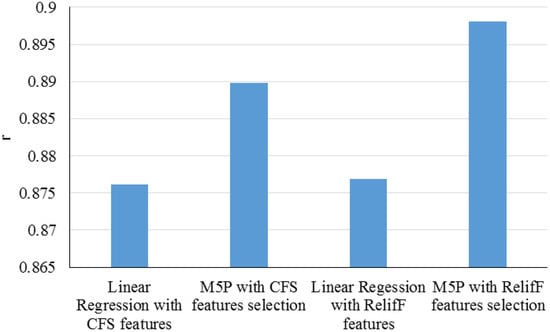
Figure 30.
Correlation coefficient values for study by Touati et al. (2017). Reproduced from [95], the Elsevier: 2017.
As is clear from Figure 30, Linear Regression and M5P tree decision algorithms have been developed for prediction proposes equipped with CFS and RelifF to select subsets of relevant and high-quality features. Based on the results, the M5P model equipped with RelifF creates more accurate predictions due to its high correlation coefficient value; on the other hand, the developed models are relatively simple and can be readily equipped to predict PV power output.
Voyant et al. (2017) [96] proposed models based on the Kalman filter to forecast global radiation time series without utilizing historical data. These methodologies were compared with other data-driven models with different time steps using RMSE values. The results claimed that the proposed model improved the prediction purposes. Voyant et al. (2017) [97] presented a method to better understand the propagation of uncertainty in the global radiation time series. In this study, the reliability index has been defined to evaluate the validity of predictions. The presented method has been applied to several meteorological stations. The comparisons were performed using RMSE factor. The results were promising for successfully applying in these stations in the Mediterranean area.
There are many novel hybrid ML models proposed to forecast solar radiation. Hybrids of the ANN method have often been used for this purpose and SVM and SVR are being used more extensively nowadays. SVM and SVR usually have the same forecasting performance. Also, the ensemble models were reported to generally deliver higher performance. SVR, GP, and NN have better forecasting performance than AR in forecasting solar radiation. The RMSE values of ELM, GANN, RF, and GRNN [18] shows that there is no meaningful difference between them in terms of forecasting performance.
In order to integrate highly volatile wind power in a power grid, precise forecasting of wind speed is crucial. This would result in less of a need to control the energy provided by wind, having battery loading strategies and planning reserve plants. ML models can predict a time interval from seconds to hours and, as a result, are essential for energy grid balancing. Table 16 shows some critical papers in this field. The estimation of the total power collected from wind turbines in a wind farm depends on several factors such as the location, hub height, and season. Cornejo-Bueno et al. (2017) [98] applied different machine learning regression techniques to predict WPREs. Variables from atmospheric reanalysis data were used as predictive inputs for the learning machine. RMSE was employed as a comparison factor among the developed models. The results have been presented in Figure 31. In general, GPR followed by MLP has the lowest RMSE compared with SVR and ELM for each farm. This shows the high prediction capability of GPR and MLP models, in line with the purpose of the study.

Table 16.
Notable hybrid ML models in wind energy systems.
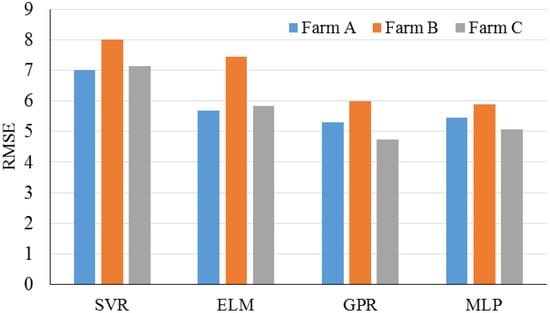
Figure 31.
RMSE values for study by Cornejo-Bueno et al. (2017). Reproduced from [98], Elsevier: 2017.
Accurate forecasting of WPREs is necessary for the efficient integration of a wind farm into an electricity system [103]. Khosravi et al. (2018) [99] developed models based on a group model of data handling type neural network, adaptive neuro-fuzzy inference system, ANFIS optimized with an ant colony, ANFIS optimized with particle swarm optimization algorithm, ANFIS optimized with genetic algorithm, and multilayer feed-forward neural network. Day, month, average air temperature, minimum and maximum air temperature, air pressure, wind speed, relative humidity, latitude, longitude, and top of atmosphere insolation. The group method of data handling-type neural network was the best-developed model. Figure 32 demonstrates the RMSE and correlation coefficient for each model for making the best comparison.
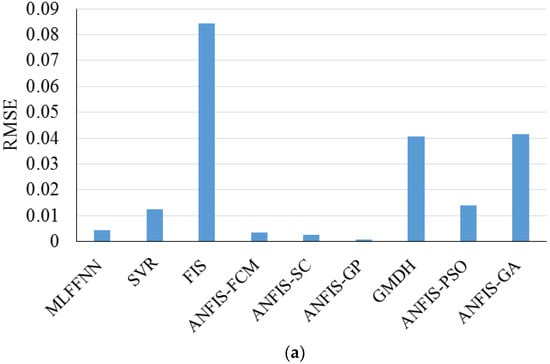
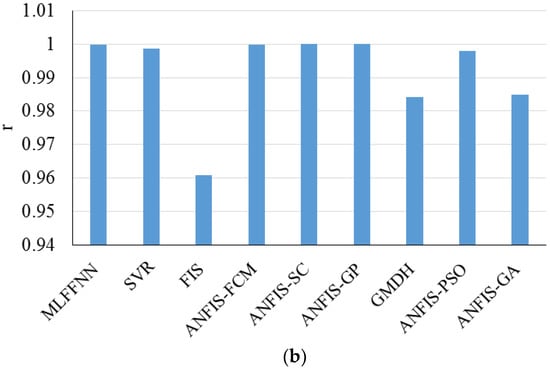
Figure 32.
(a) RMSE and (b) r values for study by Khosravi et al. (2018). Reproduced from [99], Elsevier: 2018.
Burlando et al. (2017) [100] compared a pure ANN model and a hybrid model. Both models had similar performance. Both models were validated against the wind farm SCADA data. However, the hybrid model made better predictions during high and low ranges of wind speed, and ANN better predicted medium wind speed ranges. The results were compared using the normalized root mean square error and the normalized mean absolute error. The best results (the lowest value of comparison factors) were calculated for NWP height of 100 and 200 m for both layout 1 and 2.
Pandit and Infield (2018) [101] performed a study to reduce the costs of operation and maintenance of the wind turbine. Predictive condition monitoring based on SCADA was applied to identify early failures, boost production, limit downtime, and lower the energy cost. A Gaussian Process algorithm was presented to roughly calculate operational curves, which can be utilized as a reference model to recognize critical failures of the wind turbine and enhance power performance. Figure 33 presents the correlation coefficient for the prediction results of four variables using Gaussian process compared with the target values. Based on Figure 33, this model successfully estimated the power curve compared with other variables. Sharifian et al. (2018) [102] presented a new model based on the fuzzy neural network to forecast wind power under uncertain data conditions. The proposed model was established using a particle swarm optimization algorithm. This model was based on the neural network’s learning and expert knowledge of the fuzzy system. The presented model was validated against a real wind farm. The results are presented in Figure 34 using RMSE values for each case study. As is evident, RMSE for the first case study has the lowest value and for the fifth case study has the highest value. Therefore, it can be claimed that the precision of the employed model for the first case study is higher than that of other case studies.
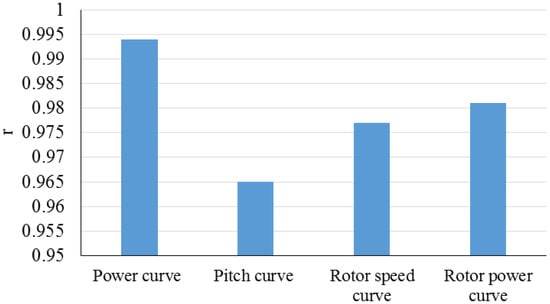
Figure 33.
Correlation coefficient values for study by Pandit and Infield (2018). Reproduced from [101], Elsevier: 2018.
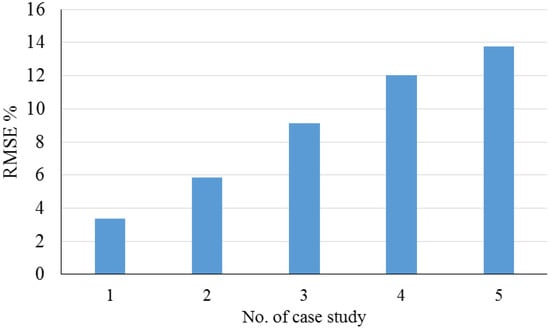
Figure 34.
RMSE values for study by Sharifian et al. (2018). Reproduced from [102], Elsevier: 2018.
For proper integration of wind power into the power grid, a high-performance forecasting model to compute the forecasting of wind speed at a reasonable speed is needed. It can be concluded that the multilayer perceptron ANN model has better forecasting performance for wind speed than SVM and regression trees [25]. Also, hybrid models such as the ANFIS model have better performance than SVR models. For wind speed forecasting, the hybridization of ANFIS with GP has better performance than its hybridization with PSO and GA [26].
ML models can provide accurate energy consumption and demand prediction, and can be used at the managerial level such as by building commissioning project managers, utility companies, and facilities managers to introduce energy-saving policies. Table 17 demonstrates some critical papers in this field.

Table 17.
Notable hybrid ML models in energy consumption and demand prediction.
Albert and Maasoumy (2016) [104] presented a predictive segmentation technique to create the targeting process and highly-interpretable segmentation for energy companies. The presented model utilized demographics, consumption and program enrollment data to make predictive patterns. This model displayed homogeneous segments that were 2- to 3-fold more productive for targeting. Alobaidi et al. (2018) [105] proposed an ensemble learning framework for household energy consumption forecasting. In this paper, a prediction framework was presented to predict individual household average daily energy consumption. The results showed the robustness of the proposed ensemble model to provide prediction performance using limited data. Figure 35 presents the results of RMSE for each model separately.
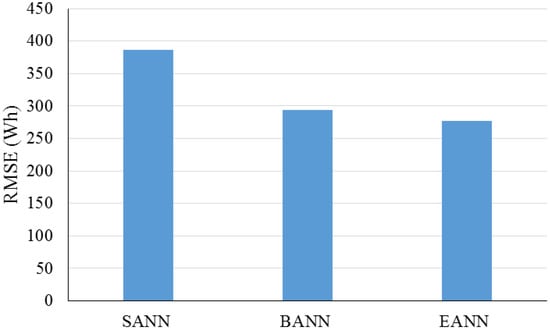
Figure 35.
RMSE values for study by Alobaidi et al. (2018). Reproduced from [105], Elsevier: 2018.
Benedetti et al. (2016) [106] introduced a new methodology for control automation of energy consumption utilizing adaptive algorithms and artificial neural networks. Three neural network structures were presented and trained to deal with an enormous amount of data. Three indicators were used to identify the best structure for creating a control tool for energy consumption. The accuracy of the model was investigated. Finally, the model was applied to a case study of a building in Rome, Italy.
Chen et al. (2018) [107] worked on a novel approach for predicting residential electricity consumption using ensemble learning. In this study, a data-driven framework was introduced to forecast the annual electricity consumption of household utilizing ensemble learning model. Ridge regression was used to combine feed-forward deep networks and extreme gradient boosting forest. Figure 36 presents the results of the study in comparison with those of the other models. As is clear from Figure 36, the proposed models have the highest accuracy with the lowest RMSE in comparison with the other models.
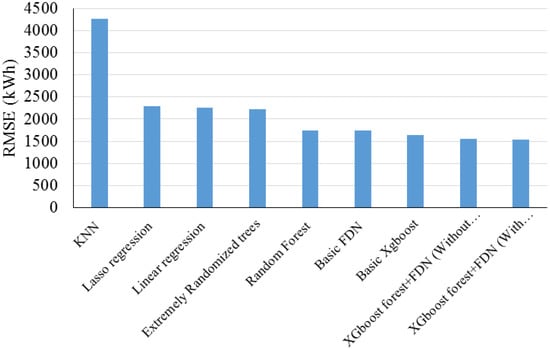
Figure 36.
RMSE values for the study by Chen et al. (2018). Reproduced from [107], Elsevier: 2018.
Kuroha et al. (2018) [108] presented an operational planning model for residential air conditioners. In this study, the focus was on automatic air conditioners for thermal comfort improvement and electricity cost reduction. An energy management methodology was introduced to provide an air conditioner operation plan by learning the installation environment characteristics from result data of the historic operation. Based on the results, the proposed model could reduce the electricity cost about 39.7% compared with that for the benchmark method.
The type of data that is available today is continuously evolving. Some data already encode information that is used as proxy metrics to predict energy consumption in buildings. For example, geometry, size, and height can be used to predict energy consumption in buildings. Wang et al. [109] developed the Unige Building Identifier to correspond attribute data and building energy to smooth the way for corresponding across datasets. Depecker et al. [110] matched the consumption of heating of the buildings and their shape. In this study, the criterion for the shape of buildings was presented. Fourteen buildings were chosen based on their shape varieties. The results demonstrated that the energy consumption of buildings is inversely proportionate to the building’s compactness. Qi and Wang [111] introduced a novel model for calculation of shape coefficient of buildings utilizing Google Earth. Astronomy principles, geometry, and GIS slope analysis were used for calculation of shape coefficient of buildings. This new model can be used for energy-saving measures in existing buildings.
ML and big data have led to believe that personally identifiable information is released when predicting energy patterns, and so forth. However, this is not often the case. The following studies show how to protect data privacy while predicting and disclosing information about energy in commercial buildings. Livingston et al. [112] presented a solution to measure the impact of modifying the utility meter aggregation threshold for dweller privacy and on buildings that are qualified for energy usage reporting. As the threshold rises, lesser buildings are qualified for disclosure of energy use data. This paper’s goal was to study the resemblance between whole-building totals and individual utility meters at various aggregation levels. Sweeney et al. [113] proposed a solution for data privacy. The solution included a formal protection model titled k-anonymity as a series of accompanying policies. For this definition of privacy, in a k-anonymized dataset, every record is identical from at least k-1 other records. Machanavajjhala et al. [114] studied two problems about k-anonymity; little diversity in sensitive attributes and background knowledge of attackers. They introduced a new privacy criterion called l-diversity that can shield against such attacks. The hybridization of ML models in energy demand field demonstrated that the accuracy of energy demand forecasting could improve significantly. Also, an ensemble model has significantly higher generalization ability than ANN and SVM models, and it has a lower uncertainty of forecasting [7,32].
3.11. Comparative Analysis of ML Models
Table 18 provides a comparative study of ML models and deep learning for prediction in different energy systems. In this table, the complexity of ML models, user-friendliness, accuracy, speed, and dataset type are summarized. Hybrid ML models are reported to be superior in terms of user-friendliness, accuracy, and speed. However, the complexity of their methodologies has increased.

Table 18.
Comparative study of ML models in energy systems.
There is not any meaningful difference in the forecasting performance of SVR, GP, and NN models [17]. Therefore, their quality of forecasting is the same. Considering the reviewed papers, these models have the same statistics of error. Also, SVM and SVR have similar performance, with no statistical forecasting performance difference among them. SVR models have lower forecasting performance than ELM, GPR, and MLP models [20]. Decision Tree models have a lower fluctuation of performance than SVM and NN models for quarter-hourly, daily, and weekly periods [46]. The RMSE value of SVM models are higher than the MLP models, and therefore it has lower forecasting performance [52]. The hybrid models have a lower RMSE value than ARIMA, EEMD-FOASVR, and EEMD-FOAGRNN [96]. Hybridizing existing methodologies and algorithm ensemble are among the most effective ways to improve the ML models.
4. Conclusions
Smart sensors, smart grid, and IoT technologies have enabled big data with new challenges and opportunities to the energy systems. The ML models have gained popularity in putting big data in the constructive use for informed-decision and more efficient models. The state of the art of ML models in energy systems identified 10 groups of ML algorithms with the highest popularity for model building in energy systems, i.e., ANN, MLP, ELM, SVM, WNN, ANFIS, decision trees, deep learning, ensembles, and advanced hybrid ML models. Diverse applications of each ML models have been reviewed showing the popularity and effectiveness of ML models almost in any energy domain. The example application of ML models include energy consumption prediction, demand prediction, cost prediction, wind speed estimation, load forecasting, solar radiation prediction, ranking, various optimization tasks, power generation forecasting, power quality estimation, time series forecasting, load perdition, wind speed forecasting, power demand prediction, risk prediction, storage planning, energy control, peak load management, dynamic energy pricing, cost minimization, battery charge estimation, price prediction and more. Further investigation of the accuracy and generalization ability of the various ML models suggested that novel hybrid models are superior to the more conventional ML models. The trend in advancement of hybrid ML models will continue to deliver higher performance and sophisticated energy models.
The progress of renewable energy systems is dependent on the advancement of ML models. Note that renewable energy systems have recently gained popularity due to climate protection and sustainability concerns, so it is more acceptable to extract energy from the wind, sun, and other renewable energy resources. The central aspect of all renewable energy resources is their dependence on the environment and huge barriers to controlling and planning. Furthermore, due to the expansion of the electricity grid, it is necessary to forecast power generation and demand. Nevertheless, fluctuations in wind and solar energies and energy demand have a negative impact on the grid and its users if not managed properly. Therefore, ML models have become essential in such energy systems. The review of these particular applications has demonstrated the promising robustness of the ML models. Based on the results, the research direction is moving toward personalized ML models designed for a particular application. This trend has shown that the highest degree of accuracy can be achieved though case-based ML model development. Although the hybrid ML models are reported as the optimal choice and the future trend in energy systems, further evaluation and comparison of various hybrid ML models are essential, considering alternative comparative performance parameters besides the RMSE and r.
Author Contributions
Review, data curation and analyzing the results, M.S., A.M., and S.F.A.; energy expertise, M.S., T.R., S.S., and A.V.-K.; machine learning expertise, A.M., S.S., A.V.-K., and S.F.A.; management, database, conceptualization, writing, administration and methodology, A.M.; visualization, S.F.A.; supervision, resources, software, expertise, revision, and verifying the results, S.S., A.V.-K. and T.R.
Conflicts of Interest
The authors declare no conflict of interest.
Acronyms
| AR | Autoregressive |
| ARMA | Autoregressive Moving Average |
| ANNs | Artificial Neural Networks |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| BANN | Back Propagation Neural Network |
| BP | Back Propagation |
| CFS | Correlation based Feature Selection |
| CGP | Cartesian Genetic Programming |
| CRBM | Conditional Restricted Boltzmann Machines |
| CRO | Coral Reefs Optimization |
| CWNN | Convolutional-Wavelet Neural Networks |
| DL | Deep Learning |
| DOPH | Direct Optimum Parallel Hybrid |
| DT | Decision trees |
| EANN | Evolutionary Artificial neural networks |
| EEMD | Ensemble Empirical Mode Decomposition |
| ELM | Extreme Learning Machine |
| EMD | Empirical Mode Decomposition |
| FCRBM | Factored Conditional Restricted Boltzmann Machine |
| FFNN | Feed Forward Neural Network |
| FIS | Fuzzy inference system |
| FOARBF | Fruit Fly Optimization Algorithm Radial Basis Function |
| FOAGRNN | Fruit Fly Optimization Algorithm Generalized Regression Neural Networks |
| FOASVR | Fruit Fly Optimization Algorithm Support Vector Regression |
| GA | Genetic Algorithm |
| GANN | Neural Networks by Genetic Algorithm |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| GHG | Greenhouse Gas |
| GFF | General Factorization Framework |
| GP | Gaussian Processes |
| GPR | Gaussian Processes Regression |
| GRNN | Generalized Regression Neural Networks |
| IDSS | Intelligent Decision Support System |
| IoT | Internet of Things |
| KELM | kernel-based extreme learning machine |
| KFCM | Kernel Fuzzy C Means |
| KNN | K-Nearest Neighbors |
| LM | Levenberg-Marquardt |
| MARS | Multivariate Adaptive Regression Splines |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MR | Multi-Resolution |
| MLR | Multiple linear regression |
| MTL | Method of transmission lines |
| MRWNN | Multi-Resolution Wavelet Neural Network |
| NARX | Nonlinear Auto-Regressive with external input |
| NDP | Neuro-Dynamic Programming |
| NN | Neural Networks |
| NWP | Numerical Weather Prediction |
| OLR | Outgoing long-wave radiation |
| PR | Persistence model |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| r | Correlation coefficient |
| RBF | Radial Basis Function |
| RBFNN | Radial Basis Function Neural Networks |
| RF | Random Forests |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| SANN | Subsequent Artificial Neural Networks |
| SAPSO | Self-Adaptive Particle Swarm Optimization |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SCADA | Supervisory Control and Data Acquisition |
| SCG | Scaled Conjugate Gradient |
| SE | Solar radiation |
| SEAT | A car manufacturing plant in Spain |
| SOC | State of Charge |
| SOFM | Self-Organizing Feature Map |
| SVM | Support Vector Machine |
| SP | Coral Reefs Optimization algorithm with species |
| SVR | Support vector regression |
| WPRE | Wind Power Ramp Events |
| WNN | Wavelet Neural Network |
References
- Deshmukh, M.; Deshmukh, S. Modeling of hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- Elgerd, O.I. Electric Energy Systems Theory: An introduction; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Gomez-Exposito, A.; Conejo, A.J.; Canizares, C. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Quaschning, V. Understanding Renewable Energy Systems; Routledge: Abingdon, UK, 2016. [Google Scholar]
- Isabella, O.; Smets, A.; Jäger, K.; Zeman, M.; van Swaaij, R. Solar Energy: The Physics and Engineering of Photovoltaic Conversion, Technologies and Systems; UIT Cambridge Limited: Cambridge, UK, 2016. [Google Scholar]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Torabi, M.; Hashemi, S.; Saybani, M.R.; Shamshirband, S.; Mosav, A. A Hybrid clustering and classification technique for forecasting short-term energy consumption. Environ. Prog. Sustain. Energy 2018, 38, 66–76. [Google Scholar] [CrossRef]
- Najafi, B.; Faizollahzadeh Ardabili, S.; Mosavi, A.; Shamshirband, S.; Rabczuk, T. An Intelligent Artificial Neural Network-Response Surface Methodology Method for Accessing the Optimum Biodiesel and Diesel Fuel Blending Conditions in a Diesel Engine from the Viewpoint of Exergy and Energy Analysis. Energies 2018, 11, 860. [Google Scholar] [CrossRef]
- Hosseini Imani, M.; Zalzar, S.; Mosavi, A.; Shamshirband, S. Strategic behavior of retailers for risk reduction and profit increment via distributed generators and demand response programs. Energies 2018, 11, 1602. [Google Scholar] [CrossRef]
- Dineva, A; Mosavi, A.; Ardabili, S.F.; Vajda, I.; Shamshirband, S.; Rabczuk, T.; Chau, K.-W. Review of soft computing models in design and control of rotating electrical machines. Energies 2019, 12, 1049. [Google Scholar] [CrossRef]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K.; Isa, D. Hybrid energy storage systems and control strategies for stand-alone renewable energy power systems. Renew. Sustain. Energy Rev. 2016, 66, 174–189. [Google Scholar] [CrossRef]
- Curry, N.; Pillay, P. Biogas prediction and design of a food waste to energy system for the urban environment. Renew. Energy 2012, 41, 200–209. [Google Scholar] [CrossRef]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1483–1488. [Google Scholar]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment. J. Atmos. Sol.-Terr. Phys. 2017, 155, 62–70. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Applications of artificial neural-networks for energy systems. Appl. Energy 2000, 67, 17–35. [Google Scholar] [CrossRef]
- Faizollahzadeh Ardabili, S.; Najafi, B.; Alizamir, M.; Mosavi, A.; Shamshirband, S.; Rabczuk, T. Using SVM-RSM and ELM-RSM Approaches for Optimizing the Production Process of Methyl and Ethyl Esters. Energies 2018, 11, 2889. [Google Scholar] [CrossRef]
- Al-Jarrah, O.Y.; Yoo, P.D.; Muhaidat, S.; Karagiannidis, G.K.; Taha, K. Efficient machine learning for big data: A review. Big Data Res. 2015, 2, 87–93. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Peng, Y.; Rysanek, A.; Nagy, Z.; Schlüter, A. Using machine learning techniques for occupancy-prediction-based cooling control in office buildings. Appl. Energy 2018, 211, 1343–1358. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Robinson, C.; Dilkina, B.; Hubbs, J.; Zhang, W.; Guhathakurta, S.; Brown, M.A.; Pendyala, R.M. Machine learning approaches for estimating commercial building energy consumption. Appl. Energy 2017, 208, 889–904. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Mosavi, A.; Lopez, A.; Varkonyi-Koczy, A.R. Industrial applications of big data: State of the art survey. In Proceedings of the International Conference on Global Research and Education, Iași, Romania, 25–28 September 2017; pp. 225–232. [Google Scholar]
- Qasem, S.N.; Samadianfard, S.; Nahand, H.S.; Mosavi, A.; Shamshirband, S.; Chau, K.W. Estimating Daily Dew Point Temperature Using Machine Learning Algorithms. Water 2019, 11, 582. [Google Scholar] [CrossRef]
- Najafi, B.; Ardabili, S.F. Application of ANFIS, ANN, and logistic methods in estimating biogas production from spent mushroom compost (SMC). Resour. Conserv. Recycl. 2018, 133, 169–178. [Google Scholar] [CrossRef]
- Faizollahzadeh Ardabili, S.; Najafi, B.; Ghaebi, H.; Shamshirband, S.; Mostafaeipour, A. A novel enhanced exergy method in analyzing HVAC system using soft computing approaches: A case study on mushroom growing hall. J. Build. Eng. 2017, 13, 309–318. [Google Scholar] [CrossRef]
- Abbas, F.; Habib, S.; Feng, D.; Yan, Z. Optimizing Generation Capacities Incorporating Renewable Energy with Storage Systems Using Genetic Algorithms. Electronics 2018, 7, 100. [Google Scholar] [CrossRef]
- Anwar, M.B.; El Moursi, M.S.; Xiao, W. Novel Power Smoothing and Generation Scheduling Strategies for a Hybrid Wind and Marine Current Turbine System. IEEE Trans. Power Syst. 2017, 32, 1315–1326. [Google Scholar] [CrossRef]
- Boukelia, T.; Arslan, O.; Mecibah, M. Potential assessment of a parabolic trough solar thermal power plant considering hourly analysis: ANN-based approach. Renew. Energy 2017, 105, 324–333. [Google Scholar] [CrossRef]
- Chatziagorakis, P.; Ziogou, C.; Elmasides, C.; Sirakoulis, G.C.; Karafyllidis, I.; Andreadis, I.; Georgoulas, N.; Giaouris, D.; Papadopoulos, A.I.; Ipsakis, D. Enhancement of hybrid renewable energy systems control with neural networks applied to weather forecasting: The case of Olvio. Neural Comput. Appl. 2016, 27, 1093–1118. [Google Scholar] [CrossRef]
- Gallagher, C.V.; Bruton, K.; Leahy, K.; O’Sullivan, D.T. The suitability of machine learning to minimise uncertainty in the measurement and verification of energy savings. Energy Build. 2018, 158, 647–655. [Google Scholar] [CrossRef]
- Faizollahzadeh Ardabili, S.; Mahmoudi, A.; Mesri Gundoshmian, T. Modeling and simulation controlling system of HVAC using fuzzy and predictive (radial basis function, RBF) controllers. J. Build. Eng. 2016, 6, 301–308. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Mohammadzadeh, S.D.; Shamshirband, S.; Hajikhodaverdikhan, P.; Mosavi, A.; Chau, K.W. Prediction of remaining service life of pavement using an optimized support vector machine. Eng. Appl. Comput. Fluid Mech. 2019, 13, 188–198. [Google Scholar]
- Faizollahzadeh Ardabili, S.; Najafi, B.; Shamshirband, S.; Minaei Bidgoli, B.; Deo, R.C.; Chau, K.-w. Computational intelligence approach for modeling hydrogen production: A review. Eng. Appl. Comput. Fluid Mech. 2018, 12, 438–458. [Google Scholar] [CrossRef]
- Ahmad, A.; Anderson, T.; Lie, T. Hourly global solar irradiation forecasting for New Zealand. Sol. Energy 2015, 122, 1398–1408. [Google Scholar] [CrossRef]
- Chahkoutahi, F.; Khashei, M. A seasonal direct optimal hybrid model of computational intelligence and soft computing techniques for electricity load forecasting. Energy 2017, 140, 988–1004. [Google Scholar] [CrossRef]
- Kazem, H.A.; Yousif, J.H. Comparison of prediction methods of photovoltaic power system production using a measured dataset. Energy Convers. Manag. 2017, 148, 1070–1081. [Google Scholar] [CrossRef]
- Loutfi, H.; Bernatchou, A.; Tadili, R. Generation of Horizontal Hourly Global Solar Radiation From Exogenous Variables Using an Artificial Neural Network in Fes (Morocco). Int. J. Renew. Energy Res. (IJRER) 2017, 7, 1097–1107. [Google Scholar]
- Shimray, B.A.; Singh, K.; Khelchandra, T.; Mehta, R. Ranking of Sites for Installation of Hydropower Plant Using MLP Neural Network Trained with GA: A MADM Approach. Comput. Intell. Neurosci. 2017, 2017, 4152140. [Google Scholar] [CrossRef] [PubMed]
- Arat, H.; Arslan, O. Optimization of district heating system aided by geothermal heat pump: A novel multistage with multilevel ANN modelling. Appl. Therm. Eng. 2017, 111, 608–623. [Google Scholar] [CrossRef]
- Bagnasco, A.; Fresi, F.; Saviozzi, M.; Silvestro, F.; Vinci, A. Electrical consumption forecasting in hospital facilities: An application case. Energy Build. 2015, 103, 261–270. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Z.; Xia, X. Estimate and characterize PV power at demand-side hybrid system. Appl. Energy 2018, 218, 66–77. [Google Scholar] [CrossRef]
- Premalatha, N.; Valan Arasu, A. Prediction of solar radiation for solar systems by using ANN models with different back propagation algorithms. J. Appl. Res. Technol. 2016, 14, 206–214. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Performance prediction of a solar thermal energy system using artificial neural networks. Appl. Therm. Eng. 2014, 73, 1348–1359. [Google Scholar] [CrossRef]
- Arabloo, M.B.A.; Ghiasi, M.M.; Lee, M.; Abbas, A.; Zendehboudi, S. A novel modeling approach to optimize oxygen-steam ratios in coal gasification process. Fuel 2015, 153. [Google Scholar] [CrossRef]
- Arikan, C.; Ozdemir, M. Classification of power quality disturbances at power system frequency and out of power system frequency using support vector machines. Prz. Elektrotech 2013, 89, 284–291. [Google Scholar]
- Ma, J.; Jiang, H.; Huang, K.; Bi, Z.; Man, K.L. Novel Field-Support Vector Regression-Based Soft Sensor for Accurate Estimation of Solar Irradiance. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 3183–3191. [Google Scholar] [CrossRef]
- Özdemir, S.; Demirtas, M.; Aydin, S. Harmonic estimation based support vector machine for typical power systems. Neural Netw. World 2016, 26, 233–252. [Google Scholar] [CrossRef]
- Pinto, T.; Sousa, T.M.; Praça, I.; Vale, Z.; Morais, H. Support Vector Machines for decision support in electricity markets’ strategic bidding. Neurocomputing 2016, 172, 438–445. [Google Scholar] [CrossRef]
- Zhang, J.; Walter, G.G.; Miao, Y.; Lee, W.N.W. Wavelet neural networks for function learning. IEEE Trans. Signal Process. 1995, 43, 1485–1497. [Google Scholar] [CrossRef]
- Doucoure, B.; Agbossou, K.; Cardenas, A. Time series prediction using artificial wavelet neural network and multi-resolution analysis: Application to wind speed data. Renew. Energy 2016, 92, 202–211. [Google Scholar] [CrossRef]
- Gu, J.; Wang, J.; Qi, C.; Min, C.; Sundén, B. Medium-term heat load prediction for an existing residential building based on a wireless on-off control system. Energy 2018, 152, 709–718. [Google Scholar] [CrossRef]
- He, Q.; Wang, J.; Lu, H. A hybrid system for short-term wind speed forecasting. Appl. Energy 2018, 226, 756–771. [Google Scholar] [CrossRef]
- Qin, F.; Li, W.; Hu, Y.; Xu, G. An Online Energy Management Control for Hybrid Electric Vehicles Based on Neuro-Dynamic Programming. Algorithms 2018, 11, 33. [Google Scholar] [CrossRef]
- Sarshar, J.; Moosapour, S.S.; Joorabian, M. Multi-objective energy management of a micro-grid considering uncertainty in wind power forecasting. Energy 2017, 139, 680–693. [Google Scholar] [CrossRef]
- Hadi Abdulwahid, A.; Wang, S. A Novel Method of Protection to Prevent Reverse Power Flow Based on Neuro-Fuzzy Networks for Smart Grid. Sustainability 2018, 10, 1059. [Google Scholar] [CrossRef]
- Bassam, A.; May Tzuc, O.; Escalante Soberanis, M.; Ricalde, L.; Cruz, B. Temperature estimation for photovoltaic array using an adaptive neuro fuzzy inference system. Sustainability 2017, 9, 1399. [Google Scholar] [CrossRef]
- Kampouropoulos, K.; Andrade, F.; Sala, E.; Espinosa, A.G.; Romeral, L. Multiobjective optimization of multi-carrier energy system using a combination of ANFIS and genetic algorithms. IEEE Trans. Smart Grid 2018, 9, 2276–2283. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.; Mansor, Z. Identifying the most significant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Sajjadi, B.; Raman, A.A.A.; Parthasarathy, R.; Shamshirband, S. Sensitivity analysis of catalyzed-transesterification as a renewable and sustainable energy production system by adaptive neuro-fuzzy methodology. J. Taiwan Inst. Chem. Eng. 2016, 64, 47–58. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Mosavi, A.; Shamshirband, S.; Kazimieras Zavadskas, E.; Rakotonirainy, A.; Chau, K.W. Sustainable Business Models: A Review. Sustainability 2019, 11, 1663. [Google Scholar] [CrossRef]
- Aguado, J.A.; Racero, A.J.S.; de la Torre, S. Optimal operation of electric railways with renewable energy and electric storage systems. IEEE Trans. Smart Grid 2018, 9, 993–1001. [Google Scholar] [CrossRef]
- Costa, D.C.; Nunes, M.V.; Vieira, J.P.; Bezerra, U.H. Decision tree-based security dispatch application in integrated electric power and natural-gas networks. Electr. Power Syst. Res. 2016, 141, 442–449. [Google Scholar] [CrossRef]
- Kamali, S.; Amraee, T. Blackout prediction in interconnected electric energy systems considering generation re-dispatch and energy curtailment. Appl. Energy 2017, 187, 50–61. [Google Scholar] [CrossRef]
- Moutis, P.; Skarvelis-Kazakos, S.; Brucoli, M. Decision tree aided planning and energy balancing of planned community microgrids. Appl. Energy 2016, 161, 197–205. [Google Scholar] [CrossRef]
- Ottesen, S.Ø.; Tomasgard, A.; Fleten, S.-E. Prosumer bidding and scheduling in electricity markets. Energy 2016, 94, 828–843. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Coelho, I.M.; Coelho, V.N.; Luz, E.J.d.S.; Ochi, L.S.; Guimarães, F.G.; Rios, E. A GPU deep learning metaheuristic based model for time series forecasting. Appl. Energy 2017, 201, 412–418. [Google Scholar] [CrossRef]
- Kim, J.; Le, T.-T.-H.; Kim, H. Nonintrusive load monitoring based on advanced deep learning and novel signature. Comput. Intell. Neurosci. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, X. Ensemble learning via negative correlation. Neural Netw. 1999, 12, 1399–1404. [Google Scholar] [CrossRef]
- Burger, E.M.; Moura, S.J. Gated ensemble learning method for demand-side electricity load forecasting. Energy Build. 2015, 109, 23–34. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Gjoreski, H.; Kaluža, B.; Gams, M.; Milić, R.; Luštrek, M. Context-based ensemble method for human energy expenditure estimation. Appl. Soft Comput. 2015, 37, 960–970. [Google Scholar] [CrossRef]
- Hasan, A.N.; Twala, B. Mine’s Pump Station Energy consumption and Underground Water Dam Levels Monitoring System Using Machine Learning Classifiers and Mutual Information Ensemble Technique. Int. J. Innov. Comput. Inf. CONTROL 2016, 12, 1777–1789. [Google Scholar]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.-w.; Faizollahzadeh Ardabili, S.; Piran, M.J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef]
- Deng, B.; Peng, D.; Zhang, H.; Qian, Y. An intelligent hybrid short-term load forecasting model optimized by switching delayed PSO of micro-grids. J. Renew. Sustain. Energy 2018, 10, 024901. [Google Scholar] [CrossRef]
- Dou, C.-X.; An, X.-G.; Yue, D. Multi-agent system based energy management strategies for microgrid by using renewable energy source and load forecasting. Electr. Power Compon. Syst. 2016, 44, 2059–2072. [Google Scholar] [CrossRef]
- Peng, L.-L.; Fan, G.-F.; Huang, M.-L.; Hong, W.-C. Hybridizing DEMD and quantum PSO with SVR in electric load forecasting. Energies 2016, 9, 221. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, K.; Wang, J.; Zhang, W.; Leng, W. A hybrid model based on ensemble empirical mode decomposition and fruit fly optimization algorithm for wind speed forecasting. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.-W. Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System. Energies 2019, 12, 289. [Google Scholar] [CrossRef]
- Mosavi, A.; Rituraj, R.; Varkonyi-Koczy, A.R. Review on the Usage of the Multiobjective Optimization Package of modeFrontier in the Energy Sector. In Proceedings of the International Conference on Global Research and Education, Iași, Romania, 25–28 September 2017; pp. 217–224. [Google Scholar]
- Moeini, I.; Ahmadpour, M.; Mosavi, A.; Alharbi, N.; Gorji, N.E. Modeling the time-dependent characteristics of perovskite solar cells. Sol. Energy 2018, 170, 969–973. [Google Scholar] [CrossRef]
- Mosavi, A.; Torabi, M.; Ozturk, P.; Varkonyi-Koczy, A.; Istvan, V. A hybrid machine learning approach for daily prediction of solar radiation. In Proceedings of the International Conference on Global Research and Education, Kaunas, Lithuania, 24–27 September 2018. [Google Scholar]
- Ijadi Maghsoodi, A.; Ijadi Maghsoodi, A.; Mosavi, A.; Rabczuk, T.; Zavadskas, E. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA Approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef]
- David, M.; Ramahatana, F.; Trombe, P.-J.; Lauret, P. Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 2016, 133, 55–72. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhang, Q.; Zhao, L.; Gong, D. Comparison of artificial intelligence and empirical models for estimation of daily diffuse solar radiation in North China Plain. Int. J. Hydrogen Energy 2017, 42, 14418–14428. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Appl. Energy 2017, 203, 897–916. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Deo, R.C.; Cornejo-Bueno, L.; Camacho-Gómez, C.; Ghimire, S. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Appl. Energy 2018, 209, 79–94. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Jiménez-Fernández, S.; Aybar-Ruiz, A.; Casanova-Mateo, C.; Sanz-Justo, J.; García-Herrera, R. A CRO-species optimization scheme for robust global solar radiation statistical downscaling. Renew. Energy 2017, 111, 63–76. [Google Scholar] [CrossRef]
- Touati, F.; Chowdhury, N.A.; Benhmed, K.; Gonzales, A.J.S.P.; Al-Hitmi, M.A.; Benammar, M.; Gastli, A.; Ben-Brahim, L. Long-term performance analysis and power prediction of PV technology in the State of Qatar. Renew. Energy 2017, 113, 952–965. [Google Scholar] [CrossRef]
- Voyant, C.; Motte, F.; Fouilloy, A.; Notton, G.; Paoli, C.; Nivet, M.-L. Forecasting method for global radiation time series without training phase: Comparison with other well-known prediction methodologies. Energy 2017, 120, 199–208. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Darras, C.; Fouilloy, A.; Motte, F. Uncertainties in global radiation time series forecasting using machine learning: The multilayer perceptron case. Energy 2017, 125, 248–257. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Cuadra, L.; Jiménez-Fernández, S.; Acevedo-Rodríguez, J.; Prieto, L.; Salcedo-Sanz, S. Wind Power Ramp Events Prediction with Hybrid Machine Learning Regression Techniques and Reanalysis Data. Energies 2017, 10, 1784. [Google Scholar] [CrossRef]
- Khosravi, A.; Machado, L.; Nunes, R. Time-series prediction of wind speed using machine learning algorithms: A case study Osorio wind farm, Brazil. Appl. Energy 2018, 224, 550–566. [Google Scholar] [CrossRef]
- Burlando, M.; Meissner, C. Evaluation of Two ANN Approaches for the Wind Power Forecast in a Mountainous Site. Int. J. Renew. Energy Res. (IJRER) 2017, 7, 1629–1638. [Google Scholar]
- Pandit, R.; Infield, D. Gaussian process operational curves for wind turbine condition monitoring. Energies 2018, 11, 1631. [Google Scholar] [CrossRef]
- Sharifian, A.; Ghadi, M.J.; Ghavidel, S.; Li, L.; Zhang, J. A new method based on Type-2 fuzzy neural network for accurate wind power forecasting under uncertain data. Renew. Energy 2018, 120, 220–230. [Google Scholar] [CrossRef]
- Baranyai, M.; Mosavi, A.; Vajda, I.; Varkonyi-Koczy, A.R. Optimal Design of Electrical Machines: State of the Art Survey. In Proceedings of the International Conference on Global Research and Education, Iași, Romania, 25–28 September 2017; pp. 209–216. [Google Scholar]
- Albert, A.; Maasoumy, M. Predictive segmentation of energy consumers. Appl. Energy 2016, 177, 435–448. [Google Scholar] [CrossRef]
- Alobaidi, M.H.; Chebana, F.; Meguid, M.A. Robust ensemble learning framework for day-ahead forecasting of household based energy consumption. Appl. Energy 2018, 212, 997–1012. [Google Scholar] [CrossRef]
- Benedetti, M.; Cesarotti, V.; Introna, V.; Serranti, J. Energy consumption control automation using Artificial Neural Networks and adaptive algorithms: Proposal of a new methodology and case study. Appl. Energy 2016, 165, 60–71. [Google Scholar] [CrossRef]
- Chen, K.; Jiang, J.; Zheng, F.; Chen, K. A novel data-driven approach for residential electricity consumption prediction based on ensemble learning. Energy 2018, 150, 49–60. [Google Scholar] [CrossRef]
- Kuroha, R.; Fujimoto, Y.; Hirohashi, W.; Amano, Y.; Tanabe, S.-I.; Hayashi, Y. Operation planning method for home air-conditioners considering characteristics of installation environment. Energy Build. 2018, 177, 351–362. [Google Scholar] [CrossRef]
- Wang, N.; Vlachokostas, A.; Borkum, M.; Bergmann, H.; Zaleski, S. Unique Building Identifier: A natural key for building data matching and its energy applications. Energy Build. 2019, 184, 230–241. [Google Scholar] [CrossRef]
- Depecker, P.; Menezo, C.; Virgone, J.; Lepers, S. Design of buildings shape and energetic consumption. Build. Environ. 2001, 36, 627–635. [Google Scholar] [CrossRef]
- Qi, F.; Wang, Y. A new calculation method for shape coefficient of residential building using Google Earth. Energy Build. 2014, 76, 72–80. [Google Scholar] [CrossRef]
- Livingston, O.V.; Pulsipher, T.C.; Anderson, D.M.; Vlachokostas, A.; Wang, N. An analysis of utility meter data aggregation and tenant privacy to support energy use disclosure in commercial buildings. Energy 2018, 159, 302–309. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A model for protecting privacy. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Perez, A.J.; Zeadally, S. PEAR: A privacy-enabled architecture for crowdsensing. In Proceedings of the International Conference on Research in Adaptive and Convergent Systems, Krakow, Poland, 20–23 September 2017; pp. 166–171. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).