Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties
Abstract
1. Introduction
2. State of the Art of Multi-Period Optimal Power Flow for Distribution Systems with Energy Storage
3. Methodology
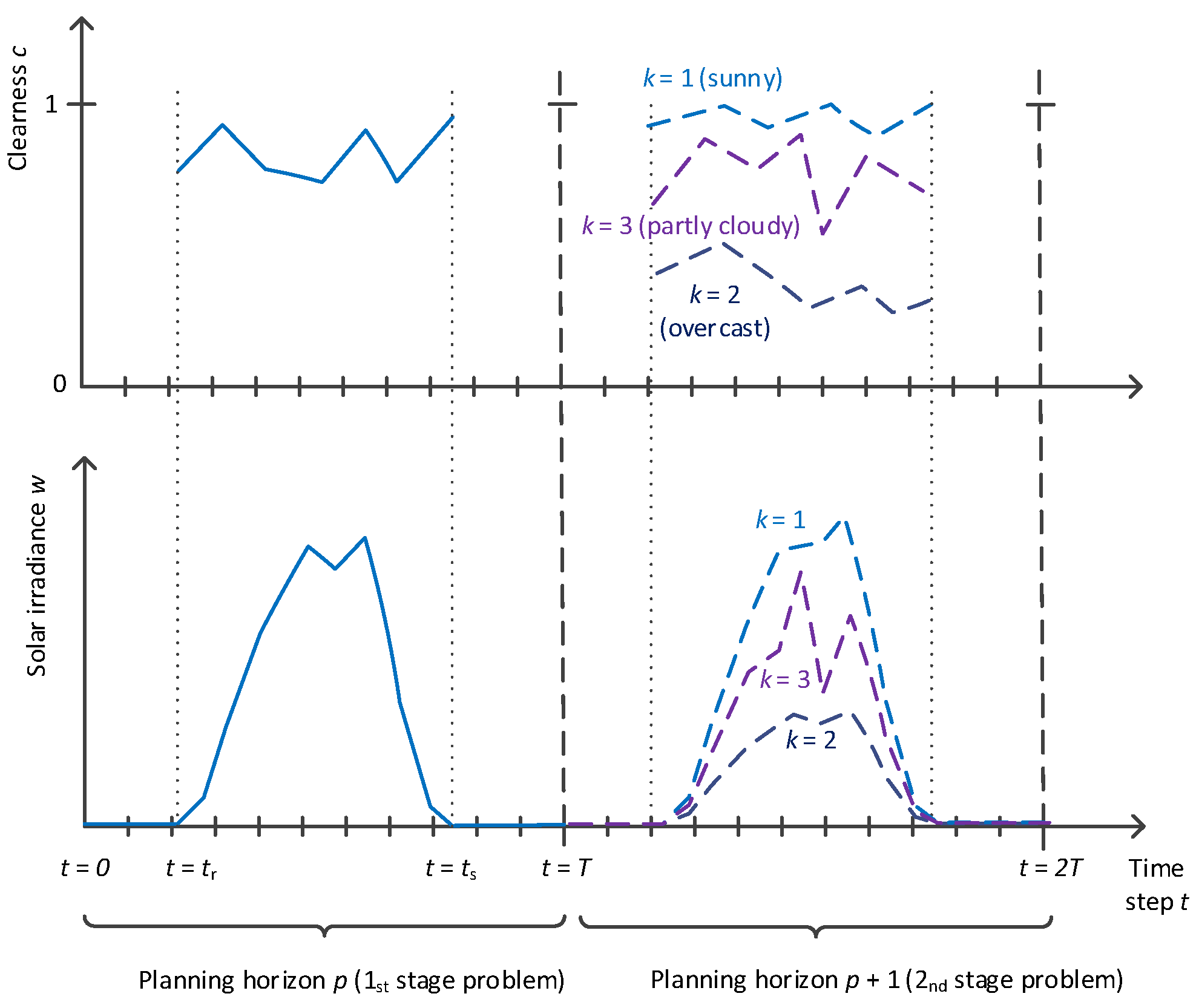
3.1. Multi-Period Optimal Power Flow Model for Distribution System with Energy Storage
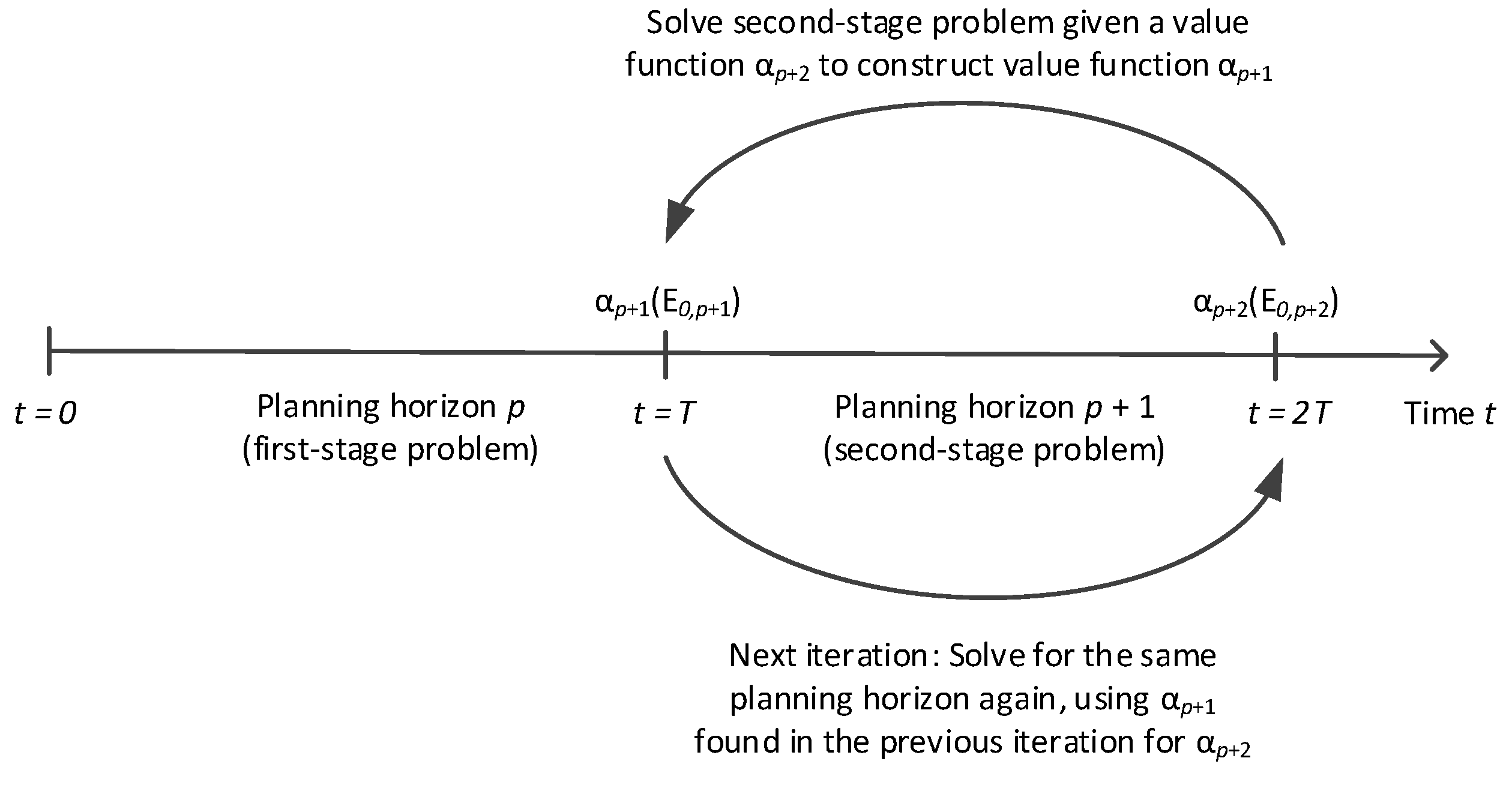
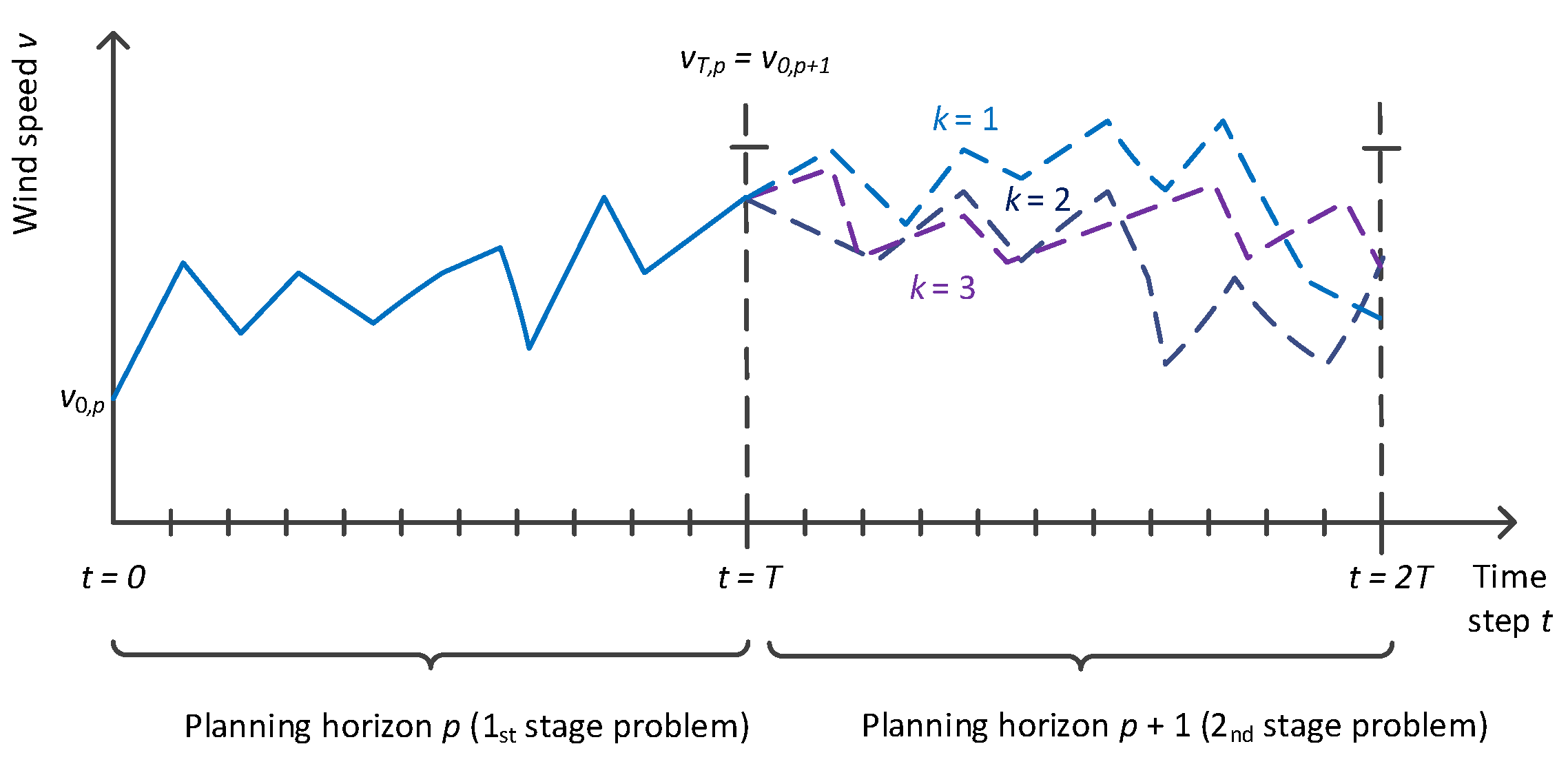
3.2. Expected Future Value Function for Stored Energy
3.3. Determining the Value Function
| Algorithm 1: Determining Value Function for Stored Energy |
| Input: Grid data for the distribution system model in Section 3.1, historic DG resource (wind speed or solar irradiance) time series data, selection of a discrete set Sx of DG state variable values ; selection of a discrete set of initial stored energy values Output: Estimates of value function parameters and for all DG state variables 1: Initialize value function parameters , for all 2: Generate synthetic time series yk for the stochastic DG resource variables for each value of 3: while and not converged for all 4: for do 5: Set DG state variable to the th value in 6: for do 7: Set initial stored energy to the th value in 8: for do 9: Use DG resource time series yk for state variable value 10: Solve second-stage problem for planning horizon () with value function parameterized by and for initial stored energy and DG resource time series yk 11: Evaluate dual value π(x, E0,p+1) 12: end for 13: end for 14: Fit dual values to a linear function of 15: Determine updated values of and 16: end for 17: end while |
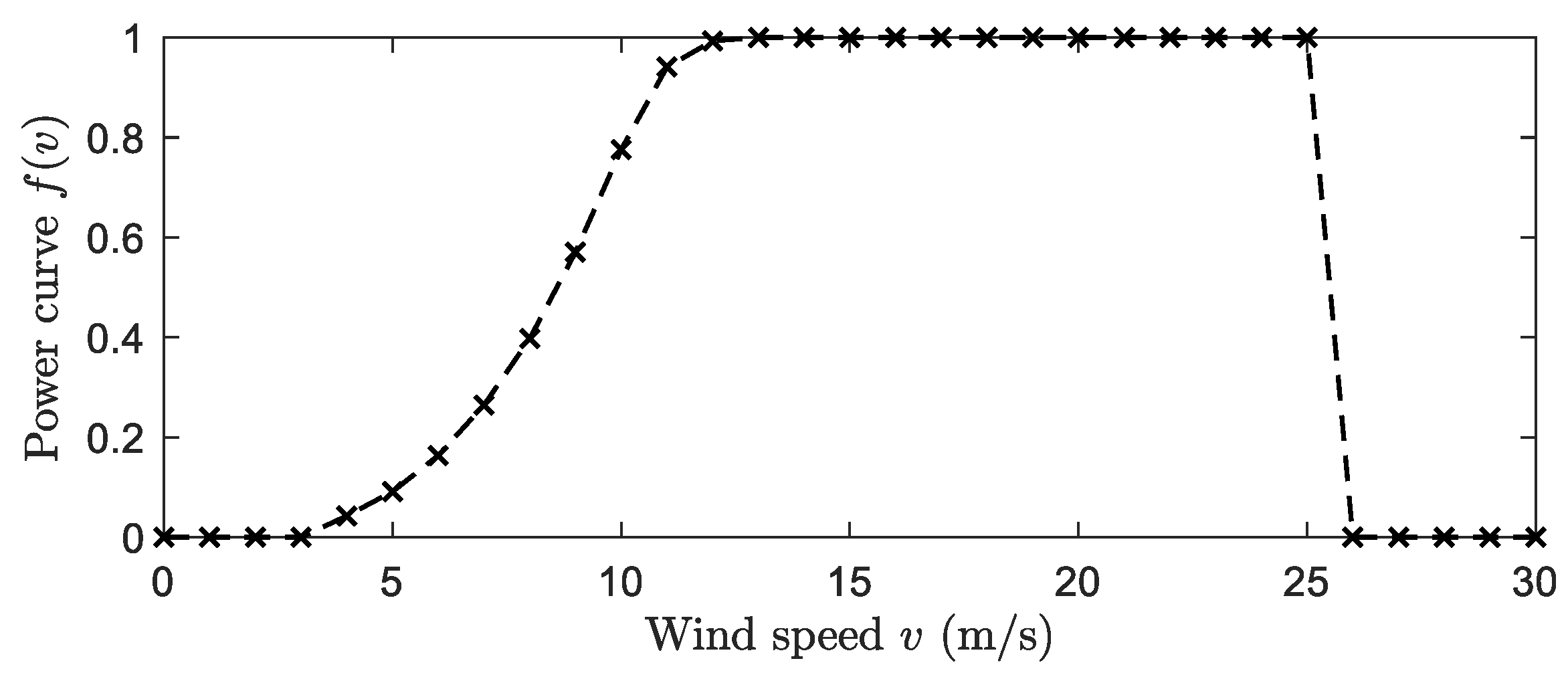
3.4. Modeling Stochasticity of Wind Power Generation
3.5. Modeling Stochasticity of Solar PV Power Generation
4. Case Study
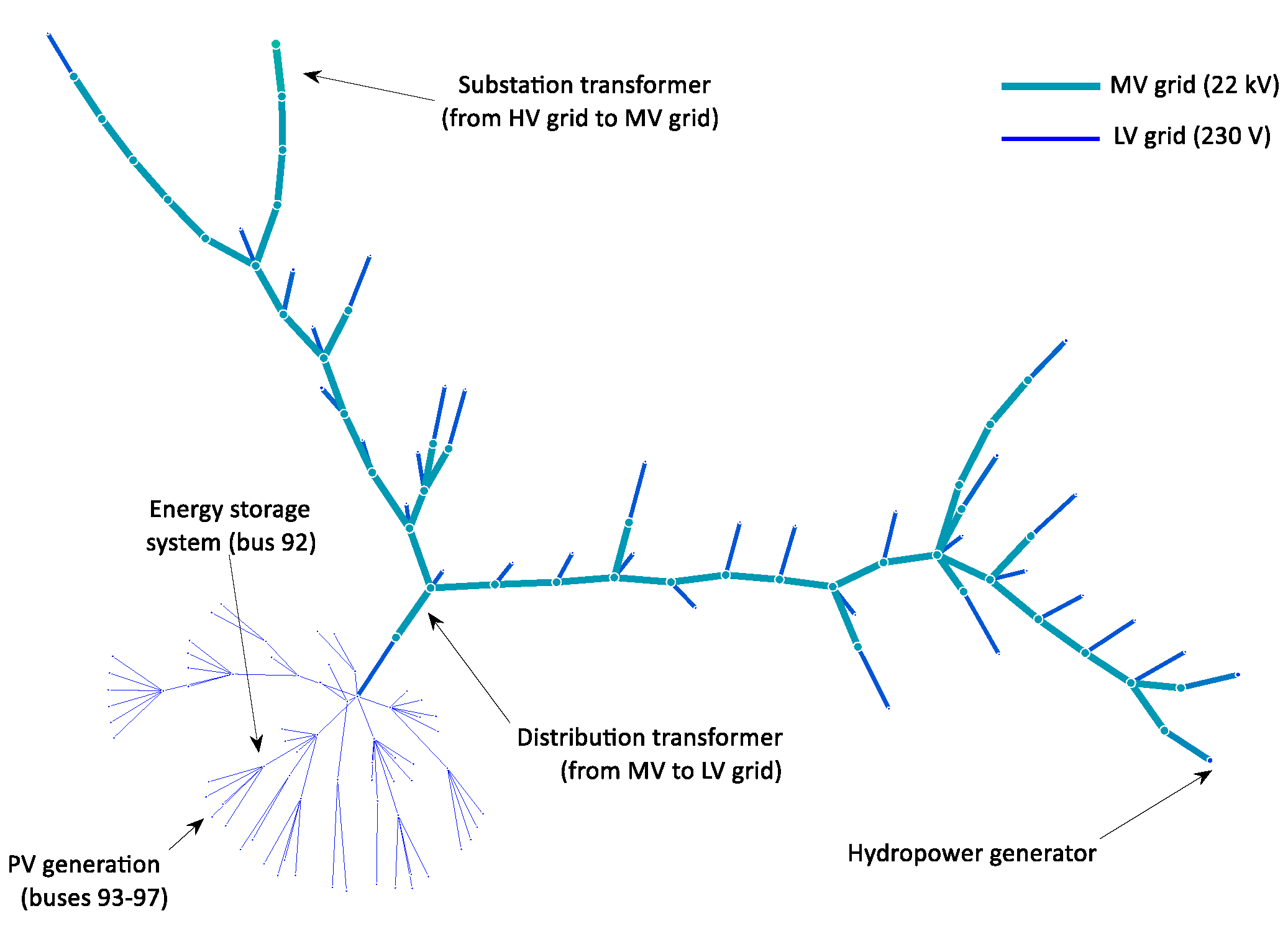
4.1. Distribution System Model
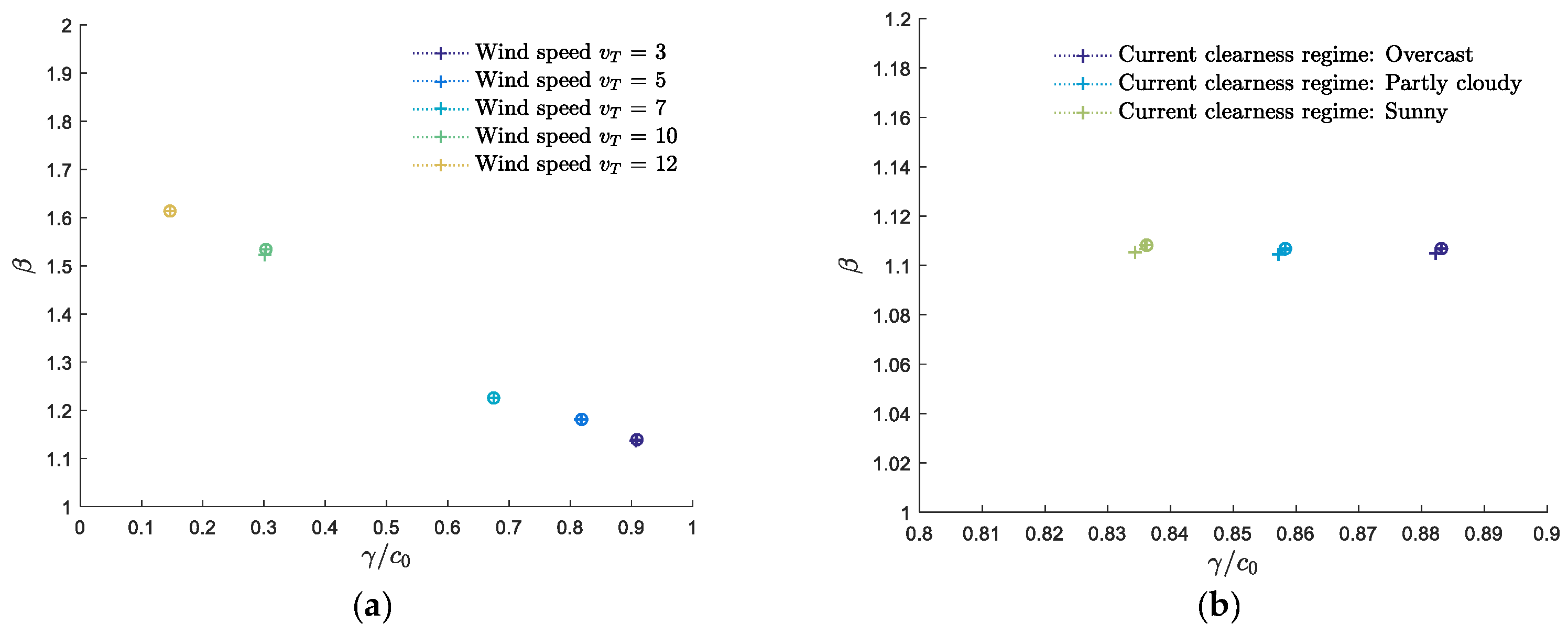
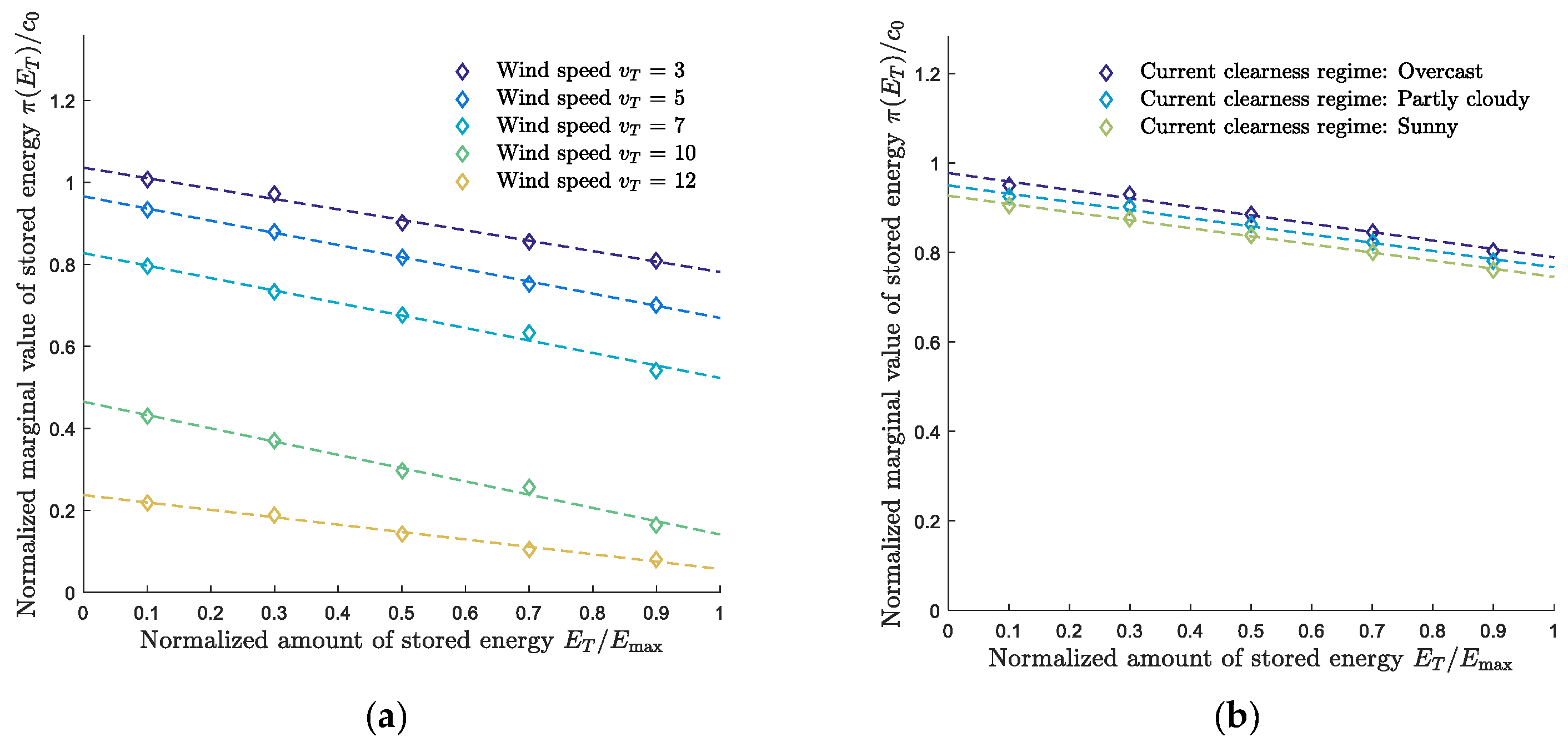
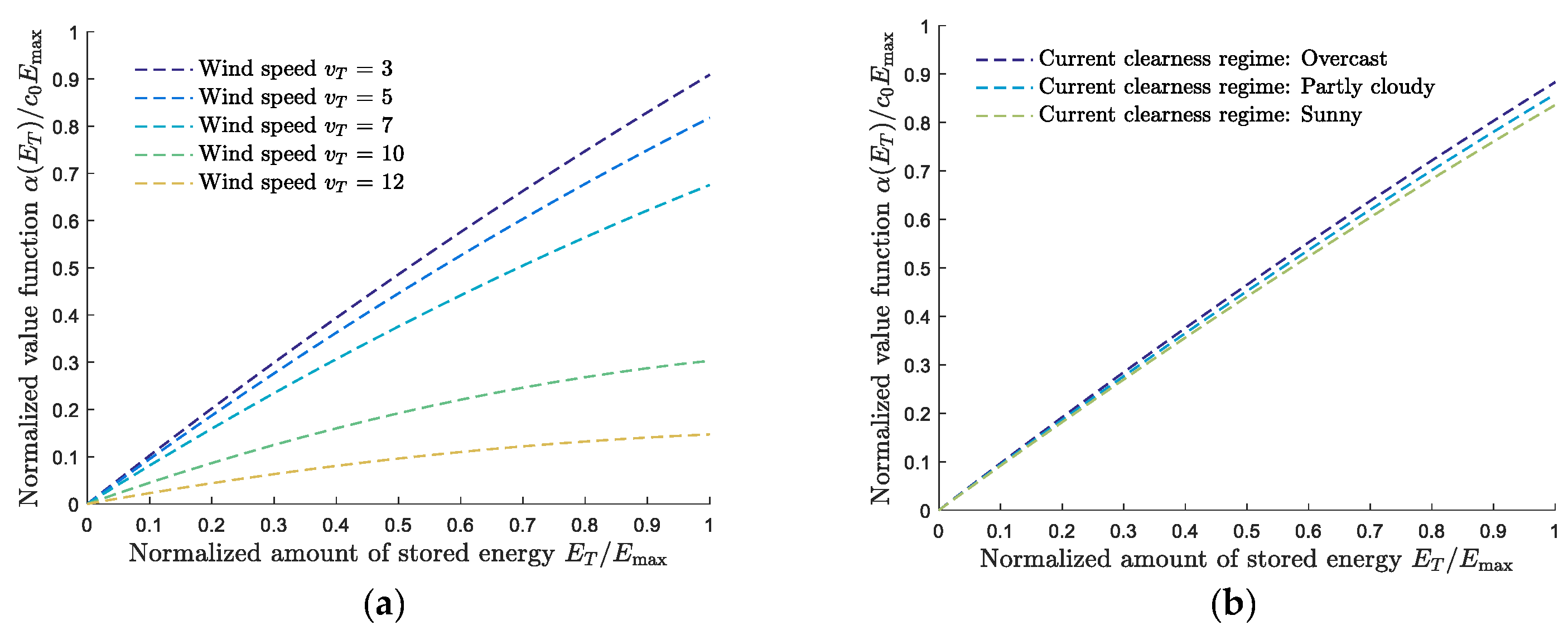
4.2. Results for the Expected Future Value of Stored Energy
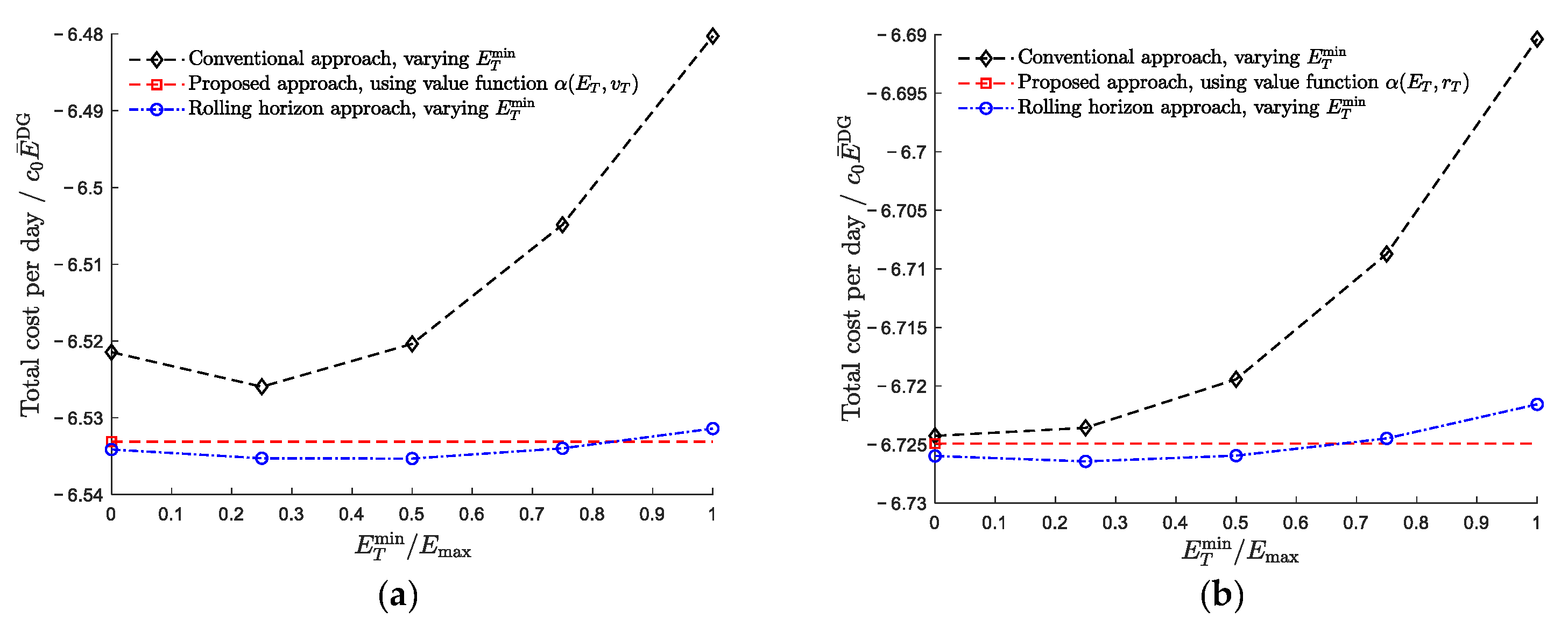
4.3. Evaluation of Energy Storage Scheduling Considering the Value of Stored Energy
5. Conclusions and Further Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zubo, R.H.A.; Mokryani, G.; Rajamani, H.-S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renew. Sustain. Energy Rev. 2017, 72, 1177–1198. [Google Scholar] [CrossRef]
- Haque, M.M.; Wolfs, P. A review of high PV penetrations in LV distribution networks: Present status, impacts and mitigation measures. Renew. Sustain. Energy Rev. 2016, 62, 1195–1208. [Google Scholar] [CrossRef]
- Engeland, K.; Borga, M.; Creutin, J.-D.; François, B.; Ramos, M.-H.; Vidal, J.-P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Shivashankar, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M. Mitigating methods of power fluctuation of photovoltaic (PV) sources—A review. Renew. Sustain. Energy Rev. 2016, 59, 1170–1184. [Google Scholar] [CrossRef]
- Malhotra, A.; Battke, B.; Beuse, M.; Stephan, A.; Schmidt, T. Use cases for stationary battery technologies: A review of the literature and existing projects. Renew. Sustain. Energy Rev. 2016, 56, 705–721. [Google Scholar] [CrossRef]
- Rocky Mountain Institute. The Economics of Battery Energy Storage; Rocky Mountain Institute: Boulder, CO, USA, 2015. [Google Scholar]
- Xia, X.; Elaiw, A.M. Optimal dynamic economic dispatch of generation: A review. Electr. Power Syst. Res. 2010, 80, 975–986. [Google Scholar] [CrossRef]
- Sperstad, I.B.; Marthinsen, H. Optimal Power Flow Methods and Their Application to Distribution Systems with Energy Storage—A Survey of Available Tools and Methods; SINTEF Energy Research: Trondheim, Norway, 2016. [Google Scholar]
- Sperstad, I.B.; Helseth, A.; Korpås, M. Valuation of stored energy in dynamic optimal power flow of distribution systems with energy storage. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016. [Google Scholar]
- Pereira, M.V.F. Optimal stochastic operations scheduling of large hydroelectric systems. Int. J. Electr. Power Energy Syst. 1989, 11, 161–169. [Google Scholar] [CrossRef]
- Gjelsvik, A.; Røtting, T.A.; Røynstrand, J. Long-term scheduling of hydro-thermal power systems. In Hydropower ’92; Broch, E., Lysne, D.K., Eds.; Balkema: Rotterdam, The Netherlands, 1992; pp. 539–546. [Google Scholar]
- Byrne, R.H.; Nguyen, T.A.; Copp, D.A.; Chalamala, B.R.; Gyuk, I. Energy Management and optimization methods for grid energy storage systems. IEEE Access 2017, 6, 13231–13260. [Google Scholar] [CrossRef]
- Mohagheghi, E.; Alramlawi, M.; Gabash, A.; Li, P. A survey of real-time optimal power flow. Energies 2018, 11, 3142. [Google Scholar] [CrossRef]
- Chandy, K.M.; Low, S.H.; Topcu, U.; Xu, H. A simple optimal power flow model with energy storage. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, Georgia, 15–17 December 2010; pp. 1051–1057. [Google Scholar]
- Lamadrid, A.J.; Mount, T.D.; Thomas, R.J. Scheduling of energy storage systems with geographically distributed renewables. In Proceedings of the Ninth IEEE International Symposium on Parallel and Distributed Processing with Applications Workshops (ISPAW), Busan, Korea, 26–28 May 2011; pp. 85–90. [Google Scholar]
- Sojoudi, S.; Low, S.H. Optimal charging of plug-in hybrid electric vehicles in smart grids. In Proceedings of the Power and Energy Society General Meeting, Detroit, Michigan, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Gabash, A.; Pu, L. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage. IEEE Trans. Power Syst. 2012, 27, 2026–2035. [Google Scholar] [CrossRef]
- Gopalakrishnan, A.; Raghunathan, A.U.; Nikovski, D.; Biegler, L.T. Global optimization of multi-period optimal power flow. In Proceedings of the American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 1157–1164. [Google Scholar]
- Baker, K.; Zhu, D.; Hug, G.; Li, X. Jacobian singularities in optimal power flow problems caused by intertemporal constraints. In Proceedings of the North American Power Symposium (NAPS), Manhatan, KS, USA, 22–24 September 2013; 2013; pp. 1–6. [Google Scholar]
- Celli, G.; Mocci, S.; Pilo, F.; Loddo, M. Optimal integration of energy storage in distribution networks. In Proceedings of the PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7. [Google Scholar]
- Carpinelli, G.; Celli, G.; Mocci, S.; Mottola, F.; Pilo, F.; Proto, D. Optimal integration of distributed energy storage devices in smart grids. IEEE Trans. Smart Grid 2013, 4, 985–995. [Google Scholar] [CrossRef]
- Murillo-Sanchez, C.E.; Zimmerman, R.D.; Anderson, C.L.; Thomas, R.J. Secure planning and operations of systems with stochastic sources, energy storage, and active demand. IEEE Trans. Smart Grid 2013, 4, 2220–2229. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E. Matpower Optimal Scheduling Tool (MOST) User’s Manual; Power Systems Engineering Research Center (PSERC): Tempe, AZ, USA, 2016. [Google Scholar]
- Khanabadi, M.; Moghadasi, S.; Kamalasadan, S. Real-time optimization of distribution system considering interaction between markets. In Proceedings of the Industry Applications Society Annual Meeting, Orlando, FL, USA, 6–11 October 2013; pp. 1–8. [Google Scholar]
- Levron, Y.; Guerrero, J.M.; Beck, Y. Optimal power flow in microgrids with energy storage. IEEE Trans. Power Syst. 2013, 28, 3226–3234. [Google Scholar] [CrossRef]
- Tant, J.; Geth, F.; Six, D.; Tant, P.; Driesen, J. Multiobjective battery storage to improve pv integration in residential distribution grids. IEEE Trans. Sustain. Energy 2013, 4, 182–191. [Google Scholar] [CrossRef]
- Gill, S.; Kockar, I.; Ault, G.W. Dynamic optimal power flow for active distribution networks. IEEE Trans. Power Syst. 2014, 29, 121–131. [Google Scholar] [CrossRef]
- Moghadasi, S.; Kamalasadan, S. Real-time optimal scheduling of smart power distribution systems using integrated receding horizon control and convex conic programming. In Proceedings of the Industry Application Society Annual Meeting, Vancouver, BC, CA, 5–9 October 2014; pp. 1–7. [Google Scholar]
- Bozchalui, M.C.; Sharma, R. Operation strategies for energy storage systems in distribution networks. In Proceedings of the PES General Meeting | Conference & Exposition, 2014, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Maffei, A.; Meola, D.; Marafioti, G.; Palmieri, G.; Iannelli, L.; Mathisen, G.; Bjerkan, E.; Glielmo, L. Optimal Power Flow model with energy storage, an extension towards large integration of renewable energy sources. In Proceedings of the 19th World Congress on International Federation of Automatic Control, Cape Town, South Africa, 2014; pp. 9456–9461. [Google Scholar]
- Maffei, A.; Srinivasan, S.; Iannelli, L.; Glielmo, L. A receding horizon approach for the power flow management with renewable energy and energ storage systems. In Proceedings of the 2015 AEIT International Annual Conference, Naples, Italy, 14–16 October 2015; pp. 1–6. [Google Scholar]
- Maffei, A.; Srinivasan, S.; Meola, D.; Palmieri, G.; Iannelli, L.; Holhjem, Ø.H.; Marafioti, G.; Mathisen, G.; Glielmo, L. A cyber-physical systems approach for implementing the receding horizon optimal power flow in smart grids. IEEE Trans. Sustain. Comput. 2018, 3, 98–111. [Google Scholar] [CrossRef]
- Meyer-Huebner, N.; Suriyah, M.; Leibfried, T. On efficient computation of time constrained optimal power flow in rectangular form. In Proceedings of the PowerTech 2015, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Nguyen, N.T.A.; Le, D.D.; Bovo, C.; Berizzi, A. Optimal power flow with energy storage systems: Single-period model vs. multi-period model. In Proceedings of the PowerTech 2015, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–635. [Google Scholar]
- Fortenbacher, P.; Zellner, M.; Andersson, G. Optimal sizing and placement of distributed storage in low voltage networks. In Proceedings of the Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Fortenbacher, P.; Mathieu, J.L.; Andersson, G. Modeling and optimal operation of distributed battery storage in low voltage grids. IEEE Trans. Power Syst. 2017, 32, 4340–4350. [Google Scholar] [CrossRef]
- Geth, F.; Leyder, S.; Marmol, C.D.; Rapoport, S. The PlanGridEV distribution grid simulation tool with EV models. In CIRED Workshop 2016; CIRED: Helsinki, Finland, 2016. [Google Scholar]
- Grillo, S.; Pievatolo, A.; Tironi, E. Optimal storage scheduling using Markov decision processes. IEEE Trans. Sustain. Energy 2016, 7, 755–764. [Google Scholar] [CrossRef]
- Marley, J.F.; Hiskens, I.A. Multi-period AC-QP optimal power flow including storage. In Proceedings of the 19th Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; 2016; pp. 1–7. [Google Scholar]
- Zaferanlouei, S.; Korpås, M.; Farahmand, H.; Vadlamudi, V.V. Integration of PEV and PV in Norway using multi-period ACOPF—Case study. In PowerTech 2017; IEEE: Manchester, UK, 2017. [Google Scholar]
- Zaferanlouei, S.; Korpås, M.; Hashemipour, N.; Aghaei, J.; Farahmand, H. Computational efficiency assessment of multi-period AC optimal power flow including energy storage systems. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal planning of distributed energy storage systems in active distribution networks embedding grid reconfiguration. IEEE Trans.Power Syst. 2018, 33, 1577–1590. [Google Scholar] [CrossRef]
- Kourounis, D.; Fuchs, A.; Schenk, O. Towards the next generation of multiperiod optimal power flow solvers. IEEE Trans. Power Syst. 2018, 33, 4005–4013. [Google Scholar] [CrossRef]
- Knezović, K.; Soroudi, A.; Keane, A.; Marinelli, M. Robust multi-objective PQ scheduling for electric vehicles in flexible unbalanced distribution grids. IET Gener. Transm. Distrib. 2017, 11, 4031–4040. [Google Scholar] [CrossRef]
- Karagiannopoulos, S.; Roald, L.; Aristidou, D.; Hug, G. Operational planning of active distribution grids under uncertainty. In Proceedings of the 10th Bulk Power Systems Dynamics and Control Symposium—IREP 2017, Espinho, Portugal, 27 August–1 September 2017. [Google Scholar]
- Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar] [CrossRef]
- Graabak, I.; Korpås, M. Variability characteristics of european wind and solar power resources—A review. Energies 2016, 9, 449. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; Lai, L.L.; Xu, Z.; McCulloch, M.D.; Wong, K.P. A comprehensive review on large-scale photovoltaic system with applications of electrical energy storage. Renew. Sustain. Energy Rev. 2017, 78, 439–451. [Google Scholar] [CrossRef]
- Crespo Del Granado, P.; Wallace, S.W.; Pang, Z. The impact of wind uncertainty on the strategic valuation of distributed electricity storage. Comput. Manag. Sci. 2016, 13, 5–27. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Pereira, M.V.F.; Pinto, L.M.V.G. Multi-stage stochastic optimization applied to energy planning. Math. Program. 1991, 52, 359–375. [Google Scholar] [CrossRef]
- Brokish, K.; Kirtley, J. Pitfalls of modeling wind power using Markov chains. In Proceedings of the2009 IEEE/PES Power Systems Conference and Exposition, 15–18 March 2009; pp. 1–6. [Google Scholar]
- Ramakrishna, R.; Scaglione, A.; Vittal, V. A stochastic model for short-term probabilistic forecast of solar photo-voltaic power. arXiv, 2017; arXiv:1706.05445. [Google Scholar]
- Kaplanis, S.N. New methodologies to estimate the hourly global solar radiation: Comparisons with existing models. Renew. Energy 2006, 31, 781–790. [Google Scholar] [CrossRef]
- Bjarghov, S.N. Utilizing EV Batteries as a Flexible Resource at End-User Level. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2017. [Google Scholar]
- Roberts, J.J.; Mendiburu Zevallos, A.A.; Cassula, A.M. Assessment of photovoltaic performance models for system simulation. Renew. Sustain. Energy Rev. 2017, 72, 1104–1123. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER’s extensible optimal power flow architecture. In Proceedings of the Power & Energy Society General Meeting 2009, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar]
- INVADE Consortium. D9.1: Review of Existing Business Models and Storage Technology Database. 2017. Available online: https://h2020invade.eu/wp-content/uploads/2017/04/D9.1-Review-of-existing-business-models-and-storage-technology-database.pdf (accessed on 3 July 2018).
- MathWorks®. Optimization Toolbox™ User’s Guide; 2015b ed.; MathWorks®: Natick, MA, USA, 2015. [Google Scholar]
- Holttinen, H.; Rissanen, S.; Larsen, X.; Løvholm, A.L. Wind and Load Variability in the Nordic Countries; VTT: Espoo, Finland, 2013. [Google Scholar]
- Sagosen, Ø. Analysis of Large Scale Integration of Electric Vehicles in Nord-Trøndelag. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Cuffe, P.; Keane, A. Visualizing the electrical structure of power systems. IEEE Syst. J. 2017, 11, 1810–1821. [Google Scholar] [CrossRef]
- Usman, M.; Coppo, M.; Bignucolo, F.; Turri, R. Losses management strategies in active distribution networks: A review. Elect. Power Syst. Res. 2018, 163, 116–132. [Google Scholar] [CrossRef]
- Nord Pool. Market data|Nord Pool. Available online: https://www.nordpoolgroup.com (accessed on 23 May 2018).
- Tesla. Powerpack|Commercial and Utility Energy Storage Solutions. Available online: https://www.tesla.com/powerpack (accessed on 9 June 2018).
- Staffell, I. Wind Turbine Power Curves; Imperial College: London, UK, 2012. [Google Scholar]
| Reference | OPF Model and Application | Handling of Stored Energy At The End Of Planning Horizon |
|---|---|---|
| [14] | AC MPOPF with small voltage angle approximation (convex problem), formulated as a finite-horizon optimal control problem | Linear penalty function in the objective function (proportional to the deviation of the amount of stored energy at the end of the planning horizon from the maximal energy capacity); 24 h horizon |
| [15] | AC MPOPF; applied to power system with wind power | Rolling horizon (24 h look-ahead horizon) |
| [16] | AC MPOPF for optimal charging of EVs | Requiring that all EVs are charged at the end of 10 h planning horizon |
| [17] | AC MPOPF (coupled real-reactive) | (24 h horizon or 120 h horizon) |
| [18] | Semidefinite programming relaxation of AC MPOPF | (8 h horizon) |
| [19] | AC MPOPF; applied to power system with wind power | Rolling horizon (10 × 5 min look-ahead horizon) |
| [20] | Scheduling of ESS (not including power flow constraints) solved by dynamic programming; genetic algorithm for sizing and siting problem as an outer loop (including checking of power flow constraints) | (24 h horizon) |
| [21] | AC MPOPF with linearized power flow constraints; genetic algorithm for sizing and siting problem as an outer loop | (24 h horizon) |
| [22] | Stochastic security-constrained AC MPOPF; implemented in the MATPOWER Optimal Scheduling Tool [23] | Linear penalty function (that is a linear combination of charged and discharged power for all time steps) |
| [24] | AC MPOPF | Rolling horizon (24 h look-ahead horizon) |
| [25] | Dynamic programming search in the time domain combined with conventional PF solver in the network domain; grid-connected microgrid with DG | n/a (72 h horizon) |
| [26] | Combined ESS scheduling and sizing problem for distribution system with PV; no power flow constraints but including linearized voltage constraints from base case power flow sensitivities | (16 week horizon) |
| [27] | AC MPOPF; applied to distribution system with DG | (24 h horizon) |
| [28] | AC MPOPF with second-order cone programming relaxation | Rolling horizon (72 h look-ahead horizon) |
| [29] | AC MPOPF for unbalanced 3-phase distribution network | (24 h horizon) |
| [30] | AC MPOPF for distribution system with wind power | Linear penalty function in the objective function for each time step (proportional to the deviation of the amount of stored energy from the maximal energy capacity); 24 h horizon |
| [31,32] | AC MPOPF; applied to distribution system with wind power | Linear penalty function in the objective function for each time step proportional to energy stored, and implicitly through rolling horizon (24 h look-ahead horizon) |
| [33] | AC MPOPF | n/a (72 h horizon) |
| [34] | AC MPOPF (comparing with solving each time step in isolation) | (24 h horizon) |
| [9] | AC MPOPF; applied to distribution system with wind power (which is treated as stochastic for the next planning horizon) | Explicit valuation of the future value of stored energy at the end of 24 h planning horizon |
| [35] | MPOPF with linearized AC power flow equations for radial distribution grids; compared with full AC power flow | n/a (up to 744 h horizon) |
| [36] | Robust MPOPF with linearized AC power flow equations for radial distribution grids; applied to LV grid with high PV penetration | Rolling horizon (24 h look-ahead horizon) combined with real-time control within each hour |
| [37] | AC MPOPF for radial distribution systems based on convex relaxation; optimizing EV charging | Requiring fully charged EV at the end of the 24 h planning horizon [31] |
| [38] | Finite-horizon optimal policy problem for Markov decision process for distribution system with PV generation, solved by stochastic dynamic programming, explicitly checking for violations of power flow constraints | Taken into account within each daily planning horizon through stochastic dynamic programming approach (not explicitly discussing the storage level at the end of the planning horizon) |
| [39] | AC-Quadratic Programming MPOPF | A quadratic penalty function penalizing the deviation from a reference storage level (with penalty coefficient and reference storage level varying over the day); up to 8 h horizons |
| [40] | AC MPOPF; optimal scheduling of EVs in distribution system with PV and wind power | Requiring fully charged EV at the end of the 33 h planning horizon |
| [41] | AC MPOPF, applied to minimizing generation costs | n/a (2 h horizon) |
| [42] | Conditionally exact convex MPOPF embedded in model for optimal sizing and siting with stochastic load, electricity prices and PV; applied to distribution system with PV | (24 h horizons for separate days with time series for the stochastic variables) |
| [43] | AC MPOPF | (up to 2880 time steps) |
| [44] | Robust AC MPOPF for unbalanced 3-phase distribution network, applied to EV charging scheduling | Requiring fully charged EV at the end of the 24 h planning horizon |
| [45] | Chance-constrained AC MPOPF for radial distribution systems | n/a (24 h planning horizon) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sperstad, I.B.; Korpås, M. Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties. Energies 2019, 12, 1231. https://doi.org/10.3390/en12071231
Sperstad IB, Korpås M. Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties. Energies. 2019; 12(7):1231. https://doi.org/10.3390/en12071231
Chicago/Turabian StyleSperstad, Iver Bakken, and Magnus Korpås. 2019. "Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties" Energies 12, no. 7: 1231. https://doi.org/10.3390/en12071231
APA StyleSperstad, I. B., & Korpås, M. (2019). Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties. Energies, 12(7), 1231. https://doi.org/10.3390/en12071231





