Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase Change Materials
2.2. Methods for the Multipurpose Thermal Investigation
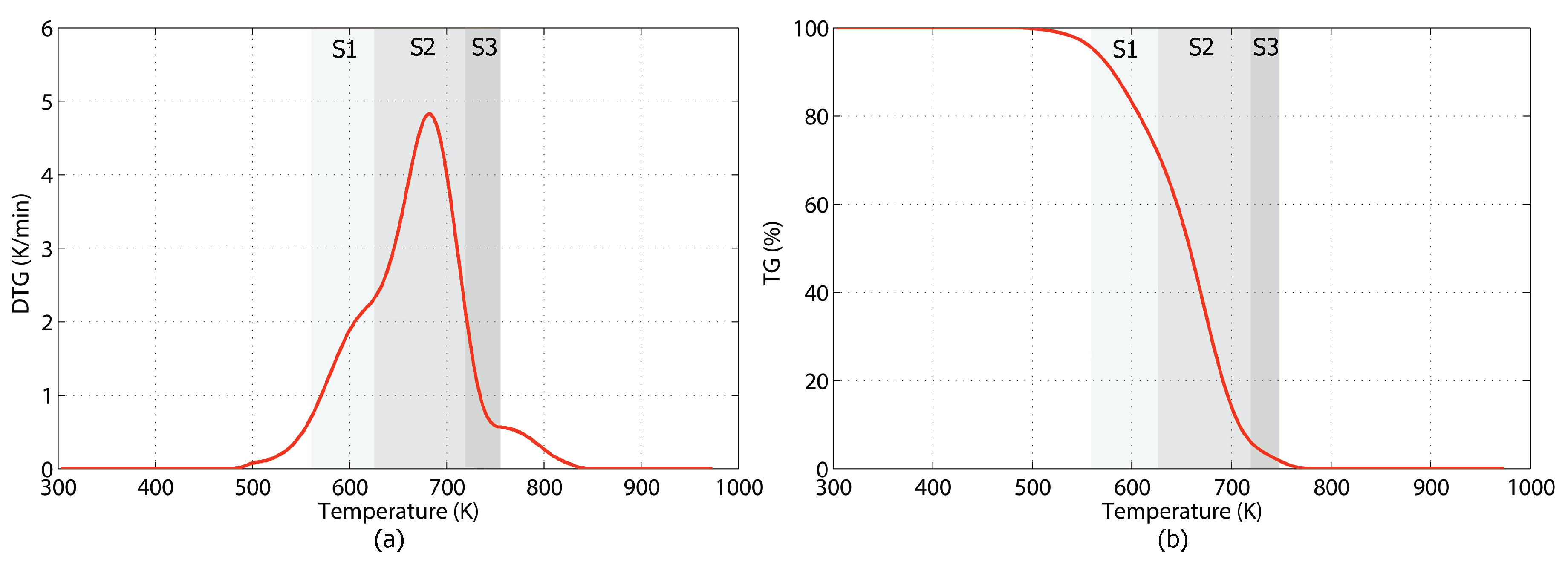
2.2.1. Thermogravimetric Analysis
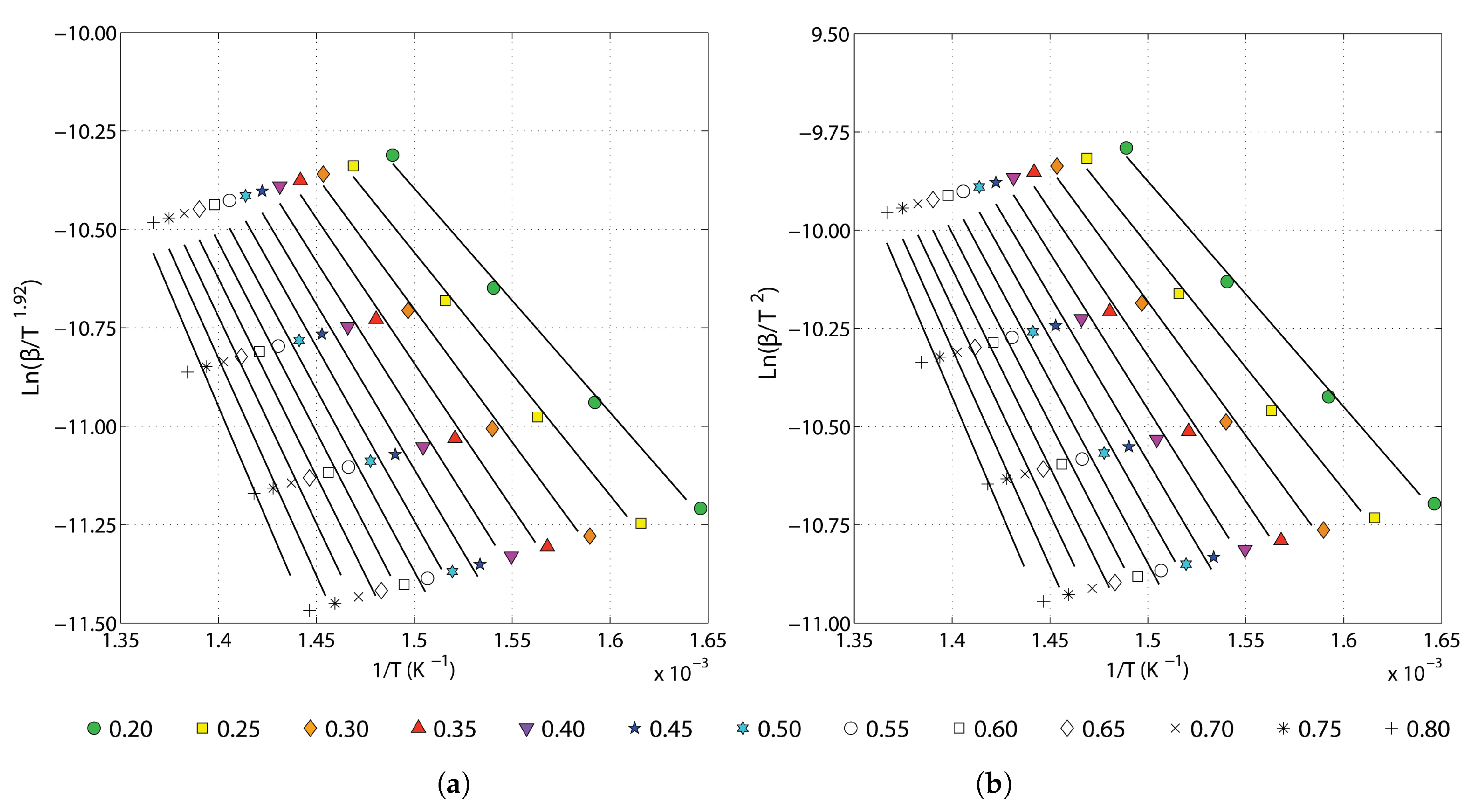
2.2.2. Kinetic Analysis
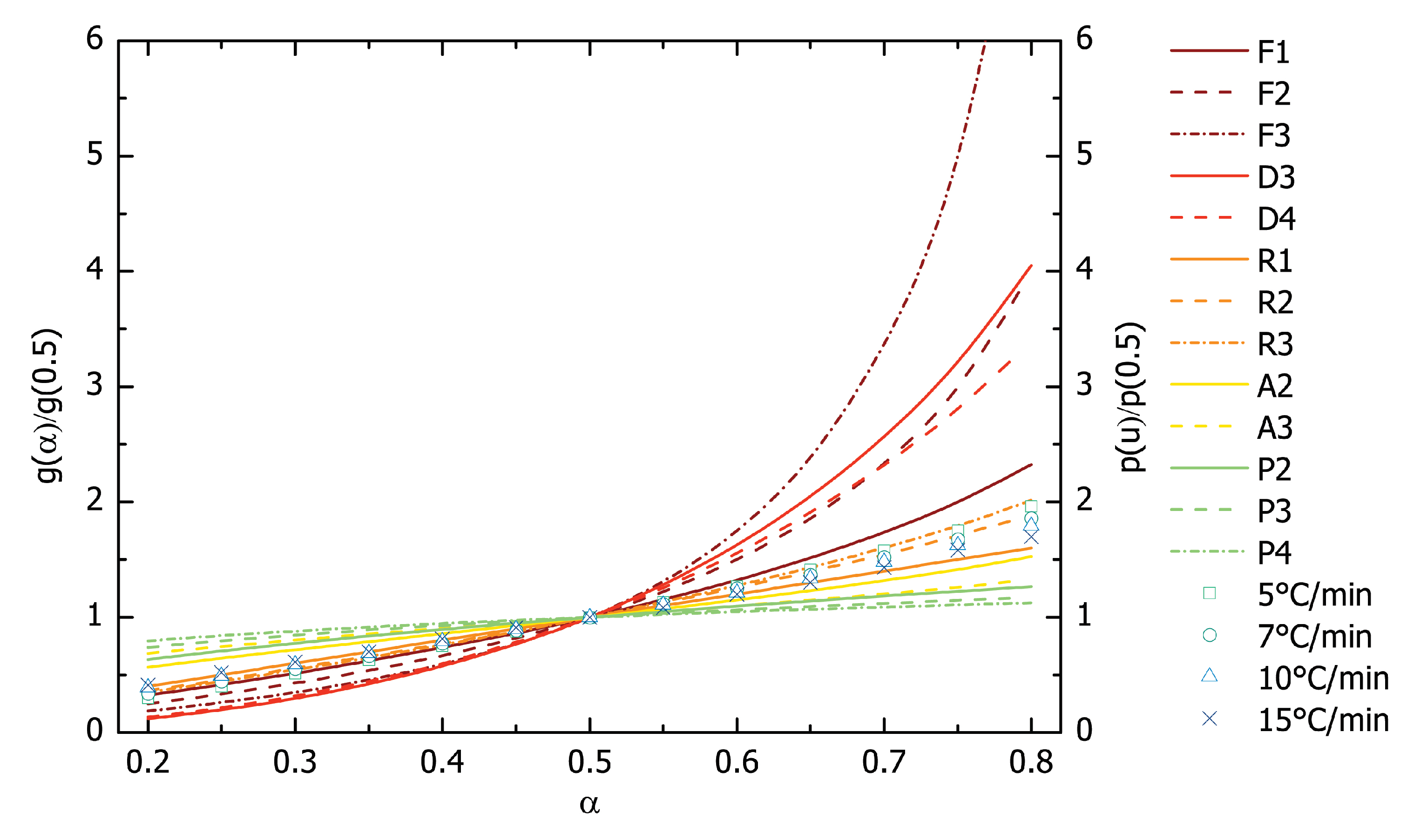
2.2.3. Reaction Model Determination Using the Master-Plots Method
2.2.4. Differential Scanning Calorimetry
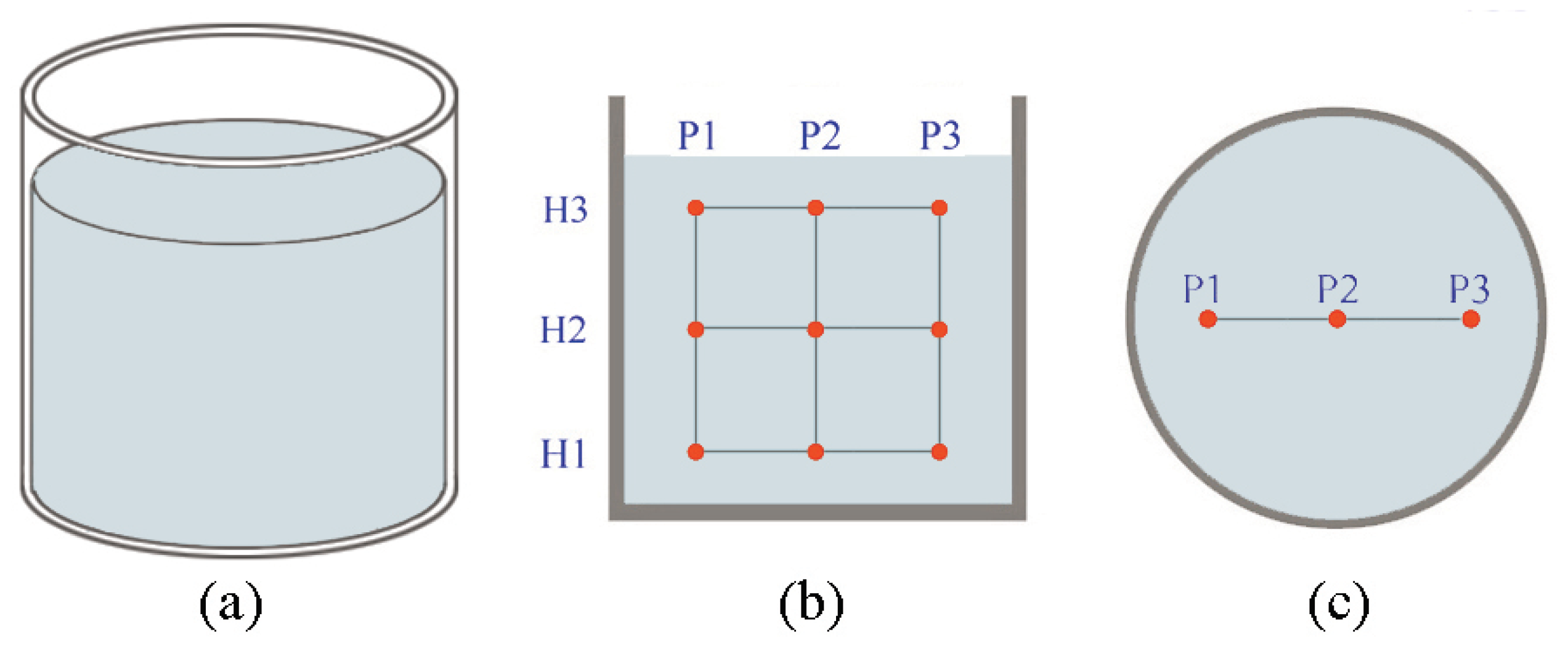
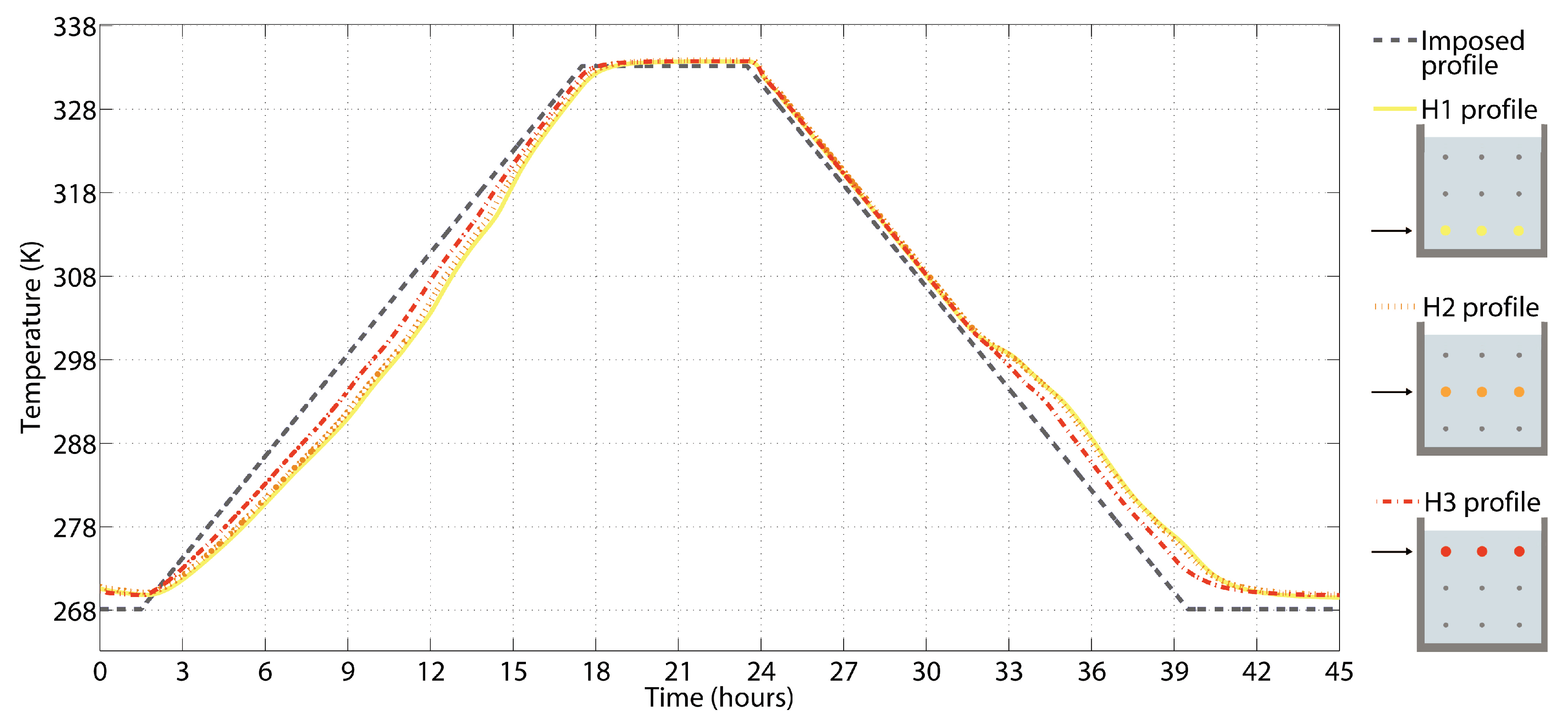
2.2.5. Thermal Monitoring in Dynamic Conditions
3. Results and Discussion
3.1. Thermal Decomposition Characteristics
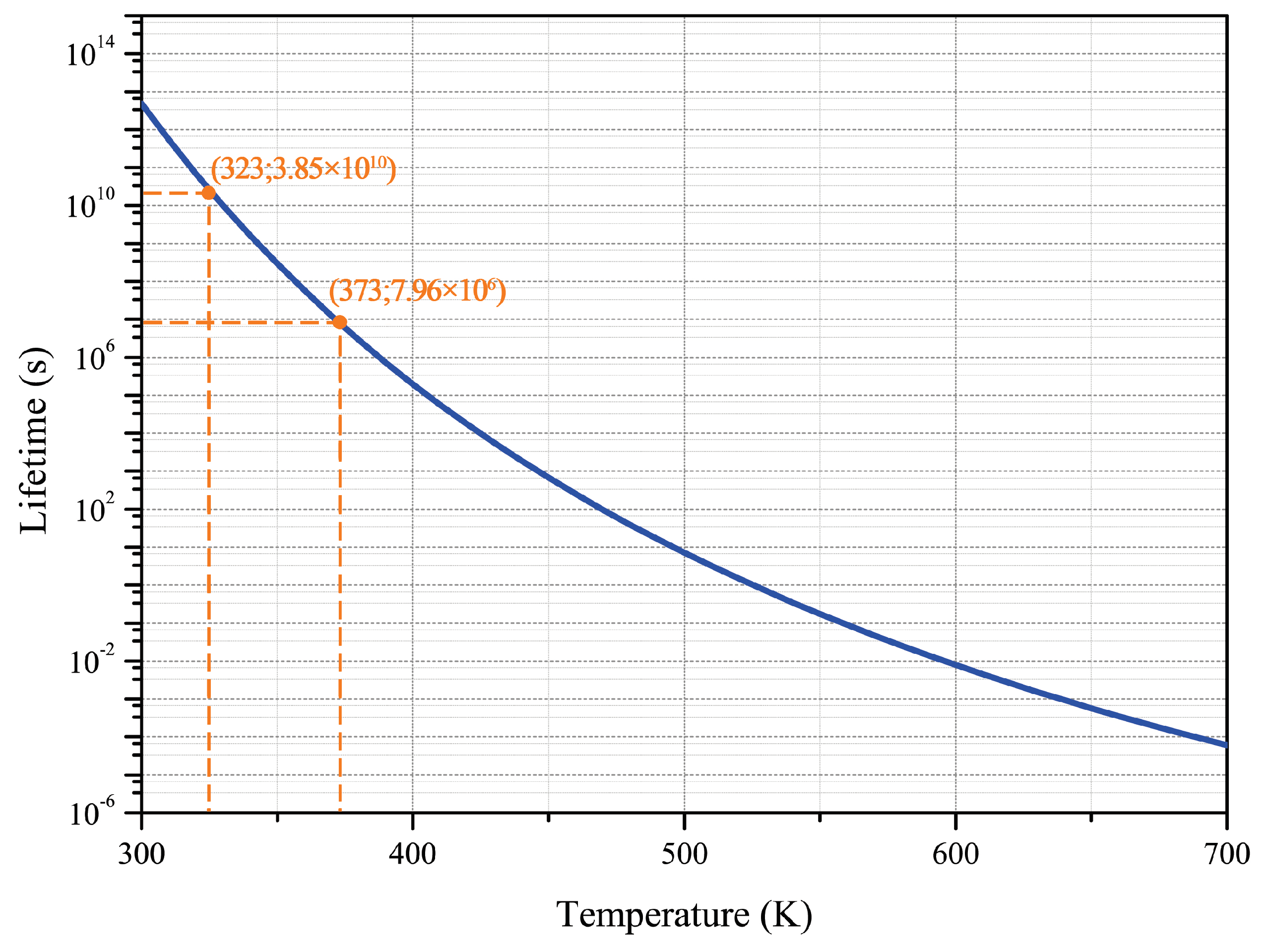
3.2. Determination of the Activation Energy
3.3. Reaction Model and Pre-Exponential Factor Determination
3.4. Results from the DSC Characterization
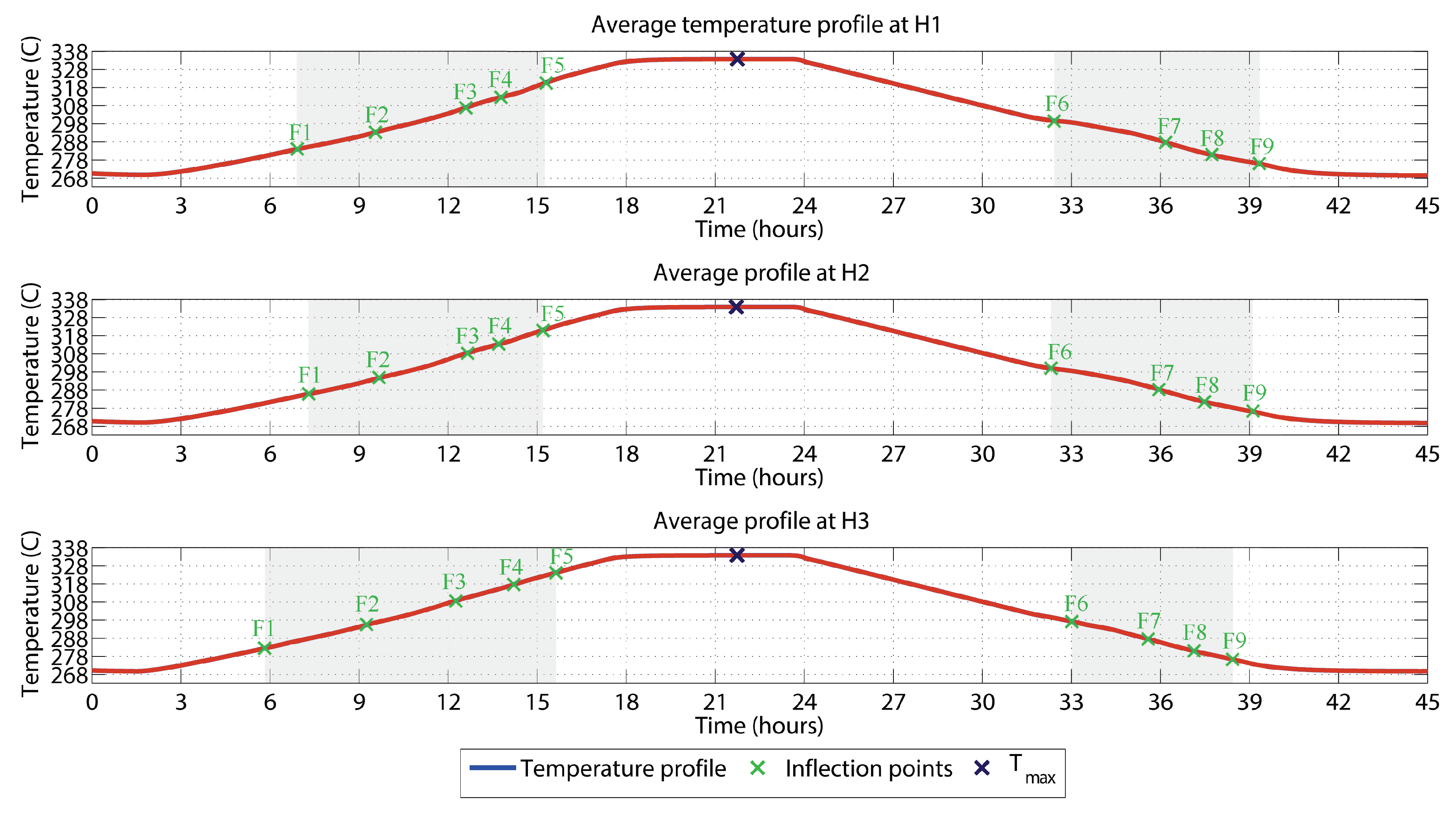
3.5. Results from the Thermal Monitoring
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aditya, L.; Mahlia, T.; Rismanchi, B.; Ng, H.; Hasan, M.; Metselaar, H.; Muraza, O.; Aditiya, H. A review on insulation materials for energy conservation in buildings. Renew. Sustain. Energy Rev. 2017, 73, 1352–1365. [Google Scholar] [CrossRef]
- Jelle, B.P. Traditional, state-of-the-art and future thermal building insulation materials and solutions—Properties, requirements and possibilities. Energy Build. 2011, 43, 2549–2563. [Google Scholar] [CrossRef]
- Schiavoni, S.; D’Alessandro, F.; Bianchi, F.; Asdrubali, F. Insulation materials for the building sector: A review and comparative analysis. Renew. Sustain. Energy Rev. 2016, 62, 988–1011. [Google Scholar] [CrossRef]
- Mehling, H.; Cabeza, L.F. Heat and Cold Storage with PCM—An up to Date Introduction into Basics and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; p. 308. [Google Scholar]
- Souayfane, F.; Fardoun, F.; Biwole, P.H. Phase change materials (PCM) for cooling applications in buildings: A review. Energy Build. 2016, 129, 396–431. [Google Scholar] [CrossRef]
- Konuklu, Y.; Ostry, M.; Paksoy, H.O.; Charvat, P. Review on using microencapsulated phase change materials (PCM) in building applications. Energy Build. 2015, 106, 134–155. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Fabiani, C.; Pisello, A.L.; Ubertini, F.; Materazzi, A.L.; Cotana, F. Innovative concretes for low-carbon constructions: A review. Int. J. Low-Carbon Technol. 2016, 12, 289–309. [Google Scholar] [CrossRef]
- Vicente, R.; Silva, T. Brick masonry walls with PCM macrocapsules: An experimental approach. Appl. Therm. Eng. 2014, 67, 24–34. [Google Scholar] [CrossRef]
- Chhugani, B.; Klinker, F.; Weinlaeder, H.; Reim, M. Energetic performance of two different PCM wallboards and their regeneration behavior in office rooms. Energy Procedia 2017, 122, 625–630. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Pisello, A.L.; Fabiani, C.; Ubertini, F.; Cotana, F. Multifunctional smart concretes with novel phase change materials: Mechanical and thermo-energy investigation. Appl. Energy 2018, 212, 1448–1461. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Tao, W.; Cao, X.; He, Y. Fatty acids as phase change materials: A review. Renew. Sustain. Energy Rev. 2014, 29, 482–498. [Google Scholar] [CrossRef]
- Kahwaji, S.; Johnson, M.B.; Kheirabadi, A.C.; Groulx, D.; White, M.A. Fatty acids and related phase change materials for reliable thermal energy storage at moderate temperatures. Sol. Energy Mater. Sol. Cells 2017, 167, 109–120. [Google Scholar] [CrossRef]
- Wang, R.; Ren, M.; Gao, X.; Qin, L. Preparation and properties of fatty acids based thermal energy storage aggregate concrete. Constr. Build. Mater. 2018, 165, 1–10. [Google Scholar] [CrossRef]
- Miró, L.; Oró, E.; Boer, D.; Cabeza, L.F. Embodied energy in thermal energy storage (TES) systems for high temperature applications. Appl. Energy 2015, 137, 793–799. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Miró, L.; Morera, J.M.; Bartolí, E.; Inés Fernández, A. Low carbon and low embodied energy materials in buildings: A review. Renew. Sustain. Energy Rev. 2013, 23, 536–542. [Google Scholar] [CrossRef]
- De Gracia, A.; Rincón, L.; Castell, A.; Jiménez, M.; Boer, D.; Medrano, M.; Cabeza, L.F. Life Cycle Assessment of the inclusion of phase change materials (PCM) in experimental buildings. Energy Build. 2010, 42, 1517–1523. [Google Scholar] [CrossRef]
- Oró, E.; Gil, A.; de Gracia, A.; Boer, D.; Cabeza, L.F. Comparative life cycle assessment of thermal energy storage systems for solar power plants. Renew. Energy 2012, 44, 166–173. [Google Scholar] [CrossRef]
- Sharma, R.K.; Ganesan, P.; Tyagi, V.V.; Metselaar, H.S.; Sandaran, S.C. Developments in organic solid-liquid phase change materials and their applications in thermal energy storage. Energy Convers. Manag. 2015, 95, 193–228. [Google Scholar] [CrossRef]
- Gallart-Sirvent, P.; Martín, M.; Villorbina, G.; Balcells, M.; Solé, A.; Barrenche, C.; Cabeza, L.F.; Canela-Garayoa, R. Fatty acid eutectic mixtures and derivatives from non-edible animal fat as phase change materials. RSC Adv. 2017, 7, 24133–24139. [Google Scholar] [CrossRef]
- Gallart-Sirvent, P.; Martín, M.; Solé, A.; Villorbina, G.; Balcells, M.; Cabeza, L.F.; Canela-Garayoa, R. Combining biocatalysts to achieve new phase change materials. Application to non-edible animal fat. Mol. Catal. 2018, 444, 76–83. [Google Scholar] [CrossRef]
- Yu, S.; Jeong, S.G.; Chung, O.; Kim, S. Bio-based PCM/carbon nanomaterials composites with enhanced thermal conductivity. Sol. Energy Mater. Sol. Cells 2014, 120, 549–554. [Google Scholar] [CrossRef]
- Kang, Y.; Jeong, S.G.; Wi, S.; Kim, S. Energy efficient Bio-based PCM with silica fume composites to apply in concrete for energy saving in buildings. Sol. Energy Mater. Sol. Cells 2015, 143, 430–434. [Google Scholar] [CrossRef]
- Crnkovic, P.M.; Koch, C.; Ávila, I.; Mortari, D.A.; Cordoba, A.M.; Moreira dos Santos, A. Determination of the activation energies of beef tallow and crude glycerin combustion using thermogravimetry. Biomass Bioenergy 2012, 44, 8–16. [Google Scholar] [CrossRef]
- Chetehouna, K.; Belayachi, N.; Rengel, B.; Hoxha, D.; Gillard, P. Investigation on the thermal degradation and kinetic parameters of innovative insulation materials using TGA-MS. Appl. Therm. Eng. 2015, 81, 177–184. [Google Scholar] [CrossRef]
- Asimakopoulou, E.K.; Kolaitis, D.I.; Founti, M.A. Fire safety aspects of PCM-enhanced gypsum plasterboards: An experimental and numerical investigation. Fire Saf. J. 2015, 72, 50–58. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Buratti, C.; Mousavi, S.; Barbanera, M.; Lascaro, E.; Cotana, F.; Bufacchi, M. Thermal behaviour and kinetic study of the olive oil production chain residues and their mixtures during co-combustion. Bioresour. Technol. 2016, 214, 266–275. [Google Scholar] [CrossRef]
- Carrasco, F.; Pags, P.; Gámez-Pérez, J.; Santana, O.O.; Maspoch, M.L. Kinetics of the thermal decomposition of processed poly(lactic acid). Polym. Degrad. Stab. 2010, 95, 2508–2514. [Google Scholar] [CrossRef]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Miura, K.; Maki, T. A simple method for estimating f(E) and k0(E) in the distributed activation energy model. Energy Fuels 1998, 12, 864–869. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Irmak Aslan, D.; Parthasarathy, P.; Goldfarb, J.L.; Ceylan, S. Pyrolysis reaction models of waste tires: Application of Master-Plots method for energy conversion via devolatilization. Waste Manag. 2017, 68, 405–411. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.C.; Cho, Y.J.; Eun, H.C.; Kim, E.H.; Kim, I.T. Kinetic study of a thermal dechlorination and oxidation of neodymium oxychloride. Thermochim. Acta 2007, 460, 53–59. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Sun, X.; Liu, Y. The mathematical prediction model for the oxidative stability of vegetable oils by the main fatty acids composition and thermogravimetric analysis. LWT 2018, 96, 51–57. [Google Scholar] [CrossRef]
- Kenda, E.S.; N’Tsoukpoe, K.E.; Ouédraogo, I.W.; Coulibaly, Y.; Py, X.; Ouédraogo, F.M.A.W. Jatropha curcas crude oil as heat transfer fluid or thermal energy storage material for concentrating solar power plants. Energy Sustain. Dev. 2017, 40, 59–67. [Google Scholar] [CrossRef]
- Gouveia De Souza, A.; Oliveira Santos, J.C.; Conceição, M.M.; Dantas Silva, M.C.; Prasad, S. A thermoanalytic and kinetic study of sunflower oil. Braz. J. Chem. Eng. 2004, 21, 265–273. [Google Scholar] [CrossRef]
- Trache, D.; Maggi, F.; Palmucci, I.; DeLuca, L.T. Thermal behavior and decomposition kinetics of composite solid propellants in the presence of amide burning rate suppressants. J. Therm. Anal. Calorim. 2018, 132, 1601–1615. [Google Scholar] [CrossRef]
- Li, H.; Niu, S.; Lu, C.; Wang, Y. Comprehensive Investigation of the Thermal Degradation Characteristics of Biodiesel and Its Feedstock Oil through TGA-FTIR. Energy Fuels 2015, 29, 5145–5153. [Google Scholar] [CrossRef]
- Galvan, D.; Orives, J.R.; Coppo, R.L.; Silva, E.T.; Angilelli, K.G.; Borsato, D. Determination of the kinetics and thermodynamics parameters of biodiesel oxidation reaction obtained from an optimized mixture of vegetable oil and animal fat. Energy Fuels 2013, 27, 6866–6871. [Google Scholar] [CrossRef]
- Mahfouz, R.M.; Bumajdad, A.; Al-Sagheer, F.A. γ-Irradiation effects on the kinetics and mechanism of the thermal decomposition of silver acetate. Radiat. Eff. Defects Solids 2009, 164, 170–177. [Google Scholar] [CrossRef]
- Turmanova, S.C.; Genieva, S.D.; Dimitrova, A.S.; Vlaev, L.T. Non-isothermal degradation kinetics of filled with rise husk ash polypropene composites. Express Polym. Lett. 2008, 2, 133–146. [Google Scholar] [CrossRef]

| Mechanism | Serial Number (k) | Symbol | ) | g() | |
|---|---|---|---|---|---|
| Order of reaction | |||||
| First-order | 1 | () | 0.462 | ||
| Second-order | 2 | () | ()−1 | 2.388 | |
| Third-order | 3 | () | /2 | 9.844 | |
| Diffusion | |||||
| One-way transport | 4 | 0.5 | 0.554 | ||
| Two-way transport | 5 | 0.990 | |||
| Three-way transport | 6 | 1.5 | 1.850 | ||
| Ginstling-Brounshtein equation | 7 | 1.5 | 1.234 | ||
| Limiting surface reaction between both phases | |||||
| One dimension | 8 | 1 | 0.183 | ||
| Two dimensions | 9 | 2 | 0.123 | ||
| Three dimensions | 10 | 3 | 0.202 | ||
| Random nucleation and nuclei growth | |||||
| Two-dimensional | 11 | 2 | 0.249 | ||
| Three-dimensional | 12 | 3 | 0.406 | ||
| Exponential nucleation | |||||
| Power law, n = 1/2 | 13 | 2 | 0.433 | ||
| Power law, n = 1/3 | 14 | 3 | 0.521 | ||
| Power law, n = 1/4 | 15 | 4 | 0.568 |
| Step | Temperature Setpoint (K) | Relative Humidity Set Point (%) | Duration (h) |
|---|---|---|---|
| S1 | 268.15 | 40 | 5.5 |
| S2 | 268.15 → 333.15 | 40 | 16 |
| S3 | 333.15 | 40 | 6 |
| S4 | 333.15 → 268.15 | 40 | 16 |
| S5 | 268.15 | 40 | 5.5 |
| Degree of Conversion () | Starink Method | Miura-Maki Method | ||
|---|---|---|---|---|
| E (kJ·mol) | R | E (kJ·mol) | R | |
| 0.20 | 47.70 | 0.9962 | 47.37 | 0.9962 |
| 0.25 | 51.72 | 0.9938 | 51.33 | 0.9937 |
| 0.30 | 56.56 | 0.9926 | 56.17 | 0.9925 |
| 0.35 | 61.58 | 0.9899 | 61.18 | 0.9898 |
| 0.40 | 66.03 | 0.9867 | 65.64 | 0.9865 |
| 0.45 | 70.23 | 0.9815 | 69.84 | 0.9813 |
| 0.50 | 73.95 | 0.9768 | 73.55 | 0.9765 |
| 0.55 | 77.20 | 0.9730 | 76.81 | 0.9727 |
| 0.60 | 80.49 | 0.9703 | 80.09 | 0.9700 |
| 0.65 | 83.92 | 0.9693 | 83.53 | 0.9690 |
| 0.70 | 87.62 | 0.9691 | 87.22 | 0.9688 |
| 0.75 | 92.08 | 0.9699 | 91.68 | 0.9696 |
| 0.80 | 97.66 | 0.9702 | 97.26 | 0.9700 |
| Average | 75.16 | 72.46 | ||
| Heating Rate (K·min) | A (s) | R |
|---|---|---|
| 5 | 5.85 × 10 | 0.9991 |
| 7 | 6.27 × 10 | 0.9968 |
| 10 | 6.66 × 10 | 0.9949 |
| 15 | 7.05 × 10 | 0.9951 |
| Average | 6.46 × 10 |
| Melting Temperature (K) | Melting Enthalpy (kJ·kg) |
|---|---|
| 275.03 | 5.67 |
| 298.30 | 23.27 |
| Position | H1 | H2 | H3 | |||
|---|---|---|---|---|---|---|
| Quantity | ||||||
| Unit | (hh:mm:ss) | (K) | (hh:mm:ss) | (K) | (hh:mm:ss) | (K) |
| F1 | 06:54:20 | 283.8 | 07:25:20 | 286.2 | 05:45:20 | 282.2 |
| F2 | 09:31:10 | 293.1 | 09:54:10 | 295.6 | 09:26:50 | 296.2 |
| F3 | 12:41:50 | 307.5 | 12:40:00 | 308.6 | 12:15:30 | 308.5 |
| F4 | 14:03:30 | 313.8 | 13:45:10 | 313.5 | 14:12:40 | 317.7 |
| F5 | 15:22:10 | 321.2 | 15:15:10 | 321.4 | 15:37:50 | 324.2 |
| F6 | 32:23:20 | 299.7 | 32:25:00 | 299.8 | 32:58:20 | 297.3 |
| F7 | 36:10:00 | 287.8 | 35:56:40 | 288.3 | 35:58:20 | 287.6 |
| F8 | 37:30:00 | 281.7 | 37:35:00 | 281.1 | 37:10:00 | 280.8 |
| F9 | 39:25:00 | 275.7 | 39:13:20 | 275.8 | 38:18:20 | 276.8 |
| Max | 22:34:40 | 333.6 | 22:30:50 | 333.6 | 22:28:05 | 333.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabiani, C.; Pisello, A.L.; Barbanera, M.; Cabeza, L.F.; Cotana, F. Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation. Energies 2019, 12, 1111. https://doi.org/10.3390/en12061111
Fabiani C, Pisello AL, Barbanera M, Cabeza LF, Cotana F. Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation. Energies. 2019; 12(6):1111. https://doi.org/10.3390/en12061111
Chicago/Turabian StyleFabiani, Claudia, Anna Laura Pisello, Marco Barbanera, Luisa F. Cabeza, and Franco Cotana. 2019. "Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation" Energies 12, no. 6: 1111. https://doi.org/10.3390/en12061111
APA StyleFabiani, C., Pisello, A. L., Barbanera, M., Cabeza, L. F., & Cotana, F. (2019). Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation. Energies, 12(6), 1111. https://doi.org/10.3390/en12061111








