Enthalpies of Hydrate Formation from Hydrate Formers Dissolved in Water
Abstract
:1. Introduction
2. Methodologies
2.1. Residual Thermodynamic Modeling of Hydrate Formation from Water and Separate Hydrate Former Phase
2.2. Residual Thermodynamic Modeling of Hydrate Formation from Water and Dissolved Hydrate Former in Water
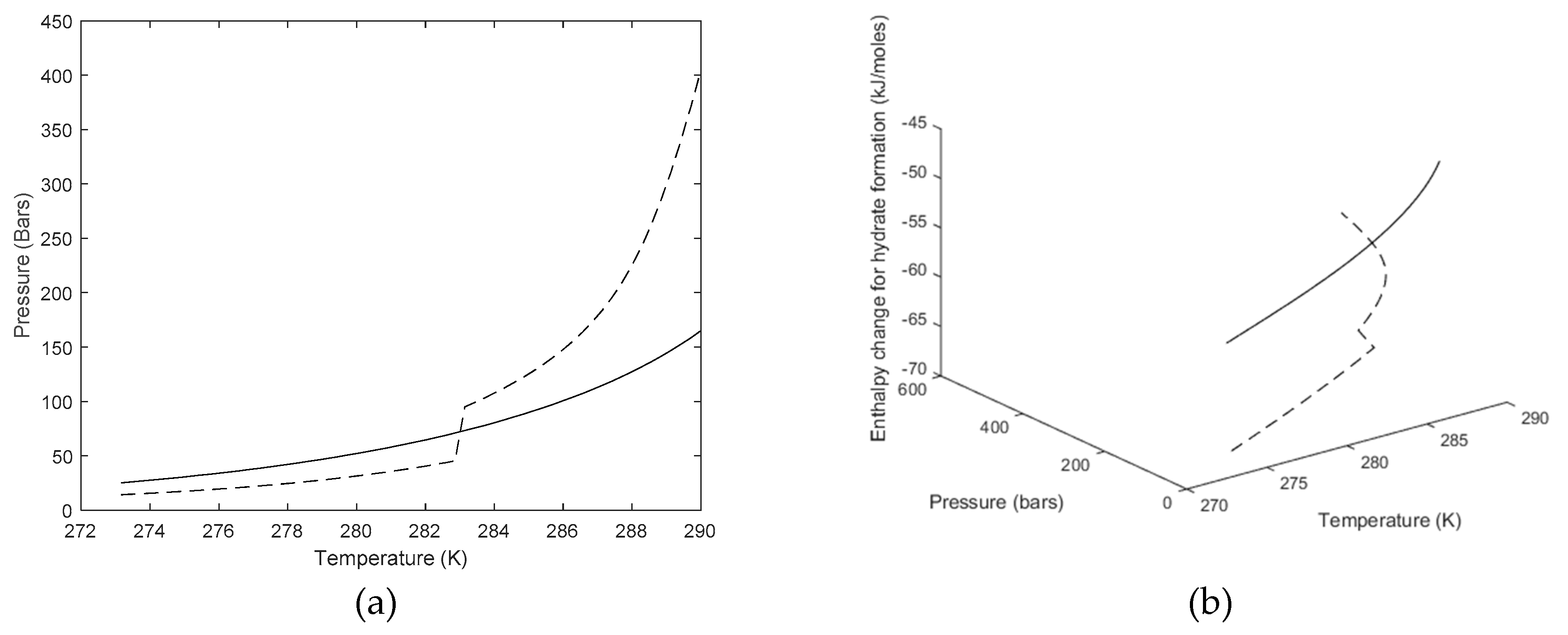
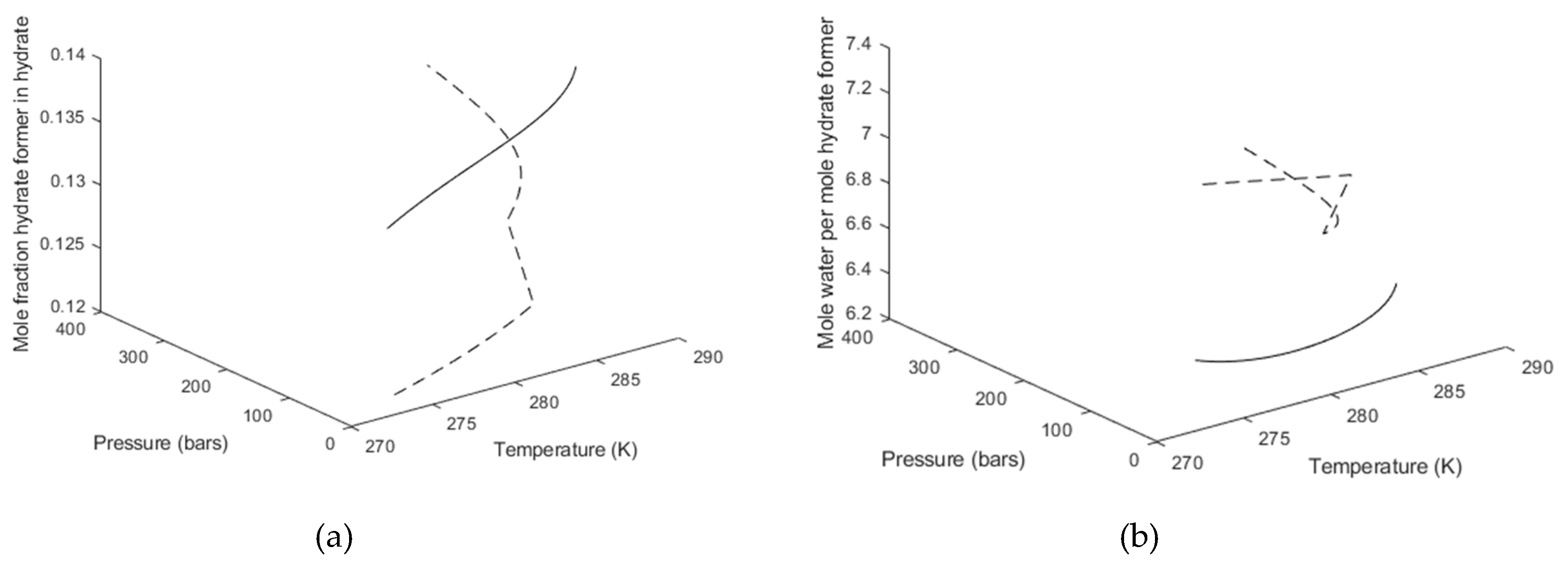
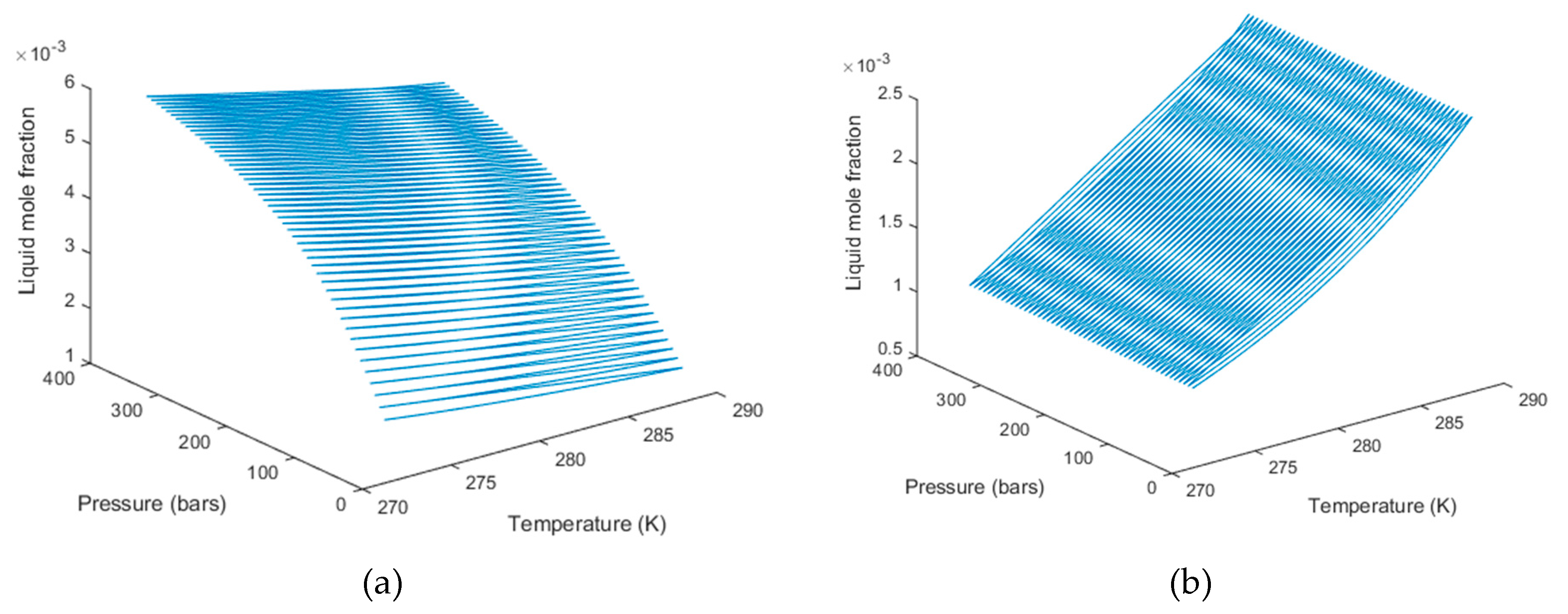
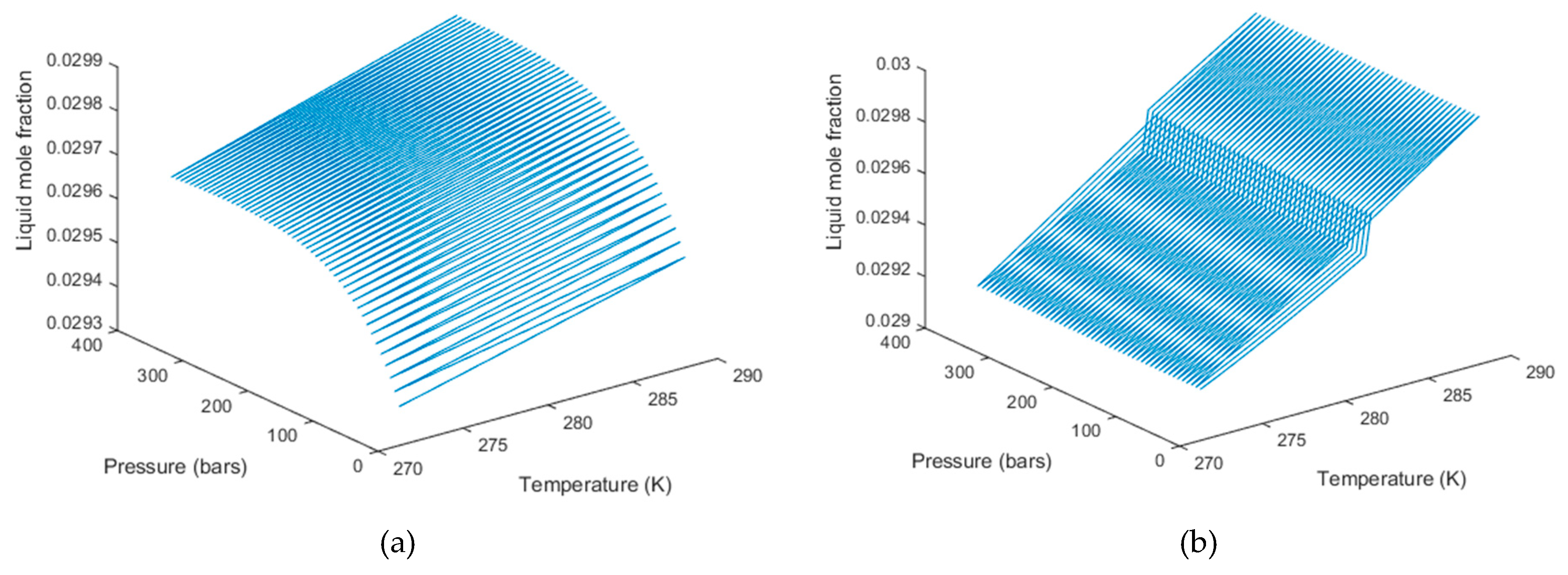
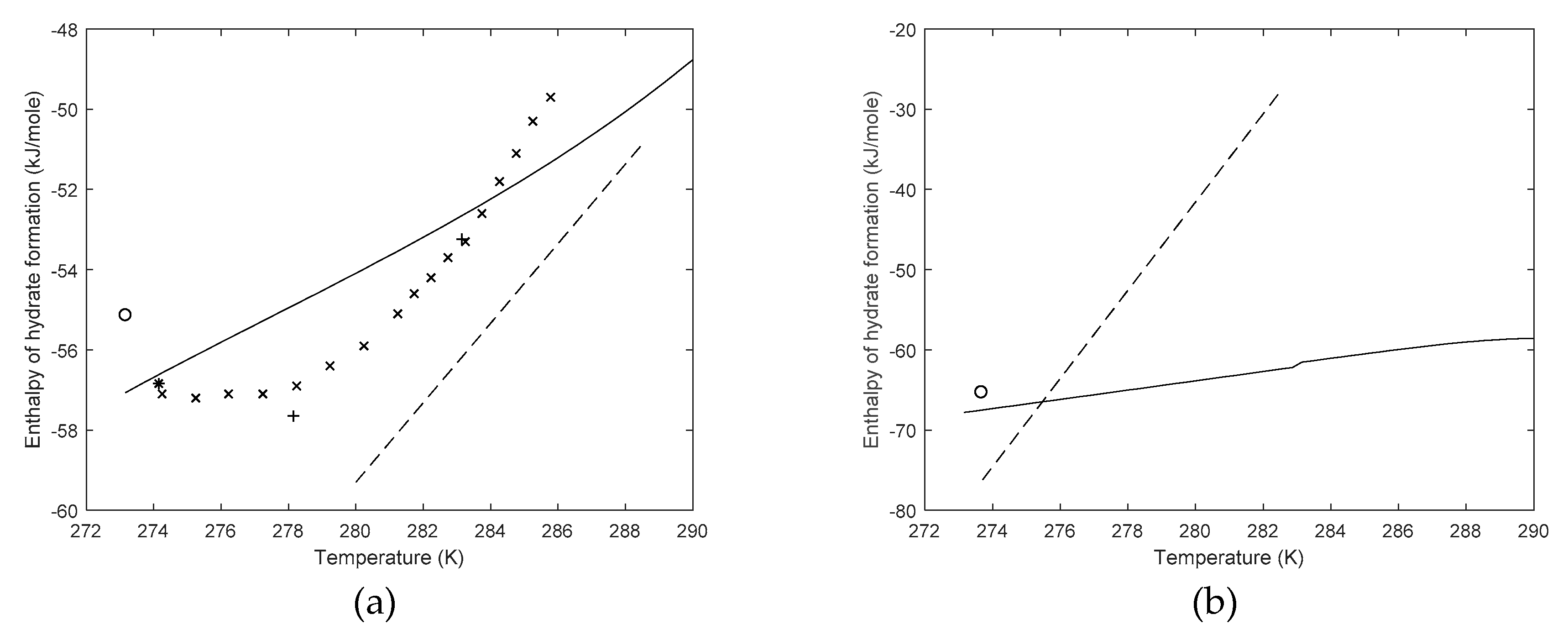
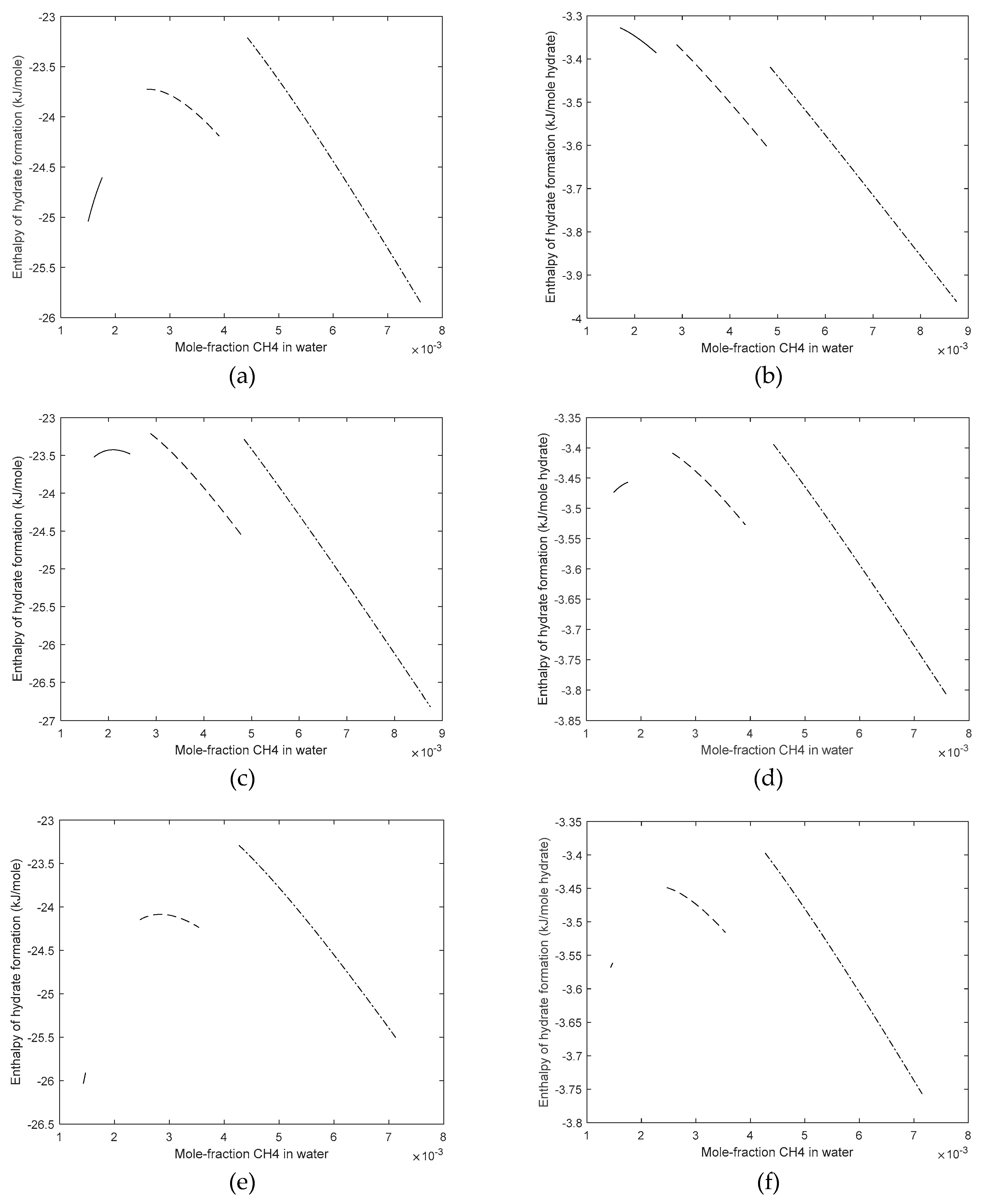
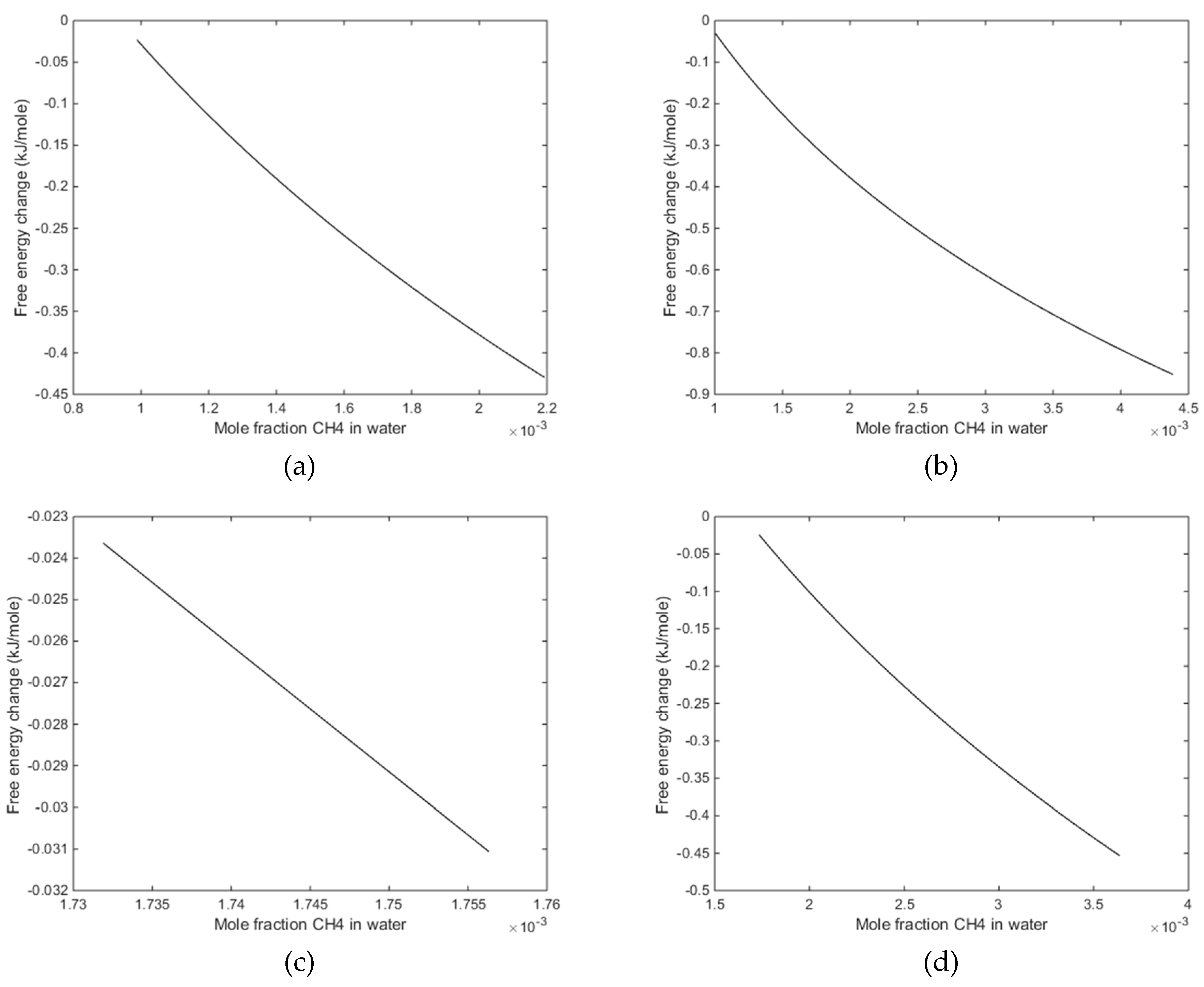
3. Results
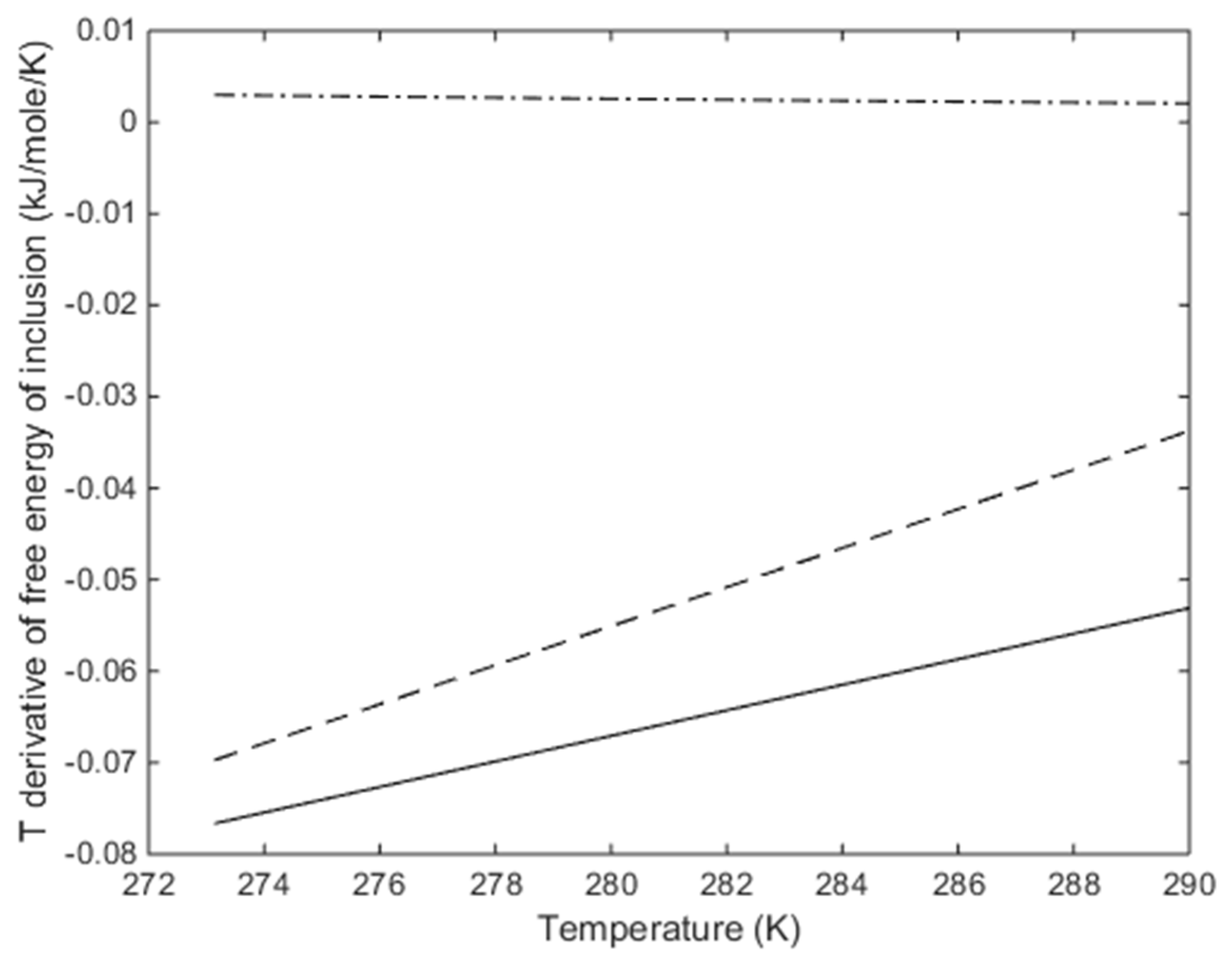
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Dallimore, S.R.; Uchida, T.; Collett, T.S. (Eds.) Scientific Results from JAPEX/JNOC/GSC Mallik 2L-38 Gas Hydrate Research Well; Geological Survey of Canada Bulletin: Mackenzie Delta, NT, Canada, 1999; Volume 544.
- Hancock, S.H.; Collett, T.S.; Dallimore, S.R.; Satoh, T.; Inoue, T.; Huenges, E.; Henninges, J.; Weatherill, B. Overview of Thermal-Stimulation Production-Test Results for the JAPEX/JNOC/GSC et al. Mallik 5l38 Gas Hydrate Production Research Well; Geological Survey of Canada: Ottawa, ON, Canada, 2005; p. 585.
- Konno, Y.; National Institute of Advanced Industrial Science and Technology (AIST), Japan. Oral Presentation at Nanotechnology and Nano-Geoscience in Oil and Gas Industry, 4–8 March 2014. Available online: https://connect.spe.org/events/eventdescription?CalendarEventKey=7b08d694-1554-4e55-a2ce-8f5538b723fc (accessed on 17 March 2019).
- Tenma, N. AIST, Tokyo, Japan, Recent Status of Methane Hydrate R&D Program in Japan. In Proceedings of the Oral presentation at 11th International Methane Hydrate Research and Development, Corpus Christie, TX, USA, 5–8 December 2017. [Google Scholar]
- Lee, H.; Seo, Y.; Seo, Y.-T.; Moudrakovski, I.L.; Ripmeester, J.A. Recovering Methane from Solid Methane Hydrate with Carbon Dioxide. Angew. Chem. Int. Ed. 2003, 115, 5202–5205. [Google Scholar] [CrossRef]
- Falenty, A.; Genov, G.; Hansen, T.C.; Kuhs, W.F.; Salamatin, A.N. Kinetics of CO2-Hydrate Formation from Water Frost at Low Temperatures: Experimental Results and Theoretical Model. J. Phys. Chem. C 2010, 115, 4022–4032. [Google Scholar] [CrossRef]
- Baig, K. Nano to Micro Scale Modeling of Hydrate Phase Transition Kinetics. PhD Thesis, University of Bergen, Bergen, Norway, 2017. [Google Scholar]
- Baig, K.; Kvamme, B.; Kuznetsova, T.; Bauman, J. The impact of water/hydrate film thickness on the kinetic rate of mixed hydrate formation during CO2 injection into CH4 hydrate. AICHE J. 2015, 61, 3944–3957. [Google Scholar] [CrossRef]
- Schoderbek, D.; Farrell, H.; Hester, K.; Howard, J.; Raterman, K.; Silpngarmlert, S.; Lloyd Martin, K.; Smith, B.; Klein, P. ConocoPhillips Gas Hydrate Production Test Final Technical Report 1 October 2008–30 June 2013; DOE Award No.: DE-NT0006553; ConocoPhillips Company for United States Department of Energy National Energy Technology Laboratory: Morgantown, WV, USA, 2013.
- Kvamme, B. Thermodynamic limitations of the CO2/N2 mixture injected into CH4 hydrate in the Ignik Sikumi field trial, 2016. J. Chem. Eng. Data 2016, 61, 1280–1295. [Google Scholar] [CrossRef]
- Kvamme, B.; Selvåg, J.; Aromada, S.A.; Saeidi, N.; Kuznetsova, T. Methanol as hydrate inhibito and hydrate activator. Phys. Chem. Chem. Phys. 2018, 20, 21968–21987. [Google Scholar] [CrossRef] [PubMed]
- Austvik, T.; Hustvedt, E.; Gjertsen, L.H. Formation and removal of hydrate plugs—Field trial at Tommeliten. In Proceedings of the 76 Annual Meeting of the Gas Processors Asso- Ciation (GPA), San Antonio, TX, USA, 10–12 March 1997. [Google Scholar]
- Gibbs, J.W. The Collected Works of J. Willard Gibbs, Thermodynamics; Yale University Press: New Haven, CT, USA, 1928; Volume 1, pp. 55–353. [Google Scholar]
- Kvamme, B.; Graue, A.; Kuznetsova, T.; Gránásy, L.; Imre Tóth, G.; Pusztaib, T.; Tegzeb, G. Kinetics of solid hydrate formation by carbon dioxide: Phase field theory of hydrate nucleation and magnetic resonance imaging. Phys. Chem. Chem. Phys. 2004, 6, 2327–2334. [Google Scholar] [CrossRef]
- Tegze, G.; Pusztai, T.; Tóth, G.; Gránásy, L.; Svandal, A.; Buanes, T.; Kuznetsova, T.; Kvamme, B. Multiscale approach to CO2 hydrate formation in aqueous solution: Phase field theory and molecular dynamics. Nucleation and growth. J. Chem. Phys. 2006, 124, 234710. [Google Scholar] [CrossRef]
- Kvamme, B.; Tanaka, H. Thermodynamic stability of hydrates for ethane, ethylene, and carbon dioxide. J. Phys. Chem. 1995, 99, 7114–7119. [Google Scholar] [CrossRef]
- Kuznetsova, T.; Kvamme, B. Grand canonical molecular dynamics for TIP4P water systems. Mol. Phys. 1999, 97, 423–431. [Google Scholar] [CrossRef]
- Kvamme, B. Feasibility of simultaneous CO2 storage and CH4 production from natural gas hydrate using mixtures of CO2 and N2. Can. J. Chem. 2015, 93, 897–905. [Google Scholar] [CrossRef]
- Kvamme, B.; Kuznetsova, T.; Sapate, A.; Qorbani, K. Thermodynamic implications of adding N2 to CO2 for production of CH4 from hydrates. J. Nat. Gas Sci. Eng. 2016, 35 Pt B, 1594–1608. [Google Scholar] [CrossRef]
- Kvamme, B.; Kuznetsova, T.; Bauman, J.M.; Sjöblom, S.; Kulkarni, A.A. Hydrate Formation during Transport of Natural Gas Containing Water and Impurities. J. Chem. Eng. Data 2016, 61, 936–949. [Google Scholar] [CrossRef]
- Aromada, S.A. New Concept for Evaluating the Risk of Hydrate Formation during Processing and Transport of Hydrocarbons. Master’s Thesis, The University of Bergen, Bergen, Norway, 2017. [Google Scholar]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Buanes, T. Mean-Field Approaches Applied to Hydrate Phase Transition. PhD Thesis, University of Bergen, Bergen, Norway, 2006. [Google Scholar]
- Svandal, A.; Kuznetsova, T.; Kvamme, B. Thermodynamic properties and phase transitions in the H2O/CO2/CH4 system. Fluid Phase Equilib. 2006, 246, 177–184. [Google Scholar] [CrossRef]
- Svandal, A. Modeling Hydrate Phase Transitions Using Mean-Field Approaches; University of Bergen: Bergen, Norway, 2006. [Google Scholar]
- Kvamme, B.; Lund, A. The influence of gas-gas interactions on the langmuir-constants for some natural gas hydrates. Fluid Phase Equilib. 1993, 90, 15–44. [Google Scholar] [CrossRef]
- Kvamme, B.; Førrisdahl, O.K. Polar guest-molecules in natural gas hydrates. Fluid Phase Equilib. 1993, 83, 427–435. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Chazallon, B.; Klapproth, A.; Pauer, F. Filling isotherms in clathrate hydrates. Rev. High Press. Sci. Technol. 1998, 7, 1147–1149. [Google Scholar] [CrossRef]
- Nasir, K.K.Q.; Lau, K.K.; Lal, B. World Academy of Science, Engineering and Technology. Int. J. Chem. Mol. Eng. 2014, 8, 4. [Google Scholar]
- Nakamura, T.; Makino, T.; Sugahara, T.; Ohgaki, K. Stability boundaries of gas hydrates helped by methane—Structure-H hydrates of methylcyclohexane and cis-1,2-dimethylcyclohexane. Chem. Eng. Sci. 2003, 58, 269–273. [Google Scholar] [CrossRef]
- Deaton, W.M.; Frost, E.M., Jr. Clathrate Hydrates and Their Relation to the Operations of Natural Gas Pipelines; US Bureau of Mines Monograph; American Gas Association: Washington, WA, USA, 1946; Volume 8. [Google Scholar]
- Kang, S.-P.; Lee, H.; Ryu, B.-J. Enthalpies of dissociation of clathrate hydrates of carbon dioxide. J. Chem. Thermodyn. 2001, 33, 513–521. [Google Scholar] [CrossRef]
- Lievois, J.S.; Perkins, R.; Martin, R.J.; Kobayashi, R. Development of An Automated, High Pressure Heat Flux Calo-rimeter and its Application to Measure the Heat of Dissociation and Hydrate Numbers of Methane Hydrate. Fluid Phase Equilib. 1990, 59, 73–79. [Google Scholar] [CrossRef]
- Kvamme, B.; Kuznetsova, T.; Pilvi-Helina Kivelæ, P.-H. Adsorption of water and carbon dioxide on Hematite and consequences for possible hydrate formation. Phys. Chem. Chem. Phys. 2012, 14, 4410–4424. [Google Scholar] [CrossRef] [PubMed]
- Van Cuong, P. Transport and Adsorption of CO2 and H2O on Calcite and Clathrate Hydrate. PhD Thesis, University of Bergen, Bergen, Norway, 2012. [Google Scholar]
- Austrheim, M.H. Evaluation of Methane and Water Structure at a Hematite Surface—A Hydrate Prevention Perspective. Master’s Thesis, University of Bergen, Bergen, Norway, 2017. [Google Scholar]
- Nesse Knarvik, A.B. Examination of Water and Methane Structuring at a Hematite Surface in the Presence of MEG. Master’s Thesis, University of Bergen, Bergen, Norway, 2017. [Google Scholar]
- Mohammad, N. Heterogeneous Hydrate Nucleation on Calcite [1014] and Kaolinite [001] Surfaces: A Molecular Dynamics Simulation Study. Master’s Thesis, University of Bergen, Bergen, Norway, 2016. [Google Scholar]
- Kvamme, B.; Svandal, A.; Buanes, T.; Kuznetsova, T. Phase field approaches to the kinetic modeling of hydrate phase transitions. In Natural Gas Hydrates—Energy Resource Potential and Associated Geologic Hazards; Collett, T., Johnson, A., Knapp, C., Boswell, R., Eds.; AAPG Memoir: Tulsa, OK, USA, 2009; Volume 89, pp. 758–769. [Google Scholar]
- Kvamme, B.; Qasim, M.; Baig, K.; Kivelä, P.-H.; Bauman, J. Phase field theory modeling of methane fluxes from exposed natural gas hydrate reservoirs. Int. J. Greenh. Gas Control 2014, 29, 263–278. [Google Scholar] [CrossRef]
- Qasim, M. Microscale Modeling of Natural Gas Hydrates in Reservoirs. Ph.D. Thesis, University of Bergen, Bergen, Norway, 2012. [Google Scholar]
| Property | CH4 | CO2 | ||
|---|---|---|---|---|
| Large Cavity | Small Cavity | Large Cavity | Small Cavity | |
| (kJ/mole) | –16.53 | –17.73 | –27.65 | –10.58 |
| Vki (Å3) | 164.2 | 89.2 | 135.6 | 76.9 |
| i | a0 | a1 |
|---|---|---|
| 1 | −139.137483 | −138.899061 |
| 3 | −76.549658 | −72.397006 |
| 5 | −20.868725 | −14.715982 |
| 7 | 18.030987 | 24.548835 |
| 9 | 44.210433 | 52.904238 |
| 11 | 63.353037 | 71.596515 |
| 13 | 74.713278 | 82.605791 |
| 15 | 80.411175 | 88.536302 |
| 17 | 82.710575 | 90.262518 |
| 19 | 82.017332 | 89.094887 |
| 21 | 79.373137 | 85.956670 |
| 23 | 75.429910 | 81.519167 |
| 25 | 70.680932 | 76.270320 |
| 27 | 65.490785 | 70.551406 |
| 29 | 60.126698 | 64.683147 |
| 31 | 54.782421 | 58.865478 |
| 33 | 49.592998 | 53.235844 |
| 35 | 44.500001 | 47.728622 |
| 37 | 39.869990 | 42.730831 |
| 39 | 35.597488 | 38.125674 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kvamme, B. Enthalpies of Hydrate Formation from Hydrate Formers Dissolved in Water. Energies 2019, 12, 1039. https://doi.org/10.3390/en12061039
Kvamme B. Enthalpies of Hydrate Formation from Hydrate Formers Dissolved in Water. Energies. 2019; 12(6):1039. https://doi.org/10.3390/en12061039
Chicago/Turabian StyleKvamme, Bjørn. 2019. "Enthalpies of Hydrate Formation from Hydrate Formers Dissolved in Water" Energies 12, no. 6: 1039. https://doi.org/10.3390/en12061039
APA StyleKvamme, B. (2019). Enthalpies of Hydrate Formation from Hydrate Formers Dissolved in Water. Energies, 12(6), 1039. https://doi.org/10.3390/en12061039





