Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region
Abstract
1. Introduction
2. Materials and Methods
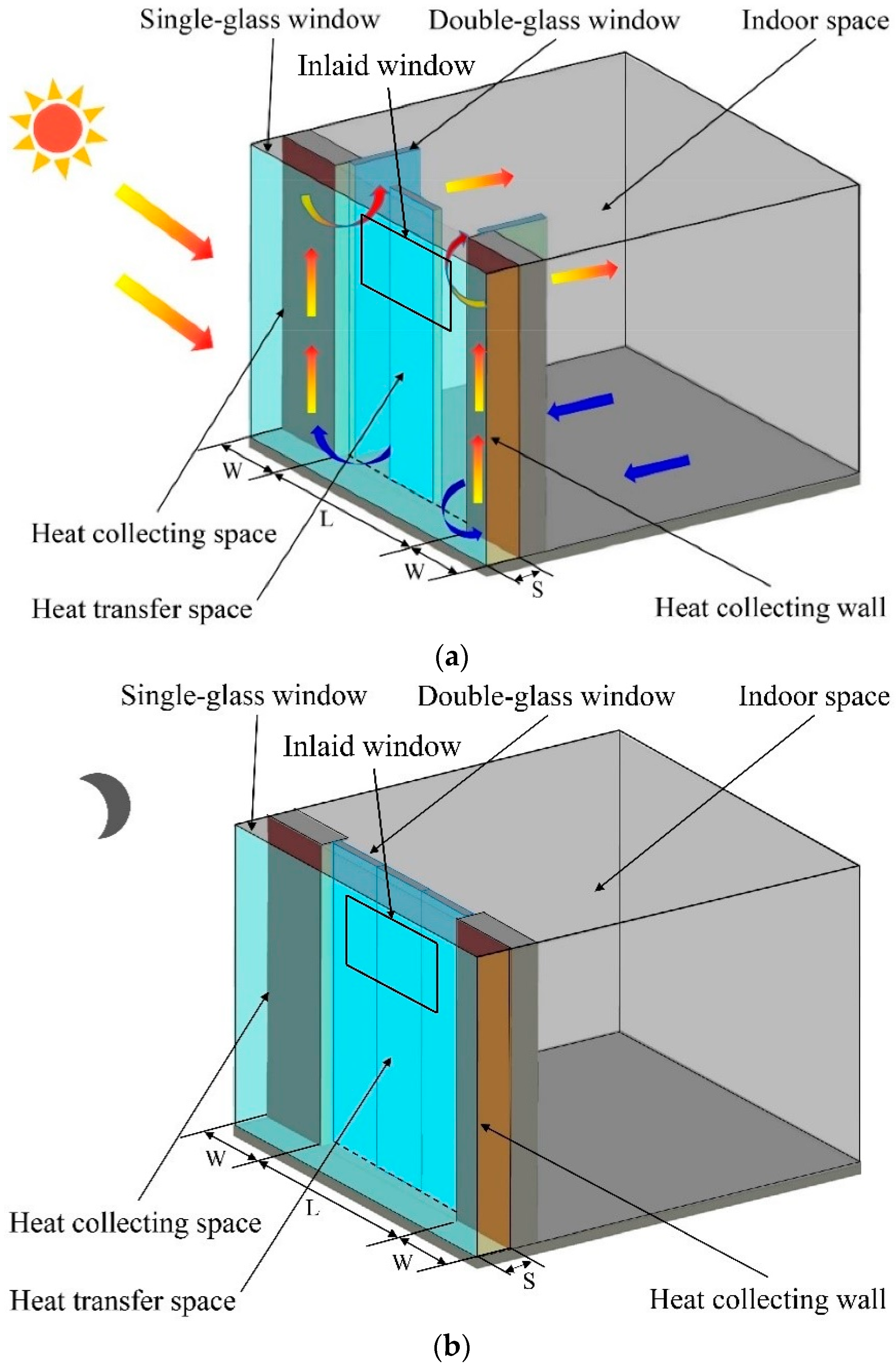
2.1. Principle of HHCF
- In a sunny day, solar energy is absorbed by the exterior surface of the heat collecting wall and converted into thermal energy for heating the air convectively within the heat collecting space. With the inner double-glass window open, the heated air in the heat collecting space rises up and reaches the top of the heat collecting space under the effect of the buoyancy force. Then, the heated air gathers at the top of the heat collecting space and increases the air pressure at the top of the heat collecting space. Finally, under the effect of the pressure difference, the heated air passes through the heat transfer space and enters into the indoor space along the horizontal direction. Meanwhile, at the bottom of the heat collecting space, the low-pressure cavity is supplied by the indoor air along the horizontal direction. In this way, thermal energy is transferred into the room space and the indoor temperature rises. Moreover, sunlight can also penetrate the windows into the indoor space directly and the solar energy is stored in the interior building construction.
- At night or during a cloudy day, the inner double-glass window should be kept closed, and it increases the thermal resistance between the indoor space and the outdoor environment. Consequently, the heat loss from the indoor space to the outdoor environment can be effectively reduced, especially at night.
2.2. Modeling of the Building with HHCF
2.2.1. Assumptions
- (1)
- Thermal properties of the building materials are kept constant.
- (2)
- Heat transfer processes through walls, floor, roof, and windows are considered as one-dimensional.
- (3)
- The heat storage of glass is ignored.
- (4)
- Air in each zone is well-mixed.
- (5)
- Mean air flow rate between the heat collecting space and the heat transfer space is identical with that between the heat transfer space and the indoor space.
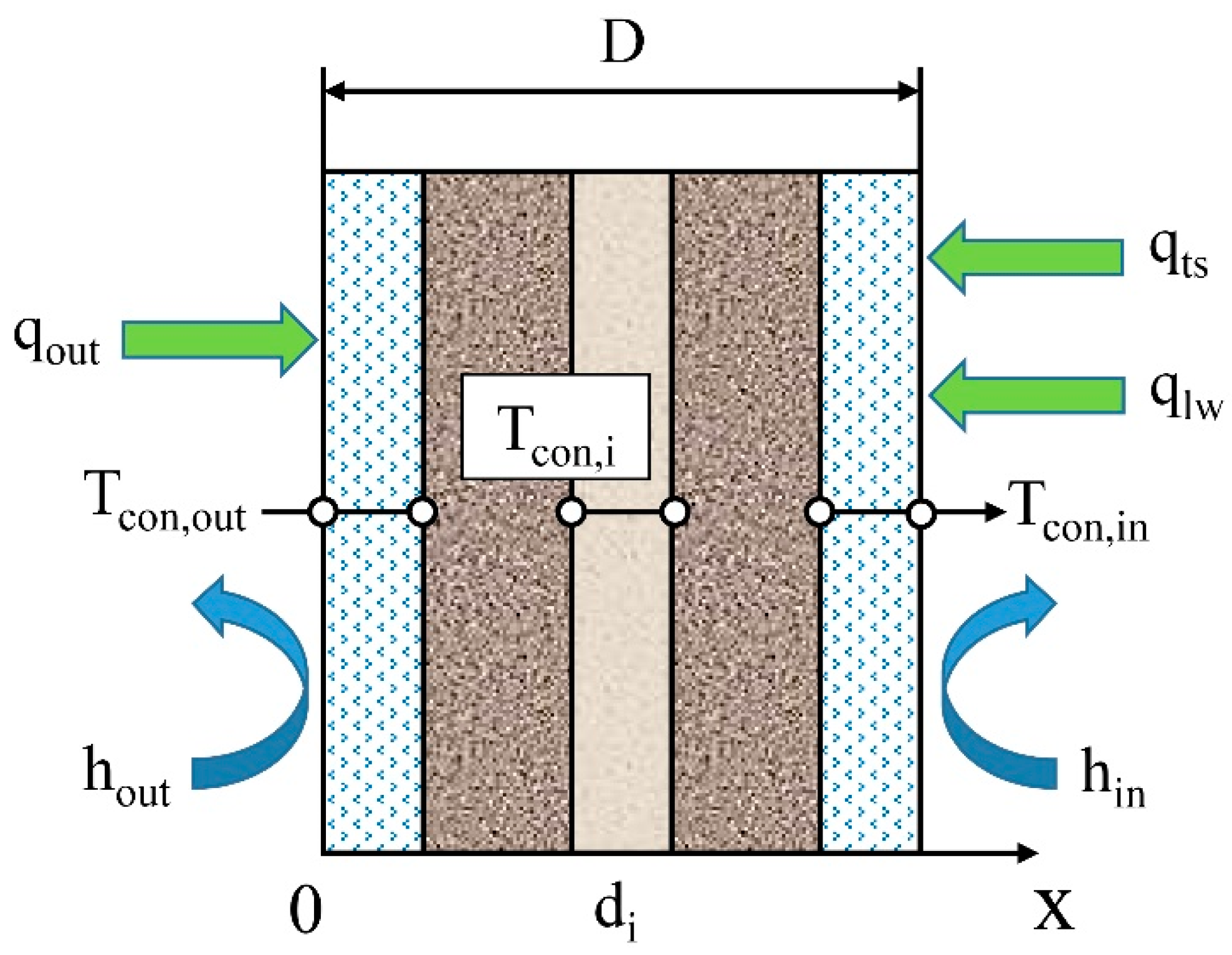
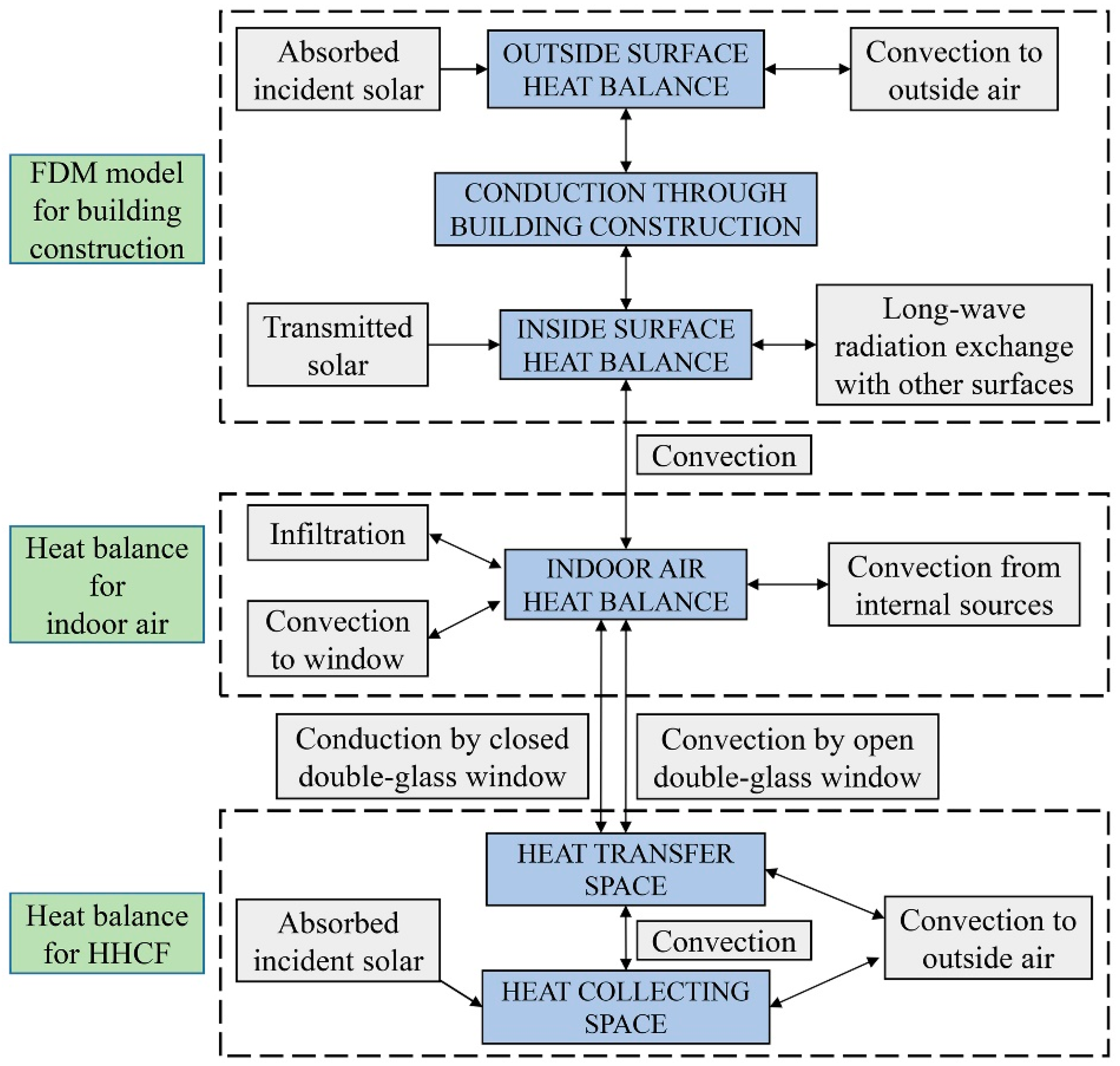
2.2.2. Energy Balance Equations
2.2.3. Validation of Heat Transfer Model
2.2.4. Energy Saving Comparison of HHCF
3. Results and Discussion
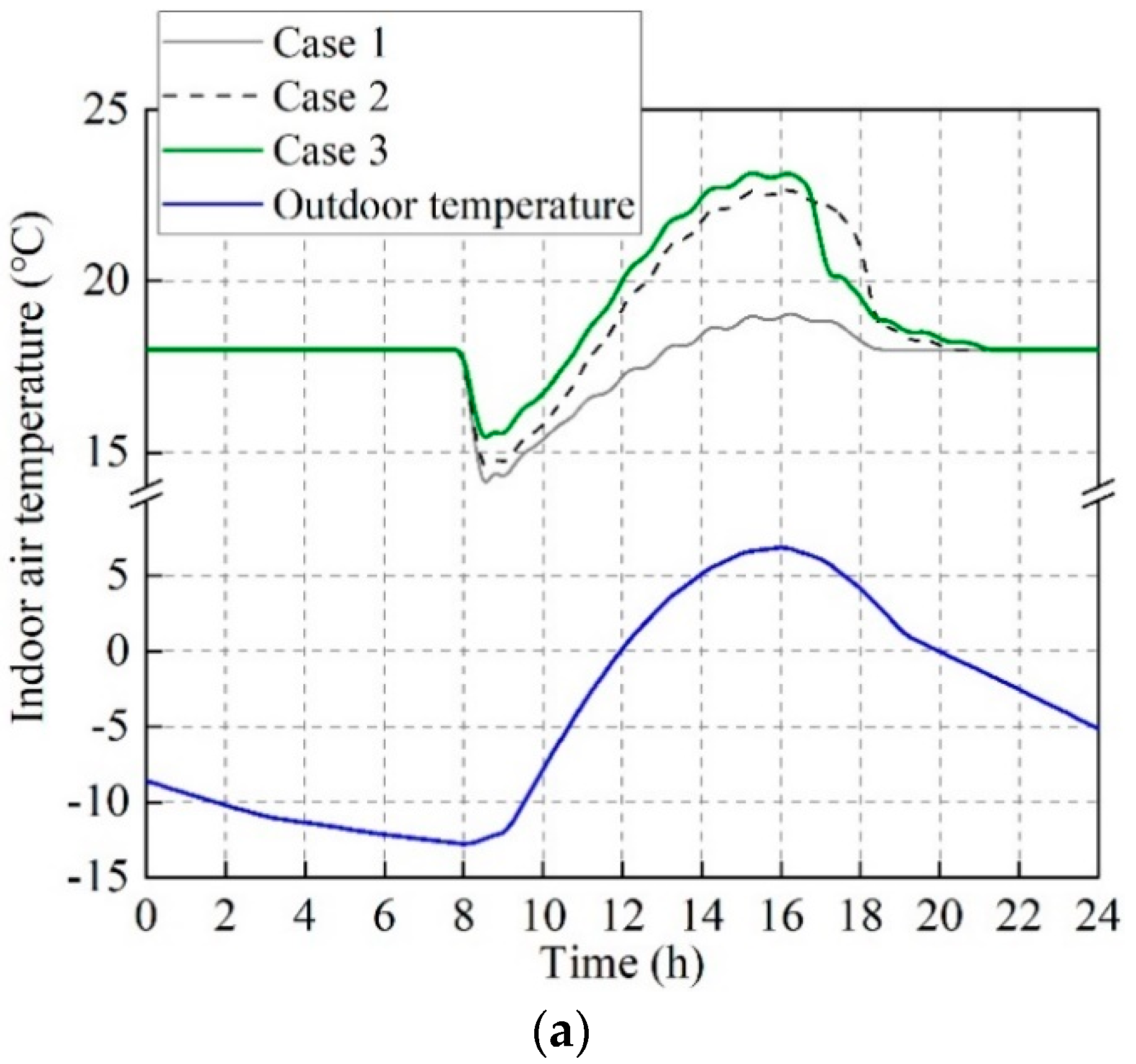
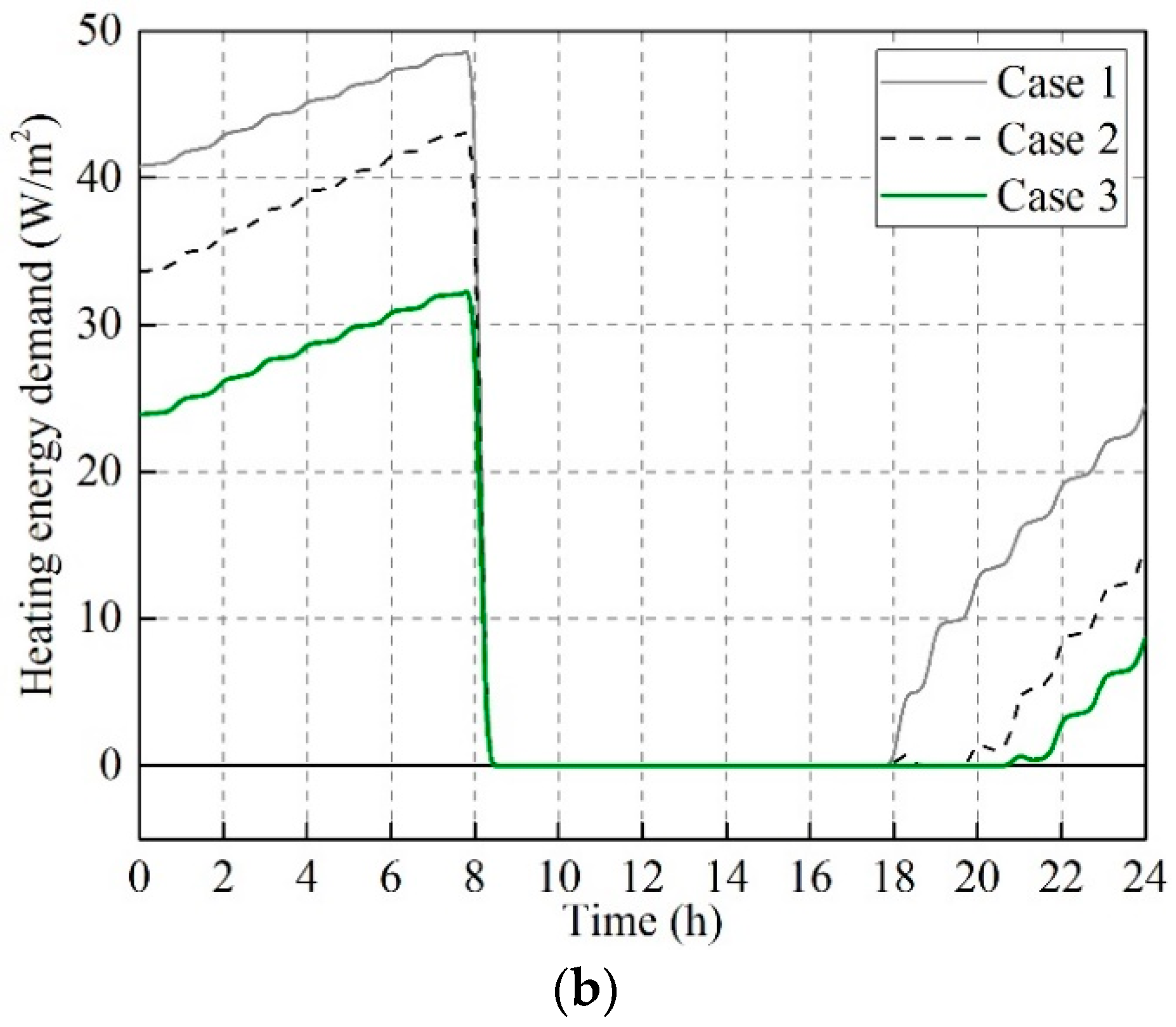
3.1. Energy Saving Potential of HHCF
3.2. Parametric Study on the Thermal Performance of a Room with a HHCF
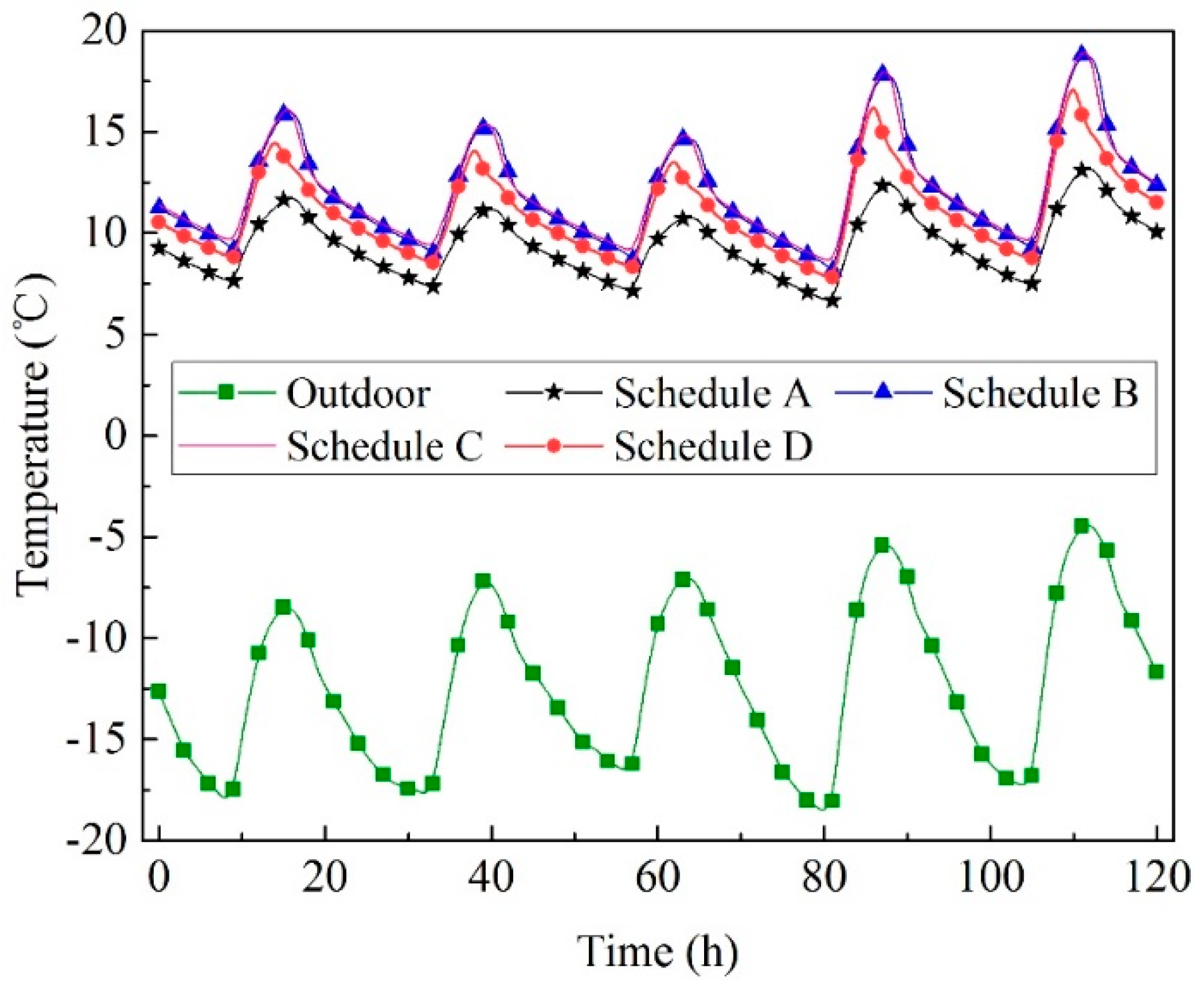
3.2.1. Effects of Window Operational Schedule
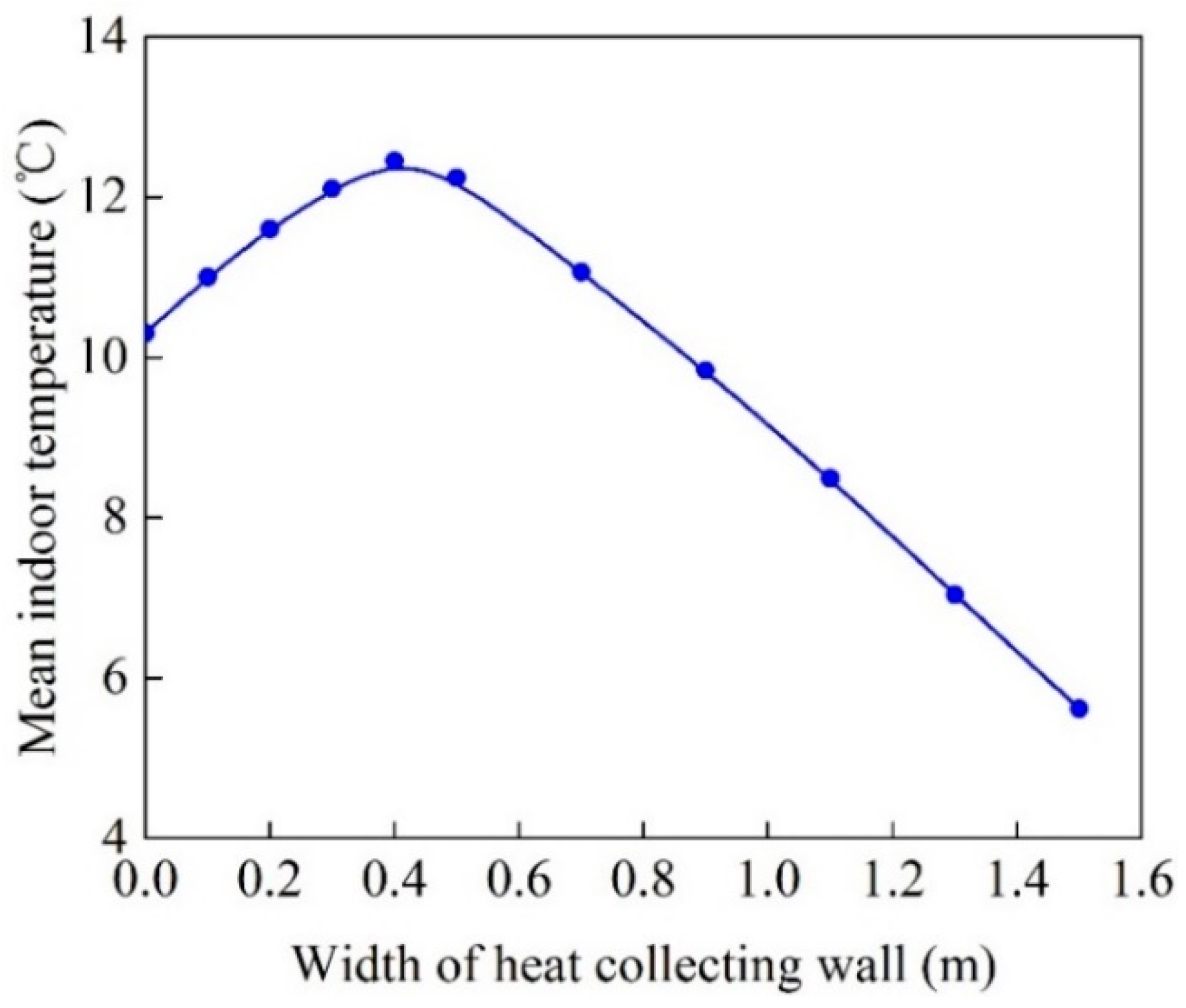
3.2.2. Effects of Width of Heat Collecting Wall
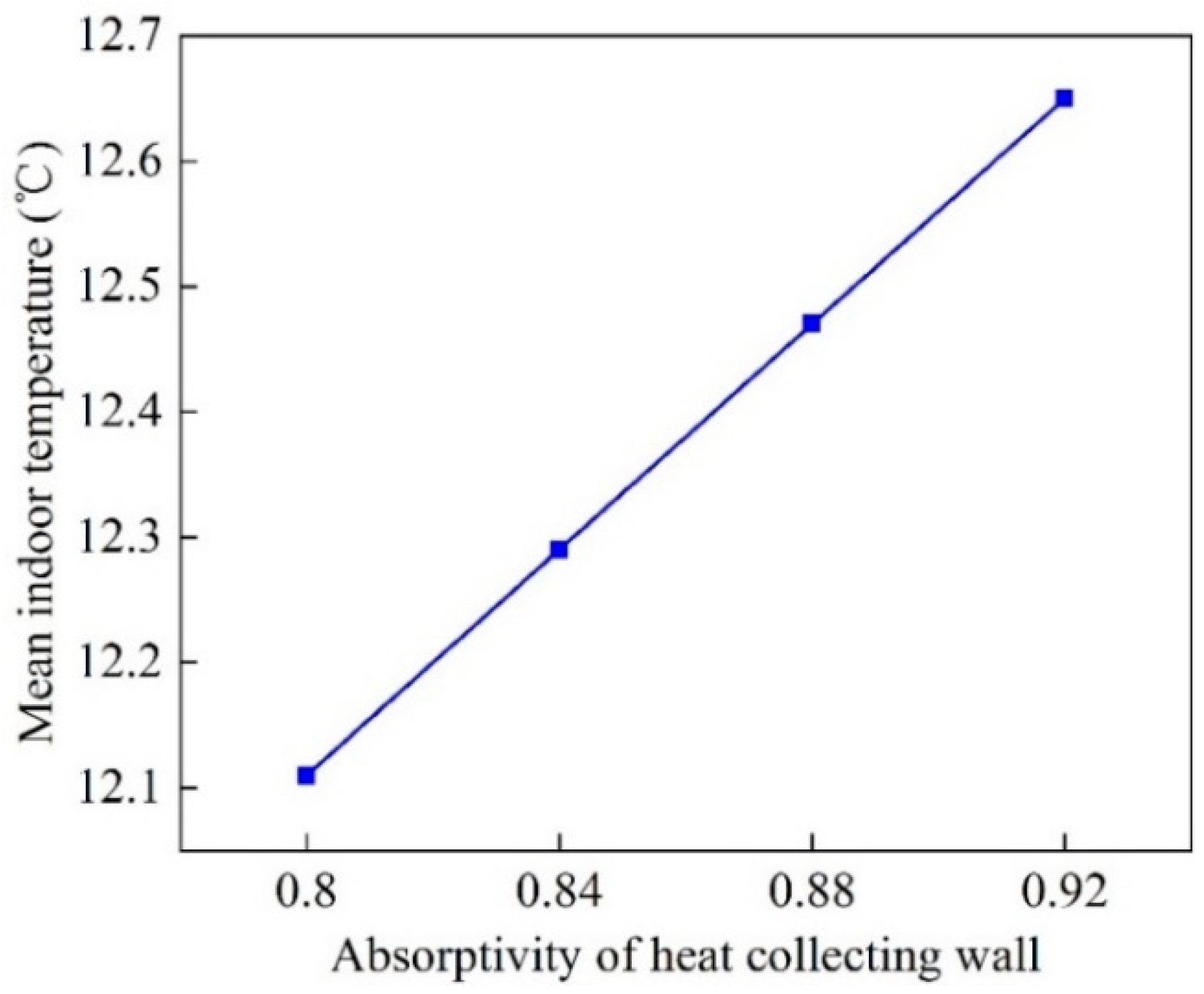
3.2.3. Effects of Absorptivity of Heat Collecting Wall
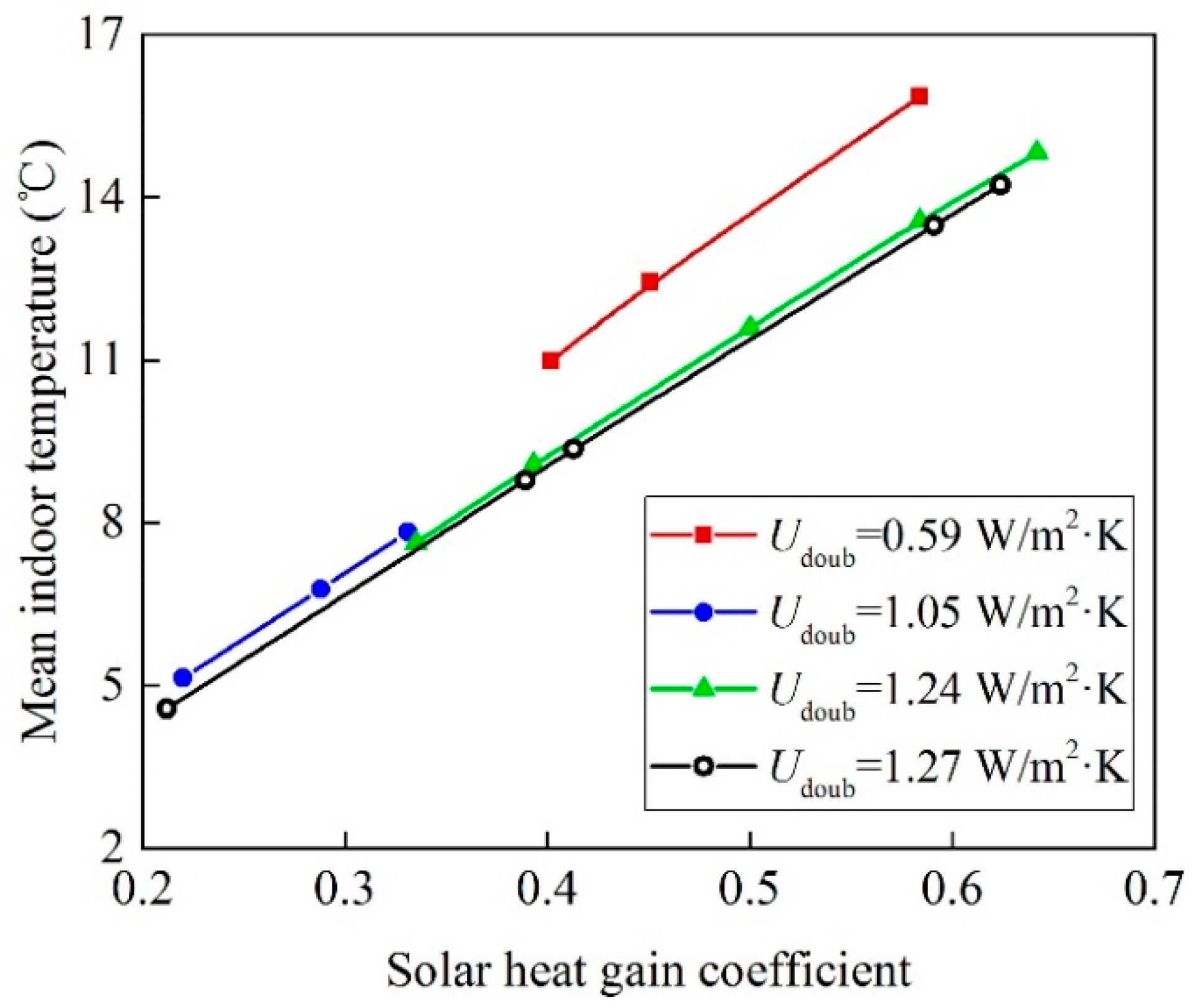
3.2.4. Effects of Thermal Performance of Inner Double-Glass Window
3.2.5. Effects of Outer Single-Glass Window
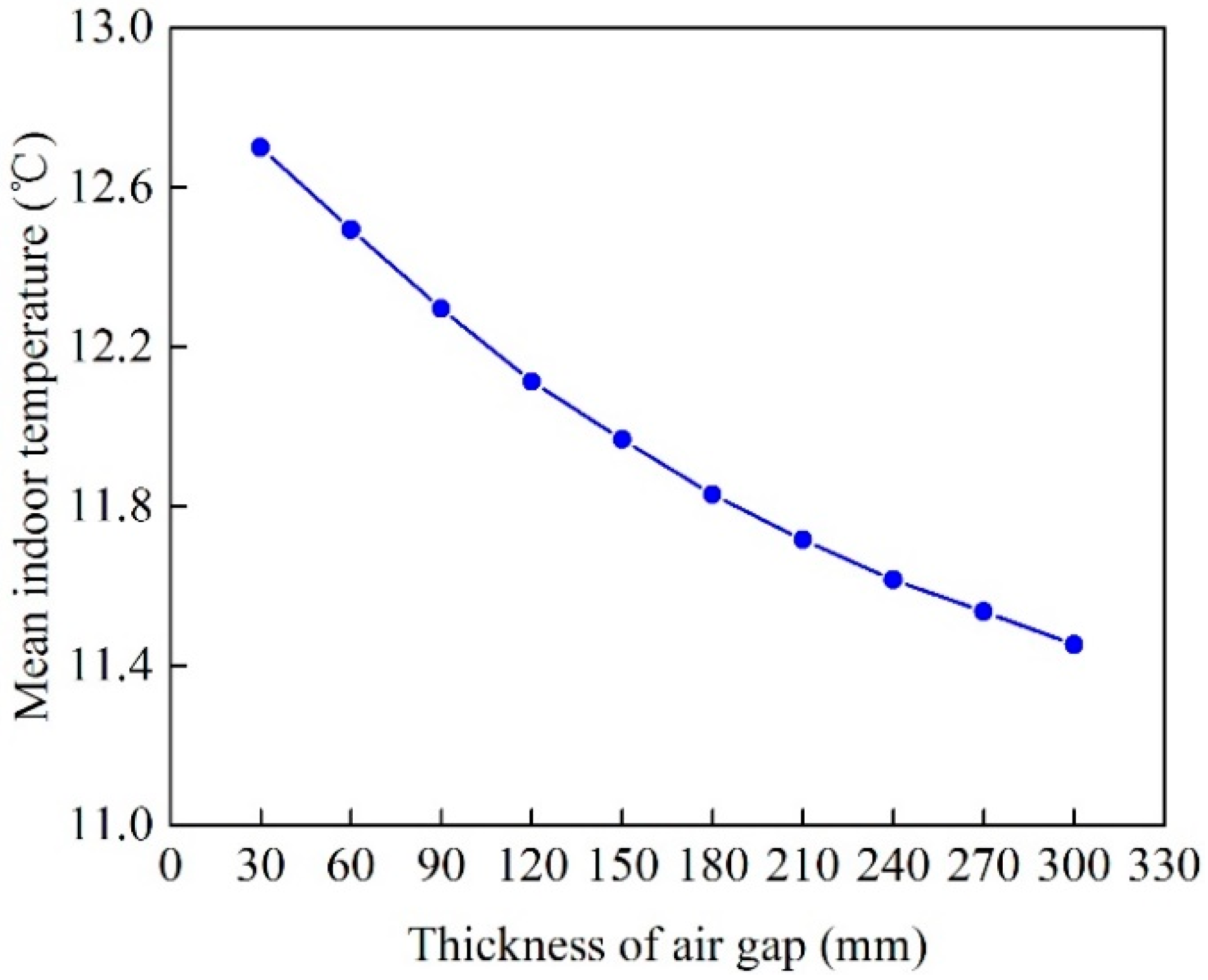
3.2.6. Effects of Air Gap Thickness
3.3. Summary of the Presented Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | building envelope area (m2) | Subscripts and superscripts | |
| ACH | air change per hour (1/h) | a | air |
| C | specific heat capacity (J/(kg·K)) | con | building construction |
| D | total thickness of building construction (m) | con, in | interior surface of building construction |
| g | gravity acceleration (m/s2) | con, out | exterior surface of building construction |
| Gr | Grashof number | clo | closed double-glass window |
| h | convective heat transfer coefficient (W/(m2·K)) | cs | horizontal cross section of the heat collecting space |
| H | height of HHCF (m) | diffuse | diffuse radiation |
| I | intensity of solar radiation (W/m2) | direct | direct radiation |
| Ir | incident radiation (W/m2) | doub | double-glass window |
| L | width of double-glass window (m) | hcs | heat collecting space |
| l | characteristic length (m) | hcs-hts | convection from heat transfer space to heat collecting space |
| m | mass flow rate of air in the heat collecting space (kg/s) | hts | heat transfer space |
| Pr | Prandtl number | hts-in | convection from heat transfer space to indoor space |
| q | heat flux (W/m2) | in | indoor |
| qts | solar radiation absorbed by the interior surface (W/m2) | interheat | indoor heat source of building |
| qtsf | transmitted solar radiation through the fenestration (W/m2) | leak | air leak from room |
| Q | heat transfer rate (W) | lw | long-wave radiation exchange |
| S | thickness of air gap (m) | ope | open double-glass window |
| SHGC | solar heat gain coefficient | out | outdoor |
| T | temperature (°C) | r | room |
| U | U-value of window (W/(m2·K)) | sig | single-glass window |
| V | volume (m3) | sig-hcs | convection from single-glass single-glass window to air in the heat collecting space |
| Vm | average wind velocity (m/s) | sig-hts | convection from single-glass single-glass window to air in the heat transfer space |
| W | width of heat collecting wall (m) | tic | conduction through closed double-glass window from heat transfer space to indoor space |
| Greek symbols | va | outlet area of the vent | |
| α | absorptivity of building surface | wa-hcs | convection from heat collecting wall to air in the gap |
| ρ | density (kg/m3) | win | window |
| λ | thermal conductivity (W/(m·K)) | ||
| τ | time (s) | ||
| ν | dynamic viscosity (Pa·s) | ||
| ε | emissivity of building surface | ||
| ξ1 | vent pressure loss coefficient | ||
| ξ2 | air gap pressure loss coefficient | ||
References
- Gil-Baez, M.; Padura, A.B.; Huelva, M.M. Passive actions in the building envelope to enhance sustainability of schools in a Mediterranean climate. Energy 2019, 167, 144–158. [Google Scholar] [CrossRef]
- Wang, R.Z.; Zhai, X.Q. Handbook of Energy Systems in Green Buildings; Springer Nature: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Athienitis, A.K.; Barone, G.; Buonomano, A.; Palombo, A. Assessing active and passive effects of façade building integrated photovoltaics/thermal systems: Dynamic modelling and simulation. Appl. Energy 2018, 209, 355–382. [Google Scholar] [CrossRef]
- Duan, S.P.; Jing, C.J.; Zhao, Z.Q. Energy and exergy analysis of different Trombe walls. Energy Build. 2016, 126, 517–523. [Google Scholar] [CrossRef]
- Barea, G.; Ganem, C.; Esteves, A. The multi-azimuthal window as a passive solar system: A study of Heat gain for the rational use of energy. Energy Build. 2017, 144, 251–261. [Google Scholar] [CrossRef]
- Schnieders, J.; Feist, W.; Rongen, L. Passive Houses for different climate zones. Energy Build. 2015, 105, 71–87. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Tran, Q.B.; Tran, D.Q.; Reiter, S. An investigation on climate responsive design strategies of vernacular housing in Vietnam. Build. Environ. 2011, 46, 2088–2106. [Google Scholar] [CrossRef]
- Zhang, T.T.; Tan, Y.F.; Yang, H.X.; Zhang, X.D. The application of air layers in building envelopes: A review. Appl. Energy 2016, 165, 707–734. [Google Scholar] [CrossRef]
- Lebied, M.; Sick, F.; Choulli, Z.; Bouardi, A.E. Improving the passive building energy efficiency through numerical simulation—A case study for Tetouan climate in northern of Morocco. Case Stud. Therm. Eng. 2018, 11, 125–134. [Google Scholar] [CrossRef]
- Shen, C.; Li, X.T. Solar heat gain reduction of double glazing window with cooling pipes embedded in venetian blinds by utilizing natural cooling. Energy Build. 2016, 112, 173–183. [Google Scholar] [CrossRef]
- Egolf, P.W.; Amacker, N.; Gottschalk, G.; Courret, G.; Noume, A.; Hutter, K. A translucent honeycomb solar collector and thermal storage module for building façades. Int. J. Heat Mass Transf. 2018, 127, 781–795. [Google Scholar] [CrossRef]
- Stevanović, S. Optimization of passive solar design strategies: A review. Renew. Sustain. Energy 2013, 25, 177–196. [Google Scholar] [CrossRef]
- Alfredo, F.G. Analysis of the thermal performance and comfort conditions produced by five different passive solar heating strategies in the United States Midwest. Sol. Energy 2007, 81, 581–593. [Google Scholar]
- Sebald, A.V.; Clinton, J.R.; Langenbacher, F. Performance effects of Trombe wall control strategies. Sol. Energy 1979, 23, 479–487. [Google Scholar] [CrossRef]
- Kara, Y.A. Diurnal performance analysis of phase change material walls. Appl. Therm. Eng. 2016, 102, 1–8. [Google Scholar] [CrossRef]
- Jaber, S.; Ajib, S. Optimum design of Trombe wall system in Mediterranean region. Sol. Energy 2011, 85, 1891–1898. [Google Scholar] [CrossRef]
- Ihm, P.; Krartib, M. Design optimization of energy efficient residential buildings in Tunisia. Build. Environ. 2012, 58, 81–90. [Google Scholar] [CrossRef]
- Naylor, D.; Foroushani, S.S.M.; Zalcman, D. Free convection heat transfer from a window glazing with an insect screen. Energy Build. 2017, 138, 206–214. [Google Scholar] [CrossRef]
- Lou, S.W.; Li, D.H.W.; Lam, J.C.; Lee, E.W.M. Estimation of obstructed vertical solar irradiation under the 15 CIE Standard Skies. Build. Environ. 2016, 106, 123–133. [Google Scholar] [CrossRef]
- Parvin, S.; Ahmed, S.; Chowdhury, R. Effect of Solar Irradiation on Forced Convective Heat Transfer through a Nanofluid Based Direct Absorption Solar Collector. In Proceedings of the 7th BSME International Conference on Thermal Engineering, Dhaka, Bangladesh, 22–24 December 2016. [Google Scholar]
- Aksoy, U.T.; Inalli, M. Impacts of some building passive design parameters on heating demand for a cold region. Build. Environ. 2006, 41, 1742–1754. [Google Scholar] [CrossRef]
- Marinoski, D.L.; Guths, S.; Pereiara, F.O.R.; Lamberts, R. Improvement of a measurement system for solar heat gain through fenestrations. Energy Build. 2007, 39, 478–487. [Google Scholar] [CrossRef]
- Zhou, G.B.; Pang, M.M. Experimental investigations on the performance of a collector–storage wall system using phase change materials. Energy Convers. Manag. 2015, 105, 178–188. [Google Scholar] [CrossRef]
- Tian, Z.C.; Zhang, X.K.; Jin, X.; Zhou, X.; Si, B.H.; Shi, X. Towards adoption of building energy simulation and optimization for passive building design: A survey and a review. Energy Build. 2018, 158, 1306–1316. [Google Scholar] [CrossRef]
- Wei, H.; Hu, Z.T.; Luo, B.Q.; Hong, X.Q.; Sun, W.; Ji, J. The thermal behavior of Trombe wall system with venetian blind: An experimental and numerical study. Energy Build. 2015, 104, 395–404. [Google Scholar]
- Gou, S.Q.; Nik, V.M.; Scartezzini, J.L.; Zhao, Q.; Li, Z.R. Passive design optimization of newly-built residential buildings in Shanghai for improving indoor thermal comfort while reducing building energy demand. Energy Build. 2018, 169, 484–506. [Google Scholar] [CrossRef]
- Harkouss, F.; Fardoun, F.; Biwole, P.H. Passive design optimization of low energy buildings in different climates. Energy 2018, 165, 591–613. [Google Scholar] [CrossRef]
- Larsen, S.F.; Rengifo, L.; Filippin, C. Double skin glazed façades in sunny Mediterranean climates. Energy Build. 2015, 102, 18–31. [Google Scholar] [CrossRef]
- Samuelson, H.; Claussnitzer, S.; Goyal, A.; Chen, Y.J.; Alejandra, R.C. Parametric energy simulation in early design: High-rise residential buildings in urban contexts. Build. Environ. 2016, 101, 19–31. [Google Scholar] [CrossRef]
- Owrak, M.; Aminy, M.; Jamal-Abad, M.T.; Dehghan, M. Experiments and simulations on the thermal performance of a sunspace attached to a room including heat-storing porous bed and water tanks. Build. Environ. 2015, 92, 142–151. [Google Scholar] [CrossRef]
- Gong, X.Z.; Akashi, Y.; Sumiyoshi, D. Optimization of passive design measures for residential buildings in different Chinese areas. Build. Environ. 2012, 58, 46–57. [Google Scholar] [CrossRef]
- Ruiz, M.C.; Romero, E. Energy saving in the conventional design of a Spanish house using thermal simulation. Energy Build. 2011, 43, 3226–3235. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A.; Mitchell, J.W.; Duffie, J.A.; Duffie, N.A.; Freeman, T.L. TRNSYS Manual; University of Wisconsin-Madison: Madison, WI, USA, 2007. [Google Scholar]
- Pantankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere: New York, NY, USA, 1980. [Google Scholar]
- Hottel, H.C.; Sarofim, A.F. Radiative Transfer; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Cengel, Y.A.; Ghajar, A.J. Fundamentals of Thermal-Fluid Sciences; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Park, B.; Krarti, M. Development of a simulation analysis environment for ventilated slab systems. Appl. Therm. Eng. 2015, 87, 66–78. [Google Scholar] [CrossRef]
- Xiao, W. Study of the Direct-Gain Solar Heating in Remote Southwest Tibet; Tsinghua University: Beijing, China, 2010. [Google Scholar]
- He, L.Q.; Ding, L.X. The Calculation Basis of Thermal Physics for SOLAR Building; Press of University of Science and Technology of China: Hefei, China, 2010. [Google Scholar]
- Klien, S.A.; Theilacker, J.C. An algorithm for calculating monthly-average radiation on inclined surfaces. J. Sol. Energy Eng. 1981, 103, 29–33. [Google Scholar] [CrossRef]
- Meteorological information center of China, Department of building technology science of Tsinghua university. Special Meteorological Data Sets for the Analysis of the Thermal Environment of Chinese Buildings; China building industry press: Beijing, China, 2005. [Google Scholar]
- TRNSYS 18 Manuals, Component Mathematical Reference. Available online: http://sel.me.wisc.edu/trnsys/user18-resources/index.html (accessed on 1 November 2018).
- Zhu, Y.X.; Yan, Q.S. Built Environment, 2nd ed.; China building industry press: Beijing, China, 2007. [Google Scholar]
- Bellos, E.; Tzivanidis, C.; Zisopoulou, E.; Mitsopoulos, G. An innovative Trombe wall as a passive heating system for a buildingin Athens—A comparison with the conventional Trombe wall and theinsulated wall. Energy Build. 2016, 133, 754–769. [Google Scholar] [CrossRef]
- Zou, H.F.; Fei, Y.C.; Yang, F.H.; Tang, H.; Zhang, Y.; Ye, S. Mathematical Modeling of Double-Skin Facade in Northern Area of China. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]




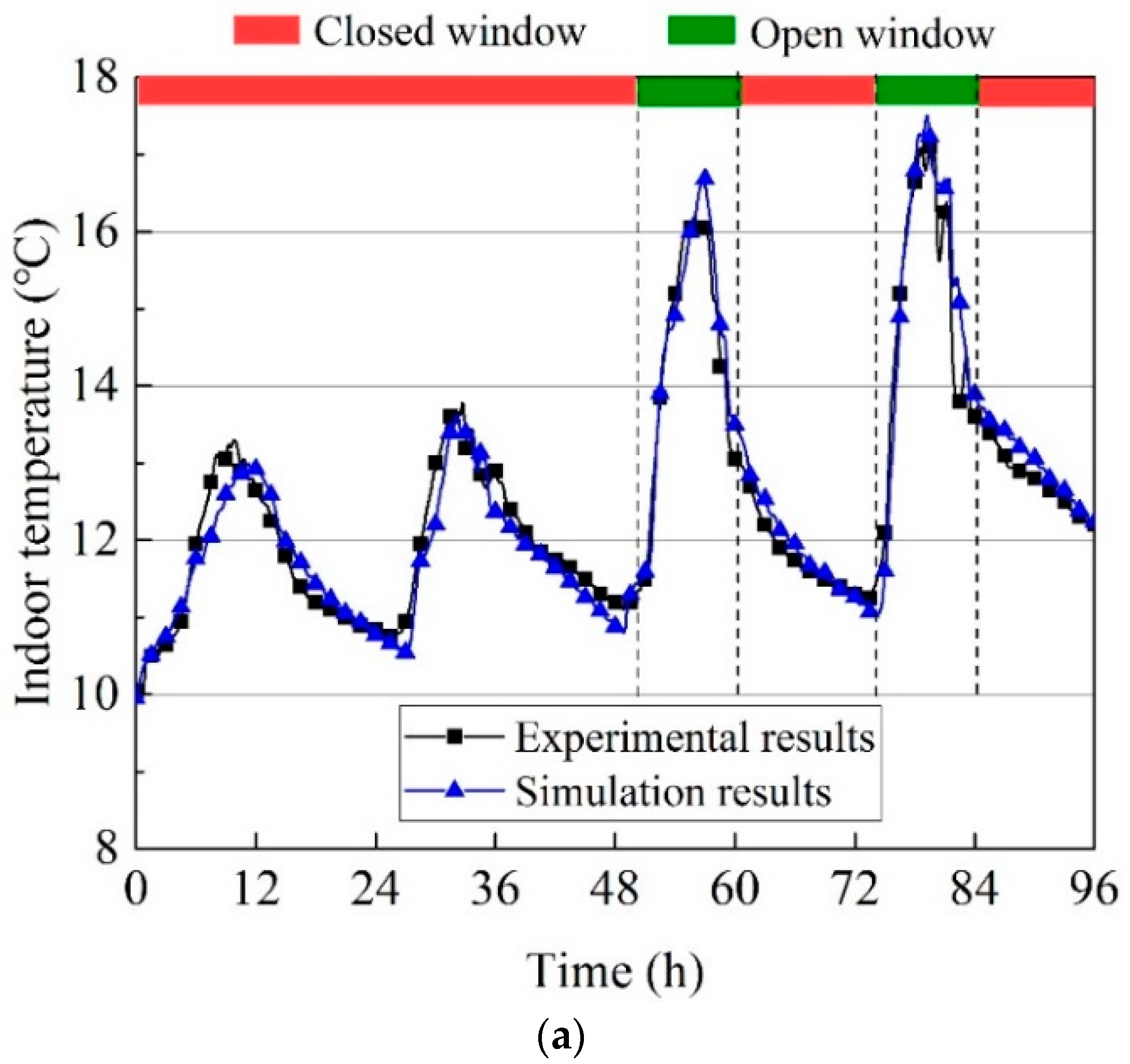
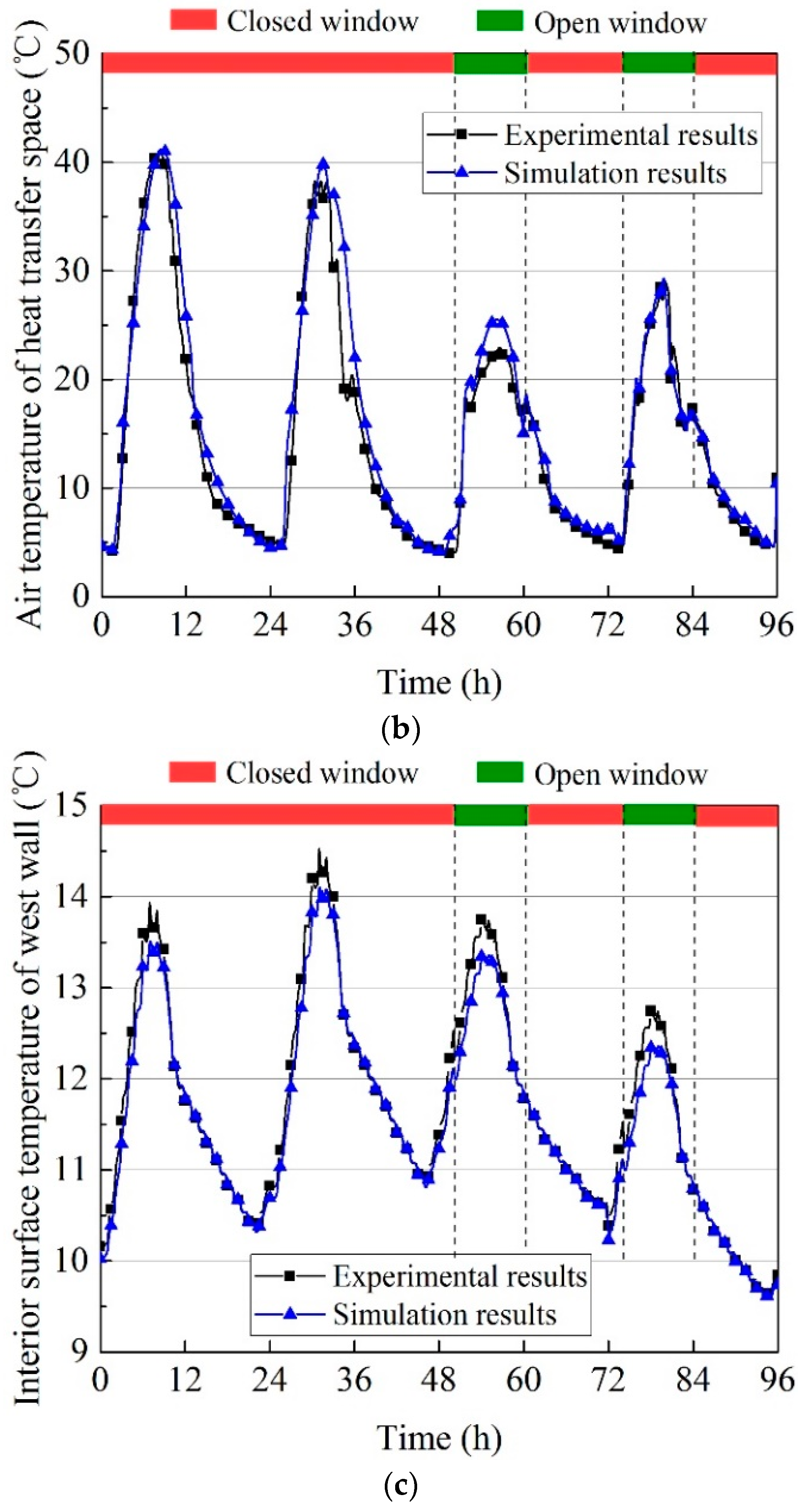

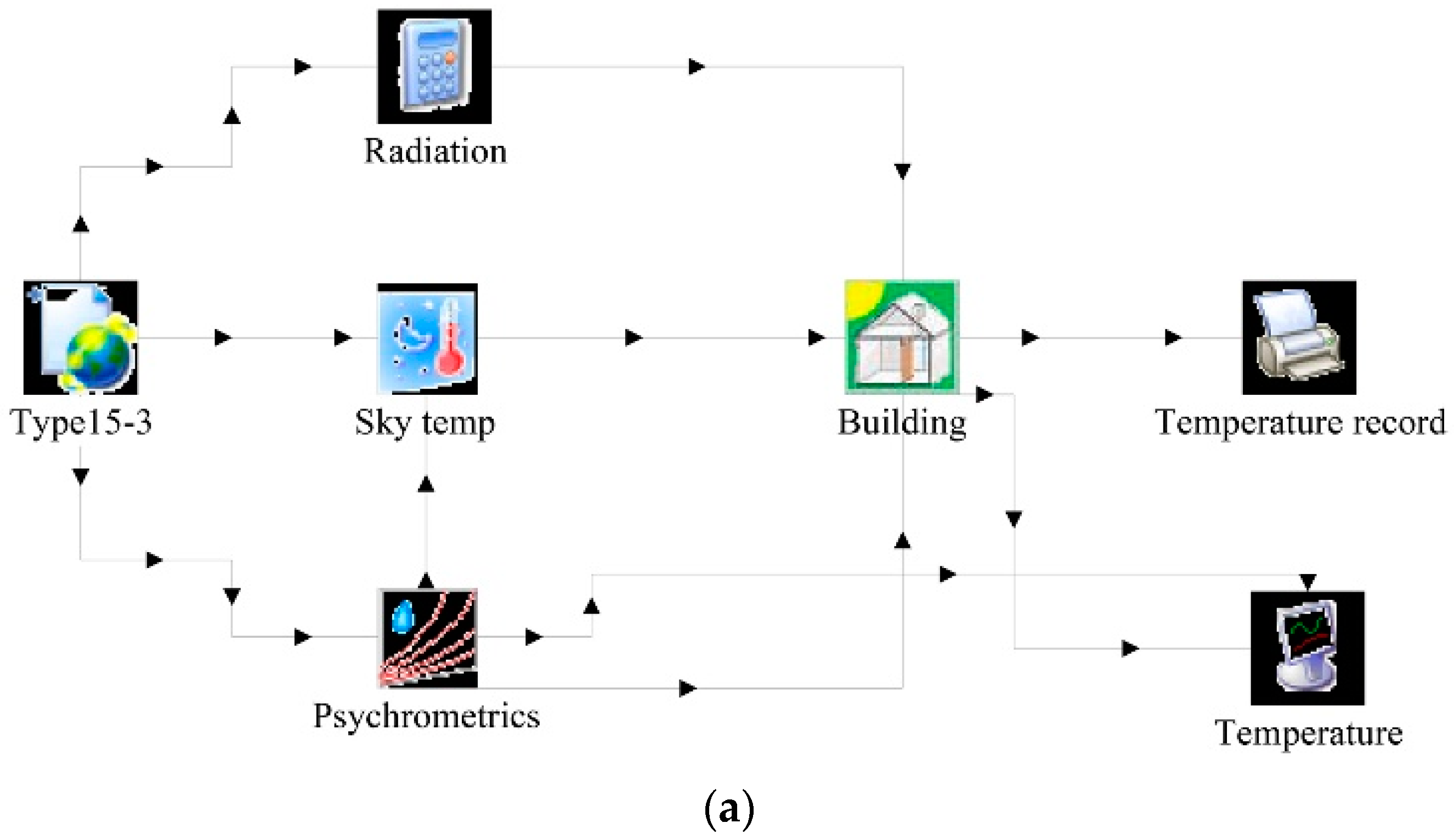
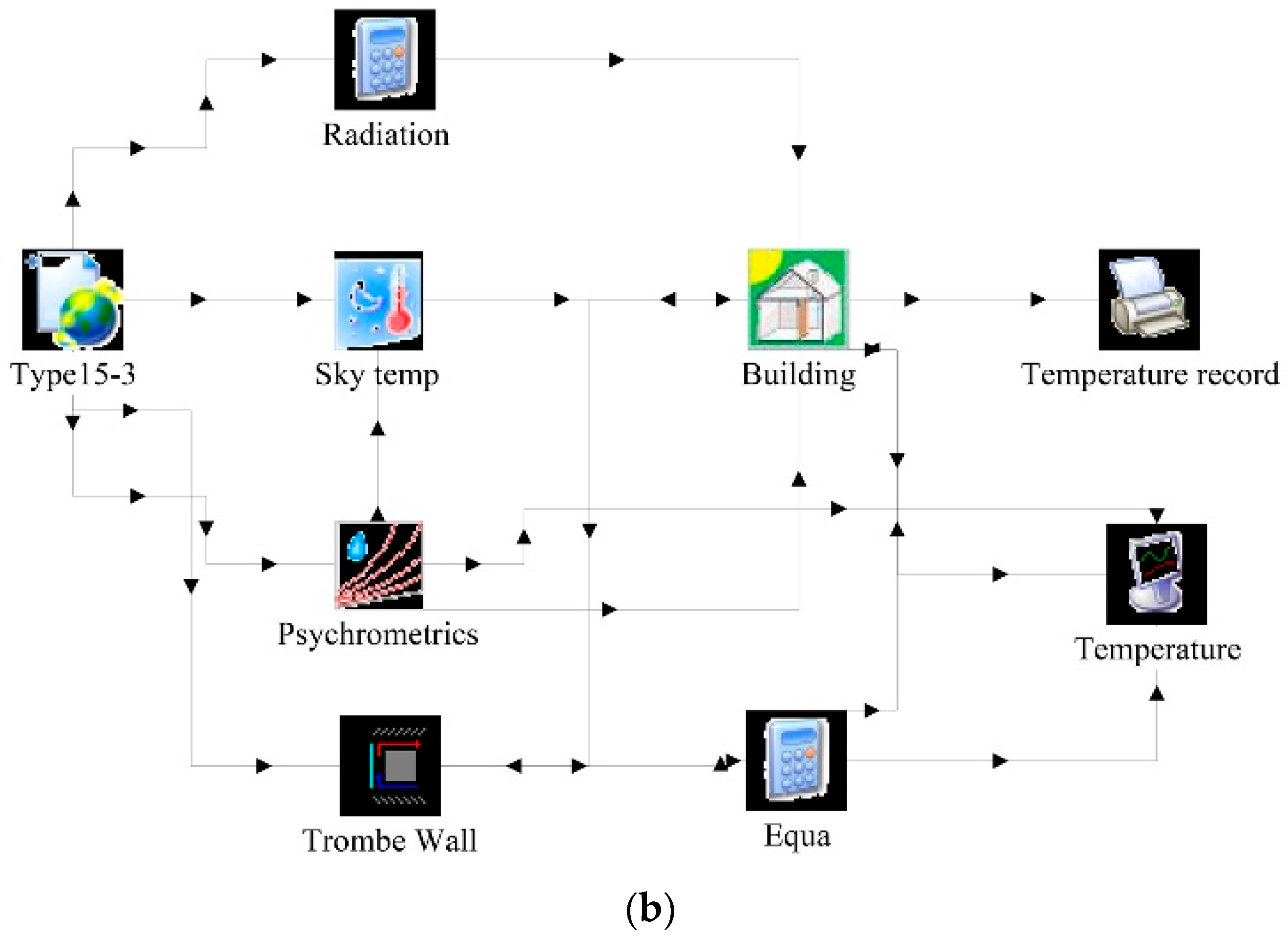


| Construction | Material | Thermal Conductivity (W/(m·K)) | Heat Capacity (J/(kg·K)) | Density (kg/m3) |
|---|---|---|---|---|
| Exterior wall | 80 mm polyurethane | 0.033 | 1380 | 40 |
| 240 mm brick wall | 0.89 | 1000 | 1800 | |
| 20 mm Cement mortar | 0.93 | 1050 | 1800 | |
| Interior wall | 20 mm Cement mortar | 0.93 | 1050 | 1800 |
| 240 mm brick wall | 0.89 | 1000 | 1800 | |
| 20 mm Cement mortar | 0.93 | 1050 | 1800 | |
| Ceiling | 20 mm Cement mortar | 0.93 | 1050 | 1800 |
| 180 mm concrete | 1.74 | 920 | 2500 | |
| 20 mm Cement mortar | 0.93 | 1050 | 1800 | |
| Door | 60 mm wood | 0.15 | 1630 | 608 |
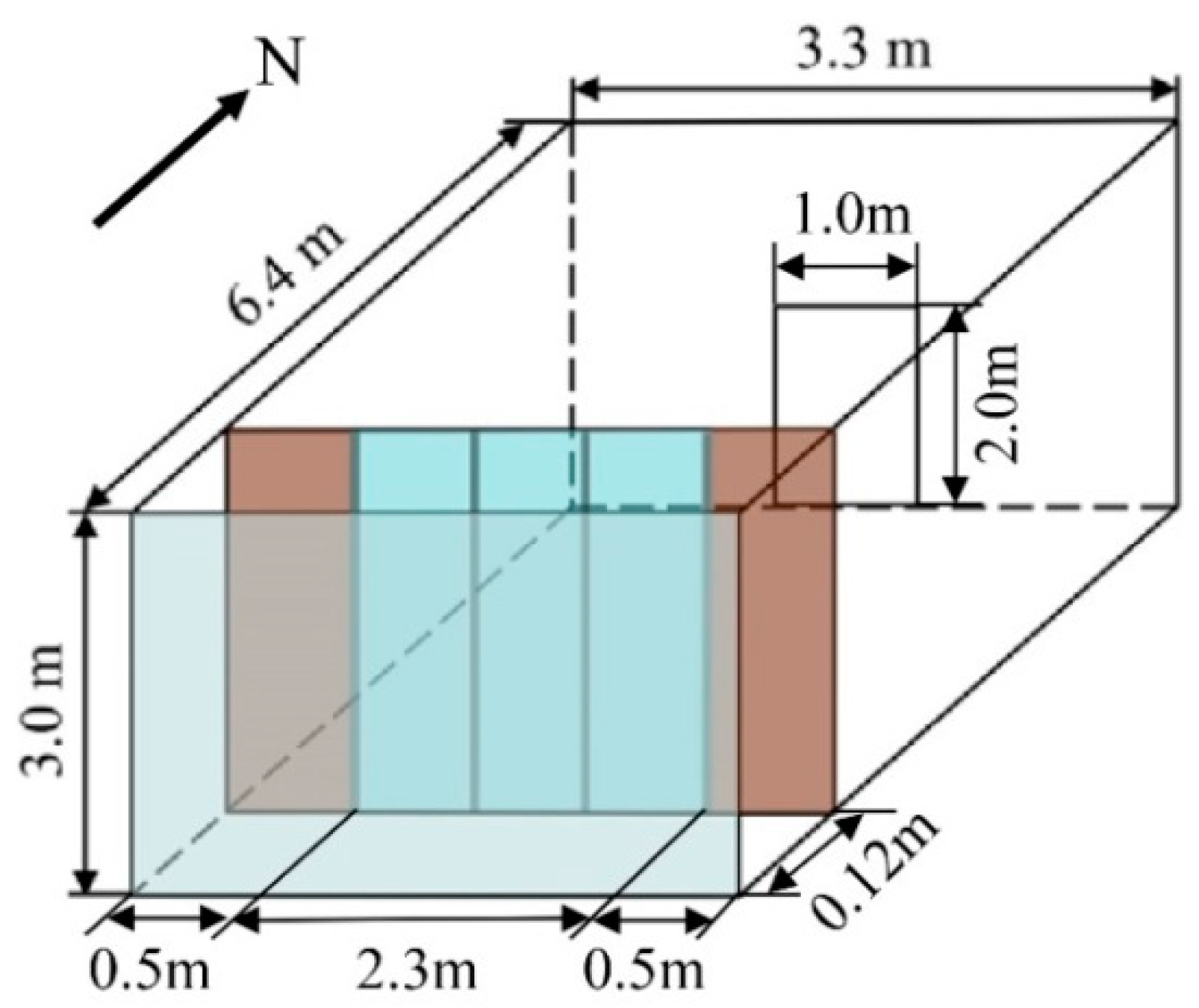
| HHCF | 3 mm single-glass window, U = 5.56 W/(m2·K); SHGC = 0.9; 120 mm-thickness air gap; 12 mm double-glass window, U = 2.83 W/(m2·K); SHGC = 0.76; 0.5 m-width for each heat collecting wall (W = 0.5 m); Materials of the heat collecting wall is the same with the exterior wall Absorptivity of the heat collecting wall is 0.8; 2.3 m-width for double-glass window (L = 2.3 m) | |||
| Indoor Air Temperature (°C) | Total Heating Energy Demand (kWh/m2) | |||
|---|---|---|---|---|
| Mean | Minimum | Maximum | ||
| Case 1 | 17.5 | 10.4 | 21.9 | 47.9 |
| Case 2 | 18.2 | 10.5 | 26.7 | 36.6 |
| Case 3 | 18.6 | 11.0 | 27.1 | 28.7 |
| Schedule A | Schedule B | Schedule C | Schedule D | |
|---|---|---|---|---|
| Time to open windows | With windows closed all day | 8:00 | 9:00 | 11:00 |
| Time to close windows | 18:00 | 17:00 | 15:00 | |
| Indoor air temperature (°C) | 6.7~13.2 | 8.2~19.0 | 8.6~19.0 | 7.8~17.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lei, B.; Bi, H.; Yu, T. Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region. Energies 2019, 12, 1038. https://doi.org/10.3390/en12061038
Wang X, Lei B, Bi H, Yu T. Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region. Energies. 2019; 12(6):1038. https://doi.org/10.3390/en12061038
Chicago/Turabian StyleWang, Xiaoliang, Bo Lei, Haiquan Bi, and Tao Yu. 2019. "Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region" Energies 12, no. 6: 1038. https://doi.org/10.3390/en12061038
APA StyleWang, X., Lei, B., Bi, H., & Yu, T. (2019). Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region. Energies, 12(6), 1038. https://doi.org/10.3390/en12061038





