1. Introduction
The expansion of volatile renewable energy (VRE) is a major project, that many countries decided to undergo as part of their commitments under the UN Paris Climate Change Conference of 2016 [
1]. Various energy system configurations (i.e., distribution of technologies, their installed rated power and capacities) are suggested to meet the goals of e.g., the German Energiewende [
2]. Energy systems can consist of VRE plants (e.g., wind, photovoltaic, concentrating solar power), of renewable storage facilities (e.g., batteries, power to gas to power, pumped hydro) and of conventional storage facilities or “primary energy storages” [
3] (e.g., combined cycle gas turbine (CCGT), coal-fired steam power plant). To avoid confusion, in this paper the term “energy storage” is used solely for renewable storage facilities or “secondary energy storages” [
3]. “Primary energy storages” are referred to as conventional power plants throughout this paper.
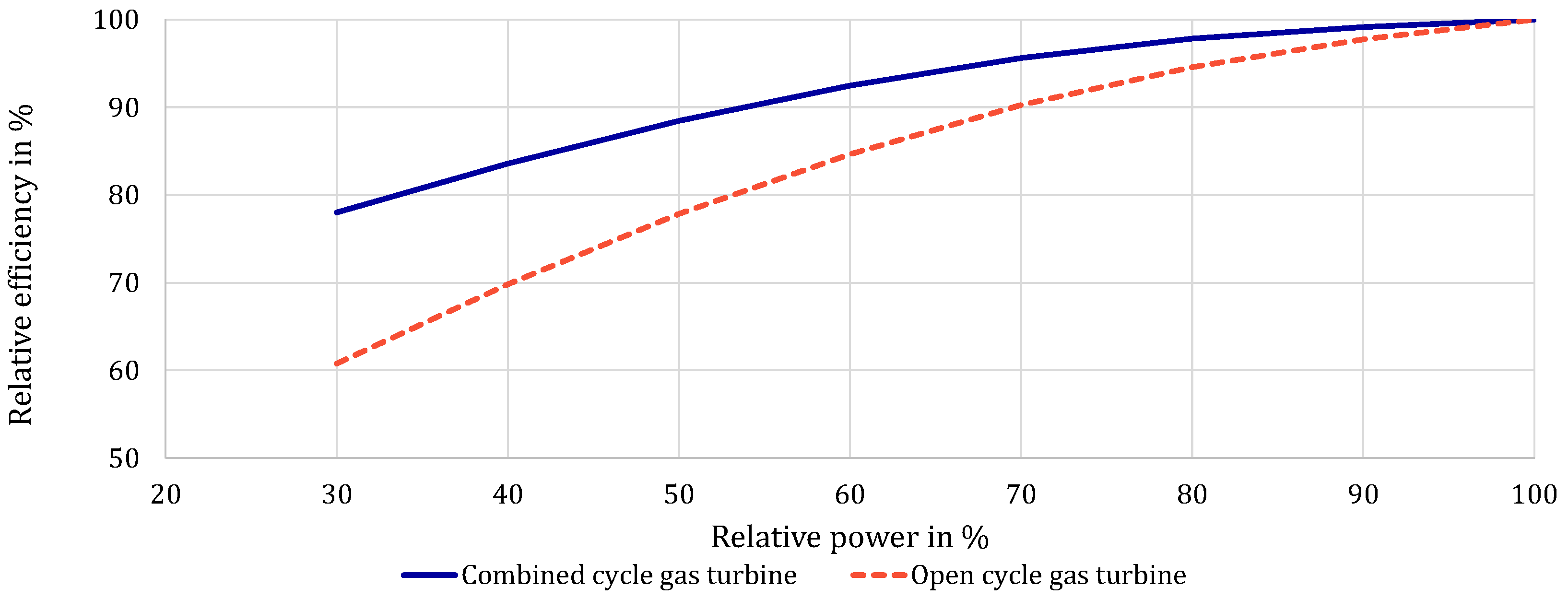
For this work a small energy system without transmission losses (often referred to as “copper plate”) and no possible external source or sink of power (often referred to as “island restriction”), in the following referred to as “copper plate island”, is the test system. The copper plate island consists of a CCGT power plant, a short-term and a long-term energy storage and varying instalments of solar and wind power. Installed solar and wind power are equally distributed across all configurations and their installed power is given as VRE power in MWeach, meaning the installed power each generation type has in a given configuration. As demand for the energy system, a constant power of 1000 MW is defined.
To utilise given energy system configurations to their maximum potential as well as test their feasibility, time series simulation is a commonly used tool. These simulations need some kind of unit commitment (UC) for dispatching the plants in the given energy system.
The methods for UC can vary from heuristic to non-linear optimisation problems, from deterministic to stochastic with all their methodical benefits and drawbacks [
4,
5]. A popular approach is the formulation of the energy system as a mixed integer linear problem (MILP) for small [
6] to larger systems [
7,
8]. Most often the optimisation problem is formulated to find the best solution for the entire time series (e.g., one year) at once, which can become very complex and time consuming and might make local computing resources incompatible [
9]. To solve this problem, the use of a rolling horizon became more and more popular in recent years [
5,
10,
11,
12].
In [
13] a comprehensive review of energy system modelling tools can be found. Seventy-five models were categorised in purpose, approach, methodology, temporal resolution, modelling horizon, spatial resolution and coverage and availability. These models were then discussed and their features listed. More than half of the presented models use a linear programming or MILP approach. The use of rolling horizons is however rarely mentioned.
Recently developed frameworks such as the one of [
11] demonstrate the significance of the rolling horizon approach. This framework was developed to show the effect of different interval lengths (e.g., five hours or four days) on a one-day unit commitment problem. It would allow for modification of the MILP results in order to adjust for uncertainties or new information, but was not used in [
10]. The framework was updated in [
14] to model start-up times and tested for different rolling horizon interval lengths between two and 24 h. [
15] presented a different framework, where the rolling horizon was implemented for a similar reason, but added an optional economic dispatch algorithm to adjust the suggested UC. This is to model market behaviour more properly.
This use of cascading UC to mimic the behaviour of a day-ahead and intra-day market was implemented by [
16]. The market behaviour was modelled by a 24 h MILP unit commitment with a stochastically generated VRE forecast for the day ahead and a 4 h non-linear point algorithm to minimise the cost associated with diverging from the day-ahead UC.
A similar approach of stochastic programming for the UC was investigated and tested against a deterministic approach by [
17]. The stochastic problem was tested in various configurations of rolling horizon lengths for the problem and solution aggregation on a larger energy system with electric grid constraints. In a similar fashion this research topic was investigated by [
18], with the difference that in [
18] various lengths for the final unit commitment—minimising the divergence from the stochastic forecast—were tested. Another difference lies in the configuration of the underlying energy system, whereby both [
17,
18] use different kinds of short-term energy storage devices and no long-term energy storage devices.
Investigation of lengths for the rolling horizon was done by [
19] to find the optimal use of power plant flexibility considering the start-up and maintenance related problems of CCGT power plants.
Focusing on a thermal energy storage device for the medium term, [
20] investigated a rolling horizon with a week-long forecast against a previous research with a day-ahead forecast and found the results to be better for the week-long unit commitment.
To adjust for non-linear behaviour of the system [
20,
21] did a piecewise linearisation of the price-effects that influenced the objective function. The focus of [
21] was the usage of upper-, lower-bound or mean value of the linearised piece from the price function.
This paper focusses on energy system feasibility for future energy systems, for which [
22] reviewed various energy system simulation models. The difference to the previously discussed systems is that future energy systems contain long-term energy storage devices. In this case, the UC might need longer forecasting lengths, as their name implies. It should be noted however, that [
16,
20,
21] still adjust their models for non-linearities despite their rather short interval length.
For a better integration of long-term storages [
23] integrates the rolling horizon approach to apply different levels of detail. For the exact UC, a complex model is used with short horizons, which is thought to not encompass the characteristics of long-term storages. A less complex model is used for the entire time frame, to set the characteristics for the exact planning.
Similarly [
24] applied the use of a less complex model, but for a whole year simulation. The research investigated the use of an evolutionary algorithm for the energy system configuration with an underlying two level MILP UC. For the lower level a one-day rolling horizon MILP UC was implemented. The parameters of the MILP were generated from a non-linear model. Unfortunately the model of [
24] does not ensure, that the long-term storage is filled to its initial state of charge (SOC) at the end of the simulation.
The rolling horizon is done here primarily to save simulation time, as [
25] proposed, where the effect of different lengths of the rolling horizon and their effect on simulation time und quality of the solution was investigated. The quality of the solution was judged against the solution of a MILP UC solution for the entire time frame at once.
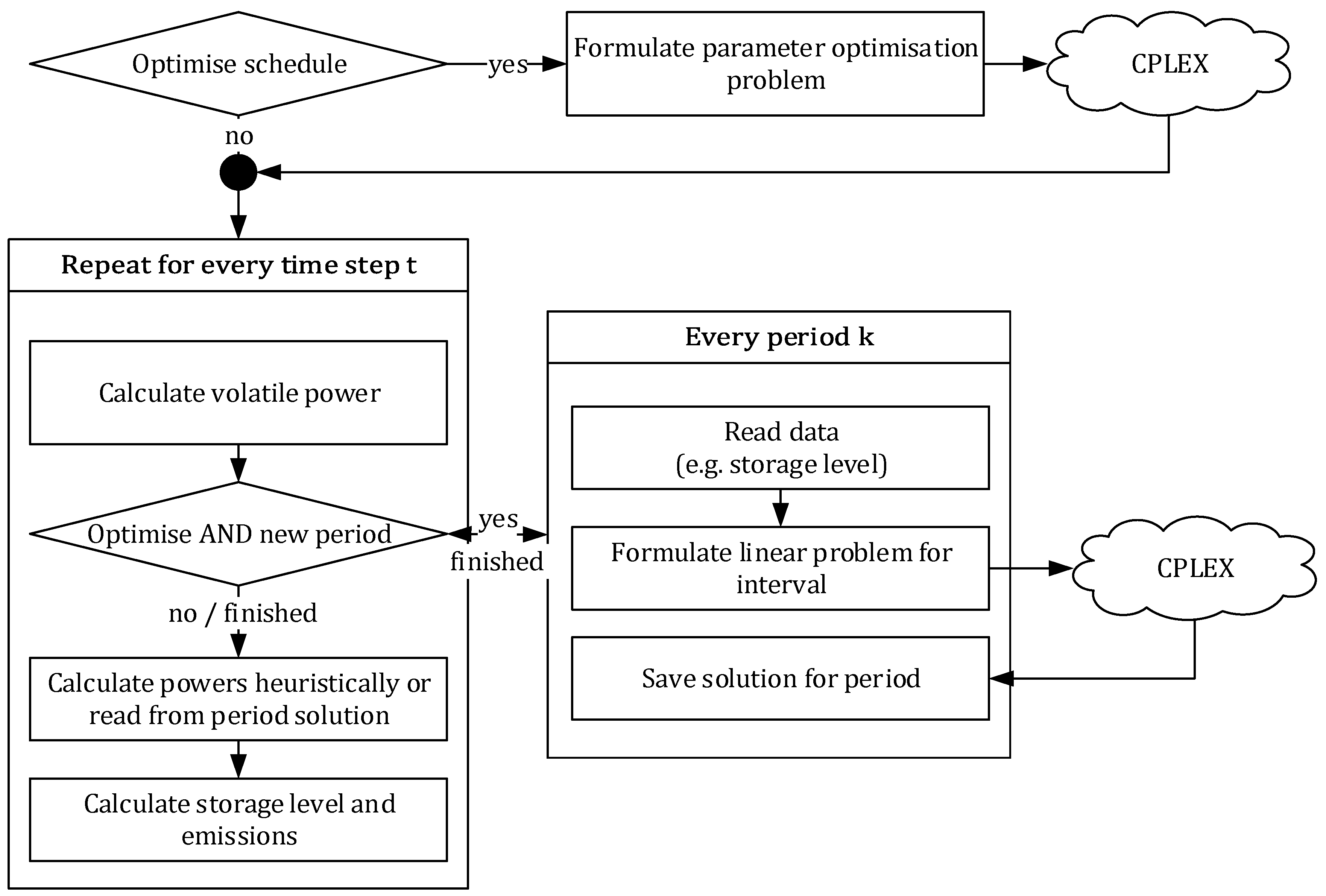
This paper introduces a different modelling approach for the solution of UC problems, in which the solution of a MILP UC is handed to a non-linear control model (NLC). That way the feasibility of the proposed UC can be tested. Further the MILP formulation uses the approach of [
26] to model part-load behaviour more correctly, where the parameters of the MILP and initial values in a rolling horizon operation are generated from the NLC. With this approach, the effect of the interval length (see
Section 2.1) in a rolling horizon problem becomes the research focus of this paper. To our knowledge, this has not been addressed with an NLC before.
To determine the effect of the interval lengths the results of MILP unit commitment optimisations (UCO) with varying temporal settings are compared to a unit commitment with a heuristic approach (UCH). The CO2 emissions of the electricity producer park are the minimisation objective of the MILP, which is why the specific CO2 emissions of the electricity producer park are used as the primary quality measure of the UC results. Additionally, the share of storages, meaning the amount of energy delivered by the energy storage devices in respect to total demand, acts as an indicator of difference between UCO and UCH.
A characteristic line model, namely CharL (see
Supplementary Materials), is inherent to the UCH and used as an NLC for the UCO, instead of simply aggregating the MILP results (see
Section 2.1).
3. Results
In a first step, the usage of the UCH is compared to the UCO with 2 days interval rolling horizon (scenario a) for all VRE power configurations.
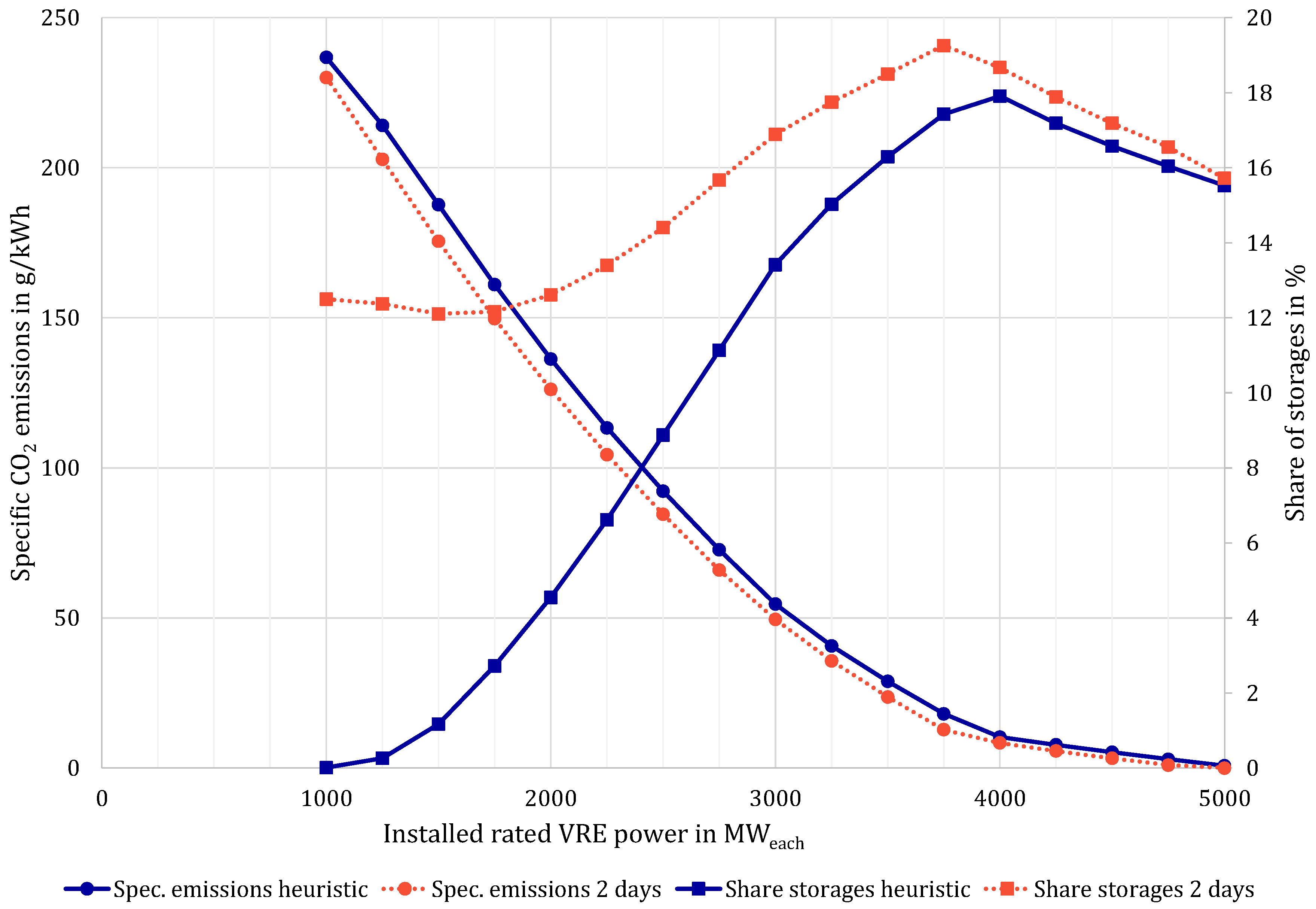
Figure 6 shows the specific CO
2 emissions (dots) of the plants of the copper plate island and the storage share (square) in dependence on installed VRE power. The results show that the UCO model (dotted lines) leads to slightly lower CO
2 emissions than the UCH (solid lines) for all configurations.
In terms of the storage share, the UCO delivers a widely different result than the UCH, with higher values in all configurations but especially for small installed VRE power. This is further discussed in
Section 3.1. Both UCH and UCO show a maximum share of storages below the maximum installed VRE power. This is due to the ever-rising share of direct VRE supply, leaving less demand to be covered by the energy storage devices.
Lastly,
Figure 6 explains why the 1000 MW
each configuration shows a lower absolute improvement than the 2000 MW
each configuration, with the storage share of the UCH. Since the UCH only integrates surplus of VRE power supply, it is obvious that the 1000 MW
each configuration has negligible surplus of VRE to be integrated, thus the UCO has only the CCGT left to optimise. In practice, this is done using the short-term storage.
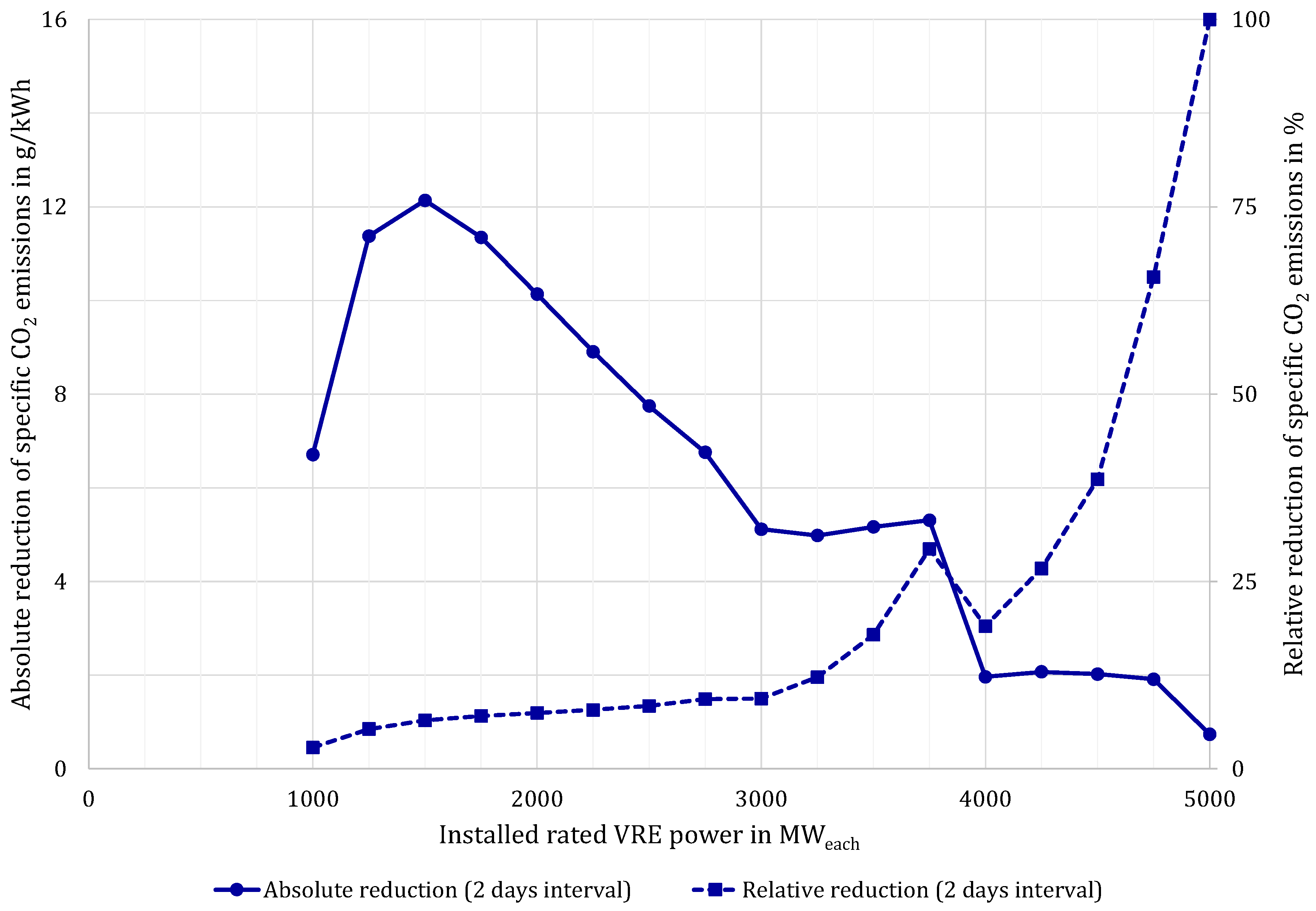
The reduction of CO
2 emissions due to optimisation in comparison to the UCH is shown in absolute and relative terms in
Figure 7 also for the interval length of two days. The figure shows that the relative CO
2 reduction through UCO for installed VRE power below 3000 MW
each is generally below 10%. Between 3000 and 3750 MW
each the absolute reduction is rather constant across VRE configurations while the relative reduction shows increasing values. For 4000 MW
each both absolute and relative reduction show lower values, which can be explained with the maximum share of storage to be integrated as seen in
Figure 6 and discussed above. For higher installed capacities, the denominator becomes so insignificant that the relative reduction is amplified while the absolute CO
2 reduction becomes remarkably small.
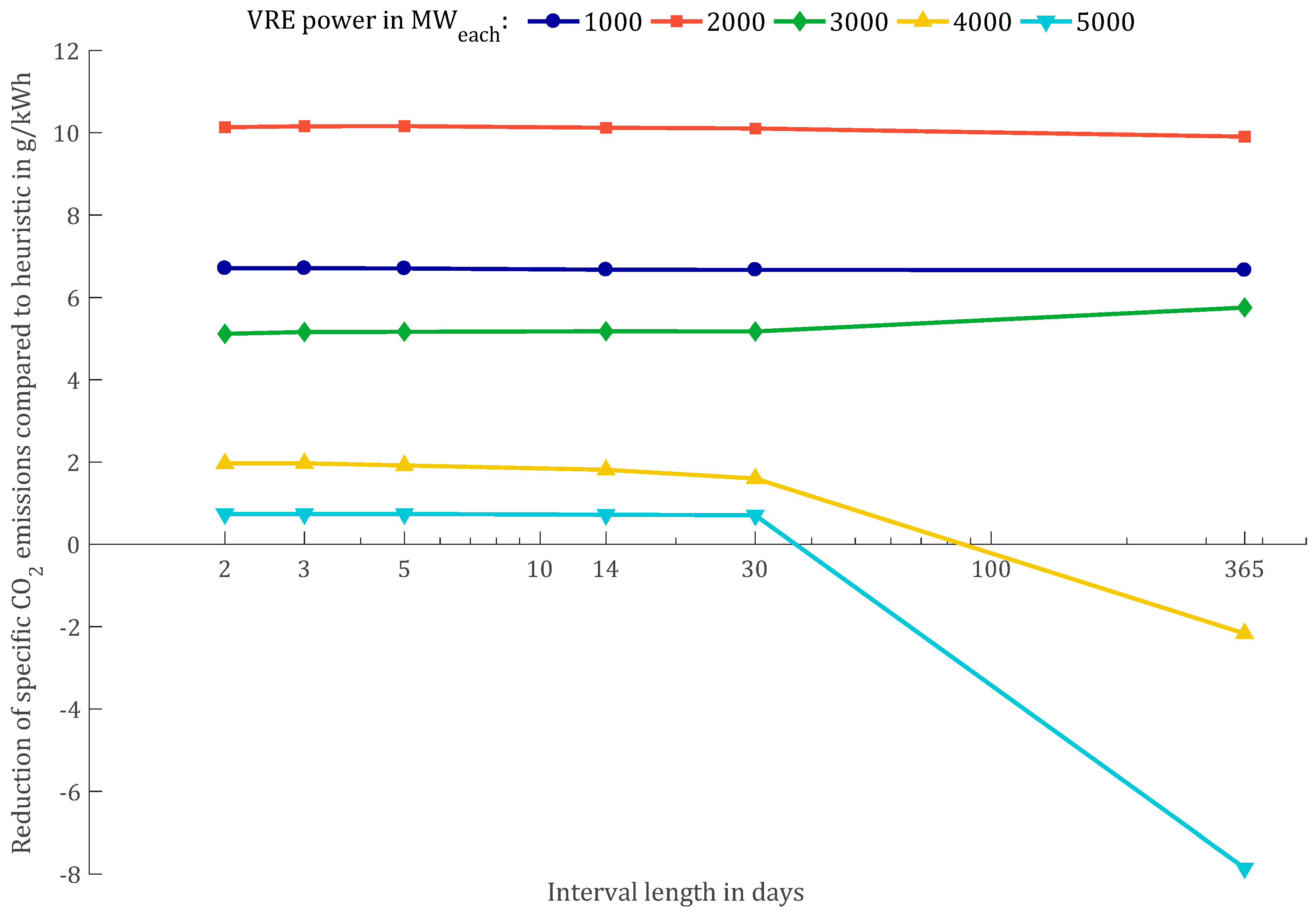
The main result can be seen in
Figure 8, where the reduction of CO
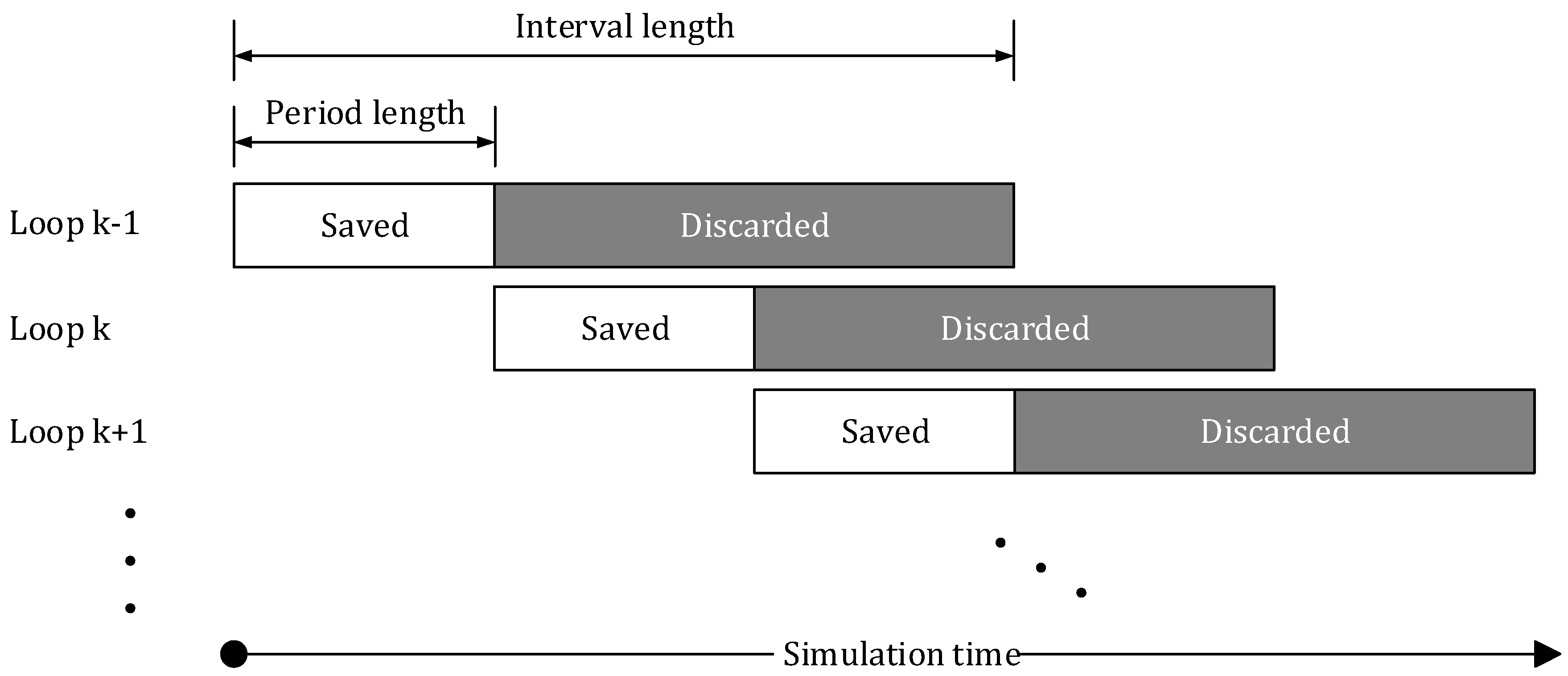
2 emissions through UCO relative to the heuristic approach (UCH) is shown in relation to the interval length, which in this context implies the corresponding period lengths of
Table 1. The configurations with 1000 MW
each (circles) and 2000 MW
each (squares) VRE power show no significant influence of the interval length across the scenarios (interval lengths). The configuration with 3000 MW
each shows a slight advantage for a whole year optimisation run, which is explicable with the maximum possible integration of storage power (see
Figure 6) for the assumed residual power units’ configuration. For the 4000 and 5000 MW
each configurations the whole year optimisation run shows, against expectations, negative emission reduction, which can be explained by the linearisation effects, that are discussed in
Section 3.2 and visible in Figure 10.
All interval lengths between 2 and 30 days with their corresponding period lengths do not seem to have a major influence on the quality of the optimisation result, but show significant changes in computational time (see
Table A3 in
Appendix A). Further, the graph shows that the absolute reduction of emissions through UC decreases with increased VRE power installation, the exception being the 2000 MW
each configuration, as discussed above.
3.1. Result of Unit Commitment
The goal of optimisation is to find non-trivial solutions [
44].
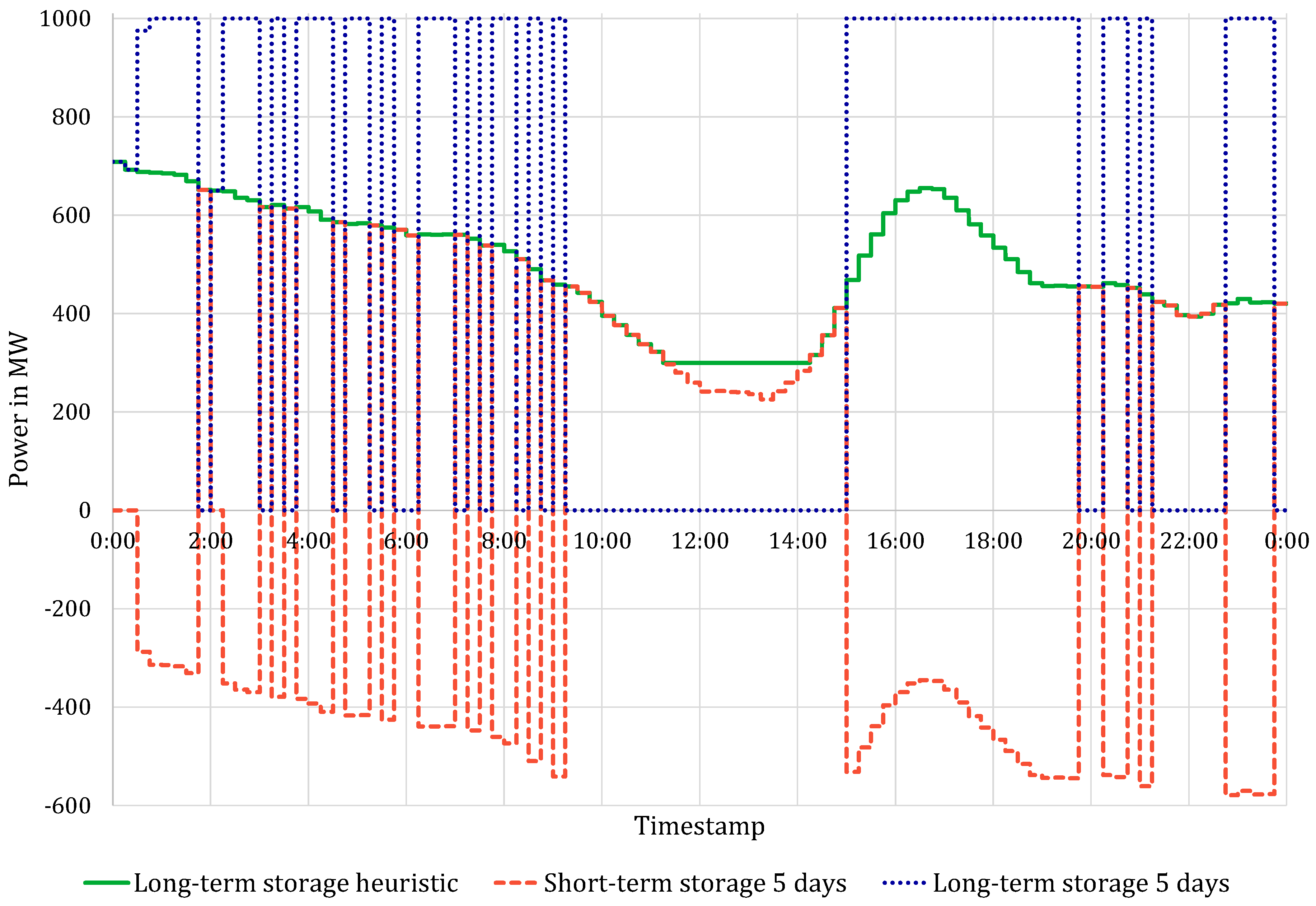
Figure 9, depicting a time series excerpt, clearly shows a non-trivial result from the implemented UCO model (dashed and dotted lines). For the UCH the long-term storage device’s discharge unit (solid line) follows the residual load as the UCH emptied the short-term storage device already at that time frame (therefore not shown), which results from the pre-set order of operation. For the hours 11:30 to 14:15 however the long-term storage device’s discharge unit cannot go below its minimum load and therefore feeds to the grid with minimum load, creating the need for curtailment. The UCO makes a better use of storage devices in that the long-term storage (dotted line) rarely follows the residual load, but rather is running mostly at full power or not at all. The short-term storage device (dashed line) is charged with the surpluses created by the long-term storage device and discharges when the long-term storage device is not utilised. This happens predominantly at low residual loads, where the long-term storage device’s discharge unit would have a relative efficiency lower than the round-trip efficiency of the short-term storage device. While this seems an unrealistic unit dispatch, it is the most efficient plan, in energy terms, for the formulated mathematical problem. Hence, this can be considered an optimal strategy—especially as the curtailment due to minimum load of the long-term storage device’s discharge unit is avoided. In
Figure 9, a scattering of the UC can be observed and is deemed unrealistic. It can be prevented by including intertemporal constraints such as minimum downtimes and start-up times in the mathematical problem formulation, which has not been implemented in the UCO version used in this paper. The resulting scattering of the tactic is further discussed in
Section 4.
As previously discussed, the biggest difference between the UCO and the UCH can be seen in the share of storage in the supplied energy. This results from the different use of the energy storage devices. While the UCH only stores surpluses of renewables, the optimisation finds non-trivial solutions where the CCGT of the long-term storage is used at its best efficiency, charging the battery to avoid a less efficient operating point later and instead discharging the battery. This is the expected behaviour of the optimisation routine, since its target is to minimise the CO2 emissions and the efficiency spread of the CCGT between minimum and maximum operating point is 20%-rel. and the losses due to battery usage lie around 10%.
3.2. Results for Different Interval Lengths
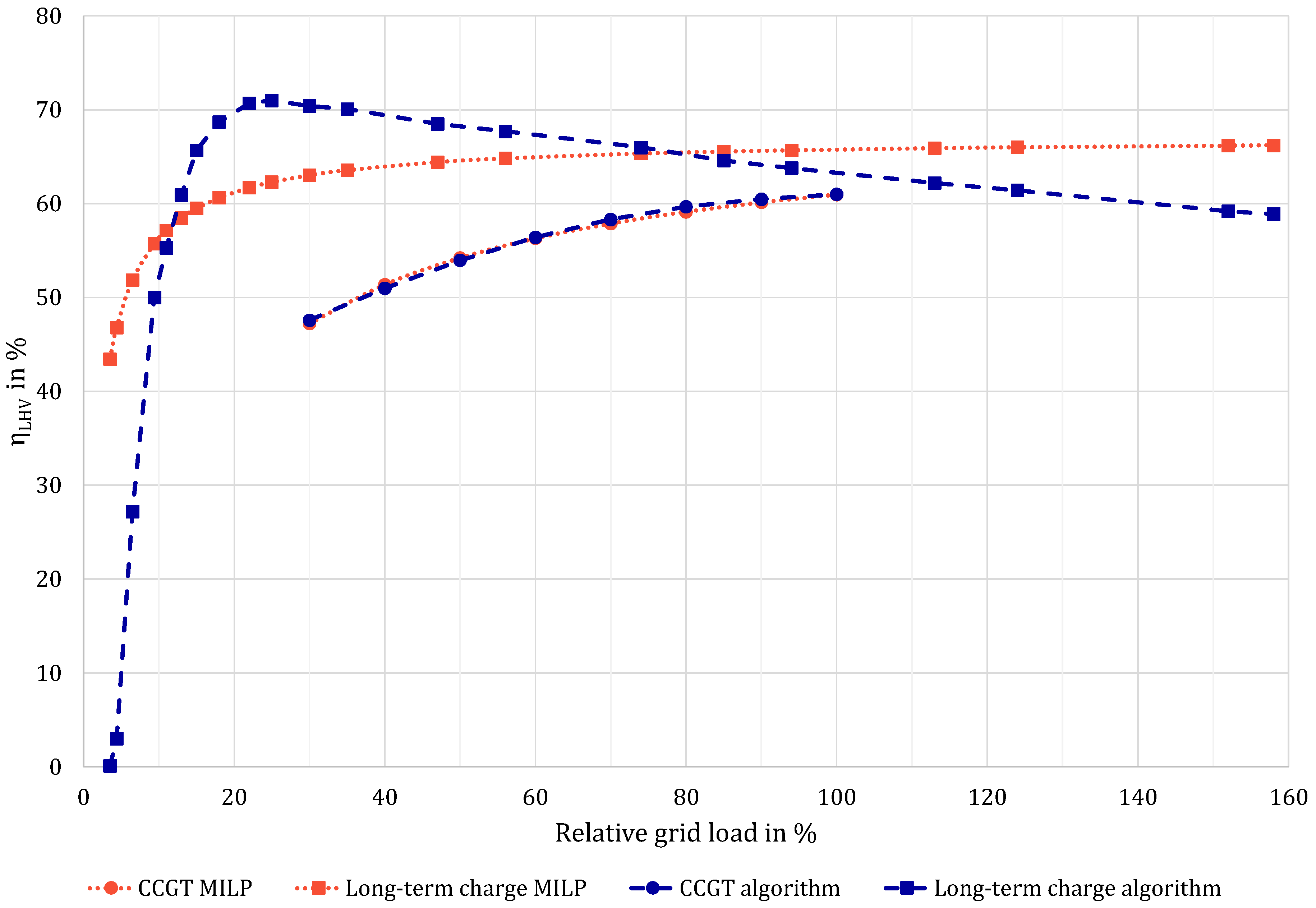
As described in
Section 3.1, the characteristic line model acts as an NLC for the optimised operation plan. While the algorithm tries to set the power of each unit according to plan, it does not use the linearised efficiency curves shown in
Figure 5 as dotted lines, but the non-linear characteristics (dashed lines). This results in differences between the direct MILP solution and the final UCO solution after non-linear control by algorithm.
For storage units that means that the storage level might be over- or underestimated and the unit is not running with the planned power or, due to those discrepancies in storage level, at all. For the conventional residual unit, the difference results in only negligibly different emissions when running as planned. Due to the storage deviations unplanned run-times may occur for the conventional units. These run-times result e.g., from timesteps, where the MILP can use the energy storage devices because of non-zero SOC, but the NLC calculated zero SOC (see
Figure 10) and needs to use the conventional power plants to cover the residual load. The timesteps and duration of the different run-times vary with interval and period length of the rolling horizon.
For a closer look, time series of the storage level are shown in
Figure 10 for the long-term storage with an installed VRE power of 3000 MW
each. The dashed lines represent the MILP results, while the solid lines show the storage level after the NLC. The time series are presented for a 5 days interval (scenario c, blue lines) and a 365 days optimization (scenario f, green lines).
It can clearly be seen, that the storage level behaviours for both scenarios differ widely, especially from the end of January to November. In case of the 5 days interval, the storage is discharged completely at the end of January. Afterwards, the energy in the storage is charged only up to 80 GWh of energy once, with various other minor peaks, but no significant accumulation of energy. Lastly, starting in November, enough renewable surplus leads to an accumulation of energy, until the initial storage level is either reached or exceeded again.
In the 365 days interval, with perfect foresight for the entire time frame, the long-term storage is not depleted at the beginning of the year, but operated between 50 and 90% SOC. The peaks throughout the year, however, qualitatively correspond to the 5 days interval time series. After a complete discharge at the end of November, both scenarios progress with an almost equal storage level.
Furthermore, it can clearly be seen that a significant difference in storage level is mounting up as long as the zero SOC point is avoided by the MILP solution. The reason lies in the parameterisation of the long-term charge unit efficiency curve, as displayed in
Figure 5. The optimiser calculates a 13 rel.-% higher efficiency for maximum power than the NLC, which in return accumulates a higher storage level for long operating hours at higher charging power (see
Figure 10). As
Figure 5 suggests we observe an underestimation for operating hours at low charging power.
When looking at the same VRE configuration, but shorter interval length of 5 days (blue lines) the differences in storage level between the MILP solution and the solution after NLC become significantly smaller. This is due to the rolling horizon, which is aligning the optimisation storage level more frequently (at the end of each optimisation period for a new interval) with the NLC results. For the 365 days interval and period length, there is no feedback loop, so that differences can accumulate (see
Figure 10).
This is also the main cause why seemingly optimal solutions for long optimisation intervals might be found, but are not necessarily feasible by the non-linear control calculation and therefore lead to higher emissions than even the simplest heuristic approach.
While the linearisation effects mainly influence scenarios with long optimisation intervals (in this paper especially the 365 days optimisation in scenario f), the VRE configuration influences the magnitude of those effects. With higher installed VRE capacity, the usage of the long-term storage with high loads increases, so that higher deviations due to linearisation effects can accumulate. This can be observed in
Figure 8.
4. Discussion
Several points need to be discussed in order to correctly categorise the findings of this paper. As previously stated, the constant power demand does not represent a real grid situation. The complexity still was deemed sufficient for the test of interval lengths, which is supported by
Figure 9, where the UCO comes to a different solution than the UCH in almost every time step. The quantitative values of specific emissions and storage share therefore do not represent a prognosis for future energy systems. Additionally, it is emphasized, that the configuration of residual power supply was not optimised. Lastly, with the chosen boundary conditions it could be argued, that either the efficiency curves or the number of units should have been adjusted to correctly represent the installed powers. This was deemed too complex within the scope of this research.
The linearisation effects presented in
Section 3.2 can mainly be attributed to the efficiency curve parameterisation in
Section 2.6.3. A different formulation of the optimisation target might resolve in a closer fit around maximum power. The results for high installed VRE power might be improved by that. An adjustment of the parameter optimisation’s objective (see Equation (15)) was not done however, since the 365 days interval is considered unrealistic and other interval lengths were matching the NLC’s result close enough (see
Figure 10). This rather shows the missing robustness of a 365 days interval length for the chosen problem.
A shorter period length for the 365 days interval might fix the previously mentioned problems, but that was considered too distant from the scope of this paper due to large computational effort. In general, the results for the different interval lengths might be tied closely to the corresponding period lengths. This difference is only addressed by the 2 and 3 days interval lengths, where no significant effect occurred.
Another point that needs discussion is the scattering observed in
Figure 9. The CCGT of the long-term storage is working for several short time periods following each other rather closely. This is a behaviour that would not be expected in reality since there are temporal constraints on down-time and maximum possible ramps to consider. This was deemed beyond of scope for this paper, but will be worked on to better approximate real behaviour. As it is expected to change the results only in quantity and appearance it is seen as a minor problem for the findings of this paper.
As a last shortcoming of the model it should be emphasized, that the implemented heuristic is very simple. It could be argued that a more complex heuristic of conditions and loops could meet the results of the optimisation more closely. A rather simple heuristic was chosen, since the results were meant to cover the baseline expectation.
5. Conclusions
In this paper, a different modelling approach for rolling horizon UC was presented. For that approach, a UCO model was implemented and its positive effect in contrast to a simple UCH could be clearly shown. As the main result it is observed, that the interval length for a rolling horizon approach has an almost negligible effect on the objective value, namely the CO
2 emissions of the energy park, with this approach, even though, the detailed unit commitment can vary significantly (see
Figure 10)). However, the difference is mainly to be found in computational effort.
A 2 days optimisation interval is therefore suggested as sufficient considering quantitative reduction of the optimisation target, computation time (see solver statistics in the
Appendix A) and realistic lengths of weather forecasts [
42,
43].
The variation of the configuration (installed volatile power capacity in this study) however has a bigger effect on the optimisation objective (CO2 emissions in this study) than the UCO. Considering the massive computation time of a UCO, it is suggested to explore configuration variations using a simple heuristic and to optimise a small set of resulting configurations with a UCO only afterwards.
The effects of the linearisation of a given system as discussed in
Section 4 make a strong case for rolling horizon and against whole-year optimisation runs. Additionally, a system configuration optimised according to a whole year optimisation run might lead to different results than a system configuration optimised according to a rolling horizon run. Since the forecast length that is inherent to a whole year run is not achievable, it is suggested to optimise an energy system configuration with a rolling horizon approach as the final configuration of any energy system should work with realistically achievable foresight.
Outlook
While the proposed optimisation model already allows a detailed technical description of the energy system, there are several possibilities for model improvement in upcoming versions. As discussed in
Section 4, the optimiser’s results tend to include scattering of generation and storage units. Intertemporal constraints could resolve that problem. Such intertemporal constraints will be included and looked upon in future versions. It is of great interest how that effects both the solution and the computation time since the problem is more complex but also tighter, which might make the decision trees of the branch-and-bound considerably smaller.
In this paper, the optimisation goal is set to minimise the CO2 emissions of the underlying energy system. Another common approach is the minimisation of (operational) costs, which is currently being implemented allowing multi-objective optimisations (costs and CO2 emissions).
A major problem with using a rolling horizon for UC problems is the control of storage levels for long-term storages, especially with short interval length, because the optimiser is not aware and therefore does not plan for eventually upcoming periods of continuously low supply of VRE power (“dark doldrums”). The use of long-term storage strategies e.g., by the use of minimum support points is an interesting topic for investigation.
Lastly, it would be interesting to see whether the findings of this paper are applicable to different configurations and more complex systems.