2.2. Methodology
Understanding the regulations of electricity markets and Denmark’s special conditions is very important in order to correctly identify price drivers and relevant variables. These are discussed in detail throughout the paper as they contain a lot of information and assumptions, and constitute an integral part of the research. The availability and the collection of the data is also crucial as it affects the implementability of the models.
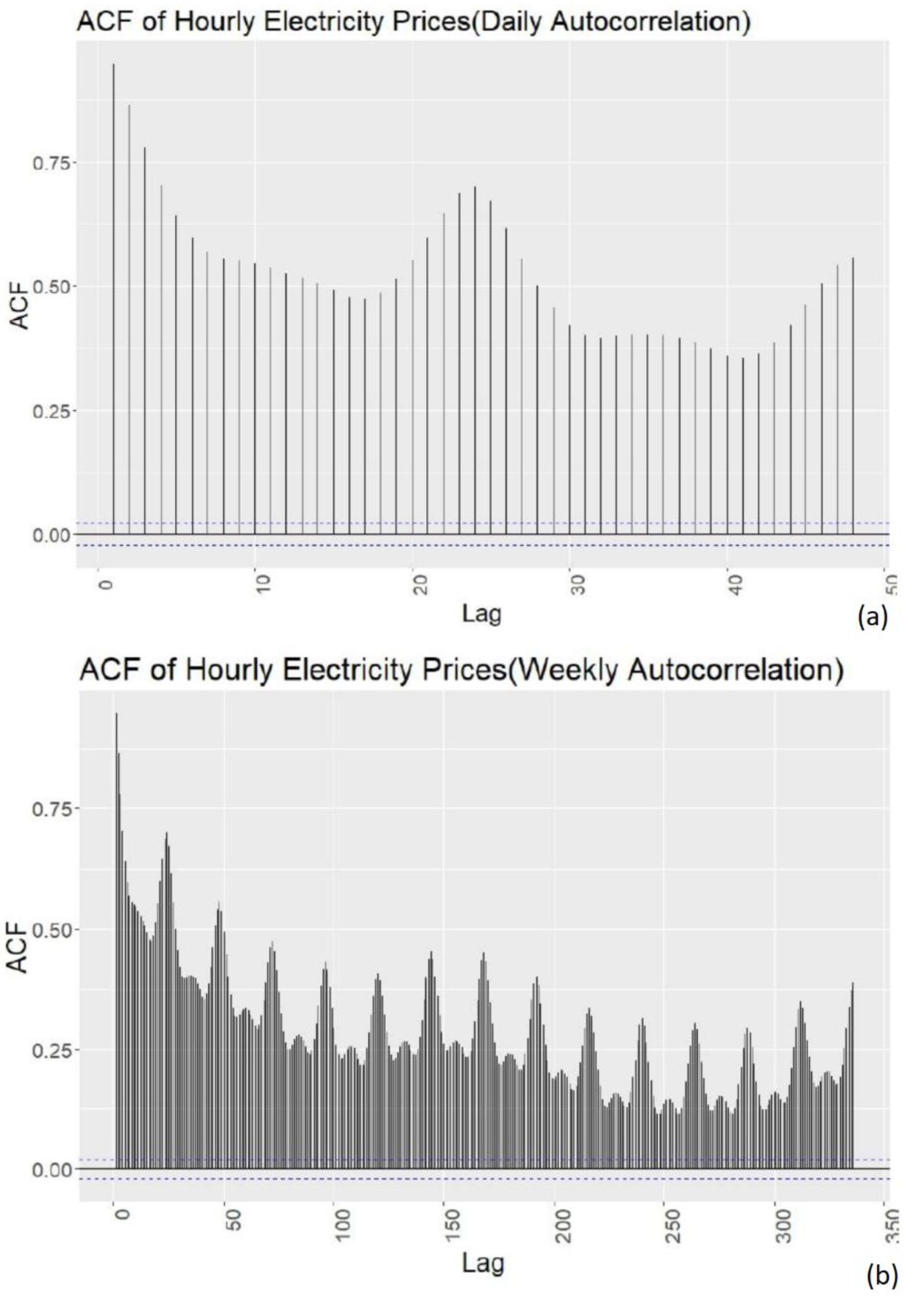
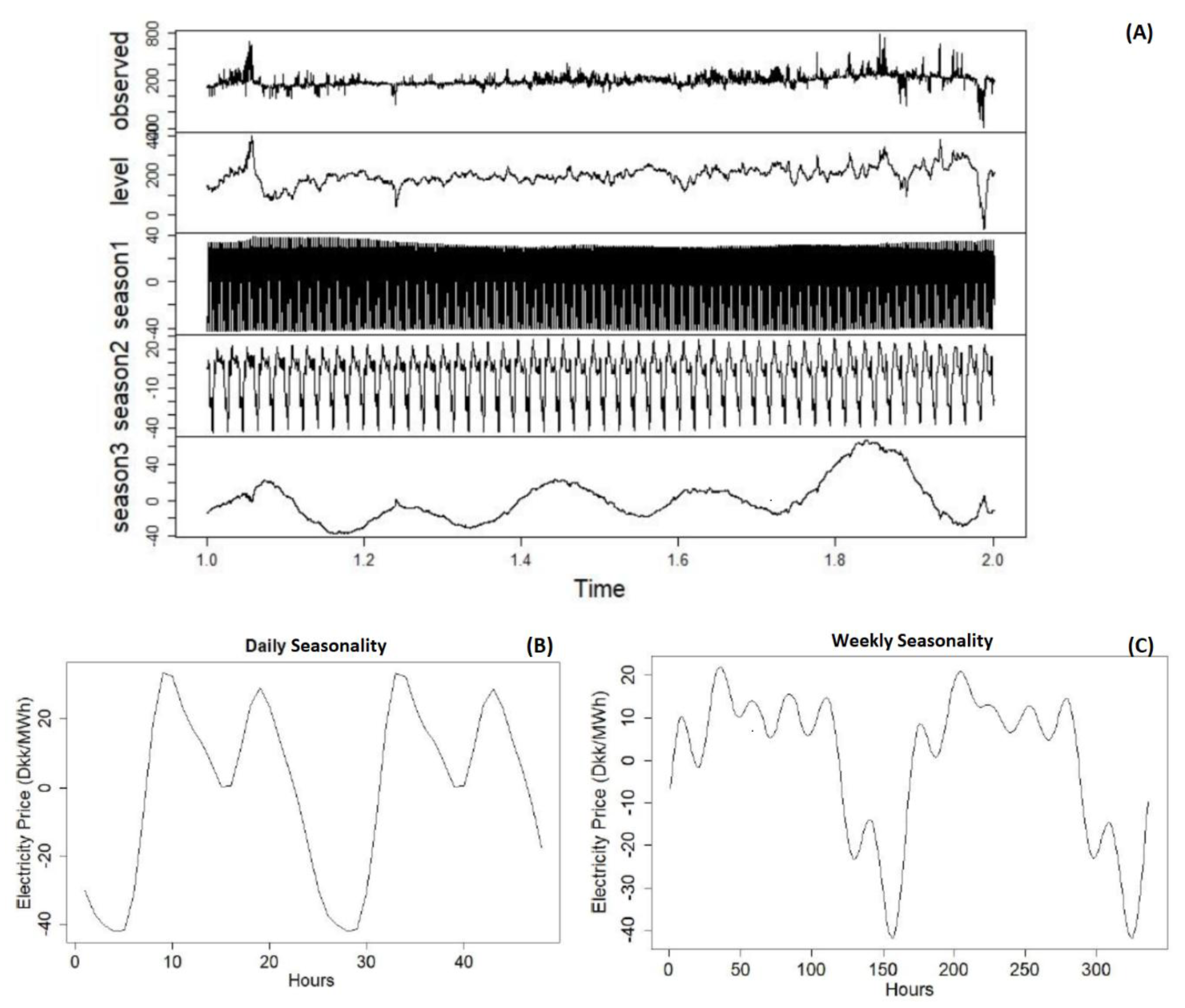
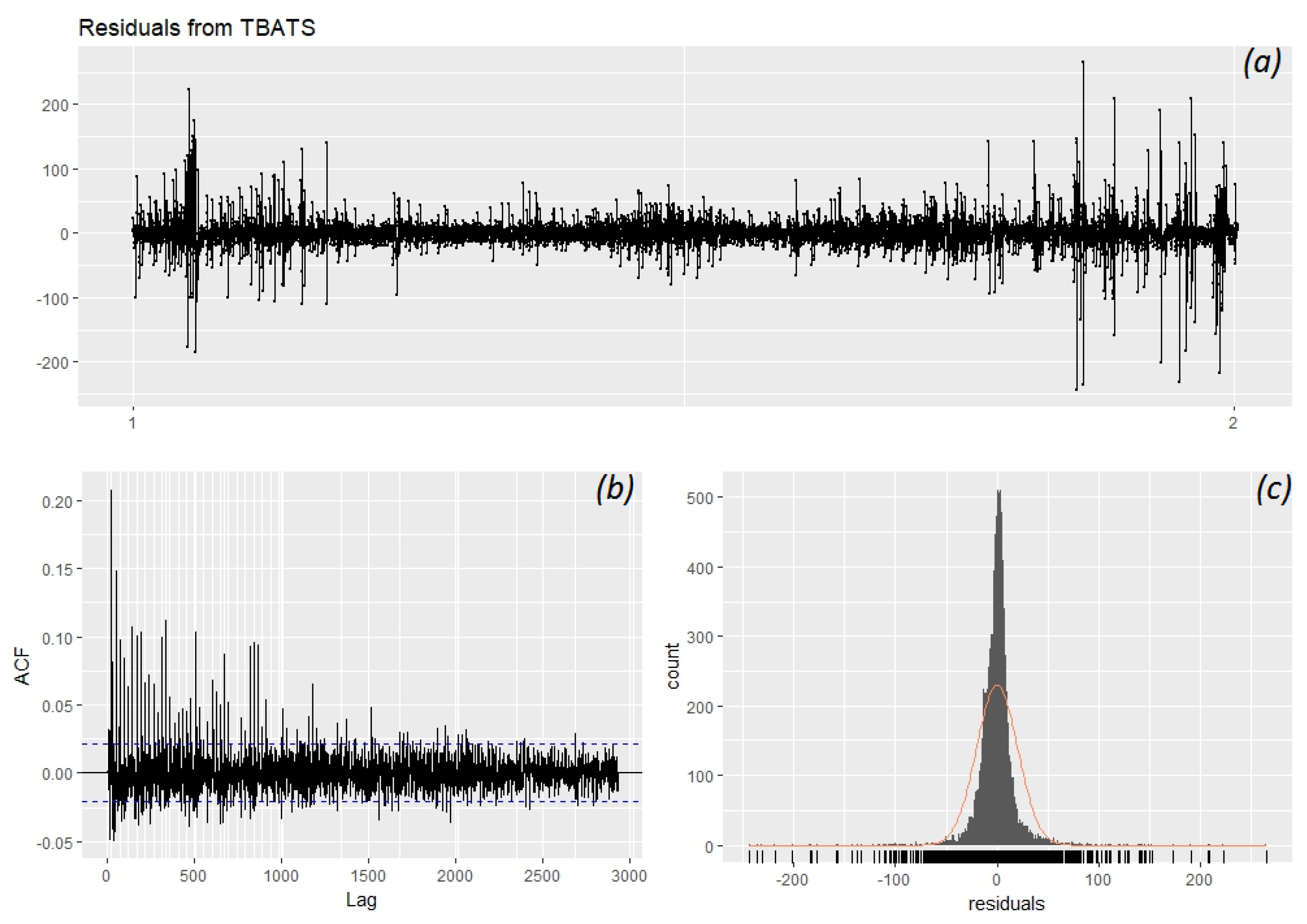
After collecting the data, preliminary data analysis is required to understand the data better. This will enable us to find good models that fit our data well. For the data analysis, tools such as correlation graphs, autocorrelation functions, comparative variable analysis, decomposition and residual analysis will be used. First the data to be used in the forecasting will be analysed using statistical tools and patterns for seasonality will be checked using autocorrelation analysis. Then the data will be decomposed and further analysis will be done on patterns and residuals. For variable analysis correlation scatterplots will be used as the main tools. Each variable and its possible effects on the data will be discussed briefly.
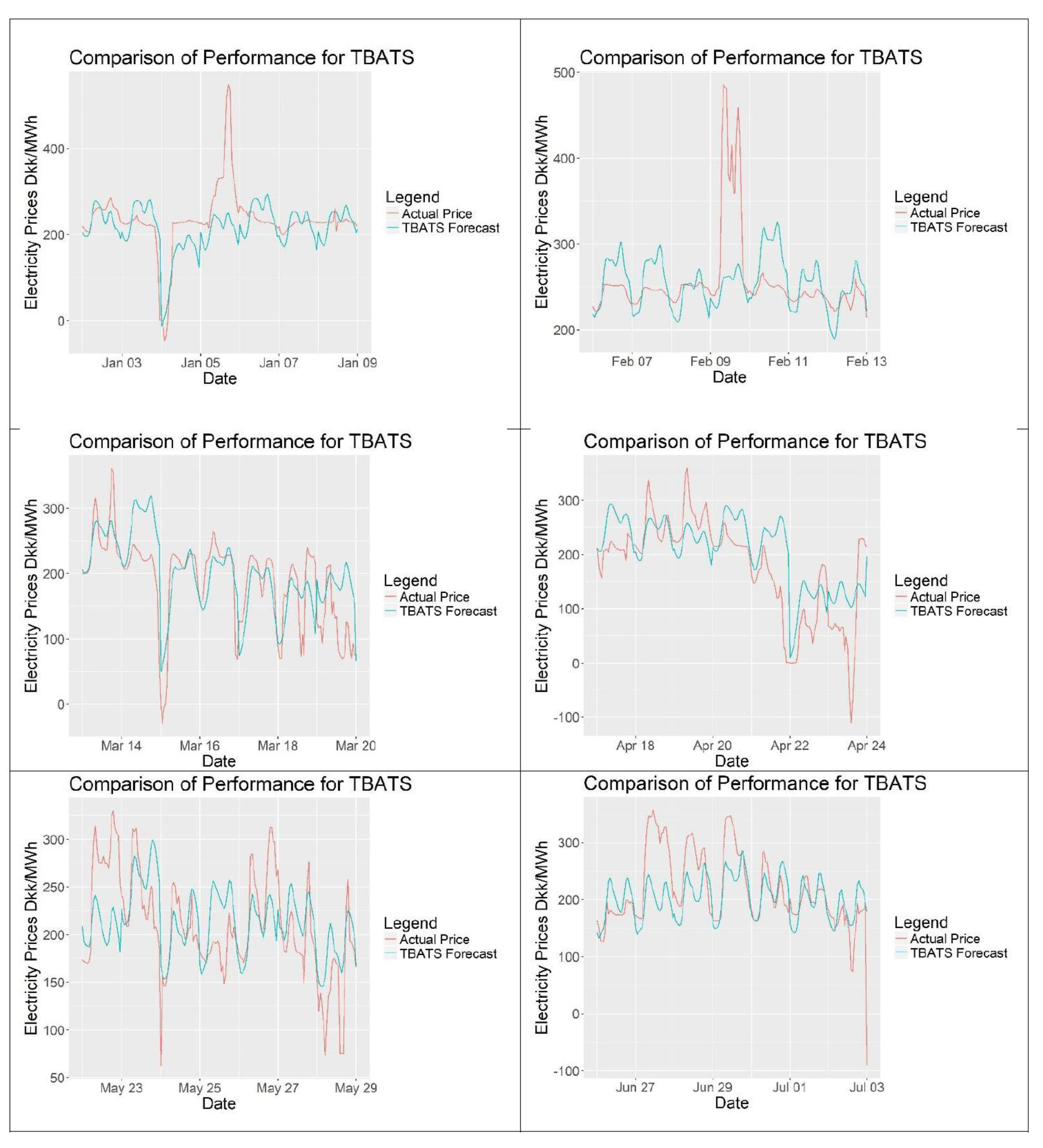
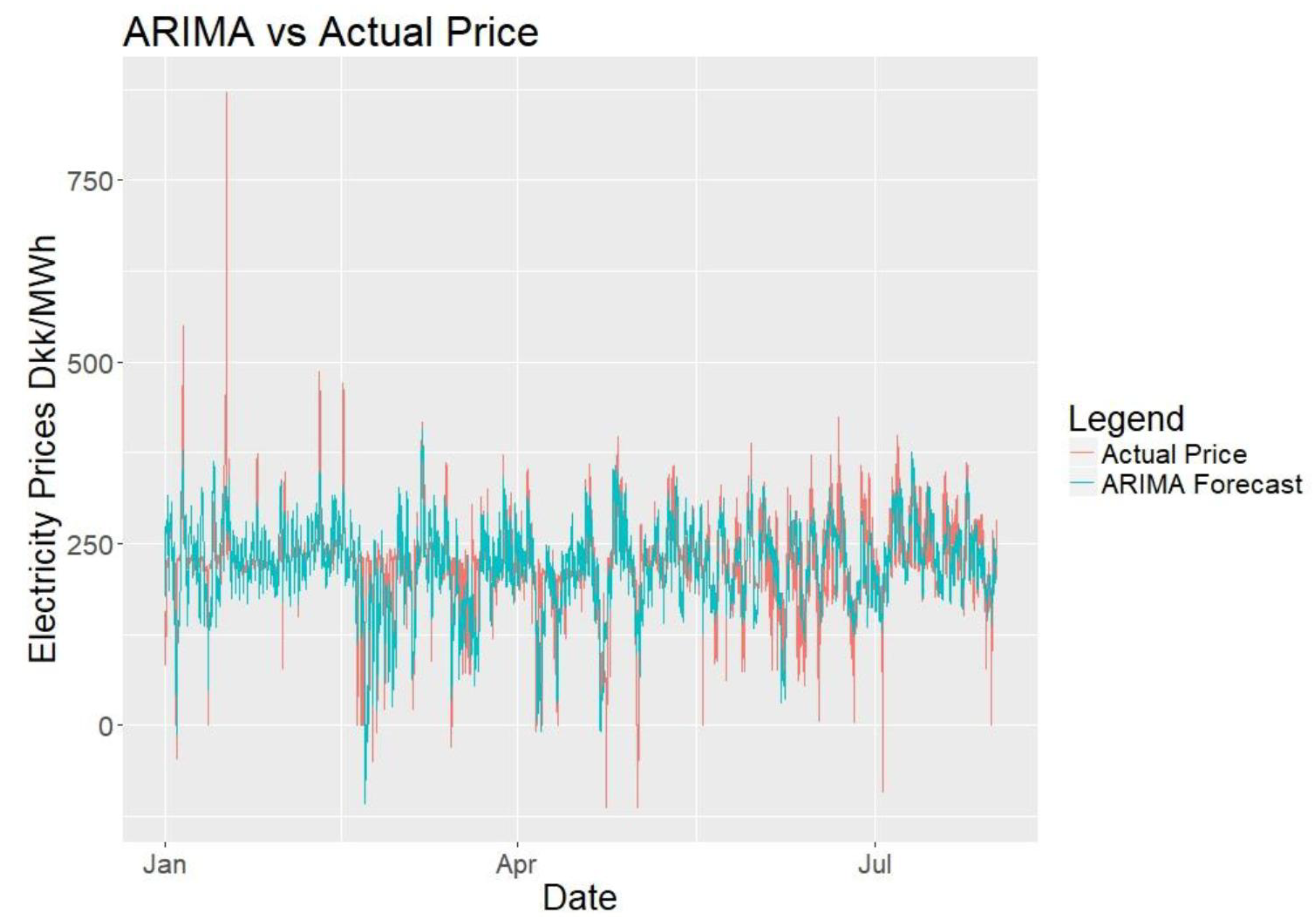
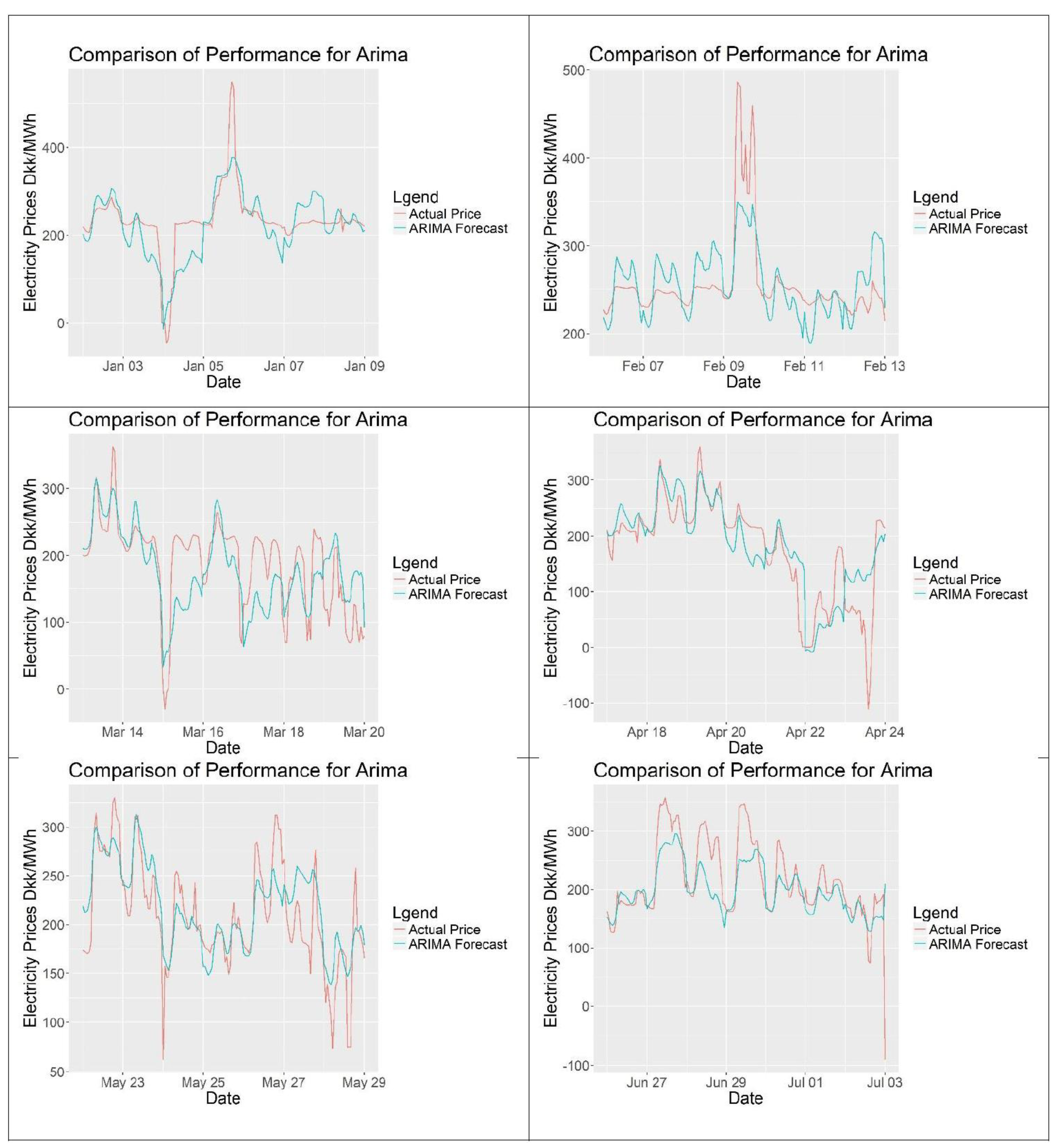
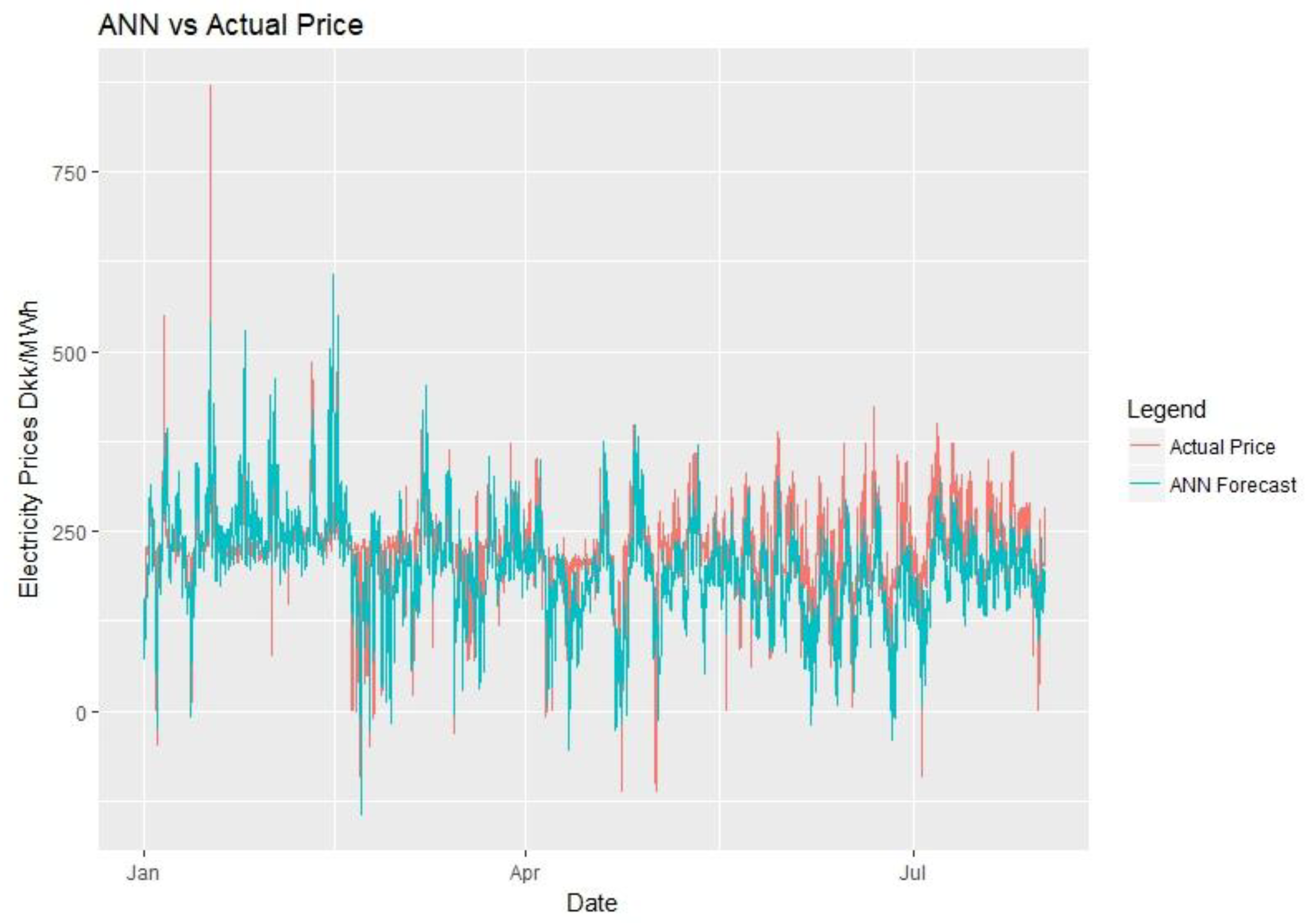
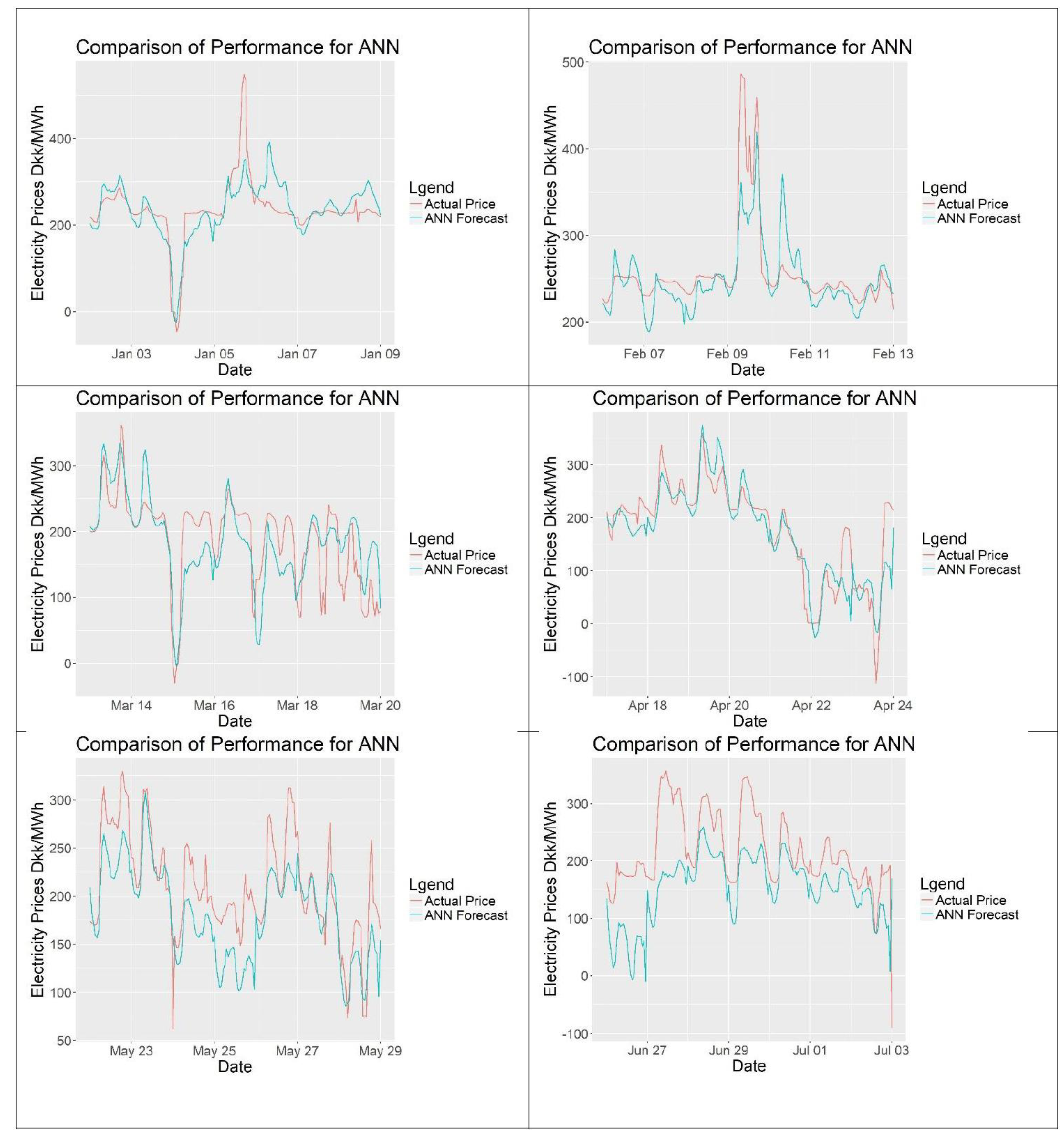
After setting up the model, the input data will be divided into two parts, one for training the model and one for testing the forecasts. The forecasting range will be 24 h with an hourly frequency. To include a full year of training data as a minimum, 2016 data will be taken as the training period. 2017 prices will be forecasted as an expanding forecast for 212 days, which is from the start of January to end of July. Expanding forecast means that after forecasting the next 24 h, that raw data is included to our training period for forecasting the day after. As mentioned by [
7,
17,
18] short and carefully selected test periods do not give any information regarding the performance of the forecasts as they are ignoring special days, holidays and general price variations. Therefore, a 7-month period for forecasting will be used for more objective and better assessment of forecasting models.
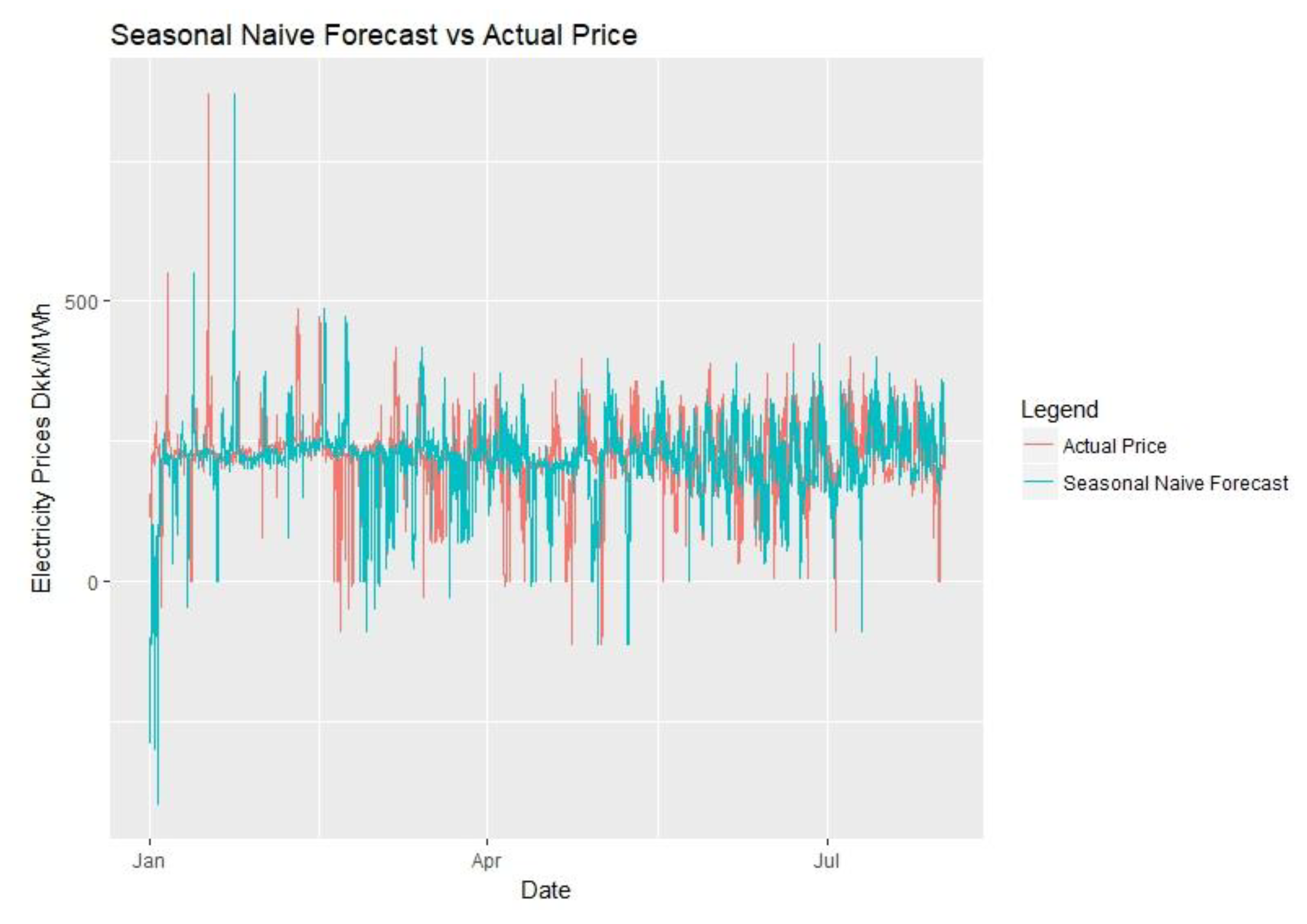
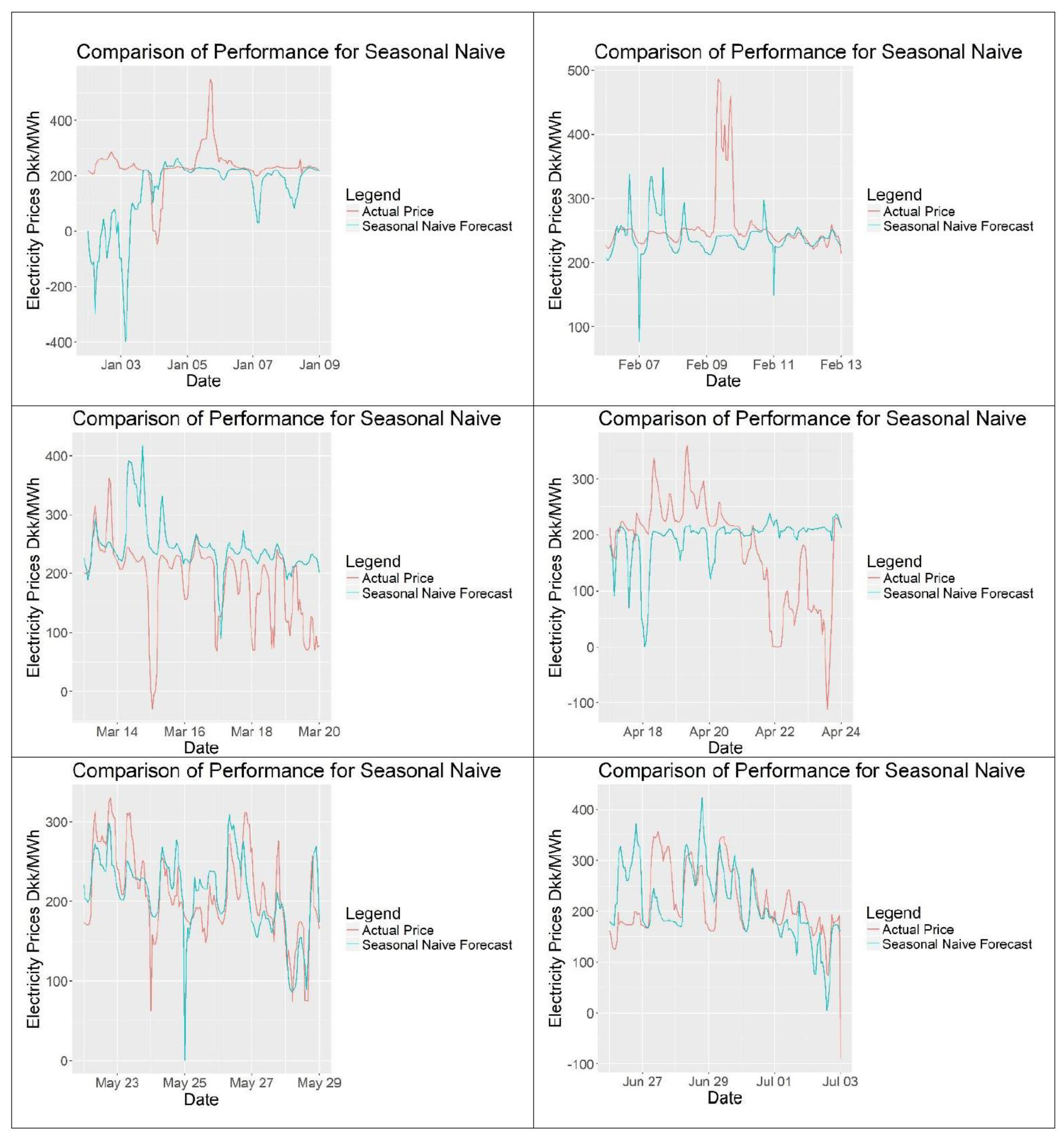
For the evaluation of the forecasts, scaled error models will be preferred over percentage error models as percentage models can yield infinite error when the actual electricity prices are 0 DKK/MWh, making them unreliable. The reader should keep in mind that the performance of the models should only be compared for the same set of data of the same time using the same error calculation model. Also for evaluation simpler forecasting methods can be used as benchmarks. One model that will be used is the seasonal naïve method, which is basically assuming that the price to be forecasted is similar to the previous period’s prices, such as previous week.
After comparing the error values and evaluating the forecasts, ways to improve the forecasting performance of the models will be investigated using backwards feature elimination. This tool will provide the removal of variables that are irrelevant to the forecasts. Then an attempt at combining the forecasts in order to gather more accurate forecasts will be realized. The paper will be finalized with conclusion, evaluation of the study and suggestions for further studies.
2.3. Forecasting Methodology
Forecasting can be defined as estimating future unknown values in an educated and systematic way using available data. As the values of the data that is to be forecasted is unknown, there are different possible values and the forecaster aims to find the most probable value(s). In case the forecast is used to obtain a single value as the most probable value the forecast is called a point forecast, whereas a probability forecast contains a range of values with the prediction intervals and densities [
19]. In this research point forecasts will be used as they are simpler and easier to interpret.
There are a variety of tools and methods for forecasting. It is important for a forecaster to be able to spot the right tools considering the data and the forecast span. To achieve this the problem should be defined clearly and relevant data should be collected. To achieve this task the following steps mentioned by [
17] will be followed. These steps are as follows: problem definition, gathering information, preliminary analysis, choosing and fitting models, and using and evaluating a forecasting model.
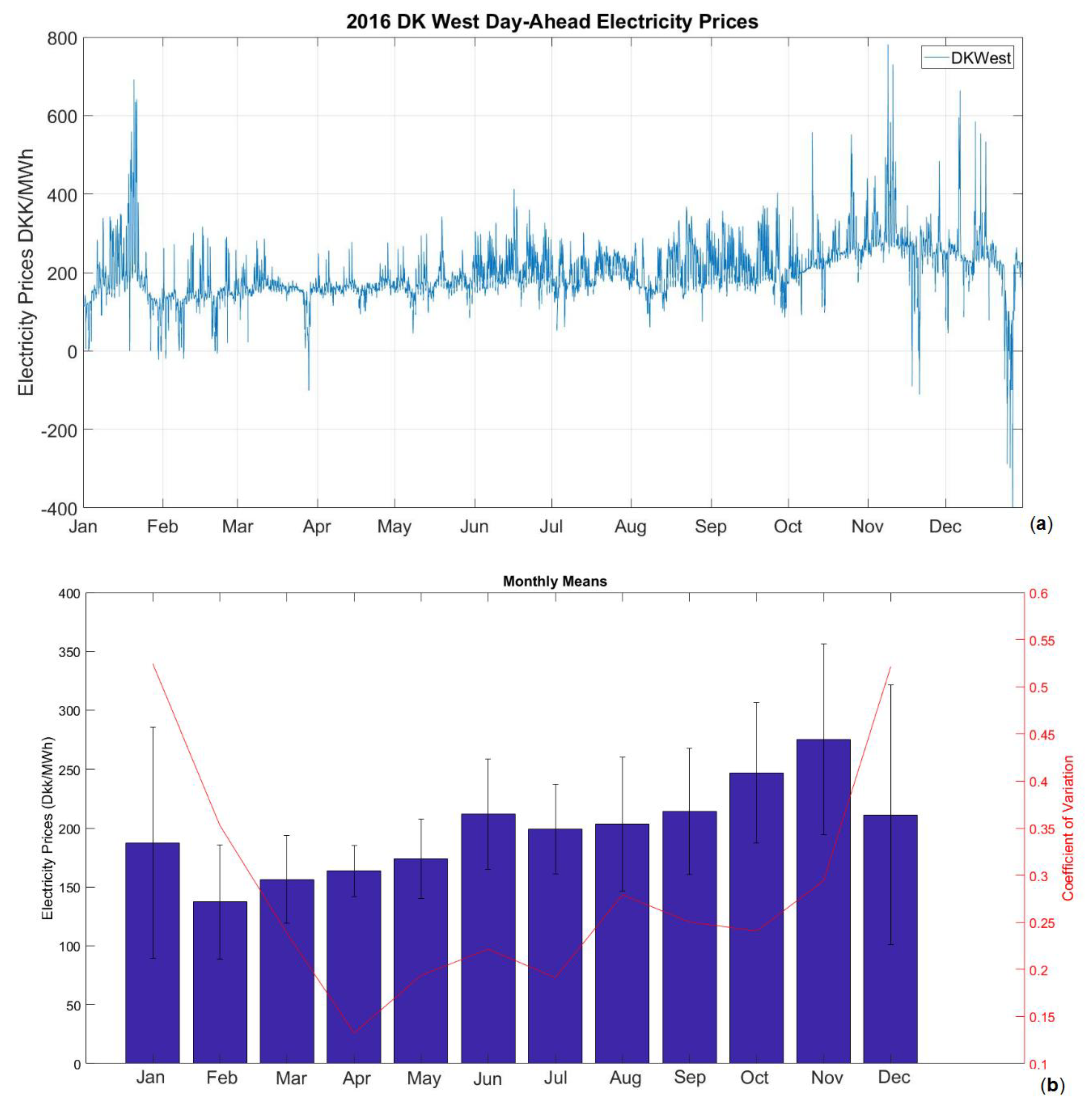
The forecasting problem of the project is to forecast day-ahead electricity prices from Denmark Jutland (including Fyn) region, commonly referred to as DK1 or DKWest in Energinet or Nordpool sources. The forecasting span has been selected as 24 h to simplify and imitate the actual bidding that takes place in Nordpool. As the aim is to forecast hourly prices using more frequent data than hourly will not be necessary. Data from 2016 will be used as training data and the first seven months of 2017 will be forecasted.
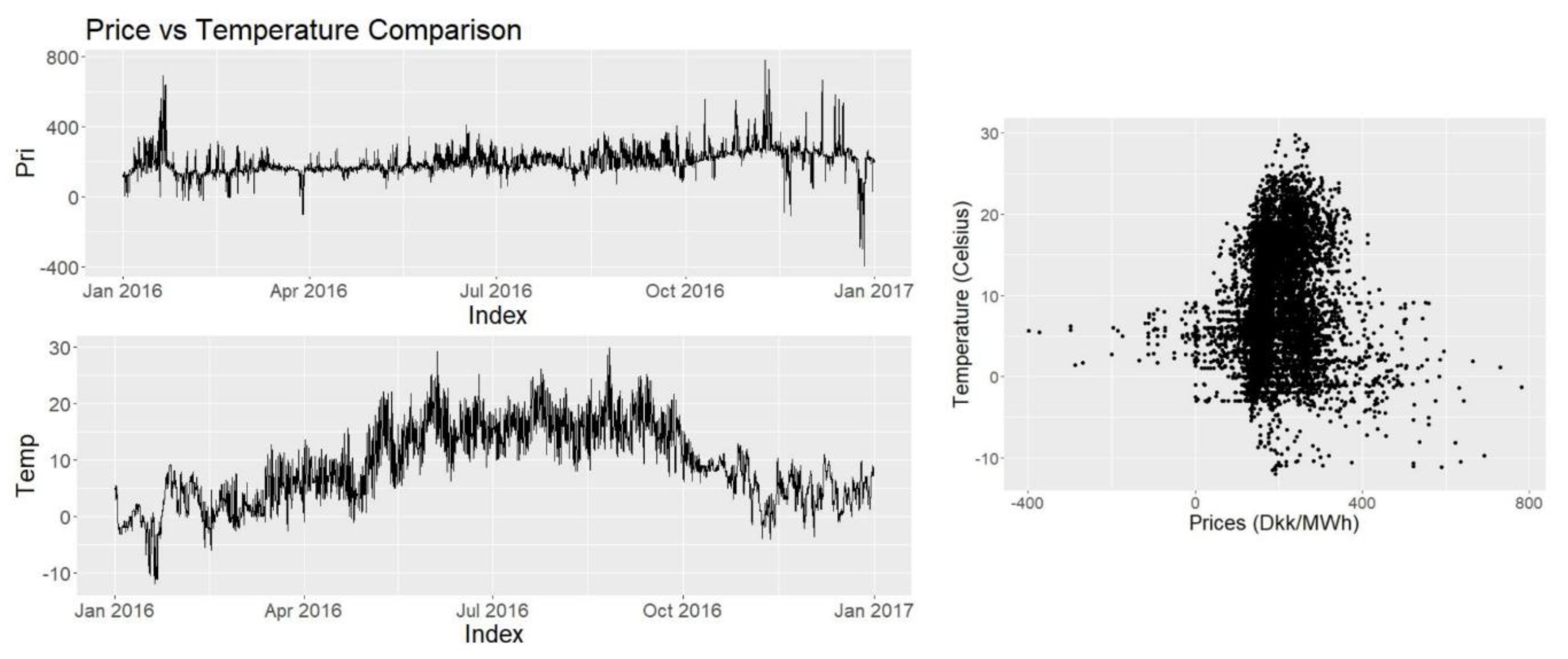
Historical data regarding electricity prices is available online at Nordpool website. For the explanatory variables different sources are being used. Temperature data is provided by Energinet for the Tange location. As this is a central location in Jutland and knowing Denmark is mostly flat it is assumed that this temperature portrays a good average for the region and the temperature across the region is highly positively correlated.
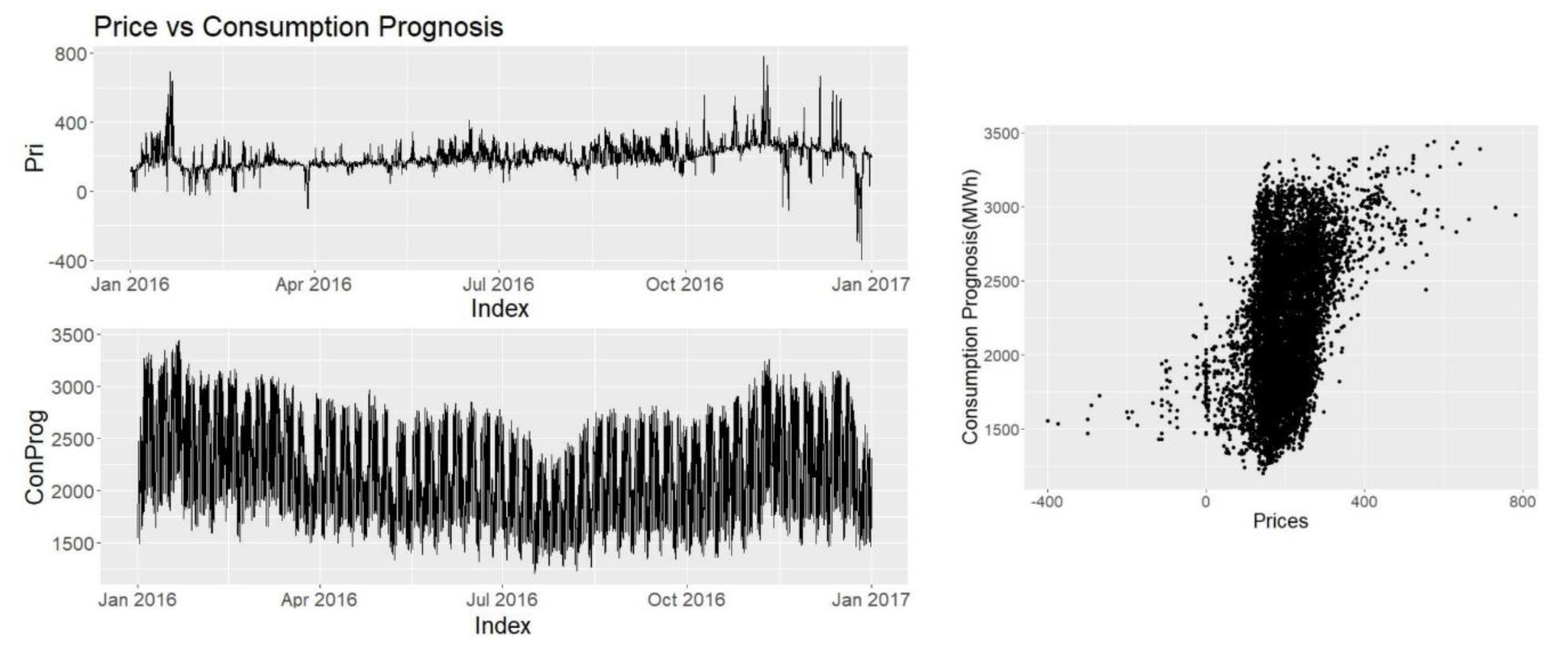
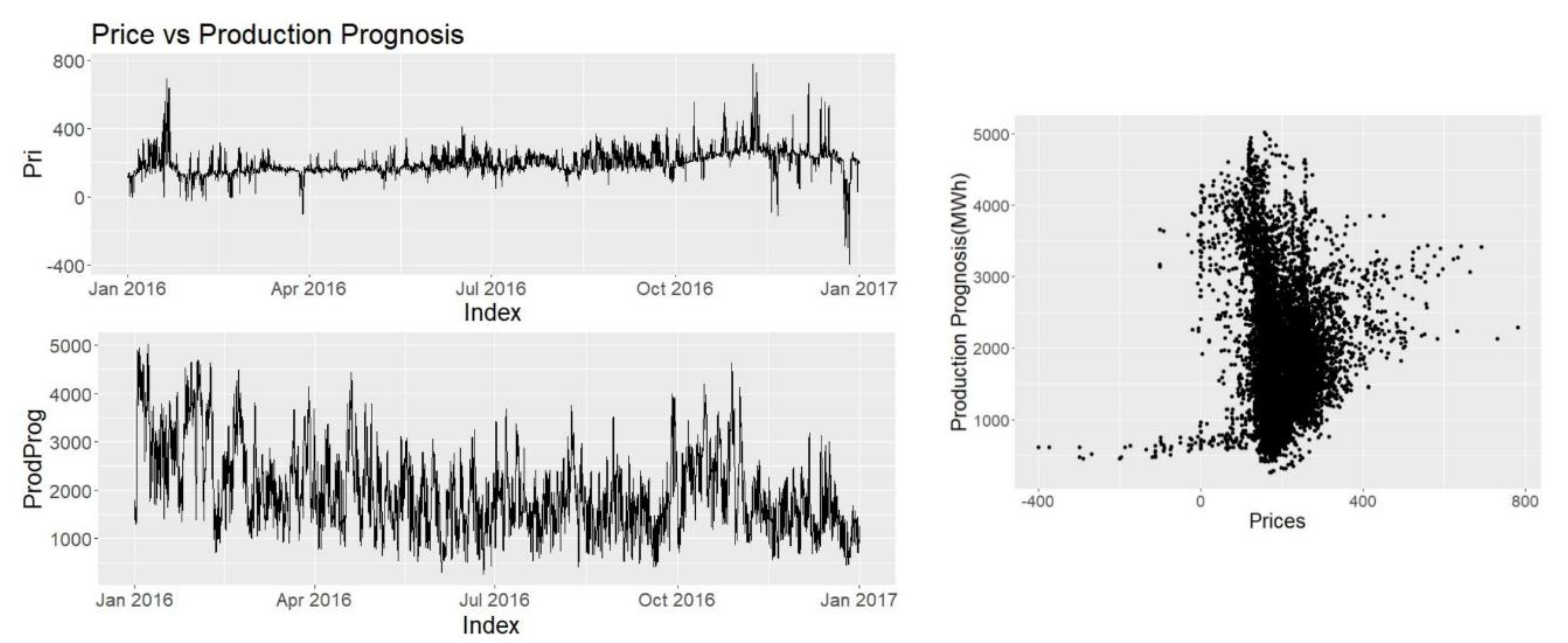
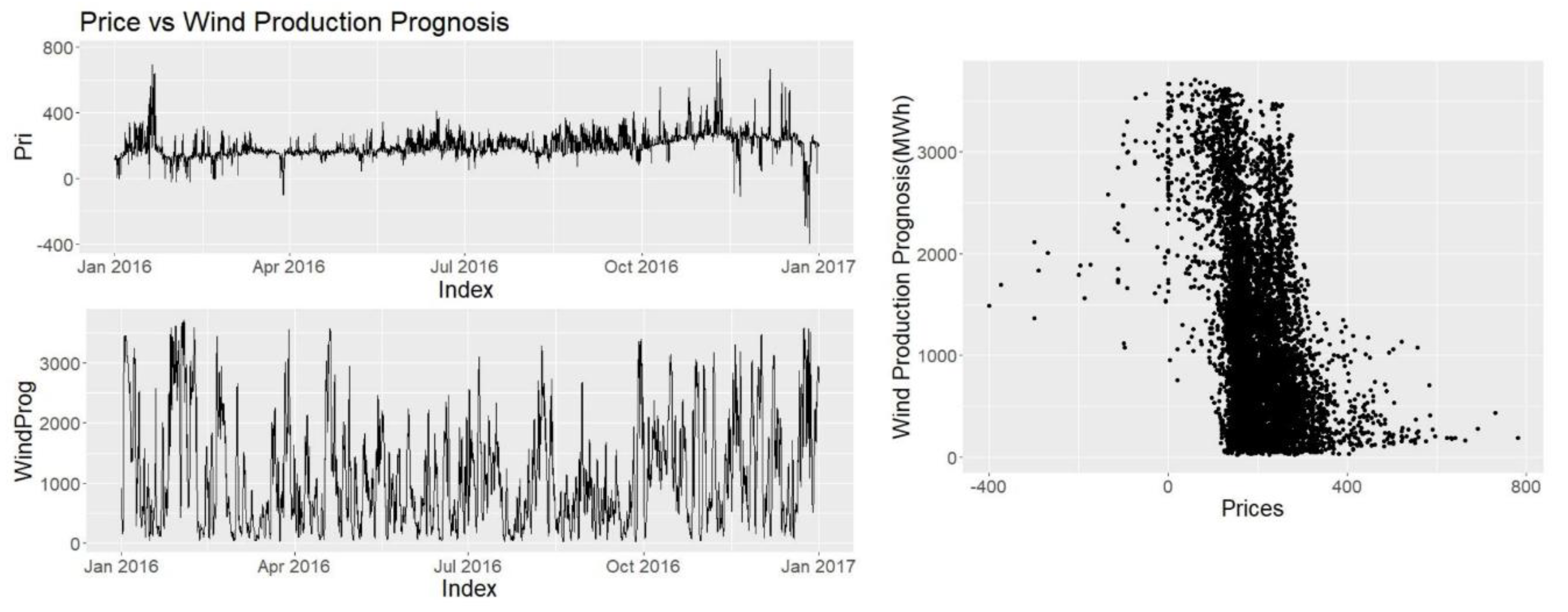
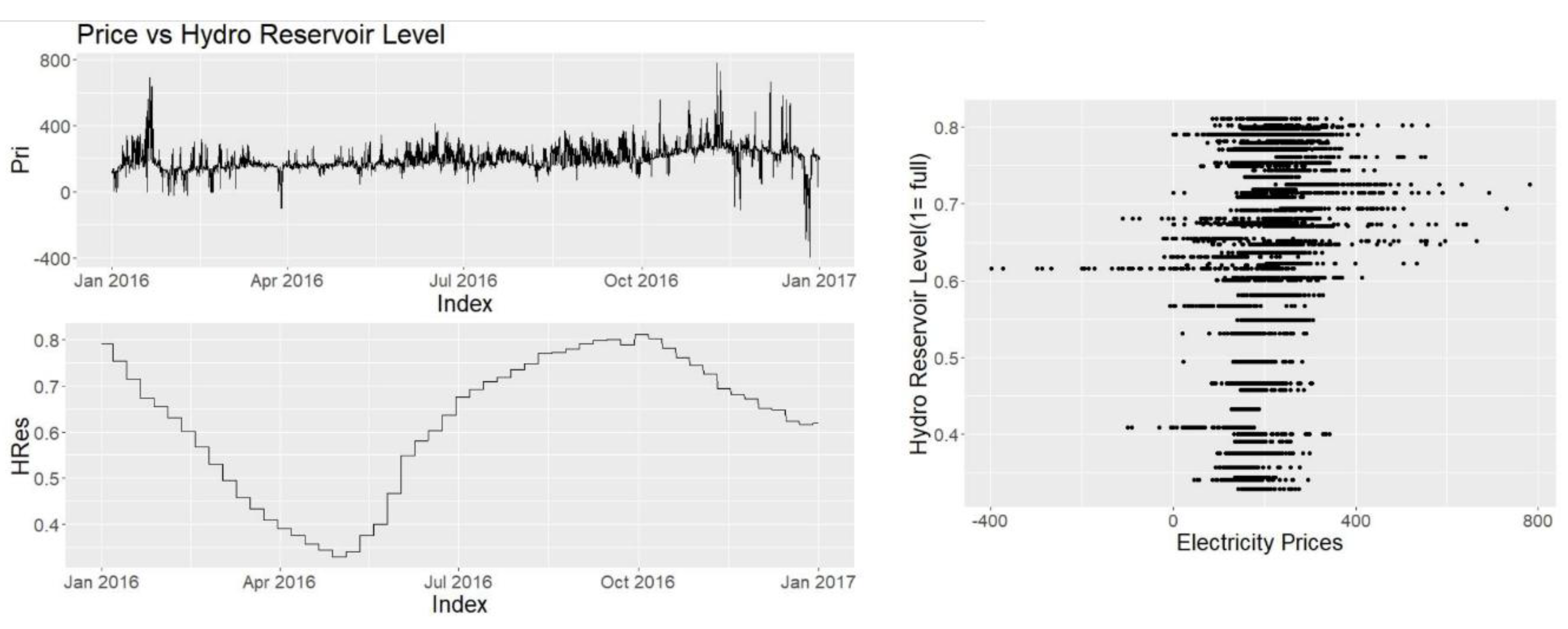
Other explanatory variables such as consumption prognosis, production prognosis, wind power prognosis and hydro reserve levels are provided by Nordpool and Energinet. Since they have direct access to the producers, and the users they are seen as highly credible and reliable sources.
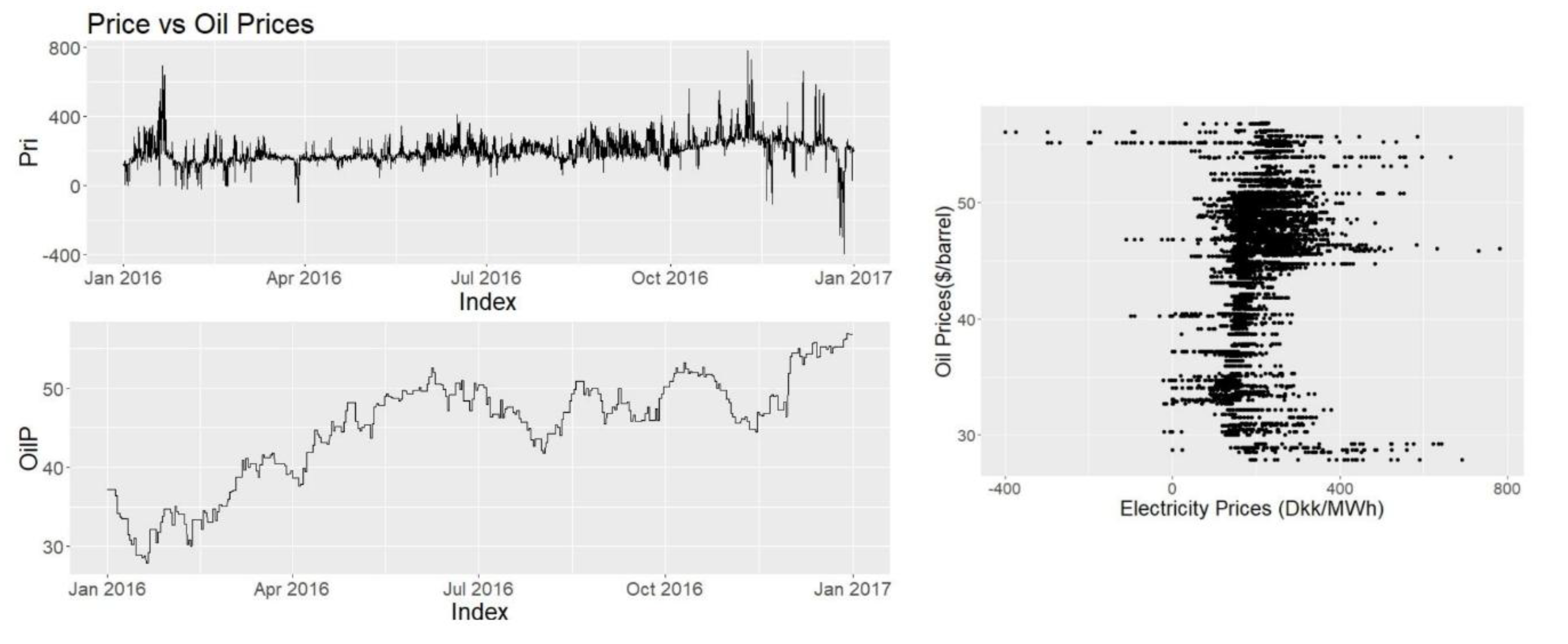
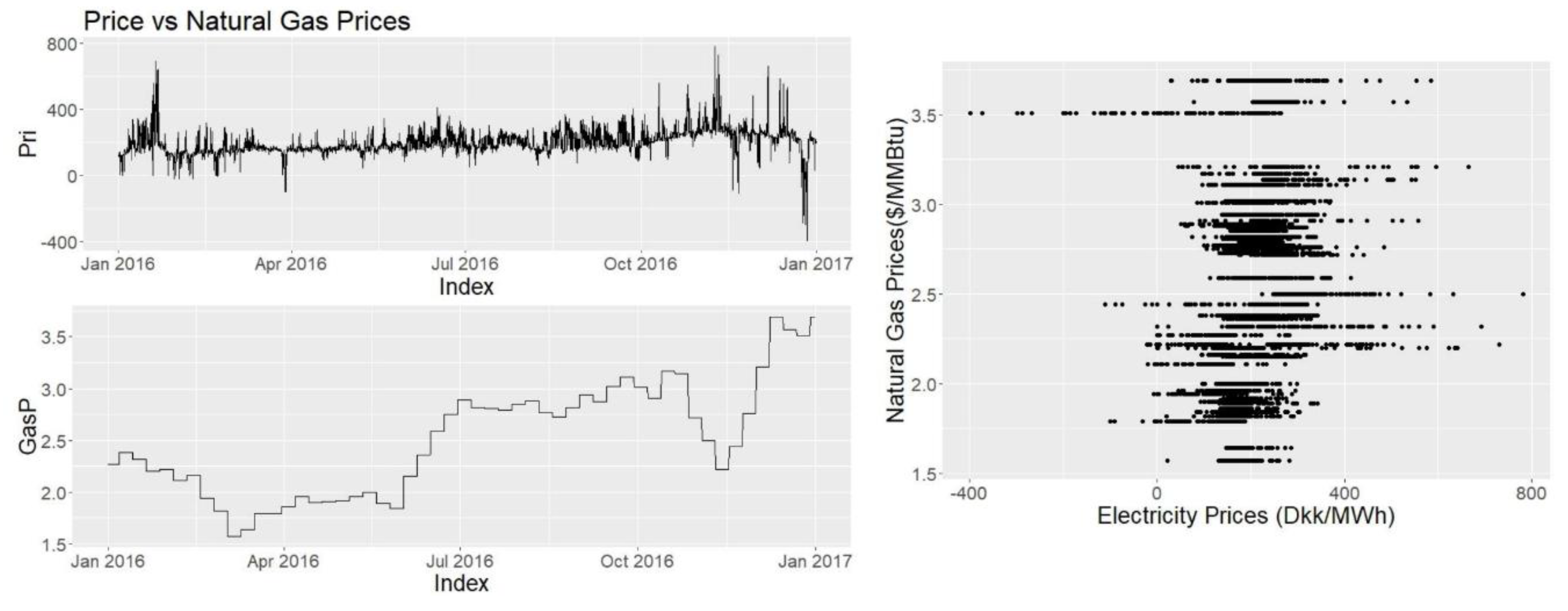
Oil and natural gas prices are taken from Fred series [
20]. For oil, “Crude Oil Prices: Brent—Europe” and for natural gas, “Henry Hub Natural Gas Spot Price” data sets are taken into consideration.
Data obtained from Fred and hydro reservoir data are weekly data where the data are copied to the corresponding values for each hour of the week. It is assumed that this data frequency is suitable these variables are not very volatile or have high variance in short time and possibly their effects are not seen hourly or daily in the corresponding data. Other data mentioned are collected and used as hourly data.
Hydro reservoir level is derived from the data collected from Nordpool. Following equation (Equation (1)) is used in order to obtain the data, where HRL is the hydro reservoir level,
NL is the amount of water in reservoirs in Norway,
SL is the amount of water in reservoirs in Sweden and
FL is the amount of water in Finish reservoirs.
NC,
SC, and
FC correspond to the total available water capacities in respective countries. Using the equation a value between 0 and 1 is reached, where 1 means that the reservoirs are full and 0 means that they are empty:
Two dummy variables are also considered in our data sets, one for weekdays and one for holidays including the weekends. Two sources are used to spot the holidays (the Office Holidays and the Public Holidays) [
21,
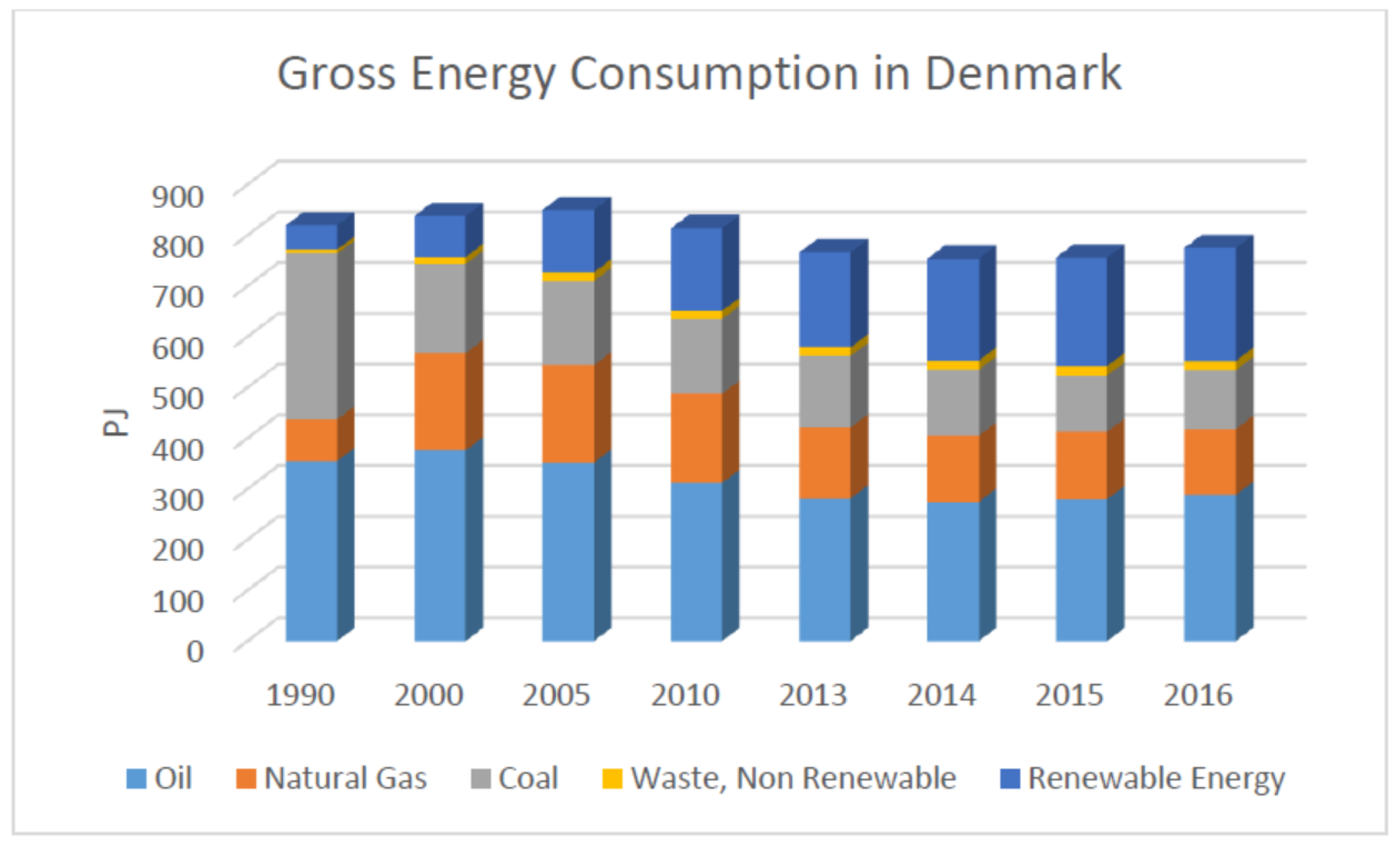
22] in order to crosscheck the validity of the data. Also, weekends that are combined with the holidays are included in the holiday data set as it is assumed that they might exhibit similar behaviours to holidays than normal weekends. There is one variable for weekdays and weekends and one for holidays and non-holidays. Therefore for the holiday variable: (a) for holiday the value is ”1”, and (b) for non-holiday the value is ”0”. For the weekday variable: (c) for a weekday the value is “0” and for the weekend the value is “1”. Using coal prices was also planned as coal constitutes a significant portion of the energy consumption however, suitable data in this regard was not accessible and therefore coal prices were omitted from the forecasts. The reason why coal prices were not attainable is because coal has many different types depending on British thermal units (BTU) and maybe it is not traded in spot markets and rather traded privately.
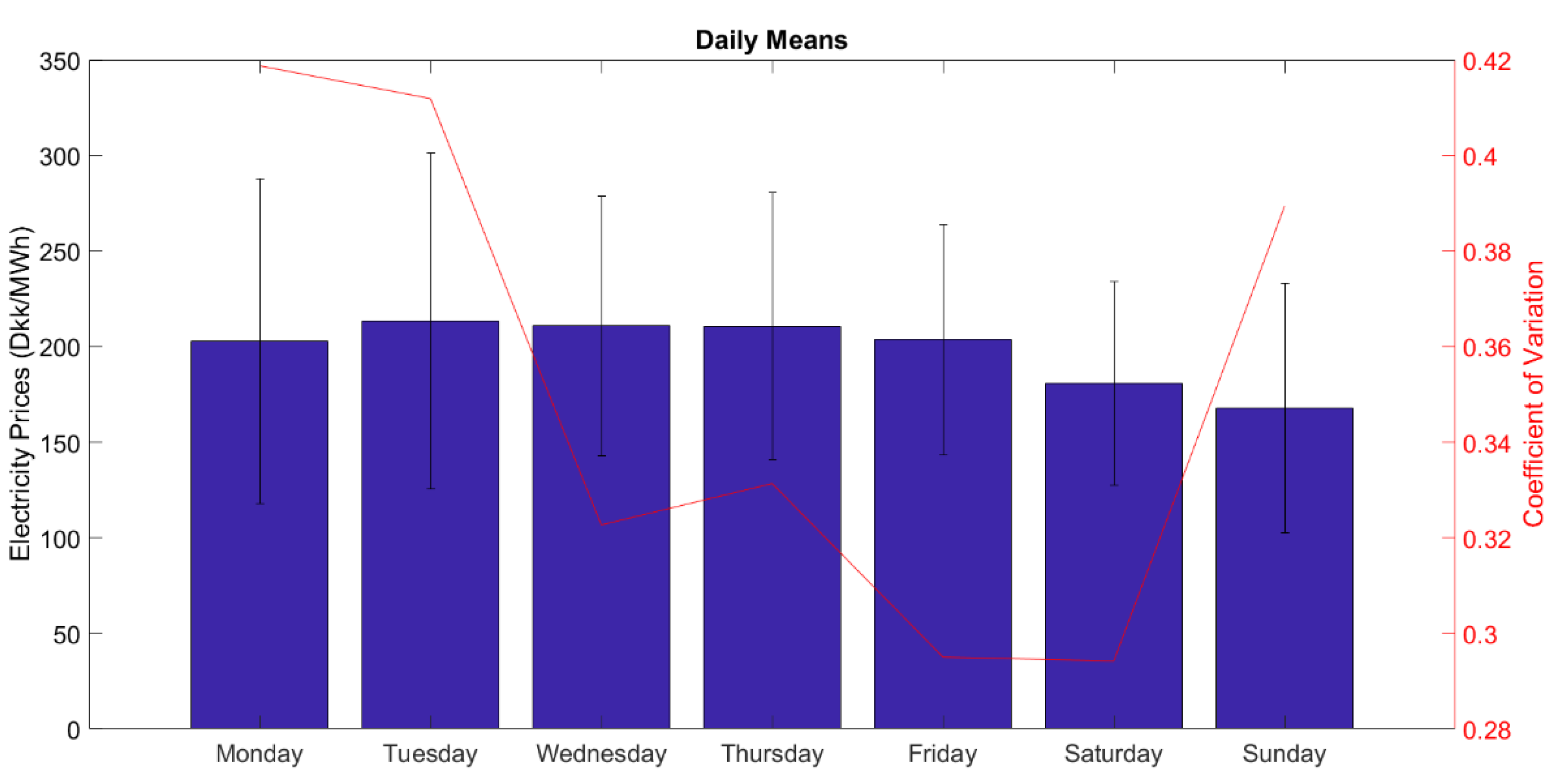
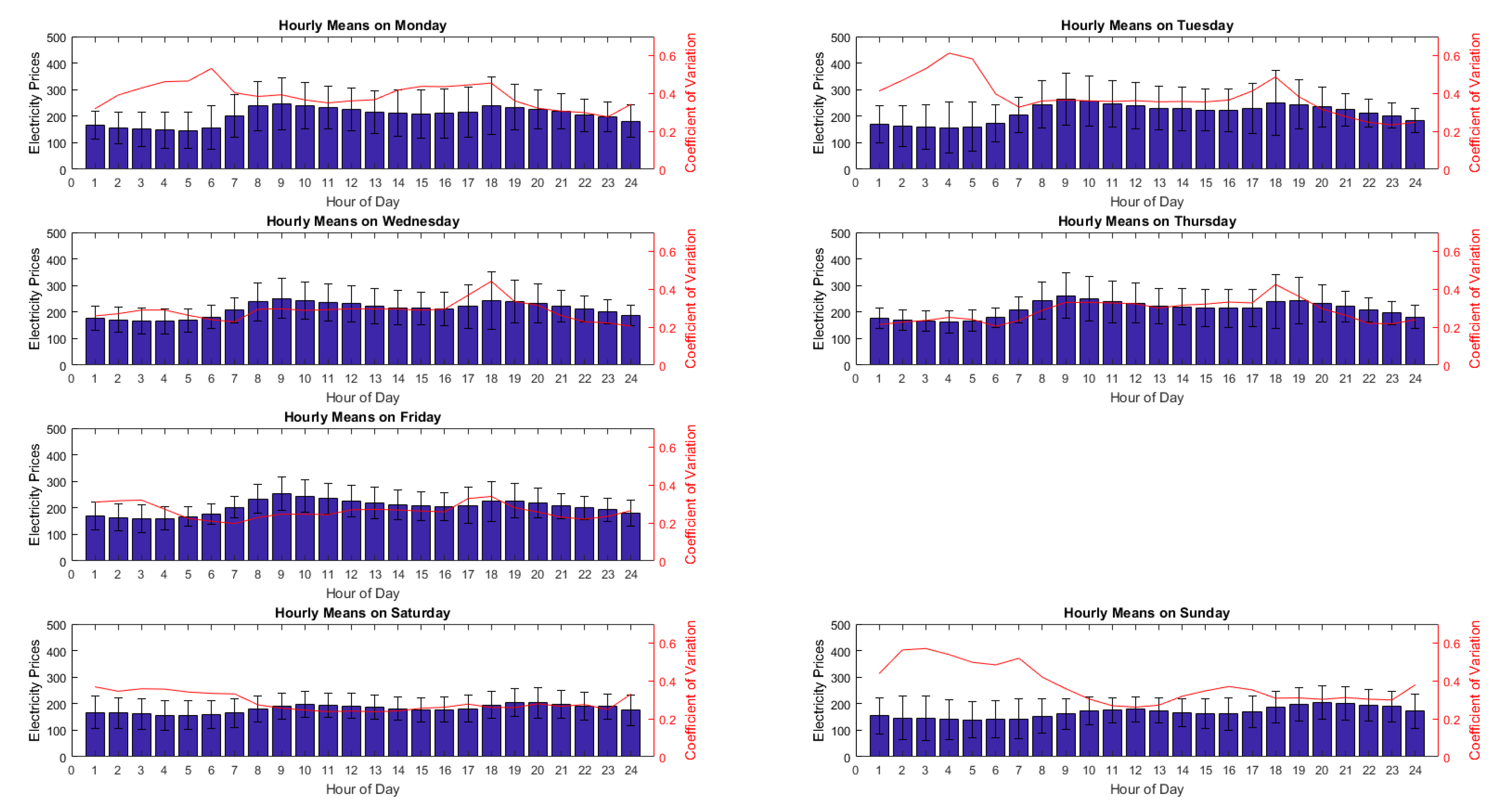
A large number of researchers used dummy variables to explain seasonal variables, such as the day of the week [
23,
24]. The latter of the two papers test consumption and production prognosis as variables. Other researchers [
25] use system loads, fuel prices, seasonal variables stressing that available hydro energy and fuel prices are variables that could be used if, and when, data are present. Other researchers took into account the natural gas prices as explanatory variable. They did also test temperature, but was found of low correlation [
26]. Others like [
27] test wind prognosis, however, it was the link to price that was mainly proven.
One very important price driver is the planned or unexpected changes in production such as planned maintenance or unexpected problems in a production plant. This information is present in Nordpool website, under the name Remit Urgent Market Messaging (UMM) however a method to make the information useful and usable is needed before incorporating it into a model. This method should compose of two parts, one to filter and download the required data and the second one to convert the data into usable quantitative information before incorporating it into the models. Due to the time limitations of the project, these data are excluded from the models.
One other factor that has an effect on the prices is the transmission of electricity. Transmission lines are used to convey electricity and because electricity is mostly brought from where the production is high and prices are low to high consumption regions, the transmission lines have an effect to smooth and bring the prices closer to each other. When the transmission capacity of the lines are close the local production and consumption becomes more important therefore the prices tend to have more spikes. As the transmission lines and the interaction between regions and markets are very complicated and not straightforward to incorporate into a regression model, they are excluded from our models as well.
Reserve margin is a metric that relates available production capacity to consumption and in some markets it seems to be a reliable predictor for spike forecasting [
7]. These data are not present in Nordpool or Energinet however if they were present, they should have been included in the model as they could have contributed when the prices are harder to forecast, at high volatility.