Planning of a Resilient Underground Distribution Network Using Georeferenced Data
Abstract
1. Introduction
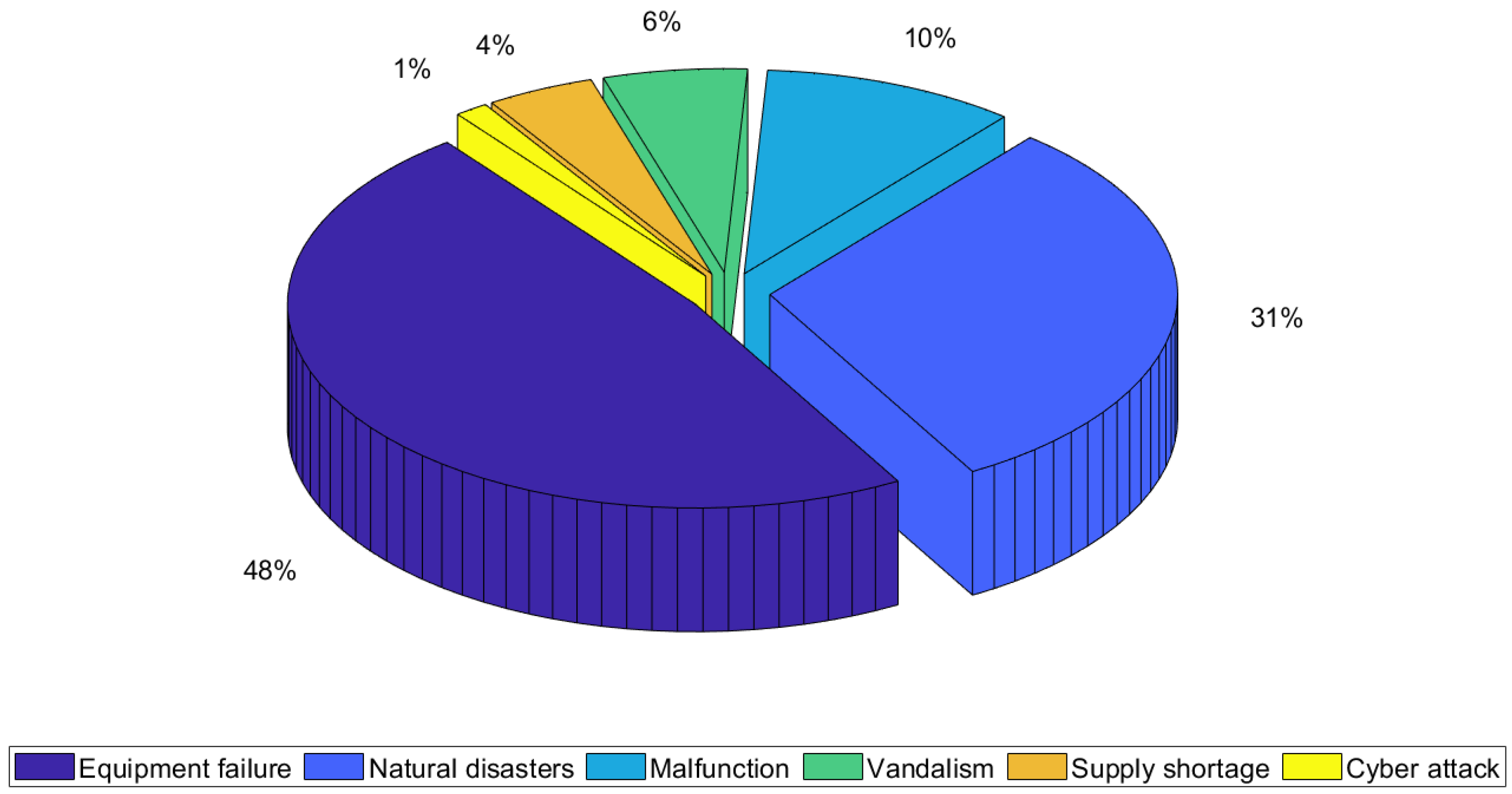
2. Resilience on Power Distribution Networks
3. Planning Distribution Networks
3.1. Types of Distribution Network Topology
3.2. Network Planning Based on Theory Graphs
4. Problem Formulation
| Algorithm 1 Planning of a Resilent Distribution Network |
|
| Algorithm 2 Routing of MV network and Switching Equipment Allocation |
|
5. Analysis and Results
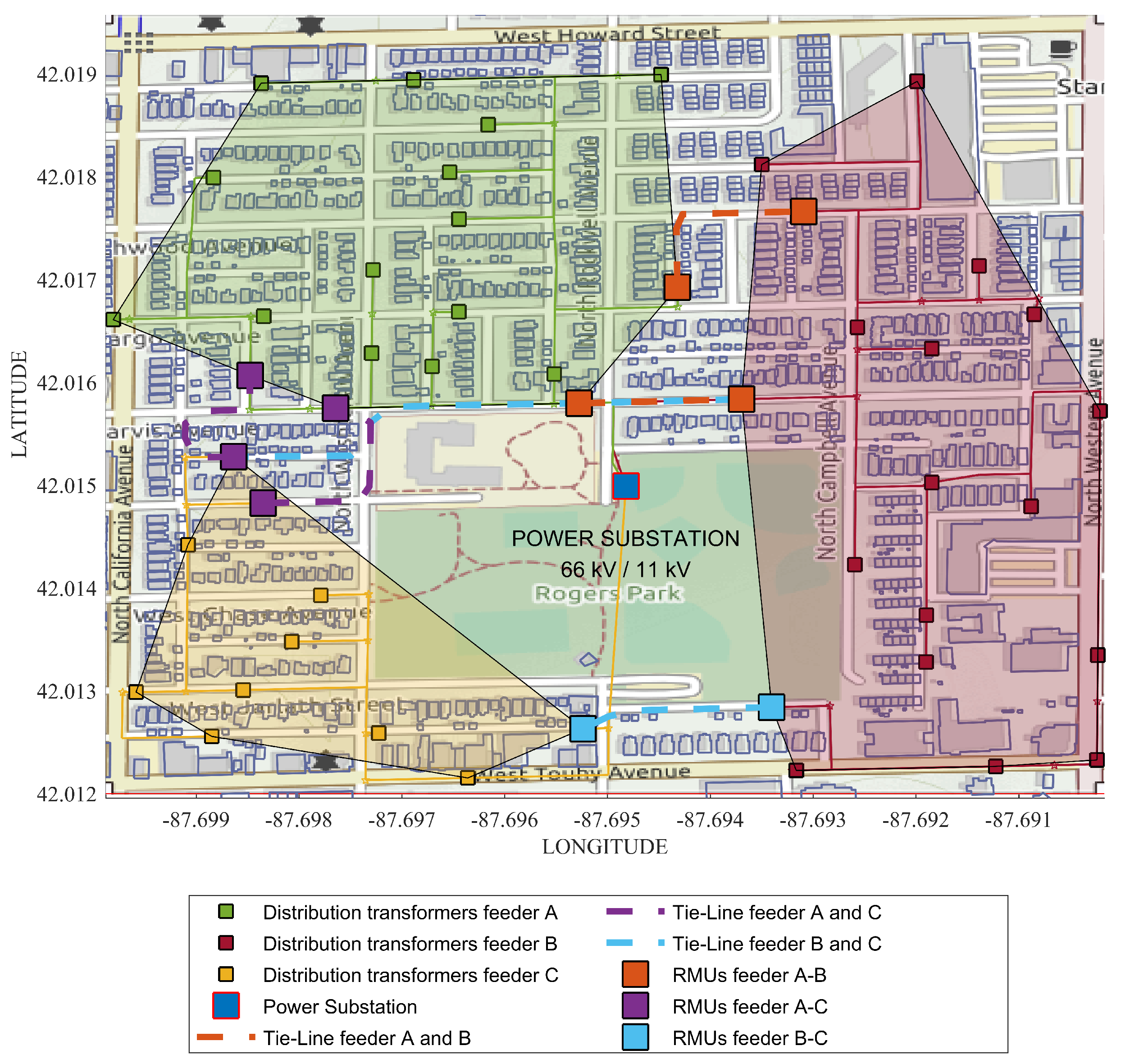
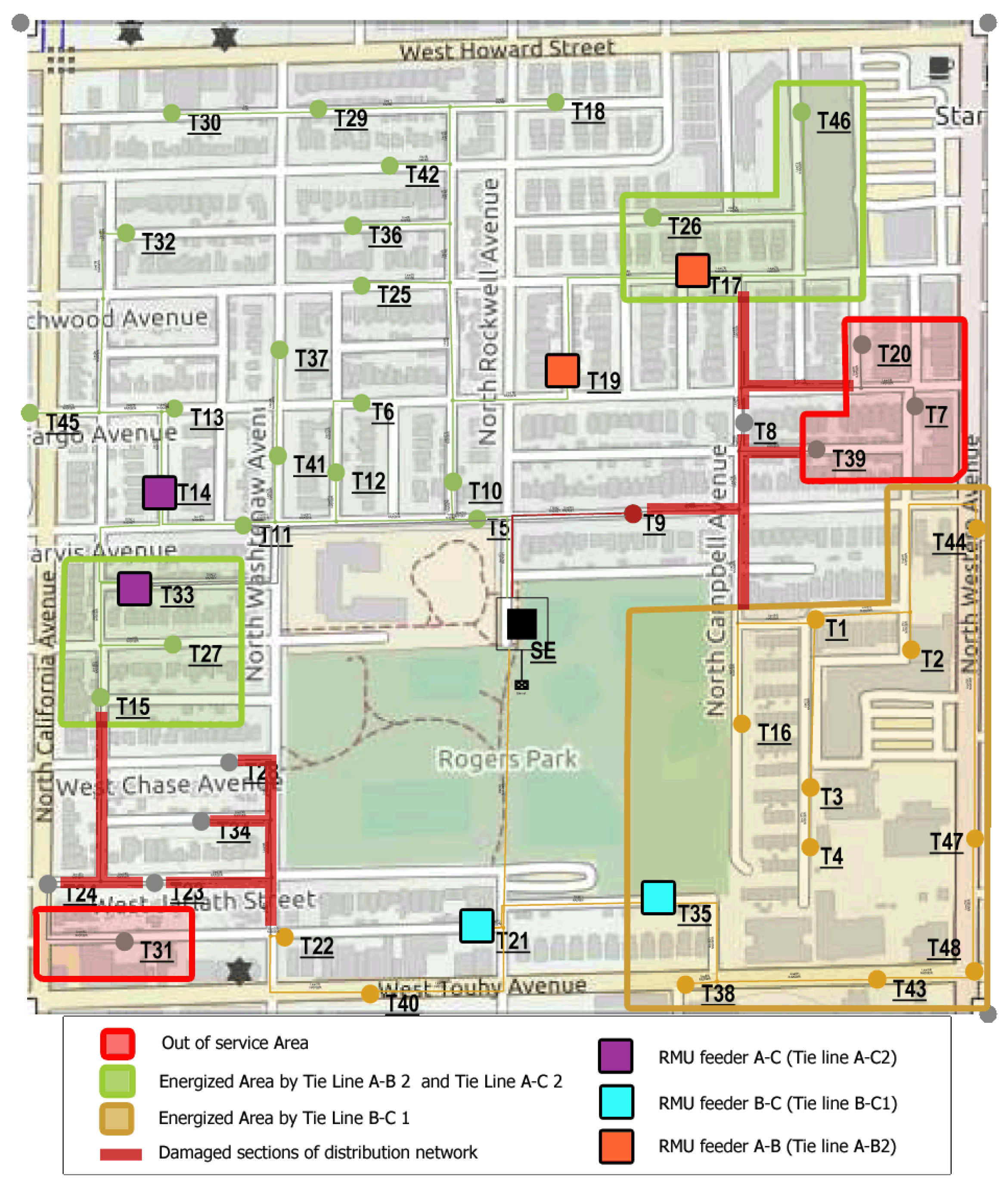
5.1. Case Study
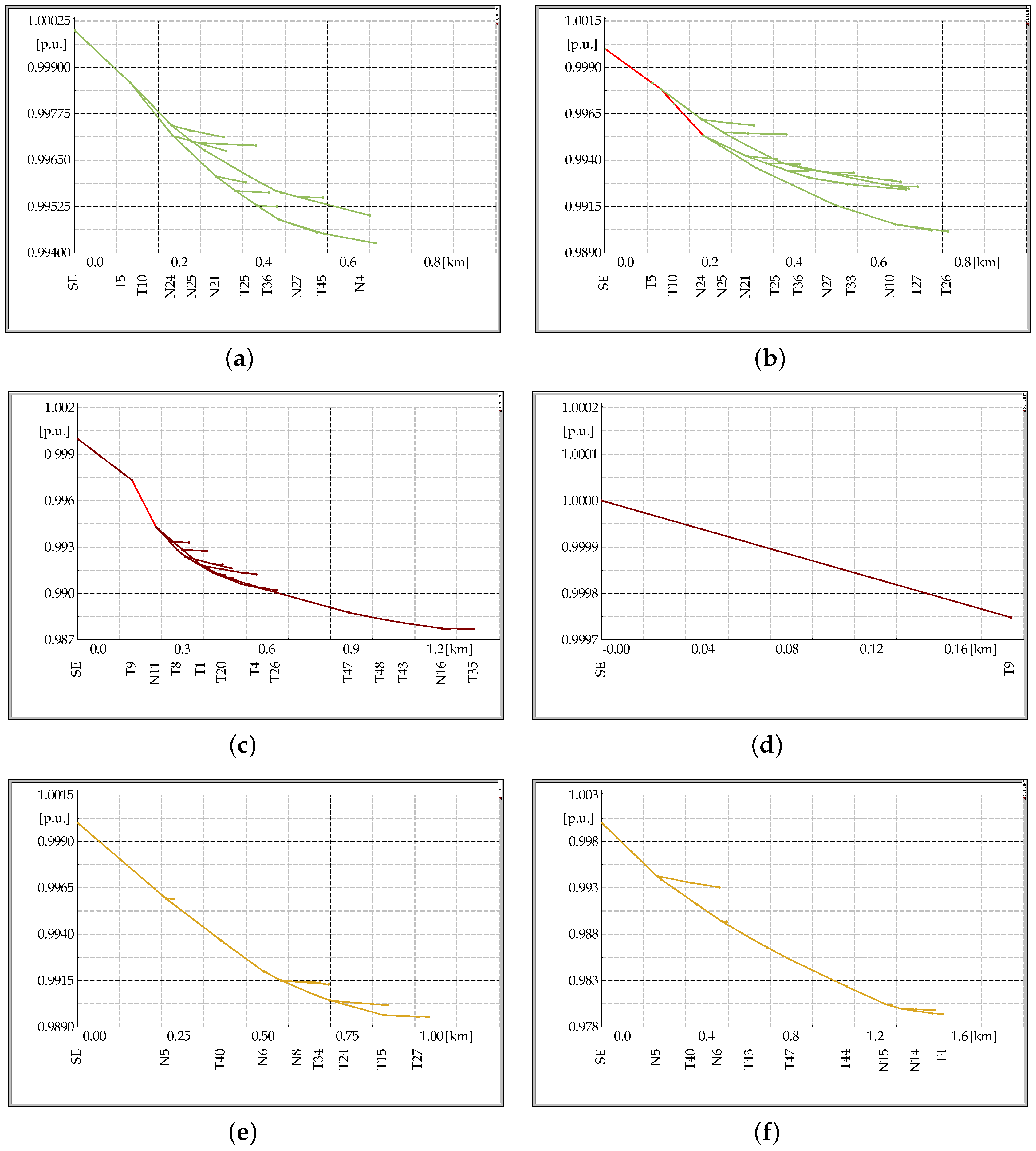
5.2. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nahman, J.; Perić, D. Path-set based optimal planning of new urban distribution networks. Int. J. Electr. Power Energy Syst. 2017, 85, 42–49. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, C.; Wang, J.; Baldick, R. Research on Resilience of Power Systems Under Natural Disasters-A Review. IEEE Trans. Power Syst. 2015, 31, 1604–1613. [Google Scholar] [CrossRef]
- Espinoza, S.; Panteli, M.; Mancarella, P.; Rudnick, H. Multi-phase assessment and adaptation of power systems resilience to natural hazards. Electr. Power Syst. Res. 2016, 136, 352–361. [Google Scholar] [CrossRef]
- Bie, Z.; Lin, Y.; Li, G.; Li, F. Battling the Extreme: A Study on the Power System Resilience. Proc. IEEE 2017, 105, 1253–1266. [Google Scholar] [CrossRef]
- Mousavizadeh, S.; Haghifam, M.R.; Shariatkhah, M.H. A linear two-stage method for resiliency analysis in distribution systems considering renewable energy and demand response resources. Appl. Energy 2018, 211, 443–460. [Google Scholar] [CrossRef]
- Salman, A.M.; Li, Y.; Stewart, M.G. Evaluating system reliability and targeted hardening strategies of power distribution systems subjected to hurricanes. Reliab. Eng. Syst. Saf. 2015, 144, 319–333. [Google Scholar] [CrossRef]
- Amraee, T.; Saberi, H. Controlled islanding using transmission switching and load shedding for enhancing power grid resilience. Int. J. Electr. Power Energy Syst. 2017, 91, 135–143. [Google Scholar] [CrossRef]
- Jia, K.; Bi, T.; Liu, B.; Thomas, D.; Goodman, A. Advanced islanding detection utilized in distribution systems with DFIG. Int. J. Electr. Power Energy Syst. 2014, 63, 113–123. [Google Scholar] [CrossRef]
- Aghamohammadi, M.R.; Shahmohammadi, A. Intentional islanding using a new algorithm based on ant search mechanism. Int. J. Electr. Power Energy Syst. 2012, 35, 138–147. [Google Scholar] [CrossRef]
- Li, J.; Ma, X.Y.; Liu, C.C.; Schneider, K.P. Distribution system restoration with microgrids using spanning tree search. IEEE Trans. Power Syst. 2014, 29, 3021–3029. [Google Scholar] [CrossRef]
- Zhai, H.F.; Yang, M.; Chen, B.; Kang, N. Dynamic reconfiguration of three-phase unbalanced distribution networks. Int. J. Electr. Power Energy Syst. 2018, 99, 1–10. [Google Scholar] [CrossRef]
- Figueroa-Candia, M.; Felder, F.A.; Coit, D.W. Resiliency-based optimization of restoration policies for electric power distribution systems. Electr. Power Syst. Res. 2018, 161, 188–198. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, L.; Zhang, Y. Electrical Power and Energy Systems Adequacy evaluation of electric power grids considering substation cyber vulnerabilities. Electr. Power Energy Syst. 2018, 96, 368–379. [Google Scholar] [CrossRef]
- Valenzuela, A.; Montalvo, I.; Barrera-singaña, C. Electrical Vehicle: Facing Future Challenges in Quito. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Quito, Ecuador, 20–22 September 2017; pp. 1–6. [Google Scholar]
- Mosbah, M.; Arif, S.; Mohammedi, R.D.; Hellal, A. Optimum dynamic distribution network reconfiguration using minimum spanning tree algorithm. In Proceedings of the 2017 5th International Conference on Electrical Engineering—Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; pp. 1–6. [Google Scholar]
- Li, H.; Mao, W.; Zhang, A.; Li, C. An improved distribution network reconfiguration method based on minimum spanning tree algorithm and heuristic rules. Int. J. Electr. Power Energy Syst. 2016, 82, 466–473. [Google Scholar] [CrossRef]
- Xie, S.; Hu, Z.; Zhou, D.; Li, Y.; Kong, S.; Lin, W.; Zheng, Y. Multi-objective active distribution networks expansion planning by scenario-based stochastic programming considering uncertain and random weight of network. Appl. Energy 2018, 219, 207–225. [Google Scholar] [CrossRef]
- Raeisi-Gahrooei, Y.; Khodabakhshian, A.; Hooshmand, R.A. A new stratified random sample customer selection for load research study in distribution networks. Int. J. Electr. Power Energy Syst. 2018, 97, 363–371. [Google Scholar] [CrossRef]
- Santos, N.; Lagarto, M.; Rodrigues, C. Innovative underground distribution cabinet for low-voltage network. CIRED-Open Access Proc. J. 2017, 2017, 256–259. [Google Scholar] [CrossRef][Green Version]
- Bajpai, P.; Chanda, S.; Srivastava, A.K. A Novel Metric to Quantify and Enable Resilient Distribution System using Graph Theory and Choquet Integral. IEEE Trans. Smart Grid 2016, 3053, 2918–2929. [Google Scholar] [CrossRef]
- Moradijoz, M.; Moghaddam, M.P.; Haghifam, M.R. A flexible active distribution system expansion planning model: A risk-based approach. Energy 2018, 145, 442–457. [Google Scholar] [CrossRef]
- Inga-Ortega, E.; Peralta-Sevilla, A.; Hincapie, R.C.; Amaya, F.; Tafur Monroy, I. Optimal dimensioning of FiWi networks over advanced metering infrastructure for the smart grid. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America, ISGT LATAM 2015, Boumerdes, Algeria, 29–31 October 2017; pp. 30–35. [Google Scholar]
- Inga, E.; Céspedes, S.; Hincapié, R.; Cárdenas, A. Scalable Route Map for Advanced Metering Infrastructure Based on Optimal Routing of Wireless Heterogeneous Networks. IEEE Wirel. Commun. 2017, 24, 26–33. [Google Scholar] [CrossRef]
- Inga, J.; Inga, E.; Ortega, A.; Hincapíé, R.; Gómez, C. Optimal Planning for Deployment of FiWi Networks based on Hybrid Heuristic Process. IEEE Latin Am. Trans. 2017, 15, 1684–1690. [Google Scholar] [CrossRef]
- Wang, G.W.; Zhang, C.X.; Zhuang, J. Clustering with Prim’s sequential representation of minimum spanning tree. Appl. Math. Comput. 2014, 247, 521–534. [Google Scholar] [CrossRef]
- Campaña, M.; Inga, E.; Hincapié, R. Optimal Placement of Universal Data Aggregation Points for Smart Electric Metering based on Hybrid Wireless. In Proceedings of the CEUR Workshop Proceedings, Como, Italy, 27–31 August 2017; Volume 1950, pp. 6–9. [Google Scholar]
- Peralta, A.; Inga, E.; Hincapié, R. Optimal Scalability of FiWi Networks Based on Multistage Stochastic Programming and Policies. J. Opt. Commun. Netw. 2017, 9, 1172. [Google Scholar] [CrossRef]
- Peralta, A.; Inga, E.; Hincapié, R. FiWi Network Planning for Smart Metering Based on Multistage Stochastic Programming. IEEE Latin Am. Trans. 2015, 13, 3838–3843. [Google Scholar] [CrossRef]
- Chuang, H.J.; Tsai, W.Y.; Chen, C.S.; Ho, C.Y. Optimal Expansion Planning of Distribution Substations Using Loading Gravity with Genetic Algorithm. In Proceedings of the 2nd International Conference on Intelligent Technologies and Engineering Systems (ICITES2013), Taiwan, China, 12–14 December 2013; Volume 293, pp. 11–19. [Google Scholar]
| Nomenclature | Description |
|---|---|
| Street point positions (Latitude and Longitude) | |
| Residential customers’ locations (Latitude and Longitude) | |
| Manhole’s position (Latitude and Longitude) | |
| Transformer’s position (Latitude and Longitude) | |
| RMUs positions (Latitude and Longitude) | |
| Distance matrix (variable dimension) | |
| Connectivity matrix | |
| Variables for loop control | |
| Temporary variables | |
| Residential customers connected to the nearest manhole | |
| Residential customer’ demand | |
| Associated manhole demand | |
| n | Number of residential customers |
| m | Capacity Restriction |
| Number of primary feeders | |
| Connectivity route for medium Voltage grid and tie-lines | |
| Route selection criteria | |
| Complementary variables |
| Item | Parameter | Value |
|---|---|---|
| Medium Voltage network | Primary feeders | 3 |
| Voltage level | 11 kV | |
| Installation Type | Underground Network | |
| Network Configuration | Radial with tie points using RMU | |
| Conductor size and type | XLPE insulated power cable 3 × 95 mm2 15 kV | |
| Ring Main Units | 1 to 4 switchgear cubicles | |
| Low Voltage network | Distribution Transformers | Oil Immersed distribution Transformers 11/0.22 kV |
| Distribution Transformers Rating | kVA {30, 50, 75, 100, 160, 250, 350, 500, 750, 1000} | |
| Voltage level | 0.22 kV | |
| Installation Type | Underground Network | |
| Network Configuration | Radial | |
| Conductor size and type | XLPE insulated power cable 2 kV | |
| Deployment features | end users information | 1155 closed-features from OSM |
| Total demand | 13.029 MW | |
| Associated junction boxes per transformer | # {5, 10, 15,20} | |
| Coverage LV network | 100% | |
| Coverage MV network | 100% |
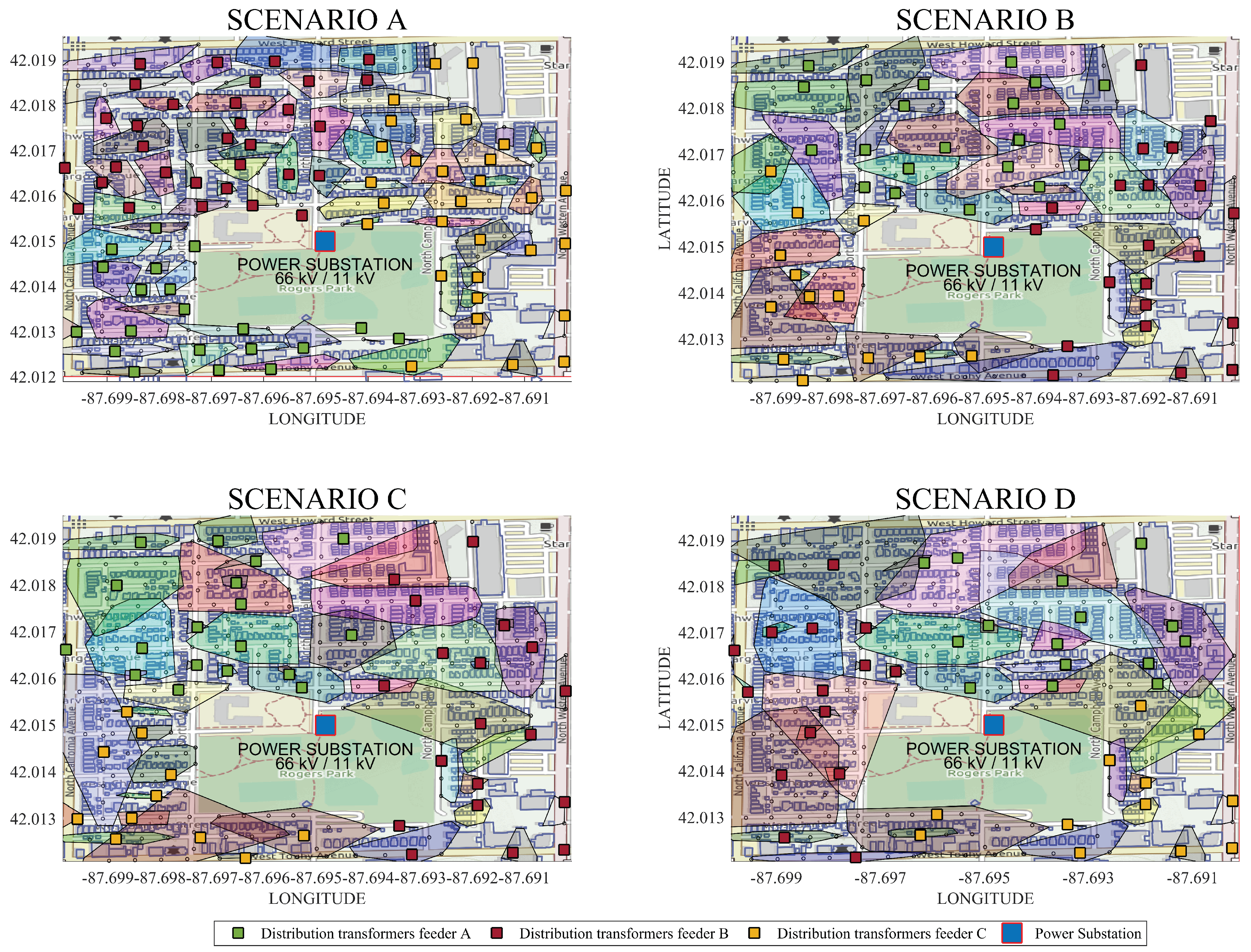
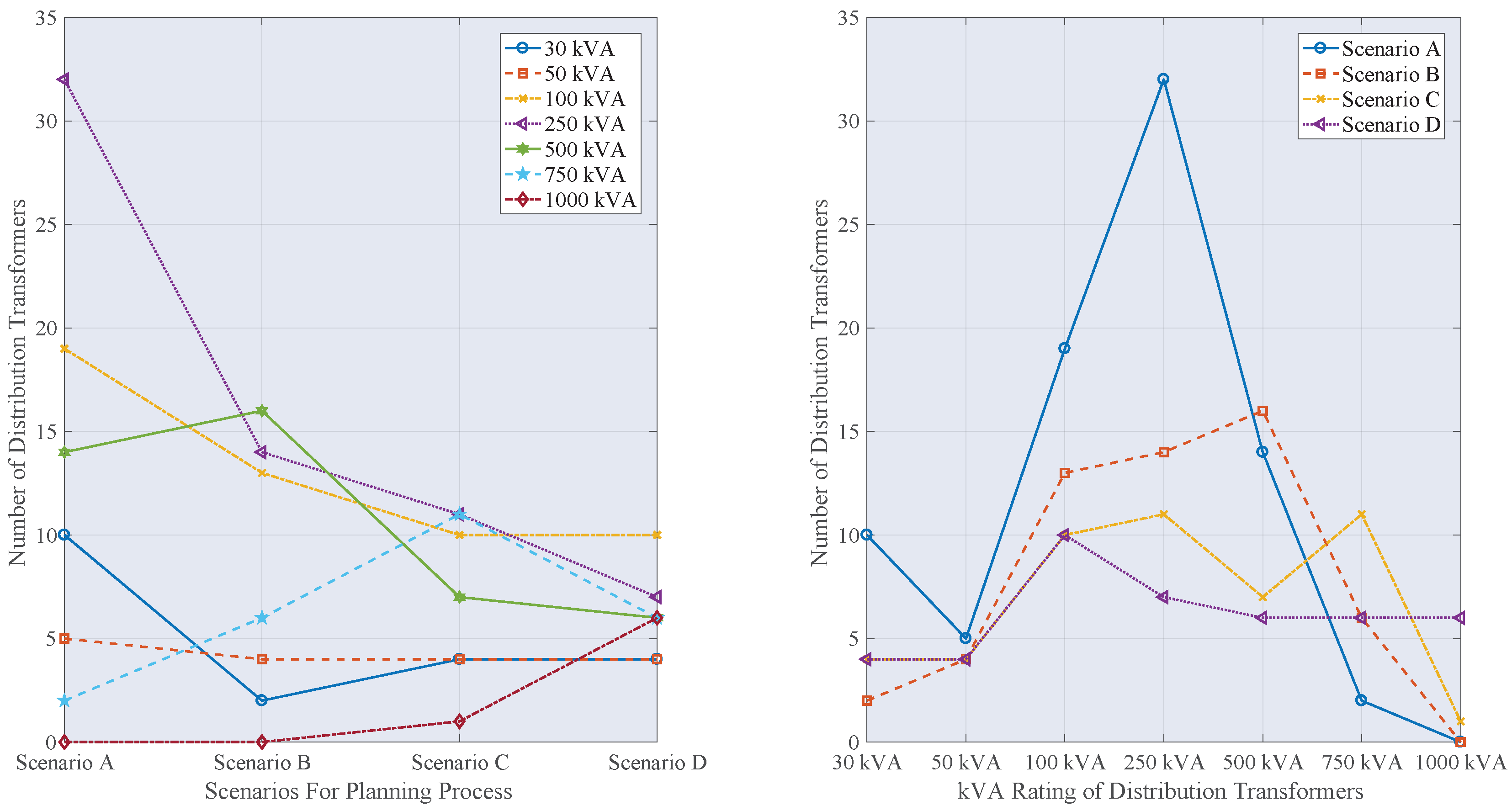
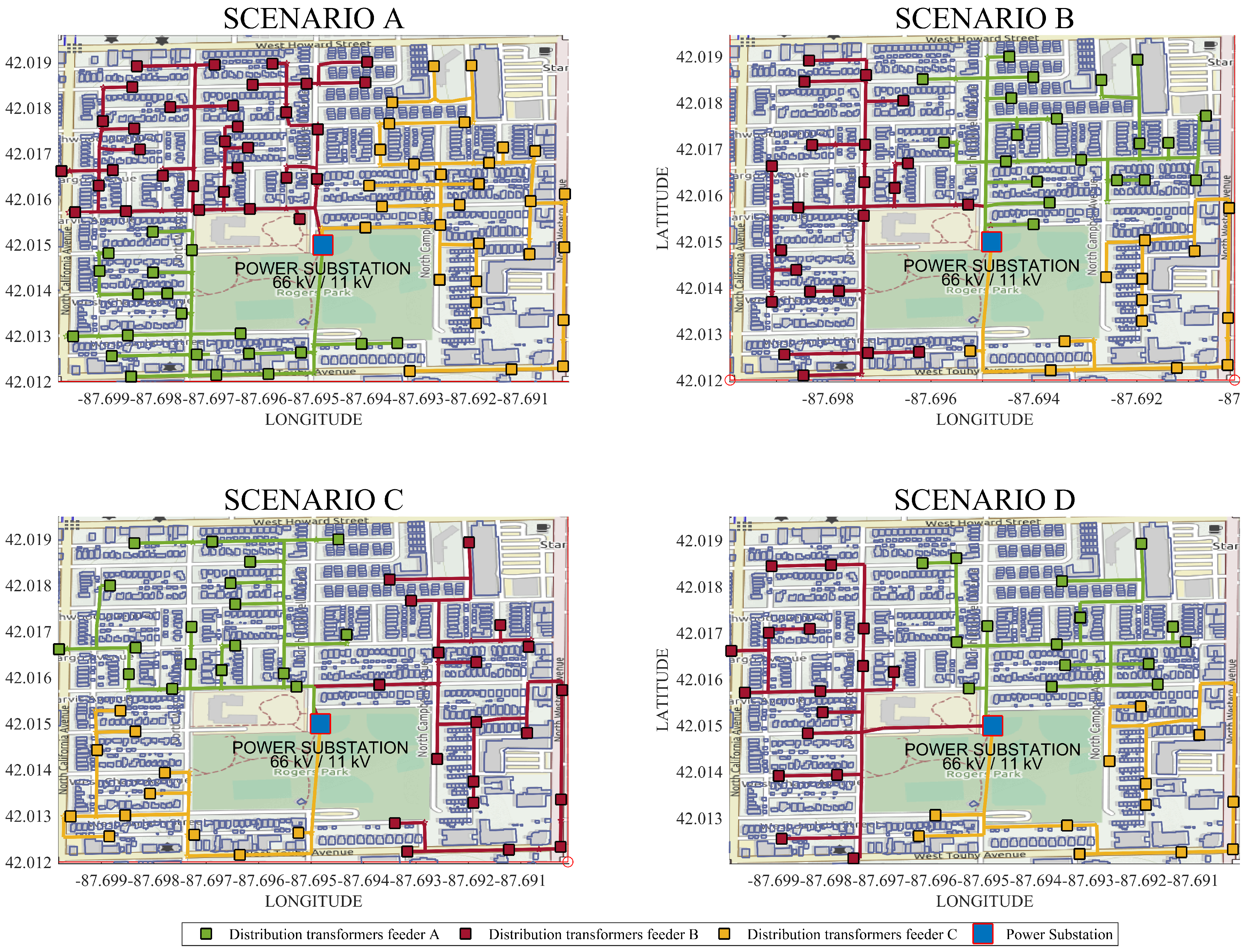
| Scenario Per Cluster # | Primary Feeder Description | Distance Transformer to End User Average | Coverage LV % | Distribution Transformer # | End Users Per Primary Feeder # | MV Grid Length km | MV Grid Voltage Drop % |
|---|---|---|---|---|---|---|---|
| SCENARIO A | PRIMARY FEEDER A | 100 | 100 | 32 | 466 | 2.524 | <1.2 |
| PRIMARY FEEDER B | 100 | 100 | 30 | 452 | 2.94 | <1.2 | |
| PRIMARY FEEDER C | 100 | 100 | 20 | 237 | 2.04 | <1.2 | |
| TOTAL | 100 | 100 | 82 | 1155 | 7.484 | <1.2 | |
| SCENARIO B | PRIMARY FEEDER A | 200 | 100 | 22 | 318 | 2.572 | <1.2 |
| PRIMARY FEEDER B | 200 | 100 | 13 | 306 | 1.799 | <1.2 | |
| PRIMARY FEEDER C | 200 | 100 | 20 | 531 | 2.234 | <1.2 | |
| TOTAL | 200 | 100 | 55 | 1155 | 6.605 | <1.2 | |
| SCENARIO C | PRIMARY FEEDER A | 300 | 100 | 19 | 444 | 2.568 | <1.2 |
| PRIMARY FEEDER B | 300 | 100 | 11 | 245 | 1.507 | <1.2 | |
| PRIMARY FEEDER C | 300 | 100 | 18 | 466 | 2.039 | <1.2 | |
| TOTAL | 300 | 100 | 48 | 1155 | 6.114 | <1.2 | |
| SCENARIO D | PRIMARY FEEDER A | 400 | 100 | 16 | 422 | 2.038 | <1.2 |
| PRIMARY FEEDER B | 400 | 100 | 12 | 249 | 2.032 | <1.2 | |
| PRIMARY FEEDER C | 400 | 100 | 15 | 484 | 1.792 | <1.2 | |
| TOTAL | 400 | 100 | 43 | 1155 | 5.862 | <1.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valenzuela, A.; Inga, E.; Simani, S. Planning of a Resilient Underground Distribution Network Using Georeferenced Data. Energies 2019, 12, 644. https://doi.org/10.3390/en12040644
Valenzuela A, Inga E, Simani S. Planning of a Resilient Underground Distribution Network Using Georeferenced Data. Energies. 2019; 12(4):644. https://doi.org/10.3390/en12040644
Chicago/Turabian StyleValenzuela, Alex, Esteban Inga, and Silvio Simani. 2019. "Planning of a Resilient Underground Distribution Network Using Georeferenced Data" Energies 12, no. 4: 644. https://doi.org/10.3390/en12040644
APA StyleValenzuela, A., Inga, E., & Simani, S. (2019). Planning of a Resilient Underground Distribution Network Using Georeferenced Data. Energies, 12(4), 644. https://doi.org/10.3390/en12040644







