Abstract
New common platforms for optimization of balancing energy activation will facilitate cross-border exchange and integrate the fragmented European balancing markets. Having a zonal market structure, these platforms will optimize balancing actions as if intra-zonal transmission constraints did not exists, leaving it to each Transmission System Operator (TSO) to manage internal congestion caused by balancing energy activations. This paper describes a new method to pre-filter balancing bids likely to cause internal congestion due to their location. Furthermore, the complementary concept of exchange domains has been developed to prevent congested and infeasible balancing situations. A numerical example illustrates both the effectiveness and limitations of each method.
1. Introduction
As European balancing markets are being integrated, common methodologies and systems are being developed to optimize activation and exchange of balancing energy across borders. Under the current target model, each TSO will submit their balancing energy needs for the upcoming imbalance settlement period, as well as a list of available bids within their own area, to a common European platform. The common platform aims to identify the most efficient set of bid activations to cover the imbalances in all areas.
Congestion in the transmission grid incurs the risk of overloads, and must be managed to avoid endangering operational security. Congestion between different market areas can be prevented through cross-zonal capacity constraints in the platform optimization, but intra-zonal—or internal—congestion may occur as a result of bid locations and initial power flows in the network. The enormous size of the interconnected European system, the limited available time in the operational phase, and the preference of zonal market coupling bodes that European balancing platforms will not include the highly detailed network models necessary to represent internal bottlenecks. Rather, the common balancing platform will select the balancing actions, but the task of managing internal congestion is left to each TSO.
This paper presents two methodologies for TSOs to prevent internal congestion caused by an integrated European balancing activation optimization. Firstly, a method for bid filtering is described. Based on extensive power flow analyses across a variety of potential situations, the method aims to detect potentially harmful bid activations and flag the corresponding bids as unavailable. Secondly, the paper introduces a new concept of exchange domains, complementing the bid filtering by ensuring feasibility and enabling more bids to be made available to the common platform.
Section 2 summarizes the development of an integrated European balancing market, and highlights earlier contributions to managing internal congestion from balancing activations. The two congestion management mechanisms are described in the subsequent sections. Section 3 explains pre-filtering balancing energy bids, introducing a new, multi-dimensional approach to assess which bids to make available to a common European balancing platform. The concept of exchange domains is introduced and explained in Section 4. Following a numerical example illustrating both methods in Section 5, the paper concludes in Section 6 with a discussion on the merits and viability of each of the concepts for a future integrated European balancing market.
2. Background
Over the last few years, the European Network of Transmission System Operators for Electricity (ENTSO-E) have developed new network codes, rules and regulations for European power markets. In particular, the Guideline on Electricity Balancing [1] specifies the target model for an integrated European balancing market, including standardization of balancing energy products across countries to facilitate exchange. Aiming to increase efficiency in resource utilization, balancing energy bids located in different areas will be collected into common merit order lists (CMOLs), from which an Activation Optimization Function (AOF) will select bids for activation to cover the imbalances of all TSOs, taking into account possibilities for netting of imbalances and available cross-zonal transmission capacity between areas.
Several European TSOs are collaborating in balancing pilot projects to develop and implement common activation and exchange optimization platforms for the different reserve products. Notably, the TERRE (Trans European Replacement Reserves Exchange) project establishes a platform for cross-border exchange of balancing energy from replacement reserves (RR) [2], while the MARI (Manually Activated Reserves Initiative) [3] and PICASSO (Platform for the International Coordination of Automated Frequency Restoration and Stable System Operation) [4] projects develop European platforms for the exchange of balancing energy from frequency restoration reserves with manual activation (mFRR) and automatic activation (aFRR), respectively. The available time between optimization and activation will be limited, restricting the possibilities for redispatch. All of these projects suggest preventing balancing actions from causing internal congestion by letting each TSO mark bids as unavailable if their activation could endanger system security, in accordance with Art. 29.14 in [5].
Congestion management is a central aspect of a zonal electricity market design, and is necessary when the price structure does not reflect the impact of grid congestion, as compared to locational marginal prices (LMPs). For zonal markets, Linnemann et al. [6] identified three main mechanisms to manage congestion: grid expansion, market splitting, and redispatch. Only the latter can be applied in an operational timeframe, and it is used in several European systems to manage internal congestion.
Several factors can impact power flows, and thereby potentially also network congestion during the balancing stage. Contingencies and power imbalances from intermittent generation are inherently stochastic. Interestingly, the balancing market itself may also have a strong effect, depending on the imbalance pricing mechanism. In a study of the German balancing market, Chaves-Ávila et al. [7] argued that using a single area-wide imbalance price signal may be adverse and misleading in the presence of internal congestion, worsening the local imbalance in part of the system, with the potential result of further congesting the network. At the same time, there may be very limited time and flexibility to effectively manage congestions through redispatch during the balancing stage.
Another crucial factor is the impact of bid activations in the balancing energy market. Some systems allow portfolio-based bids, meaning the exact locations of balancing energy injections are often unknown. For the German power system, Sprey et al. [8] concluded that the effect on congestion from reserve activation is unforeseeable, and uses simulation to assess the impact. In the Norwegian system, on the other hand, the location of each balancing bid is largely known. This allows the effect on network flows from bid activation to be predicted using power flow analyses. This is used in [9] to develop an algorithm that evaluates whether balancing bids must be skipped in the merit order to satisfy requests for balancing energy exchange from different neighboring zones. This can support decisions on which bids to make available to a European balancing platform, yet the proposed algorithm is one-dimensional, only considering balancing energy requests from a single neighboring zone at a time, i.e., no combinations or transit requests.
Finally, concerns on intra-zonal network constraints are not limited to European market designs. In the US, traditional reserve requirements have partitioned the grid into deterministic reserve zones, mainly based on ad-hoc rules [10]. Disregarding the intra-zonal constraints, and thereby the grid location of reserves procured within a zone, incurs the risk of ineffective means to handle intra-zonal congestion [11]. Moreover, since all reserves within a zone are assumed to have equal shift factors on critical lines, the true deliverability of the procured reserves will be imprecise. Acknowledging that different contingencies render different reserves undeliverable, Lyon et al. [12] demonstrated a locational reserve disqualification method to ensure adequate volumes and locations of operating reserves to cope with a range of distinct scenarios.
3. Bid Filtering
A zonal market platform will optimize balancing actions as if intra-zonal transmission constraints did not exist, in some cases leading to the activation plans that are infeasible due to internal congestion. In an attempt to prevent infeasible activation plans, the MARI platform [3] plans to allow TSOs to mark individual bids as unavailable if their activation would lead to internal congestion. Thus, each TSO needs to assess—in advance of the platform clearing—whether activating a bid would lead to congestion or not. The impact of balancing bid activations on internal congestion depends not only on the bid location, but also on the location of the request, as well as the current (or predicted) flow in the intra-zonal network. Guntermann et al. [9] showed on a realistic dataset how bid activations can often cause congestion when requested from one or more of the neighboring zones, while causing no congestion if requested from other zones.
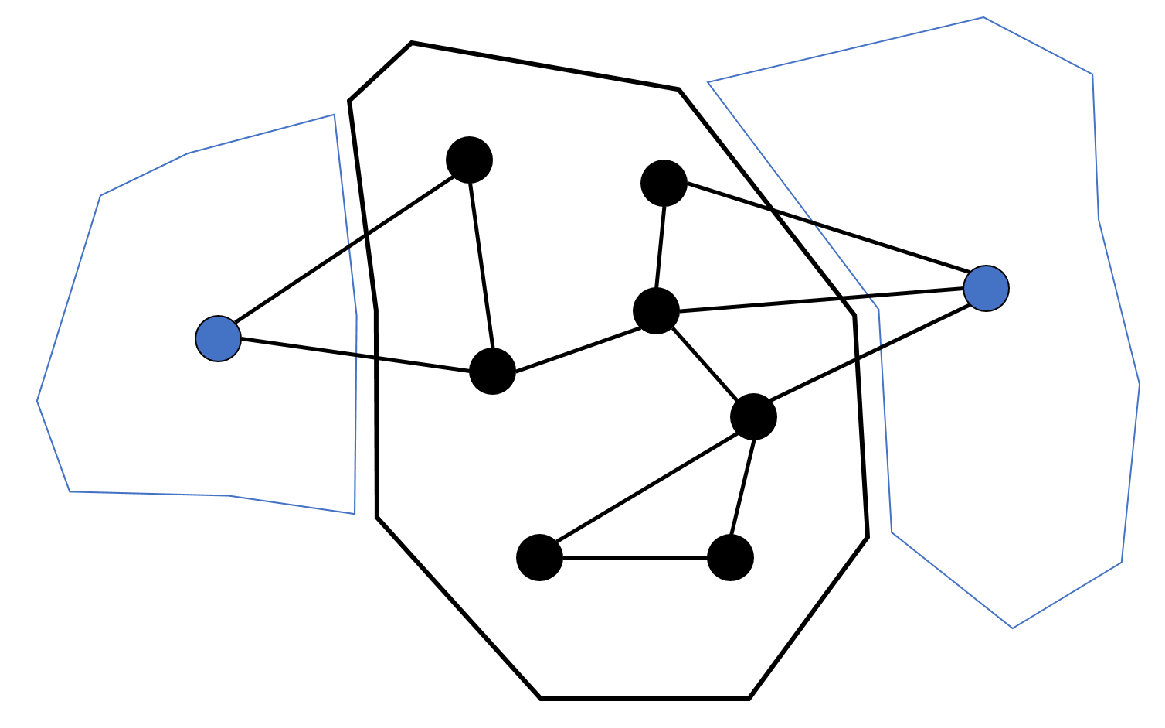
The bid filtering methodology proposed in this paper aims to determine the availability of balancing energy bids within a given bidding zone, with each neighboring area considered to be represented by a single external node (cf. Figure 1). It extends the work in [9] by considering combinations of balancing requests from multiple neighboring areas. While this is more realistic, it also increases complexity. Moreover, since these requests cannot be accurately predicted, the proposed method needs to consider a range of combined balancing energy requests from the immediate neighboring zones of a given zone. Each request combination is denoted as an exchange scenario, and the method evaluates for each of the scenarios whether avoiding internal congestion requires deviating from merit order activation.
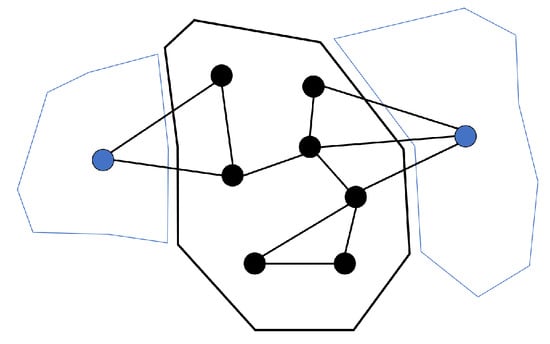
Figure 1.
Example single-area system consisting of internal nodes and external nodes representing neighboring areas.
To evaluate each exchange scenario, a local balancing activation optimization problem is solved on a detailed network model. For a given zone a, the objective function in Equation (1) minimizes the activation cost given by the bid price and activation volume of each bid b available in the local bid list . The energy balance constraint in Equation (2) requires for each internal or external node that the net imbalance is covered either by flow or bid activation from bids located at node i. The adjacency parameter ensures adequate connections between each node i and lines . Depending on the directions and volumes of imbalance volumes, upward or downward activations can be disallowed (e.g., by making sets and empty for all i) to prevent simultaneous counter-activations within a zone. The flow constraint in Equation (3) translates the balancing energy injection in each node to balancing energy flows on each line l, through the power transfer distribution factor (PTDF) , while Equation (4) limits the activation volume of each bid to its capacity . Balancing energy flows are limited by the remaining available capacities and on each line in Equation (5).
The congesting bids can be identified by considering the resulting nodal balancing prices in each evaluated scenario. The Lagrangian multiplier on each energy balance constraint in Equation (2) provides a locational marginal price on balancing energy in each node i for the minimum-cost feasible balancing dispatch. If no internal transmission constraints are binding, this dispatch will follow the merit order. If, on the other hand, congestion prevents bids from being used in the merit order, this will be visible through shadow price differences between different nodes. The locational balancing energy price on the external nodes indicate the marginal costs of exporting one more unit of balancing energy to the corresponding neighboring zone. If there is unused upward capacity with a bid price lower than these marginal exchange costs, this bid is congesting the system. The same is true with opposite price differences for congested downward resources. In these cases, it is clear that the bid price does not reflect the full cost of activation, and following the merit order would have been infeasible due to transmission constraints. In short, the bids not fully utilized although priced within the marginal cross-zonal price are the ones that would cause congestion in the particular scenario if activated in the merit order.
Bids causing congestion only when activated under special circumstances provide a dilemma. Filtering such bids from the list reduces the reserve capacity and increases balancing costs in situations where they could have been used, after all. Not filtering them would lead to congestion and distorted price signals in some cases. The detection of congested bids in individual scenarios does not provide a final answer as to which bids to make available to the platform. However, it provides insight on the degree to which each bid causes congestion when it is activated, in some cases suggesting that the bid should be filtered from the list.
The computational burden of the bid filtering process depends, among other things, on the number of exchange scenarios to be evaluated. The structure of Equations (1)–(5) is linear and largely similar to a DC OPF problem, and requires minimal computational effort. Even with time requirements in the near-operational phase, this structure should allow using detailed network models and a substantial number of exchange scenarios. The scenario selection used for the numerical example in Section 5 constitutes a trivial approach, using a matrix of equidistant exchange volumes. The size of these intervals will affect both the number of scenarios and the accuracy of the results. However, with the set of merit-order feasible scenarios forming a convex region, sensitivity analysis would require only a subset of these scenarios to be evaluated for each bid list configuration. Moreover, the method does not require exhaustive enumeration of all possible bid list configurations, but iteratively removes one bid at a time and evaluates whether more scenarios become merit-order feasible.
4. Exchange Domains
Given the bid locations and initial flow in the network, there are exchange scenarios for which internal congestion cannot be avoided. Should such a scenario materialize, the congestion must be managed through an urgent redispatch to avoid disconnections. Another approach is to attempt to prevent infeasible scenarios from materializing. Rather than filtering bids, a more adequate solution to this end would be to identify and disallow unfavorable combinations of cross-border flows.
The key idea of exchange domains is to add additional constraints in the platform optimization on balancing energy exchange volumes to neighboring areas. This can be used to eliminate the possibility of exchange requests that are found to be infeasible in the exchange scenario evaluation. Furthermore, scenarios where deviation from the merit order is necessary can also be discarded in this manner, thereby enabling many bids to be made available without causing the platform to give incorrect price signals. Constraints describing exchange domains would need to be submitted to the platform together with the list of available bids.
The selection of an exchange domain for a given area can be based on the same exchange scenario analyses as for bid filtering, and needs to take into account the final list of available bids. A robust approach is to select a domain such that all scenarios are included for which merit order activation of the available bids is feasible. Since lists of upward and downward bids are used exclusively in their direction of activation, upward and downward domains must be considered separately as well. A possible step-by-step method is summarized below.
4.1. Determine List of Available Bids
The exchange domain will be tailored towards a filtered list of bids. In principle, any bid filtering method can be applied before this step.
4.2. Evaluate Exchange Scenarios
Precalculating the local balancing dispatch for different combinations of balancing energy exchange provides a discrete approximation of the feasibility region. This enables identifying the borderline of feasibility, and also where the available bids can be used in the merit order.
4.3. Convex Hull Transformation
Each evaluated exchange scenario can be represented as a point, with coordinates given by the balancing exchange volumes to neighboring zones in the particular scenario. If the set S contains all points representing exchange scenarios evaluated as merit-order feasible for the filtered bid list, then the convex hull (Convex hulls are efficiently calculated from a finite set of points using the Quickhull algorithm [13], even for higher dimensions.) is the smallest convex polytope containing all these points.
4.4. Define Linear Constraints
Each facet in the convex hull corresponds to a supporting hyperplane defining a half-space, and all the points in S are enclosed by the intersection of these half-spaces. The inequalities describing each half-space directly comprises a finite set of linear constraints, efficiently describing the feasible region of exchange situations, or exchange domain.
5. Numerical Example
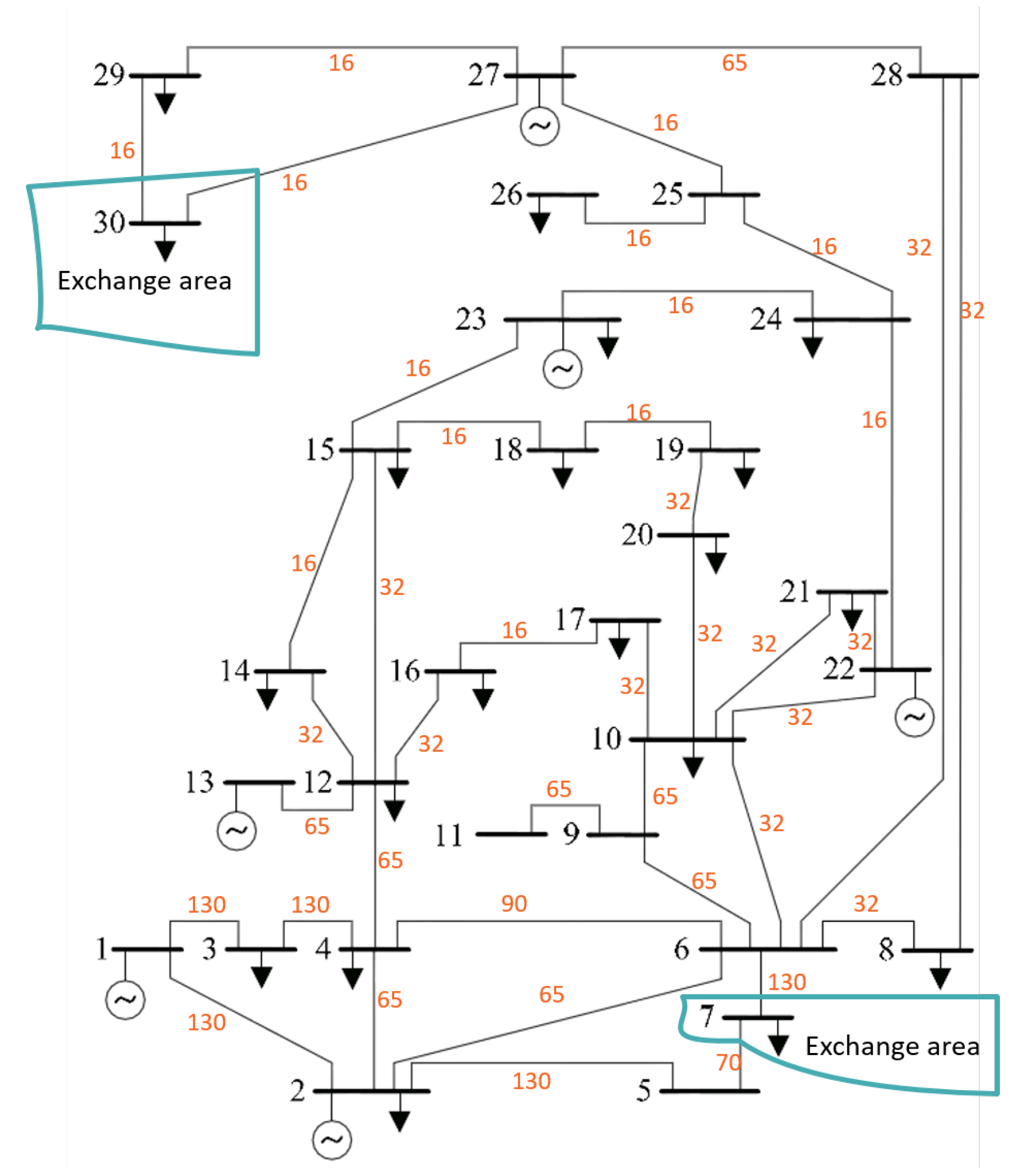
Based on the work in [14], this numerical example highlights the important steps in the bid filtering method and the relation to exchange domains. A test system based on the IEEE 30-bus network is used, with two of the nodes (7 and 30) assumed to represent neighboring zones (cf. Figure 2). The flow in the transmission network is already initialized by an economic dispatch, with no lines being initially congested. Six generators at different nodes serve 156 MW of local load, in addition exporting 23 MW and 11 MW on exchange nodes 7 and 30, respectively.
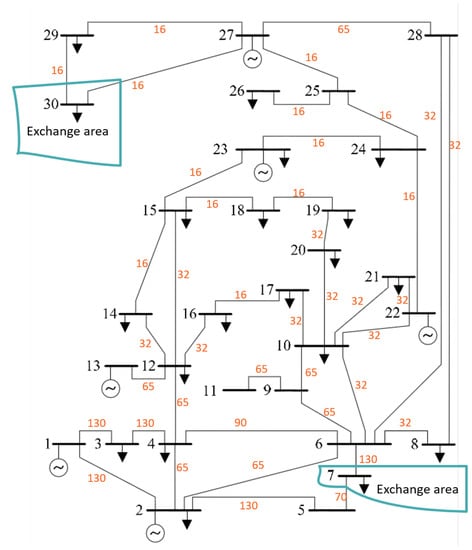
Figure 2.
Single line diagram of the test system used, indicating bus numbers (black) and rated line capacities in MW (orange).30-bus system single line diagram
5.1. Bid Filtering
This example focuses on determining the availability of six upward bids. Downward bids could have been evaluated using broadly the same methodology [14], and have been omitted here for brevity. All bids have a capacity of 10 MW, and carry names Bid #1–Bid #6 according to their position in the merit order, given by bid prices.
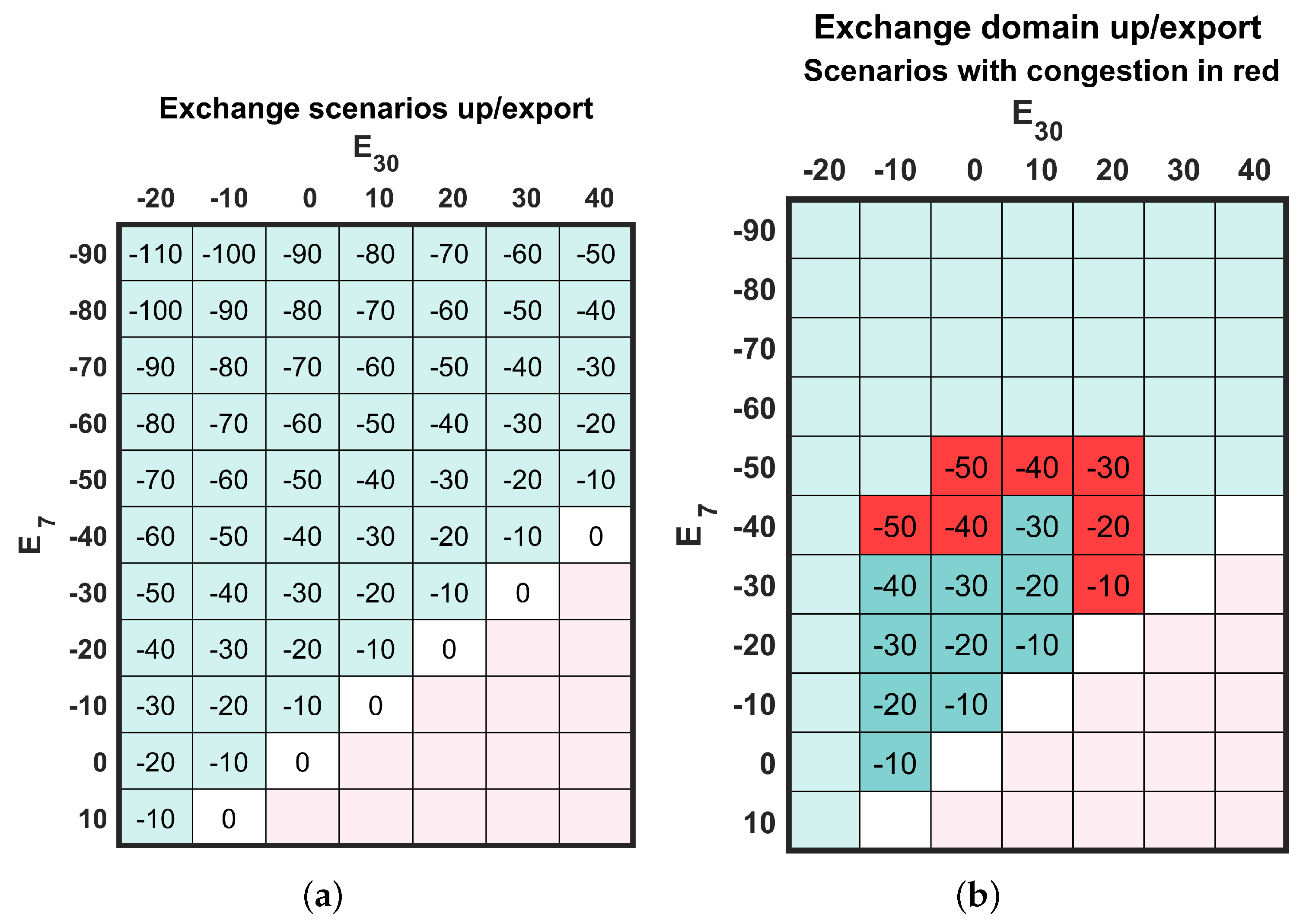
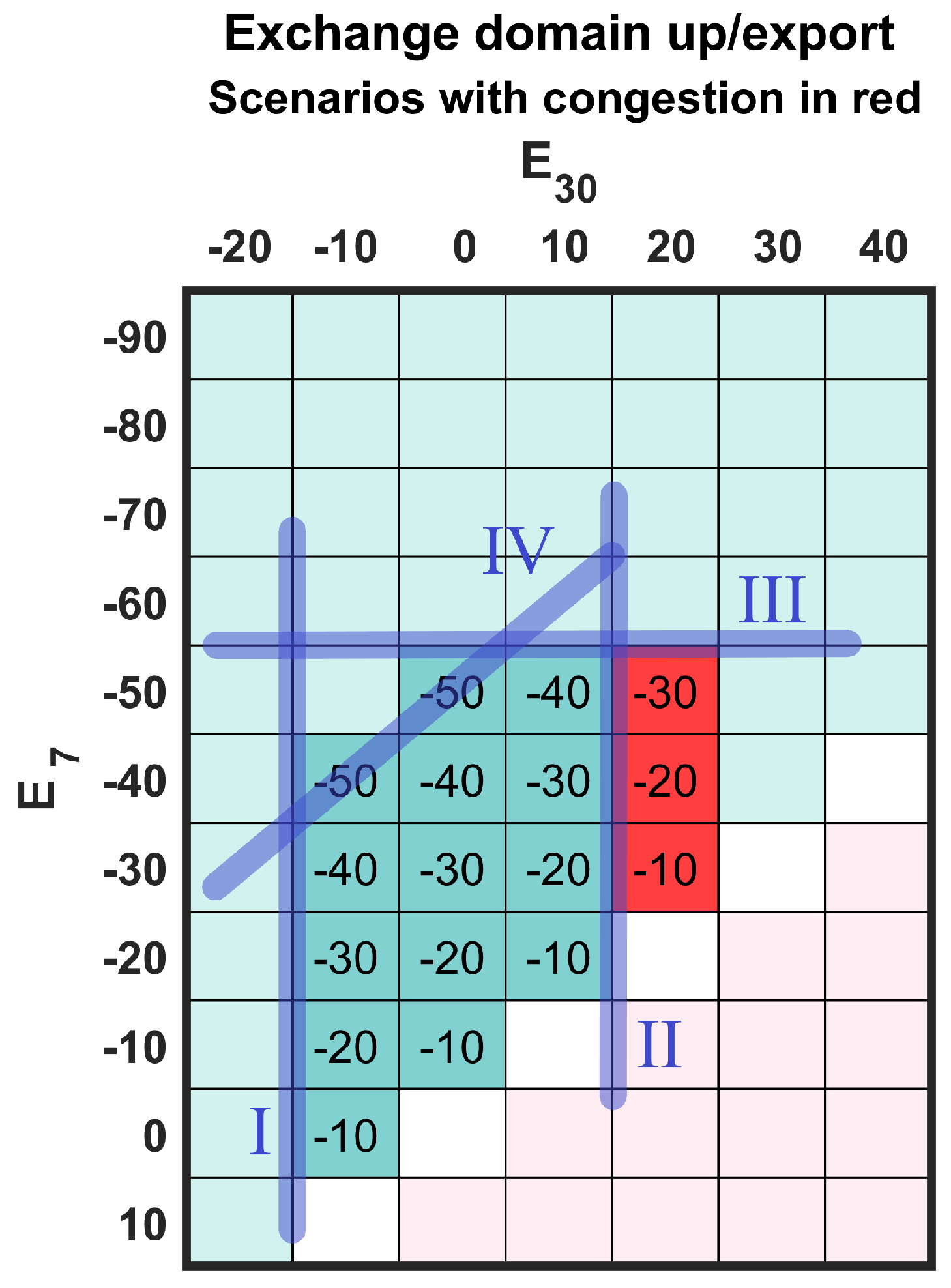
The selection of which exchange scenarios to evaluate should in principle cover all possible balancing exchange outcomes from the European balancing platform, i.e., limited by cross-zonal capacities to neighboring zones in both directions. Without sufficient bid capacity to cover many of the resulting rather extreme scenarios, this example considers a reduced set of exchange scenarios, given by the net injections and at the exchange nodes, with 10 MW steps between scenarios (cf. Figure 3a).
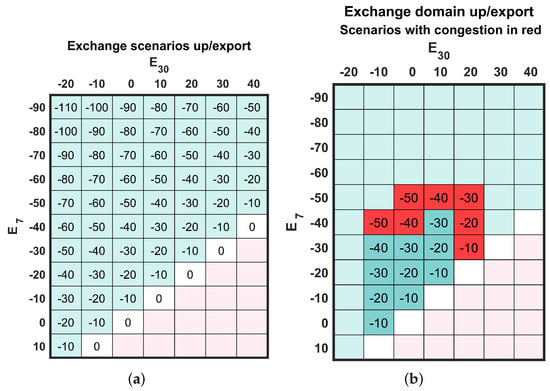
Figure 3.
Net balancing activation volumes in the considered exchange scenarios: (a) All exchange scenarios; (b) Feasible scenarios.Exchange matrices for up and down regulation
Upon evaluating these scenarios using the optimization in Equations (1)–(5), only a subset of them can be balanced given the initial flow in the network and the bid list at hand. The cells with numerical values in Figure 3b represent exchange scenarios for which there exists a feasible balancing dispatch. Some of these scenarios are congested (shown in red), and require deviating from the merit order, i.e., one or more bids must be (at least partially) skipped to avoid overloading the network.
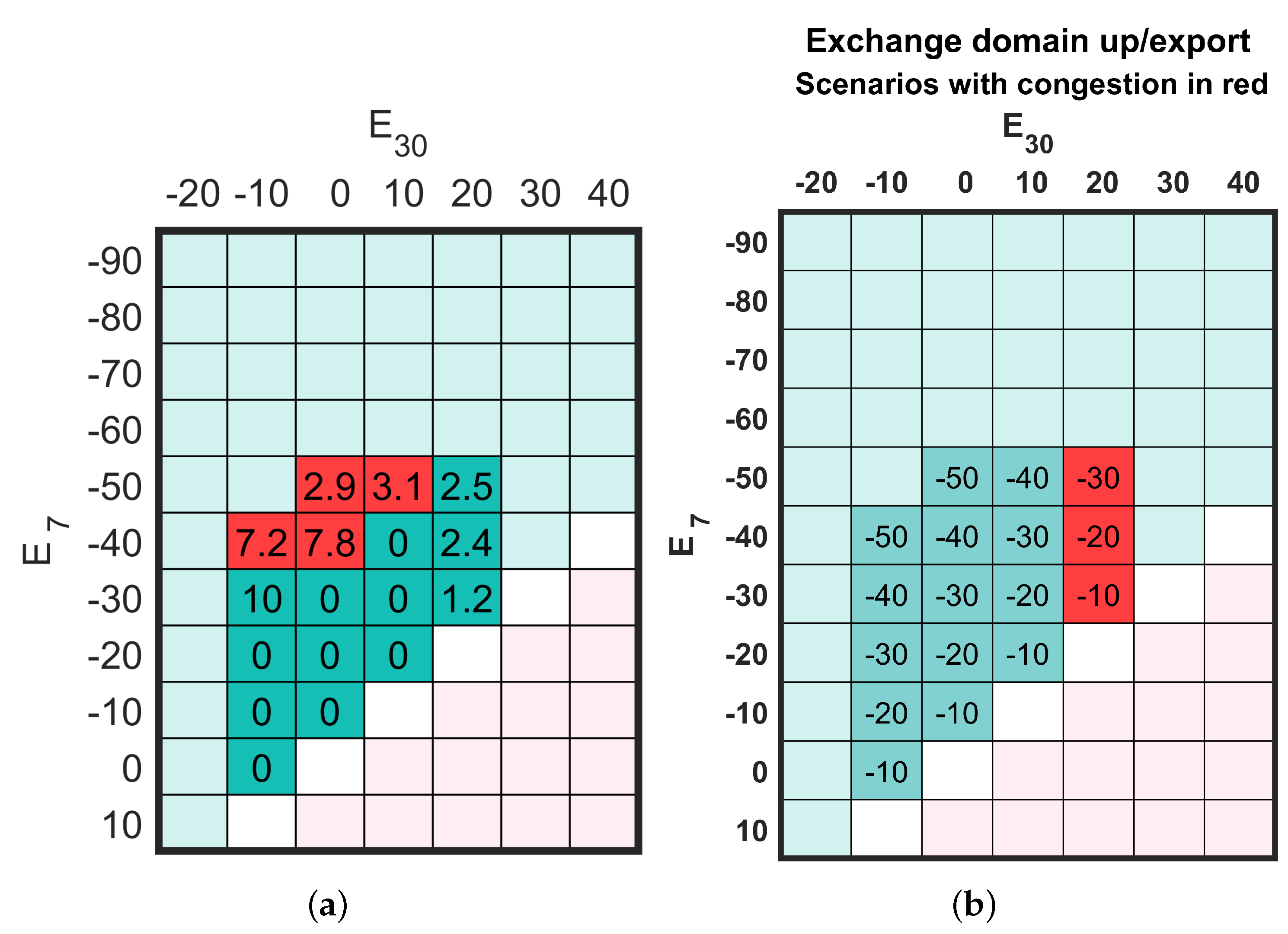
Comparing shadow prices on balancing energy exchange with bid prices in the different scenarios reveals that one of the bids, Bid #4, located on bus 22, causes congestion in several of the congested scenarios. These scenarios are marked as red in Figure 4a. Filtering this bid from the list and re-evaluating the exchange scenarios shows the scenarios previously congested by Bid #4 are now merit-order feasible (cf. Figure 4b).
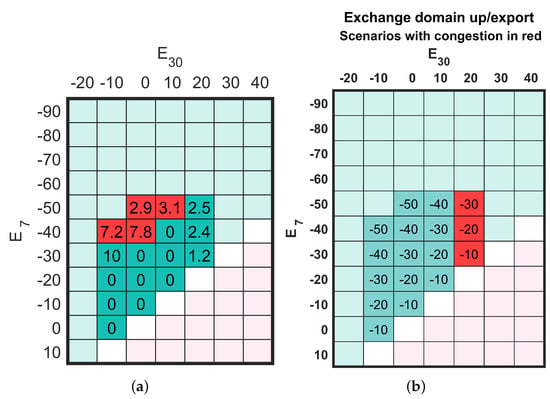
Figure 4.
(a) Activation volume of Bid #4, causing congestion in red scenarios; (b) Feasible exchange scenarios after filtering Bid #4.
In this example, the three red scenarios for cannot be made merit-order feasible by filtering any of the bids. Moreover, there is no efficient way of filtering bids to avoid most infeasible scenarios. For example, preventing the combination requires making all upward bids unavailable. This scenario requires only 10 MW of activated balancing energy, so reserve capacity is not an issue here, but the transit flow is.
5.2. Exchange Domains
Following the steps in Section 4, an exchange domain can be specified to prevent infeasible and congested exchange flow combinations. Here, exchange domains are calculated for the full upward bid list, and a list where Bid #4 is filtered.
5.2.1. All Six Upward Bids Made Available
The linear constraints corresponding to the convex hull is found using the Quickhull algorithm [13] with a list of coordinates corresponding to feasible exchange scenarios. Assuming only merit-order feasible scenarios should be included, these scenarios correspond to the green cells with numeric values in Figure 3b. The linear constraints enclosing the desired domain will be
Although computed by Quickhull, these constraints can easily be manually verified in this example, since the vertices of the convex hull can be identified directly from Figure 3b as and .
5.2.2. Bid #4 Made Unavailable
After withholding Bid #4, a larger set of exchange scenarios become merit-order feasible. (cf. Figure 4b). The scenarios in the red cells are still congested. Using Quickhull on the list of merit-order feasible scenarios eventually provides the hyperplanes constraining the feasible region (cf. Figure 5).
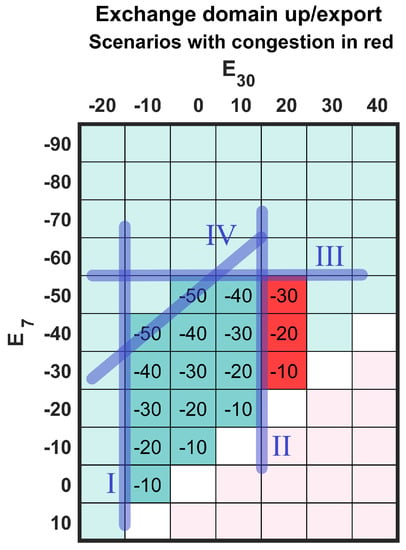
Figure 5.
Exchange domain defined by linear constraints after filtering Bid #4.
Compared to the case with all bids available, the convex hull has different vertices: and . One more linear constraint is needed, but the resulting exchange domain is larger.
The same procedure also applies for areas with more neighboring areas, albeit with more variables due to higher dimensionality of the exchange scenarios. Including these constraints to the common platform optimization enables making the balancing bids available without the risk of activation or transit flow leading to internal congestion.
6. Discussion
The impact of balancing energy activation on internal congestion depends strongly on the location of the imbalance. With the possibility of the balancing energy recipient being several different combinations of neighboring zones, bid locations cannot be seen as singular predictors for internal congestion due to balancing actions. Cross-border balancing exchange flows, including transit flows, appear to have similar, or higher importance.
For the balancing platforms being developed, filtering congested bids is currently the preferred mechanism for avoiding internal congestion. The method for bid filtering proposed in this paper takes the uncertainty in exchange flows into account by considering a large number of discrete exchange scenarios. For each scenario, a balancing dispatch followed by a nodal price analysis detects which bids would cause congestion with the given exchange flows. While bids causing congestion are obvious candidates for being filtered from the common merit order list, the picture is rarely black and white; bids can lead to congestion under some scenarios while being perfectly safe to use in many others.
The evaluation of an exchange scenario for a given bid list distinguishes between three outcomes: infeasible, congested, or merit-order feasible. While the latter indicates that the available bids can safely be activated for the exchange flows at hand, congested scenarios require skipping bids and deviating from the merit order. Infeasible scenarios simply cannot be balanced with any combination of bids from the list, and redispatch would be critical to avoid overloading the transmission network should such a scenario materialize. Whereas making specific bids unavailable can make congested scenarios merit-order feasible, bid filtering is ineffective in preventing infeasible platform outcomes.
Exchange domains provide restrictions on cross-zonal balancing energy flow combinations. These cannot make more exchange scenarios feasible, but effectively prevent infeasible or congested situations from occurring. In this regard, the concept is complementary to bid filtering. An exchange domain must be tailored to the list of available bids, and the domains calculated for specific lists of bids can also help determine which bids to filter. More importantly, the ability to discard congested scenarios without filtering bids also enables making more bids available to the platform.
An exchange domain is described by a set of linear inequalities, and these would act as additional constraints in the platform optimization. The impact on the computational burden from these additional constraints would be negligible. The concept is newly developed and thus has not been proposed as a candidate method in the design drafts of any of the European balancing platforms being implemented. Nevertheless, the importance of cross-border balancing flows on internal congestion infers that including such a mechanism should be considered in the future.
Author Contributions
The paper was partly based on the MSc thesis of H.B., with individual contributions including: conceptualization, M.H.; methodology, M.H. and H.B.; software, H.B.; validation, H.B., M.H. and G.D.; formal analysis, H.B.; investigation, H.B.; resources, H.B., M.H.; data curation, H.B.; writing—original draft preparation, M.H.; writing—review and editing, M.H.; visualization, H.B.; supervision, M.H. and G.D.; project administration, G.D.; and funding acquisition, G.D.
Funding
This research was funded by the Norwegian Research Council grant number 248291.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| aFRR | Automatically activated Frequency Restoration Reserves |
| AOF | Activation Optimization Function |
| CMOL | Common Merit Order List |
| ENTSO-E | European Network of Transmission System Operators for Electricity |
| LMP | Locational Marginal Price |
| mFRR | Manually activated Frequency Restoration Reserves |
| MARI | Manually Activated Reserves Initiative |
| PICASSO | Platform for the International Coordination of Automated Frequency Restoration and Stable |
| System Operation | |
| PTDF | Power Transfer Distribution Factor |
| RR | Replacement Reserves |
| TERRE | Trans European Replacement Reserves Exchange |
| TSO | Transmission System Operator |
References
- European Commission. Guideline on Electricity Balancing; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- ADMIE; National Grid; REE; REN; RTE; Terna; SwissGrid. Public Consultation Document for the Design of the TERRE (Trans European Replacement Reserves Exchange) Project Solution. 2016. Available online: https://consultations.entsoe.eu/markets/public-consultation-document-for-the-design-of-the/results/terre-public-consultation-assessment.pdf (accessed on 3 February 2019).
- MARI. First Consultation—Call For Input. 2017. Available online: https://consultations.entsoe.eu/markets/mari-first-consultation-call-for-input/supporting_documents/20171121_%20MARI%20First%20Consultation_Final.pdf (accessed on 3 February 2019).
- 50 Hertz; Amprion; APG; Elia; RTE; TenneT; Transnet BW. Consultation on the Design of the pLatform for Automatic Frequency Restoration Reserve (aFRR) of PICASSO Region. 2017. Available online: https://docstore.entsoe.eu/Documents/Network%20codes%20documents/Implementation/picasso/PICASSO-Consultation_document.pdf (accessed on 3 February 2019).
- ENTSO-E. Guideline on Electricity Balancing (May 2017 Version). 2017. Available online: https://electricity.network-codes.eu/network_codes/eb/ (accessed on 3 February 2019).
- Linnemann, C.; Echternacht, D.; Breuer, C.; Moser, A. Modeling optimal redispatch for the European Transmission grid. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; number chapter IV. pp. 1–8. [Google Scholar] [CrossRef]
- Chaves-Ávila, J.P.; van der Veen, R.A.C.; Hakvoort, R.A. The interplay between imbalance pricing mechanisms and network congestions—Analysis of the German electricity market. Util. Policy 2014, 28, 52–61. [Google Scholar] [CrossRef]
- Sprey, J.D.; Drees, T.; vom Stein, D.; Moser, A. Impact of balancing energy on network congestions. In Proceedings of the 2015 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015; pp. 1–6. [Google Scholar]
- Guntermann, C.; Gunderson, N.W.; Lindeberg, E.; Håberg, M. Detecting unavailable Balancing Energy Bids due to Risk of Internal Congestions. In Proceedings of the 18th International Conference on Environment and Electrical Engineering (EEEIC), Palermo, Italy, 12–15 June 2018. [Google Scholar]
- Wang, F.; Hedman, K.W. Reserve zone determination based on statistical clustering methods. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Lyon, J.D.; Hedman, K.W.; Zhang, M. Reserve Requirements to Efficiently Manage Intra-Zonal Congestion. IEEE Trans. Power Syst. 2014, 29, 251–258. [Google Scholar] [CrossRef]
- Lyon, J.D.; Zhang, M.; Hedman, K.W. Locational reserve disqualification for distinct scenarios. IEEE Trans. Power Syst. 2015, 30, 357–364. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Bood, H. Exchange Domains for Cross-border Activation of Balancing Bids—Preventing Internal Congestion in an Integrated EUropean Balancing Activation Optimization. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).