Heat Recovery for a Textile Stenter: CFD Analysis of Air Curtain Benefits
Abstract
1. Introduction
1.1. Waste Heat Utilization in the Textile Industry
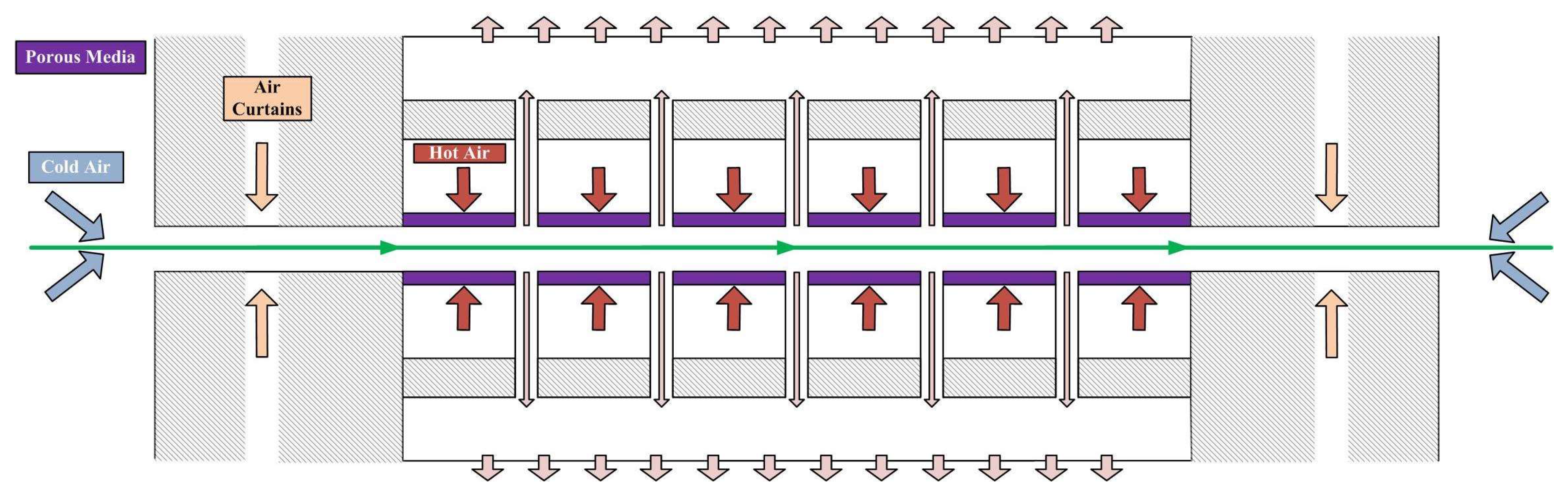
1.2. Air Curtains Possible Use in Stenters
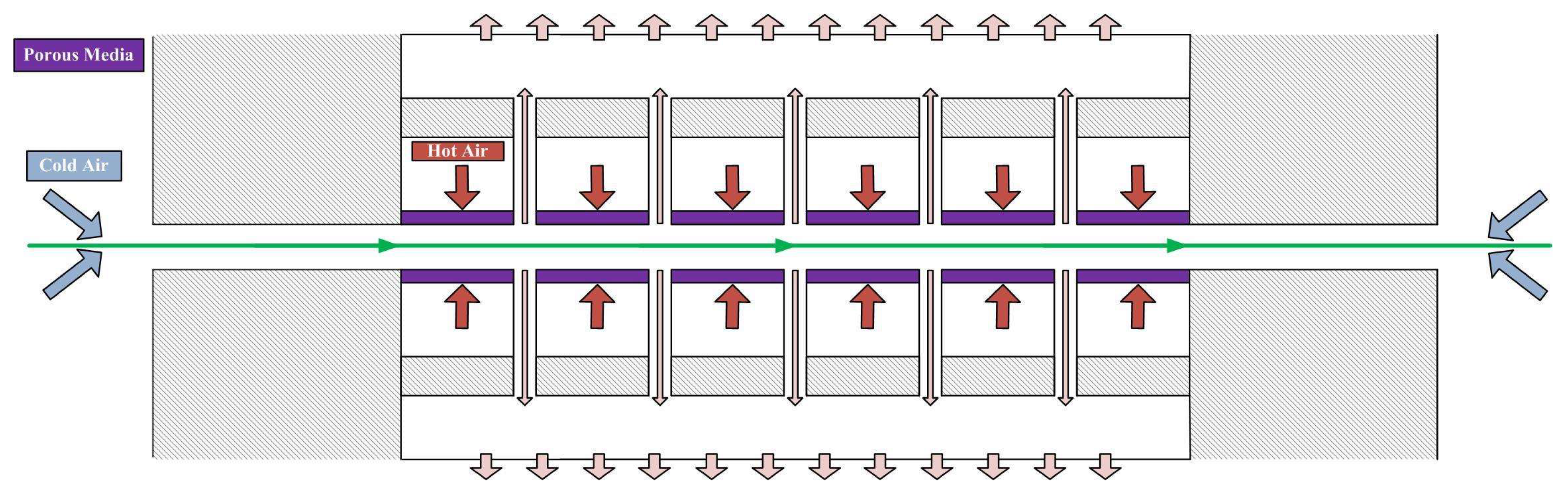
2. Description of the Application
2.1. Stenter Geometry
2.2. Stenter Model
3. Methodology
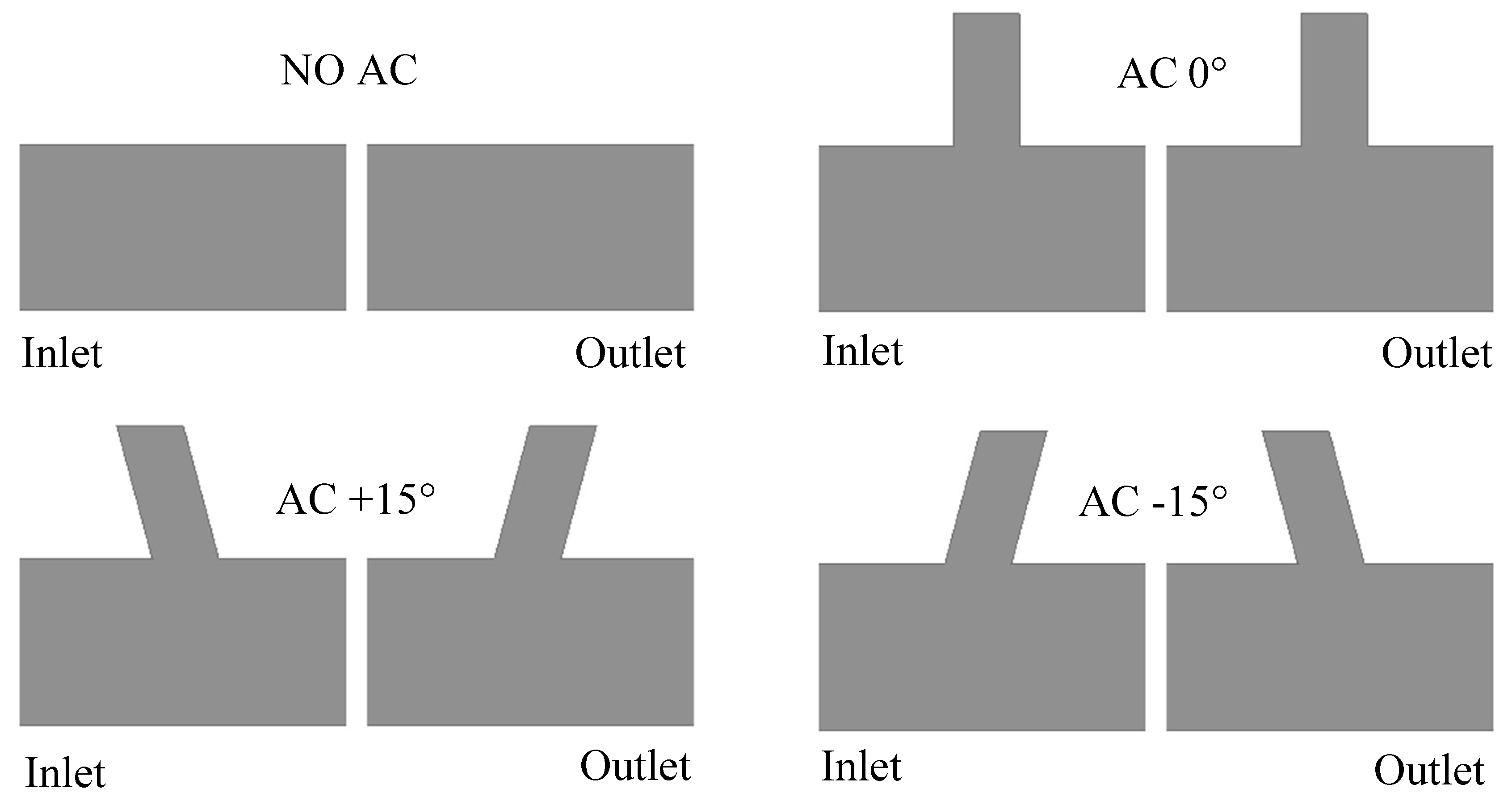
3.1. Stenter Configurations
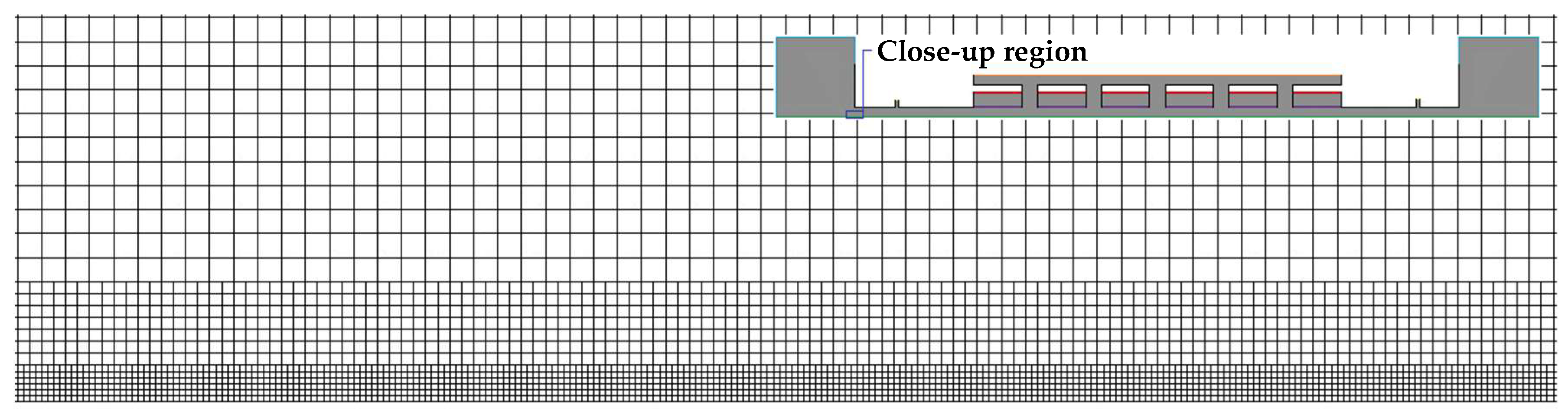
3.2. Numerical Setup
3.3. Performance Indicators
4. Results
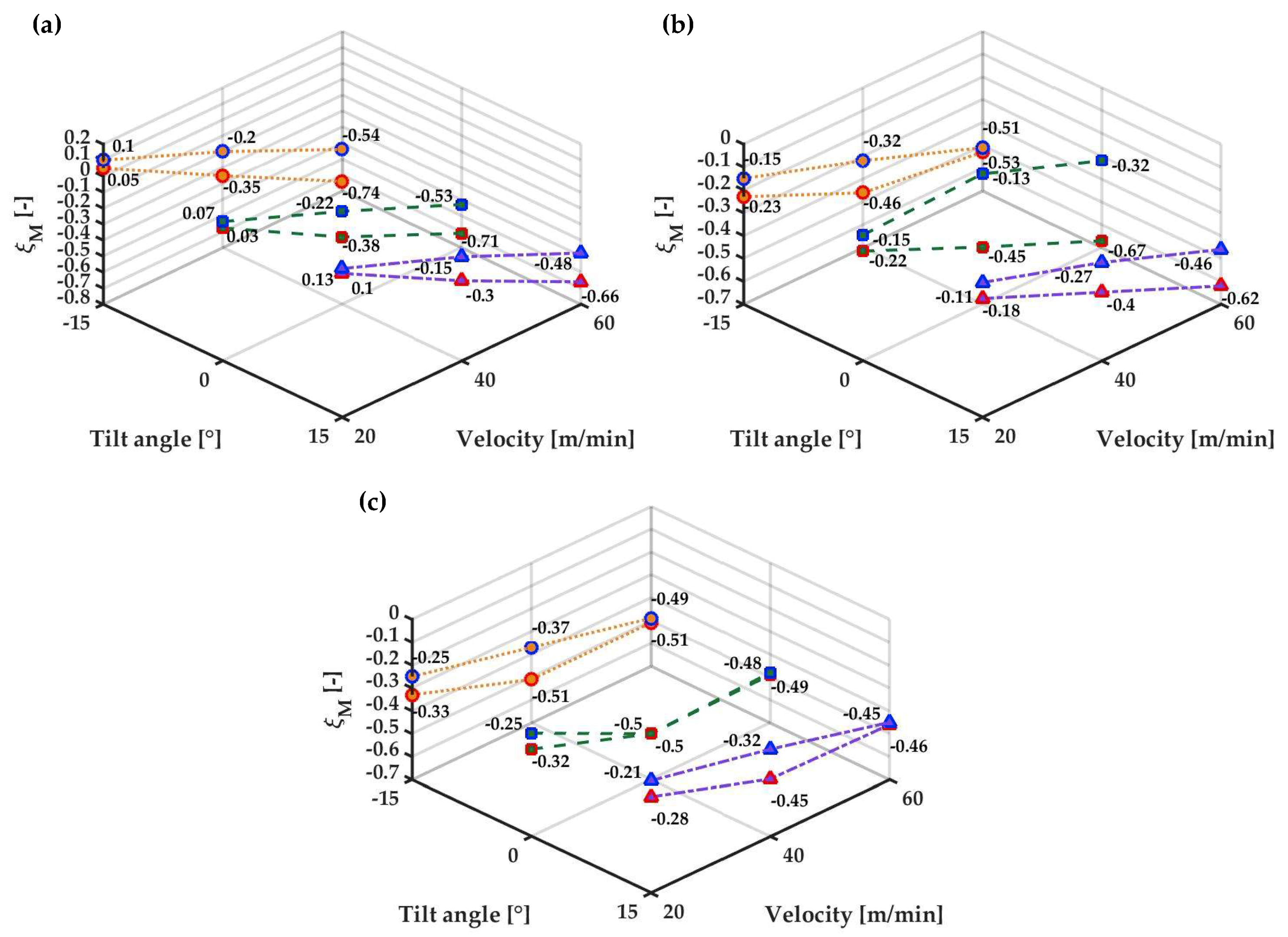
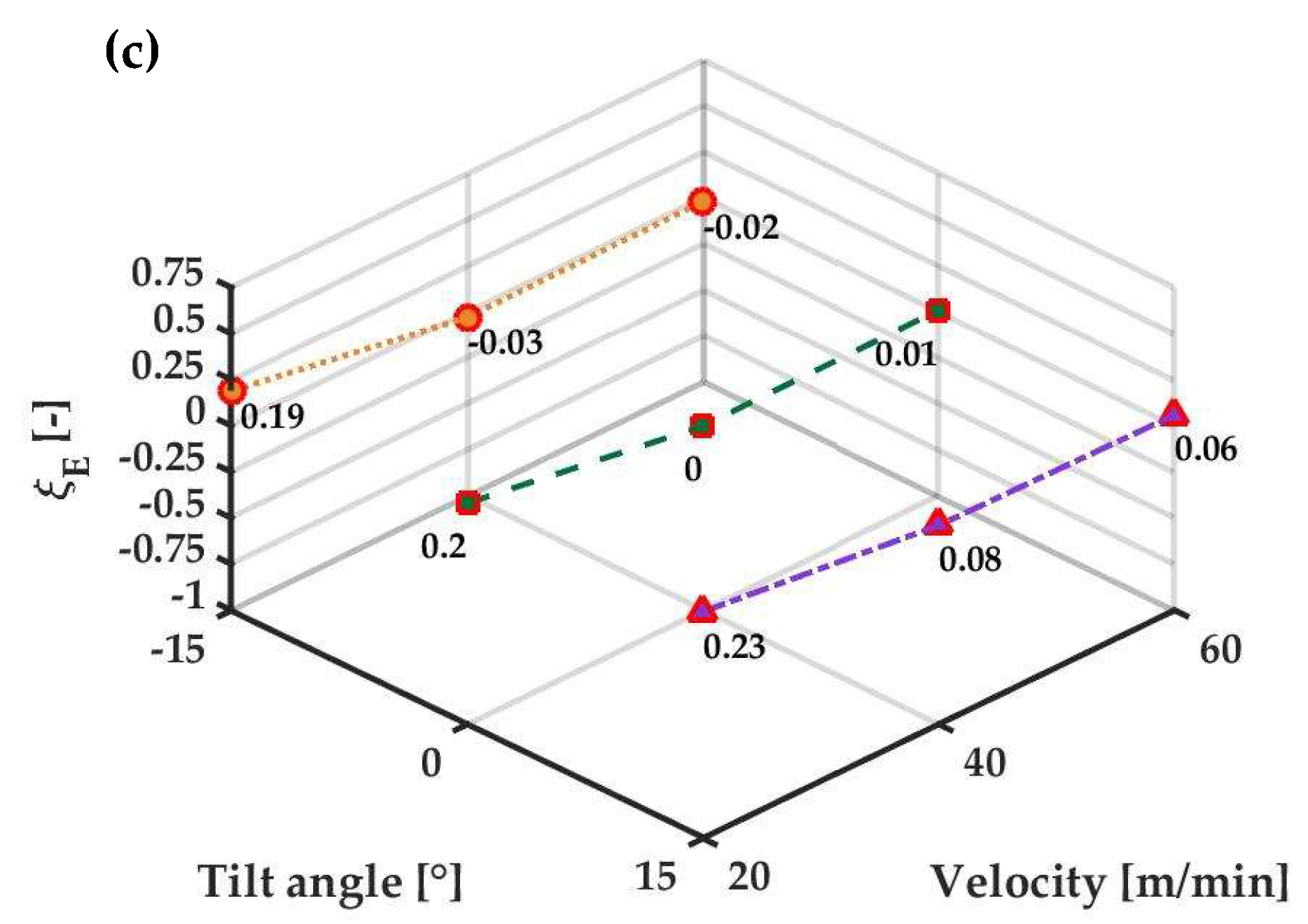
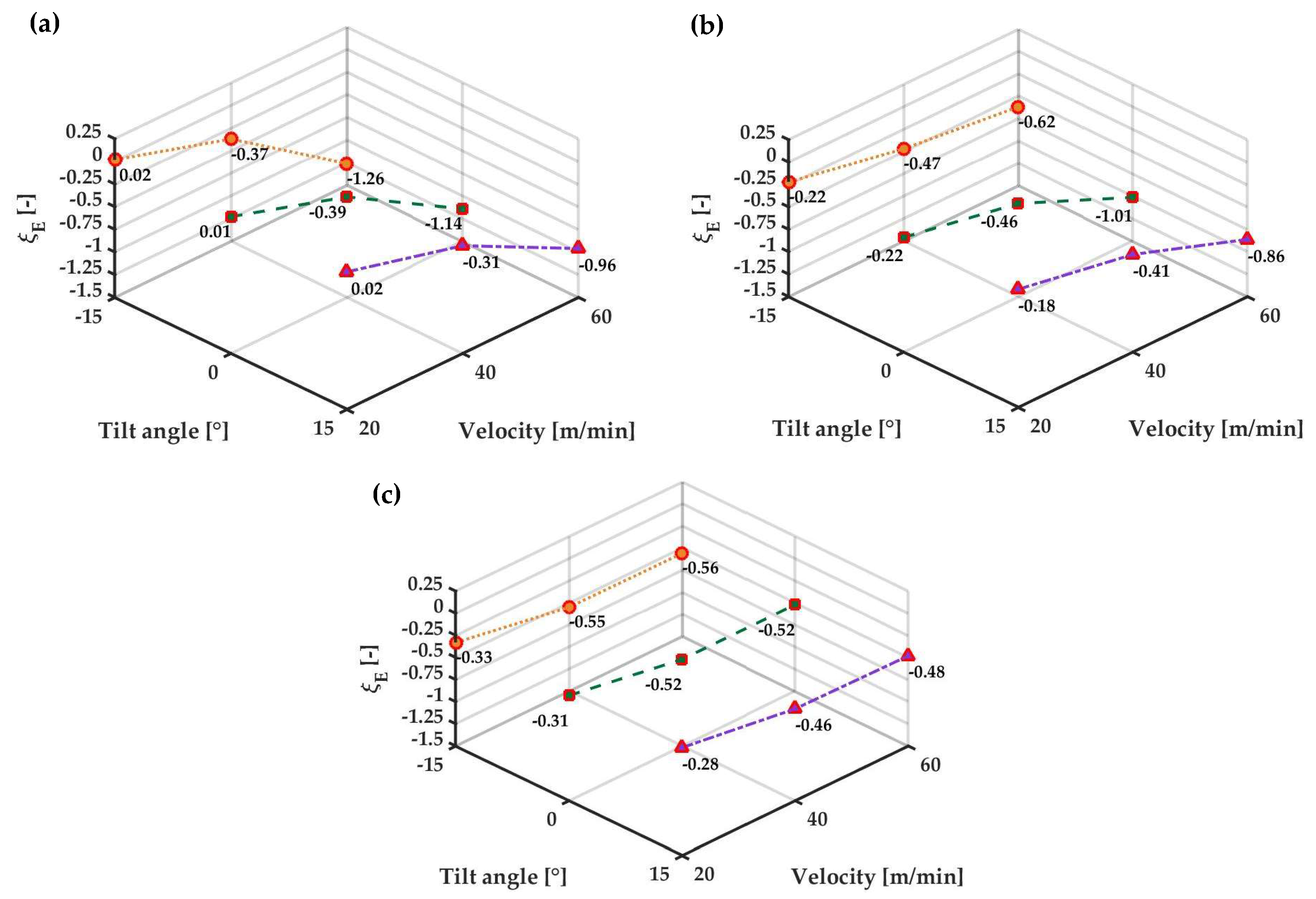
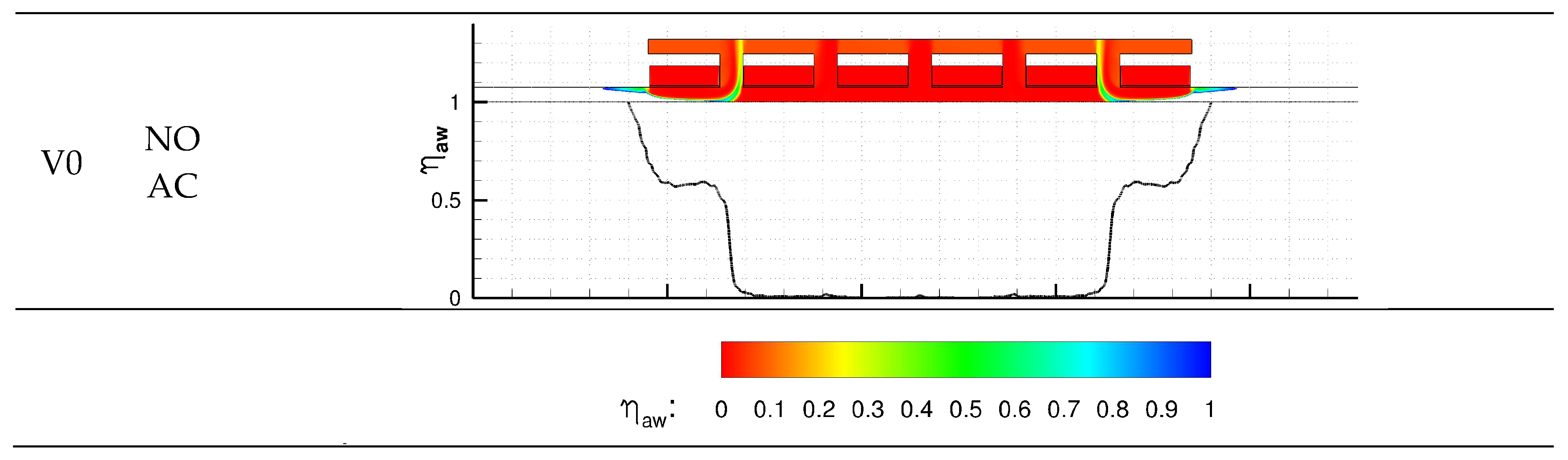
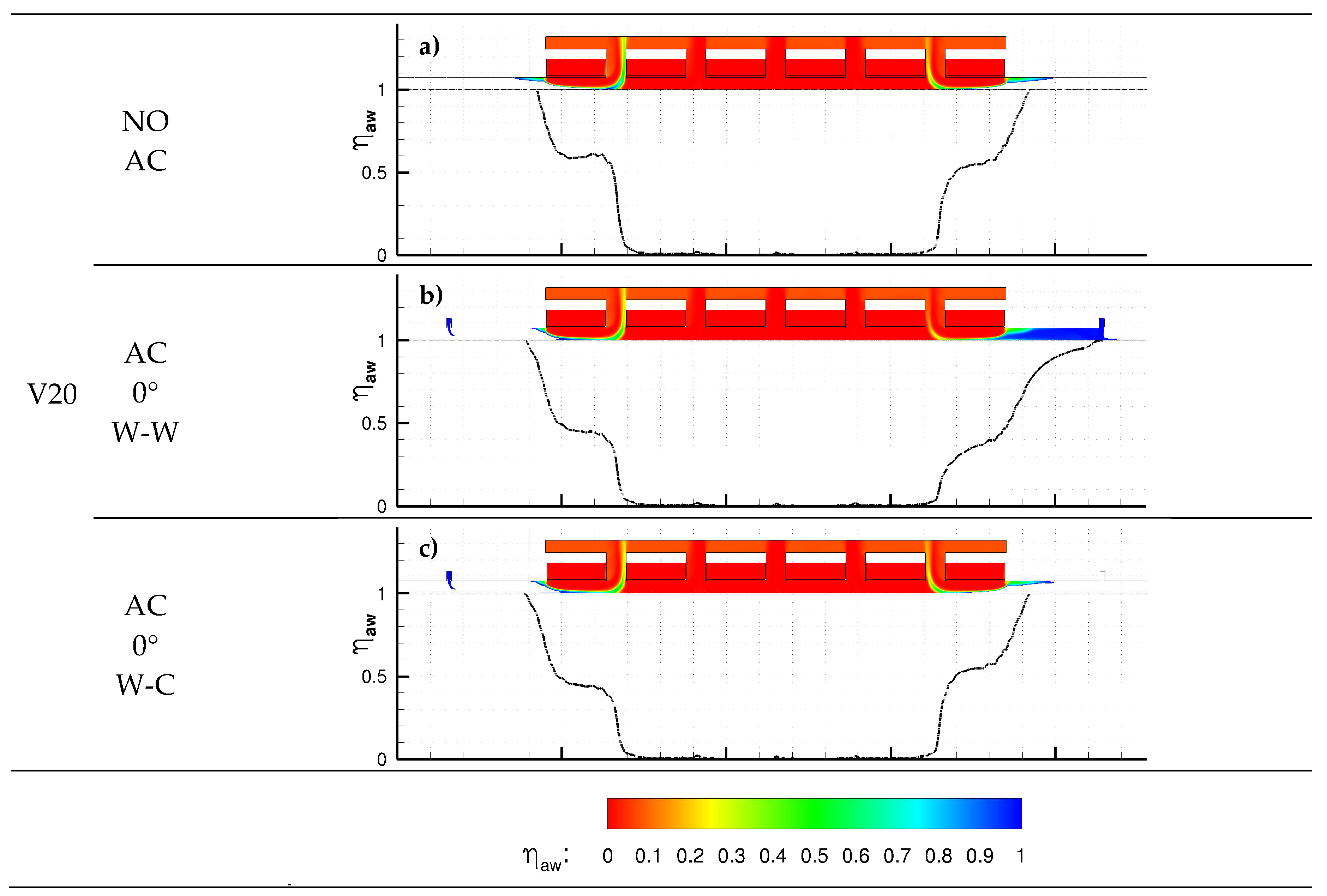
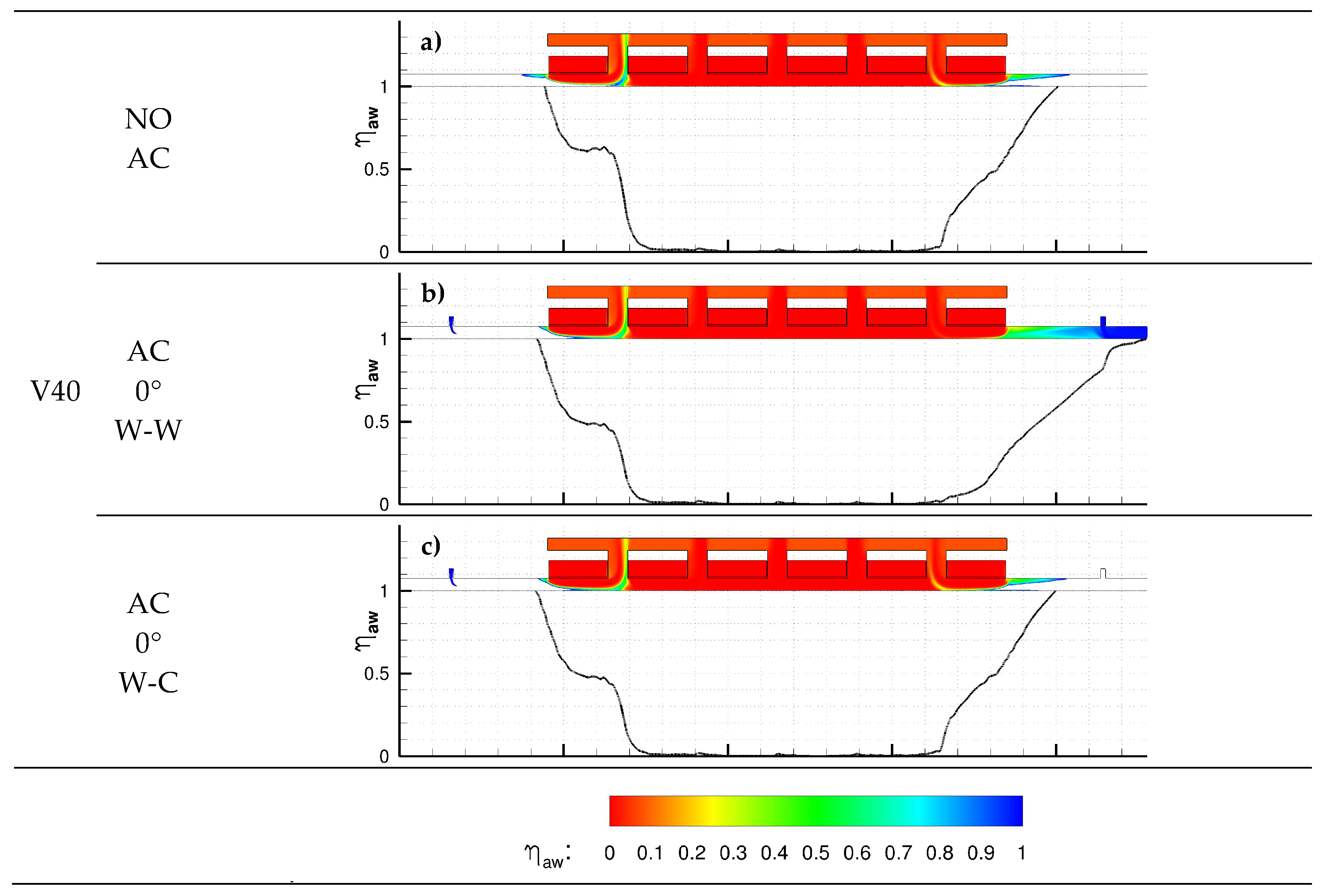
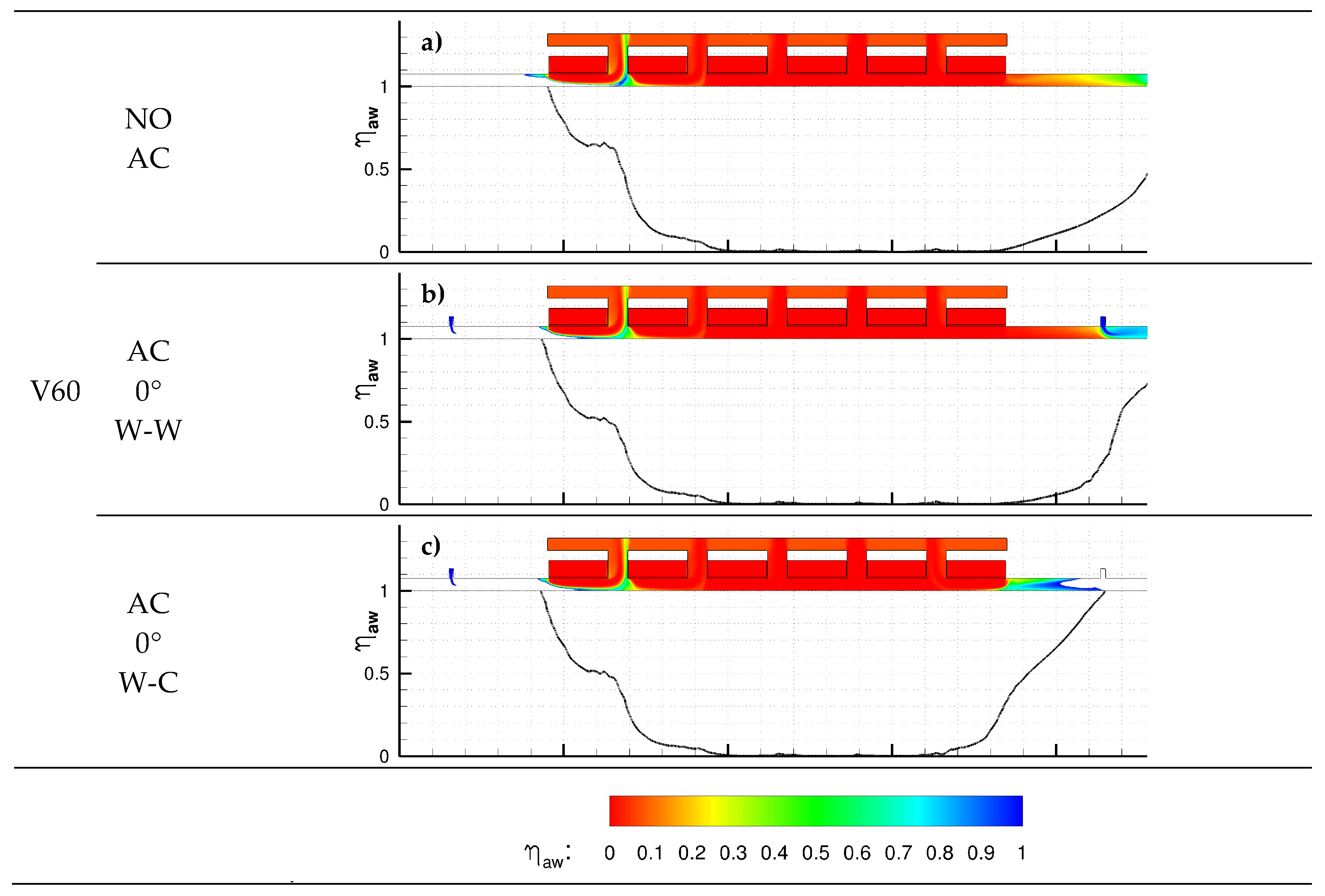
4.1. Mass Sealing Effectiveness
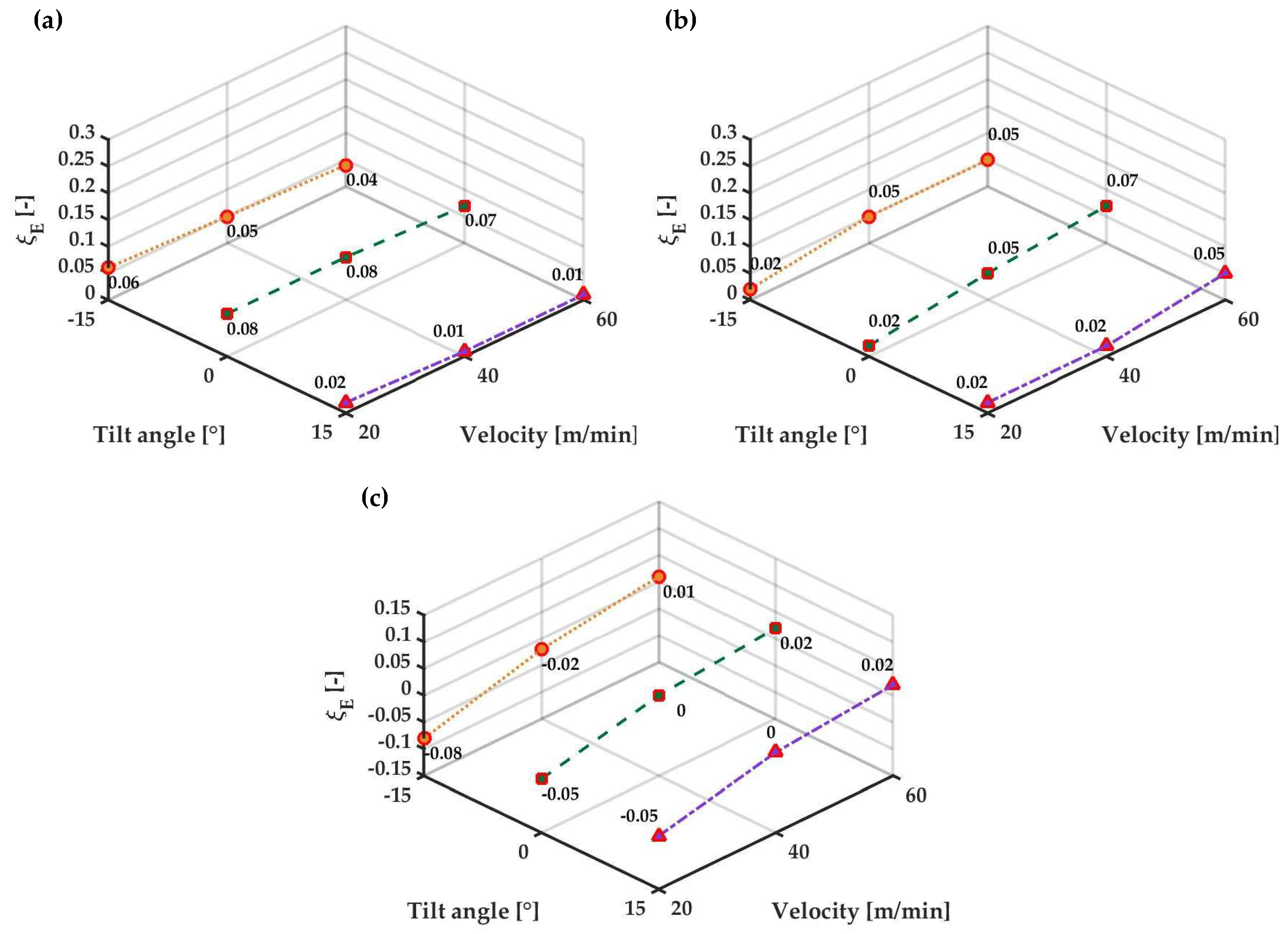
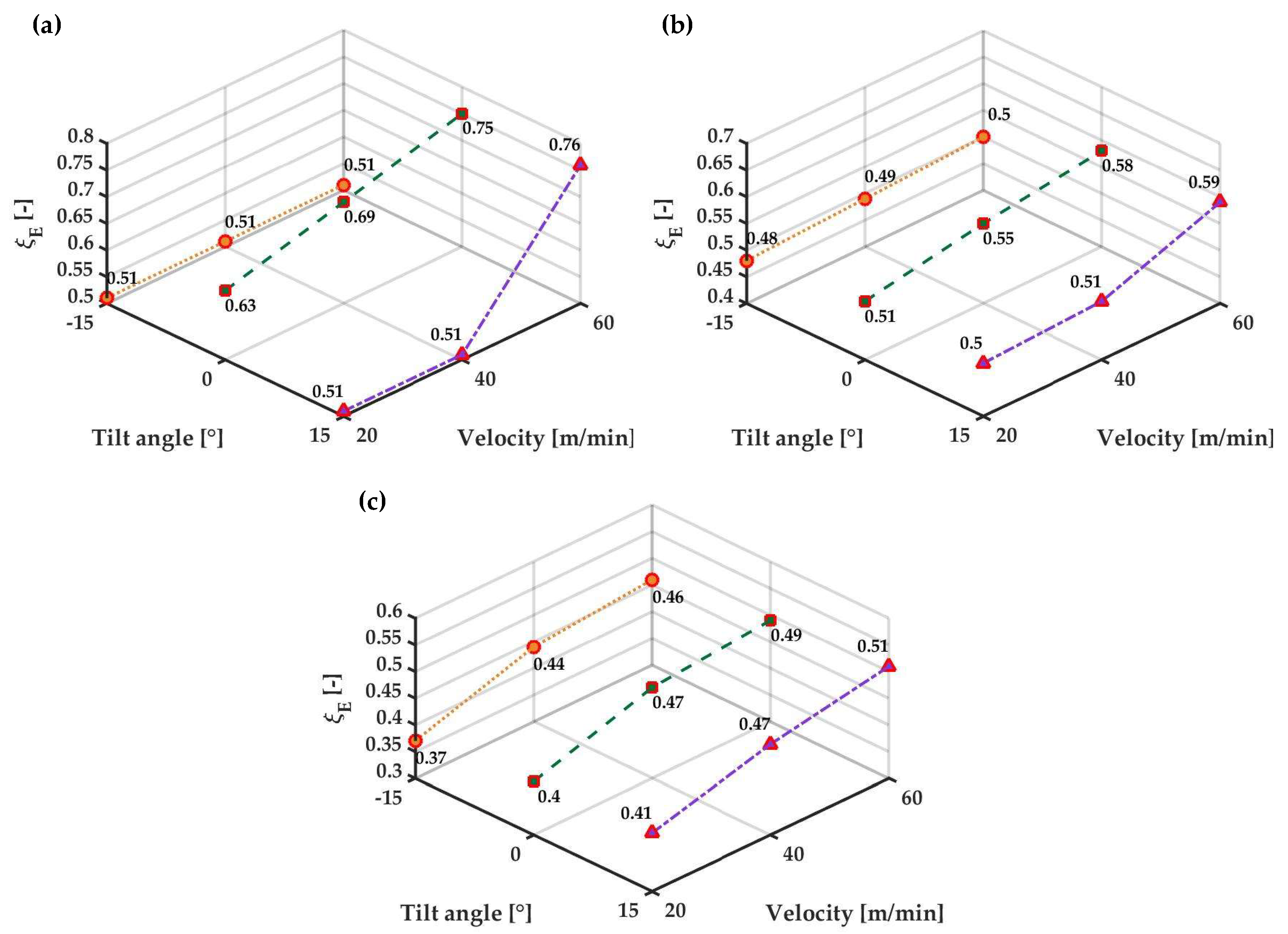
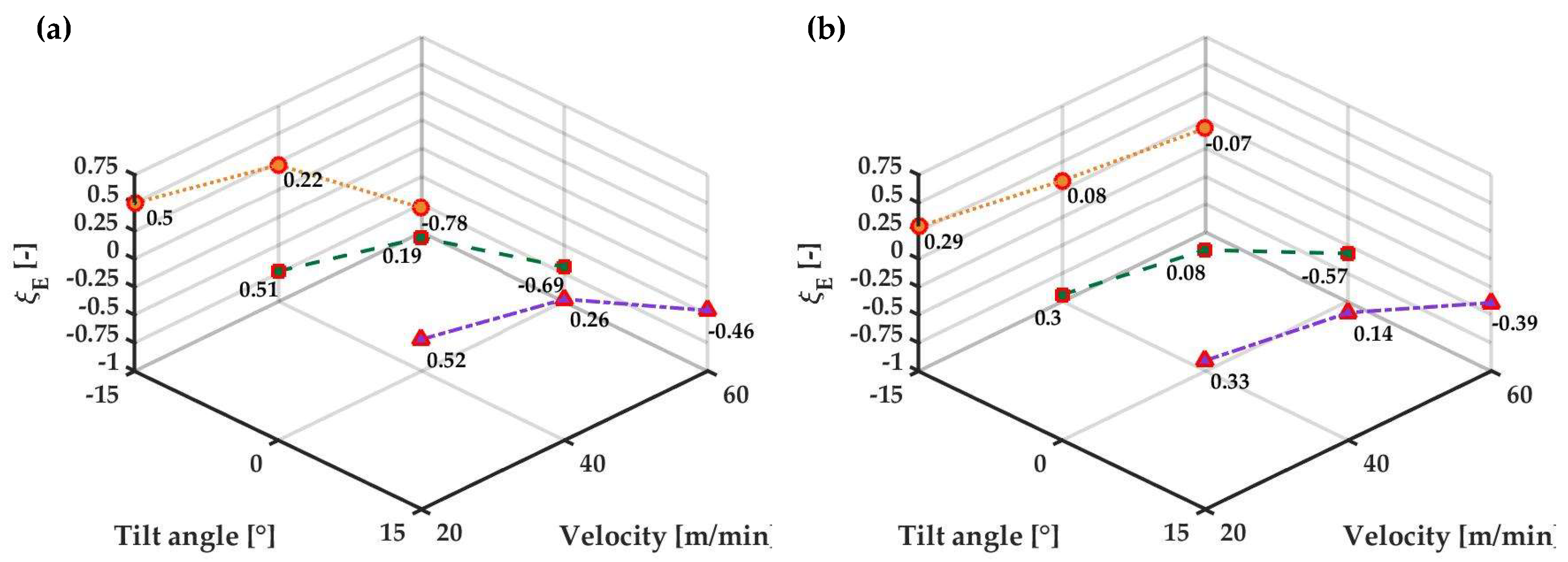
4.2. Energy Effectiveness
4.3. Temperature Distribution
5. Conclusions
- 60 different configurations were analyzed, determining that the most influencing parameters for air curtains effectiveness are mass flow rate and temperature;
- The tilt angle of the air curtains (−15°, 0° and +15°) has a moderate effect on the machine performance;
- A high AC mass flow rate can result in a negative effect for the stenter, as the recovered heat could be leaked to the environment, as the values of ξM and ξE are negatively affected;
- The ACs determine an effective reduction of air suction from the environment compared to the reference case without air curtains;
- The use of ACs reduces the energy loss with respect to the reference case and part of the sensible heat used in the ACs is effectively recovered.
- A warm AC is always preferable at the stenter inlet (warm air is ingested by the machine and regeneration is effective)
- At large fabric speeds (above 40 m/min), entrainment of hot gases at the outlet from inside the machine becomes relevant, and a cold AC is recommended at the outlet to improve sealing performance; regeneration can be promoted boosting the flow rate at the inlet warm AC.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| cp | Specific heat capacity (J/(kg·K)) |
| Mass flow rate (kg/s) | |
| h | Specific enthalpy (J/kg) |
| Acronyms | |
| 2D | Two-dimensional |
| AC | Air curtain |
| AW | Adiabatic wall |
| CFD | Computational fluid dynamics |
| CS | Control section |
| Greek Letters | |
| α, β, γ, δ | Control sections |
| ξM | Mass sealing effectiveness coefficient |
| ξE | Energy effectiveness coefficient |
| ηAW | Adiabatic wall effectiveness coefficient |
| Abbreviations | |
| Amb | Ambient |
References
- U.S. Energy Information Administration. International Energy Outlook. 2013. Available online: http://www.eia.gov/outlooks/ieo/pdf/0484(2013).pdf (accessed on 30 November 2018).
- Zuazua-Ros, A.; Martín Gómez, C.; Ramos, J.C.; Bermejo-Busto, J. Towards cooling systems integration in buildings: Experimental analysis of a heat dissipation panel. Renew. Sustain. Energy Rev. 2017, 72, 73–82. [Google Scholar] [CrossRef]
- Tello, P.; Weerdmeester, R. Spire Roadmap. 2013. Available online: https://www.spire2030.eu/sites/default/files/pressoffice/spire-roadmap.pdf (accessed on 30 November 2018).
- Beers, D.V.; Biswas, W.K. A regional synergy approach to energy recovery: The case of the Kwinana industrial area, Western Australia. Energy Convers. Manag. 2008, 49, 3051–3062. [Google Scholar] [CrossRef]
- Hasanbeigi, A.; Price, L. A review of energy use and energy efficiency technologies for textile industry. Renew. Sustain. Energy Rev. 2012, 16, 3648–3665. [Google Scholar] [CrossRef]
- Hong, G.B.; Su, T.L.; Lee, J.D.; Hsu, T.C.; Chen, H.W. Energy conservation potential in Taiwanese textile industry. Energy Policy 2010, 38, 7048–7053. [Google Scholar] [CrossRef]
- Rakib, M.I.; Saidur, R.; Mohamad, E.N.; Afifi, A.M. Waste-heat utilization—The sustainable technologies to minimize energy consumption in Bangladesh textile sector. J. Clean. Prod. 2017, 142, 1867–1876. [Google Scholar] [CrossRef]
- Alkaya, E.; Demirer, G.N. Sustainable textile production: A case study from a woven fabric manufacturing mill in Turkey. J. Clean. Prod. 2014, 65, 595–603. [Google Scholar] [CrossRef]
- Pulat, E.; Etemoglu, A.B.; Can, M. Waste-heat recovery potential in Turkish textile industry: Case study for city of Bursa. Renew. Sustain. Energy Rev. 2009, 13, 663–672. [Google Scholar] [CrossRef]
- Ozturk, E.; Koseoglu, H.; Karaboyaci, M.; Yigit, N.O.; Yetis, U.; Kitis, M. Sustainable textile production: Cleaner production assessment/eco-efficiency analysis study in a textile mill. J. Clean. Prod. 2016, 138, 248–263. [Google Scholar] [CrossRef]
- Shiwanthi, S.; Lokupitiya, E.; Peiri, S. Evaluation of the environmental and economic performances of three selected textile factories in Biyagama Export Processing Zone Sri Lanka. Environ. Dev. 2018, 27, 70–82. [Google Scholar] [CrossRef]
- Cay, A.; Tarakcioglu, I.; Hepbasli, A. Exergetic performance assessment of a stenter system in a textile finishing mill. Int. J. Energy Res. 2007, 31, 1251–1265. [Google Scholar] [CrossRef]
- Cay, A.; Tarakcioglu, I.; Hepbasli, A. A study on the exergetic analysis of continuous textile dryer. Int. J. Exergy 2009, 6, 422–439. [Google Scholar] [CrossRef]
- Cay, A.; Tarakcioglu, I.; Hepbasli, A. Exergetic analysis of textile convective drying with stenters by subsystem models: Part 1—Exergetic modelling and evaluation. Dry. Technol. 2010, 28, 1359–1367. [Google Scholar] [CrossRef]
- Cay, A.; Tarakcioglu, I.; Hepbasli, A. Exergetic analysis of textile convective drying with stenters by subsystem models: Part 2—Parametric study on exergy analysis. Dry. Technol. 2010, 28, 1368–1376. [Google Scholar] [CrossRef]
- Oǧulata, R.T. Utilization of waste-heat recovery in textile drying. Appl. Energy 2014, 79, 41–49. [Google Scholar] [CrossRef]
- Sekkeli, M.; Keçecioglu, O.F. Scada based an energy saving approach to operation of stenter machine in a textile plant using waste-heat recovery system. J. Text. Appar./Tekstil ve Konfeksiyon 2012, 22, 248–257. [Google Scholar]
- Fiaschi, D.; Manfrida, G.; Russo, L.; Talluri, L. Improvement of waste heat recuperation on an industrial textile dryer: Redesign of heat exchangers network and components. Energy Convers. Manag. 2017, 150, 924–940. [Google Scholar] [CrossRef]
- Van Kennel, T. Means for Excluding Drafts from Open Doorways. U.S. Patent 774,730, 8 November 1904. [Google Scholar]
- Krajewki, G.; Wegrzynski, W. Air curtain as a barrier for smoke in case of fire: Numerical modelling. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 145–153. [Google Scholar]
- Yu, L.X.; Liu, F.; Beji, T.; Weng, M.C.; Merci, B. Experimental study of the effectiveness of air curtains of variable width and injection angle to block fire-induced smoke in a tunnel configuration. Int. J. Therm. Sci. 2018, 134, 13–26. [Google Scholar] [CrossRef]
- Liu, Q.; Nie, W.; Hua, Y.; Peng, H.; Liu, C.; Wei, C. Research on tunnel ventilation systems: Dust diffusion and pollution behavior by air curtains based on CFD technology and field measurement. Build. Environ. 2019, 147, 444–460. [Google Scholar] [CrossRef]
- Van Belleghem, M.; Verhaehe, G.; T’Joen, C.; Huisseune, H.; De Jaeger, P.; De Paepe, M. Heat transfer through vertically downward-blowing single-jet air curtains for cold rooms. Heat Transf. Eng. 2012, 33, 1196–1206. [Google Scholar] [CrossRef]
- Goncalves, J.C.; Costa, J.J.; Figueiredo, A.R.; Lopes, A.M.G. Study of the aerodynamic sealing of a cold store—Experimental and numerical approaches. Energy Build. 2012, 55, 779–789. [Google Scholar] [CrossRef]
- Foster, A.M.; Swain, M.J.; Barrett, R.; D’Agaro, P.; James, S.J. Effectiveness and optimum jet velocity for a plane jet air curtain used to restrict cold room infiltration. Int. J. Refrig. 2006, 29, 692–699. [Google Scholar] [CrossRef]
- Moureh, J.; Yataghene, M. Numerical and experimental investigations on jet characteristics and airflow patterns related to an air curtain subjected to external lateral flow. Int. J. Refrig. 2016, 67, 355–372. [Google Scholar] [CrossRef]
- Neto, L.P.C.; Gameiro Silva, M.C.; Cost, J.J. On the use of infrared thermography in studies with air curtain devices. Energy Build. 2006, 38, 1194–1199. [Google Scholar] [CrossRef]
- Hayes, F.C.; Stoecker, W.F. Heat transfer characteristics of the air curtain. ASHRAE Trans. 1969, 1, 153–167. [Google Scholar]
- Gil-Lopez, T.; Castejon-Navas, J.; Galvez-Huerta, M.A.; O’Donohoe, P.G. Energetic, environmental and economic analysis of climatic separation by means of air curtains in cold storage rooms. Energy Build. 2014, 74, 8–16. [Google Scholar] [CrossRef]
- Cordis, Air Curtains on Textile Stenters. Available online: https://cordis.europa.eu/project/rcn/14616/factsheet/en (accessed on 10 January 2018).
- Sicurfad, Nobilitazione Tessile. Manuale per la Formazione degli Operai. Available online: http://www.sicurfad.it/strumenti/documenti/sicurfadS00.pdf (accessed on 30 November 2018).
- ANSYS Fluent Theory Guide, ANSYS Inc. Southpointe 2600 ANSYS Drive Canonsburg, PA 15317. January 2019. Available online: http://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node3.htm (accessed on 15 January 2019).
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: Milton Park, Didcot, UK; Abingdon, UK, 1980; ISBN 978-0-89116-522-4. [Google Scholar]
- Montomoli, F.; Massini, M.; Salvadori, S.; Martelli, F. Geometrical Uncertainty and Film Cooling: Fillet Radii. ASME J. Turbomach. 2012, 134, 011019. [Google Scholar] [CrossRef]



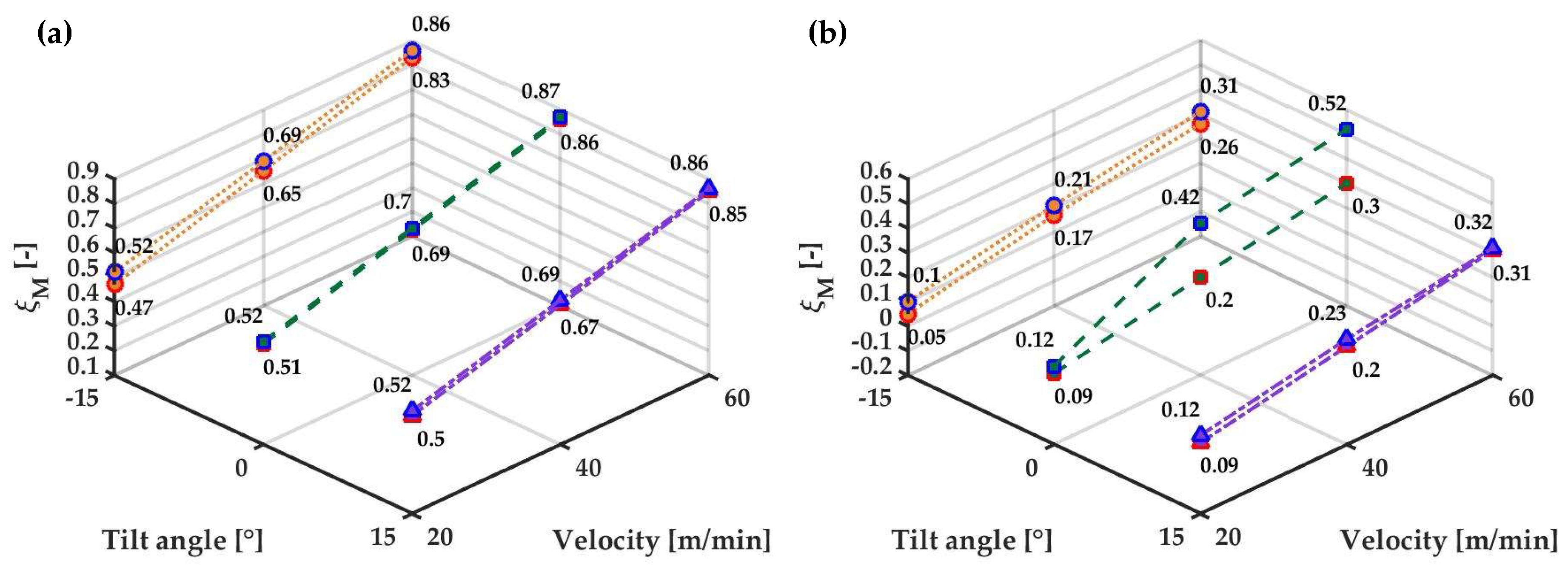
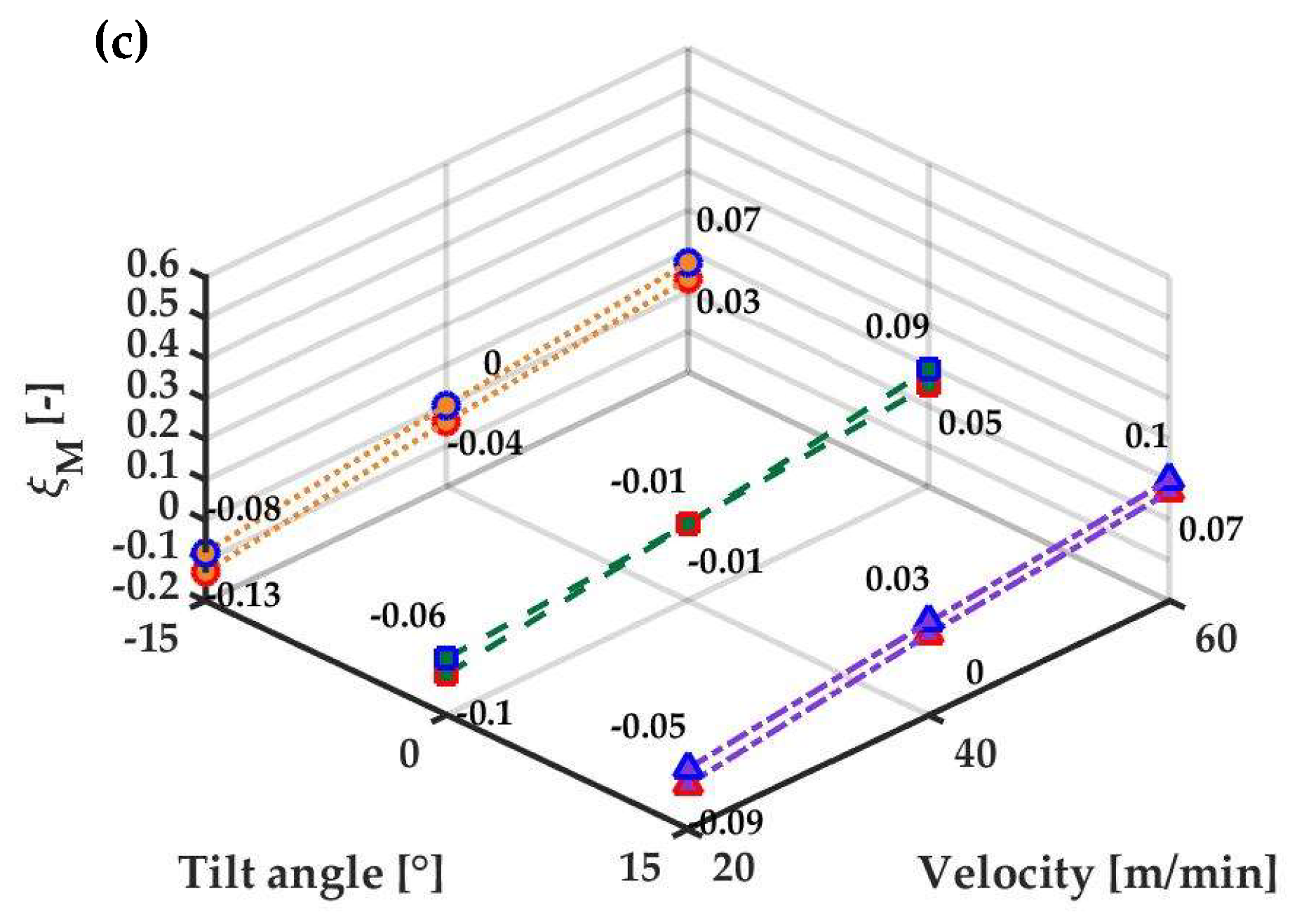
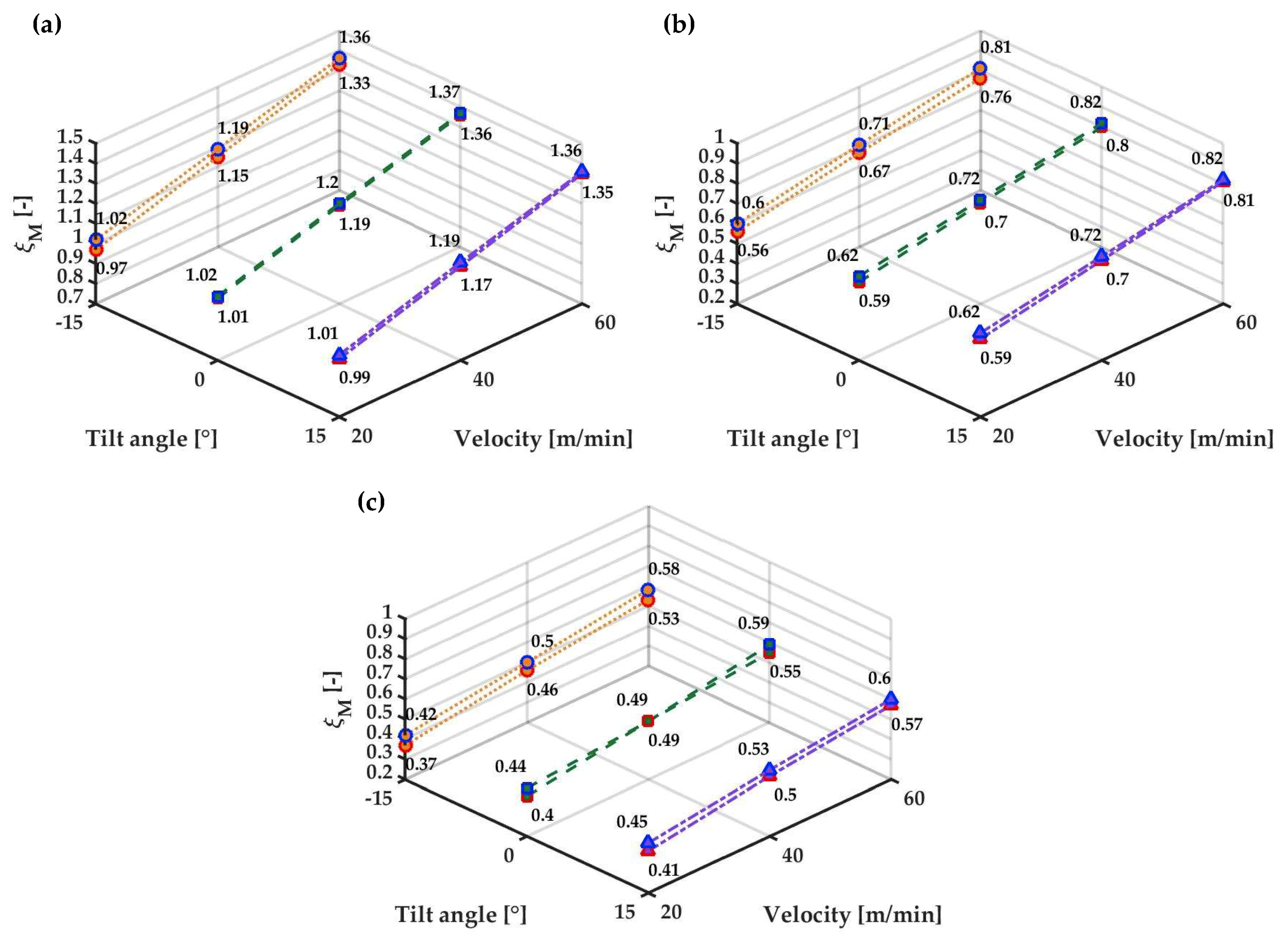
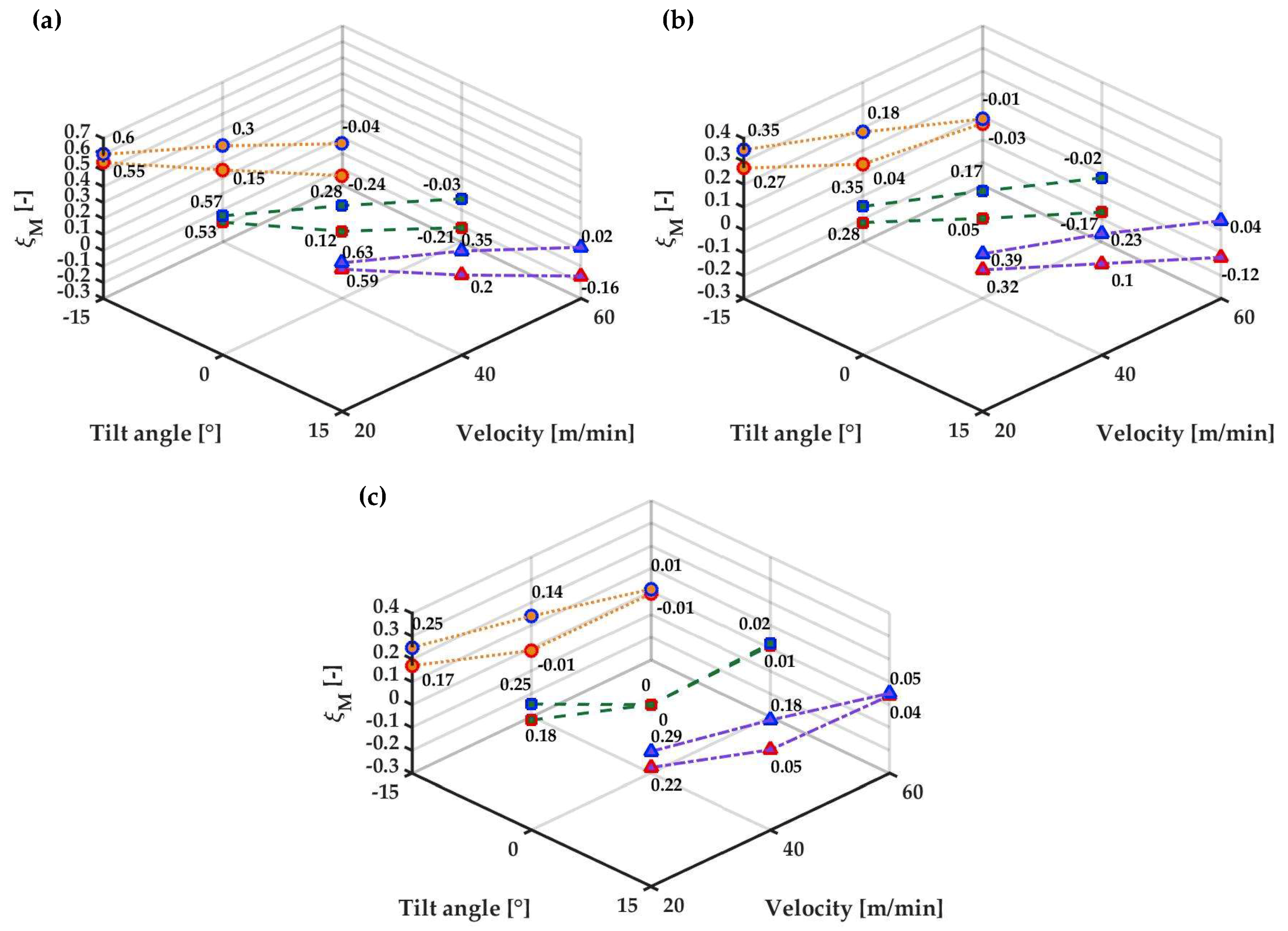
| AC Tilt Angle (°) | AC Temperature (°C) | AC/Ambient Flow Ratio (%) | Fabric Velocity (m/min) |
|---|---|---|---|
| −15 0 +15 | 15 | 3 5 7 | 0 |
| 20 | |||
| 70 | 40 | ||
| 60 |
| Blower Number (-) | Plate Total Area (m2) | Plate Open Area (m2) | Plate Porosity (%) |
|---|---|---|---|
| 12 | 0.7 | 0.0245 | 3.5 |
| AC Tilt Angle | AC Temperature | AC/Ambient Flow Ratio | Fabric Velocity |
|---|---|---|---|
| −15 0 +15 | C | L M H | V0 |
| V20 | |||
| W | V40 | ||
| V60 |
| Boundary | Mass Flow Rate (kg/(s*m)) | Total Pressure (Pa) | Total Temperature (K) | Static Pressure (Pa) |
|---|---|---|---|---|
| Ambient (Inlet) | 0.03093 | - | 288.15 | - |
| Blowers (Inlet) | 0.5588 | - | 473.15 | - |
| Extraction (Outlet) | - | - | - | 0 |
| Boundary | Mass Flow Rate (kg/(s·m)) | Total Pressure (Pa) | Total Temperature (K) | Static Pressure (Pa) |
|---|---|---|---|---|
| Ambient (Inlet) | 2.71 | 288.15 | ||
| Air curtains (Inlet) | 0.01856 (3%) | - | 288.15 or 343.15 | - |
| 0.03093 (5%) | - | 288.15 or 343.15 | - | |
| 0.04330 (7%) | - | 288.15 or 343.15 | - | |
| Blowers (Inlet) | 0.5588 | - | 473.15 | - |
| Extraction (Outlet) | - | - | - | 0 |
| Configuration | ξE for CS α (-) | ξE for CS β (-) | ξE for CS γ (-) | ξE for CS δ (-) |
|---|---|---|---|---|
| AC0WWMV20 | 0.09 | 0.59 | 0.28 | −0.22 |
| AC0WWMV40 | 0.20 | 0.70 | 0.05 | −0.45 |
| AC0WWMV60 | 0.30 | 0.80 | −0.17 | −0.67 |
| AC0WCMV20 | 0.08 | 0.57 | 0.36 | −0.14 |
| AC0WCMV40 | 0.19 | 0.69 | 0.18 | −0.32 |
| AC0WCMV40 | 0.28 | 0.78 | 0.01 | −0.49 |
| Configuration | ξE for CS α (-) | ξE for CS β (-) | ξE for CS γ (-) | ξE for CS δ (-) |
|---|---|---|---|---|
| AC0WWMV20 | 0.02 | 0.51 | 0.30 | −0.22 |
| AC0WWMV40 | 0.05 | 0.55 | 0.08 | −0.46 |
| AC0WWMV60 | 0.07 | 0.58 | −0.57 | −1.01 |
| AC0WCMV20 | 0.02 | 0.49 | - | - |
| AC0WCMV40 | 0.04 | 0.51 | - | - |
| AC0WCMV40 | 0.05 | 0.52 | - | - |
| Configuration | Average Temperature (K) | Temperature Ratio (-) | Mass Flow Rate ratio at CS β (-) | Mass Flow Rate Ratio at CS γ (-) |
|---|---|---|---|---|
| NOACV20 | 440.53 | - | - | - |
| NOACV40 | 442.05 | - | - | - |
| NOACV60 | 443.67 | - | - | - |
| AC0WWMV20 | 451.65 | 11.12 | 0.96 | 0.78 |
| AC0WWMV40 | 452.14 | 10.09 | 0.98 | 0.27 |
| AC0WWMV60 | 453.51 | 9.84 | 0.96 | 2.03 |
| AC0WCMV20 | 446.94 | 6.40 | 0.94 | 1.01 |
| AC0WCMV40 | 448.31 | 6.26 | 0.96 | 1.03 |
| AC0WCMV60 | 449.17 | 5.50 | 0.93 | −0.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciappi, L.; Fiaschi, D.; Manfrida, G.; Salvadori, S.; Smolka, J.; Talluri, L. Heat Recovery for a Textile Stenter: CFD Analysis of Air Curtain Benefits. Energies 2019, 12, 482. https://doi.org/10.3390/en12030482
Ciappi L, Fiaschi D, Manfrida G, Salvadori S, Smolka J, Talluri L. Heat Recovery for a Textile Stenter: CFD Analysis of Air Curtain Benefits. Energies. 2019; 12(3):482. https://doi.org/10.3390/en12030482
Chicago/Turabian StyleCiappi, Lorenzo, Daniele Fiaschi, Giampaolo Manfrida, Simone Salvadori, Jacek Smolka, and Lorenzo Talluri. 2019. "Heat Recovery for a Textile Stenter: CFD Analysis of Air Curtain Benefits" Energies 12, no. 3: 482. https://doi.org/10.3390/en12030482
APA StyleCiappi, L., Fiaschi, D., Manfrida, G., Salvadori, S., Smolka, J., & Talluri, L. (2019). Heat Recovery for a Textile Stenter: CFD Analysis of Air Curtain Benefits. Energies, 12(3), 482. https://doi.org/10.3390/en12030482









