Abstract
Single Inductor (SI) converters with the advantage of using one inductor for any number of inputs/outputs find wide applications in portable electronic gadgets and electrical vehicles. SI converters can be used in Single Input Multiple Output (SIMO) and Multiple Input Multiple Output (MIMO) configurations but they need controllers to achieve good transient and steady state responses, to improve the stability against load and line disturbances and to reduce cross regulation. Cross regulation is the change in an output voltage due to change in the load current at another output and it is an added constraint in SI converters. In this paper, Single Input Dual Output (SIDO) and Dual Input Dual Output (DIDO) converters with applications capable of handling high load current working in Continuous Conduction Mode (CCM) of operation are taken under study. Conventional multivariable PID and optimal Linear Quadratic Regulator (LQR) controllers are developed and their performances are compared for the above configurations to meet the desired objectives. Generalized mathematical models for SIMO and MIMO are developed and a Genetic Algorithm (GA) is used to find the parameters of a multivariable PID controller and the weighting matrices of optimal LQR where the objective function includes cross regulation as a constraint. The simulated responses reveal that LQR controller performs well for both the systems over multivariable PID controller and they are validated by hardware prototype model with the help of DT9834® Data Acquisition Module (DAQ). The methodologies used here generate a fresh dimension for the case of such converters in practical applications.
1. Introduction
A Single Input Multi Output (SIMO) and Multi Input Multi Output (MIMO) DC-DC converters have the ability to provide different voltage and current levels and eliminate the drawbacks of having bulky inductors for each output. MIMO converters can have two or more diversified renewable energy sources with variable dc voltage and current characteristics. The outputs of the converters can be configured either independently where all the output ports share the same ground or the outputs can be connected in series fashion. Both the converters can be operated either in Continuous Conduction Mode (CCM) or in Discontinuous Conduction Mode (DCM) and mode selection depends on the load current rating and the amount of ripples in the output voltages. In this paper, CCM mode capable of handling the large current load with lesser ripples is taken. Like all converters, compensators and/or controllers are essential to improve the time and frequency domain specifications with the additional constraint of reducing cross regulation. To achieve these goals different control techniques are available in the literature for both the converter types.
For SIMO converters, to achieve good regulation performance over wide load current and voltage ranges with fewer ripples and high efficiency, different control algorithms are developed based on the output voltages or inductor current. In reference [1], cross-regulation is minimized by operating in hysteresis mode with additional circuitry, but there is a reduction in efficiency due to the flow of current in the freewheeling switch. In reference [2], time multiplexing techniques to regulate the multiple output voltages and to reduce cross-regulation are proposed but the output voltages have higher amount of ripples. To reduce ripples and cross regulation, the zero current switching lagging leg is added which makes the circuit more complex [3]. In reference [4], the Single Inductor Dual Output (SIDO) boost converter with discrete pulse width modulation is proposed which occupies lesser area and operates at higher efficiency only when the system works for low power applications. In reference [5], to increase the voltage gain, two half bridge converters are formed in series manner with clamp circuit such that the soft switching is obtained with reduced stress on switches. Modelling of SIMO dc-dc converters in particular for two outputs is done in [6] and most of the researchers have used this model only to design the controllers for SIDO Buck converter [7]. Also, in reference [7], multivariable digital control for SIDO converter is designed using the model in [6] where a system open loop transfer function matrix is shaped by convex minimization method to decouple the system. In another research, an inductor current ripple-based modelling approach is proposed to model and analyze the converter accurately. The control, cross coupling, and cross regulation transfer functions, generated with the model has been portrayed in [8]. However, the procedure involved is very complex and lengthy. A ripple-based modelling of the SIDO buck converter is developed for cross derivative state feedback control methodology in [9]. The number of compensators required is two times that of the outputs and the parameters of the compensators are obtained using trial and error method. The algorithm used to develop a model is complex and limited to two outputs. The analysis is done only for SIDO system and there is no generalized mathematical model of SIMO and MIMO converters for ‘n’ number of outputs. This emphasis necessitates the development of a generalized mathematical model for SIMO dc-dc converter with n number of independent outputs considering the on-state losses of the switches. It helps to analyze the steady state and dynamic performance of the converter.
Electric vehicles, energy harvesting applications, and DC micro-grids are typical examples of MIMO system where the inputs can be from various sources and the loads will have different voltage/current specifications. MIMO converters are cost effective solutions and can be operated in DCM or CCM modes. In DCM, the limitation is with the maximum inductor current and thereby high-power applications are not possible. In reference [10], the topology is introduced to interface the multiple output dc-dc converters with diode clamped inverter but the detailed analysis on control strategies is not present. The analysis on the design of a multivariable controller for MIMO system is introduced in [11]. But the outputs are connected in a series manner and there is no generalized mathematical model for ‘n’ number of outputs. A linearized small signal ac model is developed for two outputs in which the outputs are connected in series configuration [11]. The above model has to include n + 2 number of variables for the design of controllers. Therefore, a new topology is developed in which the outputs are connected independently and share lesser number of switches.
To eliminate the complexity in designing controller for higher number of outputs, linear, non-linear and intelligent controllers separately in multi loop mode are proposed [12]. Naturally, multivariable controllers are suited for the SIMO and MIMO converters [13]. Multivariable control, which reduces the number of controllers used in the system, appears to be a promising technology for the targeted space restricted applications.
The suitability of multivariable control for the SIMO and MIMO systems with Evolutionary Algorithms can be found in [14] which uses a Artificial Bee Colony algorithm with variable population size. Its focus is mainly on the convergence of the algorithm for a Multivariable PID controller applied in a Distillation Column Systems, a 2 × 2 multivariate process with strong interactions between the inputs and outputs. Particle Swarm Optimization-based multivariable PID controller performance [15] is found to be better than the Ziegler Nicholas method for a MIMO process. A Twin Rotor System where LQR whose weighted matrix elements are found by a Bacterial Foraging Algorithm is shown to be better than a manually calculated/found weighting matrix [16]. In reference [17], a randomized algorithm is presented for the design of an optimal PID controller for MIMO systems such that the closed loop poles are placed at desired locations to obtain the desired performance specifications. Therefore, simplicity and availability of global optimization techniques to search for best parameters and design procedure using the model of the system are the compelling reasons for studying multivariable PID and optimal LQR for the SIMO and MIMO systems. Ninety percent of the controllers used are PID controllers which is most discussed, analyzed and tested with flexibility and robustness for most of the applications. Optimal LQR controller for MIMO systems are extensively studied in the literature and the superiority of the controller over other controllers are well documented [18].
In this paper, the simplified small signal mathematical models of SIMO and MIMO converters including on-state resistance of the switches are developed for n number of outputs. From these models, small signal models of the converter for any number of outputs can be obtained. These models also used to obtain the control inputs to output voltages and input voltages to output voltages transfer functions of both SIMO and MIMO dc-dc converters for any number of outputs. Here multivariable PID and optimal LQR controllers are developed for SIDO and DIDO converters. The parameters of these controllers are obtained with the help of GA based optimization tool using developed small signal models of the converter and reduction in the coupling between the outputs are done. Gershgorin bands drawn for the converters before and after adding the controller serve as a tool to show the amount of coupling between the outputs. The designed controllers are validated by using DT 9834® Data Acquisition Module. From both the simulated and hardware results, it is revealed that LQR performs well for both the systems.
2. Converter Description and Mathematical Modelling
2.1. System diagram and Modes of operations
The circuit diagram of the SIMO converter shown in Figure 1a includes ‘n’ number of outputs V1, V2 … Vn which are taken across loads R1, R2 … Rn and share the inductor L which gets charged from the battery Vin. The circuit diagram of the MIMO converter shown in Figure 1b includes a ‘n’ number of outputs V1, V2 … Vn taken across loads R1, R2 … Rn and share the inductor L which gets charged from the same number of inputs as Vin1, Vin2 … Vinn.
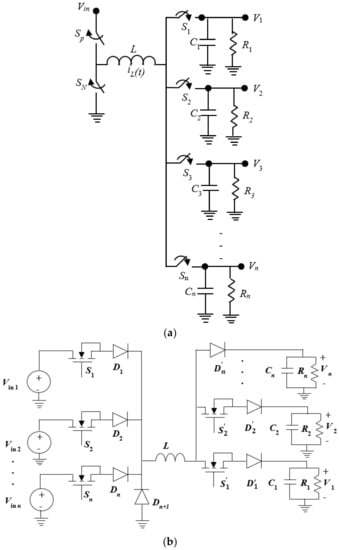
Figure 1.
(a) Single Input Multi Output dc-dc Converter (b) Multi Input Multi Output dc-dc Converter.
Continuous Conduction Mode of operation is selected for both the converters and the timing diagram of inductor current for (n + 1) modes of operations is shown in Figure 2. For one switching cycle in both the systems, inductor gets charged through respective outputs from sources and discharged through the n-th output.
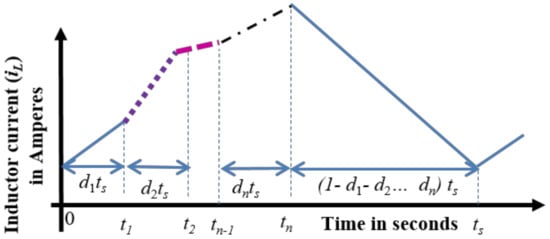
Figure 2.
Timing diagram of various modes of operations of SIMO and MIMO converters.
The state space description is used to develop mathematical model of non-linear system. With the help of the state space description of each switching interval and state space averaging technique, the state space averaged equations of dc-dc converters are developed. From this averaged model, linearized small signal ac model is developed. The state space model of the converter for each mode of operation is obtained using Kirchhoff’s voltage and current laws by considering n output voltages (v1, v2, v3 … vn) and inductor current (iL) as state variables. The duty cycles d1, d2, d3 … dn are independent control variables. The disturbances are observed at the input voltages and the load currents (i1, i2, i3 … in). R is the parameter included in the modelling of the converter to represent the on-state resistance of the conducting switches.
2.2. Average Model of the SIMO/MIMO DC-DC Converter
The averaging of the converter dynamics over an entire switching cycle is required as the converter switches among (n + 1) modes during each switching cycle. The procedure used to obtain the average state space model of SIMO and MIMO DC-DC converters is represented as a block diagram in Figure 3.
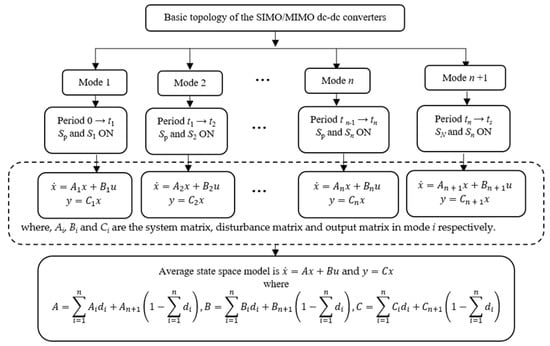
Figure 3.
Block diagram of average state space model.
The state space averaged model of the SIMO Buck converter is stated in Equations (1) and (2):
Equation (1) is known as state space equation and its output equation can be formulated as shown in Equation (2), where A (see Figure 3) is the system matrix of order p × p where p denotes the number of state variables B is the disturbance matrix of order p × m where m denotes the number of disturbance variables, and C is the output matrix of order n × p where n denotes the number of outputs, x is the state vector of order (p × 1), u is the disturbance vector of order (m × 1) and y is the output vector of order (n × 1).
2.3. Small Signal Perturbation and Linearization
The state space representation of the system stated in Equation (1) is non-linear as the matrices are the functions of the duty cycle di where i = 1, 2, 3 … n. Equations are non-linear because they involve multiplications of time varying quantities. The capacitor current depends on the product of the duty cycles and the low frequency component of the inductor current in one switching cycle [19]. Considering small perturbations around the equilibrium point, it becomes necessary to linearize the system equations. The independent control inputs and the disturbances observed at the input voltages and the load currents are considered to be time varying around their quiescent operating points. This linearized model helps to obtain the control inputs to outputs and disturbance variables to outputs transfer function.
The state vector and the output vector are represented as in Equation (3):
With the help of state space representation, the system can be perturbed and represented as Equation (4):
After removing the steady state DC values, Equation (5) is written by considering only the linear and non-linear terms. The perturbed output equation is given in Equation (6):
Similarly, after removing steady state DC values, the output equation can be stated as (7):
From the above analysis, the state space representation can be stated as Equation (8):
where, is system matrix of linearized system of order p × p, is the disturbance matrix of the linearized system of order p × m, is the output matrix of linearized system of order n × p and is the input matrix of linearized system of order p × n, where is the control input vector of order n × 1 and ]:
By using the expressions obtained from modes 1 to (n + 1), the small signal model of the system can be obtained as shown below:
The same procedure explained in Section 2.2 is used to formulate the steady state averaged model of MIMO dc-dc converter. The state space averaged model of the MIMO dc-dc converter is formulated in Equations (12) and (13) as:
The analysis that is carried out on SIMO in Section 2.3 is repeated for MIMO system and a small signal ac model is constructed at the quiescent operating point (I, V) assuming u and duty ratios to be some given quiescent value with small superimposed ac variations. The small signal model of the system can be represented as shown in Equations (14) and (15):
Equations (14) and (15) can be rewritten as
where, is system matrix of the linearized system of order p × p, is the disturbance matrix of the linearized system of order p × m, is the output matrix of linearized system of order n × p and is the input matrix of linearized system of order p × n. From this generalized mathematical model for ‘n’ number of outputs, the Small signal ac model for Single Input Dual Output (SIDO) and Dual Input Dual Output (DIDO) dc-dc converters can be obtained as in [20,21]. The specifications for both (SIDO) and (DIDO) are given in Table 1 and Table 2 respectively.

Table 1.
Specifications for SIDO converter.

Table 2.
Specifications for DIDO converter.
For the above specifications, using MATLAB–m file coding, the control inputs to their respective output voltages transfer functions for both SIDO and DIDO converters are obtained from the derived linearized small signal model.
For a SIDO converter, they are given in Equations (16) and (17):
For a DIDO converter, the output voltage with respect to duty ratio is given in Equation (18):
The output voltage with respect to duty ratio is represented in Equation (19):
3. Study on Coupling and Stability
Gershgorin and Relative Gain Array (RGA) are two techniques to identify the coupling between the outputs and control inputs. Gershgorin circle is drawn at each point of the Nyquist plot of the diagonal elements gii(s) with the following radius or where n is number of inputs and outputs to check for coupling where the coupling denotes the presence of the cross regulation. The set of circles drawn with above radius enclosing the locus of gii(ω) is called as Gershgorin bands. Gershgorin theorem reveals that the bands catch the unions of the Nyquist diagram and moreover helps to say that there will be as many Nyquist diagrams trapped in a region as many Gershgorin bands are there. The stability of the system is identified by counting the number of endings made by the bands around the point (−1, 0). If the bands are thin and exclude the origin then it is found that the system is diagonally dominant which is diagonalized as a de-coupled system [22]. Such Gershgorin bands are drawn for g11(s) and g22(s) of SIDO and DIDO converters and shown in Figure 4.
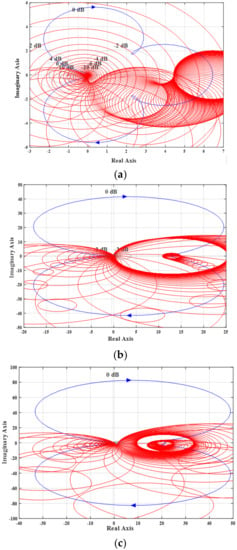
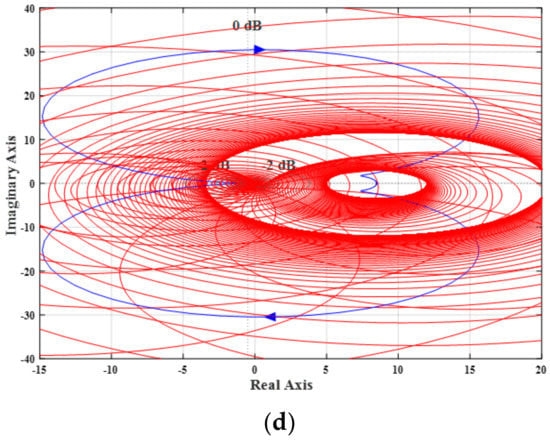
Figure 4.
Gershgorin bands of converters in open loop for SIDO (a) g11(s) (b) g12(s) and DIDO (c) g11(s) (d) g12(s).
It is found that the bands are enclosing the origin as the system is not diagonal dominance, that is, it’s a coupled system and hence a controller is required to make the system as decoupled. Moreover, RGA, denoted as ⋏ is used as a parameter to measure the inputs and outputs interactions. RGA for both the systems are given in Equations (20) and (21):
From Equations (20) and (21), it is found that both the matrices are not diagonal which indicates that the output one gets varied due to change in both the control inputs.
4. System Realization in Matlab and Hardware
The interfacing between the prototype models and the controller developed in MATLAB® SIMULINK® are done with the help of data acquisition module DT 9834®. The hardware setup is shown in Figure 5.

Figure 5.
Laboratory setup (a) SIDO (b) DIDO.
Data Acquisition (DAQ) module is a high speed, high performance USB based device compatible with LABVIEW® and MATLAB® software packages. The output voltages of the converter are given to the analog input of the data acquisition module which is interfaced to MATLAB/Simulink®. Then the output voltages are compared with the reference voltages and the error signal is applied to the compensator developed in MATLAB/Simulink® and the control voltage signals are applied to the analog output of the DAQ module. The pulse width modulation generator and driver circuit avail the data from DAQ module to generate the pulses for the MOSFET switches in the power module. Figure 5a,b show the laboratory setups of SIDO and DIDO converters interfaced with DT9834® DAQ module respectively.
5. Genetic Algorithms for Finding Parameters of Multivariable PID and LQR Controllers
Genetic Algorithm (GA) is an optimization tool which mimics natural evolution in finding the best solution. It is useful when the search space is large and unknown with local minima’s [23]. It starts with a set of solutions (population) represented as bit strings or rational numbers and by processes such as crossover, mutation and selection evolves to a better solution. In this paper, the population is rational numbers and the tuning of GA process is done for fast convergence as per the steps followed in [24]. SIMO and MIMO are non-linear systems where tuning of controller parameters becomes extremely difficult when the number of inputs and/or outputs increases. They have mutual interferences which have to be nullified and tuning of controller parameters has to decouple the same. In these systems, GA is used to find cyclic matrix of multivariable PID and weighting matrix of optimal LQR controllers. These matrices are multimodal in nature with many dimensions [24] and this is where conventional optimization techniques fail whereas global optimization algorithms such as GA accommodate these constraints [25,26]. In addition, GA are computationally simple and have inherent parallelism. Successful applications are further seen related to multivariable PID and optimal LQR for MIMO process in [27,28,29].
The objective function can be either Integral Square Error (ISE), Integral Absolute Error (IAE), Integrated Time Absolute Error (ITAE) or a combination of all and has to be minimized. The objective function is the sum of various parameters related to time response such as Rise Time, Settling Time, Overshoot, Peak Time and Undershoot [30]. The parameters used to study the performance analysis of the controllers are Overshoot, Undershoot, Settling Time, Ripples and Cross Regulation. Overshoot, Undershoot and Ripples relate to the quality of the response whereas Settling Time measures the speed of the response. In SIMO and MIMO converters the main parameter to consider is the Cross Regulation which is change of desired level in an output due to disturbance in other outputs or inputs. Each parameter has to be given a weight (Wn) since some parameters values are relatively very high and dominate the convergence and weights are found out by trial and error method. Another method is running the GA with few dominant parameters and then stopping the GA and continuing it again with all parameters from the population until it is stopped:
Equation (22) gives the objective function taken for this problem in which the overshoot_2 (which is cross regulation) is taken as the dominant factor.
6. Controllers for SIMO and MIMO Converters
SIMO and MIMO converters are multivariable systems as they have n number of control inputs and n number of outputs. A multivariable PID controller has the parameters Kp, Ki and Kd as matrices of order n × n. In literature, these parameters (proportional, integral and derivative matrices) of the conventional multivariable PID controller are obtained using trial and error procedures, but in this paper, the generalized design procedure using the proposed mathematical model is developed to tune the parameters of the controllers with the help of optimization technique. Multivariable PID controller increases the order of the system from number of state variables to the number of summations of state variables and output variables. Linear Quadratic Regulator (LQR) is an optimal control method in which the system dynamics represented as set of linear differential equations. In LQR controller, a cost function which is the deviation from the desired setting of the process/plant is quadratic in nature. The advantage of LQR controller is generation of a state feedback gain matrix K which leads to keeping the closed loop and original plant/process to have same order. LQR also guarantees phase margin greater than 60° which is a demand in design of good controllers. The main challenge in the LQR controller is the determination of cost matrices Q and R. In this paper, the generalized design procedure using the proposed mathematical model is developed to tune the parameters of the weighting matrix Q with the help of optimization technique.
Multivariable PID Control
The designed PID controller is shown as a block diagram in Figure 6 in which the integral term acts on the error (desir–d-actual) and the proportional and derivative terms act on the output (actual). Due to the addition of PID controller the order of the system is increased from p to (n + p). The additional state variable is the integral of error:
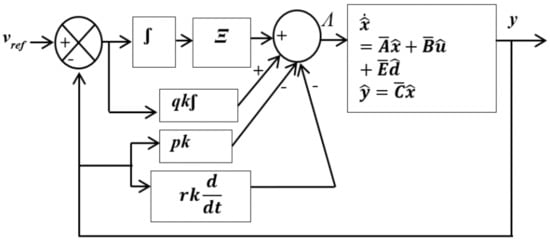
Figure 6.
Block diagram representation of the multivariable PID controller.
Therefore, the derivatives of the state variables are the errors of the outputs and given as Equation (24):
so, the open loop system is augmented by the n numbers of integrators as shown in Equations (25) and (26):
To meet the desired objectives the following conditions have to be met [13]:
- The augmented system matrix should be controllable and observable.
- The controller matrix is restricted to have unit rank.
- The augmented system matrix should be cyclic which is made possible by initial application of control law given in Equation (27):
The new system matrix is now cyclic and given by Equation (29):
7. Design Algorithm
Let λ1, λ2 … λn+p be the desired poles. The desired characteristic polynomial is:
where and
Equating the Equations (30) and (31), the parameters of the PID controller can be obtained. The (n + p)th order state model of the closed loop system is then given by:
The design procedure is summarized as follows:
- (1)
- The system description (, , ) and the desired pole positions λ1, λ2 … λn + p are obtained from the mathematical model.
- (2)
- Genetic Algorithm-based optimization is used to obtain the value of Ξ matrix.
- (3)
- Develop a coding procedure to find the control signal Λ.
- (4)
- Check the response of the system for a unit step input.
- (5)
- If desired objectives are not obtained, tuning of GA is performed again to obtain the new value of Ξ either by changing the values of closed loop poles or by k matrix.
The matrix found for SIDO is given by the Equation (34):
The corresponding Kp, Ki and Kd values obtained are given in Equations (34)–(36), respectively:
The Multivariable PID controller is able to make the closed loop poles to lie at the following locations: P1 = (−1500 + 1000i), P2 = (−1500 − 1000i), P3 = (−1000 + 200i), P4 = (−1000 − 200i) and P5 = (−500).
Similarly, the matrix found for DIDO is given by the Equation (38):
The corresponding Kp, Ki and Kd values derived from the Q matrix are given in Equations (39)–(41):
Similarly, the closed loop poles obtained after adding multivariable PID controller are given below: P1 = (−500 + 2171.5i), P2 = (−500 − 2171.5i), P3 = (−335.9 + 571.1i), P4 = (−335.9 − 571.1i) and P5 = (−806.3).
The response of the unit step function for the controllers taken into study using MATLAB® m-file coding is shown in Figure 7a,b for SIDO and DIDO, respectively.

Figure 7.
Response of unit step function (a) Multivariable PID – SIDO converter (b) Multivariable PID–DIDO converter.
Figure 7a,b reveal that the system has become decoupled one due to the addition of multivariable PID controller. Figure 7a (i) and (iv) and Figure 7b (i) and (iv) show that both the output voltages V1 and V2 obey only for their respective control inputs d1 and d2 respectively. Figure 7a (ii) and (iii) and Figure 7b (ii) and (iii) reveal that the output voltages V1 and V2 do not respond to the control inputs d2 and d1 respectively and produce zero outputs as the system has become decoupled one. The converters and the multivariable PID controller are developed using discrete components available in MATLAB SIMULINK®. The results are shown in Figure 8 for SIDO converter and in Figure 9 for DIDO converter.
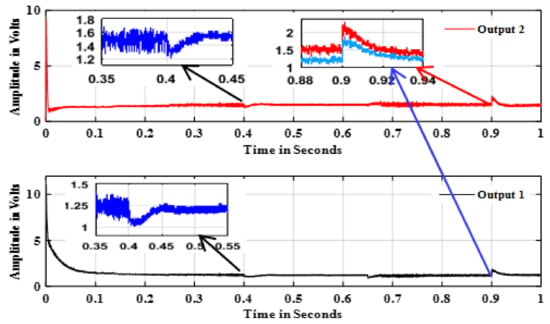
Figure 8.
Closed loop response of the SIDO converter with Multivariable PID controller with load and line disturbances.
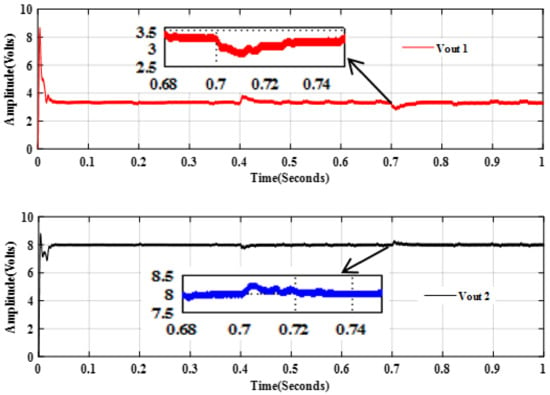
Figure 9.
Closed loop response of the DIDO converter with Multivariable PID controller with load and line disturbances.
Load disturbance is given at t = 0.4 s in output 2 by increasing the current from 0.5 A to 1.05 A and the output 2 takes 0.03 s to come back to the value of 1.5 volts. The output 1 has undershoot and takes 0.05 s to come back to the same value. Load disturbance is given at t = 0.65 s in output 1 by increasing the current from 0.3 A to 0.65 A and the output 2 has overshoot and comes back to the same value with the time period of 0.03 s. The output 1 has undershoot and comes back to the same value in 0.03 s. The supply voltage is increased to 15 V from 12 V and both the outputs have overshoot of increase in 1 V and they settle within 0.03 s. Thus, from Figure 8, it is evident that the cross regulation is minimized. Good dynamic response (except peak overshoot) is obtained from the multivariable PID controller.
Similarly, for DIDO converters, load disturbance is given at t = 0.4 s in output 2 by increasing the current from 2 A to 2.5 A and the output 1 takes 0.017 s to come back to the value of 3.3 Volts. The output 2 has undershoot and takes 0.032 s to come back to the value of 8 V. Load disturbance is given at t = 0.7 s in output 1 by increasing the current from 2 A to 2.5 A and the output 2 takes 0.02 s to return to the value of 8 V. The output 1 has undershoot and takes 0.03 s to return to the same value.
Optimal LQR Controller
Figure 10 shows the block diagram representation of the closed loop system with LQR controller, where the control signal is:
where k is the feedback gain matrix of order d × p and ki is the integral matrix of order n × d. The state space model of the closed loop system is given as:
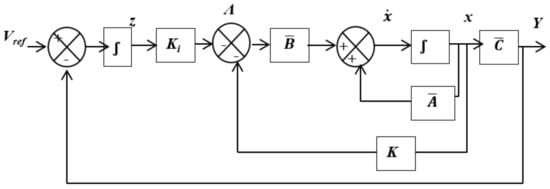
Figure 10.
Block diagram representation of multivariable LQR controllers.
The design procedure can be summarized as follows:
- The augmented system matrices are entered and their controllability and observability are checked.
- The values of Q and R are obtained using GA based optimization technique.
- The value of Ki is assigned based on the knowledge from PID Controller
- Algorithm is developed to find the values of the state feedback gain matrix, which is in the order of p × n and check the response for a unit step input.
- If desired objectives are not met, tuning of GA is performed.
The K matrix found for SIDO and is given by the Equation (46):
The corresponding Ki value used to derive K matrix and given as Equation (47):
Similarly, the K matrix found is for DIDO and given by the Equation (48):
The corresponding Ki value used Q matrix and given as Equation (49):
The response of the unit step function for the controllers taken into study using MATLAB® m-file coding is shown in Figure 11a,b for SIDO and DIDO, respectively.
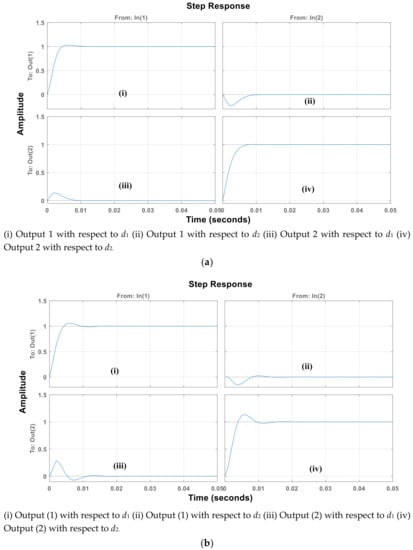
Figure 11.
Response of unit step function (a) SIDO (b) DIDO converters.
Figure 11a,b reveal that both the output voltages obey only for their respective control inputs due to the addition of Optimal LQR controller and the outputs are zero due to other inputs. The converters and the optimal LQR controller are developed using discrete components available in MATLAB SIMULINK®. The results are shown in Figure 12 for the SIDO converter and in Figure 13 for the DIDO converter.
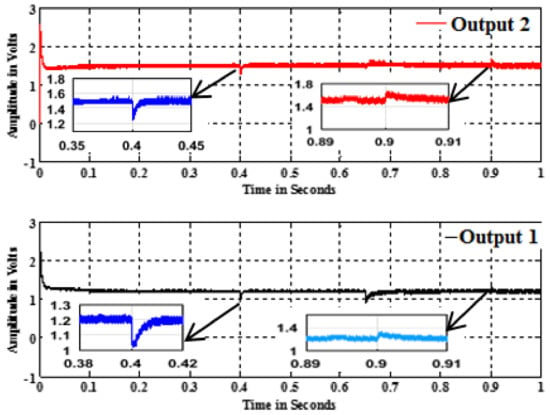
Figure 12.
Closed loop response of the SIDO converter with LQR controller with load disturbances.
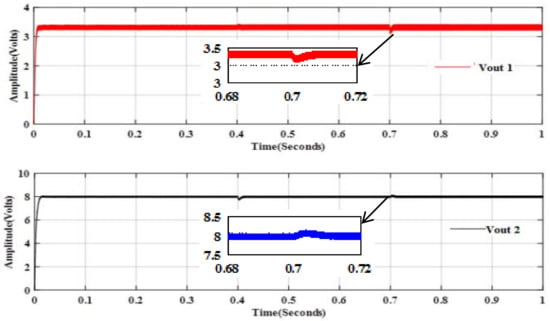
Figure 13.
Closed loop response of the DIDO converter with LQR controller with load disturbances.
The SIDO system performance for load disturbances is given in Figure 12. Load disturbance is given at t = 0.4 s in output 2 by increasing the current from 0.5 A to 1.05 A and the output 2 takes 0.01 s to revert to the value of 1.5 V. Output 1 has the undershoot and takes 0.01 s to revert to the same value of 1.2 V. Load disturbance is given at t = 0.65 s in output 1 by increasing the current from 0.3 A to 0.6 A and the output 2 has overshoot and comes back to the same value with the time period of 0.005 s. Output 1 has undershoot and comes back to the same value in 0.02 s. The supply voltage is increased to 15 V from 12 V and both the outputs have overshoot increase of 0. 1 V and they settle within 0.003 s.
The DIDO system performance for load disturbances is given in Figure 13. Load disturbance is given at t = 0.4 s in output 2 when the current is increased from 2 A to 2.5 A and the output 1 has overshoot and takes 0.007 s to come back to the value of 3.3 Volts. The output 2 has undershoot and takes 0.003 s to come back to the value of 8 V. Load disturbance is injected at t = 0.7 s in output 1 when the current is increased from 2 A to 2.5 A and the output 1 has undershoot and it takes 0.01 s to come back to the value of 3.3 Volts. The output 2 has overshoot and takes 0.005 s to return to the same value.
8. Performance Comparison
Performance comparison of Multivariable PID and Optimal LQR controllers for SIDO and DIDO are done in terms of Settling Time, Ripples and Cross Regulation. Table 3 clearly indicates the amount of cross regulation in output 2 when load disturbance is given at output 1 and proves that LQR controller performs well for both the converters.

Table 3.
Cross regulation analysis for multivariable PID and LQR controller.
Figure 14 and Figure 15 show the bar graph which indicates the settling time and ripple of both the converters respectively when both multivariable PID and LQR controllers are used at the operating point.
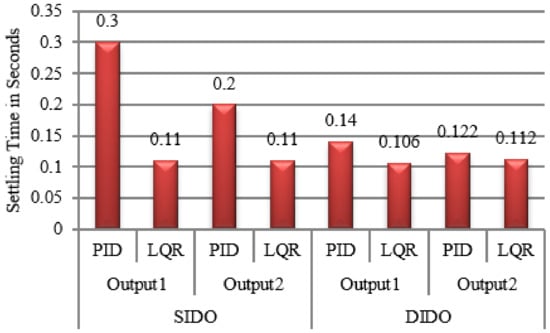
Figure 14.
Performance comparison of SIDO and DIDO Converters with LQR and PID controllers.
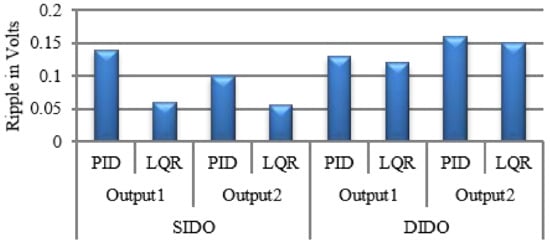
Figure 15.
Performance comparison of SIDO and DIDO Converter with LQR and PID controllers.
The graph clearly says that settling time is comparatively less when LQR controller is used at the desired operating point.
From Figure 15, it is clearly found that the ripples are low for LQR. Table 3 clearly indicates that the cross regulation between the outputs is reduced for LQR controller. In terms of peak overshoot, the output voltages have less amount of peak overshoot when LQR controller is used. As the LQR controller performs well for both the converters in terms of settling time, ripple and cross regulation, the simulated results are validated with the help of DAQ module. Figure 16a,b show the validation of the simulated results with the prototype model of the converters using DAQ module.
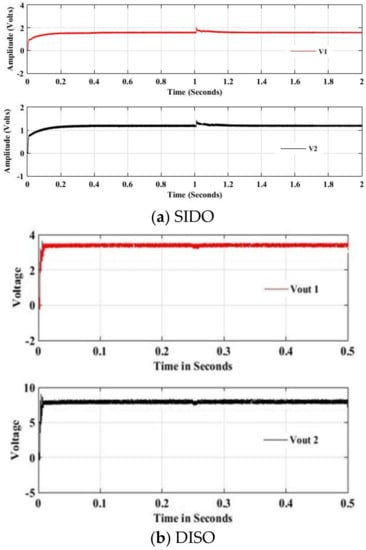
Figure 16.
Output Voltages Responses from prototype model of the converters for LQR controller with load disturbances.
Figure 16a clearly shows that the output voltages have very good transient responses and minimal cross regulation of 0.1 V increase at output 2 when load disturbance is given at t = 1 s in output 1 and comes back to the operating point within a time period of fewer than 5 milliseconds. The Figure 16b reveals that the simulation results of the DIDO converter with LQR controller in Figure 13 is validated. Figure 17 shows the Gershgorin bands of the transfer function matrix with LQR optimal controllers.
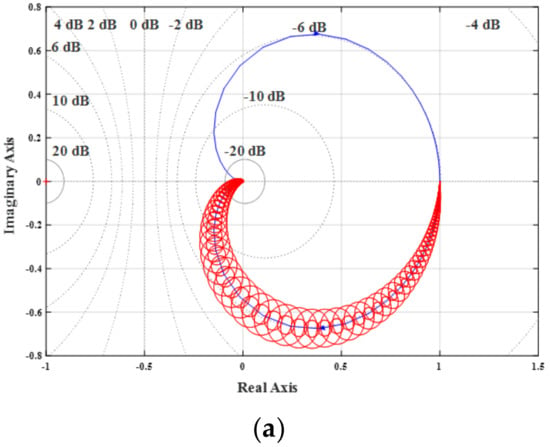
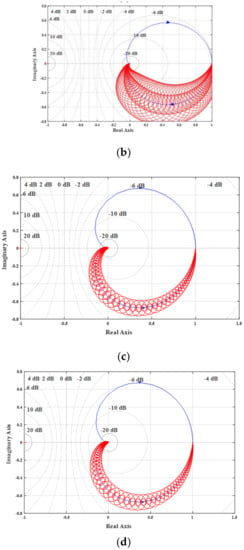
Figure 17.
Gershgorin bands of converters with controller for SIDO (a) g11(s) (b) g12(s) and DIDO (c) g11(s) (d) g12(s).
It is found that the system is diagonal dominance as the bands have become narrower and moreover the system has become stable at all frequencies. Again, RGA is used as a parameter to measure the inputs and outputs interactions. RGA for both the systems is given in Equation (50):
As the RGA matrix for both the systems is diagonal, the system has become decoupled due to the addition of a controller. This implies that the cross regulation is minimized using LQR controller.
9. Conclusions
In this paper, Single Inductor Single Input, Multiple Inputs/Outputs systems are analyzed. To design the controllers and to determine the coupling between the outputs, the linearized mathematical models are developed using state space averaging technique for both the converters with ‘n’ number of outputs including the on-state resistance of the switches. Gershgorin bands-based analysis of Single Input Dual Output and Dual Input Dual Output configurations reveal the need for controllers. Multivariable PID and LQR controllers naturally suit the configurations and their parameters are found by Genetic Algorithms. In these systems, GA is used to find cyclic matrix of multivariable PID and weighting matrix of optimal LQR controllers. Even though the controller is centralized, the design procedure involved is very simple and can be applied to any number of outputs as the generalized mathematical model is proposed. The designs are simulated and prototyped as well. It is found that optimal LQR controller performs better than multivariable PID controller in terms of settling time and ripple. The cross regulation in the output voltages is reduced with both the controllers but it is almost negligible for LQR controller. The hardware prototype assembled with the aid of a DT9834® Data Acquisition Module confirms the MATLAB/SIMULINK® simulations.
Author Contributions
S.A.L. conceptualized the problem and provided the methodology and investigated on a real hardware. The results and original draft were also prepared. N.S. reviewed and edited the manuscript and provided valuable insights in hardware design. K.V. supervised the research.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, M.; Chen, K. Single-inductor multi-output (SIMO) DC–DC converters with high light-load efficiency and minimized cross-regulation for portable devices. IEEE J. Sol. State Circuits 2009, 44, 1099–1111. [Google Scholar] [CrossRef]
- Pizzutelli, A.; Ghioni, M. Novel control technique for single inductor multiple output converters operating in CCM with reduced cross-regulation. In Proceedings of the 23rd Annual IEEE Applied Power Electronics Conference and Exposition 2008 (APEC ’08), Austin, TX, USA, 24–28 February 2008; pp. 1502–1507. [Google Scholar]
- Chen, Y.; Kang, Y.; Nie, S.; Pei, X. The multiple-output DC–DC converter with shared ZCS lagging leg. IEEE Trans. Power Electron. 2011, 26, 2278–2294. [Google Scholar] [CrossRef]
- Park, Y.J.; Khan, Z.H.N.; Oh, S.J.; Jang, B.G.; Ahmad, N.; Khan, D.; Abbasizadeh, H.; Shah, S.A.A.; Pu, Y.G.; Hwang, K.C.; et al. Single inductor-multiple output DPWM DC–DC boost converter with a high efficiency and small area. Energies 2018, 11, 725. [Google Scholar] [CrossRef]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O. A soft-switched DC/DC converter using integrated dual half-bridge with high voltage gain and low voltage stress for DC microgrid applications. Inventions 2018, 3, 63. [Google Scholar] [CrossRef]
- Lin, K.; Huang, C.; Chen, D.; Liu, K. Modeling and design of feedback loops for a voltage-mode single-inductor dual-output buck converter. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3389–3395. [Google Scholar]
- Dasika, D.; Bahrani, B.; Saeedifard, M.; Karimi, A.; Rufer, A. Multivariable control of single-inductor dual-output buck converters. IEEE Trans. Power Electron. 2014, 29, 2061–2070. [Google Scholar] [CrossRef]
- Patra, P.; Patra, A.; Misra, N. A single-inductor multiple-output switcher with simultaneous buck, boost, and inverted outputs. IEEE Trans. Power Electron. 2012, 27, 1936–1951. [Google Scholar] [CrossRef]
- Patra, P.; Ghosh, J.; Patra, A. Control scheme for reduced cross-regulation in single-inductor multiple-output DC–DC converters. IEEE Trans. Ind. Electron. 2013, 60, 5095–5104. [Google Scholar] [CrossRef]
- Nami, A.; Zare, F.; Ghosh, A.; Blaabjerg, F. Multiple-output DC–DC converters based on diode-clamped converters configuration: Topology and control strategy. IET Power Electron. 2010, 3, 197–208. [Google Scholar] [CrossRef]
- Behjati, H.; Davoudi, A. A multiple-input multiple-output DC–DC converter. IEEE Trans. Ind. Appl. 2013, 49, 1464–1480. [Google Scholar] [CrossRef]
- Lindiya, S.A.; Palani, S.; Vijayarekha, K. Multi loop controllers for single inductor multiple output DC–DC buck converters—A comparative study. Int. J. Control Autom. 2017, 10, 89–104. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control Analysis and Design, 2nd ed.; John Wiley & Sons: Chichester, UK, 1996; ISBN 978-0-470-01167-6. [Google Scholar]
- Elkhateeb, N.A.; Badr, R.I. Optimal design of multivariable controller for nonlinear systems using variable population artificial bee colony algorithm. WSEAS Trans. Syst. Control 2016, 11, 12–19. [Google Scholar]
- Taeib, A.; Lateif, A.; Chaari, A. A PSO approach for optimum design of multivariable PID controller for nonlinear systems. Eng. Technol. 2013, 2, 206–210. [Google Scholar]
- Agarwal, A.K. Optimal Controller Design for Twin Rotor MIMO System. Master’s Tech Thesis, National Institute of Technology, Rourkela, India, June 2014. Available online: http://ethesis.nitrkl.ac.in/5443/1/211EE3333.pdf (accessed on 3 March 2016).
- Peretz, Y. A randomized algorithm for optimal PID controllers. Algorithms 2018, 11, 81. [Google Scholar] [CrossRef]
- Phillips, F.S. Optimal Control of Twin Rotor MIMO System using LQR with Integral Action. In Proceedings of the World Automation Congress, Waikoloa, HI, USA, 3–7 August 2014; pp. 114–119. [Google Scholar]
- Erickson, R.; Maksimović, D. Fundamentals of Power Electronics; Kluwer Academic: Norwell, MA, USA, 2001; ISBN 978-0-306-48048-5. [Google Scholar]
- Lindiya, S.A.; Palani, S.; Vijayarekha, K. A simplified small signal model of a non-ideal single inductor multiple output buck converter. Int. Rev. Model. Simul. 2015, 8, 599–609. [Google Scholar] [CrossRef]
- Lindiya, S.A.; Palani, S.; Vijayarekha, K. A reduced switch count model for a multi input multi output DC-DC buck converter. In Proceedings of the IEEE Conference PESTSE 2018-Power and Energy System: Towards Sustainable Energy, Bengaluru, India, 18–20 January 2018. [Google Scholar]
- Vivero, O.; Liceaga-Castro, J. MIMO toolbox for MATLAB. In Proceedings of the Annual IEEE Student Paper Conference, Aalborg, Denmark, 15–26 February 2008; pp. 1–5. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Babu, S.P.K.; Salleh, M.F.M.; Ghani, F. Reduced complexity optimum detector for Block Data Transmission Systems. IEICE Electron. Express. 2009, 6, 1649–1655. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic Algorithms in Control Systems Engineering. In Proceedings of the 12th IFAC Triennial World Congress, Sydney, Australia, 18–23 July 1993; pp. 605–612. [Google Scholar]
- Hunt, K.J. Optimal control system synthesis with genetic algorithms. In Parallel Problem Solving from Nature 2; Männer, R., Manderick, B., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; pp. 381–389. [Google Scholar]
- Saptarshi, D.; Indranil, P.; Kaushik, H.; Shantanu, D.; Amitava, G. LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index. Appl. Math. Model. 2013, 37, 4253–4268. [Google Scholar]
- Arruda, L.V.R.; Swiech, M.C.S.; Delgado, M.R.B.; Neves, F., Jr. PID control of MIMO process based on rank niching genetic algorithm. Appl. Intell. 2008, 29, 290–305. [Google Scholar] [CrossRef]
- Wael, N.A.; Barry, G. Genetic algorithm optimization of PID controllers for a multivariable process. Int. J. Recent Contrib. Eng. Sci. IT (iJES) 2017, 5, 77–96. [Google Scholar]
- Mohammadloo, S.; Alizadeh, M.; Jafari, M. Multivariable autopilot design for sounding rockets using intelligent Eigen structure Assignment technique. Int. J. Control Autom. Syst. 2014, 12, 208–219. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).