100 Years of Symmetrical Components
Abstract
:1. Introduction
2. Formulations of the Fortescue Transformation
2.1. Symmetrical Components for Polyphase Systems
2.2. Instantaneous Symmetrical Components
2.3. Generalized Symmetrical Components
3. Applications to Power and Distribution System Analysis
4. Applications to Harmonic Analysis
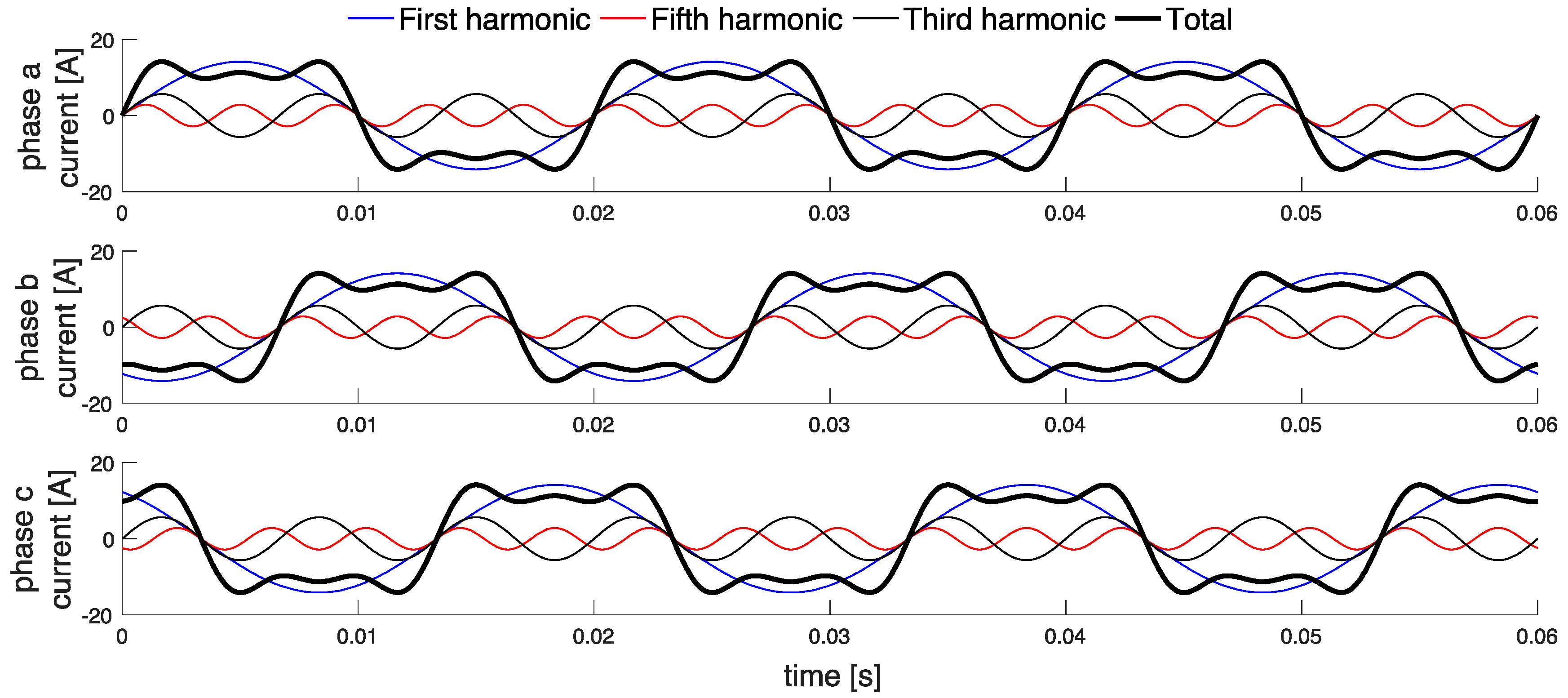
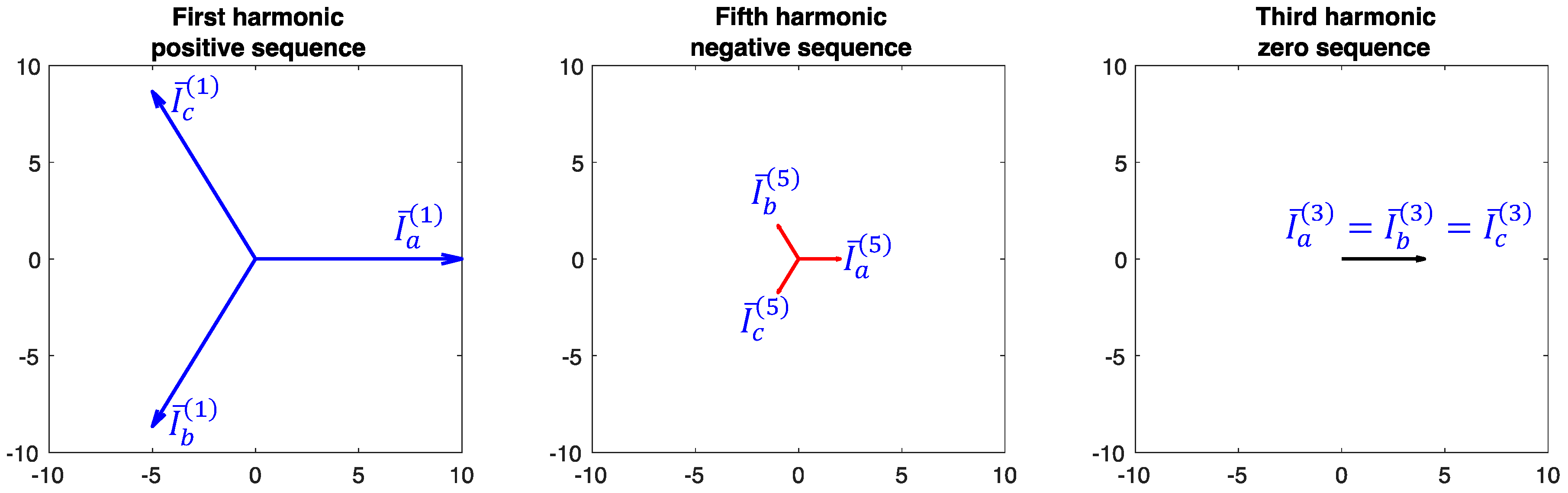
4.1. Symmetrical Components and Harmonics
4.2. Extension to Interharmonics
5. Recent Applications of the Fortescue Transformation
5.1. Electrical Machines
5.2. Distribution Systems with Distributed Energy Resources
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fortescue, C.L. Method of symmetrical co-ordinates applied to the solution of poly-phase networks (with discussion). Presented at the 34th Annual Convention of the AIEE (American Institute of Electrical Engineers), Atlantic City, NJ, USA, 28 June 1918; Volume 37, pp. 1027–1140. [Google Scholar]
- Wagner, C.F.; Butler, J.W.; Crary, S.B.; Hobson, J.E.; Huntington, E.K.; Johnson, A.A.; Kroneberg, A.A.; Miller, M.C.; Sels, H.K.; Trueblood, H.M. Silver anniversary of symmetrical components. Electr. Eng. 1943, 62, 294–295. [Google Scholar]
- Brittain, J.E.; Charles, L.G. Fortescue and the method of symmetrical components [Scanning the Past]. Proc. IEEE 1998, 86, 1020–1021. [Google Scholar] [CrossRef]
- Furfari, F.A. Charles LeGeyt Fortescue and the method of symmetrical components. IEEE Ind. Appl. Mag. 2002, 8, 7–9. [Google Scholar] [CrossRef]
- Kilgore, L.A. Calculation of Synchronous Machine Constants- Reactances and Time Constants Affecting Transient Characteristics. Trans. Am. Inst. Electr. Eng. 1931, 50, 1201–1213. [Google Scholar] [CrossRef]
- Stokvis, M.L.G. Sur la création des harmoniques 3 dans les alternateurs par suite du déséquilibrage des phases. In Proceedings of the Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences, Paris, France, 15 June 1914; Volume 159, p. 46. [Google Scholar]
- Fortescue, C.L. Polyphase Power Representation by Means of Symmetrical Coordinates. Trans. Am. Inst. Electr. Eng. 1920, 39, 1481–1484. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Electromagnetic Compatibility (EMC)—Environment—Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Low-Voltage Power Supply Systems; Standard IEC 61000-2-2; IEC: Geneva, Switzerland, 2002. [Google Scholar]
- Wagner, C.F.; Evans, R.D. Symmetrical Components; Mc-Graw-Hill: New York, NY, USA, 1933. [Google Scholar]
- Kimbark, E.W. Symmetrical-component impedance notation. Electr. Eng. 1938, 57, 431. [Google Scholar] [CrossRef]
- Pipes, L.A. Transient analysis of symmetrical networks by the method of symmetrical components. Electr. Eng. 1940, 59, 457–459. [Google Scholar] [CrossRef]
- Pipes, L.A. Discussion of “Transient analysis of symmetrical networks by the method of symmetrical components”. Electr. Eng. 1940, 59, 1107–1110. [Google Scholar] [CrossRef]
- Villamagna, N.; Crossley, P.A. A CT saturation detection algorithm using symmetrical components for current differential protection. IEEE Trans. Power Deliv. 2006, 21, 38–45. [Google Scholar] [CrossRef]
- Phadke, A.G.; Ibrahim, M.; Hlibka, T. Fundamental basis for distance relaying with symmetrical components. IEEE Trans. Power Appar. Syst. 1977, 96, 635–646. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S.; Adamiak, M.G. A New Measurement Technique for Tracking Voltage Phasors, Local System Frequency, and Rate of Change of Frequency. IEEE Trans. Power Appar. Syst. 1983, 102, 1025–1038. [Google Scholar] [CrossRef]
- Degens, A.J. Microprocessor-implemented digital filters for the calculation of symmetrical components. IEE Proc. C Gener. Transm. Distrib. 1982, 129, 111–118. [Google Scholar] [CrossRef]
- Sharma, P.; Ahson, S.I.; Henry, J. Microprocessor implementation of fast Walsh-Hadamard transform for calculation of symmetrical components. Proc. IEEE 1988, 76, 1385–1388. [Google Scholar] [CrossRef]
- Yazdani, D.; Mojiri, M.; Bakhshai, A.; Joós, G. A Fast and Accurate Synchronization Technique for Extraction of Symmetrical Components. IEEE Trans. Power Electron. 2009, 24, 674–684. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M.E. On the application of wavelet transform for symmetrical components computations in the presence of stationary and non-stationary power quality disturbances. Electr. Power Syst. Res. 2011, 81, 1373–1380. [Google Scholar] [CrossRef]
- Petit, M.; Le Pivert, X.; Garcia-Santander, L. Directional relays without voltage sensors for distribution networks with distributed generation: Use of symmetrical components. Electr. Power Syst. Res. 2010, 80, 1222–1228. [Google Scholar] [CrossRef]
- Naidoo, R.; Pillay, P.; Visser, J.; Bansal, R.C.; Mbungu, N.T. An adaptive method of symmetrical component estimation. Electr. Power Syst. Res. 2018, 158, 45–55. [Google Scholar] [CrossRef]
- Das, J.C. Understanding Symmetrical Components for Power System Modeling, 1st ed.; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- Lewis Blackburn, J. Symmetrical Components for Power Systems Engineering; Marcel Dekker: New York, NY, USA, 1993. [Google Scholar]
- Yeung, K.S. A New Look at the Method of Symmetrical Components. IEEE Trans. Educ. 1983, 26, 68–70. [Google Scholar]
- Lyon, W.V. Transient Analysis of Alternating-Current Machinery; John Wiley: New York, NY, USA, 1954. [Google Scholar]
- Leva, S. Power Network Asymmetrical Faults Analysis Using Instantaneous Symmetrical Components. J. Electromagn. Anal. Appl. 2009, 1, 205–213. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Karimi, H. Processing of Symmetrical Components in Time-Domain. IEEE Trans. Power Syst. 2007, 22, 572–579. [Google Scholar] [CrossRef]
- Paap, G.C. Symmetrical components in the time domain and their application to power network calculations. IEEE Trans. Power Syst. 2000, 15, 522–528. [Google Scholar] [CrossRef] [Green Version]
- Stankovic, A.M.; Aydin, T. Analysis of asymmetrical faults in power systems using dynamic phasors. IEEE Trans. Power Syst. 2000, 15, 1062–1068. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, A. A new approach to load balancing and power factor correction in power distribution system. IEEE Trans. Power Deliv. 2000, 15, 417–422. [Google Scholar] [CrossRef]
- Iravani, M.R.; Karimi-Ghartemani, M. Online estimation of steady state and instantaneous symmetrical components. IEE Proc. Gener. Transm. Distrib. 2003, 150, 616–622. [Google Scholar] [CrossRef]
- Rao, U.K.; Mishra, M.K.; Ghosh, A. Control Strategies for Load Compensation Using Instantaneous Symmetrical Component Theory Under Different Supply Voltages. IEEE Trans. Power Deliv. 2008, 23, 2310–2317. [Google Scholar] [CrossRef]
- Tenti, P.; Willems, J.L.; Mattavelli, P.; Tedeschi, E. Generalized symmetrical components for periodic non-sinusoidal three-phase signals. Electr. Power Qual. Util. J. 2007, XIII, 9–15. [Google Scholar]
- Húngaro Costa, L.L.; Amaral Serni, P.J.; Pinhabel Marafão, F. An analysis of Generalized Symmetrical Components in non sinusoidal three phase systems. In Proceedings of the XI Brazilian Power Electronics Conference, Natal, Brazil, 11–15 September 2011; pp. 502–507. [Google Scholar]
- Liberado, E.V.; Pomilio, J.A.; Alonso, A.M.S.; Tedeschi, E.; Marafão, F.P.; Guerreiro, J.F. Three/Four-leg Inverter Current Control Based on Generalized Symmetrical Components. In Proceedings of the IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018. [Google Scholar]
- Karami, E.; Gharehpetian, G.B.; Madrigal, M.; de Jesus Chavez, J. Dynamic Phasor-Based Analysis of Unbalanced Three-Phase Systems in Presence of Harmonic Distortion. IEEE Trans. Power Syst. 2018, 33, 6642–6654. [Google Scholar] [CrossRef]
- Mikulović, J.; Škrbić, B.; Đurišić, Ž. Power definitions for polyphase systems based on Fortescue’s symmetrical components. Int. J. Electr. Power Energy Syst. 2018, 98, 455–462. [Google Scholar] [CrossRef]
- Paranavithana, P.; Perera, S.; Koch, R.; Emin, Z. Global voltage unbalance in MV networks due to line asymmetries. IEEE Trans. Power Deliv. 2009, 24, 2353–2360. [Google Scholar] [CrossRef]
- Lyon, W.V. Applications of the Method of Symmetrical Components; McGraw Hill: New York, NY, USA, 1937. [Google Scholar]
- Clarke, E. Circuit analysis of A.C. Power Systems: Symmetrical Components; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Gandelli, A.; Leva, S.; Morando, A.P. Topological considerations on the symmetrical components transformation. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 1202–1211. [Google Scholar] [CrossRef]
- Bellan, D.; Superti-Furga, G.; Pignari, S.A. Circuit representation of load and line asymmetries in three-phase power systems. Int. J. Circuits Syst. Signal Process. 2015, 9, 75–80. [Google Scholar]
- Jabr, R.A.; Dzafic, I. A Fortescue approach for real-time short circuit computation in multiphase distribution networks. IEEE Trans. Power Syst. 2015, 30, 3276–3285. [Google Scholar] [CrossRef]
- Strezoski, L.; Prica, M.; Loparo, K.A. Sequence Domain Calculation of Active Unbalanced Distribution Systems Affected by Complex Short Circuits. IEEE Trans. Power Syst. 2018, 33, 1891–1902. [Google Scholar] [CrossRef]
- Desmet, J.J.M.; Sweertvaegher, I.; Vanalme, G.; Stockman, K.; Belmans, R.J.M. Analysis of the neutral conductor current in a three-phase supplied network with nonlinear single-phase loads. IEEE Trans. Ind. Appl. 2003, 39, 587–593. [Google Scholar] [CrossRef] [Green Version]
- Zheng, T.; Makram, E.B.; Girgis, A.A. Evaluating power system unbalance in the presence of harmonic distortion. IEEE Trans. Power Deliv. 2003, 18, 393–397. [Google Scholar] [CrossRef]
- Chicco, G.; Postolache, P.; Toader, C. Analysis of three-phase systems with neutral under distorted and unbalanced conditions in the symmetrical component-based framework. IEEE Trans. Power Deliv. 2007, 22, 674–683. [Google Scholar] [CrossRef]
- Chicco, G.; Postolache, P.; Toader, C. Triplen harmonics: Myths and reality. Electr. Power Syst. Res. 2011, 81, 1541–1549. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Electromagnetic Compatibility (EMC)—Part 4–7: Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; Standard IEC 61000-4-7; IEC: Geneva, Switzerland, 2002. [Google Scholar]
- Langella, R.; Testa, A.; Emanuel, A.E. Unbalance definition for electrical power systems in the presence of harmonics and interharmonics. IEEE Trans. Instrum. Meas. 2012, 61, 2622–2631. [Google Scholar] [CrossRef]
- Thomas, J.P.; Revuelta, P.S.; Vallés, A.P.; Litrán, S.P. Practical evaluation of unbalance and harmonic distortion in power conditioning. Electr. Power Syst. Res. 2016, 141, 487–499. [Google Scholar] [CrossRef]
- Chicco, G.; Pons, E.; Russo, A.; Spertino, F.; Porumb, R.; Postolache, P.; Toader, C. Assessment of unbalance and distortion components in three-phase systems with harmonics and interharmonics. Electr. Power Syst. Res. 2017, 147, 201–212. [Google Scholar] [CrossRef]
- Guzman, H.; Gonzalez, I.; Barrero, F.; Durán, M. Open-Phase Fault Operation on Multiphase Induction Motor Drives. In Indution Motors, 1st ed.; Gregor, R., Ed.; Intech: London, UK, 2015; pp. 327–356. [Google Scholar]
- Jerkan, D.G.; Reljic, D.D.; Marcetic, D.P. Broken Rotor Bar Fault Detection of IM Based on the Counter-Current Braking Method. IEEE Trans. Energy Convers. 2017, 32, 1356–1366. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A survey of condition monitoring and protection methods formedium voltage induction motors. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3165–3174. [Google Scholar]
- Martinez, J.; Belahcen, A.; Arkkio, A. Broken bar indicators for cage induction motors and their relationship with the number of consecutive broken bars. IET Electr. Power Appl. 2013, 7, 633–642. [Google Scholar] [CrossRef]
- Bouzid, M.B.K.; Champenois, G. New Expressions of Symmetrical Components of the Induction Motor Under Stator Faults. IEEE Trans. Ind. Electron. 2013, 60, 4093–4102. [Google Scholar] [CrossRef]
- St-Onge, X.; Cameron, J.A.D.; Saleh, S.A.M.; Scheme, E.J. A Symmetrical Component Feature Extraction Method for Fault Detection in Induction Machines. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Kroupa, M.; Ondrusek, C.; Huzlik, R. Load Torque Analysis of Induction Machine. MM Sci. J. 2016, 887–891. [Google Scholar] [CrossRef]
- Yun, J.; Lee, K.; Lee, K.-W.; Lee, S.B.; Yoo, J.-Y. Detection and Classification of Stator Turn Faults and High-Resistance Electrical Connections for Induction Machines. IEEE Trans. Ind. Appl. 2009, 45, 666–675. [Google Scholar] [CrossRef]
- Bruzzese, C. Analysis and Application of Particular Current Signatures (Symptoms) for Cage Monitoring in Nonsinusoidally Fed Motors With High Rejection to Drive Load, Inertia, and Frequency Variations. IEEE Trans. Ind. Electron. 2008, 55, 4137–4155. [Google Scholar] [CrossRef]
- Siraki, A.G.; Gajjar, C.; Khan, M.A.; Barendse, P.; Pillay, P. An Algorithm for Nonintrusive In Situ Efficiency Estimation of Induction Machines Operating With Unbalanced Supply Conditions. IEEE Trans. Ind. Appl. 2012, 48, 1890–1900. [Google Scholar] [CrossRef]
- Anwari, M.; Hiendro, A. New Unbalance Factor for Estimating Performance of a Three-Phase Induction Motor with Under- and Overvoltage Unbalance. IEEE Trans. Energy Convers. 2010, 25, 619–625. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, H.; Yang, Y.; Mu, X. Study of a Novel Energy Efficient Single-Phase Induction Motor with Three Series-Connected Windings and Two Capacitors. IEEE Trans. Energy Convers. 2010, 25, 433–440. [Google Scholar] [CrossRef]
- Madawala, U.K.; Baguley, C.A. Transient Modeling and Parameter Estimation of Field Aligned Starting. IEEE Trans. Energy Convers. 2008, 23, 15–24. [Google Scholar] [CrossRef]
- Murthy, S.S.; Singh, B.; Gupta, S.; Gulati, B.M. General steady-state analysis of three-phase self-excited induction generator feeding three-phase unbalanced load/single-phase load for stand-alone applications. IEE Proc. Gener. Transm. Distrib. 2003, 150, 49–55. [Google Scholar] [CrossRef]
- Chan, T.F.; Lai, L.L. A Novel Excitation Scheme for a Stand-Alone Three-Phase Induction Generator Supplying Single-Phase Loads. IEEE Trans. Energy Convers. 2004, 19, 136–143. [Google Scholar] [CrossRef]
- Ge, Y.; Song, B.; Pei, Y.; Mollet, Y.; Gyselinck, J. Analytical Expressions of Isolation Indicators for Permanent-Magnet Synchronous Machines Under Stator Short-Circuit Faults. IEEE Trans. Energy Convers. 2018. [Google Scholar] [CrossRef]
- Xiao, L.; Sun, H.; Gao, F.; Hou, S.; Li, L. A New Diagnostic Method for Winding Short-Circuit Fault for SRM Based on Symmetrical Component Analysis. Chin. J. Electr. Eng. 2018, 4, 74–82. [Google Scholar]
- Salomon, C.P.; Santana, W.C.; Lambert-Torres, G.; Borges da Silva, L.E.; Bonaldi, E.L.; de Lacerda de Oliveira, L.E.; Borges da Silva, J.G.; Pellicel, A.L.; Figueiredo, G.C.; Araujo Lopes, M.A. Discrimination of Synchronous Machines Rotor Faults in Electrical Signature Analysis Based on Symmetrical Components. IEEE Trans. Ind. Appl. 2017, 53, 3146–3155. [Google Scholar] [CrossRef]
- Hosobata, T.; Yamamoto, A.; Higuchi, T. Modeling and Analysis of a Linear Resonant Electrostatic Induction Motor Considering Capacitance Imbalance. IEEE Trans. Ind. Electron. 2014, 61, 3439–3447. [Google Scholar] [CrossRef]
- Chaudari, N.B.; Fernandes, B.G. Performance of line start permanent magnet synchronous motor with single-phase supply system. IEE Proc. Gener. Transm. Distrib. 2004, 151, 83–90. [Google Scholar] [CrossRef]
- Ma, M.; Li, L.; He, Z.; Chan, C.C. Influence of Longitudinal End-Effects on Electromagnetic Performance of a Permanent Magnet Slotless Linear Launcher. IEEE Trans. Plasma Sci. 2013, 41, 1161–1166. [Google Scholar] [CrossRef]
- White, D.; Woodson, H. Electromechanical Energy Conversion; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Lorenzani, E.; Bellini, A.; Fornasiero, E. Evaluation of Combined Reference Frame Transformation for Interturn Fault Detection in Permanent-Magnet Multiphase Machines. IEEE Trans. Ind. Electron. 2015, 62, 1912–1920. [Google Scholar] [CrossRef]
- Arafat, A.K.M.; Choi, S.; Baek, J. Open-Phase Fault Detection of a Five-Phase Permanent Magnet Assisted Synchronous Reluctance Motor Based on Symmetrical Components Theory. IEEE Trans. Ind. Electron. 2017, 64, 6465–6474. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Daoud, M.I.; Ahmed, S.; Elserougi, A.A.; Massoud, A.M. Parameter Identification of Five-Phase Induction Machines with Single Layer Windings. IEEE Trans. Ind. Electron. 2014, 61, 5139–5154. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Z.; Xu, L.; Wang, K.; Li, Y. Current Balance Control for Symmetrical Multiphase Inverters. IEEE Trans. Power Electron. 2016, 31, 4005–4012. [Google Scholar] [CrossRef]
- Kamh, M.Z.; Iravani, R. Unbalanced model and power flow analysis of microgrids and active distribution systems. IEEE Trans. Power Del. 2010, 25, 2851–2858. [Google Scholar] [CrossRef]
- Kamh, M.Z.; Iravani, R. A Unified Three-Phase Power-Flow Analysis Model for Electronically Coupled Distributed Energy Resources. IEEE Trans. Power Deliv. 2011, 26, 899–909. [Google Scholar] [CrossRef]
- Arboleya, P.; Garcia, P.; Mohamed, B.; Gonzalez-Moran, C. Distributed resources coordination inside nearly-zero energy buildings providing grid voltage support from a symmetrical component perspective. Electr. Power Syst. Res. 2017, 144, 208–214. [Google Scholar] [CrossRef]
- Howard, D.F.; Habetler, T.G.; Harley, R.G. Improved Sequence Network Model of Wind Turbine Generators for Short-Circuit Studies. IEEE Trans. Energy Convers. 2012, 27, 968–977. [Google Scholar] [CrossRef]
- Rodríguez, A.; Bueno, E.J.; Mayor, Á.; Rodríguez, F.J.; García-Cerrada, A. Voltage support provided by STATCOM in unbalanced power systems. Energies 2014, 7, 1003–1026. [Google Scholar]
- Chicco, G.; Corona, F.; Porumb, R.; Spertino, F. Experimental Indicators of Current Unbalance in Building-Integrated Photovoltaic Systems. IEEE J. Photovolt. 2014, 4, 924–934. [Google Scholar] [CrossRef] [Green Version]
- Cupertino, A.F.; Xavier, L.S.; Brito, E.M.S.; Mendes, V.F.; Pereira, H.A. Benchmarking of power control strategies for photovoltaic systems under unbalanced conditions. Int. J. Electr. Power Energy Syst. 2019, 106, 335–345. [Google Scholar] [CrossRef]
- Chung, S.K. A phase tracking system for three phase utility interface inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef]
- Ali, Z.; Christofides, N.; Hadjidemetriou, L.; Kyriakides, E.; Blaabjerg, F. Three-phase phase-locked loop synchronization algorithms for grid-connected renewable energy systems: A review. Renew. Sustain. Energy Rev. 2018, 90, 434–452. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled double synchronous reference frame PLL for power converters control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Reyes, M.; Rodriguez, P.; Vazquez, S.; Luna, A.; Teodorescu, R.; Carrasco, J.M. Enhanced decoupled double synchronous reference frame current controller for unbalanced grid-voltage conditions. IEEE Trans. Power Electron. 2012, 27, 3934–3943. [Google Scholar] [CrossRef]
- Feola, L.; Langella, R.; Testa, A. On the Effects of Unbalances, Harmonics and Interharmonics on PLL Systems. IEEE Trans. Instrum. Meas. 2013, 62, 2399–2409. [Google Scholar] [CrossRef]
- Vo, T.; Ravishankar, J.; Nurdin, H.I.; Fletcher, J. A novel controller for harmonics reduction of grid-tied converters in unbalanced networks. Electr. Power Syst. Res. 2018, 155, 296–306. [Google Scholar] [CrossRef]
- Hui, N.; Wang, D.; Li, Y. An Efficient Hybrid Filter-Based Phase-Locked Loop under Adverse Grid Conditions. Energies 2018, 11, 703. [Google Scholar] [CrossRef]
- Tummuru, N.R.; Mishra, M.K.; Srinivas, S. Multifunctional VSC controlled microgrid using instantaneous symmetrical components theory. IEEE Trans. Sustain. Energy 2014, 5, 313–322. [Google Scholar] [CrossRef]
- Manoj Kumar, M.V.; Mishra, M.K.; Kumar, C. A Grid-Connected Dual Voltage Source Inverter with Power Quality Improvement Features. IEEE Trans. Sustain. Energy 2015, 6, 482–490. [Google Scholar] [CrossRef]
- Chilipi, R.S.R.; Al Sayari, N.; Al Hosani, K.H.; Beig, A.R. Adaptive Notch Filter-Based Multipurpose Control Scheme for Grid-Interfaced Three-Phase Four-Wire DG Inverter. IEEE Trans. Ind. Appl. 2017, 53, 4015–4027. [Google Scholar] [CrossRef]
- Gude, S.; Chu, C.-C. Three-Phase PLLs by Using Frequency Adaptive Multiple Delayed Signal Cancellation Pre-filters under Adverse Grid Conditions. IEEE Trans. Ind. Appl. 2018, 54, 3832–3844. [Google Scholar] [CrossRef]
- Yallamilli, R.S.; Mishra, M.K. Instantaneous Symmetrical Component Theory based Parallel Grid Side Converter Control Strategy for Microgrid Power Management. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Ren, B.; Sun, X.; Chen, S.; Liu, H. A Compensation Control Scheme of Voltage Unbalance Using a Combined Three-Phase Inverter in an Islanded Microgrid. Energies 2018, 11, 2486. [Google Scholar] [CrossRef]
- Najafi, F.; Hamzeh, M.; Fripp, M. Unbalanced Current Sharing Control in Islanded Low Voltage Microgrids. Energies 2018, 11, 2776. [Google Scholar] [CrossRef]
- Hao, T.; Gao, F.; Xu, T. Fast Symmetrical Component Extraction from Unbalanced Three-Phase Signals Using Non-Nominal dq-Transformation. IEEE Trans. Power Electron. 2018, 33, 9134–9141. [Google Scholar] [CrossRef]
- Zhao, X.; Guerrero, J.M.; Savaghebi, M.; Vasquez, J.C.; Wu, X.H.; Sun, K. Low-Voltage ride-through operation of power converters in grid-interactive microgrids by using negative-sequence droop control. IEEE Trans. Power Electron. 2018, 32, 3128–3142. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, X.; Wang, F.; Cao, R.; Ni, H. Analysis and Control of Neutral-Point Voltage for Transformerless Three-Level PV Inverter in LVRT Operation. IEEE Trans. Power Electron. 2017, 32, 2347–2359. [Google Scholar] [CrossRef]

| Language | Terms Used for the Sequences |
|---|---|
| English | positive, negative, zero |
| Italian | diretta, inversa, omopolare |
| French | direct, indirect, homopolaire |
| Portuguese | directa, inversa, homopolar |
| Romanian | directă, inversă, homopolară |
| Spanish | directa, inversa, homopolar |
| Harmonic Order | Radian Frequency | Sequence | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3h − 2 | (3h − 2) ω1 | positive (+) | |||||||||||||||||||||||||||||||||||||||
| 3h − 1 | (3h − 1) ω1 | negative (-) | |||||||||||||||||||||||||||||||||||||||
| 3h | 3h ω1 | zero (0) | |||||||||||||||||||||||||||||||||||||||
| Harmonic (h) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Sequence (h) | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + |
| Harmonic order h | 0 | 1 | 2 | 3 | 4 | ||||||||||||||||||||||||||||||||||||
| Interharmonic z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Sequence (z) | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + | − | 0 | + |
| Sequence (h) | 0 | + | − | 0 | + |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chicco, G.; Mazza, A. 100 Years of Symmetrical Components. Energies 2019, 12, 450. https://doi.org/10.3390/en12030450
Chicco G, Mazza A. 100 Years of Symmetrical Components. Energies. 2019; 12(3):450. https://doi.org/10.3390/en12030450
Chicago/Turabian StyleChicco, Gianfranco, and Andrea Mazza. 2019. "100 Years of Symmetrical Components" Energies 12, no. 3: 450. https://doi.org/10.3390/en12030450
APA StyleChicco, G., & Mazza, A. (2019). 100 Years of Symmetrical Components. Energies, 12(3), 450. https://doi.org/10.3390/en12030450






