Coal Strength Development with the Increase of Lateral Confinement
Abstract
:1. Introduction
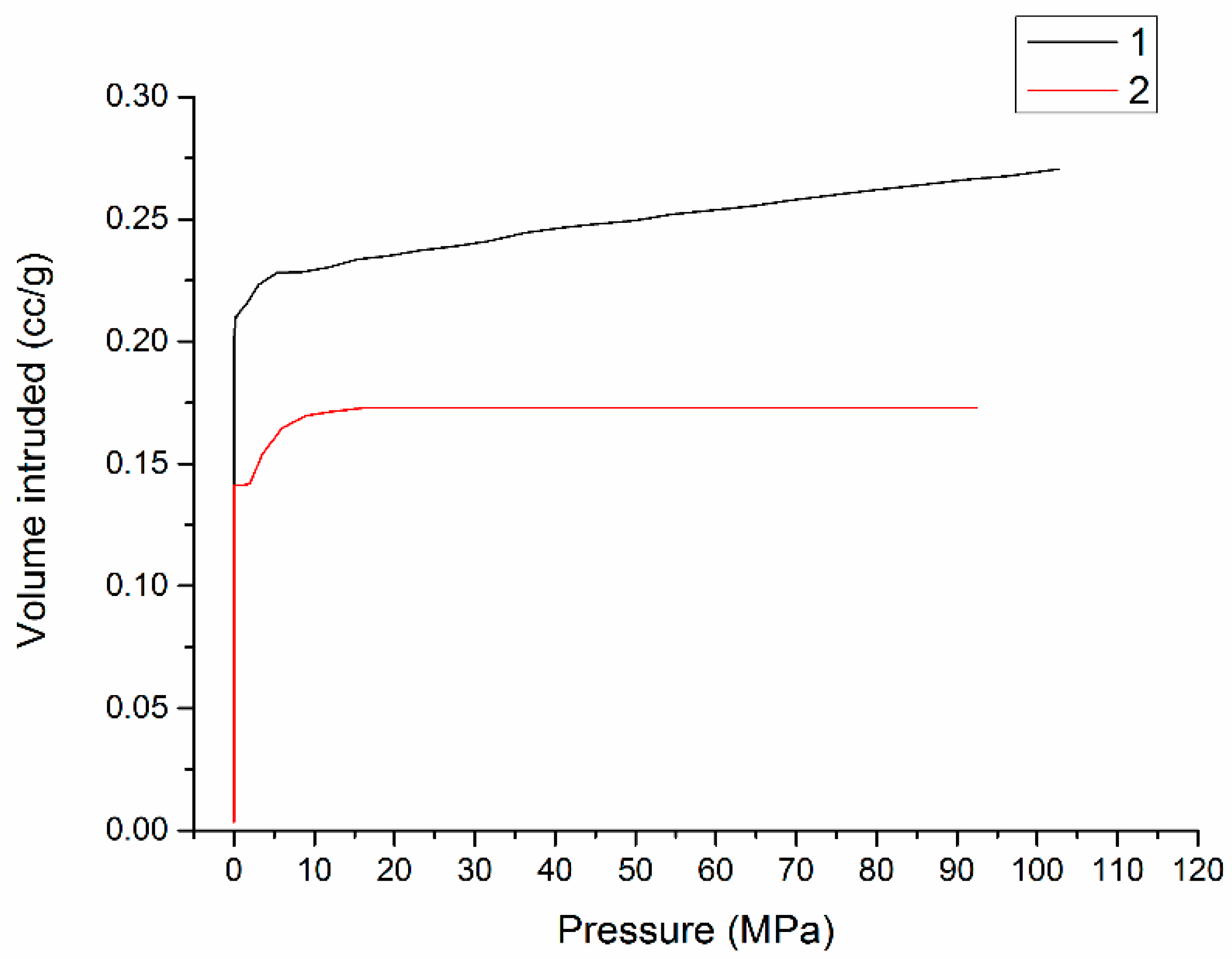
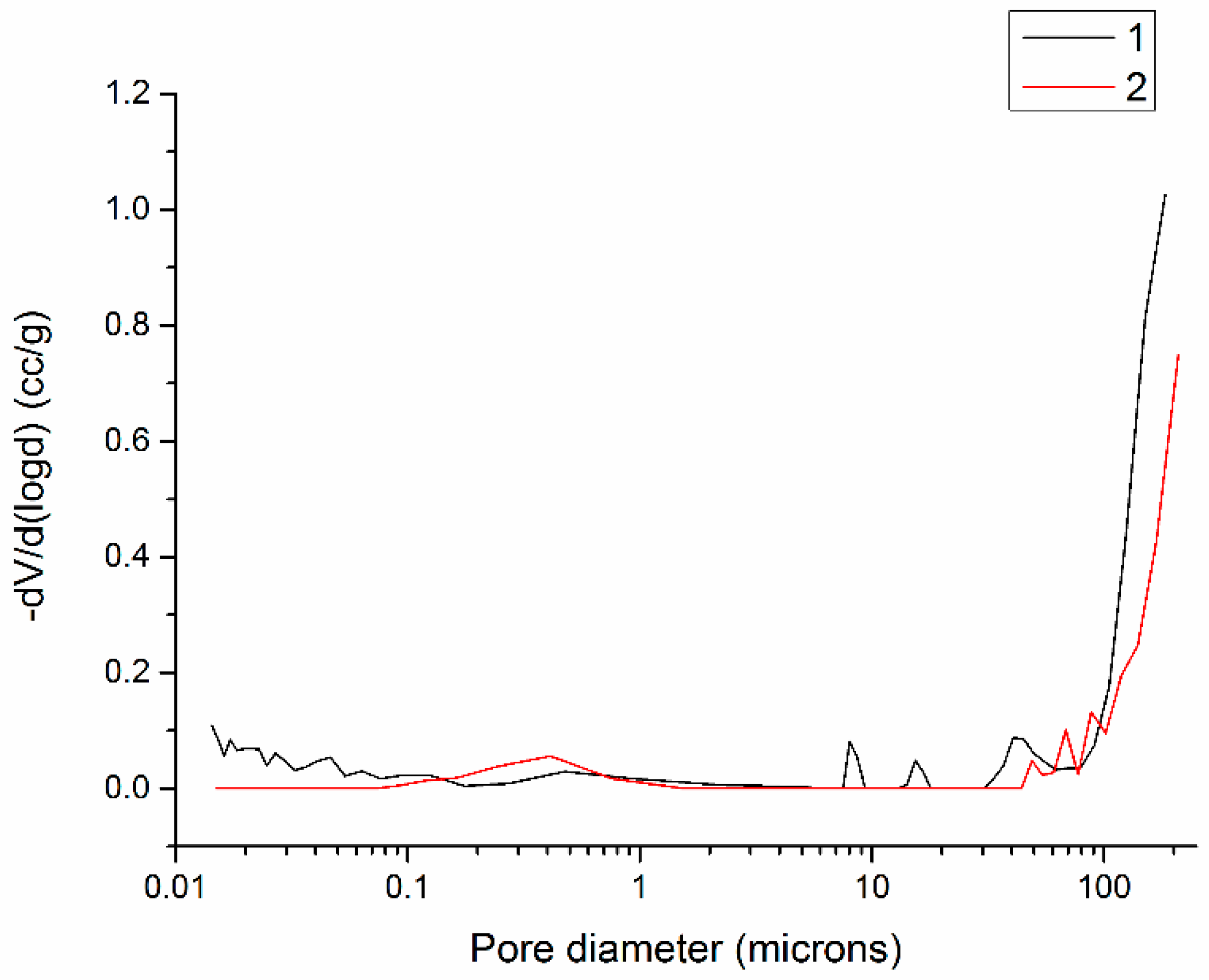
2. Sample Information and Description
3. Sampling and Experimental Procedure
3.1. Specimen Preparation
3.2. Triaxial Compressive Test Set-Up and Procedure
4. Results
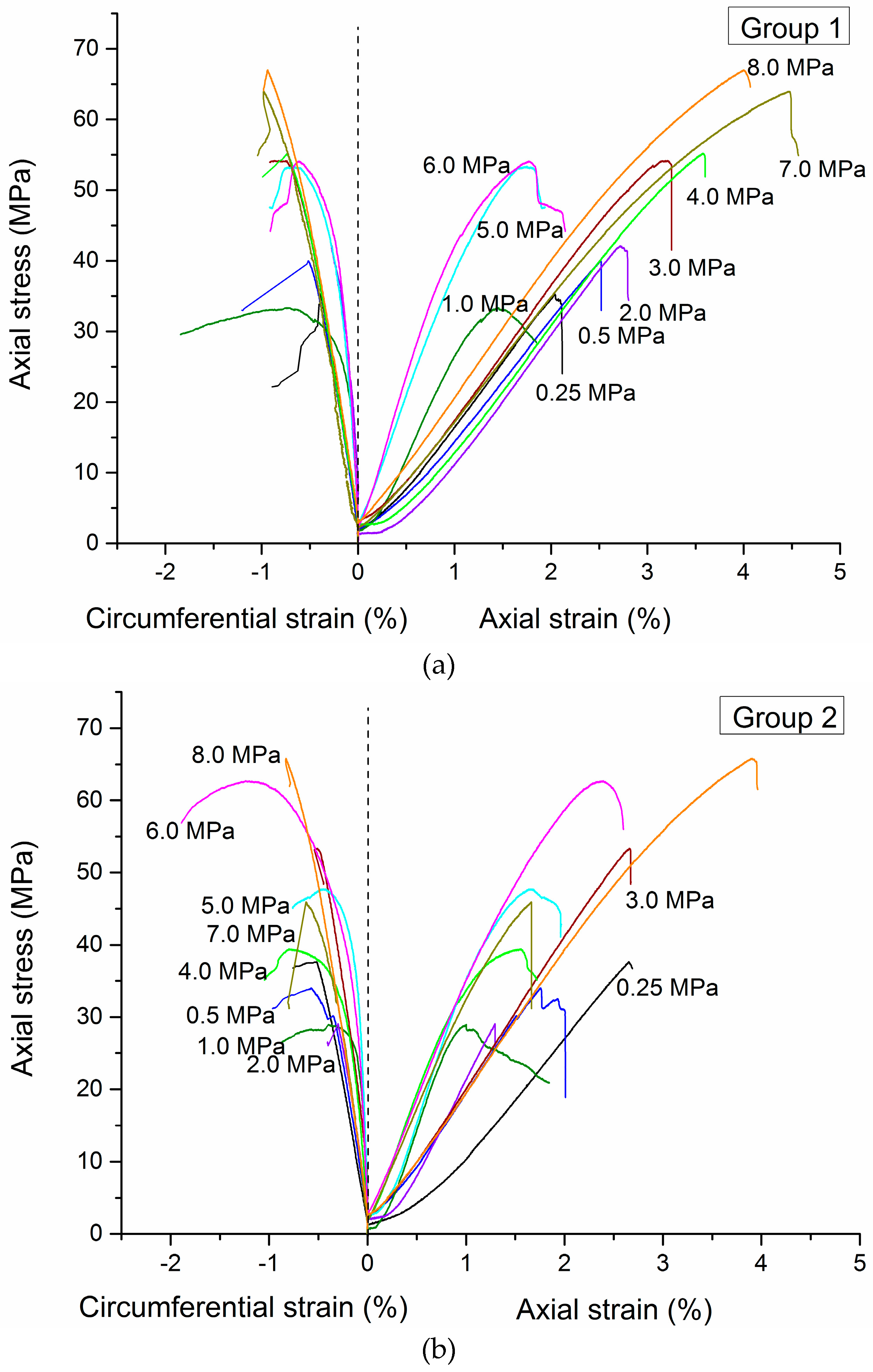
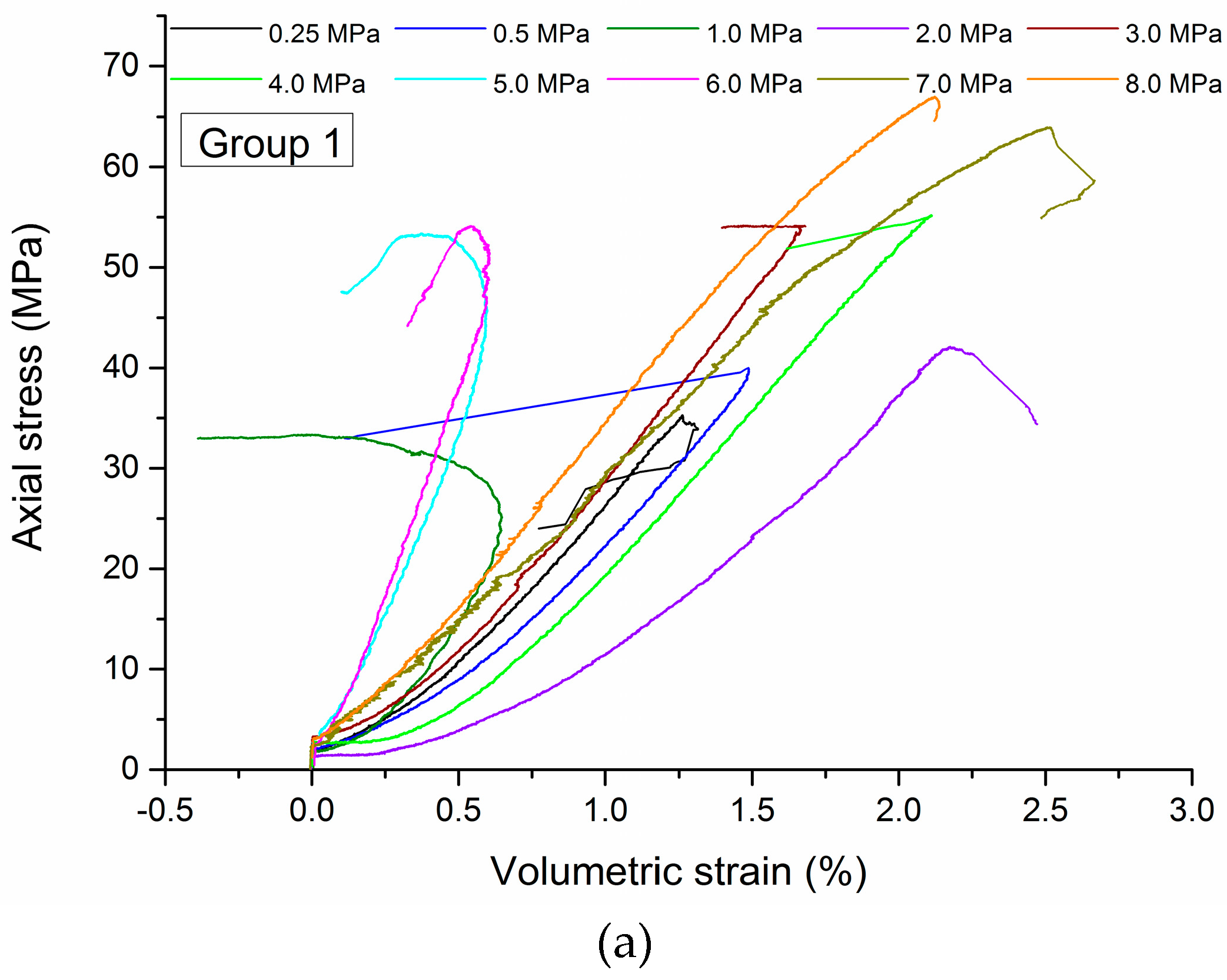
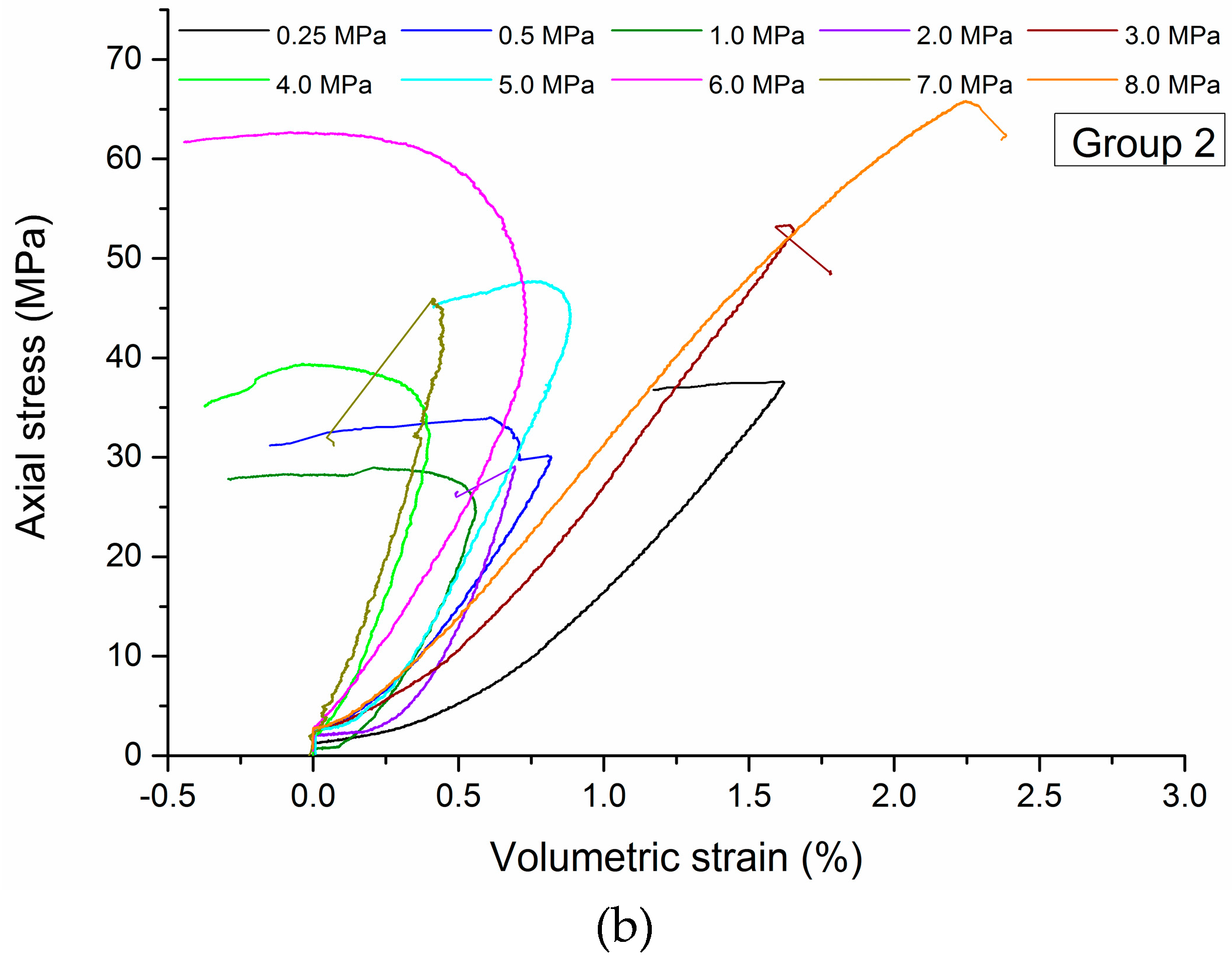
4.1. Stress-Strain Curves
4.2. Failure Mode
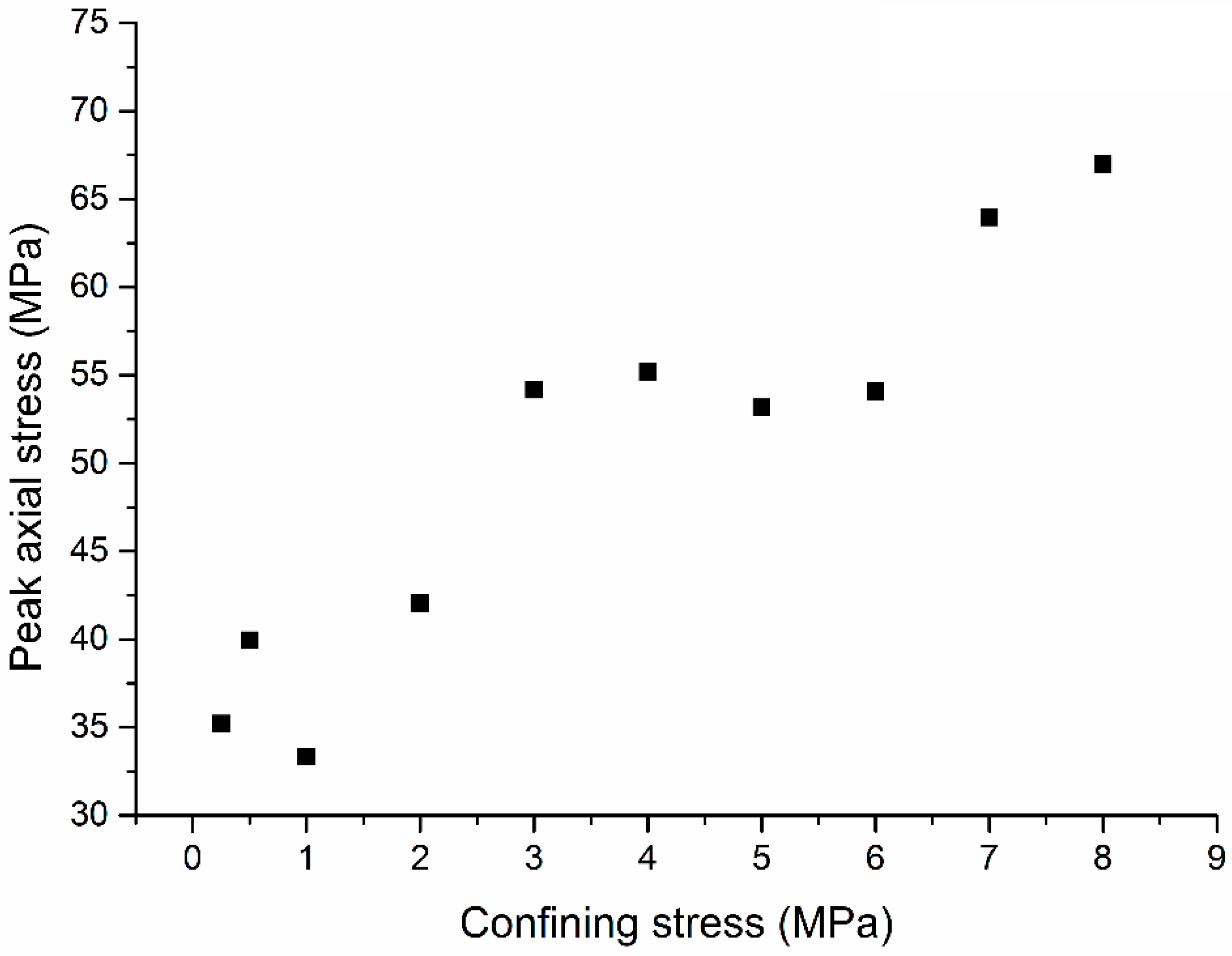
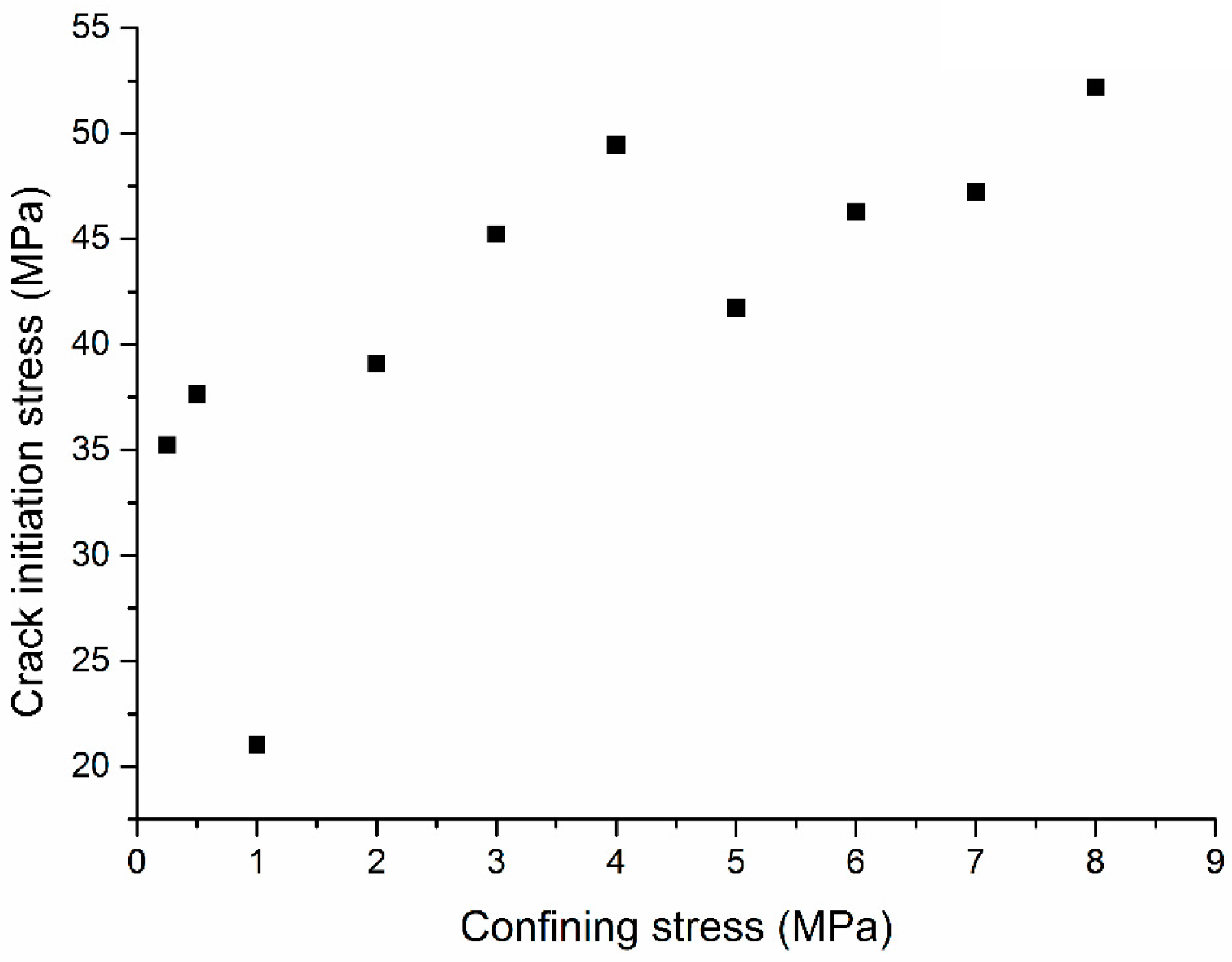
4.3. Confinement-Dependent Strength Behavior
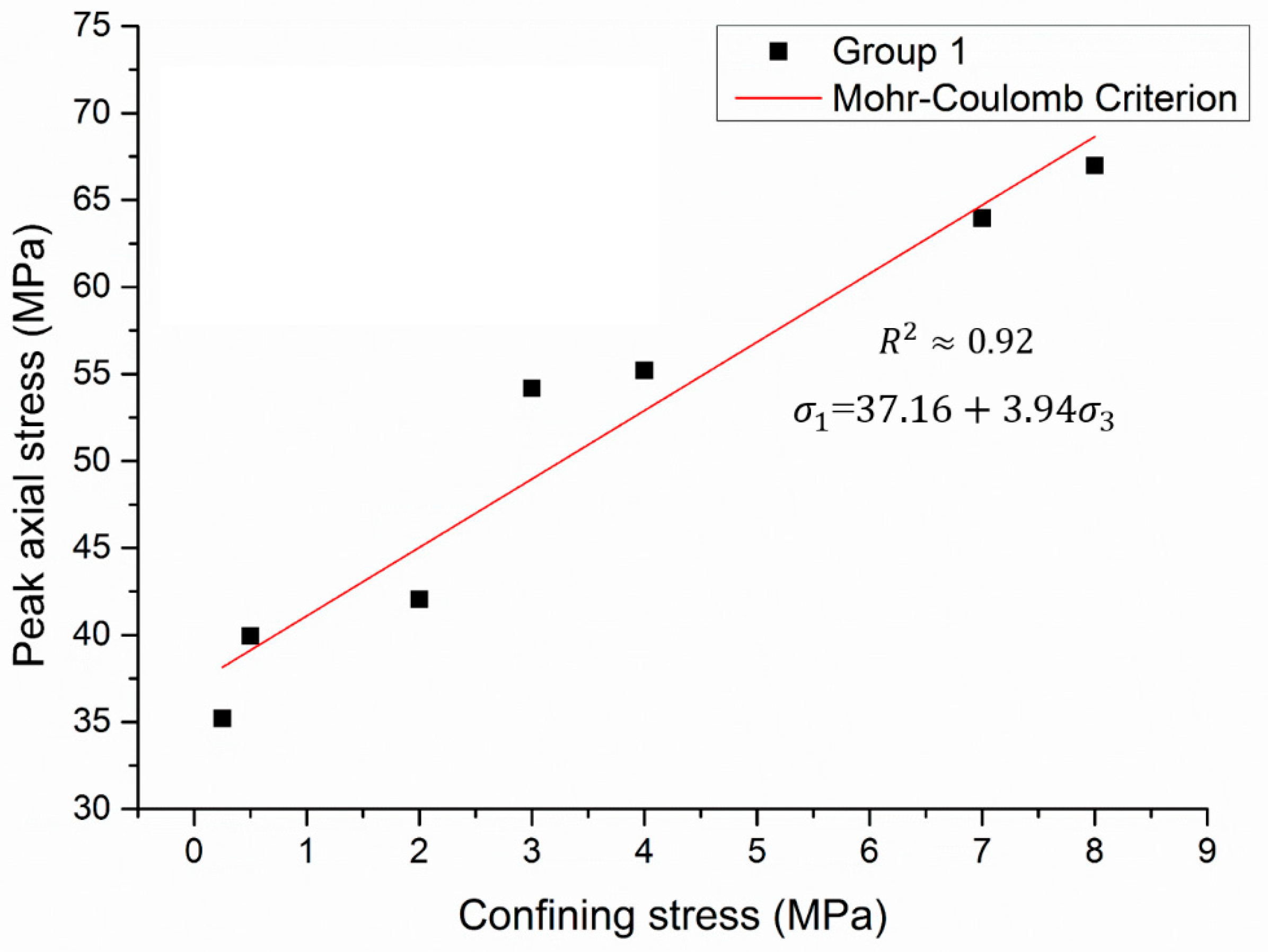
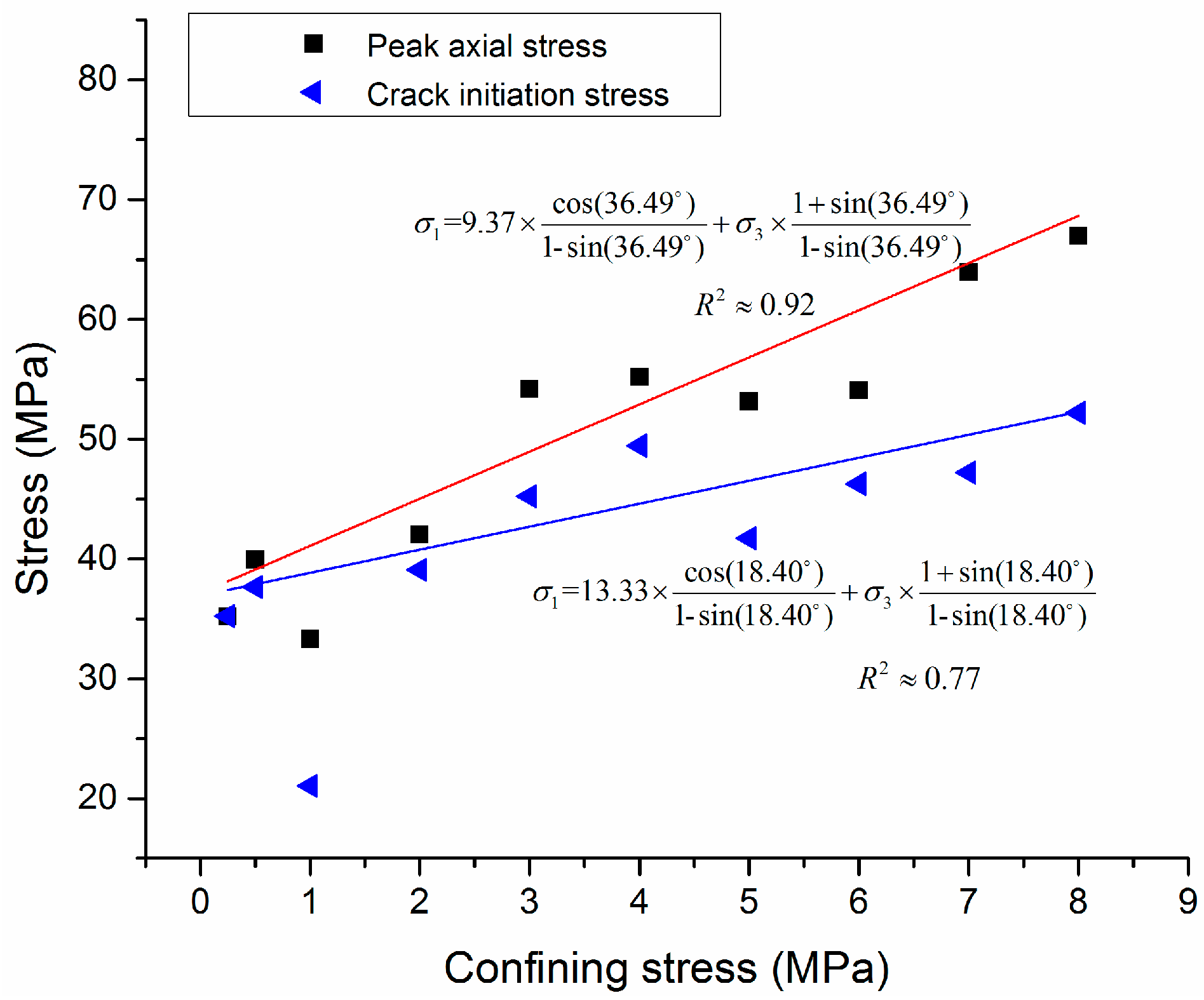
4.4. Failure Envelope
5. Discussion
5.1. Mechanism of Strength Enhancement
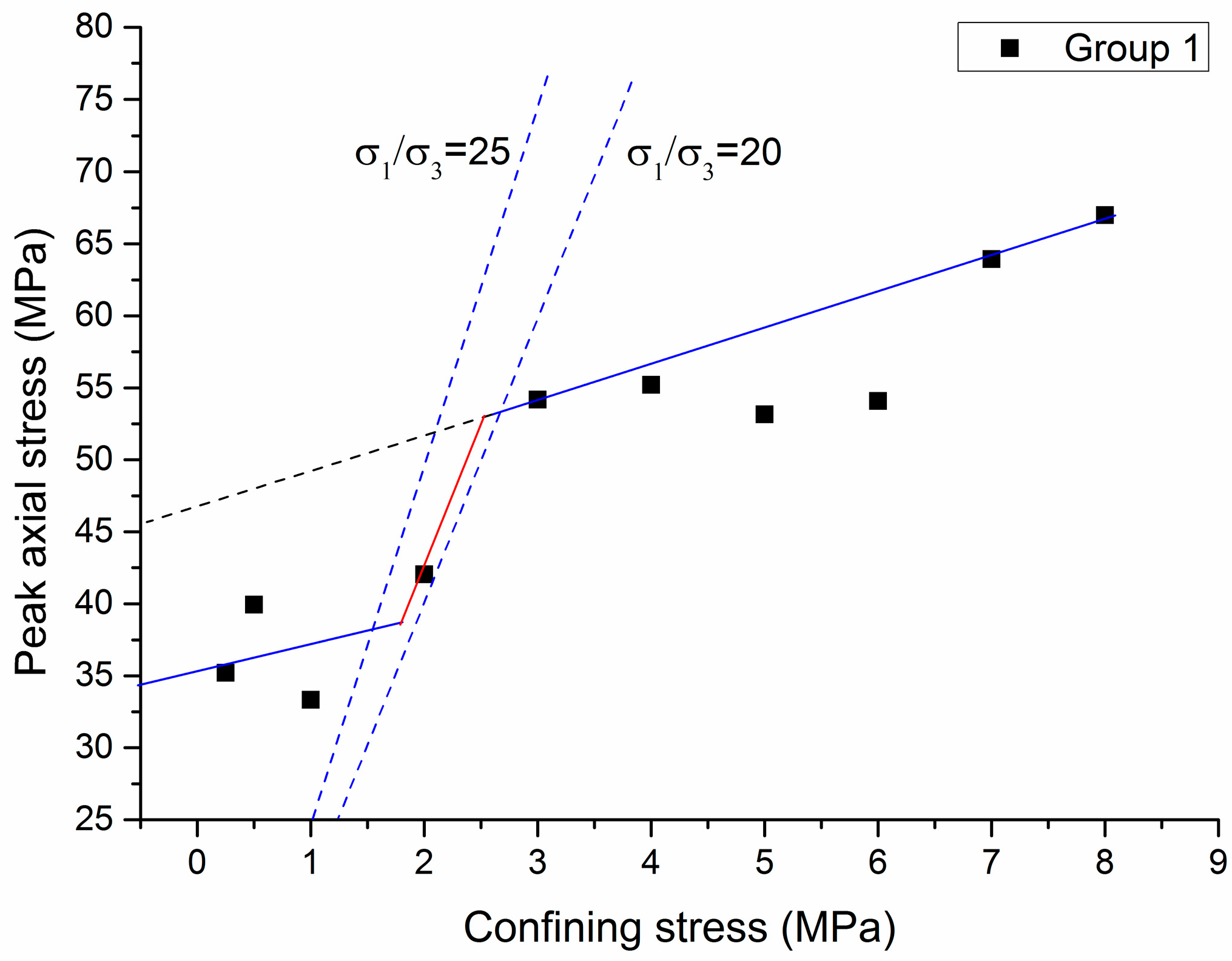
5.2. Strength Characterization
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of symbols:
| UCS | Uniaxial compressive strength |
| εv | Volumetric strain |
| εc | Circumferential strain |
| εa | Axial strain |
| Volume change | |
| V0 | Initial volume |
| σ1 | Major principal stress |
| σ3 | Minor principal stress/confining stress |
| c | Cohesion |
| ϕ | Internal friction angle |
| m | Empirical parameter in Hoek-Brown criterion |
| s | Empirical parameter in Hoek-Brown criterion |
| a | constant in Hoek-Brown criterion |
| ACS | Apparent uniaxial compressive strength |
| C | Constant |
| k2 | Slope of the linear fit of UCS to high confinement data |
References
- Kaiser, P.K.; Kim, B.H.; Bewick, R.P.; Valley, B. Rock mass strength at depth and implications for pillar design. Min Technol. 2011, 120, 170–179. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, Z.; Kuang, T.; Liu, J. Stress changes and deformation monitoring of longwall coal pillars located in weak ground. Rock Mech. Rock Eng. 2016, 49, 3293–3305. [Google Scholar] [CrossRef]
- Nara, Y. Effect of Anisotropy on the long-term strength of granite. Rock Mech. Rock Eng. 2014, 48, 959–969. [Google Scholar] [CrossRef]
- Peng, J.; Rong, G.; Cai, M.; Yao, M.; Zhou, C. Comparison of mechanical properties of undamaged and thermal-damaged coarse marbles under triaxial compression. Int. J. Rock Mech. Min. Sci. 2016, 83, 135–139. [Google Scholar] [CrossRef]
- Yang, S.; Jing, H.; Wang, S. Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression. Rock Mech. Rock Eng. 2012, 45, 583–606. [Google Scholar] [CrossRef]
- Amann, F.; Kaiser, P.; Button, E.A. Experimental study of brittle behavior of clay shale in rapid triaxial compression. Rock Mech. Rock Eng. 2011, 45, 21–33. [Google Scholar] [CrossRef]
- Rybacki, E.; Reinicke, A.; Meier, T.; Makasi, M.; Dresen, G. What controls the mechanical properties of shale rocks?—Part I: Strength and Young’s modulus. J. Pet. Sci. Eng. 2015, 135, 702–722. [Google Scholar] [CrossRef]
- Ishii, E.; Sanada, H.; Iwatsuki, T.; Sugita, Y.; Kurikami, H. Mechanical strength of the transition zone at the boundary between opal-A and opal-CT zones in siliceous rocks. Eng. Geol. 2011, 122, 215–221. [Google Scholar] [CrossRef]
- Li, D.; Wong, L.N.Y.; Liu, G.; Zhang, X. Influence of water content and anisotropy on the strength and deformability of low porosity meta-sedimentary rocks under triaxial compression. Eng. Geol. 2012, 126, 46–66. [Google Scholar] [CrossRef]
- Peng, J.; Cai, M.; Rong, G.; Zhou, C.; Wang, X. Author’s reply to discussion of the paper “an empirical failure criterion for intact rocks” by Peng et al. Rock Mech. Rock Eng. 2014, 47, 825–834. [Google Scholar] [CrossRef]
- Peng, J.; Rong, G.; Cai, M.; Wang, X.; Zhou, C. An empirical failure criterion for intact Rocks. Rock Mech. Rock Eng. 2014, 47, 347–356. [Google Scholar] [CrossRef]
- Heidari, M.; Khanlari, G.R.; Torabi-Kaveh, M.; Kargarian, S.; Saneie, S. Effect of porosity on rock brittleness. Rock Mech. Rock Eng. 2013, 47, 785–790. [Google Scholar] [CrossRef]
- Baud, P.; Wong, T.; Zhu, W. Effects of porosity and crack density on the compressive strength of rocks. Int. J. Rock Mech. Min. Sci. 2014, 67, 202–211. [Google Scholar] [CrossRef]
- Hsieh, A.; Dyskin, A.V.; Dight, P. The increase in Young’s modulus of rocks under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2014, 70, 425–434. [Google Scholar] [CrossRef]
- Shang, J.; Hu, J.; Zhou, K.; Luo, X.; Aliyu, M.M. Porosity increment and strength degradation of low-porosity sedimentary rocks under different loading conditions. Int. J. Rock Mech. Min. Sci. 2015, 75, 216–223. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Kim, B.H. Rock mechanics changes in underground construction and mining. In Proceedings of the 1st South Hemisphere International Rock Mechanics Symposium, Perth, Australia, 16–19 September 2008; pp. 1–14. [Google Scholar]
- Kim, B.H.; Kaiser, P.K. Rock strength characterization for excavation in brittle failing rock. In Proceedings of the 3rd CANUS Rock Mechanics Symposium, Toronto, ON, Canada, 9–15 May 2009; p. 3946. [Google Scholar]
- Hajiabdolmajid, V.; Kaiser, P.; Martin, C.D. Mobilised strength components in brittle failure of rock. Géotechnique 2003, 53, 327–336. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K. In-situ rock spalling strength near excavation boundaries. Rock Mech. Rock Eng. 2013, 47, 659–675. [Google Scholar] [CrossRef]
- Buzzi, O.; Sieffert, Y.; Mendes, J.; Liu, X.; Giacomini, A.; Seedsman, R. Strength of an Australian coal under low confinement. Rock Mech. Rock Eng. 2013, 47, 2265–2270. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for determining the strength of rock materials in triaxial compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 47–51. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.; Sego, D. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Xu, X.; Wu, S.; Gao, Y.; Xu, M. Effects of Micro-structure and Micro-parameters on Brazilian Tensile Strength Using Flat-Joint Model. Rock Mech. Rock Eng. 2016, 49, 3575–3595. [Google Scholar] [CrossRef]
- Fakhimi, A.; Villegas, T. Application of dimensional analysis in calibration of a discrete element model for rock deformation and fracture. Rock Mech. Rock Eng. 2007, 40, 193–211. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Liu, G.; Rong, G.; Peng, J.; Zhou, C.B. Numerical simulation on undrained triaxial behavior of saturated soil by a fluid coupled-DEM model. Eng. Geol. 2015, 193, 256–266. [Google Scholar] [CrossRef]
- Brace, W.F.; Paulding, B.R.; Scholz, C. Dilatancy in fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Kim, B.H. Characterization of strength of intact brittle rock considering confinement-dependent failure processes. Rock Mech. Rock Eng. 2015, 48, 107–119. [Google Scholar] [CrossRef]
- Hoek, E. Rock Fracture under Static Stress Conditions. PhD Thesis, University of Cape Town, Cape Town, South Africa, 1965. [Google Scholar]







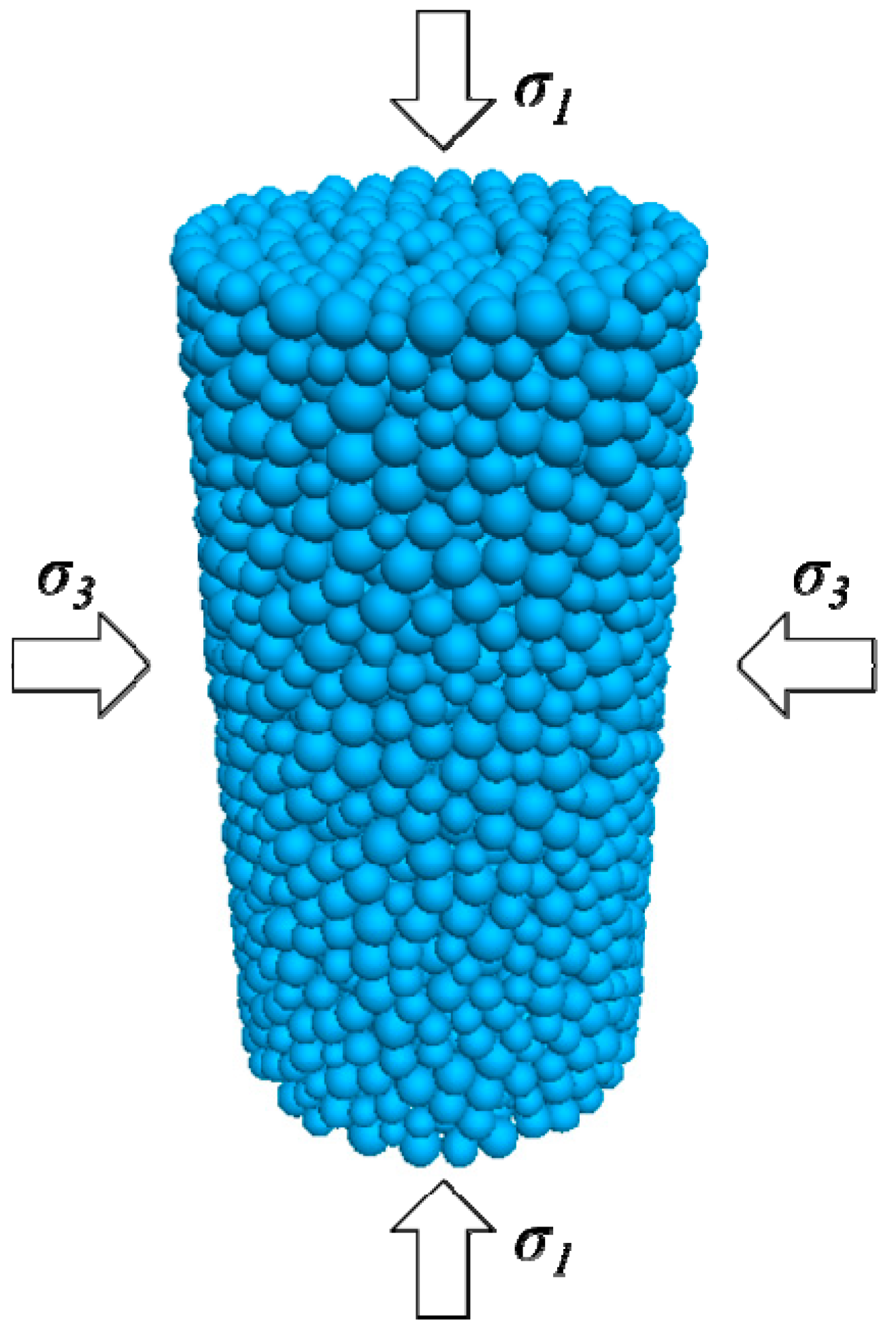
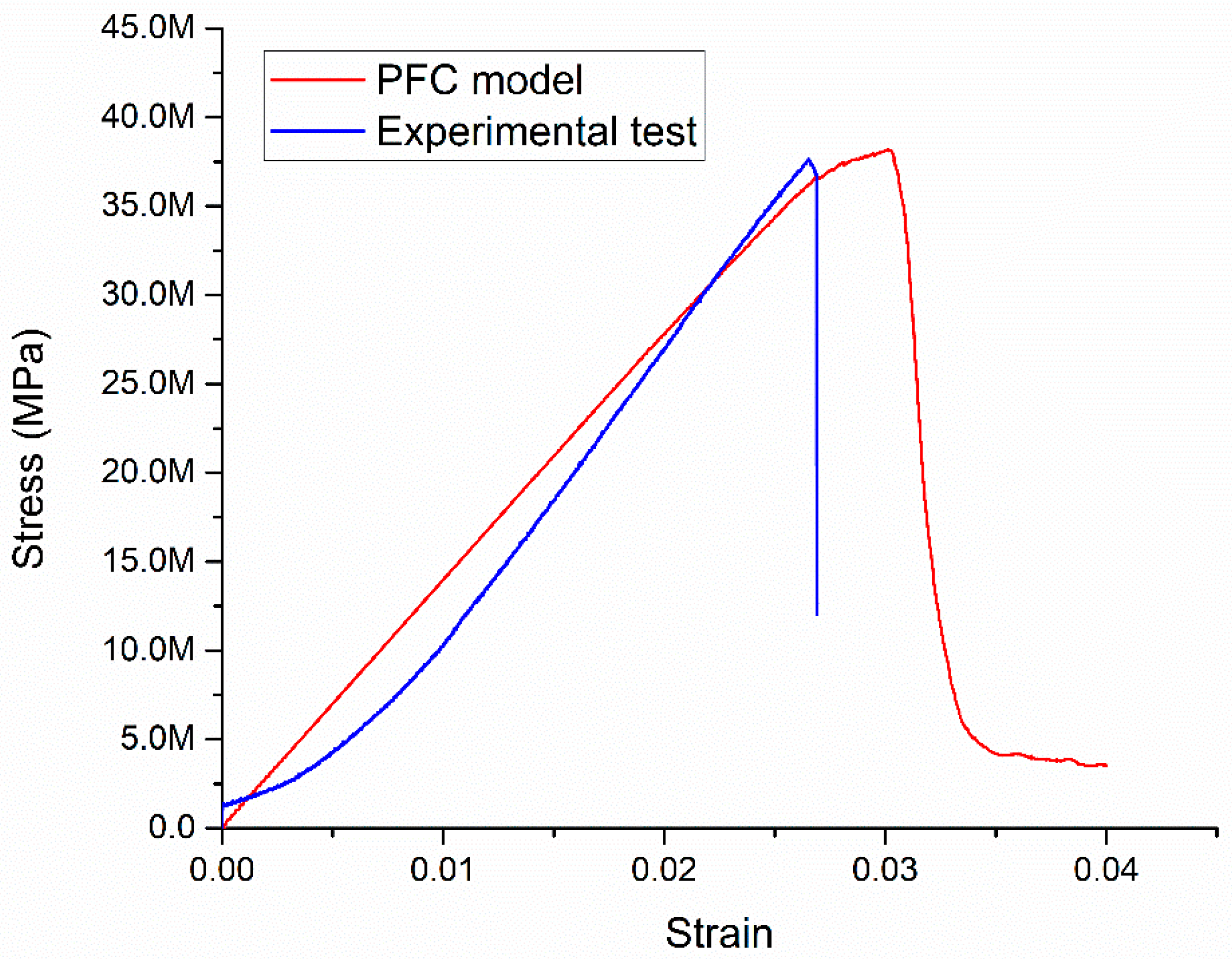
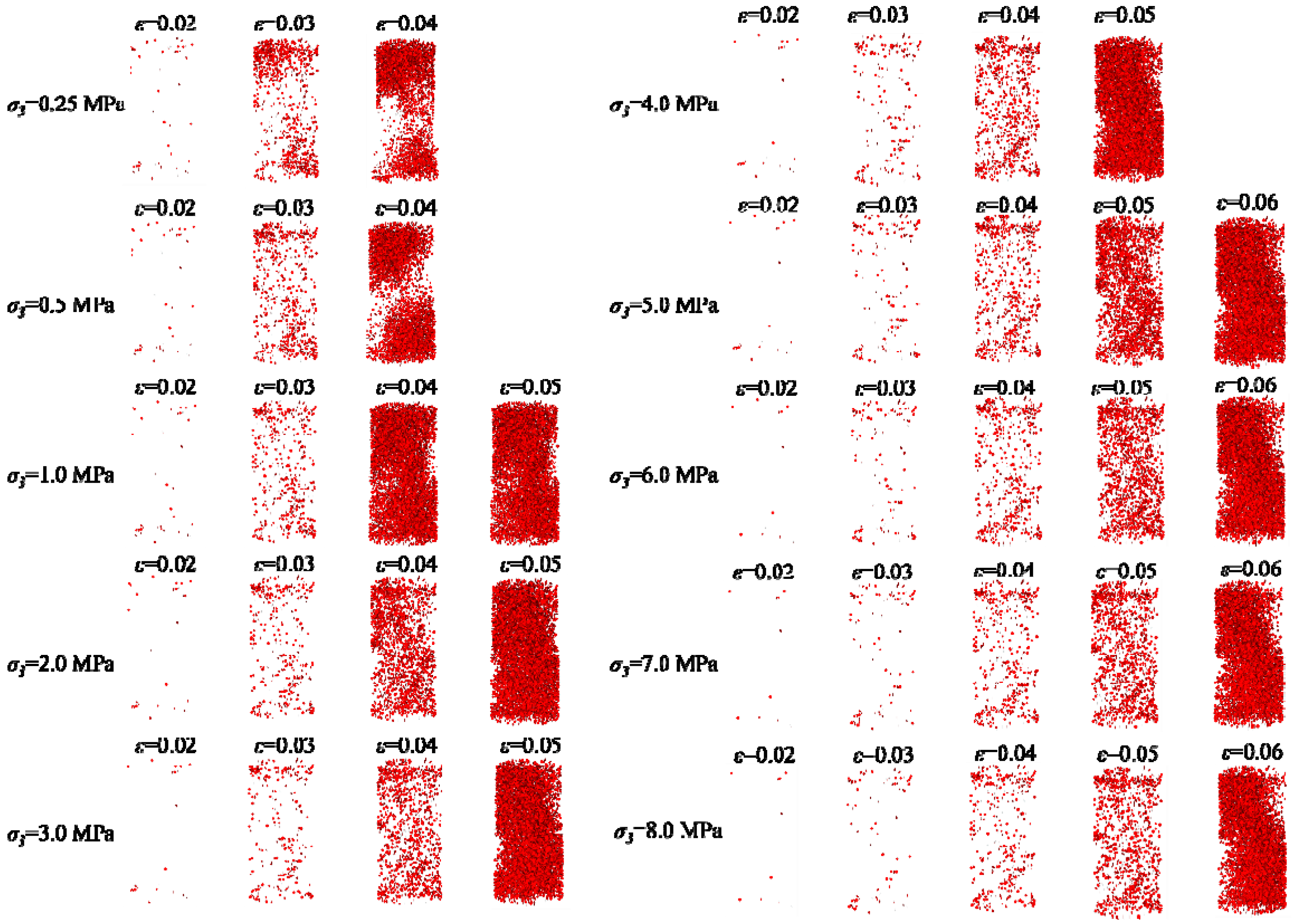

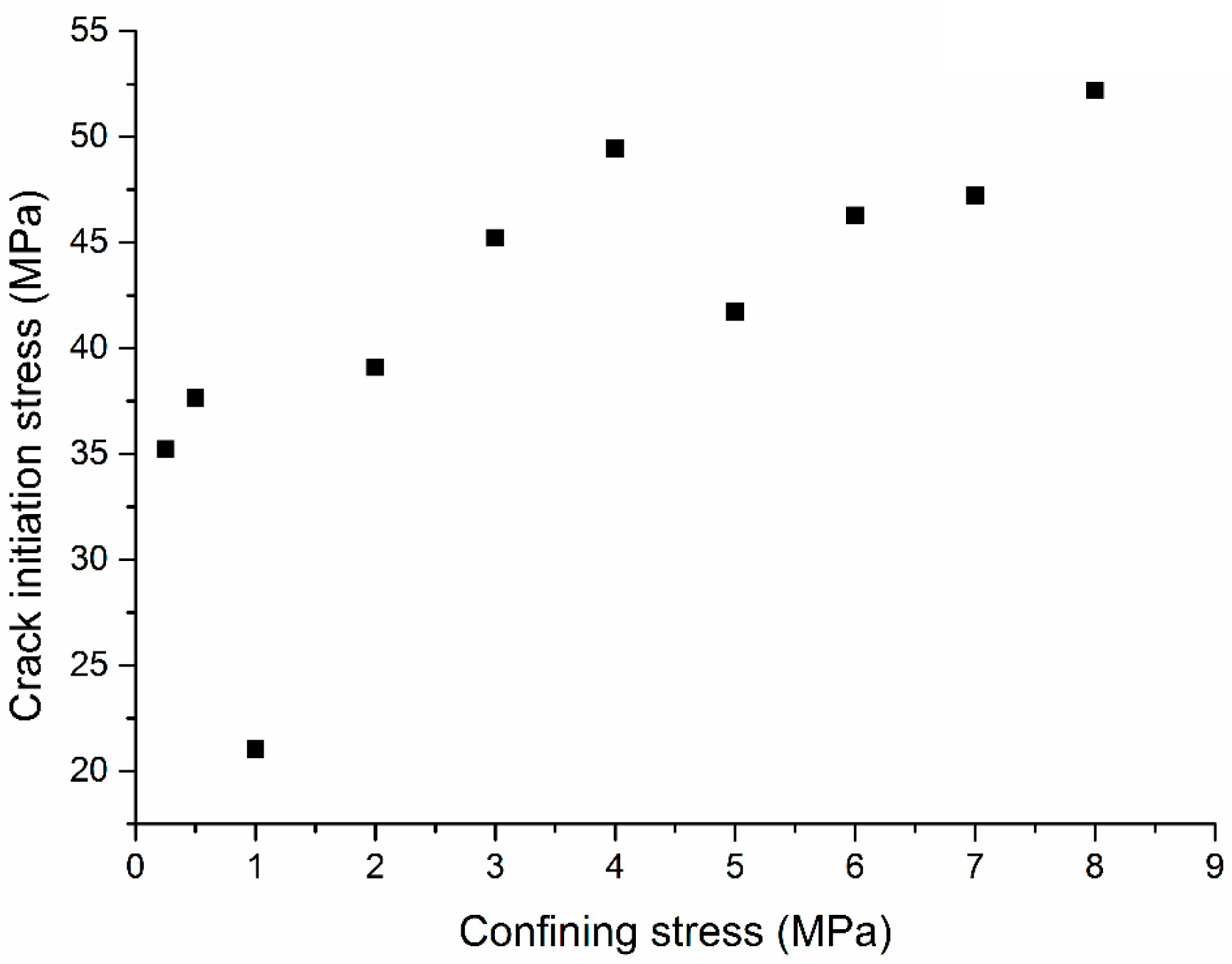

| Specimen Numbering | Confining Stress (MPa) | Axial Loading Rate (mm/min) | Diameter (mm) | Height (mm) | Note |
|---|---|---|---|---|---|
| 1-1 | 0.25 | 0.15 | 49.00 | 100.00 | Group 1 |
| 1-2 | 0.25 | 0.15 | 49.91 | 100.00 | Group 2 |
| 2-1 | 0.5 | 0.15 | 49.05 | 100.00 | Group 1 |
| 2-2 | 0.5 | 0.15 | 49.35 | 100.00 | Group 2 |
| 3-1 | 1.00 | 0.15 | 49.55 | 100.00 | Group 1 |
| 3-2 | 1.00 | 0.15 | 49.39 | 100.00 | Group 2 |
| 4-1 | 2.00 | 0.15 | 48.66 | 100.00 | Group 1 |
| 4-2 | 2.00 | 0.15 | 49.55 | 100.00 | Group 2 |
| 5-1 | 3.00 | 0.15 | 49.2 | 100.03 | Group 1 |
| 5-2 | 3.00 | 0.15 | 49.39 | 100.00 | Group 2 |
| 6-1 | 4.00 | 0.15 | 49.63 | 100.00 | Group 1 |
| 6-2 | 4.00 | 0.15 | 49.35 | 100.00 | Group 2 |
| 7-1 | 5.00 | 0.15 | 49.29 | 100.00 | Group 1 |
| 7-2 | 5.00 | 0.15 | 49.56 | 100.02 | Group 2 |
| 8-1 | 6.00 | 0.15 | 49.40 | 100.00 | Group 1 |
| 8-2 | 6.00 | 0.15 | 49.30 | 100.02 | Group 2 |
| 9-1 | 7.00 | 0.15 | 49.59 | 100.00 | Group 1 |
| 9-2 | 7.00 | 0.15 | 49.43 | 100.00 | Group 2 |
| 10-1 | 8.00 | 0.15 | 49.80 | 100.00 | Group 1 |
| 10-2 | 8.00 | 0.15 | 49.70 | 100.00 | Group 2 |
| Micro Parameters | Value |
|---|---|
| Particle density (kg/m3) | 1960 |
| Effective modulus (GPa) | 1.0 |
| Normal-to-shear stiffness ratio | 1.5 |
| Friction coefficient | 0.4 |
| Gap interval | 0.0 |
| Radius multiplier | 1.0 |
| Bond effective modulus (GPa) | 1.0 |
| Bond effective modulus (GPa) | 1.5 |
| Moment contribution factor | 1.0 |
| Tensile strength (MPa) | 10.0 |
| Cohesion (MPa) | 40.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, Y. Coal Strength Development with the Increase of Lateral Confinement. Energies 2019, 12, 405. https://doi.org/10.3390/en12030405
Zhang J, Li Y. Coal Strength Development with the Increase of Lateral Confinement. Energies. 2019; 12(3):405. https://doi.org/10.3390/en12030405
Chicago/Turabian StyleZhang, Junwen, and Yulin Li. 2019. "Coal Strength Development with the Increase of Lateral Confinement" Energies 12, no. 3: 405. https://doi.org/10.3390/en12030405
APA StyleZhang, J., & Li, Y. (2019). Coal Strength Development with the Increase of Lateral Confinement. Energies, 12(3), 405. https://doi.org/10.3390/en12030405





