Sensitivity Analysis of Rock Electrical Influencing Factors of Natural Gas Hydrate Reservoir in Permafrost Region of Qilian Mountain, China
Abstract
1. Introduction
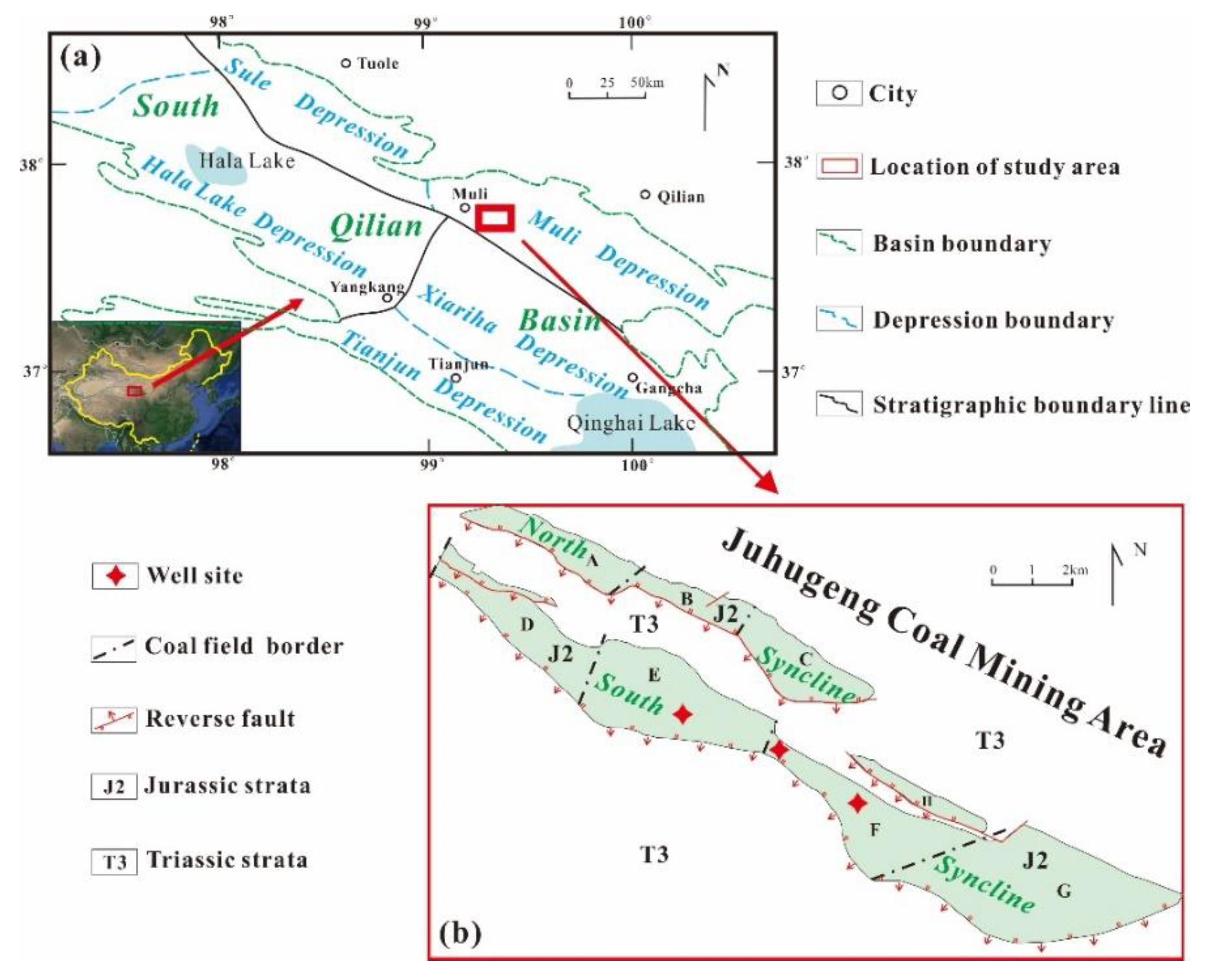
2. Geological Background
3. Methods
4. Results and Discussion
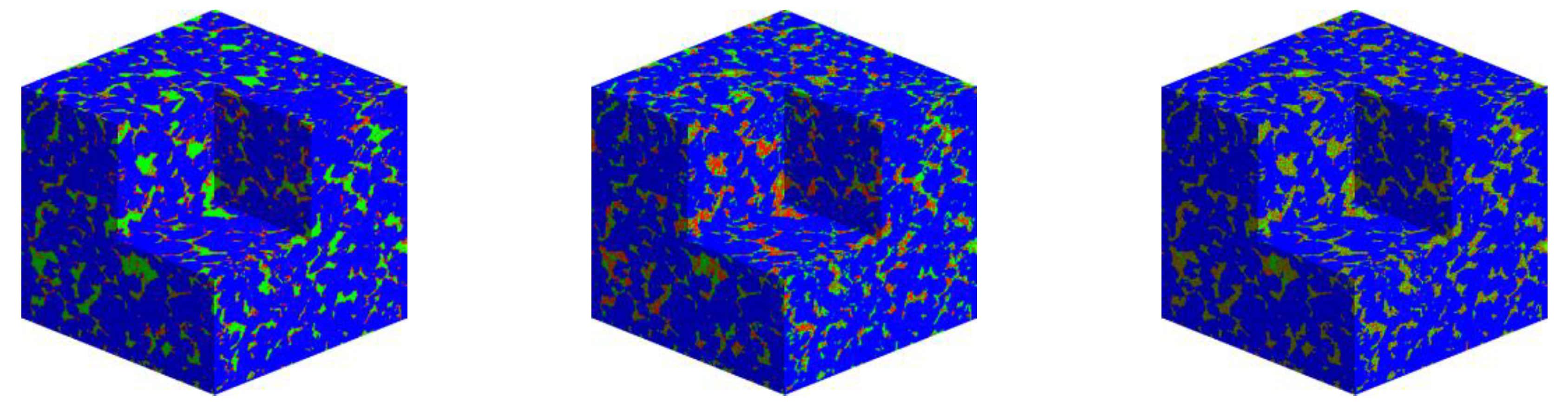
4.1. Digital Rock Models Construction
4.2. Rock Electrical Properties Sensitivity Analysis
- (1)
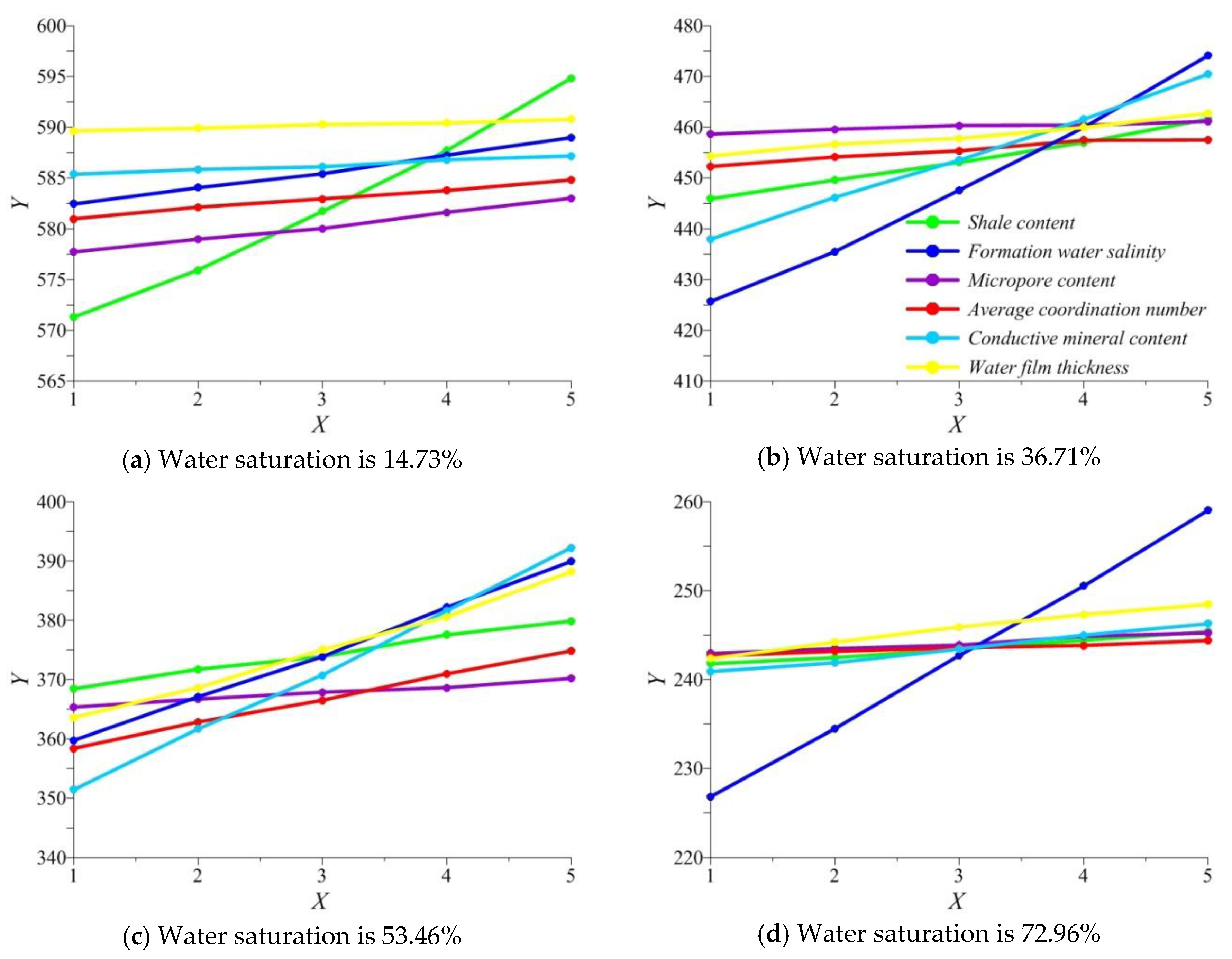
- Under different water saturation conditions, with the increase of the level difference of the influencing factors, there was a difference in the average value of the resistivity statistical variables. The greater the increase, the stronger the sensitivity of the rock electrical properties to the influencing factors.
- (2)
- At low water saturation (Sw < 30%), the largest increase in amplitude was the shale content and the smallest was the water film thickness. It is speculated that at low water saturation, the shale will form an additional conductive path, forming a double conductive path with the formation water, which has an important influence on the resistivity of the rock, so it is the most sensitive factor at this time. In contrast, due to the additional conductive action of the mud, the conductivity of the water film is greatly impaired, so the water film thickness is the most inferior to the resistivity.
- (3)
- In moderate water saturation (30% ≤ Sw ≤ 60%), the largest increase in amplitude was the formation water salinity and the smallest was the micropore content. It is speculated that in the case of moderate water saturation, since the hydrate fills part of the pore space of the rock, the micropores lose their conductivity, so it is the least sensitive factor at this time. In contrast, the formation water salinity has an important influence on the conductive properties of rocks.
- (4)
- At high water saturation (Sw > 60%), the maximum increase in amplitude was the formation water salinity, and the smallest was the average coordination number. It is speculated that in the case of high water saturation, the rock pore space is almost occupied by the formation water, so the formation water mineralization degree is the most sensitive, because the formation water mineralization has great influence on the conductivity, especially if the conductive path is relatively thin, even if the coordination number is higher, it has no effect on conductivity, so it is in the most insensitive position.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kvenvolden, K.A.; Lorenson, T.D. The Global Occurrence of Natural Gas Hydrate; American Geophysical Union: Washington, DC, USA, 2001; pp. 2–10. [Google Scholar]
- Dong, H.; Sun, J.; Zhu, J.; Liu, L.; Lin, Z.; Golsanami, N.; Cui, L.; Yan, W. Developing a new hydrate saturation calculation model for hydrate-bearing sediments. Fuel 2019, 248, 27–37. [Google Scholar] [CrossRef]
- Milkov, A.A.; Sassen, R. Economic geology of offshore gas hydrate accumulations and provinces. Mar. Pet. Geol. 2002, 19, 1–11. [Google Scholar] [CrossRef]
- Milkov, A.V.; Sassen, R. Preliminary assessment of resources and economic potential of individual gas hydrate accumulations in the Gulf of Mexico continental slope. Mar. Pet. Geol. 2003, 20, 111–128. [Google Scholar] [CrossRef]
- Milkov, A.V. Global estimates of hydrate-bound gas in marine sediments: How much is really out there? Earth Sci. Rev. 2004, 66, 183–197. [Google Scholar] [CrossRef]
- Fang, H.; Xu, M.; Lin, Z.; Zhong, Q.; Bai, D.; Liu, J.; Pei, F.; He, M. Geophysical characteristics of gas hydrate in the Muli area, Qinghai province. J. Nat. Gas Sci. Eng. 2017, 37, 539–550. [Google Scholar] [CrossRef]
- Lin, Z.; Pan, H.; Fang, H.; Gao, W.; Liu, D. High-altitude well log evaluation of a permafrost gas hydrate reservoir in the Muli area of Qinghai, China. Sci. Rep. 2018, 8, 12596. [Google Scholar] [CrossRef] [PubMed]
- Arns, C.H.; Bauget, F.; Ghous, A. Digital core laboratory: Petrophysical analysis from 3D images of reservoir core fragments. Petrophysics 2005, 46, 260–277. [Google Scholar]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Lee, H.; Shin, J.; Ha, S. Frost formation on a plate with different surface hydrophilicity. Int. J. Heat Mass Transf. 2004, 47, 4881–4893. [Google Scholar] [CrossRef]
- Qu, K.; Komori, S.; Jiang, Y. Local variation of frost layer thickness and morphology. Int. J. Heat Mass Transf. 2006, 45, 116–123. [Google Scholar] [CrossRef]
- Liu, X.; Sun, J.; Wang, H. Numerical simulation of rock electrical properties based on digital cores. Appl. Geophys. 2009, 6, 1–7. [Google Scholar] [CrossRef]
- Kong, Q.; Zhou, C.; Zhang, Y.; Li, X.; Li, C.; Hu, F. Numerical simulation methods of rock electrical properties based on digital cores: A review. Prog. Geophys. 2015, 30, 718–724. [Google Scholar]
- Collett, T.S.; Lee, M.W. Gulf of Mexico gas hydrate joint industry project leg II logging-while-drilling data acquisition and analysis. Mar. Pet. Geol. 2012, 34, 41–61. [Google Scholar] [CrossRef]
- Ning, F.; Liu, L.; Li, S. Well logging assessment of natural gas hydrate reservoirs and relevant influential factors. Acta Pet. Sin. 2013, 34, 591–606. [Google Scholar]
- Max, M.D.; Johnson, A.H. Hydrate petroleum system approach to natural gas hydrate exploration. Pet. Geosci. 2014, 20, 187–199. [Google Scholar] [CrossRef]
- Majumdar, U.; Ann, E.C.; Mackenzie, S. Semi-quantitative gas hydrate assessment from petroleum industry well logs in the northern Gulf of Mexico. Mar. Pet. Geol. 2017, 85, 233–241. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Wen, H.; Lu, Z.; Wang, P. Gas hydrate in the Qilian Mountain permafrost and their basic characteristics. Acta Geol. Sin. 2010, 31, 7–16. [Google Scholar]
- Pang, S. Relationship Between Tectonic, Sedimentation Characteristics and Distribution of Gas Hydrate in Muli Coalfield of Qilian Mountain; China University of Geosciences: Beijing, China, 2012; p. 58. [Google Scholar]
- Lu, Z.; Zhu, Y.; Zhang, Y. Basic geological characteristics of gas hydrates in Qilian Mountain permafrost area, Qinghai Province. Miner. Depos. 2010, 29, 182–191. [Google Scholar]
- Lu, Z.; Li, Y.; Wang, W. Study on the accumulation pattern for permafrost-associated gas hydrate in sanlutian of Muli, Qinghai. Geoscience 2015, 29, 1014–1023. [Google Scholar]
- Wen, H.; Lu, J.; Shang, L. A sequence stratigraphic discussion of the jurassic coal measures in the Juhugeng coalmine area in Qinghai Province. Coal Geol. China 2006, 18, 19–21. [Google Scholar]
- Cai, Y.; Xing, Y.; Hu, D. On sensitivity analysis. J. Beijing Norm. Univ. (Nat. Sci.) 2008, 44, 9–16. [Google Scholar]
- Chen, Q. Analysis on limit state equations for reliability design of side slope of embankment and parameter sensitivity. Rock Soil Mech. 1995, 16, 13–21. [Google Scholar]
- Zhang, X.; Gong, X.; Xu, R. Orthogonality analysis method of sensibility on factor of slope stability. China J. Highw. Transp. 2003, 16, 36–39. [Google Scholar]
- Ji, D.; Yang, Q. Studies on sensibilities of factors influencing on reinforced uniform slope stability. Rock Soil Mech. 2004, 25, 1089–1092. [Google Scholar]
- Zhang, Y.; Du, X. Simple sensitivity measures of reliability to system parameters. J. TongJi Univ. 1996, 24, 475–480. [Google Scholar]
- Hsu, C.; Yang, C.; Wang, H. Multi-threshold level set model for image segmentation. EURASIP J. Adv. Signal Process. 2010, 2010, 950438. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Lebedev, M.; Sarmadivaleh, M.; Barifcani, A.; Iglauer, S. Multi-scale x-ray computed tomography analysis of coal microstructure and permeability changes as a function of effective stress. Int. J. Coal Geol. 2016, 165, 149–156. [Google Scholar] [CrossRef]
- Dong, H.; Sun, J.; Lin, Z.; Cui, L.; Yan, W. Quantitative characterization and characteristics analysis of microscopic pore structure in natural gas hydrate based on CT scanning. J. China Univ. Pet. 2018, 42, 40–49. [Google Scholar]
- Dong, H.; Sun, J.; Lin, Z.; Fang, H.; Li, Y.; Cui, L.; Yan, W. 3D pore-type digital rock modeling of natural gas hydrates for permafrost and numerical simulation of electrical properties. J. Geophys. Eng. 2018, 15, 275–285. [Google Scholar] [CrossRef]
- Lv, H.; Li, X.; Gu, B. Origins and log responses of neogene of low-resistivity oil pays in Bohai sea. China Offshore Oil Gas 2006, 18, 97–102. [Google Scholar]
- Deng, J.; Wang, Z.; Gao, C. Estimation of sensitivity of Chang 2 reservoir in Zhanghan area. J. North West Univ. (Nat. Sci. Ed.) 2011, 41, 285–290. [Google Scholar]
- Feng, J. An analysis of the factors to influence electrical properties of rocks based on a digital petrophysical experiment: A case of the middle-shallow sandstone reservoirs in Pearl river mouth basin (the eastern area). China Offshore Oil Gas 2012, 24, 12–16. [Google Scholar]
- Meng, Z.P.; Zhang, J.X.; Liu, H. Productivity model of CBM wells considering the stress sensitivity and its application analysis. J. China Coal Soc. 2014, 39, 593–599. [Google Scholar]
| Influence Factor Level | Influencing Factors | |||||
|---|---|---|---|---|---|---|
| Shale Content (%) | Conductive Mineral Content (%) | Formation Water Salinity (mg/L) | Micropore Content (%) | Average Coordination Number | Water Film Thickness (um) | |
| 1 | +20% (10.470) | +20% (4.406) | +20% (9600) | +20% (5.237) | +20% (8.809) | +20% (0.317) |
| 2 | +10% (9.598) | +10% (4.039) | +10% (8800) | +10% (4.800) | +10% (8.075) | +10% (0.290) |
| 3 | 0% (8.725) | 0% (3.672) | 0% (8000) | 0% (4.364) | 0% (7.341) | 0% (0.264) |
| 4 | −10% (7.853) | −10% (3.305) | −10% (7200) | −10% (3.928) | −10% (6.607) | −10% (0.238) |
| 5 | −20% (6.980) | −20% (2.938) | −20% (6400) | −20% (3.491) | −20% (5.873) | −20% (0.211) |
| Calculation Scheme | Influencing Factors | Rock Resistivity | ||||||
|---|---|---|---|---|---|---|---|---|
| Shale Content | Conductive Mineral Content | Formation Water Salinity | Micropore Content | Average Coordination Number | Water Film Thickness | Water Saturation | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 14.73% | 72.96% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 333.220 | 104.496 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 356.301 | 111.178 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 384.360 | 118.014 |
| 4 | 1 | 4 | 4 | 4 | 4 | 4 | 418.197 | 124.476 |
| 5 | 1 | 5 | 5 | 5 | 5 | 5 | 457.893 | 130.667 |
| 6 | 2 | 1 | 2 | 3 | 4 | 5 | 364.890 | 113.273 |
| 7 | 2 | 2 | 3 | 4 | 5 | 1 | 393.076 | 121.002 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 | 427.412 | 128.659 |
| 9 | 2 | 4 | 5 | 1 | 2 | 3 | 429.735 | 135.731 |
| 10 | 2 | 5 | 1 | 2 | 3 | 4 | 366.786 | 107.990 |
| 11 | 3 | 1 | 3 | 5 | 2 | 4 | 403.096 | 123.621 |
| 12 | 3 | 2 | 4 | 1 | 3 | 5 | 402.340 | 132.680 |
| 13 | 3 | 3 | 5 | 2 | 4 | 1 | 437.083 | 141.502 |
| 14 | 3 | 4 | 1 | 3 | 5 | 2 | 379.830 | 110.945 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 | 406.179 | 118.312 |
| 16 | 4 | 1 | 4 | 2 | 5 | 3 | 410.955 | 136.060 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 | 446.940 | 147.001 |
| 18 | 4 | 3 | 1 | 4 | 2 | 5 | 392.275 | 113.866 |
| 19 | 4 | 4 | 2 | 5 | 3 | 1 | 420.935 | 121.618 |
| 20 | 4 | 5 | 3 | 1 | 4 | 2 | 416.102 | 130.750 |
| 21 | 5 | 1 | 5 | 4 | 3 | 2 | 460.085 | 151.657 |
| 22 | 5 | 2 | 1 | 5 | 4 | 3 | 404.812 | 116.471 |
| 23 | 5 | 3 | 2 | 1 | 5 | 4 | 398.357 | 124.259 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 | 427.312 | 133.643 |
| 25 | 5 | 5 | 4 | 3 | 2 | 1 | 460.719 | 144.842 |
| Influencing Factor | Shale Content | Conductive Mineral Content | Formation Water Salinity | Micropore Content | Average Coordination Number | Water Film Thickness |
|---|---|---|---|---|---|---|
| K1j | 2856.69 | 2926.39 | 2911.89 | 2887.53 | 2905.47 | 2948.44 |
| K2j | 2880.18 | 2928.52 | 2918.89 | 2893.63 | 2909.87 | 2948.32 |
| K3j | 2906.46 | 2930.42 | 2926.35 | 2899.98 | 2914.01 | 2950.20 |
| K4j | 2937.87 | 2932.27 | 2934.98 | 2907.18 | 2918.21 | 2951.28 |
| K5j | 2972.66 | 2934.16 | 2944.25 | 2914.18 | 2922.40 | 2952.62 |
| K1j | 571.34 | 585.28 | 582.38 | 577.51 | 581.09 | 589.69 |
| K2j | 576.04 | 585.70 | 583.78 | 578.73 | 581.97 | 589.86 |
| K3j | 581.29 | 586.08 | 585.27 | 579.99 | 582.80 | 590.04 |
| K4j | 587.57 | 586.45 | 586.99 | 581.42 | 583.64 | 590.26 |
| K5j | 594.53 | 586.83 | 588.85 | 582.84 | 584.48 | 590.52 |
| Sj | 1499.55 | 356.59 | 1427.60 | 69357.84 | 29.25 | 622.79 |
| Influencing Factor | Shale Content | Conductive Mineral Content | Formation Water Salinity | Micropore Content | Average Coordination Number | Water Film Thickness |
|---|---|---|---|---|---|---|
| K1j | 1209.99 | 1204.21 | 1135.35 | 1215.11 | 1214.84 | 1213.34 |
| K2j | 1214.26 | 1210.81 | 1173.37 | 1217.72 | 1217.24 | 1221.13 |
| K3j | 1218.23 | 1217.52 | 1214.50 | 1220.48 | 1219.47 | 1229.10 |
| K4j | 1222.42 | 1224.66 | 1253.73 | 1223.54 | 1221.86 | 1236.73 |
| K5j | 1226.50 | 1231.69 | 1296.24 | 1226.64 | 1224.58 | 1243.99 |
| K1j | 241.99 | 240.84 | 227.07 | 243.02 | 242.97 | 242.67 |
| K2j | 242.85 | 242.16 | 234.67 | 243.54 | 243.45 | 244.23 |
| K3j | 243.65 | 243.50 | 242.90 | 244.10 | 243.89 | 245.82 |
| K4j | 244.48 | 244.93 | 250.75 | 244.71 | 244.37 | 247.35 |
| K5j | 245.30 | 246.34 | 259.25 | 245.33 | 244.92 | 248.79 |
| Sj | 11840.97 | 122.87 | 3230.31 | 13.65 | 9.37 | 793.75 |
| Water Saturation | Influencing Factor | Deviation Sum of Squares/Sj | Degree of Freedom/fj | Mean Sum of Square/Sj | Fj Value | Significance |
|---|---|---|---|---|---|---|
| 14.73% | Shale content | 1499.55 | 4 | 374.89 | 59.02 | Highly sensitive |
| Conductive mineral content | 356.59 | 4 | 89.15 | 14.03 | Very sensitive | |
| Formation water salinity | 1427.60 | 4 | 356.90 | 56.19 | Highly sensitive | |
| Micropore content | 69,357.84 | 4 | 17,339.46 | 2729.72 | Highly sensitive | |
| Average coordination number | 29.25 | 4 | 7.31 | 1.15 | Insensitive | |
| Water film thickness | 622.79 | 4 | 155.70 | 24.51 | Very sensitive | |
| 72.96% | Shale content | 11,840.97 | 4 | 2960.24 | 1597.54 | Highly sensitive |
| Conductive mineral content | 122.87 | 4 | 30.72 | 16.58 | Highly sensitive | |
| Formation water salinity | 3230.31 | 4 | 807.58 | 435.82 | Highly sensitive | |
| Micropore content | 13.65 | 4 | 3.41 | 1.84 | Insensitive | |
| Average coordination number | 9.37 | 4 | 2.34 | 1.26 | Insensitive | |
| Water film thickness | 793.75 | 4 | 198.44 | 107.09 | Highly sensitive |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Dong, H.; Fang, H.; Sun, J.; Wang, X. Sensitivity Analysis of Rock Electrical Influencing Factors of Natural Gas Hydrate Reservoir in Permafrost Region of Qilian Mountain, China. Energies 2019, 12, 4592. https://doi.org/10.3390/en12234592
Lin Z, Dong H, Fang H, Sun J, Wang X. Sensitivity Analysis of Rock Electrical Influencing Factors of Natural Gas Hydrate Reservoir in Permafrost Region of Qilian Mountain, China. Energies. 2019; 12(23):4592. https://doi.org/10.3390/en12234592
Chicago/Turabian StyleLin, Zhenzhou, Huaimin Dong, Hui Fang, Jianmeng Sun, and Xiaojiang Wang. 2019. "Sensitivity Analysis of Rock Electrical Influencing Factors of Natural Gas Hydrate Reservoir in Permafrost Region of Qilian Mountain, China" Energies 12, no. 23: 4592. https://doi.org/10.3390/en12234592
APA StyleLin, Z., Dong, H., Fang, H., Sun, J., & Wang, X. (2019). Sensitivity Analysis of Rock Electrical Influencing Factors of Natural Gas Hydrate Reservoir in Permafrost Region of Qilian Mountain, China. Energies, 12(23), 4592. https://doi.org/10.3390/en12234592




