Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models
Abstract
:1. Introduction
2. Large-Eddy Simulation Framework
2.1. Governing Equations
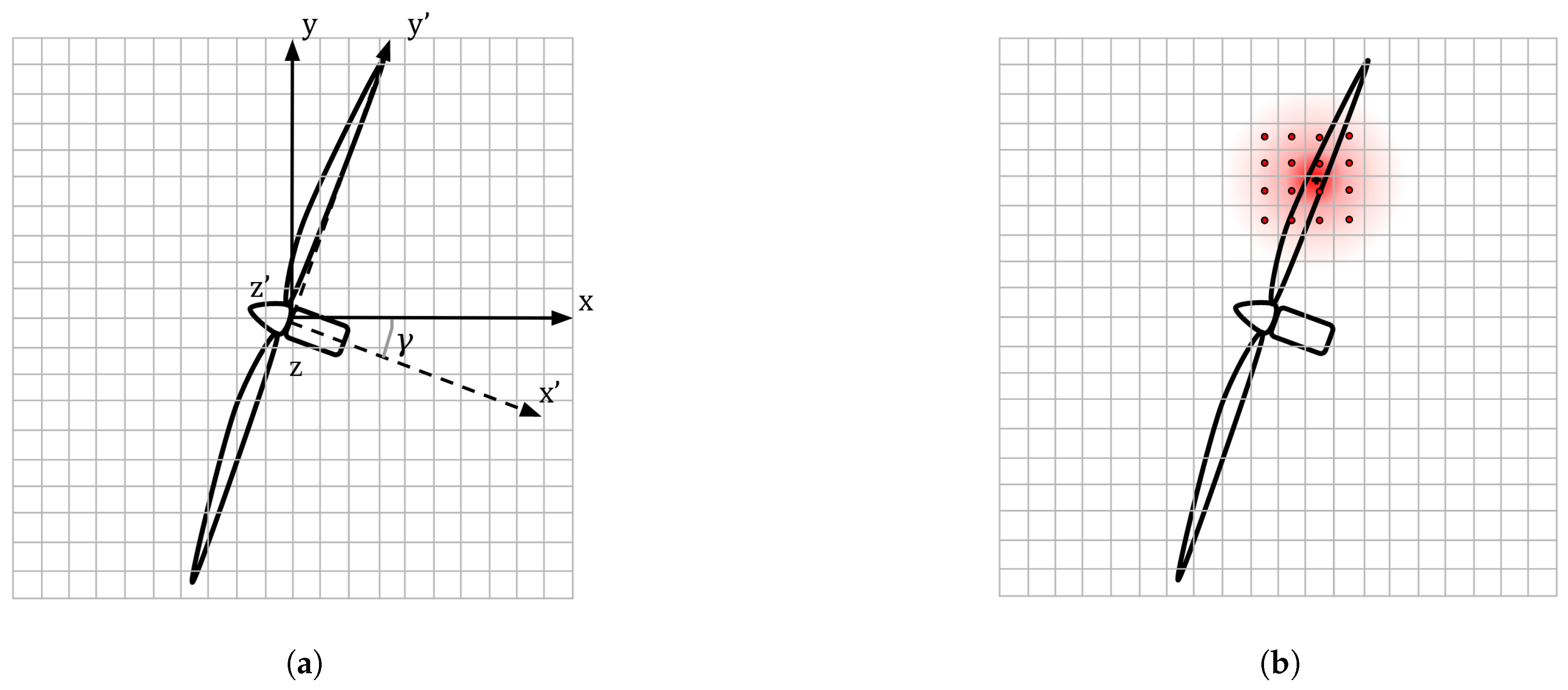
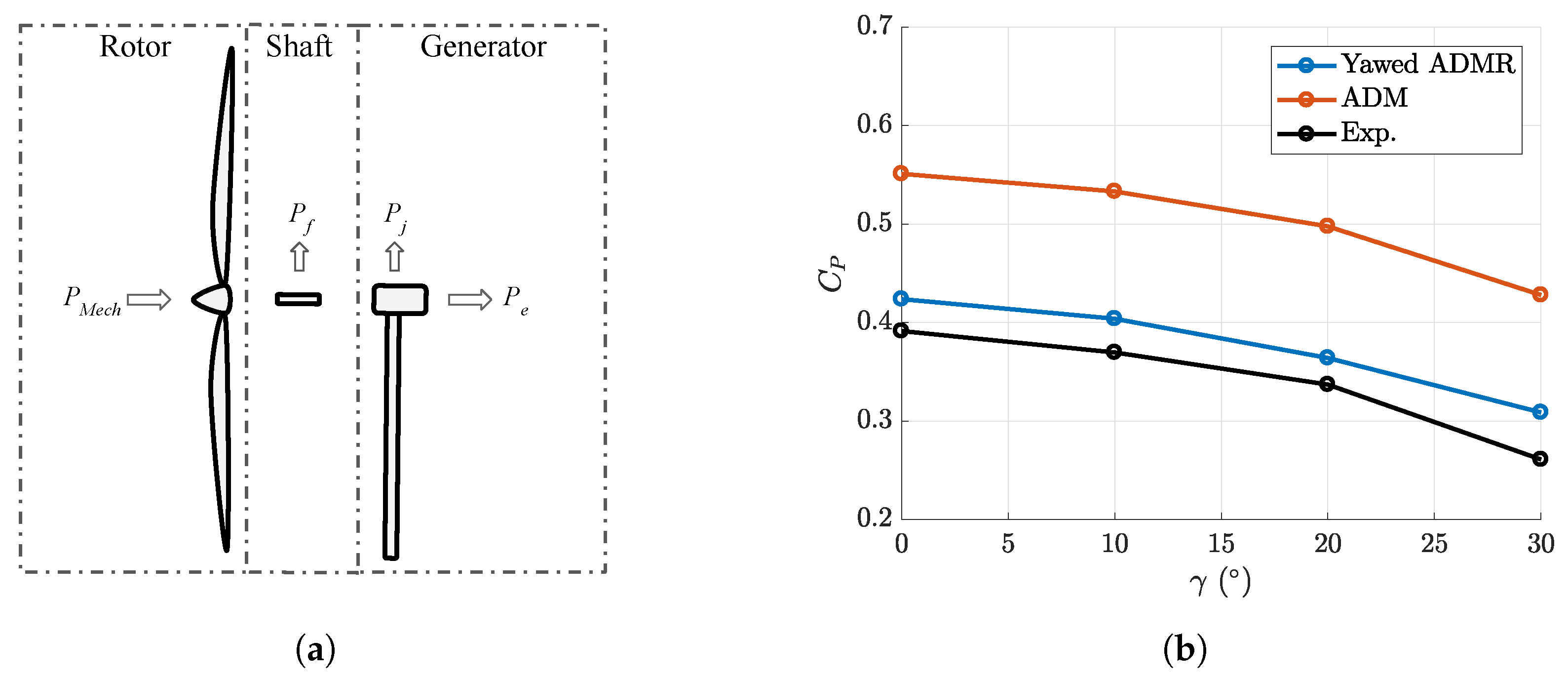
2.2. Wind Turbine Parameterisation
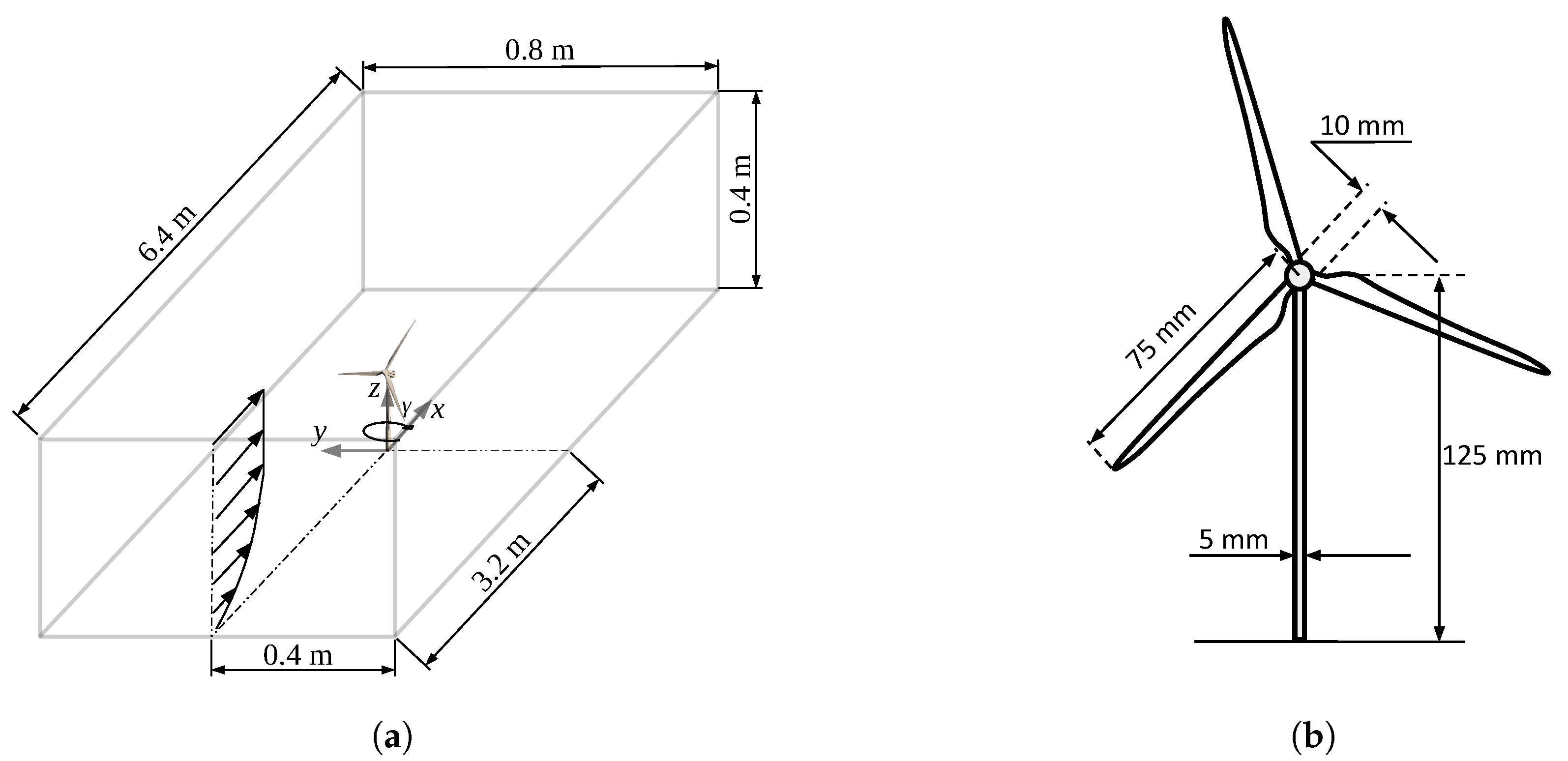
2.3. Numerical Setup
3. Results
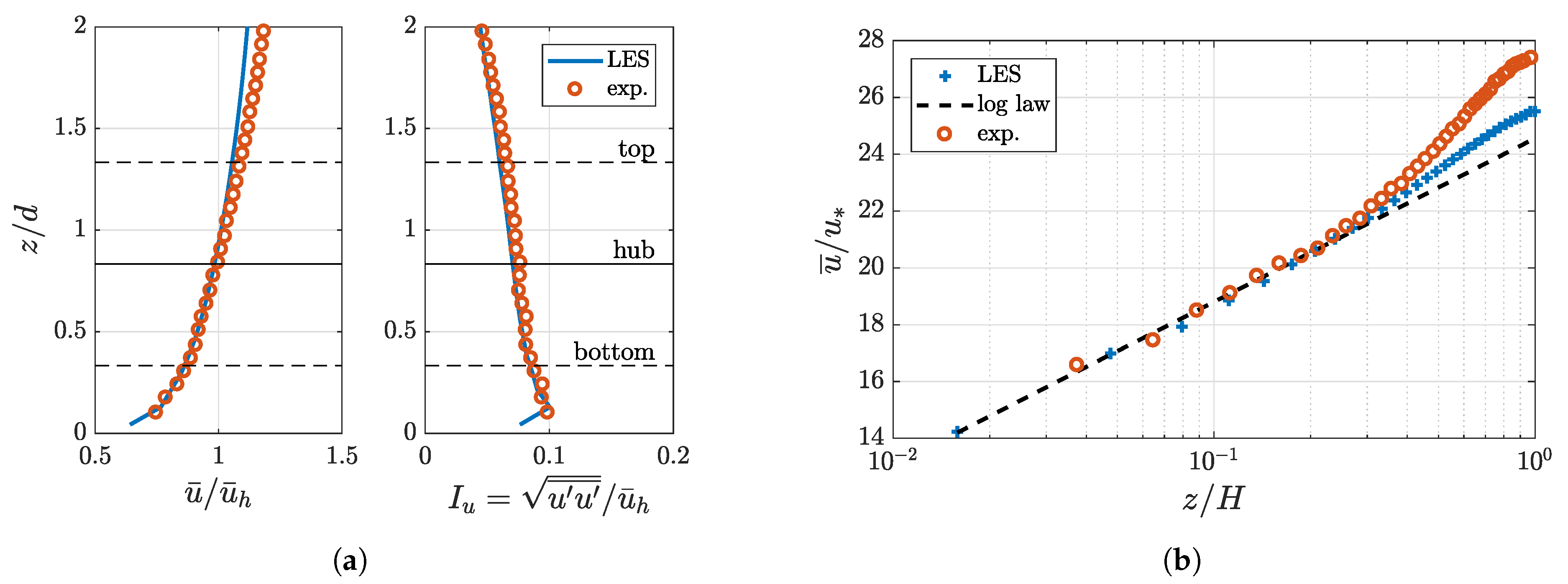
3.1. Inflow Conditions
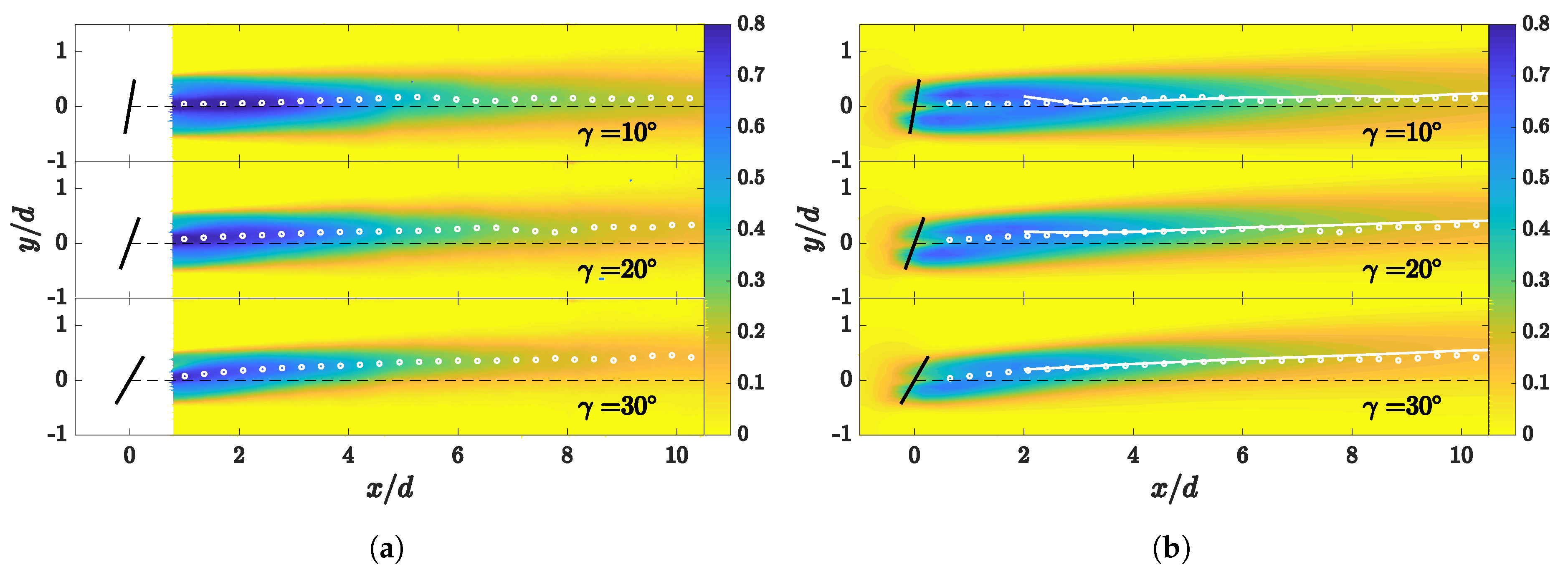
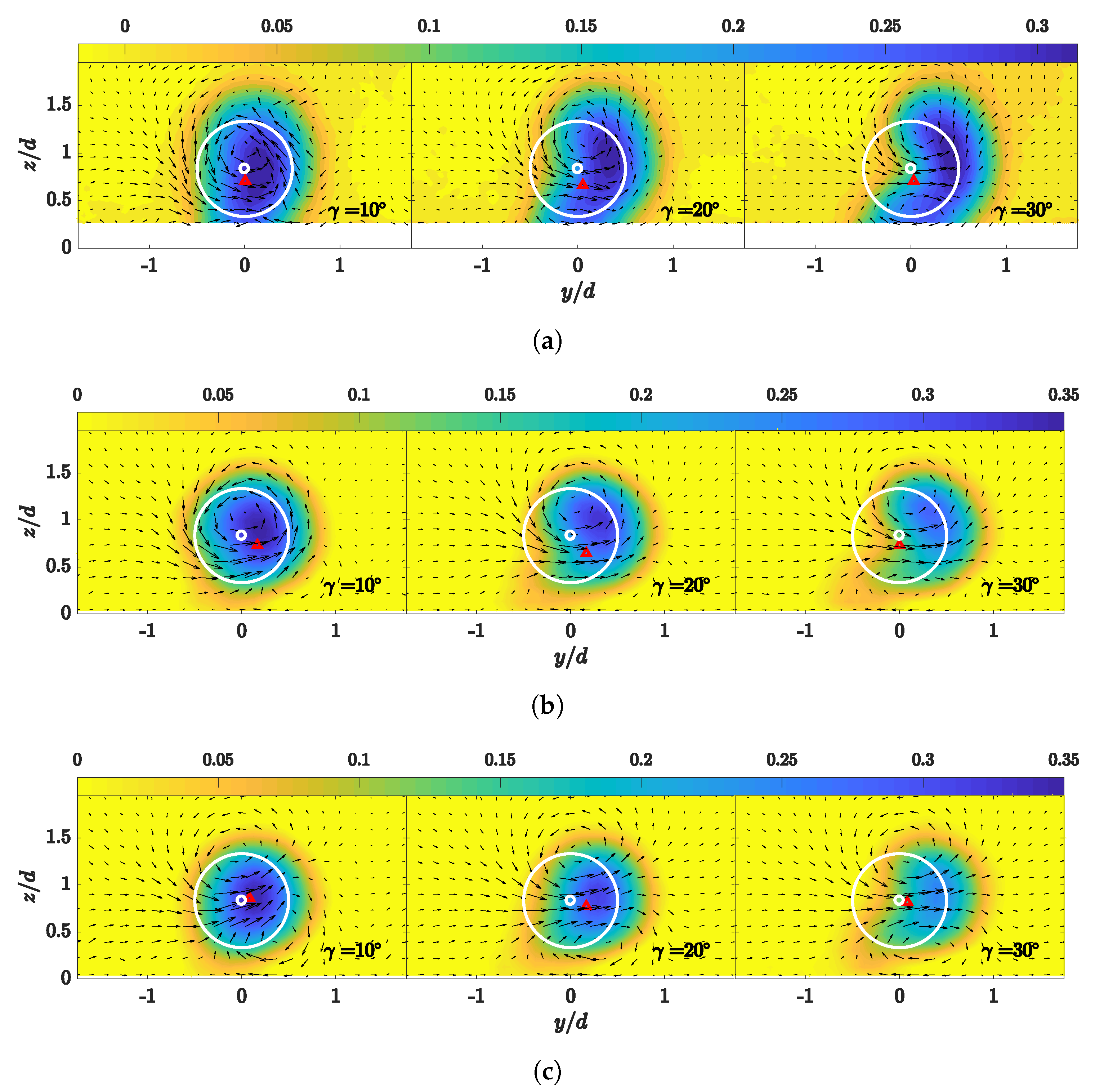
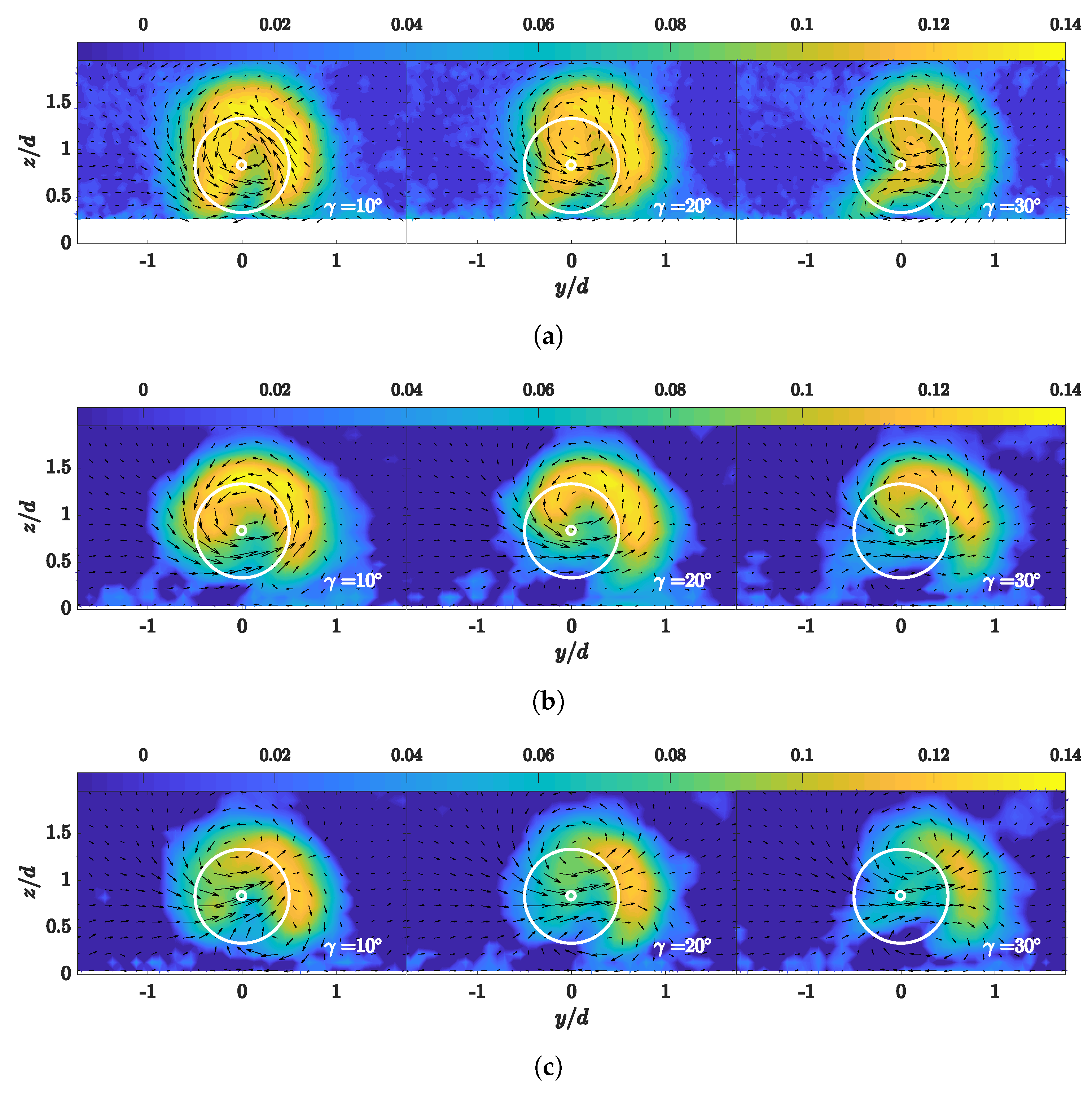
3.2. Velocity Deficit and Turbulence Intensity Contours
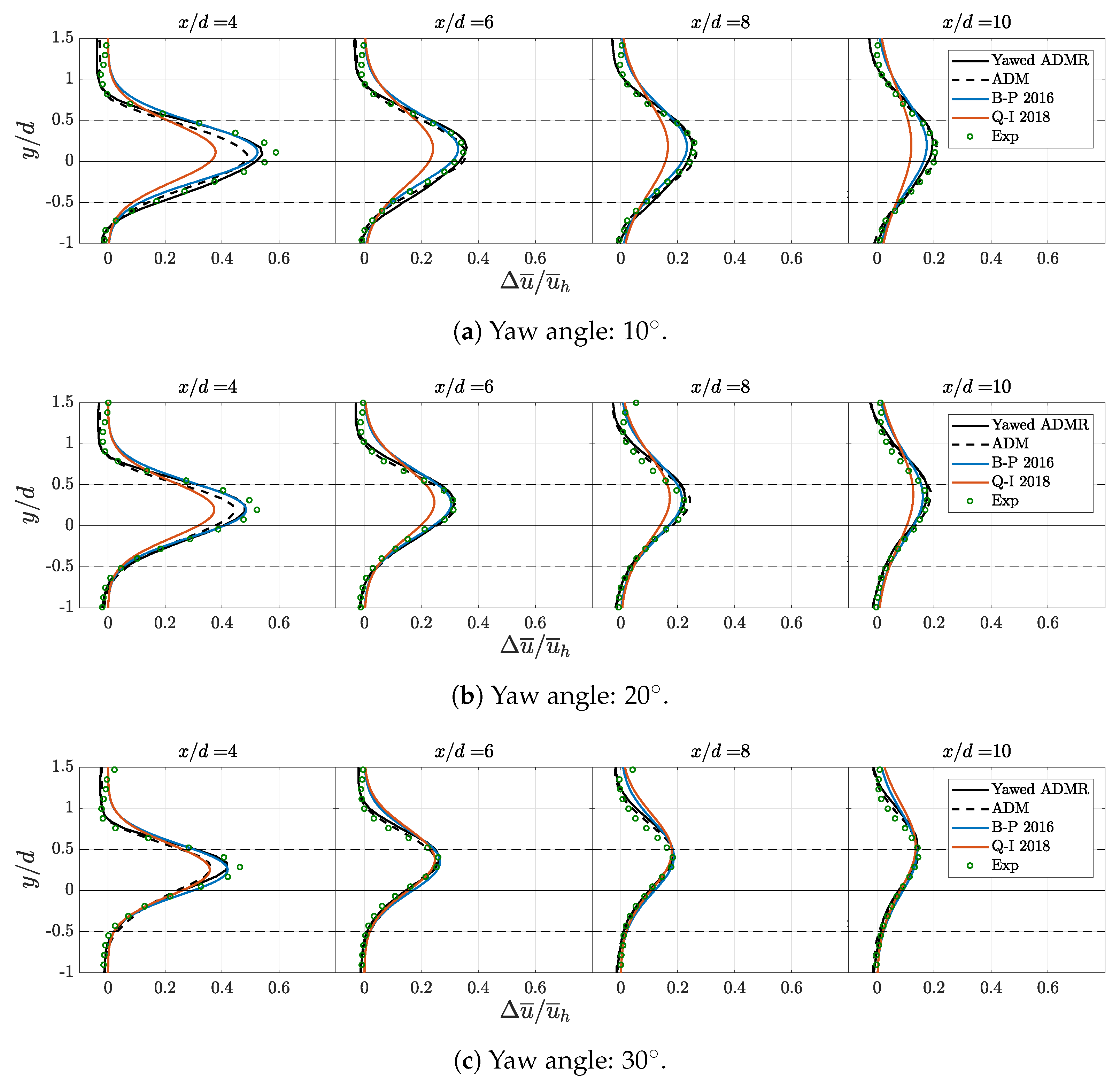
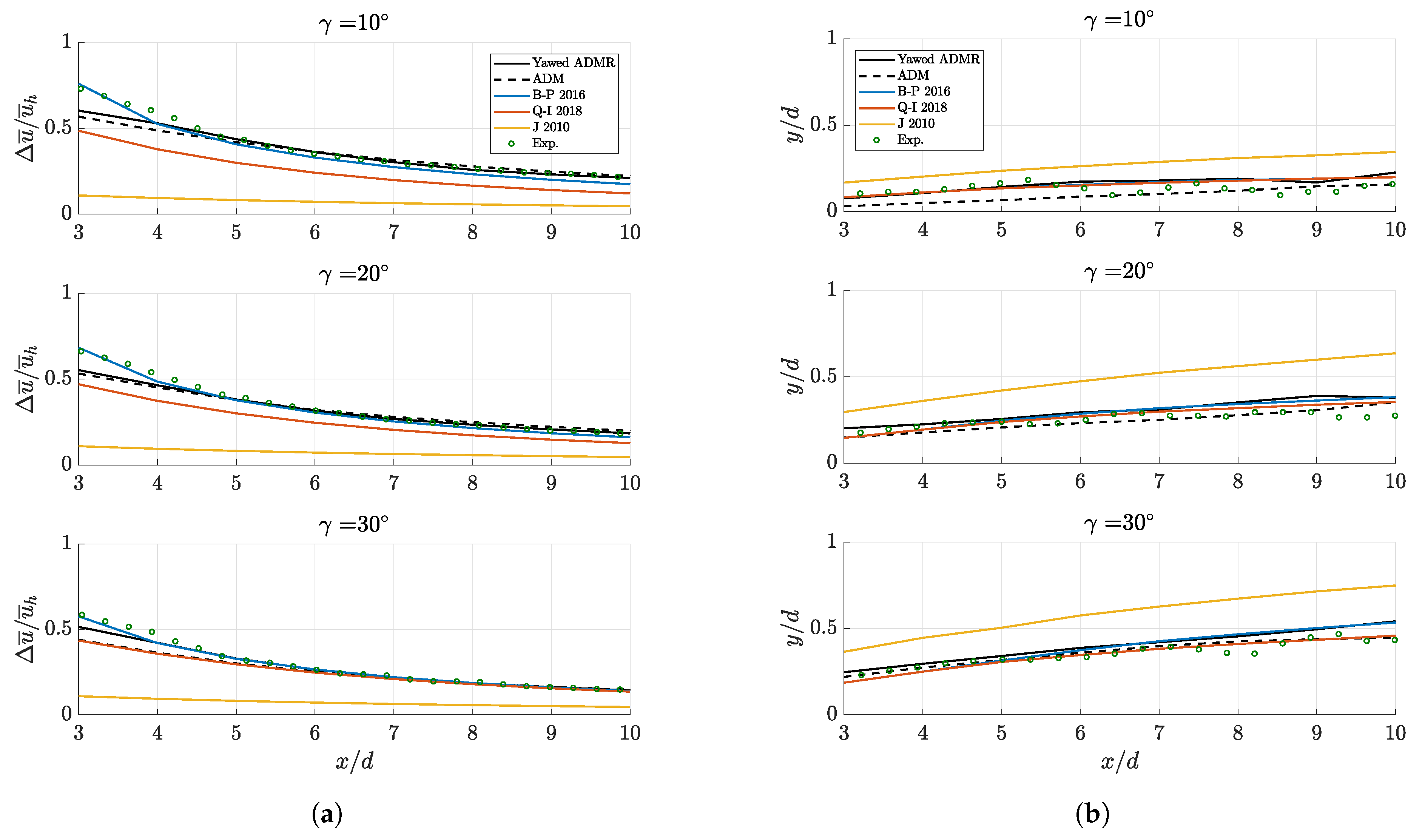
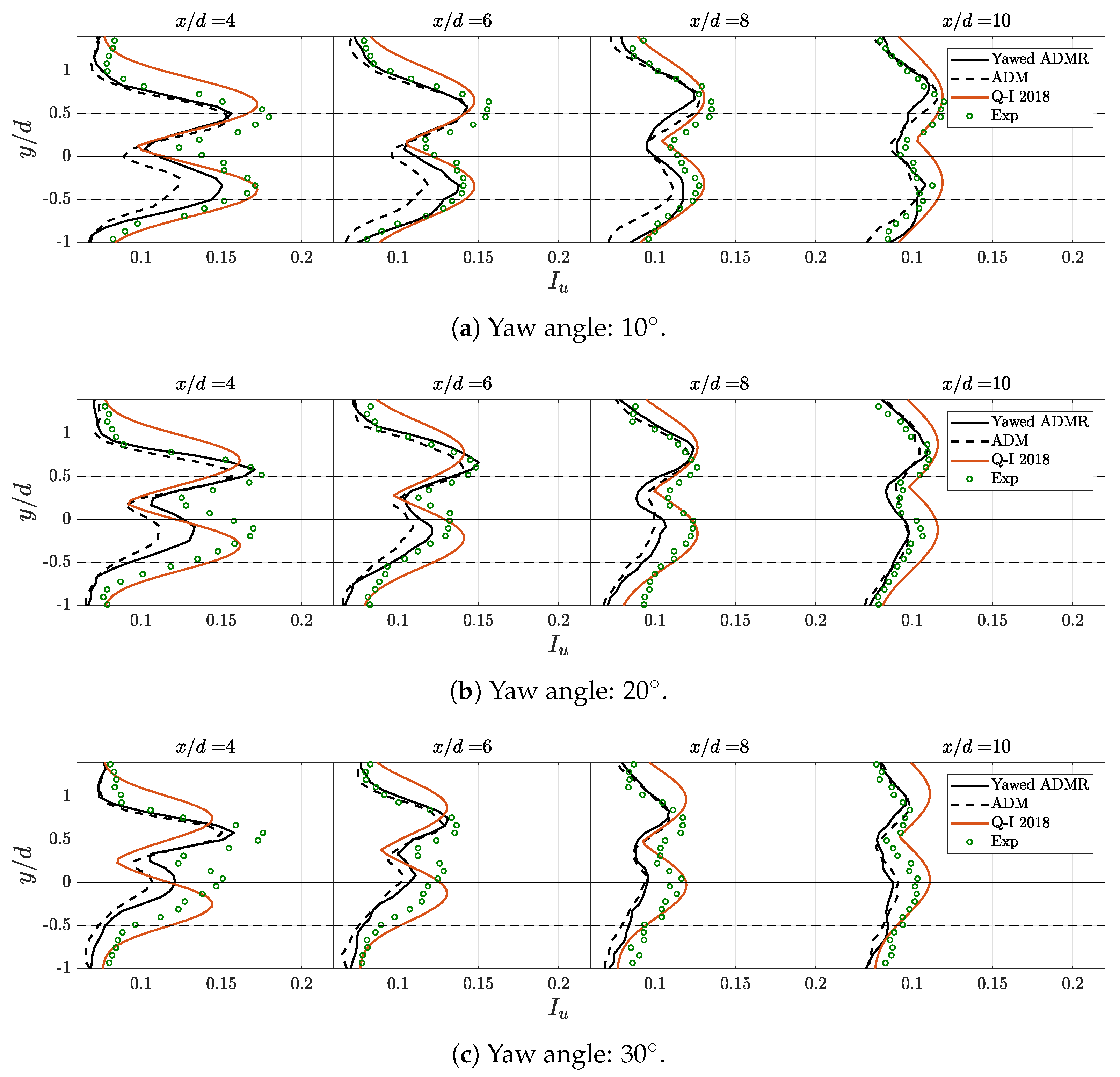
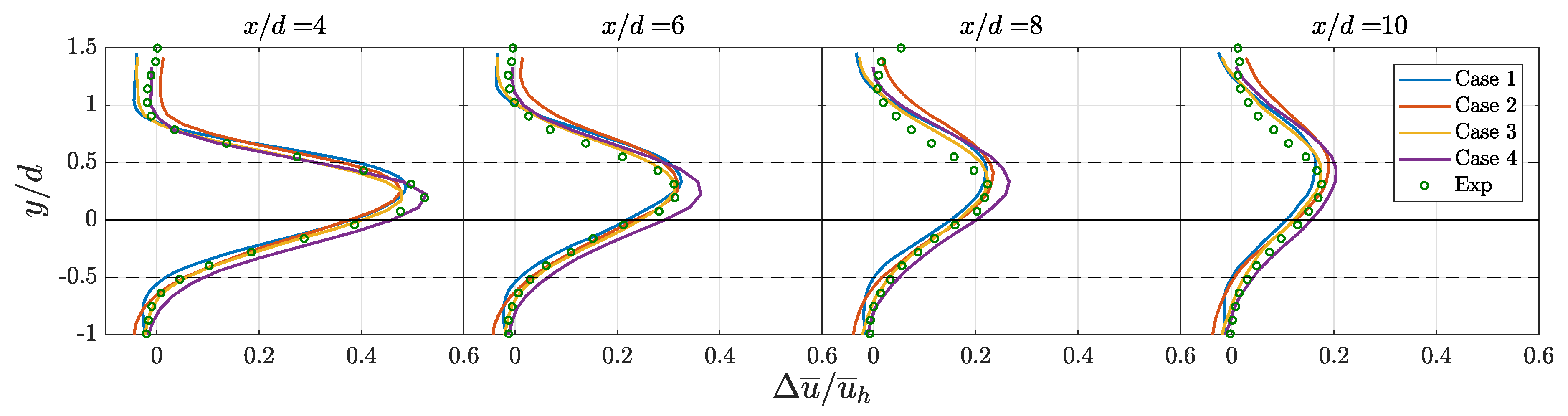
3.3. Spanwise Velocity Deficit and Turbulence Intensity Profiles
3.4. Mechanical Power Predictions
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stevens, R.J.; Meneveau, C. Flow structure and turbulence in wind farms. Annu. Rev. Fluid Mech. 2017, 49, 311–339. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Available online: https://doi.org/10.1007/s10546-019-00473-0 (accessed on 7 September 2019).
- Lavely, A.W.; Vijayakumar, G.; Craven, B.; Jayaraman, B.; Paterson, E.G.; Nandi, T.N.; Brasseur, J. Towards a blade-resolved hybrid URANS-LES of the NREL 5-MW wind turbine rotor within large eddy simulation of the atmospheric boundary layer. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014; p. 0869. [Google Scholar]
- Jiménez, A.; Crespo, A.; Migoya, E.; García, J. Advances in large-eddy simulation of a wind turbine wake. J. Phys. Conf. Ser. 2007, 75, 012041. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound.-Layer Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Mikkelsen, R.F.; Henningson, D.S.; Ivanell, S.; Sarmast, S.; Andersen, S.J. Simulation of wind turbine wakes using the actuator line technique. Philos. Trans. R. Soc. A 2015, 373. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Leonardi, S. Large eddy simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy 2015, 18, 1047–1060. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Martínez-Tossas, L.A.; Meneveau, C. Comparison of wind farm large eddy simulations using actuator disk and actuator line models with wind tunnel experiments. Renew. Energy 2018, 116, 470–478. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Lu, H.; Wu, Y.T. A large-eddy simulation framework for wind energy applications. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010; Volume 23. [Google Scholar]
- Jiménez, Á.; Crespo, A.; Migoya, E. Application of a LES technique to characterize the wake deflection of a wind turbine in yaw. Wind Energy 2010, 13, 559–572. [Google Scholar] [CrossRef]
- Munters, W.; Meyers, J. Dynamic strategies for yaw and induction control of wind farms based on large-eddy simulation and optimization. Energies 2018, 11, 177. [Google Scholar] [CrossRef]
- Boersma, S.; Doekemeijer, B.; Siniscalchi-Minna, S.; van Wingerden, J. A constrained wind farm controller providing secondary frequency regulation: An LES study. Renew. Energy 2019, 134, 639–652. [Google Scholar] [CrossRef]
- Fleming, P.; Annoni, J.; Churchfield, M.; Martinez-Tossas, L.A.; Gruchalla, K.; Lawson, M.; Moriarty, P. A Simulation Study Demonstrating the Importance of Large-Scale Trailing Vortices in Wake Steering; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Fleming, P.A.; Gebraad, P.M.O.; Lee, S.; van Wingerden, J.W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Evaluating techniques for redirecting turbine wakes using SOWFA. Renew. Energy 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Wang, J.; Foley, S.; Nanos, E.M.; Yu, T.; Campagnolo, F.; Bottasso, C.L.; Zanotti, A.; Croce, A. Numerical and experimental study of wake redirection techniques in a boundary layer wind tunnel. J. Phys. Conf. Ser. 2017, 854, 012048. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Bastankhah, M.; Porté-Agel, F. Experimental and theoretical study of wind turbine wakes in yawed conditions. J. Fluid Mech. 2016, 806, 506–541. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Shapiro, C.R.; Gayme, D.F.; Meneveau, C. Modelling yawed wind turbine wakes: A lifting line approach. J. Fluid Mech. 2018, 841, R1. [Google Scholar] [CrossRef]
- Qian, G.W.; Ishihara, T. A New Analytical Wake Model for Yawed Wind Turbines. Energies 2018, 11, 665. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Annoni, J.; Fleming, P.A.; Churchfield, M.J. The aerodynamics of the curled wake: A simplified model in view of flow control. Wind Energy Sci. 2019, 4, 127–138. [Google Scholar] [CrossRef]
- Bay, C.; King, J.; Fleming, P.; Mudafort, R. Unlocking the Full Potential of Wake Steering: Implementation and Assessment of a Controls-Oriented Model; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2019.
- Howland, M.F.; Bossuyt, J.; Martínez-Tossas, L.A.; Meyers, J.; Meneveau, C. Wake structure in actuator disk models of wind turbines in yaw under uniform inflow conditions. J. Renew. Sustain. Energy 2016, 8, 043301. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulation: Application to a neutral atmospheric boundary layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef]
- Stoll, R.; Porté-Agel, F. Dynamic subgrid-scale models for momentum and scalar fluxes in large-eddy simulations of neutrally stratified atmospheric boundary layers over heterogeneous terrain. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Revaz, T.; Lin, M.; Porté-Agel, F. Aerodynamic Data of WiRE-01 Blade. 2019. Available online: https://zenodo.org/record/3460877#.XdyLmtK-uUk (accessed on 25 September 2019).
- Sørensen, J.N.; Shen, W.Z.; Munduate, X. Analysis of wake states by a full-field actuator disc model. Wind Energy 1998, 1, 73–88. [Google Scholar] [CrossRef]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines; Technical University of Denmark: Kongens Lyngby, Denmark, 2003. [Google Scholar]
- Smith, R.A.; Moon, W.T.; Kao, T. Experiments on flow about a yawed circular cylinder. J. Basic Eng. 1972, 94, 771–776. [Google Scholar] [CrossRef]
- Wei, T.; Willmarth, W. Static Pressure Distribution on Long Cylinders as Function of Angle of Yaw and Reynolds Number; Technical Report; Department of Aerospace Engineering, University of Michigan: Ann Arbor, MI, USA, 1983. [Google Scholar]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 1982, 118, 341–377. [Google Scholar] [CrossRef]
- Moeng, C.H. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Biringen, S. Active control of transition by periodic suction-blowing. Phys. Fluids 1984, 27, 1345–1347. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Atmospheric turbulence effects on wind-turbine wakes: An LES study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Simulation of turbulent flow inside and above wind farms: Model validation and layout effects. Bound.-Layer Meteorol. 2013, 146, 181–205. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A New Miniature Wind Turbine for Wind Tunnel Experiments. Part I: Design and Performance. Energies 2017, 10, 908. [Google Scholar] [CrossRef]
- Chow, F.K.; Street, R.L.; Xue, M.; Ferziger, J.H. Explicit filtering and reconstruction turbulence modeling for large-eddy simulation of neutral boundary layer flow. J. Atmos. Sci. 2005, 62, 2058–2077. [Google Scholar] [CrossRef]
- Allaerts, D.; Meyers, J. Large eddy simulation of a large wind-turbine array in a conventionally neutral atmospheric boundary layer. Phys. Fluids 2015, 27, 065108. [Google Scholar] [CrossRef] [Green Version]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13. [Google Scholar] [CrossRef]
- Zong, H.; Porté-Agel, F. A point vortex transportation model for yawed wind turbine wakes. J. Fluid Mech. 2019. submitted. [Google Scholar]
- Hansen, M.O. Aerodynamics of Wind Turbines; Routledge: Abingdon, UK, 2015. [Google Scholar]
- Munters, W.; Meyers, J. An optimal control framework for dynamic induction control of wind farms and their interaction with the atmospheric boundary layer. Philos. Trans. R. Soc. A 2017, 375. [Google Scholar] [CrossRef] [Green Version]
| Inflow Characteristic | Value |
|---|---|
| Boundary-layer height (H) | 0.4 m |
| Hub-height incoming velocity () | 4.88 m/s |
| Hub-height turbulence intensity () | 7% |
| Surface roughness length () | 0.022 mm |
| Friction velocity () | 0.22 m/s |
| Case No. | |||||
|---|---|---|---|---|---|
| 1 | 256 | 128 | 64 | 24 | 24 |
| 2 | 128 | 64 | 64 | 12 | 24 |
| 3 | 128 | 64 | 32 | 12 | 12 |
| 4 | 96 | 48 | 24 | 9 | 9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, M.; Porté-Agel, F. Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models. Energies 2019, 12, 4574. https://doi.org/10.3390/en12234574
Lin M, Porté-Agel F. Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models. Energies. 2019; 12(23):4574. https://doi.org/10.3390/en12234574
Chicago/Turabian StyleLin, Mou, and Fernando Porté-Agel. 2019. "Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models" Energies 12, no. 23: 4574. https://doi.org/10.3390/en12234574
APA StyleLin, M., & Porté-Agel, F. (2019). Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models. Energies, 12(23), 4574. https://doi.org/10.3390/en12234574






