Recent Approaches of Forecasting and Optimal Economic Dispatch to Overcome Intermittency of Wind and Photovoltaic (PV) Systems: A Review
Abstract
1. Introduction
2. Forecasting of Wind Power Generation
2.1. Wind Power Generation Fundamentals
2.2. Weibull Distribution (WD) for Wind Power Forecasting
2.3. Review of Wind Power Forecasting without NN
2.4. Review of Wind Power Forecasting with the Incorporation of NN
3. Forecasting Solar PV Power Generation
3.1. Solar PV Power Generation Fundamentals
3.2. Weibull Distribution (WD) for Solar (PV) Forecasting
3.3. Review of PV Power Forecasting without NN
3.4. Review of PV Power Forecasting with the Incorporation of NN
4. Optimal Economic Dispatching (OED) using PSO
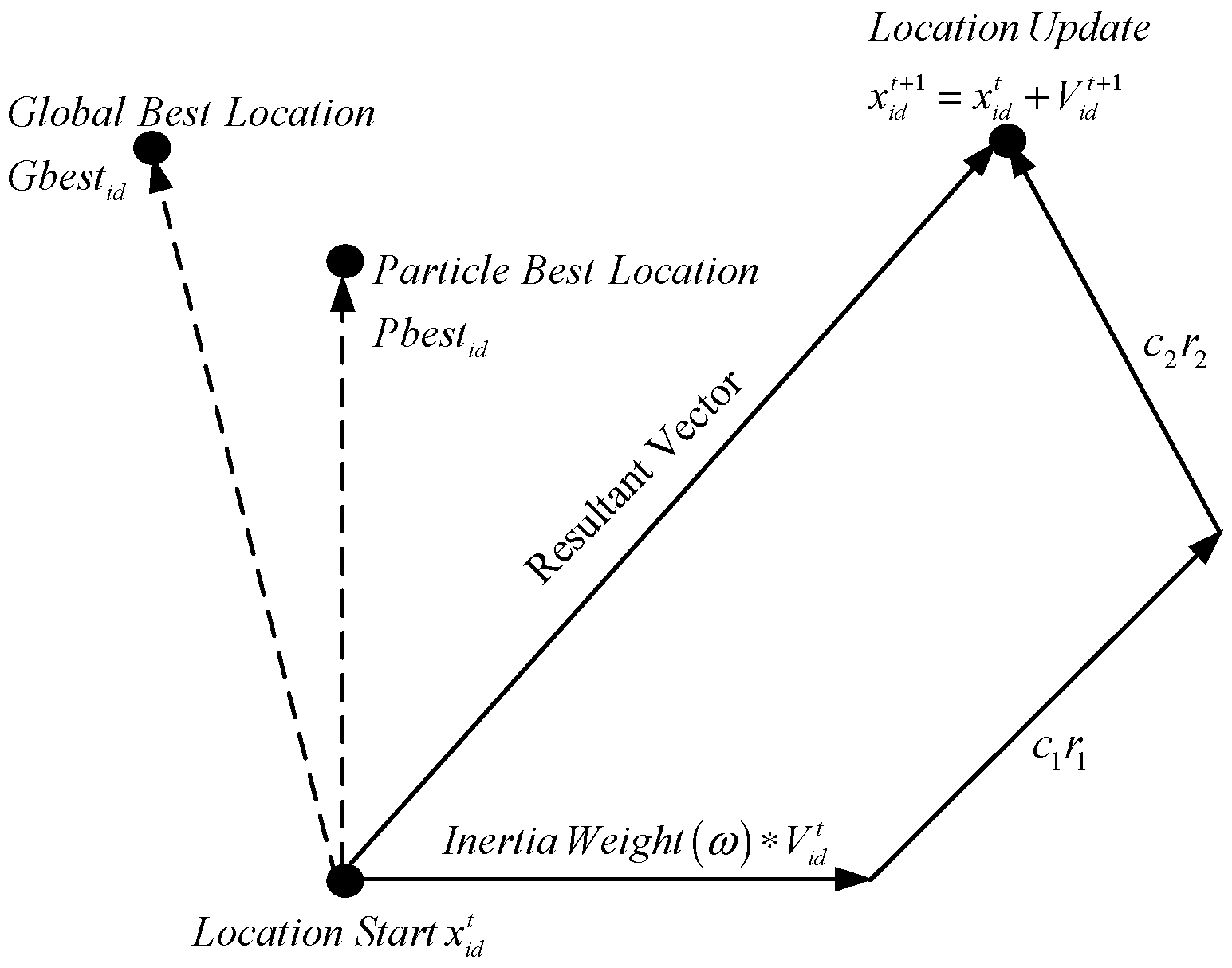
4.1. A Brief Review of PSO Algorithm
4.2. Review of PSO Applied to OED Incorporating RESs
4.3. Constraints Handling by PSO
4.3.1. Compensation for Load and Voltage Variation
4.3.2. Control of Frequency Fluctuations
4.3.3. Regulation of Ramp-Rate Limits
4.3.4. Storage Mechanism as a Solution
- (i)
- Thermal Power Generation is dependable, but it presents major issues such as a rise in carbon emissions, an increase in fuel cost, and special consideration is required in system coordination. We cannot use thermal plants as backup generation only as they take a significant amount of time in their start-up, and fuel cost for spinning reserve contributes to disturbing the economic dispatch that is a major concern in current power system.
- (ii)
- Battery Storage compensation through batteries is a modern age replacement of backup thermal plants. It requires a properly designed storage system to provide adequate power to supply the load when power from RESs is lesser than the demand. The battery storage system also provides an additional benefit of peak shaving as RES starts supplying an excessive supply for storage [117,118]. The major concern is of designing a properly designed storage system to achieve the optimum cost-saving and stability of the power system.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Networks |
| ANFIS | Artificial Neuro Fuzzy Inference System |
| CNN | Convolutional Neural Networks |
| CEED | Combined Emission Economic Dispatch |
| DED | Dynamic Economic Dispatch |
| DWPSO | Double Weighted Particle Swarm Optimization |
| DNI | Direct Normal Solar Irradiation |
| ED | Economic Dispatch |
| EDP | Economic Dispatch Problem |
| ERCOT | Electric Reliability Council of Texas |
| ESRMC | Energy and Spinning Reserve Market Cleaning |
| EMD | Empirical Mode Decomposition |
| GHI | Graphical Horizontal Solar Irradiation |
| GP | Genetic Programming |
| HANN | Hybrid Artificial Neural Network |
| ICA | Independent Component Analysis |
| LUBE | Lower-Upper Bound Estimation |
| MLFFNN | Multi-layer Feed-forward Neural Networks |
| MAPE | Model Predictive Control |
| MG | Micro-grid |
| MMG | Multi Micro-grid |
| MOM | Method of Moments |
| NN | Neural Networks |
| NWP | Numerical Weather Predictor |
| OED | Optimal Economic Dispatch |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaics |
| PDEM | Part Density Energy Method |
| PI | Prediction Interval |
| PCA | Principal Component Analysis |
| RES | Renewable Energy Sources |
| RF | Reliability Factor |
| RBFNN | Radial Basis Function Neural Networks |
| RMSE | Root Mean Squared Error |
| SVM | Support Vector Machine |
| SD | Standard Deviation |
| SVR | Support Vector Regression |
| SSER | Small-Scale Energy Resource |
| WD | Weibull Distribution |
| WT | Wind Turbine |
| WTG | Wind Turbine Generator |
| WEC | World Energy Council |
References
- Hansen, J.; Kharecha, P.; Sato, M.; Masson-Delmotte, M.; Ackerman, F.; Beerling, J.D.; Hearty, P.J.; Hoegh-Guldberg, O.; Hsu, S.L.; Parmesan, C.; et al. Assessing dangerous climate change, required reduction of carbon emissions to protect young people, future generations and nature. PLoS ONE 2013, 8, e81648. [Google Scholar] [CrossRef] [PubMed]
- Nuclear Power: Totally Unqualified to Combat Climate Change. Available online: https://worldbusiness.org/ (accessed on 21 December 2018).
- Ela, E.; O’Malley, M. Studying the variability and uncertainty impacts of variable generation at multiple timescales. IEEE Trans. Power Syst. 2012, 27, 1324–1333. [Google Scholar] [CrossRef]
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Milligan, M.; Kirby, B. Calculating Wind Integration Costs: Separating Wind Energy Value from Integration Cost Impacts; No. NREL/TP-550-46275; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2009.
- Rondina, J.M. Technology Alternative for Enabling Distributed Generation. IEEE Lat. Am. Trans. 2016, 14, 4089–4096. [Google Scholar] [CrossRef]
- Distributed Generation. Environmental & Energy Study Institute. Available online: https://www.eesi.org/topics/distributed-generation/description (accessed on 27 December 2018).
- Libra, M.; Beránek, V.; Sedláček, J.; Poulek, V.; Tyukhov, I.I. Roof photovoltaic power plant operation during the solar eclipse. Sol. Energy 2016, 140, 109–112. [Google Scholar] [CrossRef]
- Distributed Generation. OFGEM. Available online: https://www.ofgem.gov.uk/electricity/distribution-networks/connections-and-competition/distributed-generation (accessed on 27 December 2018).
- Microgrids. Grid Integration group, Energy Storage and Distributed Sources Division. Available online: https://building-microgrid.lbl.gov/microgrid-definitions (accessed on 29 December 2018).
- Khan, I.; Zhang, Y.; Xue, H.; Nasir, M. A Distributed Coordination Framework for Smart Microgrids. In Smart Microgrids; Springer: Cham, Switzerland, 2019; pp. 119–136. [Google Scholar]
- Wan, Q.; Zhang, W.; Xu, Y.; Khan, I. Distributed control for energy management in a microgrid. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Zhaoyun, Z.; Wenjun, Z.; Mei, Y.; Li, K.; Zhi, Z.; Yang, Z.; Guozhong, L.; Na, Y. Application of Micro-Grid Control System in Smart Park. J. Eng. 2019, 2019, 3116–3119. [Google Scholar] [CrossRef]
- Weibull Analysis, An Overview of Basic Concepts. Available online: https://www.weibull.com/ (accessed on 22 December 2018).
- More, A.; Deo, M.C. Forecasting wind with neural networks. Mar. Struct. 2003, 16, 35–49. [Google Scholar] [CrossRef]
- Kirschen, D.S.; Ma, J.; Silva, V.; Belhomme, R. Optimizing the flexibility of a portfolio of generating plants to deal with wind generation. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Gerven, M.V.; Bohte, S. Artificial neural networks as models of neural information processing. Front. Comput. Neurosci. 2018, 11, 114. [Google Scholar] [CrossRef]
- Stergiou, C.; Siganos, D. Neural Networks. Available online: http://www.imperial.ac.uk/computing (accessed on 22 December 2018).
- Nasle, A.; Nasle, A. Systems and Methods for Real-Time Forecasting and Predicting of Electrical Peaks and Managing the Energy, Health, Reliability, and Performance of Electrical Power Systems Based on an Artificial Adaptive Neural Network. U.S. Patent 9,846,839, 19 December 2017. [Google Scholar]
- Jordehi, A.R. How to deal with uncertainties in electric power systems? A review. Renew. Sustain. Energy Rev. 2018, 96, 145–155. [Google Scholar] [CrossRef]
- Ba˜nos, R.; Agugliarob, F.M.; Montoyab, F.G.; Gila, C.; Alcaydeb, A.; Gómezc, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Gamarra, C.; Guerrero, J.M. Computational optimization techniques applied to micro-grids planning: A review. Renew. Sustain. Energy Rev. 2015, 48, 413–424. [Google Scholar] [CrossRef]
- Alizadeh, M.I.; Moghaddam, M.P.; Amjady, N.; Siano, P.; Eslami, M.K.S. Flexibility in future power systems with high renewable penetration: A review. Renew. Sustain. Energy Rev. 2016, 57, 1186–1193. [Google Scholar] [CrossRef]
- García, F.; Bordons, C. Optimal economic dispatch for renewable energy microgrids with hybrid storage using Model Predictive Control. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7932–7937. [Google Scholar]
- Bai, Q. Analysis of Particle Swarm Optimization Algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Settles, M. An introduction to particle swarm optimization; University of Idaho: Moscow, Russia, 2005. [Google Scholar]
- Rini, D.P.; Shamsuddin, S.M.; Yuhaniz, S.S. Particle swarm optimization: Technique, system and challenges. Int. J. Comput. Appl. 2011, 14, 19–26. [Google Scholar] [CrossRef]
- Abbas, G.; Gu, J.; Farooq, U.; Asad, M.U.; El-Hawary, M. Solution of an Economic Dispatch Problem Through Particle Swarm Optimization: A Detailed Survey—Part I. IEEE Access 2017, 5, 15105–15141. [Google Scholar] [CrossRef]
- Abbas, G.; Gu, J.; Farooq, U.; Raza, A.; Asad, M.U.; El-Hawary, M. Solution of an Economic Dispatch Problem Through Particle Swarm Optimization: A Detailed Survey—Part II. IEEE Access 2017, 5, 24426–24445. [Google Scholar] [CrossRef]
- Jordehi, A.R. Particle swarm optimisation (PSO) for allocation of FACTS devices in electric transmission systems: A review. Renew. Sustain. Energy Rev. 2015, 52, 1260–1267. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Kirby, B.; Hirst, E. Customer-Specific Metrics for the Regulation and Load-Following Ancillary Services; ORNL/CON-474; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2000.
- Kariyawasam, K.; Karunarathna, K.; Karunarathne, R.; Kularathne, M.; Hemapala, K. Design and Development of a Wind Turbine Simulator Using a Separately Excited DC Motor. Smart Grid Renew. Energy 2013, 4, 259–265. [Google Scholar] [CrossRef][Green Version]
- Genc, A.; Erisoglu, M.; Pekgor, A.; Oturanc, G.; Hepbasli, A.; Ulgen, K. Estimation of Wind Power Potential Using Weibull Distribution. Energy Sources 2005, 27, 809–822. [Google Scholar] [CrossRef]
- Zhang, J.; Hodge, B.-M.; Miettinen, J.; Holttinen, H.; Lázaro, E.G.; Cutululis, N.; L-Palima, M.; Sorensen, P.; Lovholm, A.L.; Berge, E.; et al. Analysis of Variability and Uncertainty in Wind Power Forecasting: An International Comparison. In Proceedings of the 12th International Workshop on Large-Scale Integration of Wind Power into Power Systems, London, UK, 22–24 October 2013. [Google Scholar]
- Reza, S.E.; Zaman, P.; Ahammad, A.; Ifty, I.Z.; Nayan, M.F. A study on data accuracy by comparing between the Weibull and Rayleigh distribution function to forecast the wind energy potential for several locations of Bangladesh. In Proceedings of the 4th International Conference on the Development in the in Renewable Energy Technology (ICDRET), IEEE, Dhaka, Bangladesh, 7–9 January 2016; pp. 1–5. [Google Scholar]
- Stoutenburg, E.D.; Jenkins, N.; Jacobson, M.Z. Variability and uncertainty of wind power in the California electric power system. Wind Energy 2014, 17, 1411–1424. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Reliability Basics: Reliability Engineering Resources. The eMagzine for Reliability Professional. Issue 7. 2001. Available online: https://www.weibull.com/ (accessed on 22 December 2018).
- Ela, E.; Kirby, B. ERCOT Event on February 26, 2008, Lessons Learned; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
- Papoulis, A.; Papoulis, S. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: Boston, MA, USA, 2002; ISBN 0-07-366011-6. [Google Scholar]
- Jiang, R.; Murthy, D.N.P. A study of Weibull shape parameter: Properties and significance. Reliab. Eng. Syst. Saf. 2011, 96, 1619–1626. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society and Oxford University Press: Providence, RI, USA, 2000; p. 206. ISBN 0-8218-0531-2. [Google Scholar]
- Galambos, J.; Simonelli, I. Products of Random Variables: Applications to Problems of Physics and to Arithmetical Functions; Marcel Dekker, Inc.: New York, NY, USA, 2004; Volume 1, pp. 139–140. ISBN 0-8247-5402-6. [Google Scholar]
- Clarkson, E. Comparison of Weibull and Normal Distributions; NCAMP Documents/Publications, NCAMP (NASA), Technical Presentations; NASA: Washington, DC, USA, 2013.
- Merovci, F.; Elbatal, I. Weibull Rayleigh Distribution: Theory and Applications. Appl. Math. Inf. Sci. 2015, 9, 2127–2137. [Google Scholar]
- Pishgar-Komleh, S.H.; Keyhani, A.; Sefeedpari, P. Wind speed and power density analysis based on Weibull and Rayleigh distributions (A case study: Firouzkooh county of Iran). Renew. Sustain. Energy Rev. 2015, 42, 313–322. [Google Scholar] [CrossRef]
- Ahmad, M.A.; Raqab, M.Z.; Kundu, D. Discriminating between the Generalized Rayleigh and Weibull Distributions: Some Comparative Studies. Commun. Stat. Simul. Comput. 2017, 46, 4880–4895. [Google Scholar] [CrossRef]
- Fu, T.; Wang, C. A hybrid wind speed forecasting method and wind energy resource analysis based on a swarm intelligence optimization algorithm and an artificial intelligence model. Sustainability 2018, 10, 3913. [Google Scholar] [CrossRef]
- Saxena, B.K.; Rao, K.V.S. Comparison of Weibull parameters computation methods and analytical estimation of wind turbine capacity factor using polynomial power curve model: Case study of a wind farm. Renew. Wind Water Sol. 2015, 2, 3. [Google Scholar] [CrossRef]
- Carrillo, C.; Cidrás, J.; Díaz-Dorado, E.; Montaño, A.F.O. An Approach to Determine the Weibull Parameters for Wind Energy Analysis: The Case of Galicia (Spain). Energies 2014, 7, 2676–2700. [Google Scholar] [CrossRef]
- Anuradha, M.; Keshavan, B.K.; Ramu, T.S.; Sankar, V. Probabilistic modeling and forecasting of wind power. Int. J. Perform. Eng. 2016, 12, 353–368. [Google Scholar]
- Nikmehr, N.; Ravadanegh, S.N. Optimal Power Dispatch of Multi-Microgrids at Future Smart Distribution Grids. IEEE Trans. Smart Grid 2015, 6, 1648–1657. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Joint Energy and Spinning Reserve Market Clearing Incorporating Wind Power and Load Forecast Uncertainties. IEEE Syst. J. 2015, 9, 152–164. [Google Scholar] [CrossRef]
- Azada, A.K.; Rasul, M.G.; Alam, M.M.; Uddin, S.M.A.; Mondal, S.K. Analysis of wind energy conversion system using Weibull distribution. Procedia Eng. 2014, 90, 725–732. [Google Scholar] [CrossRef]
- Kim, C.; Gui, Y.; Chung, C.C.; Kang, Y. Model predictive control in dynamic economic dispatch using Weibull distribution. In Proceedings of the IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Celik, A.K. A statistical analysis of wind power density based on the Weibull and Rayleigh models at the southern region of Turkey. Renew. Energy 2004, 29, 593–604. [Google Scholar] [CrossRef]
- Sağbaş, A.; Karamanlıoğlu, T. The Application of Artificial Neural Networks in the Estimation of Wind Speed: A Case Study. In Proceedings of the 6th International Advanced Technologies Symposium (IATS’11), Elazığ, Turkey, 18 May 2011; 2011; pp. 16–18. [Google Scholar]
- Ata, R. Artificial neural networks applications in wind energy systems: A review. Renew. Sustain. Energy Rev. 2015, 49, 534–562. [Google Scholar] [CrossRef]
- Kadhem, A.A.; Wahab, N.I.A.; Aris, I.; Jasni, J.; Abdalla, A.N. Advanced Wind Speed Prediction Model Based on a Combination of Weibull Distribution and an Artificial Neural Network. Energies 2017, 10, 1744. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-Term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303–315. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A.; Nahavandi, S.; Creighton, D. Construction of Neural Network-Based Prediction Intervals for Short-Term Electrical Load Forecasting. In 2013 IEEE Computational Intelligence Applications in Smart Grid (CIASG); IEEE: Piscataway, NJ, USA, 2013; pp. 66–72. [Google Scholar]
- Peng, H.; Liu, F.; Yang, X. A hybrid strategy of short term wind power prediction. Renew. Energy 2012, 50, 590–595. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Yee, P.L.; Petkovi, D.; Zamani, M.; Chaudary, S. Predicting the wind power density based upon extreme learning machine. Energy 2015, 86, 232–239. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mohammadi, K.; Tong, C.W.; Petković, D.; Porcu, E.; Mostafaeipour, A.; Chaudary, S.; Sedaghat, A. Application of extreme learning machine for estimation of wind speed distribution. Clim. Dyn. 2016, 46, 1893–1907. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, L.; Ni, Y. Deep-learning-based scenario generation strategy considering correlation between multiple wind farms. J. Eng. 2017, 13, 2207–2210. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A short-term wind speed forecasting model by using artificial neural networks with stochastic optimization for renewable energy systems. Energies 2018, 11, 2777. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Zhao, Y.; Gao, S. Wind speed prediction with RBF neural network based on PCA and ICA. J. Electr. Eng. 2018, 69, 148–155. [Google Scholar] [CrossRef]
- Khan, G.M.; Ali, J.; Mahmud, S.A. Wind power forecasting—An application of machine learning in renewable energy. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 1130–1137. [Google Scholar]
- World Energy Sources, Solar-2016. World Energy Council. Available online: https://www.worldenergy.org/wp-content/uploads/2017/03/WEResources_Solar_2016.pdf (accessed on 1 October 2019).
- Shi, G. A Data Driven Approach to Solar Generation Forecasting. 2017. Thesis. ALL. 156. Available online: https://surface.syr.edu/thesis/156/ (accessed on 1 October 2019).
- Bushong, S. Advantages and Disadvantages of a Solar Tracker System; Solar Power World: Cleveland, OH, USA, 2016. [Google Scholar]
- Beránek, V.; Olšan, T.; Libra, M.; Poulek, V.; Sedláček, J.; Dang, M.Q.; Tyukhov, I. New monitoring system for photovoltaic power plants’ management. Energies 2018, 11, 2495. [Google Scholar] [CrossRef]
- Zhang, J.; Florita, A.; Hodge, B.; Lu, S.; Hamann, H.F.; Banunarayanan, V.; Brockway, A.M. A suite of metrics for assessing the performance of solar power forecasting. Sol. Energy 2015, 111, 157–175. [Google Scholar] [CrossRef]
- Geoffrey, H. Reflections--The Economics of Renewable Energy in the United States. Rev. Environ. Econ. Policy 2009, 4, 139–154. [Google Scholar]
- Kumara, S.; Sarkara, B. Design for reliability with weibull analysis for photovoltaic modules. Int. J. Curr. Eng. Technol. 2013, 3, 129–134. [Google Scholar]
- Langella, R.; Proto, D.; Testa, A. Solar Radiation Forecasting, Accounting for Daily Variability. Energies 2016, 9, 200. [Google Scholar] [CrossRef]
- Peruchena, C.M.F.; Ramı´rez, L.; Silva-Pe´rez, M.A.; Lara, V.; Bermejo, D.; Gasto´n, M.; Moreno-Tejera, S.; Pulgar, J.; Liria, J.; Macı´as, S.; et al. A statistical characterization of the long-term solar resource: Towards risk assessment for solar power projects. Sol. Energy 2016, 123, 29–39. [Google Scholar] [CrossRef]
- Basri, M.J.M.; Abdullah, S.; Azrulhisham, E.A.; Harun, K. Higher order statistical moment application for solar PV potential analysis. In Proceedings of the AIP Conference Proceedings AIP Publishing, Penang, Malaysia, 10–12 April 2016; Volume 1782, p. 050004. [Google Scholar]
- Munkhammar, J.; Widén, J.; Rydén, J. On a probability distribution model combining household power consumption, electric vehicle home-charging and photovoltaic power production. Appl. Energy 2015, 142, 135–143. [Google Scholar] [CrossRef]
- Ayodele, T.R. Determination of Probability Distribution Function for Global Solar Radiation: Case Study of Ibadan, Nigeria. Int. J. Appl. Sci. Eng. 2015, 13, 233–245. [Google Scholar]
- Maraj, A.; Londo, A.C.; Firat, C.; Karapici, R. Solar Radiation Models for the City of Tirana, Albania. Int. J. Renew. Energy Res. 2014, 4, 413–420. [Google Scholar]
- Arias-Rosales, A.; Mejía-Gutiérrez, R. Optimization of V-Trough photovoltaic concentrators through genetic algorithms with heuristics based on Weibull distributions. Appl. Energy 2018, 212, 122–140. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Behravesh, V.; Keypour, R.; Foroud, A.A. Stochastic analysis of solar and wind hybrid rooftop generation systems and their impact on voltage behavior in low voltage distribution systems. Sol. Energy 2018, 166, 317–333. [Google Scholar] [CrossRef]
- Chiteka, K.; Enweremadu, C.C. Prediction of global horizontal solar irradiance in Zimbabwe using artificial neural networks. J. Clean. Prod. 2016, 135, 701–711. [Google Scholar] [CrossRef]
- Gairaa, K.; Khellaf, A.; Messlem, Y.; Chellali, F. Estimation of the daily global solar radiation based on Box Jenkins and ANN models: A combined approach. Renew. Sustain. Energy Rev. 2016, 57, 238–249. [Google Scholar] [CrossRef]
- Li, F.F.; Wang, S.Y.; Wei, J.H. Long term rolling prediction model for solar radiation combining empirical mode decomposition (EMD) and artificial neural network (ANN) techniques. J. Renew. Sustain. Energy 2018, 10, 013704. [Google Scholar] [CrossRef]
- Rodriguez, F.; Fleetwood, A.; Galarza, A.; Fontan, L. Predicting solar energy generation through artificial neural networks using weather forecasts for micro-grid control. Renew. Energy 2018, 126, 855–864. [Google Scholar] [CrossRef]
- Kuo, P.H.; Huang, C.J. A High Precision Artificial Neural Networks Model for Short-Term Energy Load Forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L.; Pabon, J.J.G. Prediction of hourly solar radiation in Abu Musa Island using machine learning algorithms. J. Clean. Prod. 2018, 176, 63–75. [Google Scholar] [CrossRef]
- Economic Dispatch and Technological Change. Report to Congress United States Department of Energy 2015. Washington, DC, USA. Available online: https://www.energy.gov/oe/articles/20142015-economic-dispatch-and-technological-change-report-congress-now-available (accessed on 26 December 2018).
- Sigarchian, S.G.; Paleta, R.; Malmquist, A.; Pina, A. Feasibility study of using a biogas engine as backup in a decentralized hybrid (PV/wind/battery) power generation system–Case study Kenya. Energy 2015, 90, 1830–1841. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R. Real time economic dispatch considering renewable energy resources. Renew. Energy 2015, 83, 1215–1226. [Google Scholar] [CrossRef]
- Zhang, J.M.; Xie, L. Particle swarm optimization algorithm for constrained problems. Asia-Pac. J. Chem. Eng. 2009, 4, 437–442. [Google Scholar] [CrossRef]
- Jeyakumar, D.N.; Jayabarathi, T.; Raghunathan, T. Particle swarm optimization for various types of economic dispatch problems. Int. J. Electr. Power Energy Syst. 2006, 28, 36–42. [Google Scholar] [CrossRef]
- Gaing, Z.L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Elsaiah, S.; Benidris, M.; Mitra, J.; Cai, N. Optimal economic power dispatch in the presence of intermittent renewable energy sources. In Proceedings of the IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Huynh, D.C.; Nair, N. Chaos PSO algorithm based economic dispatch of hybrid power systems including solar and wind energy sources. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar]
- Gholami, A.; Ansari, J.; Jamei, M.; Kazemi, A. Environmental/economic dispatch incorporating renewable energy sources and plug-in vehicles. IET Gener. Transm. Distrib. 2014, 8, 2183–2198. [Google Scholar] [CrossRef]
- Kheshti, M.; Ding, L.; Ma, S.; Zhao, B. Double weighted particle swarm optimization to non-convex wind penetrated emission/economic dispatch and multiple fuel option systems. Renew. Energy 2018, 125, 1021–1037. [Google Scholar] [CrossRef]
- Nikmehr, N.; Najafi-Ravadanegh, S. Probabilistic Optimal Power Dispatch in Multi-Microgrids Using Heuristic Algorithms. In 2014 Smart Grid Conference (SGC); IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Huynh, D.C.; Ho, L.D. Optimal Generation Rescheduling of Power Systems with Renewable Energy Systems using a Dynamic PSO Algorithm. Int. Adv. Res. J. Sci. Eng. Technol. 2016, 3, 73–78. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, L.; Wang, B.; Wang, Z.; Shafie-khah, M.; Catalao, J.P. Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Micro-grid. Appl. Sci. 2017, 7, 754. [Google Scholar] [CrossRef]
- Mudumbai, R.; Dasgupta, S.; Cho, B.B. Distributed Control for Optimal Economic Dispatch of a Network of Heterogeneous Power Generators. IEEE Trans. Power Syst. 2012, 27, 1750–1760. [Google Scholar] [CrossRef]
- Shivashankar, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M. Mitigating methods of power fluctuation of photovoltaic (PV) sources– A review. Renew. Sustain. Energy Rev. 2016, 59, 1170–1184. [Google Scholar] [CrossRef]
- Senjyu, T.; Datta, M.; Yona, A.; Sekine, H.; Funabashi, T. A coordinated control method for leveling output power fluctuations of multiple PV systems. In Proceedings of the 7th International Conference on Power Electronics, Daegu, Korea, 22–26 October 2007; pp. 445–450. [Google Scholar]
- Zhao, C.; Mallada, E.; Dorfler, F. Distributed frequency control for stability and economic dispatch in power networks. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2359–2364. [Google Scholar]
- Zhua, X.; Xiaa, M.; Chiang, H.-D. Coordinated sectional droop charging control for EV aggregator enhancing frequency stability of microgrid with high penetration of renewable energy sources. Appl. Energy 2018, 210, 936–943. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.; Baldick, R. Ramp Rates Control of Wind Power Output Using a Storage System and Gaussian Processes; University of Texas at Austin, Electrical and Computer Engineering: Austin, TX, USA, September 2012. [Google Scholar]
- Maleki, A.; Rosen, M.A.; Pourfayaz, F. Optimal operation of a grid-connected hybrid renewable energy system for residential applications. Sustainability 2017, 9, 1314. [Google Scholar] [CrossRef]
- ElDesouky, A.A. Security and Stochastic Economic Dispatch of Power System Including Wind and Solar Resources with Environmental Consideration. Int. J. Renew. Energy Res. 2013, 3, 951–958. [Google Scholar]
- Khan, N.A.; Sidhu, G.A.S.; Gao, F. Optimizing Combined Emission Economic Dispatch for Solar Integrated Power Systems. IEEE Access 2016, 4, 3340–3348. [Google Scholar] [CrossRef]
- Solomon, A.A.; Child, M.; Caldera, U.; Breyer, C. ow much energy storage is needed to incorporate very large intermittent renewables? Energy Procedia 2017, 135, 283–293. [Google Scholar] [CrossRef]
- Optimizing Battery Management in Renewable Energy Storage Systems. Pulse Power Electronics. Available online: https://www.power.pulseelectronics.com/optimizing-battery-management-in-renewable-energy-storage-systems (accessed on 31 December 2018).
- Abdelrahman, A.; Lamont, L.; El-Chaar, L. Energy Storage for Intermittent Renewable Energy Systems; MDPI Sustainability Foundation: Basileia, Switzerland, 2012. [Google Scholar]
- Pickard, W.F.; Abbott, D. Addressing the intermittency challenge: Massive energy storage in a sustainable future. Proc. IEEE 2012, 100, 317–321. [Google Scholar] [CrossRef]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Zentkó, L.; Birkner, Z.; Máté, K.; Pintér, G. Intermittent Renewable Energy Sources: The Role of Energy Storage in the European Power System of 2040. Electronics 2019, 8, 729. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Fu, Q.; Yu, D.C.; Zhang, L. Economic Allocation for Energy Storage System Considering Wind Power Distribution. IEEE Trans. Power Syst. 2015, 30, 644–652. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Zhao, H.; Wua, Q.; Hu, S.; Xu, H.; Rasmussen, C.N. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- IEC. Electrical energy storage white paper. Tech report. 2011. [Google Scholar]
- Galván, L.; Navarro, J.M.; Galván, E.; Carrasco, J.M.; Alcántara, A. Optimal Scheduling of Energy Storage Using a New Priority-Based Smart Grid Control Method. Energies 2019, 12, 579. [Google Scholar] [CrossRef]
- Rui, L.I.; Wei, W.; Zhe, C.; Xuezhi, W.U. Optimal planning of energy storage system in active distribution system based on fuzzy multi-objective bi-level optimization. J. Mod. Power Syst. Clean Energy 2018, 6, 342–355. [Google Scholar]
- Hemmati, R.; Saboori, H.; Jirdehi, M.A. Stochastic planning and scheduling of energy storage systems for congestion management in electric power systems including renewable energy resources. Energy 2017, 133, 380–387. [Google Scholar] [CrossRef]
| Characteristics | Weibull Distribution (WD) | Rayleigh Distribution (RD) | Gaussian/Normal Distribution (ND) | Ref. No. |
|---|---|---|---|---|
| Mathematical representation & parameters | > 0 is the scale parameter of the distribution. | is the scale parameter of the distribution. | is the mean, whereas σ is the standard deviation. | [41,42,43,44] |
| Flexibility | WD is very flexible as a small sample size; the estimated shape of the distribution may be altered considerably. | Not flexible as a response to the out of range parameters are strict. | Not flexible as the shape doesn’t vary. | [45,46,47,48,49] |
| Accuracy | Fatigue test results follow WD, showing it to be more accurate. It is effective for both values above and below the sample size N. | Close to WD. | Effective only for values below the sample size N. | |
| Reliability | WD is more reliable even in situations where distribution parameters (shape and scale) tend to vary. | RD loses its effectiveness in situations where variables undergo variation. | Reliability in ND suffers severely at the hands of variation in variables. |
| Wind Speed Probability Distribution | Wind Power Distribution | Explanation |
|---|---|---|
| where is electric output power of WT; , and represent cut-in, cut-out, and the rated wind speed, respectively [50,51]. | ||
| The authors suggest that wind velocity follows Rayleigh distribution, whereas the power follows Weibull distribution [52]. | ||
| where is generated power at speed , and , and are wind turbine parameters [53]. | ||
| Here and are the shape and scale parameters; is power output against wind speed [54,56]. | ||
| [55] | ||
| [57] | ||
| Resource/Power Forecasting Model | Prediction Error | Description |
|---|---|---|
| Here , and are mean wind speed, standard deviation, and gamma function, respectively. Also, , and are total input and output pairs, forecasted wind speed, and actual wind speed for one hour, respectively [61]. | ||
| Here n denotes the specified time period Pi,pred and Pi,means are predicted and calculated wind powers [64]. | ||
| [65] | ||
| Here denotes the specified time period, and and are predicted and calculated wind powers, respectively [66]. |
| Solar Distribution Functions for Prediction | PV Power Production | Reference |
|---|---|---|
| are the reliability function, slope, location and scale parameters, respectively [78] stand for solar active power, amount of solar irradiance, efficiency, the total area of PV modules, PV cell temperature’s forecast error, and co-efficient of the temperature, respectively. | ||
| and η are active power, active power-voltage relationship, and converter efficiency, respectively [80]. | ||
| [81] | ||
| is the solar irradiance function [83]. |
| Model Used for Power Production or Resource/Power Forecasting | Prediction Error | Reference |
|---|---|---|
| are voltage fluctuations and voltage imbalance factor, respectively [85]. | ||
| Here are measured and predicted solar irradiations respectively [86]. | ||
| Here are estimated, measured, and average estimated and measured values, respectively [87]. | ||
| hist and pred historical and predicted results [88] stand for solar active power, amount of solar irradiance, efficiency, total area of PV modules, PV cell temperature’s forecast error, and co-efficient of the temperature, respectively. |
| Constraints | Presented Model | Objective Function | Reference |
|---|---|---|---|
| Load and Voltage Variations | are the load demand, transmission losses, solar and wind powers, respectively [103,104]. | ||
| Frequency Fluctuations | [105,106,107,108,109] | ||
| Ramp-Rate Limits | [110,111,112,113] | ||
| Storage Mechanism | [114,115,116,117,118,119,120,121,122,123,124,125] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellahi, M.; Abbas, G.; Khan, I.; Koola, P.M.; Nasir, M.; Raza, A.; Farooq, U. Recent Approaches of Forecasting and Optimal Economic Dispatch to Overcome Intermittency of Wind and Photovoltaic (PV) Systems: A Review. Energies 2019, 12, 4392. https://doi.org/10.3390/en12224392
Ellahi M, Abbas G, Khan I, Koola PM, Nasir M, Raza A, Farooq U. Recent Approaches of Forecasting and Optimal Economic Dispatch to Overcome Intermittency of Wind and Photovoltaic (PV) Systems: A Review. Energies. 2019; 12(22):4392. https://doi.org/10.3390/en12224392
Chicago/Turabian StyleEllahi, Manzoor, Ghulam Abbas, Irfan Khan, Paul Mario Koola, Mashood Nasir, Ali Raza, and Umar Farooq. 2019. "Recent Approaches of Forecasting and Optimal Economic Dispatch to Overcome Intermittency of Wind and Photovoltaic (PV) Systems: A Review" Energies 12, no. 22: 4392. https://doi.org/10.3390/en12224392
APA StyleEllahi, M., Abbas, G., Khan, I., Koola, P. M., Nasir, M., Raza, A., & Farooq, U. (2019). Recent Approaches of Forecasting and Optimal Economic Dispatch to Overcome Intermittency of Wind and Photovoltaic (PV) Systems: A Review. Energies, 12(22), 4392. https://doi.org/10.3390/en12224392









