1. Introduction
The effects of climate change and the continuous depletion of fossil fuels require a change in the global economy that should be based on the use of renewable resources. The implementation of processes based on the production, supply and processing of biomass can boost that change, reducing environmental impacts and ensuring the conservation of finite resources. Thus, the concept of bioeconomy emerges as a suitable opportunity to link economic growth with sustainable development [
1,
2]. The European Commission defines the bioeconomy concept as “the production of renewable biological resources and the conversion of these resources and waste streams into value added products, such as food, feed, bio-based products, and bioenergy” [
3].
The bioeconomy created a turnover of 2.3 trillion € in the European Union (EU) in 2015, with the bio-based electricity and forestry sectors having the greatest growth rates [
4]. Thus, the correct exploitation of forest resources can contribute to provide a sustainable source of energy, promoting the development of rural areas and jobs creation [
5]. In particular, bioenergy options based on wood feedstocks are presented as a convenient solution for residential heating, especially in countries like Portugal where forest resources are still abundant [
6,
7,
8]. Several wood-based technologies are currently available in the market for residential heating, from traditional fireplaces to wood/pellet stoves [
9,
10,
11]. An appropriate selection of these technologies in terms of sustainability will be crucial for paving the way to a future wide deployment of the European bioeconomy.
When taking into consideration the sustainability of energy systems, the search for logical and optimal solutions is a complex process since it involves: (i) many sources of uncertainty at different scales (e.g., at technology, company or policy level), (ii) probably long time frames according to the lifespan of energy systems, (iii) capital intensive investments, and (iv) a large number of stakeholders with different views and preferences [
12]. In this sense, multiple criteria are needed to reflect the complexity of the sustainability assessment for decision-makers and to create an adequate basis for a quality and comprehensive decision. This means taking into account not only environmental criteria but also economic and social indicators (covering the main dimensions of the sustainability concept). In this respect, approaches with a life-cycle perspective are considered as effective sources for supplying performance indicators in one dimension or in all dimensions of sustainability [
13,
14].
In addition to indicators, methods are needed to reduce the complexity of integrating and interpreting multiple criteria and preferences of stakeholders. Multi-criteria decision analysis (MCDA) arises as an operational evaluation and decision support approach that is suitable for addressing complex problems (e.g., energy and environmental issues) featuring high uncertainty, conflicting objectives, different forms of data and information, multiple interests and perspectives, and the accounting for complex and evolving biophysical and socio-economic systems [
15,
16]. According to Ibáñez-Forés et al. [
17], MCDA methods can be classified into two broad groups: Multi-Attribute Decision Analysis (MADA) and Multi-Objective Decision Analysis (MODA). The former is used when the decision-maker has to choose between a finite number of options, while the latter implies setting the value of decision variables (implicitly defining an infinite number of alternatives). Within the MADA, which fits better with the interest of the present study, the most popular are the following: Multi-Attribute Utility Theories (MAUT), the Outranking methods, Analytical Hierarchy Process (AHP) method, and other multiple attribute decision-making (OMADM) methods (such as distance-to-target approaches) [
12,
18,
19].
MCDA tools have been widely applied for supporting the choice of more sustainable energy solutions, mainly in the following areas: energy policy and management, evaluation of power generation technologies, evaluation of other energy systems, and electrical regional planning [
20,
21]. However, there is a lack in the existing literature concerning the use of MCDA tools for providing robust and sustainable choices within the bioenergy context [
21]. According to the review conducted by Scott et al. [
22], the most common topic studied in MCDA applied to bioenergy is the selection of the technology to use, comparing between technologies or between equipment within the same technology. The sustainability of bioenergy was only evaluated in 14% of the reviewed literature. This trend remains at present with only few studies addressing sustainable choices in the MCDA application to bioenergy systems (mainly application to biomass conversion routes [
23,
24]). In addition, little attention has been paid to MCDA studies of energy systems for heating in residential buildings [
25,
26,
27]. These studies are mainly based on the use of economic and environmental indicators for the MCDA analysis.
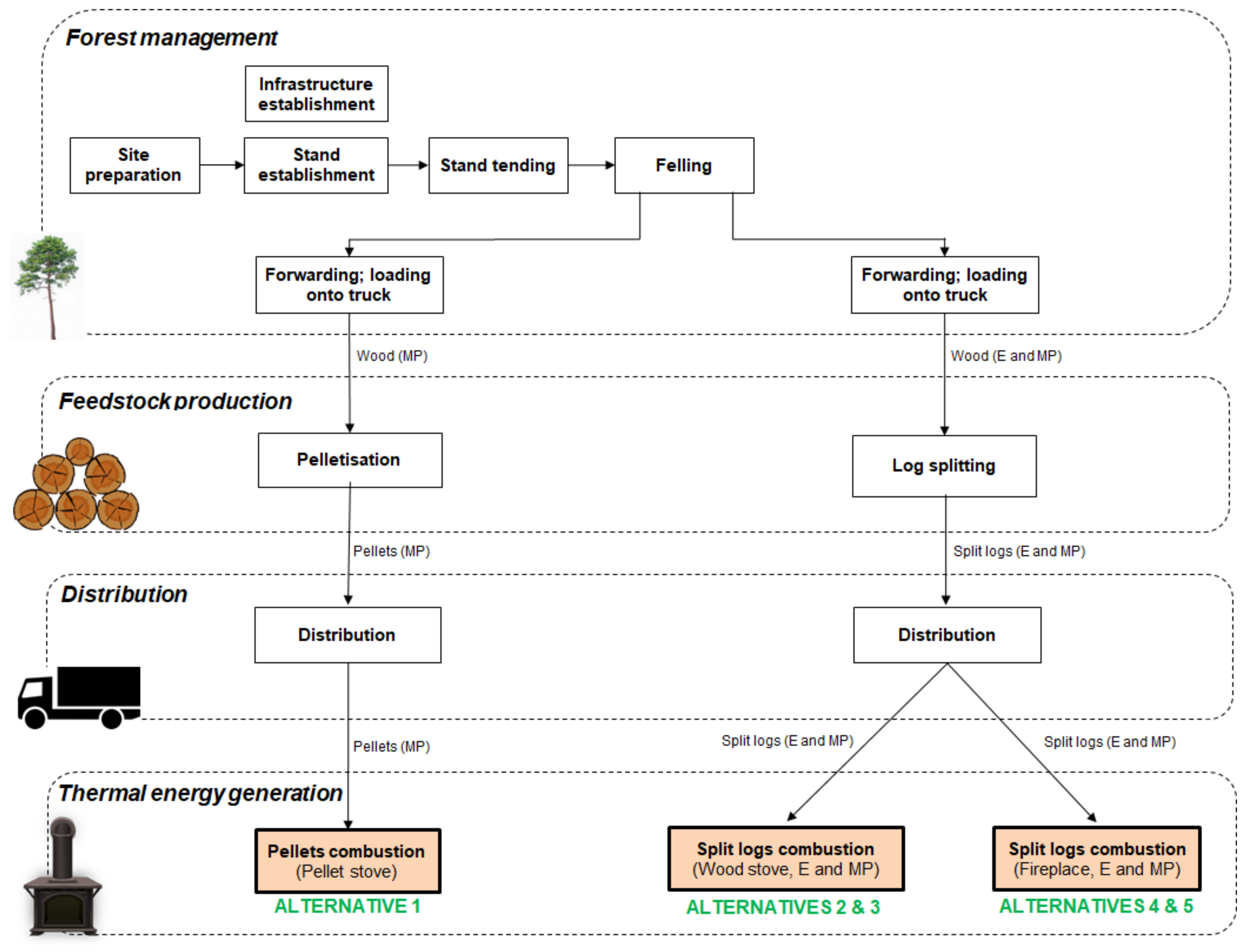
This paper aims to fill the knowledge gap in the literature regarding the application of MCDA tools for bioenergy systems, as well as to provide recommendations for the selection of the best bioenergy options for residential heating in Southern Europe. Five different wood-based residential heating alternatives based on the work conducted by Quinteiro et al. [
8] are evaluated in this study through the combination of three commercial technologies (pellet stove, wood stove and traditional fireplace) and the use of two different feedstocks widely available in the selected region (eucalypt and maritime pine species). In order to follow a sustainability perspective, the environmental analysis of the alternatives carried out in Quinteiro et al. [
8] is complemented in this study with the evaluation of the economic and social dimensions for the prioritisation of alternatives, considering eight indicators (four environmental, two economic and two social). Moreover, an exploratory MCDA analysis is carried out in this work to obtain a synthesis of the results encompassing the three sustainability dimensions. Because of the wide availability of options concerning MCDA methods and weighting vectors, this exploratory analysis applies four of the most commonly used MCDA methods: Weighted Sum Method (WSM) [
28], TOPSIS [
29], ELECTRE [
30], and PROMETHEE [
31]. The sensitivity of the obtained rankings concerning the weighting approach is also carried out. Together, these analyses allow assessing the influence of the MCDA modelling options (method and weighting approach) on the recommended choice.
3. Results and Discussion
In the present section, firstly the sustainability profiles of each wood-based system are presented. Then, the alternatives are prioritised through the four MCDA methods selected: WSM, TOPSIS, ELECTRE, and PROMETHEE. Finally, a sensitivity analysis of the rankings obtained with regard to the weighting approach is carried out. In this respect, the weights are modified—each “weighting scenario” emphasizes a different dimension of sustainability—to evaluate their influence in the original ranking (where an equal-weighted approach is taken).
3.1. Sustainability Assessment of Wood-Based Alternatives
Table 3 contains the results obtained for each indicator of the sustainability assessment. The highest impact values for the environmental criteria are associated with the alternatives based on the use of a fireplace. In particular, the alternative based on eucalypt feedstock (F–E) presents the greatest impacts in all the environmental indicators considered, negatively affecting its sustainability performance. This unfavourable performance is strongly linked to an inefficient combustion of wood split logs, which requires a higher amount of feedstock and involves a higher emission of gaseous pollutants per MJ of thermal energy produced in comparison with the rest of alternatives. Regarding the identification of the best alternative in terms of environmental criteria there is not a clear trend, with the pellet stove alternative (PS–MP) being the most favourable in global warming (env1) and ozone formation (human health) (env4), while wood stove (eucalypt, WS–E and maritime pine, WS–MP) performs better in terms of terrestrial acidification (env2) and freshwater eutrophication (env3).
In the case of economic criteria, it is not possible to identify a best or worst alternative. Despite presenting the lowest installation costs, PS–MP is the worst alternative in terms of annualised capital costs (ec1) due to its high market price in comparison with the remaining alternatives (more than 1300 € on average). On the other hand, operation and maintenance costs (ec2) are strongly affected by the annual feedstock costs. Thus, the systems based on the use of a fireplace to meet the residential heat demand (especially in the case of F–E with higher prices of the biomass feedstock) are identified as the worst alternatives because they require the largest amounts of biomass fuel within the set of options evaluated.
Finally, a similar not-dominant trend is found in the case of social criteria. In contrast to the remaining indicators, the annual working hours (soc1) should be maximised with the aim of contributing to the local economic development. Fireplace alternatives are the most favourable systems in terms of annual working hours (mainly F–E) due to the longer working times employed in these alternatives to provide the annual amount of biomass feedstock (more than 4 tonnes of eucalypt or maritime pine). For this indicator, wood stove alternatives emerge as the worst systems with the lowest working hours (especially WS–MP). It should be noted that longer working times are associated with a higher probability of accidents [
44]. For this reason, fireplace alternatives are identified as the worst alternatives when days of absence due to non-fatal work accidents are estimated. The observed variability of indicators results makes it difficult to select directly the most sustainable bioenergy systems. Therefore, the use of MCDA tools emerges as necessary and convenient to prioritise the set of wood-based alternatives according to the multiple criteria evaluated.
3.2. MCDA Prioritisation of Wood-Based Alternatives
The data presented in
Table 3 constitute the matrix which is the input for an own-developed MCDA model implemented in Excel to compute the scores. The results obtained with the four different tools (viz., WSM, TOPSIS, ELECTRE, and PROMETHEE) applying the same weights for all the indicators are presented in
Table 4. The scores obtained have different scales due to the specific mathematical formulation of each method (
Section 2.3).
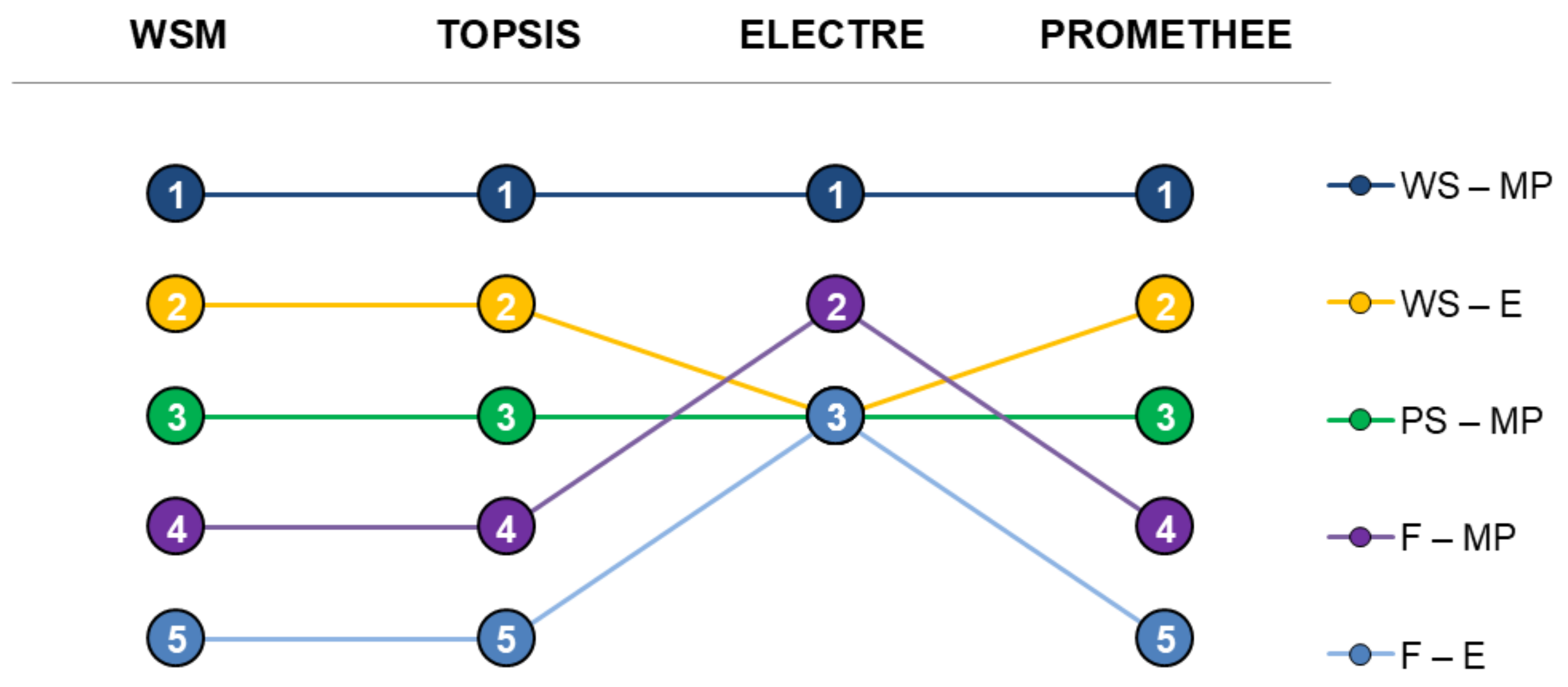
Differences in the ranking of alternatives due to the application of the different MCDA tools can be observed in
Figure 2. In this sense, the best alternative according to their position in the four rankings is WS–MP. This alternative presents the highest scores calculated through the application of the four MCDA tools included in the analysis. Despite this fact, the scores are similar between the two wood stoves alternatives (with exception of the application of ELECTRE method). Thus, both WS–MP and WS–E could be considered as appropriate bioenergy systems for residential heating in terms of sustainability performance. Regarding the worst alternative, F–E is ranked last in all rankings (in the case of ELECTRE, tied in the last position with the wood stove and fireplace alternatives based on the combustion of eucalypt split logs).
The similarity between rankings shows that the results are quite robust relative to the choice of the MCDA tools used for the present case study. The only differences are found when the ELECTRE method is applied for the prioritisation of the alternatives. These differences stem from the strong non-compensatory nature of the discordance condition in ELECTRE. Since the pellet and wood stove options (PS–MP, WS–E, and WS–MP) are much worse than the fireplace options (F–E and F–MP) on the indicators annualised capital costs (ec1) and annual working hours (soc1), none of the former three alternatives can outrank the latter two. On the other hand, since the fireplace options F–E and F–MP are so much worse on the remaining indicators, neither can outrank PS–MP, WS–E or WS–MP. These form two incomparable groups, according to ELECTRE. In the first group, PS–MP and WS–E are outranked by WS–MP and outrank no other alternative; hence they are placed in the third (viz., last) position with a net flow of -1. On the other hand, F–MP benefits because it is capable of outranking the other fireplace alternative F–E while no other alternative outranks it.
3.3. Influence of Weighting
The results presented in the previous section correspond to considering equal weights for all the indicators. However, in MCDA, different decision-makers will have other preferences. Depending on the perspective, they might wish to emphasise environmental, economic, or social criteria, possibly leading to different results than those obtained by considering equal weighting. It is therefore important to analyse how sensitive the results are to changes in the sample of weights.
A possible way of assessing the effect of using different weight vectors is to consider different “weighting scenarios”, each one overweighting a given sustainability dimension.
Table 5 presents an example of this strategy, placing 75% of the total weight on a single dimension at a time (i.e., the weight of each dimension is the triple of the other two dimensions together). This is a common strategy to represent the preference of a decision-maker in a specific dimension. Computing the results for these weights using the same methods as before does not lead to major changes. In fact, the rankings presented in
Figure 2 are maintained in the majority of the cases. When the weights prioritising the environmental dimension are used, all the rankings remain unchanged except in the case of ELECTRE, placing the WS–E alternative in the last position. When the weights prioritising the economic dimension are used, the ranking changes for the WSM, ELECTRE and PROMETHEE, with PS–MP falling from 3rd to 5th place (F–MP and F–E therefore climb one position). When the weights prioritising the social dimension are used, the ranking changes only for the TOPSIS method, with PS–MP climbing from 3rd to 1st place (WS–MP and WS–E therefore drop one position to become 2nd and 3rd). In the latter case, however, the scores of PS–M become very close to the scores of WS–MP and WS–E.
Rather than selecting a few different weighting vectors as described above, it is also possible to perform a stochastic analysis simulating thousands of weight vectors drawn randomly from a uniform distribution [
48,
51]. Using Monte-Carlo simulation, it is then possible to obtain statistics about the results corresponding to these stochastic weights.
Table 6 shows the Monte-Carlo simulation results (obtained with the @Risk software) for 50,000 random weight vectors uniformly distributed on the simplex defined by the constraints that weights are non-negative and their sum is equal to 1, following the process of Butler et al. [
52]. Since ELECTRE yields tie into the rankings frequently (e.g.,
Figure 2), in this stochastic analysis the number of “losses” was used as a tie-breaking procedure (but some ties still remain when the number of “losses” is the same among tied alternatives).
It can be observed that the rankings presented in
Figure 2 are rather stable, but in extreme cases they can be quite different. Just as an example, according to the WSM, PS–MP is ranked 3rd for 79.2% of the random weights, but for weights such as, e.g.,
w = (0.21, 0.02, 0.01, 0.36, 0.01, 0.03, 0.35, and 0.01) it is ranked 1st and for weights such as, e.g.,
w = (0.15, 0.02, 0.22, 0.03, 0.01, 0.01, 0.49, and 0.07) it is ranked 5th. The probability of obtaining the same rankings of
Figure 2 is higher for the WSM and PROMETHEE, but TOPSIS and ELECTRE also establish the ranking positions in
Figure 2 with high probability.
3.4. Influence of Hierarchy
The analysis reported so far considers all the sustainability dimensions on an equal standing, but this ignores a potential issue: The environmental dimension is represented by four criteria, whereas the economic dimension and the social dimension are represented by only two criteria each. This means that the results presented in
Section 3.2, considering equal weights, are in fact overweighting the environmental dimension.
If decision-makers wish that all the sustainability dimensions have the same weight (1/3), then a different weighting vector should be applied: dividing 1/3 by four yields a weight of 1/12 for each one of the four environmental indicators; dividing 1/3 by two yields a weight of 1/6 for each one of the two economic indicators, and the same weights apply to the two social indicators. Given this weighting vector, the scores in
Table 4 would be changed to those in
Table 7. Nevertheless, the ranking of the alternatives (
Figure 2) would remain the same except in the case of ELECTRE, with PS–MP falling from 3rd to 5th place (F–E drop one position to become 4th).
The same consideration is in order if a stochastic weights analysis is performed. Indeed, since there are more environmental criteria than economic or social ones, the environment dimension will on average have more weight than the economic or the social dimension. Correcting this requires a two-step strategy to generate random weights. In a first step, the total weight of each dimension (wEnv, wEc, wSoc) is generated randomly such that (wEnv, wEc, wSoc) ≥ 0 and wEnv + wEc + wSoc = 1. Then, the relative sub-weights of the four environmental indicators (senv1, senv2, senv3, senv4) are randomly generated such that (senv1, senv2, senv3, senv4) ≥ 0 and senv1 + senv2 + senv3 + senv4 = 1. Setting the sub-weights for the economic indicators requires only one random value, sec1, drawn from the uniform distribution in [0,1], and then setting sec2 = 1 − sec1. Similarly, a random value, ssoc1 is generated, allowing to define ssoc2 = 1 – ssoc1. Finally, dimension weights and sub-weights are combined so that wEnv1 = wEnv.senv1,…, wEnv4 = wEnv.senv4, wEc1 = wEc.sec1, wEc2 = wEc.sec2, wSoc1 = wSoc.ssoc1, and wSoc2 = wSoc.ssoc2.
Considering the stochastic weights as described above, the probability results in
Table 6 are replaced by the probability results in
Table 8. In every case, the most likely rank has a probability greater than about 60% and these most likely rankings still coincide with
Figure 2. However, by comparing
Table 6 with
Table 8 one can observe that the latter rankings are less stable in all the cases, i.e., the most likely ranking has less probability. The reason for this is that respecting the hierarchical structure increases the role of the economic and social indicators in the final result, and indicators ec1 and soc1 do not favour the top-ranked alternatives. Since now they have more chances of influencing the result, the scores of the top-ranked three alternatives tend to decrease and so they can more often be surpassed by other alternatives.
Even though TOPSIS places WS–MP in the first position with a relatively low probability of 65.7% (
Table 8), the analysis carried out in the present section corroborates the results from
Figure 2. Overall, the main conclusion that WS–MP is the most preferred option for all the methods is still fairly robust.
3.5. Final Remarks
The current development of energy policies, roadmaps or plans at all levels (i.e., national, regional, local, etc.) should be in line with the Sustainable Development Goals (SDGs) agreed by the United Nations [
53]. The exploratory MCDA analysis conducted in the present study for the sustainability-oriented prioritisation of wood-based bioenergy systems can contribute to set strategies aligned with those SDGs. In particular, it facilitates the decision-making process and the provision of plans that address most of the targets covered by both SDG7 (access to affordable and clean energy) and SDG13 (climate change mitigation). Additionally, links with some of the targets related to well-being (SDG3), decent work and economic growth (SDG8), and sustainable regions (SDG11) could also be identified if the outcomes of this study are taken into account by decision-makers in the elaboration of plans. It is important to note that the relevance of the outcomes of this research is not limited to energy actors in Portugal, but they are relevant to any decision-maker considering the development of energy plans, roadmaps or strategies under sustainability aspects.
The significant involvement of stakeholders (e.g., policy-makers, actors from biomass-related sector, local community or consumers) usually found in the energy sector encompasses a wide range of views which could significantly vary the outcomes of the prioritisation. The weighting scenarios reported in this study allow visualising the influence of different actors’ preferences (i.e., criteria weights) leading to contrasting and practical recommendations. Regarding the choice of indicators (e.g., type and number per sustainability dimension) and technical options within the MCDA methods (e.g., normalisation, concordance and discordance thresholds, etc.), special attention should be paid to the selection of these elements due to their influence on the final results. In this study, indicators and technical options were chosen by academics, but a future involvement of decision-makers at company or policy level may have modified those elements. Thus, a sensitivity analysis on the choice of indicators and technical MCDA options should be further studied. In addition, the incorporation of a life-cycle perspective into the economic and social criteria is also a future direction to explore.
4. Conclusions
An MCDA exploratory analysis was carried out to prioritise five bioenergy alternatives for residential heating in Southern Europe filling a gap in the MCDA application to bioenergy systems. The highest impacts for the environmental criteria were identified for the fireplace due to inefficient combustion of wood split logs, while there was not a preferred environmental performance option. Regarding the economic and social dimensions, no clear trend was found as the alternatives present favourable or unfavourable performances depending on the criterion evaluated. This fact strongly supported the need to apply MCDA methods for the prioritisation of alternatives in terms of sustainability.
The MCDA prioritisation revealed the wood stove options (similar scores for combustion of maritime pine or eucalypt logs) as the most appropriate alternatives in terms of sustainability performance. Regarding the worst alternative, fireplaces based on the combustion of eucalypt logs were ranked last in all MCDA rankings. Furthermore, analyses in terms of how sensitive were the results to changes in weighting were carried out in order to incorporate the vision of decision-makers and to facilitate their role in the prioritisation of bioenergy alternatives for residential heating. These analyses confirmed wood stoves with the combustion of maritime pine logs as the leading alternative and the key role of the analysts within this type of MCDA studies. Therefore, an appropriate prioritisation of bioenergy alternatives in terms of sustainability was demonstrated to be relevant for paving the way to a future wide deployment of the European bioeconomy sector, being the role of the analyst key to provide robust and reliable decisions.