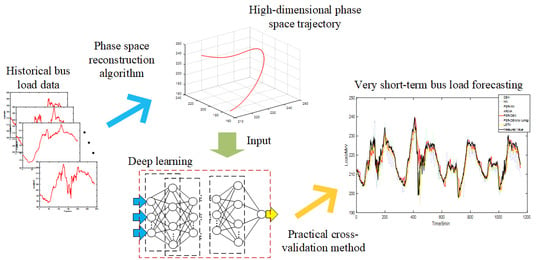
Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting
Abstract
1. Introduction
- A novel hybrid VSTLF model based on phase space reconstruction ensemble deep belief network is proposed, which can maintain high prediction accuracy in the case of high distributed power penetration and large fluctuation of bus load.
- The Levenberg-Marquardt backpropagation (LMBP) algorithm is used to fine-tune the DBN, which can make DBN convergence faster and more accurate, compared with a BP algorithm.
- A practical method based on cross-validation is proposed to tune the structure of DBN for better forecasting performance.
- The PSR algorithm is adopted to make a regular pattern that could not be obtained in one-dimensional time series appear in a high-dimensional phase space, which improves the adaptability of a forecasting model to different forecasting horizons, especially long estimation.
2. Methodology
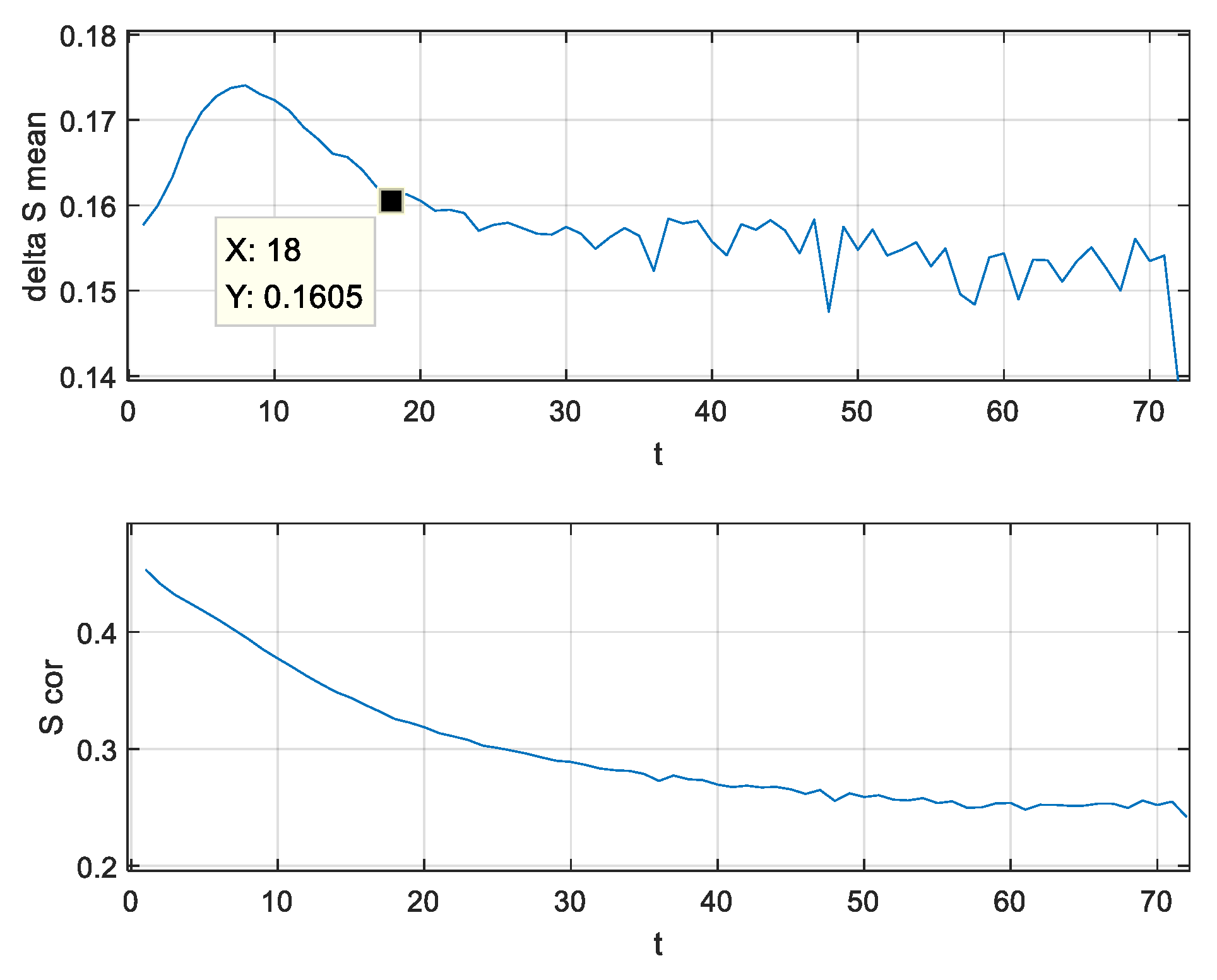
2.1. Phase Space Reconstruction (PSR)
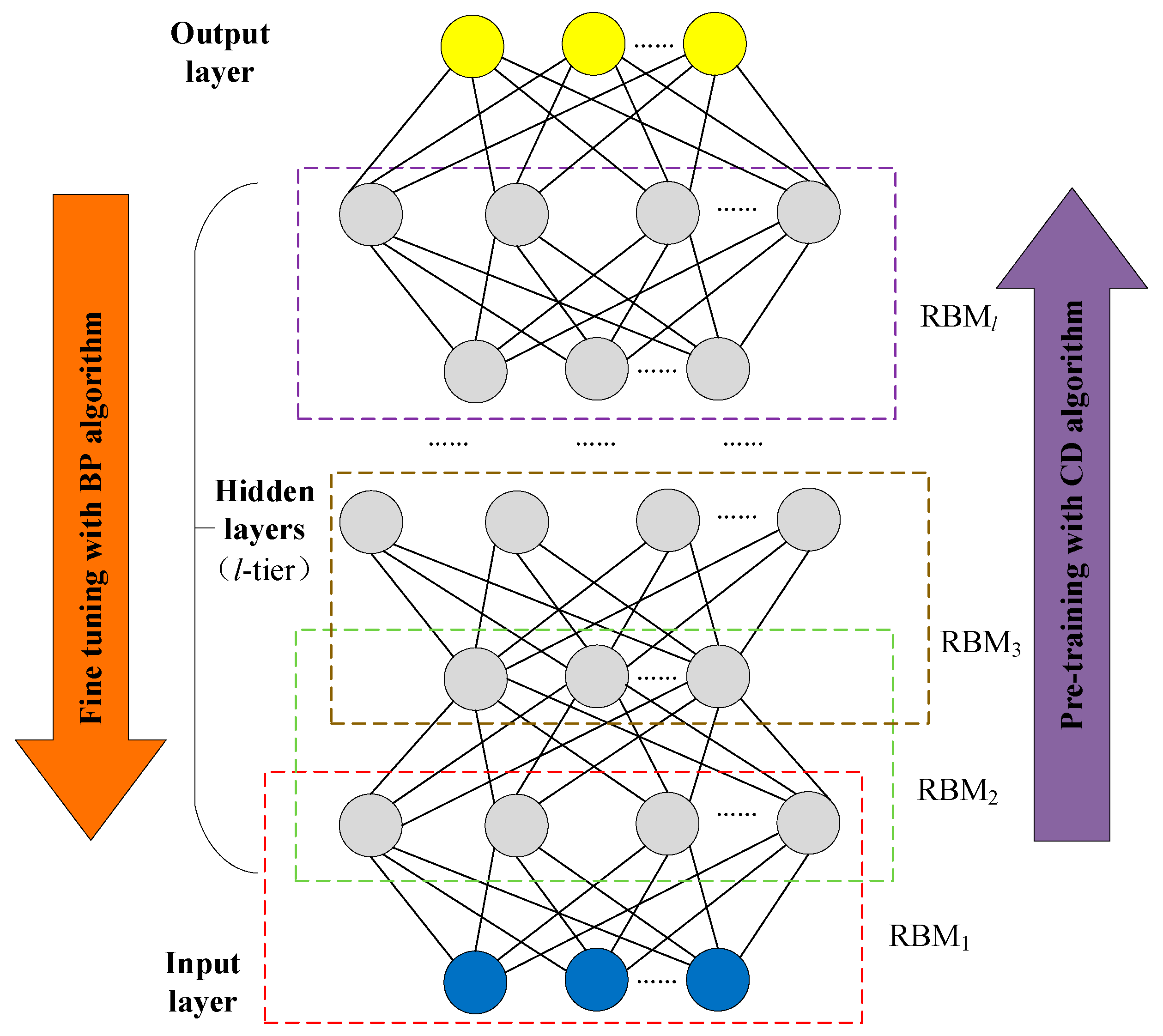
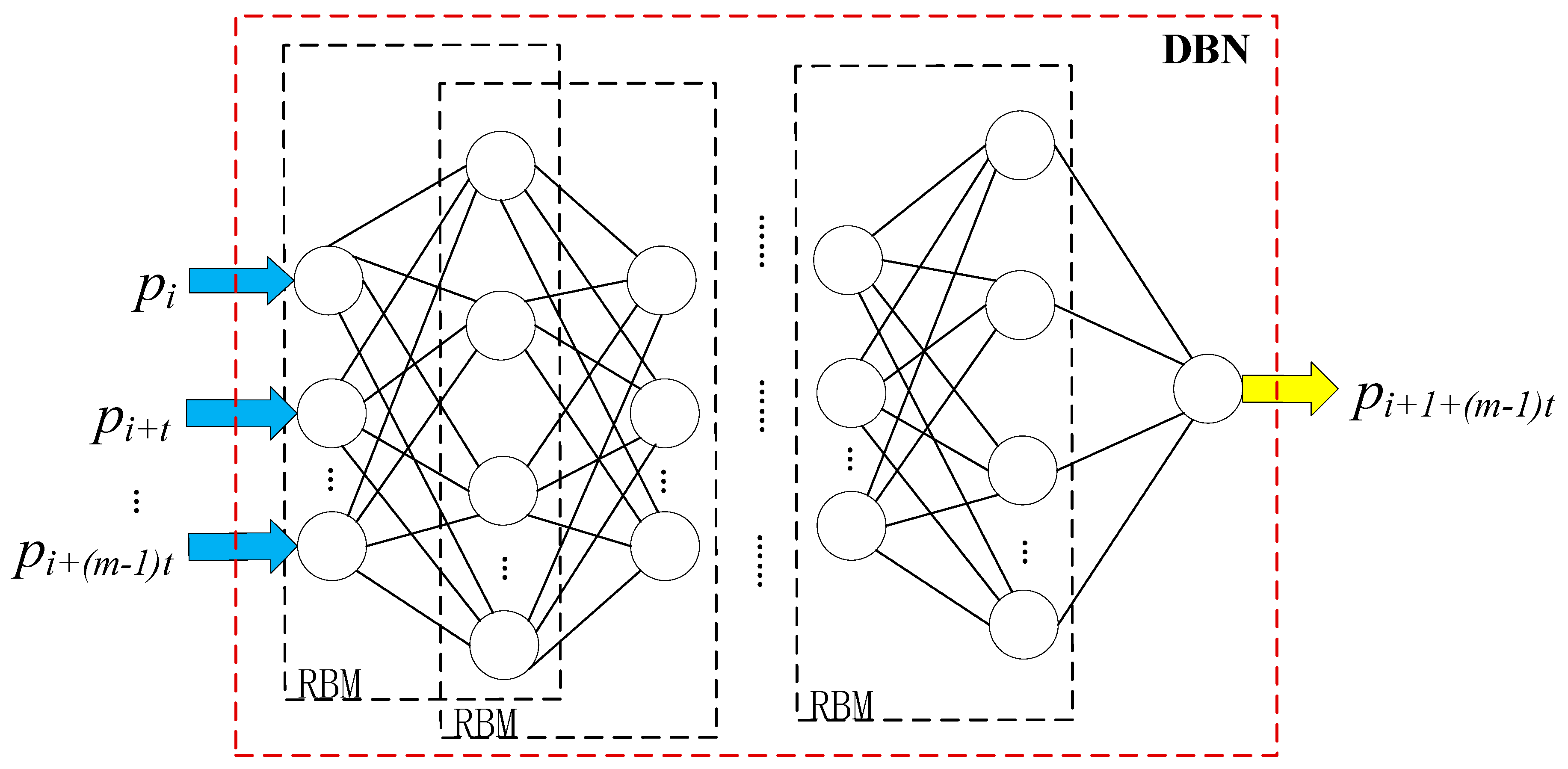
2.2. Deep Belief Network (DBN)
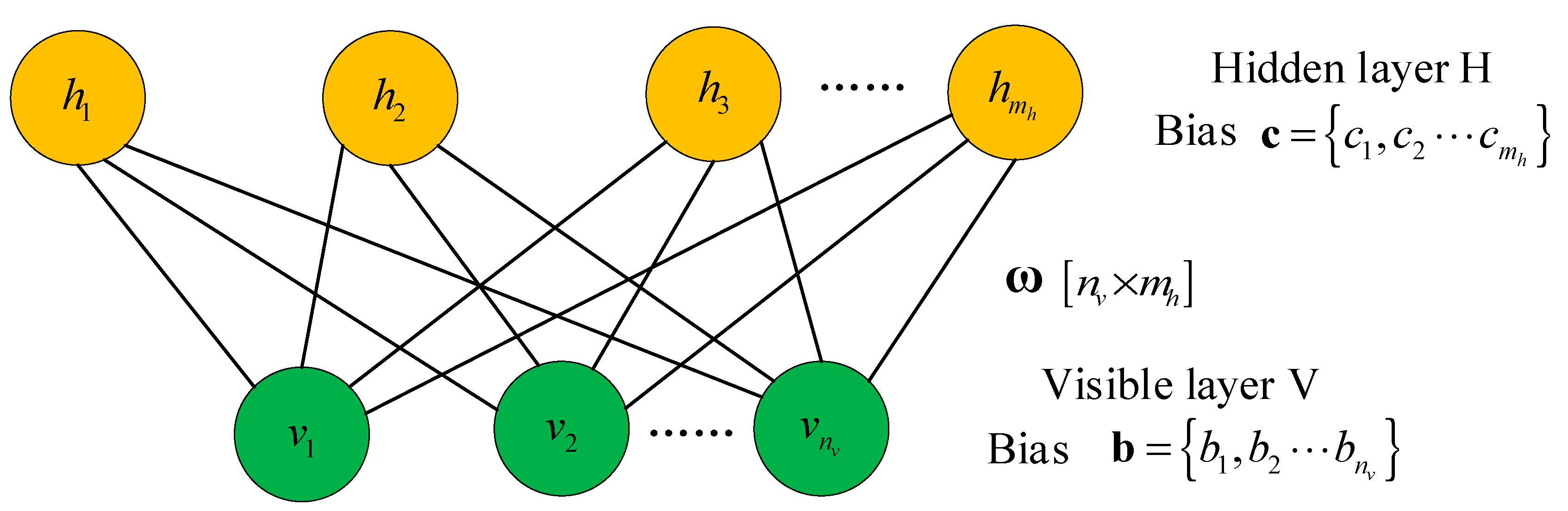
2.2.1. Restricted Boltzmann Machine (RBM)
2.2.2. DBN based on Levenberg-Marquardt backpropagation (LMBP) Algorithm
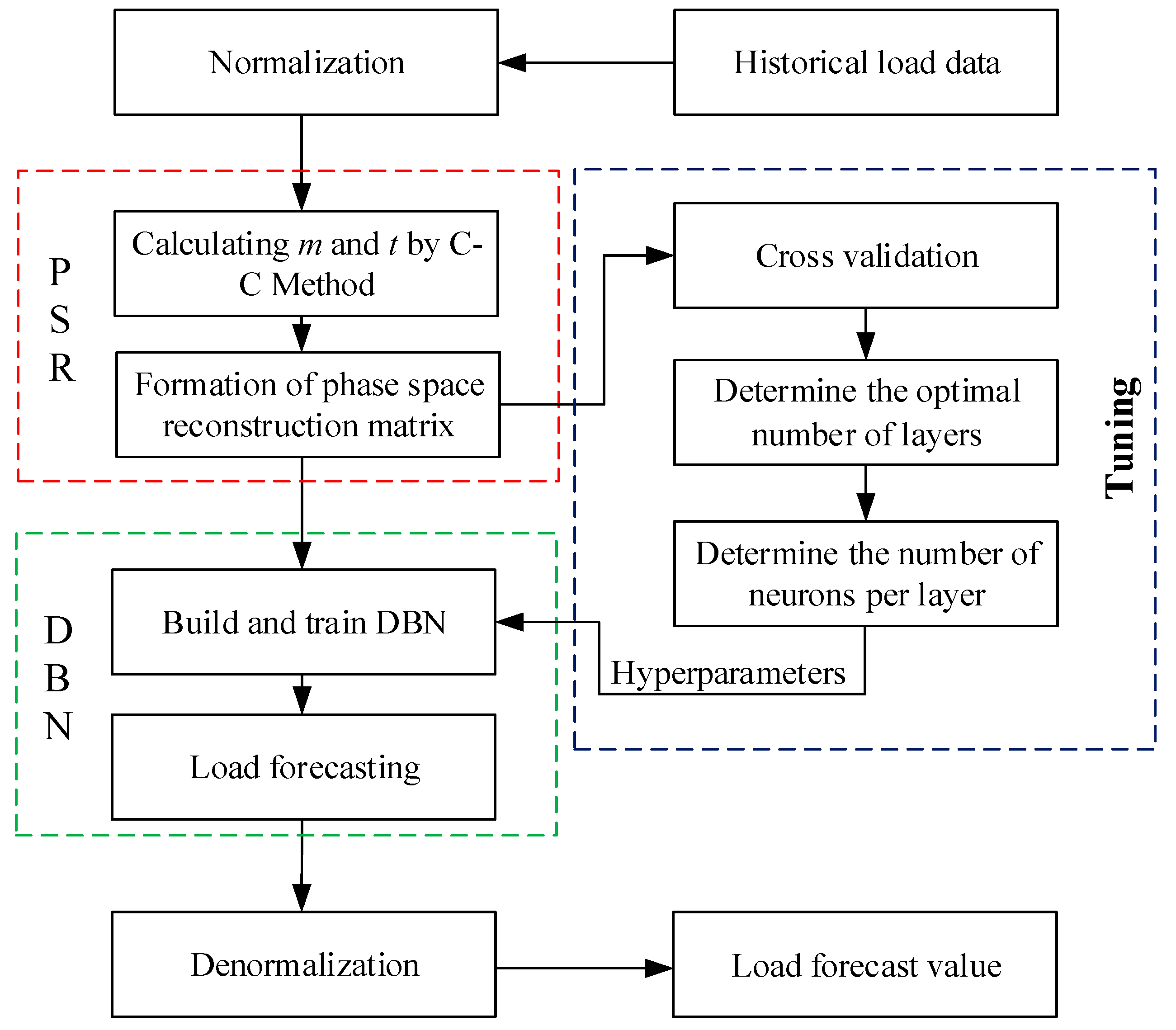
3. PSR-DBN Forecasting Model
3.1. The Procedure of the PSR-DBN Model
3.2. Determination of DBN Network Structure
- Cross-validation method: Considering that the load data is a time series, it is not appropriate to use a K-fold cross-validation method to disrupt the order. Therefore, the last part of the training set is eliminated and used as a verification set by hold-out cross-validation. The rest of the data is kept as a training set.
- Determine the optimal number of layers: The enumeration is used to determine the optimal number of hidden layers. Many researchers find that a shallow network requires exponential width (number of neurons in each layer) to implement a function that a deep network of polynomial width could implement [32]. That is, compared with the number of layers, the number of neurons in each layer has less influence on prediction, so it is fixed during the enumeration. The number of neurons in each layer is set to be 2m, and the number of hidden layers is increased layer by layer until a significant over-fitting occurs. Then the number of hidden layers with the smallest forecasting error is selected.
- Determine the number of neurons in each layer: Since the forecasting performance of DBN varies with the initial value, the effect of changing the number of neurons one by one on forecasting performance is easily submerged in the fluctuation of forecasting performance caused by different initial values. Therefore, this paper uses a fixed step size to search for the superior number of neurons roughly. After determining the number of hidden layers according to step 2, the combination of the number of neurons with minimum prediction error is searched in steps of m in each layer. Because too many neurons will make the training of network slow and bring the risk of over-fitting, the selected search range of this paper is m to 5m, and a good combination of the number of neurons is determined by testing.
4. Case Study
4.1. Bus Load Data
4.2. Forecasting Evaluation Index
4.3. PSR Reconstruction Results
4.4. DBN Hyperparameter Setting
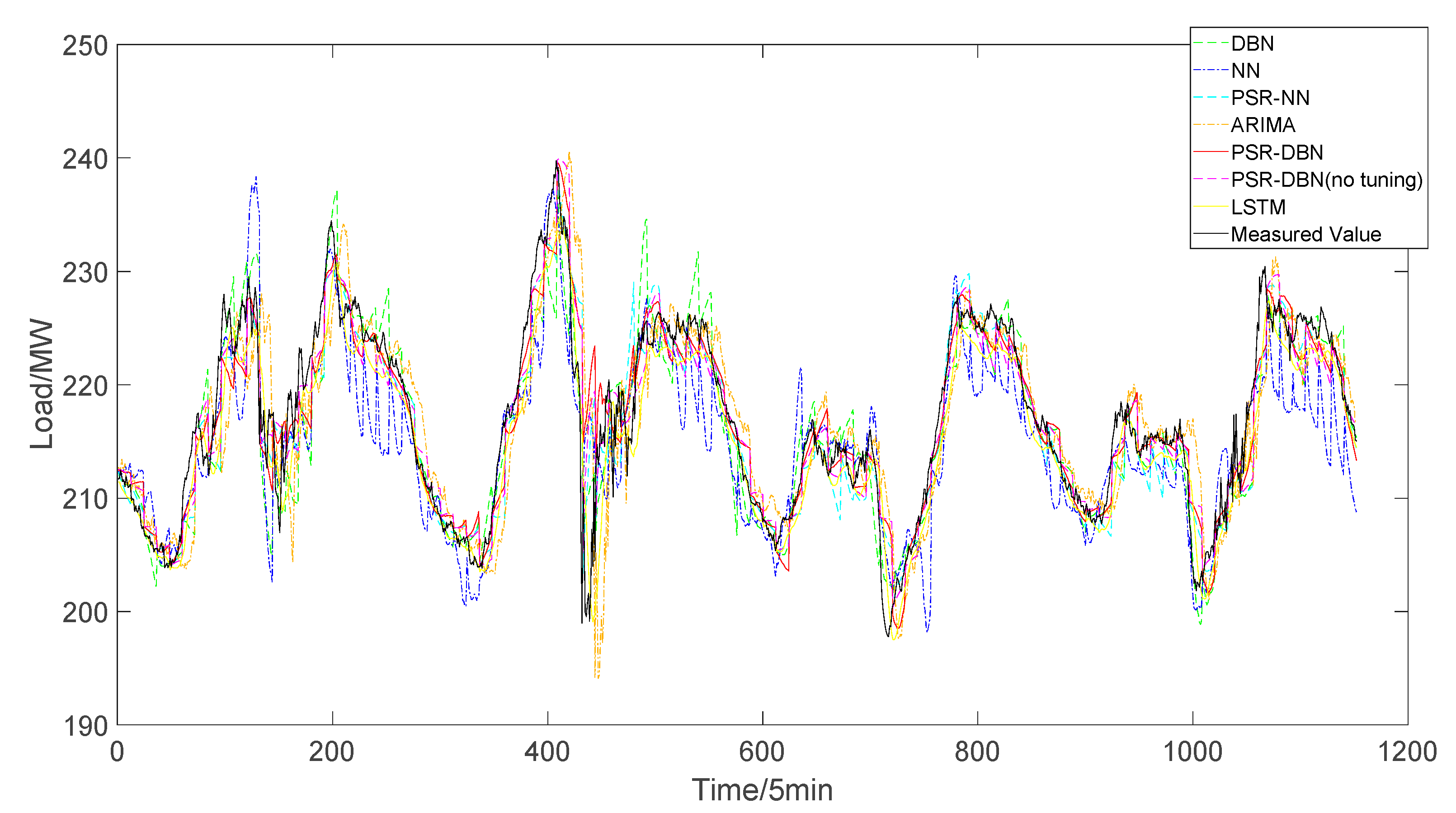
4.5. Forecasting Result
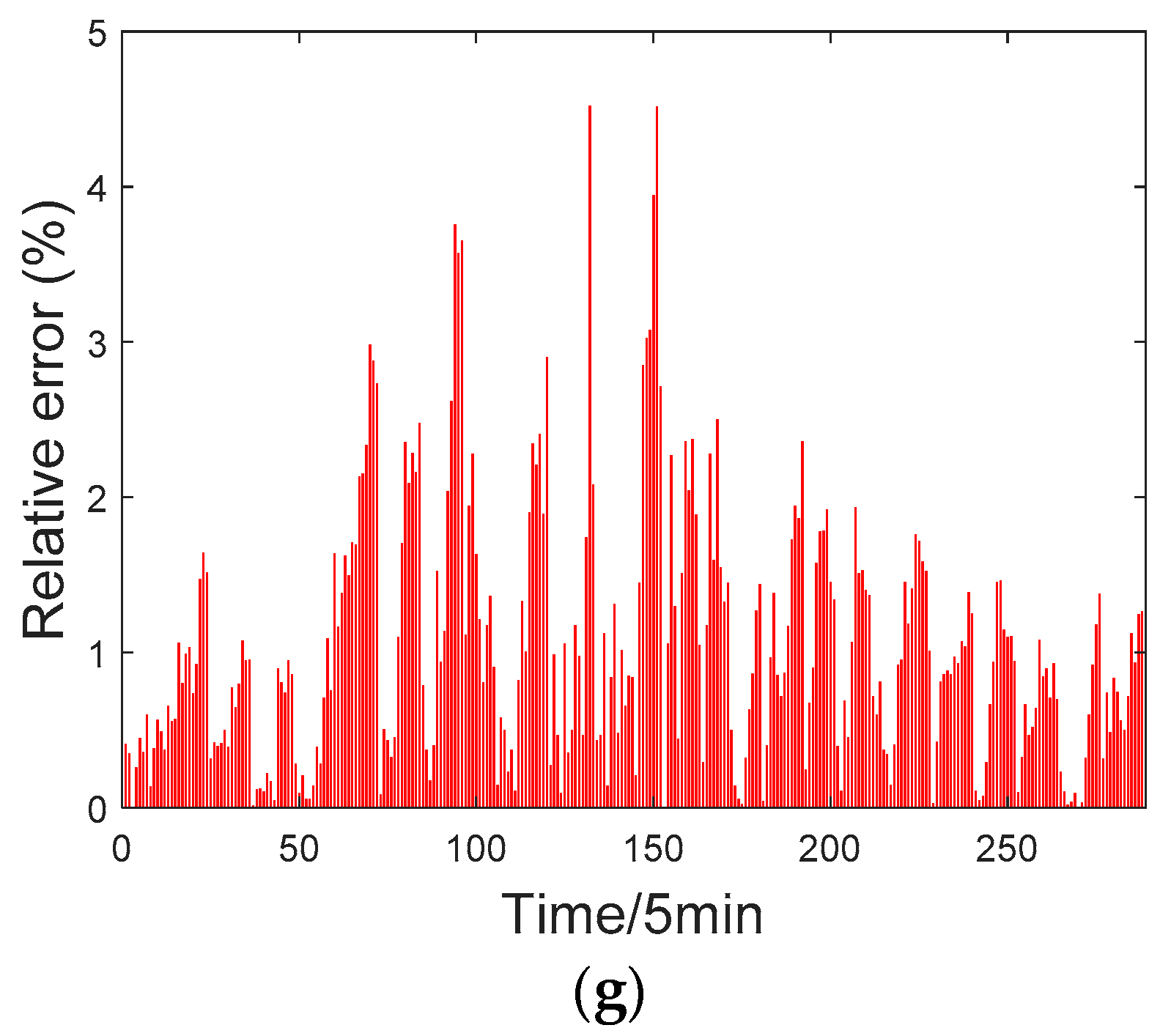
4.5.1. One Hour Ahead Load Forecasting
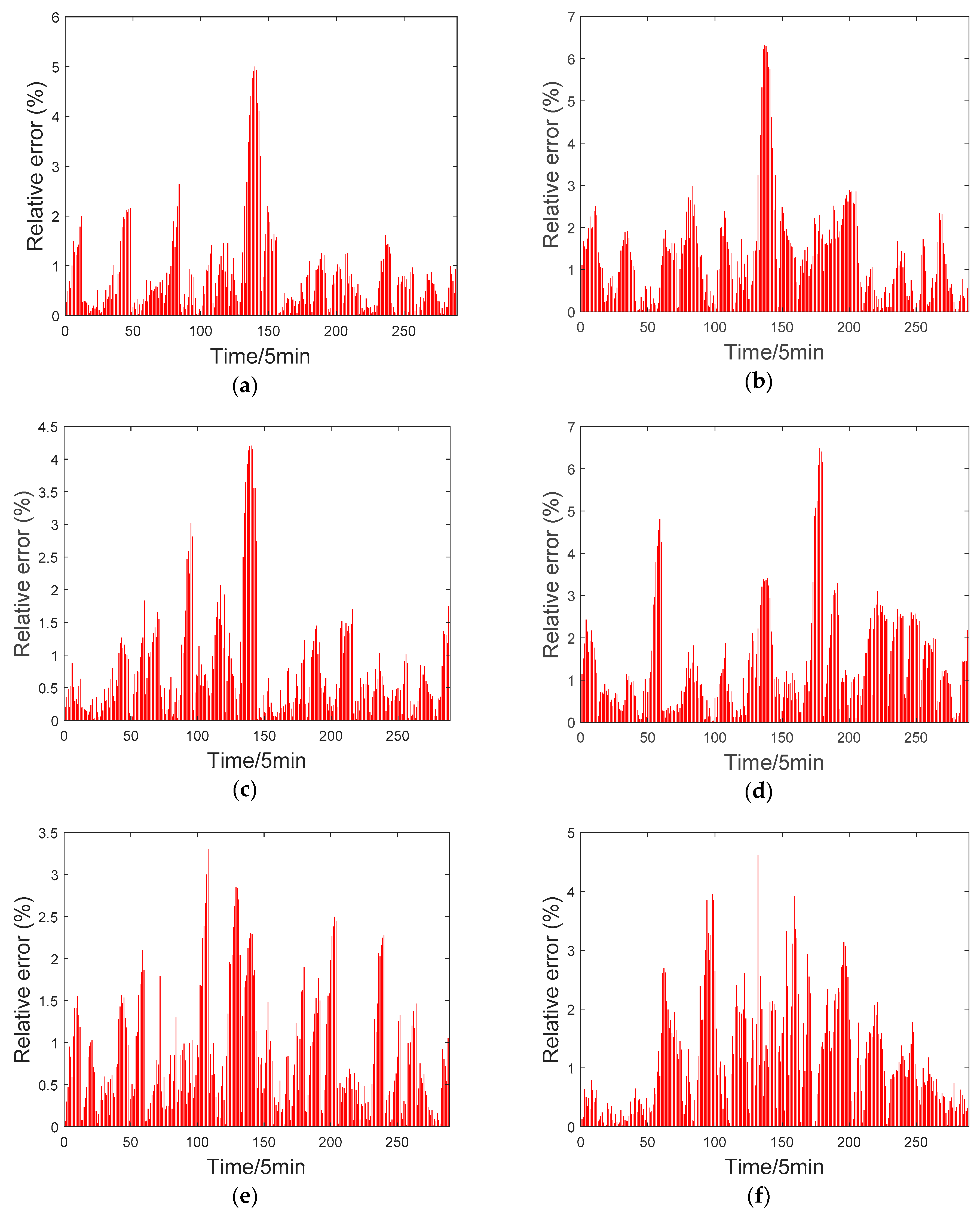
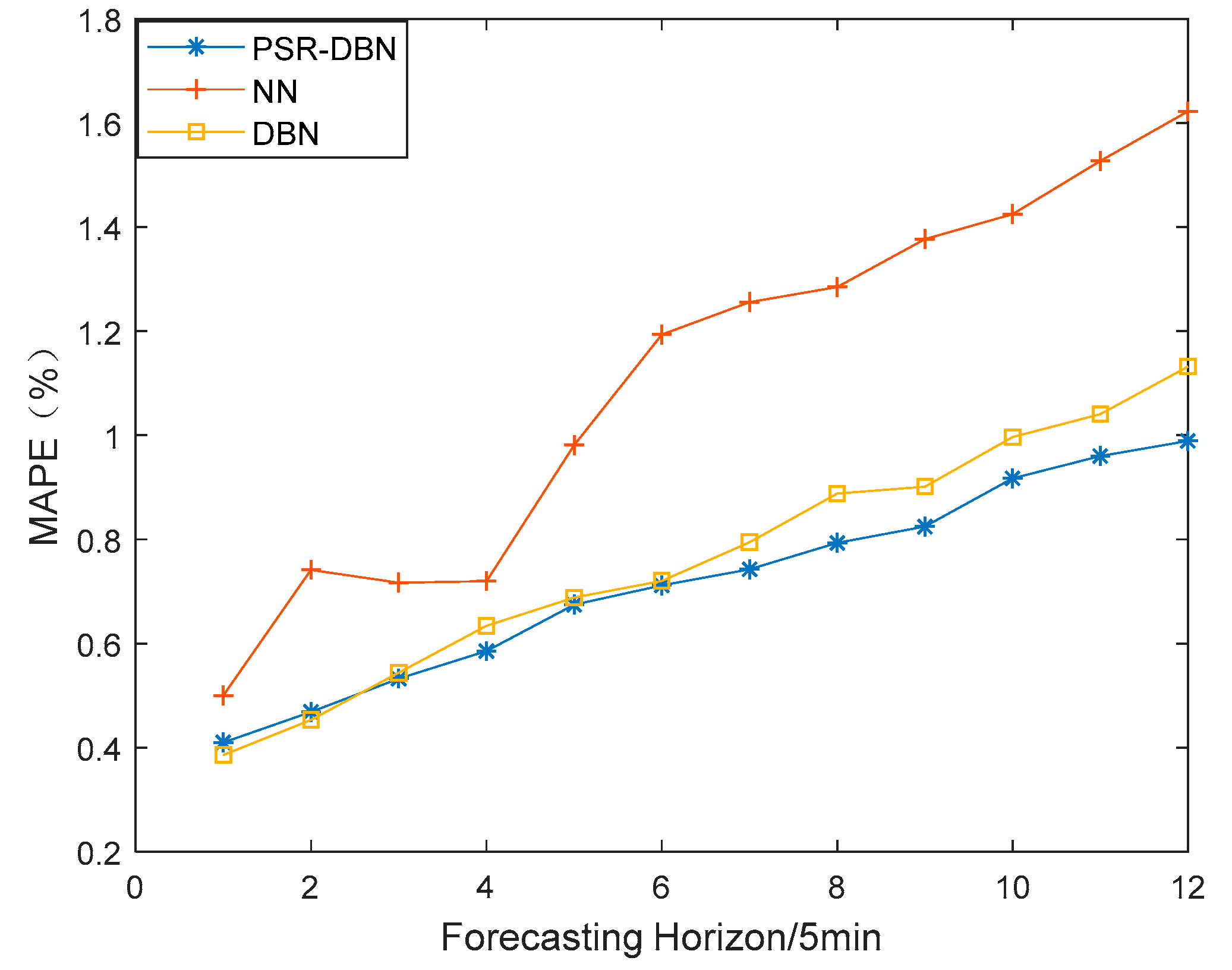
4.5.2. Prediction of Different Forecasting Horizons (5 min to 1 h ahead)
5. Conclusions
- The PSR-DBN forecasting model proposed in this paper can still maintain relatively high prediction accuracy under the condition of high distributed power penetration and large fluctuation of bus load. The prediction accuracy of the proposed model is greatly improved, when compared to the ARIMA model of traditional time series models and the general neural network model.
- The proposed practical tuning method, which is based on cross-validation, can effectively improve prediction accuracy of the model compared with the random structure selection strategy.
- Under different forecasting horizons (5 min to 1 h), the PSR-DBN model proposed in this paper can still have a small prediction error. Compared with the model only using DBN, the phase-space reconstruction technique improves the adaptability of the model to long forecasting horizons. Therefore, the PSR-DBN model in this paper can maintain a small prediction error even in long forecasting horizons.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, K.Y.; Cha, Y.T.; Park, J.H.; Kurzyn, M.S.; Park, D.C.; Mohammed, O.A. Short-term load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1992, 7, 124–132. [Google Scholar] [CrossRef]
- Kang, C.; Xia, Q.; Zhang, B. Review of power system load forecasting and its development. Autom. Electr. Power Syst. 2004, 28, 1–11. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Moghram, I.; Rahman, S. Analysis and evaluation of 5 short-term load forecasting techniques. IEEE Trans. Power Syst. 1989, 4, 1484–1491. [Google Scholar] [CrossRef]
- Ding, Q.; Lu, J.; Qian, Y.; Zhang, J.; Liao, H. A practical method for ultra-short term load forecasting. Autom. Electr. Power Syst. 2004, 28, 83–85. [Google Scholar]
- Fard, A.K.; Akbari-Zadeh, M.-R. A hybrid method based on wavelet, ANN and ARIMA model for short-term load forecasting. J. Exp. Theor. Artif. Intell. 2014, 26, 167–182. [Google Scholar] [CrossRef]
- Lee, C.-M.; Ko, C.-N. Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl. 2011, 38, 5902–5911. [Google Scholar] [CrossRef]
- Douglas, A.P.; Breipohl, A.M.; Lee, F.N.; Adapa, R. The impacts of temperature forecast uncertainty on Bayesian load forecasting. IEEE Trans. Power Syst. 1998, 13, 1507–1513. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Muljadi, E.; Zhang, J.J.; Gao, D.W. A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization. IEEE Trans. Smart Grid 2018, 9, 3341–3350. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y. A hybrid model of EMD and PSO-SVR for short-term load forecasting in residential quarters. Math. Probl. Eng. 2016, 2016, 9895639. [Google Scholar] [CrossRef]
- Bento, P.M.R.; Pombo, J.A.N.; Calado, M.R.A.; Mariano, S.J.P.S. Optimization of neural network with wavelet transform and improved data selection using bat algorithm for short-term load forecasting. Neurocomputing 2019, 358, 53–71. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, X.; Meng, Y. Short-term load forecasting with tensor partial least squares-neural network. Energies 2019, 12, 990. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Zhang, T.; Liu, Y.; Zha, Y. Short-term load forecasting using a novel deep learning framework. Energies 2018, 11, 1554. [Google Scholar] [CrossRef]
- Pan, Y.; Mei, F.; Miao, H.; Zheng, J.; Zhu, K.; Sha, H. An approach for HVCB mechanical fault diagnosis based on a deep belief network and a transfer learning strategy. J. Electr. Eng. Technol. 2019, 14, 407–419. [Google Scholar] [CrossRef]
- Yu, R.; Gao, J.; Yu, M.; Lu, W.; Xu, T.; Zhao, M.; Zhang, J.; Zhang, R.; Zhang, Z. LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 2019, 93, 33–42. [Google Scholar] [CrossRef]
- Yang, L.; Yang, H. Analysis of different neural networks and a new architecture for short-term load forecasting. Energies 2019, 12, 1433. [Google Scholar] [CrossRef]
- Panapakidis, I.P. Application of hybrid computational intelligence models in short-term bus load forecasting. Expert Syst. Appl. 2016, 54, 105–120. [Google Scholar] [CrossRef]
- Panapakidis, I.P. Clustering based day-ahead and hour-ahead bus load forecasting models. Int. J. Electr. Power Energy Syst. 2016, 80, 171–178. [Google Scholar] [CrossRef]
- Fan, G.-F.; Peng, L.-L.; Hong, W.-C. Short term load forecasting based on phase space reconstruction algorithm and bi-square kernel regression model. Appl. Energy 2018, 224, 13–33. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, W.; Zhou, Y.; Liao, F.; Xu, C.; Cheng, Y.; Yao, J. Application of indirect forecasting method in bus load forecasting. Power Syst. Technol. 2011, 35, 177–182. [Google Scholar]
- He, Y.; Qin, Y.; Lei, X.; Feng, N. A study on short-term power load probability density forecasting considering wind power effects. Int. J. Electr. Power Energy Syst. 2019, 113, 502–514. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Y.; Sun, L.; Xue, H. Ultra-short term prediction model of photovoltaic output power based on chaos-RBF neural network. Power Syst. Technol. 2018, 42, 1110–1116. [Google Scholar]
- Wang, H.Z.; Wang, G.B.; Li, G.Q.; Peng, J.C.; Liu, Y.T. Deep belief network based deterministic and probabilistic wind speed forecasting approach. Appl. Energy 2016, 182, 80–93. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay times, and embedding windows. Phys. D Nonlinear Phenom. 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Kim, H.S.; Kang, D.S.; Kim, J.H. The BDS statistic and residual test. Stoch. Environ. Res. Risk Assess. 2003, 17, 104–115. [Google Scholar] [CrossRef]
- Durlauf, S.N. Nonlinear dynamics, chaos, and instability—Statistical-theory and economic evidence. J. Econ. Lit. 1993, 31, 232–234. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, J.; Liu, Y.; Wen, L.; Wang, Z.; Ning, S. Transformer load forecasting based on adaptive deep belief network. Proc. Chin. Soc. Electr. Eng. 2019, 39, 4049–4060. [Google Scholar]
- Bengio; Y, Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [CrossRef]
- Mei, F.; Wu, Q.; Shi, T.; Lu, J.; Pan, Y.; Zheng, J. An ultrashort-term net load forecasting model based on phase space reconstruction and deep neural network. Appl. Sci. 2019, 9, 1487. [Google Scholar] [CrossRef]
- Zhong, G.; Ling, X.; Wang, L.-N. From shallow feature learning to deep learning: Benefits from the width and depth of deep architectures. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1255. [Google Scholar] [CrossRef]
- Hyndman, R.J. Another look at forecast accuracy metrics for intermittent demand. Foresight Int. J. Appl. Forecast. 2006, 4, 43–46. [Google Scholar]
| Number of Hidden Layers | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| MAPE | 1.0387 | 1.0129 | 0.9358 | 1.0443 | 1.0413 | 1.0857 | 1.1336 |
| Hyperparameter | Value |
|---|---|
| DBN Network structure | [5, 25, 15, 20, 15] |
| learning rate | 0.8 |
| Maximum epochs of RBM | 100 |
| NN Network structure | [5, 25, 15, 20, 15, 1] |
| LMBP() | 0.001 |
| Maximum epochs of NN | 150 |
| Model | MAPE (%) | RMSE | MASE | sMASE | GMAE | Training Time (s) |
|---|---|---|---|---|---|---|
| PSR-DBN | 0.9892 | 3.2316 | 2.5403 | 0.9856 | 1.2027 | 12.3397 |
| PSR-NN | 1.0125 | 3.2310 | 2.6098 | 1.0126 | 1.2259 | 18.9233 |
| DBN | 1.1322 | 3.4684 | 2.9353 | 1.1358 | 1.3815 | 7.2980 |
| ARIMA | 1.5929 | 4.8657 | 4.0986 | 1.5922 | Inf | 20.0625 |
| NN | 1.6222 | 4.6757 | 4.2132 | 1.6333 | Inf | 15.1189 |
| LSTM | 1.0736 | 3.3266 | 2.7877 | 1.0799 | Inf | 17.2867 |
| PSR-DBN (no tuning) | 1.0380 | 3.2792 | 2.6737 | 1.0358 | 1.3279 | 10.2336 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, T.; Mei, F.; Lu, J.; Lu, J.; Pan, Y.; Zhou, C.; Wu, J.; Zheng, J. Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting. Energies 2019, 12, 4349. https://doi.org/10.3390/en12224349
Shi T, Mei F, Lu J, Lu J, Pan Y, Zhou C, Wu J, Zheng J. Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting. Energies. 2019; 12(22):4349. https://doi.org/10.3390/en12224349
Chicago/Turabian StyleShi, Tian, Fei Mei, Jixiang Lu, Jinjun Lu, Yi Pan, Cheng Zhou, Jianzhang Wu, and Jianyong Zheng. 2019. "Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting" Energies 12, no. 22: 4349. https://doi.org/10.3390/en12224349
APA StyleShi, T., Mei, F., Lu, J., Lu, J., Pan, Y., Zhou, C., Wu, J., & Zheng, J. (2019). Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting. Energies, 12(22), 4349. https://doi.org/10.3390/en12224349