Study on Thermal Energy Conversion Theory in Drilling Process of Coal and Rock Mass with Different Stresses
Abstract
:1. Introduction
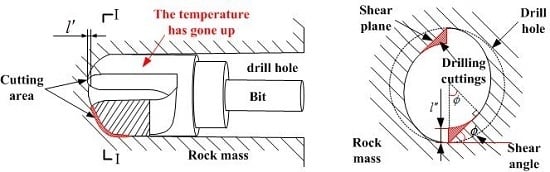
2. Factors and Causes of Heat Generation in Drilling
3. Theory of Temperature Field Evolution of the Drill Bit
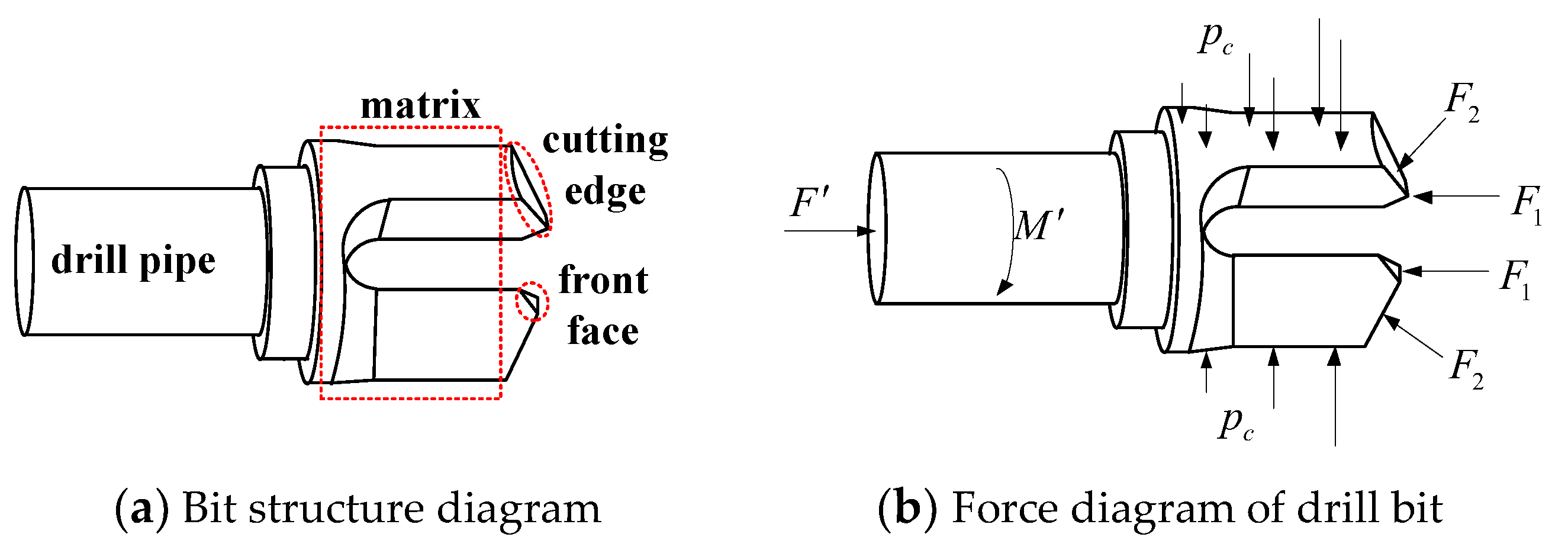
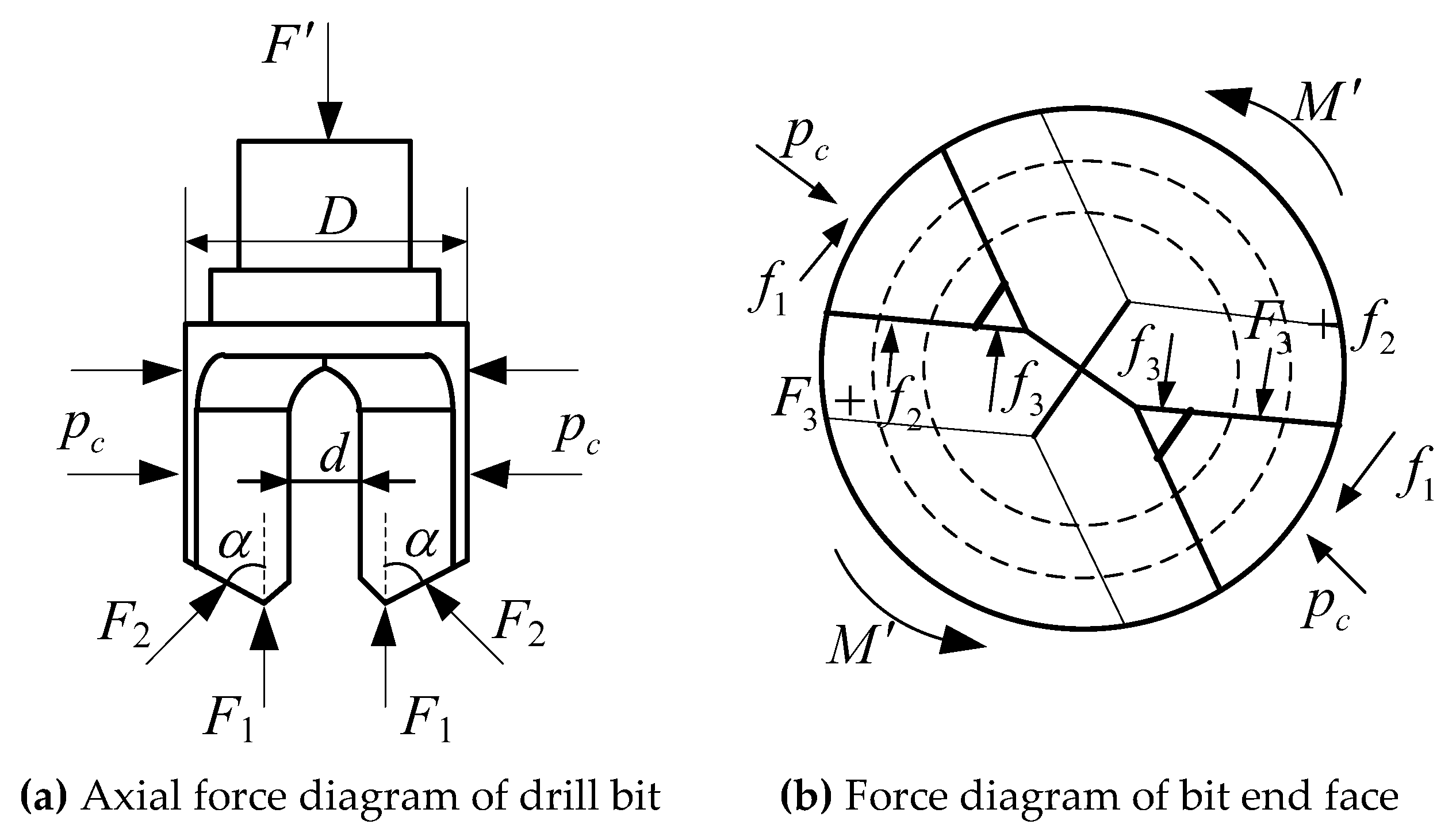
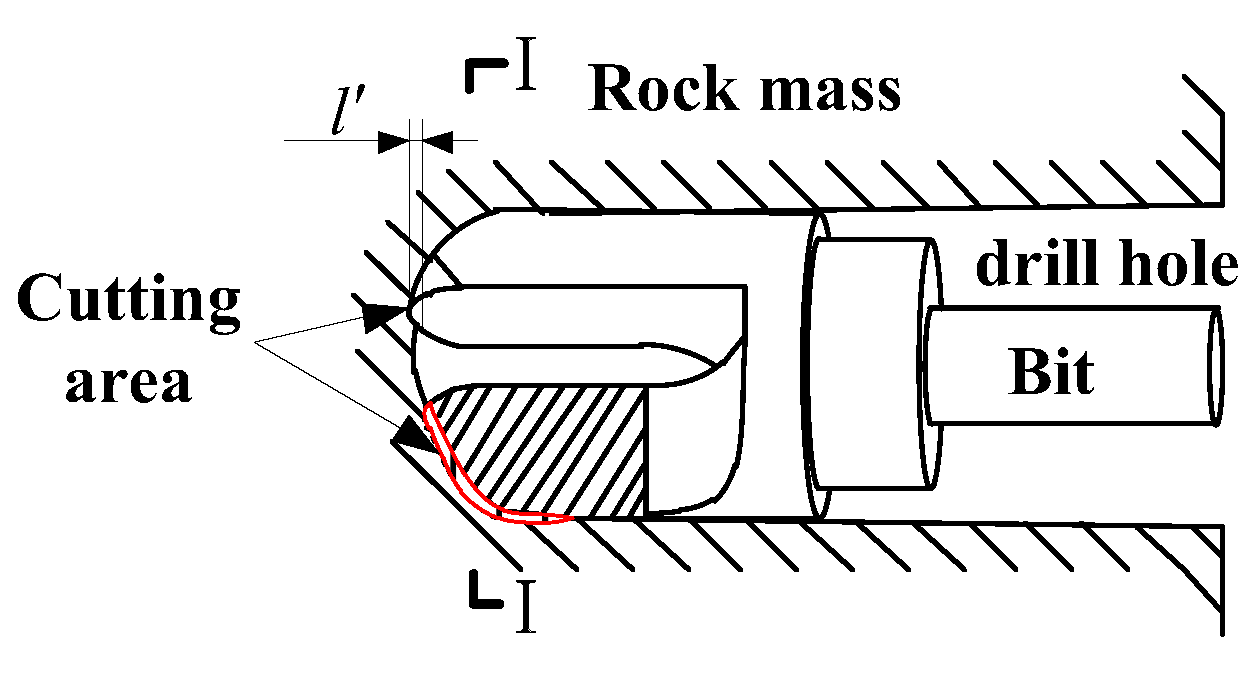
3.1. Mechanical Analysis of the Drilling Process
- (1).
- The coal and rock mass is a homogeneous and isotropic continuous medium;
- (2).
- The drilling process follows the limit stress equilibrium condition;
- (3).
- The drill bit is a homogeneous isotropic continuous medium.
3.2. Generation and Distribution of Heat
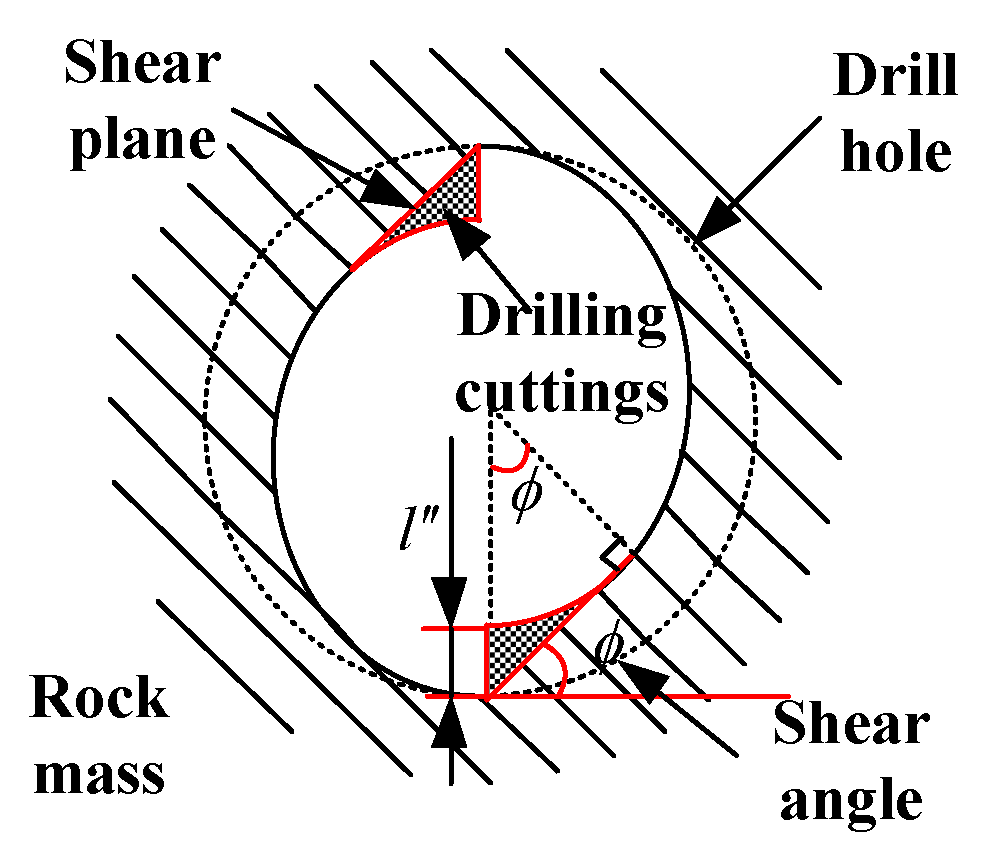
3.2.1. Generation of Friction Heat
3.2.2. Generation of Shear Heat
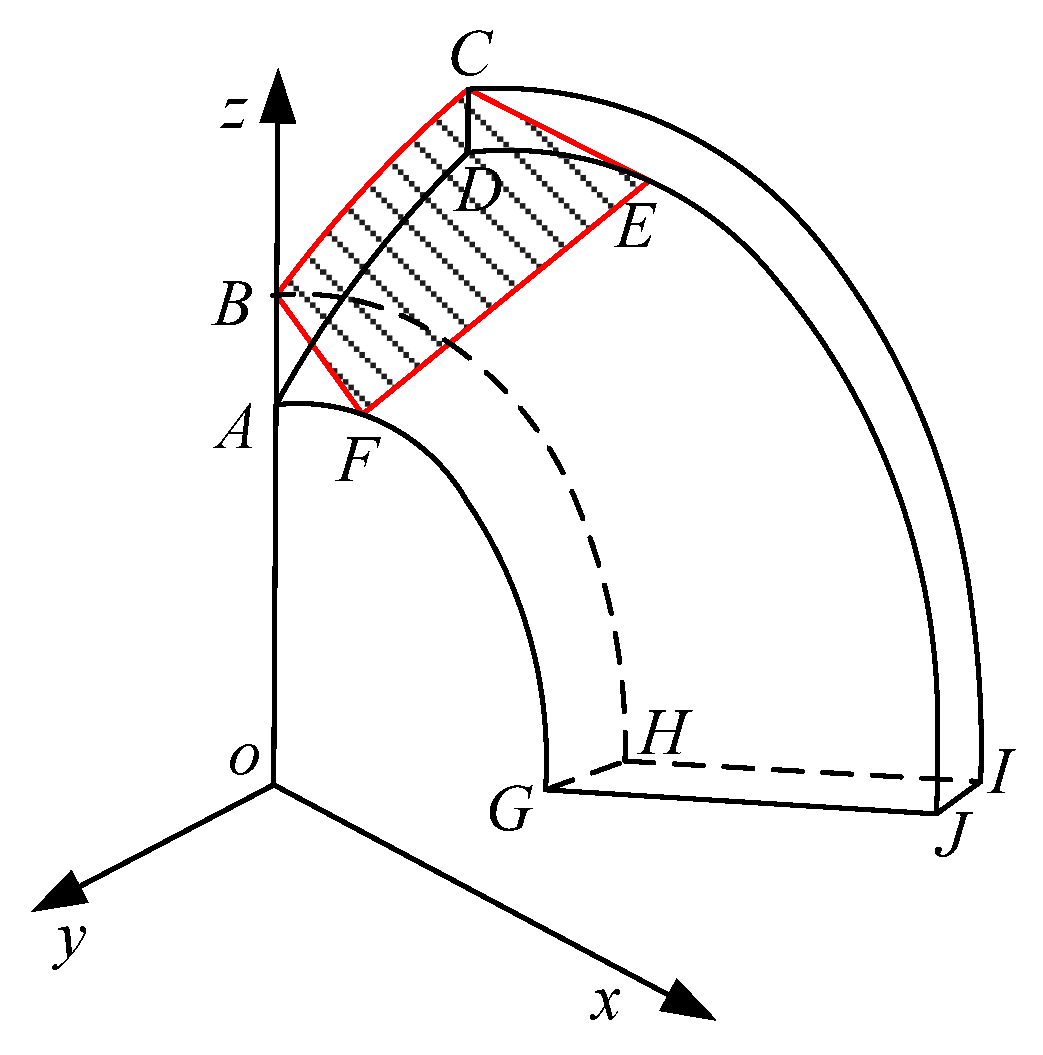
3.2.3. The Distribution of Heat
3.3. Bit Temperature Rise Condition Model
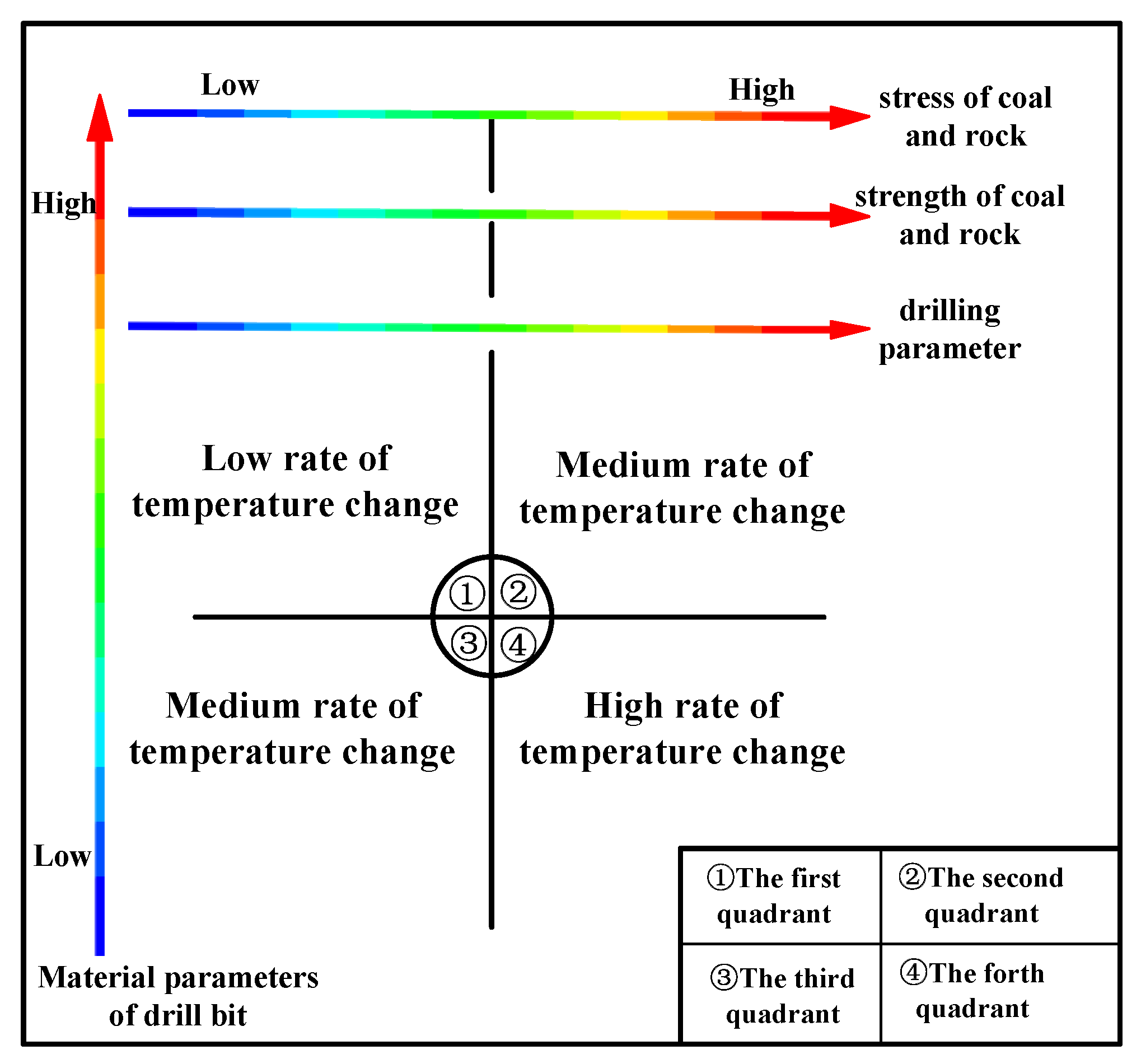
3.4. The Relation between Coal Rock Stress and the Bit Temperature Rise
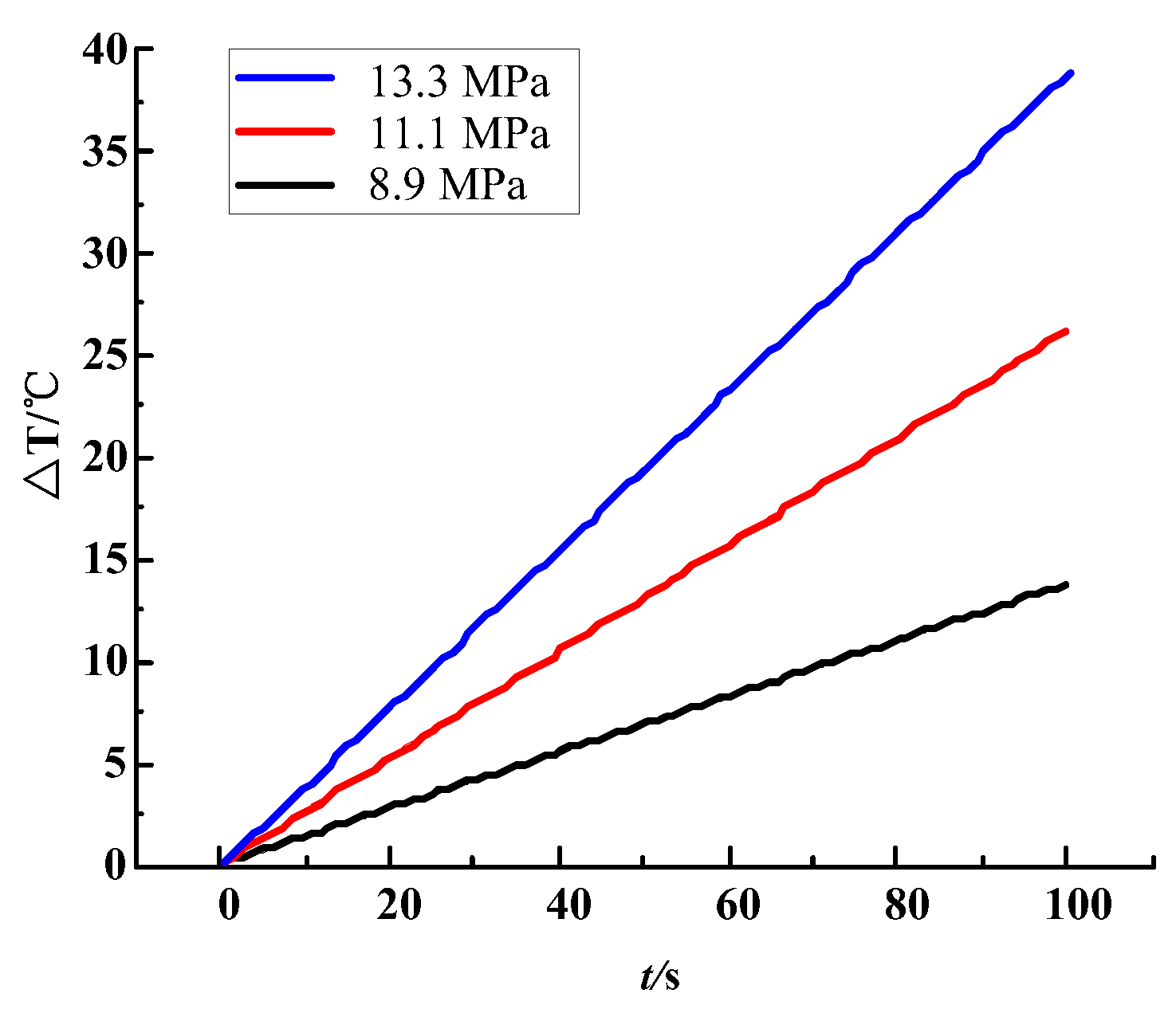
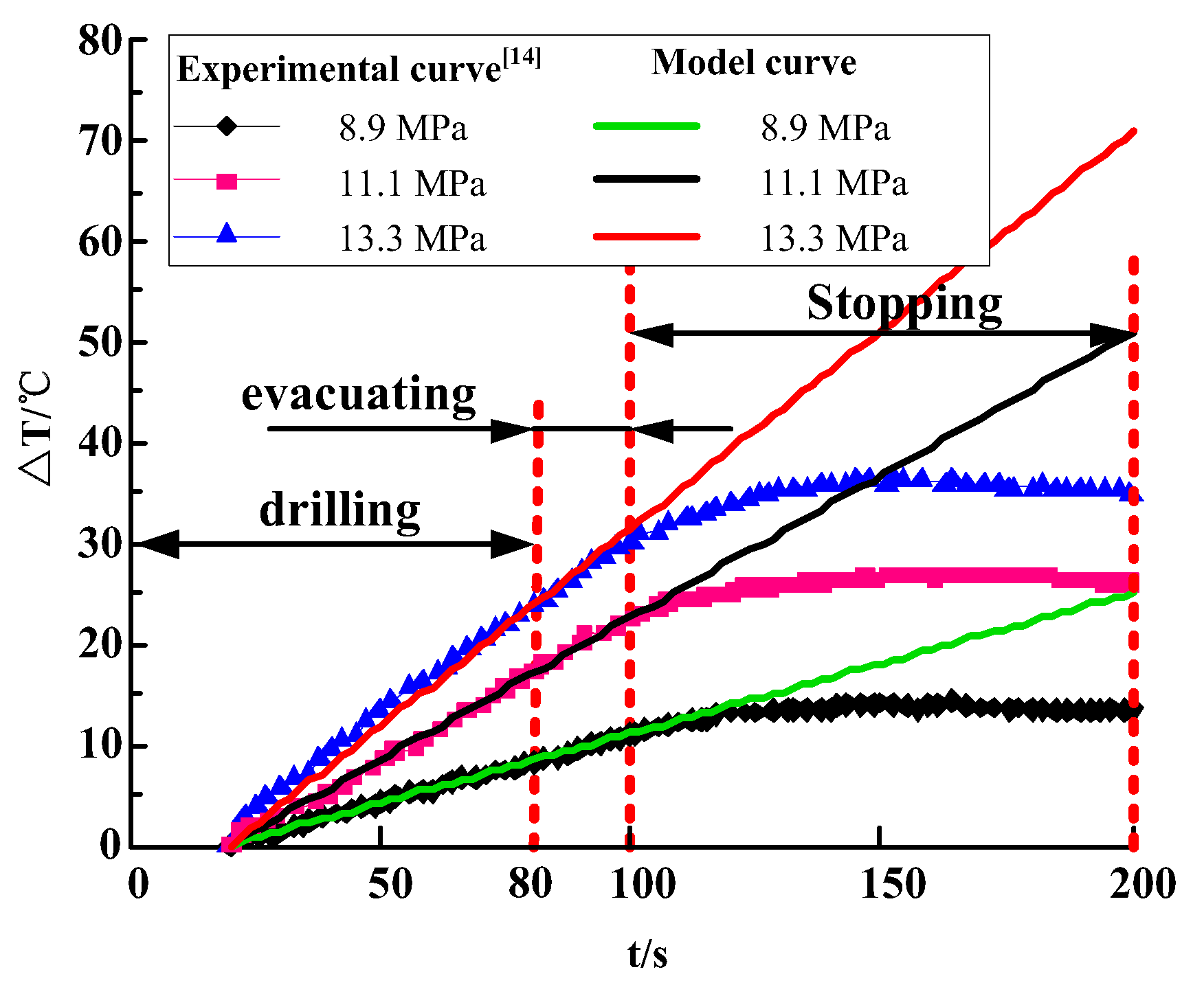
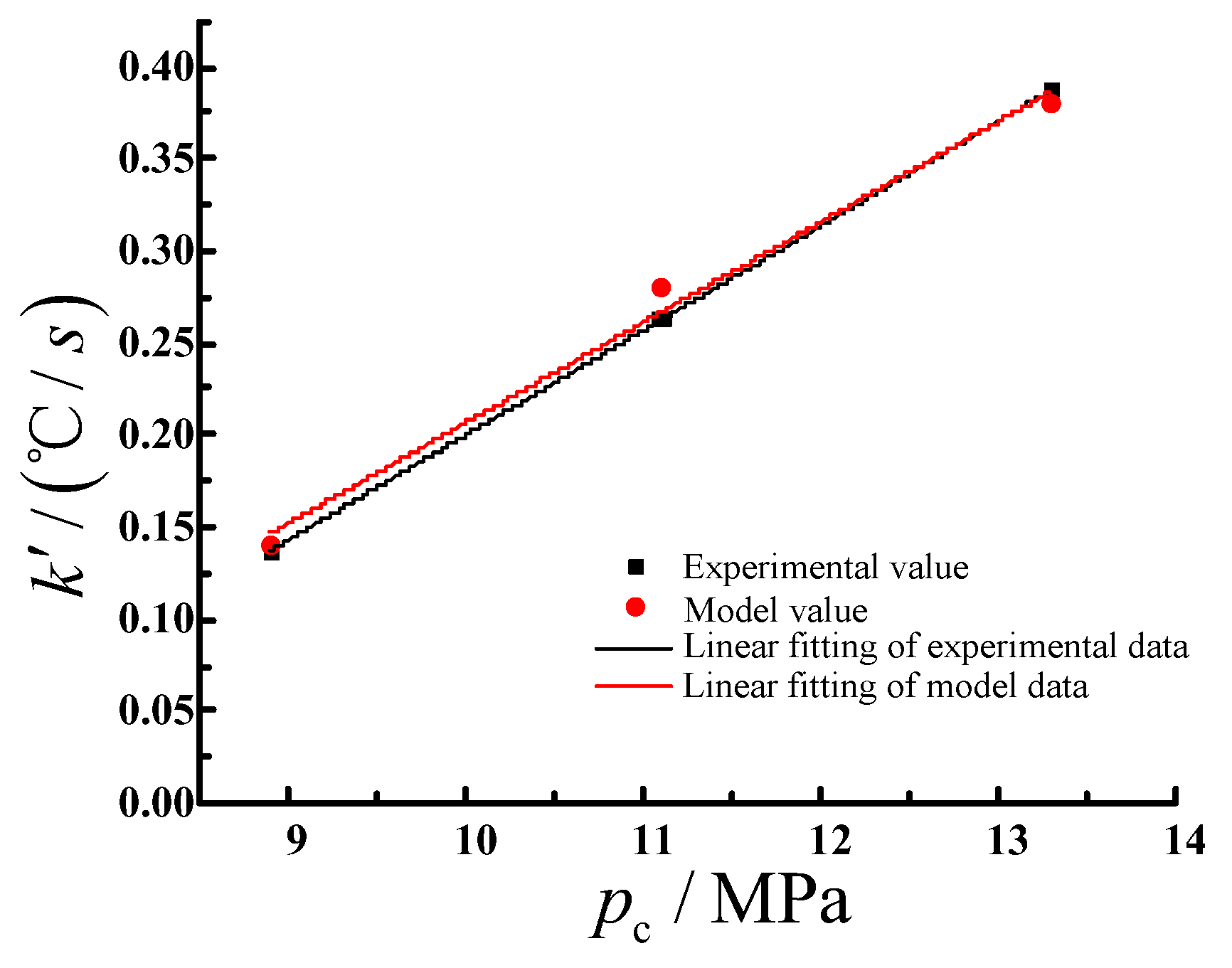
4. Verification of the Relationship between the Rate of Bit Temperature Change and the Stress of the Coal and Rock Mass
5. Conclusions
- (1).
- By studying the detection of the drilling process, the mechanism and factors of heat generation during the interaction between the drill bit and coal and rock mass are analyzed. The influences of coal and rock mass stress, coal and rock mass strength, bit motion parameters and bit material parameters on bit temperature change were obtained qualitatively, which provides a basis for the quantitative study of the relationship between the stress of coal and rock mass and the rate of bit temperature change.
- (2).
- On the basis of the mechanical analysis of the bit during drilling and the principle of energy conservation and thermal energy conversion theory, the conditional model of bit temperature rise and the coal stress identification model were established, and a linear expression between the coal stress and the bit temperature rate was obtained.
- (3).
- The variation law of bit temperature obtained from the stress identification model of the coal body is consistent with the experimental data, fully demonstrating the feasibility of using temperature as a discriminant stress index of coal. This provides a direct and effective reference for delineating dangerous areas of rock burst and testing the effect of anti-outburst measures.
- (4).
- In the process of using the bit temperature rate as the index to judge the coal stress value, a theoretical research method was adopted. The research results are preliminary and need to be further revised and deepened by practical application under specific engineering conditions.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, H.T.; Xian, X.F.; He, J.M.; Lv, Y.C.; Ji, R.S.; Zhang, J.G. Inquisition of Forecasting Dangerousness of Heading Face Outburst by Drillings and Coalbed Temperature Indices. J. Chongqing Univ. (Nat. Sci. Ed.) 1999, 22, 34–38. [Google Scholar]
- Liu, S.W.; Fu, M.; Jia, H.S.; Li, W.B.; Luo, Y.F. Numerical simulation and analysis of drill rods vibration during roof bolt hole drilling in underground mines. Int. J. Min. Sci. Technol. 2018, 28, 877–884. [Google Scholar] [CrossRef]
- Liu, S.W.; Zhu, Q.K.; Jia, H.S.; Zhu, X.T. Characteristics and recognition of the dynamic response of strata interfaces to anchorage hole drilling in coal roadway roof. J. Min. Saf. Eng. 2017, 34, 748–753, 759. [Google Scholar]
- Liu, S.W.; Liu, D.L.; Feng, Y.L.; Li, X.T.; Shang, P.X. Influence of stress states on drilling velocity of anchorage hole on coal roadway roof. J. China Coal Soc. 2014, 39, 608–613. [Google Scholar]
- Liu, S.W.; Luo, Y.F.; Jia, H.S. Energy response characteristics of rock interface under drilling of roof anchorage borehole in coal roadway. J. China Univ. Min. Technol. 2018, 47, 88–96. [Google Scholar]
- Eunhye, K.; Kerwin, H.; Demetryus, O.; Andrew, K. Effects of the skew angle of conical bits on bit temperature, bit wear, and rock cutting performance. Int. J. Rock Mech. Min. Sci. 2017, 100, 263–268. [Google Scholar]
- Sajjad, K.; Alireza, B.; Hamid, H. An analytical model for estimating rock strength parameters from smallscale drilling data. J. Rock Mech. Geotech. Eng. 2019, 11, 135–145. [Google Scholar]
- Feng, Y.L.; Liu, D.L. Model Test on Dynamic Response Characteristics in Drilling Anchorage Borehole of Roadway Roof. Chin. J. Undergr. Sp. Eng. 2016, 12, 525–531. [Google Scholar]
- Feng, Y.L.; Liu, D.L.; Luo, Y.F. Experimental study on dynamic response characteristics in drilling sedimentary rocks of coal roadway roof. J. Saf. Sci. Technol. 2016, 12, 31–37. [Google Scholar]
- Yang, X.F.; Kang, Y.; Wang, X.C. Analytical dynamic model of the drill bit in rock drilling. J. China Coal Soc. 2012, 37, 1596–1600. [Google Scholar]
- Yang, X.F.; LI, X.H.; Lu, Y.Y. Temperature analysis of drill bit in rock drilling. J. Central South Univ. (Sci. Technol.) 2011, 42, 3164–3169. [Google Scholar]
- Jurij, S.; Primoz, M.; Mitja, P.; Goran, V.; Zeljko, V. The characterization of wear in roller cone drill bit by rock material—Sandstone. J. Petroleum Sci. Eng. 2019, 173, 1355–1367. [Google Scholar]
- Alexander, M.; Elena, S.; Llya, N. Choice of lubricating and cooling action of cutting fluids by the thermomechanical model. Adv. Mater. Res. 2014, 1036, 405–410. [Google Scholar]
- Pan, Y.S.; Xv, L.M.; Li, G.Z.; Li, Z.H. Experimental study on the effect of coal intensity on drillings temperature. J. China Coal Soc. 2012, 37, 463–466. [Google Scholar]
- Pan, Y.S.; Xv, L.M. Experimental investigation on temperature of drilling cuttings to predict rock burst. Chin. J. Geotech. Eng. 2012, 34, 2228–2232. [Google Scholar]
- Xu, L.M.; Li, Q.; Pan, Y.S.; Li, Z.H.; Li, G.Z.; Ma, X. Study on forecasting rock burst of the drill pipe torque method. Eng. Mech. 2014, 31, 251–256. [Google Scholar]
- Pradeep, L.M.; Michael, R.L.; Ilya, V.A.; Jeen, S.L.; Higgs, C.F. Studies on the formation of discontinuous chips during rock cutting using an explicit finite element model. Int. J. Adv. Manuf. Technol. 2014, 70, 635–648. [Google Scholar]
- Babak, A.; Stefan, M. The effects of chamfer and back rake angle on PDC cutters friction. J. Nat. Gas Sci. Eng. 2016, 35, 347–353. [Google Scholar]
- Xu, S.Q.; Tan, Z.Y. Numerical Simulation and Design Optimization of Expansive Soil Cutting Slope Reinforced by Bolt Frame Pier. Subgrade Eng. 2014, 175, 66–70. [Google Scholar]
- Zhou, Y.N.; Zhang, W.; Isaac, G.; Lin, J.S. Mechanical specific energy versus depth of cut in rock cutting and drilling. Int. J. Rock Mech. Min. Sci. 2017, 100, 287–297. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E. Rock cutting characteristics on soft-to-hard rocks under different cutter inclinations. Int. J. Rock Mech. Min. Sci. 2016, 87, 85–89. [Google Scholar] [CrossRef]
- AbuBakara, M.Z.; Buttb, I.A.; Majeedc, Y. Penetration Rate and Specific Energy Prediction of Rotary—Percussive Drills Using Drill Cuttings and Engineering Properties of Selected Rock Units. J. Min. Sci. 2018, 54, 270–284. [Google Scholar] [CrossRef]
- Chen, J.H.; Feng, Y.; Zeng, Y.J.; Han, Y.N.; Wang, Y.; Niu, C.C. Continuous rock drillability measurements using scratch tests. J. Pet. Sci. Eng. 2017, 159, 783–790. [Google Scholar] [CrossRef]
- Jerzy, R. Discrete element thermomechanical modelling of rock cutting with valuation of tool wear. Comput. Part. Mech. 2014, 1, 71–84. [Google Scholar]
- Ritto, T.G.; Escalante, M.R.; Rubens, S.; Rosales, M.B. Drill-string horizontal dynamics with uncertainty on the frictional force. J. Sound Vib. 2013, 332, 145–153. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, J.; Nie, R.; Zeng, Y.; Xu, B.; Sun, X. A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush. Appl. Sci. 2019, 9, 2195. [Google Scholar] [CrossRef]
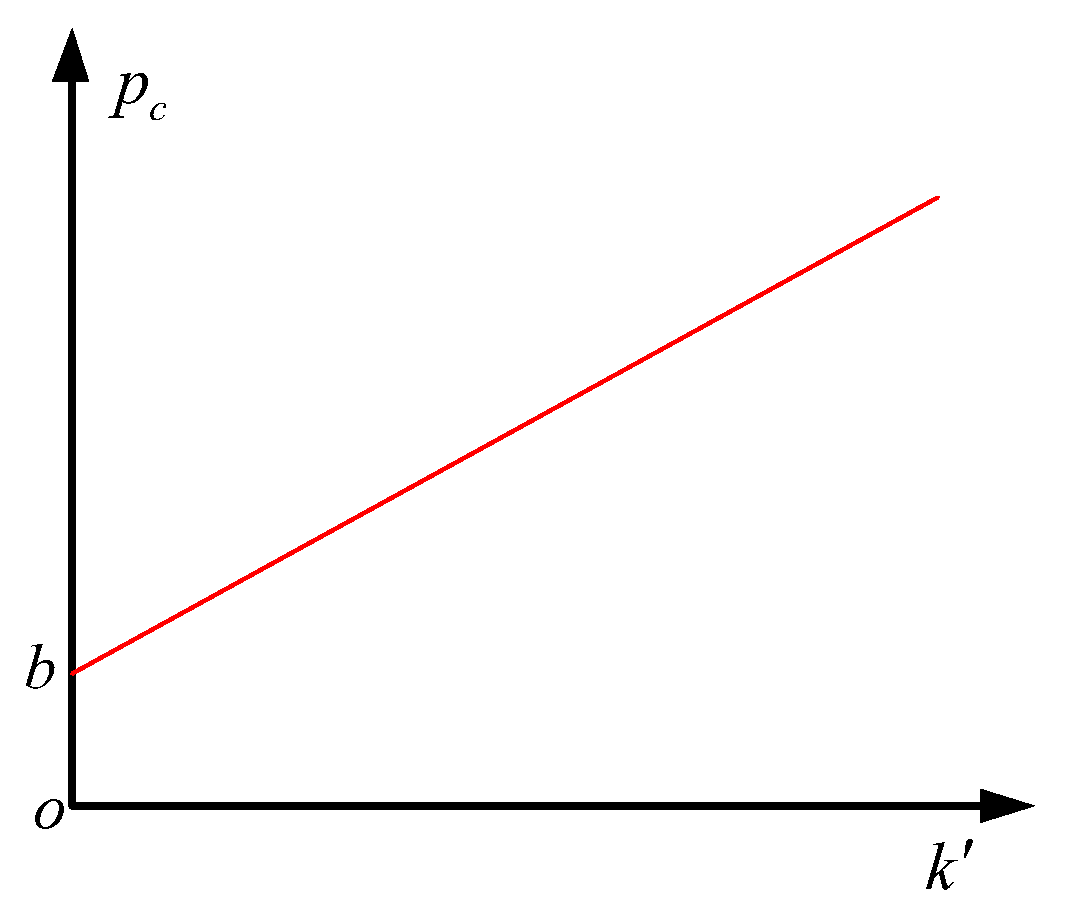
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, P.; Li, X.; Ning, J.; Wang, J.; Yang, S. Study on Thermal Energy Conversion Theory in Drilling Process of Coal and Rock Mass with Different Stresses. Energies 2019, 12, 4282. https://doi.org/10.3390/en12224282
Qiu P, Li X, Ning J, Wang J, Yang S. Study on Thermal Energy Conversion Theory in Drilling Process of Coal and Rock Mass with Different Stresses. Energies. 2019; 12(22):4282. https://doi.org/10.3390/en12224282
Chicago/Turabian StyleQiu, Pengqi, Xuehui Li, Jianguo Ning, Jun Wang, and Shang Yang. 2019. "Study on Thermal Energy Conversion Theory in Drilling Process of Coal and Rock Mass with Different Stresses" Energies 12, no. 22: 4282. https://doi.org/10.3390/en12224282
APA StyleQiu, P., Li, X., Ning, J., Wang, J., & Yang, S. (2019). Study on Thermal Energy Conversion Theory in Drilling Process of Coal and Rock Mass with Different Stresses. Energies, 12(22), 4282. https://doi.org/10.3390/en12224282