Nonlinear Analysis and Performance of Electret-Based Microcantilever Energy Harvesters
Abstract
1. Introduction
2. Problem Formulation
2.1. Single-Degree-of-Freedom (SDOF) Model
2.2. Static, Dynamic and Eigenvalue Problems
3. Electrostatic Energy Harvester Performance and Characteristics
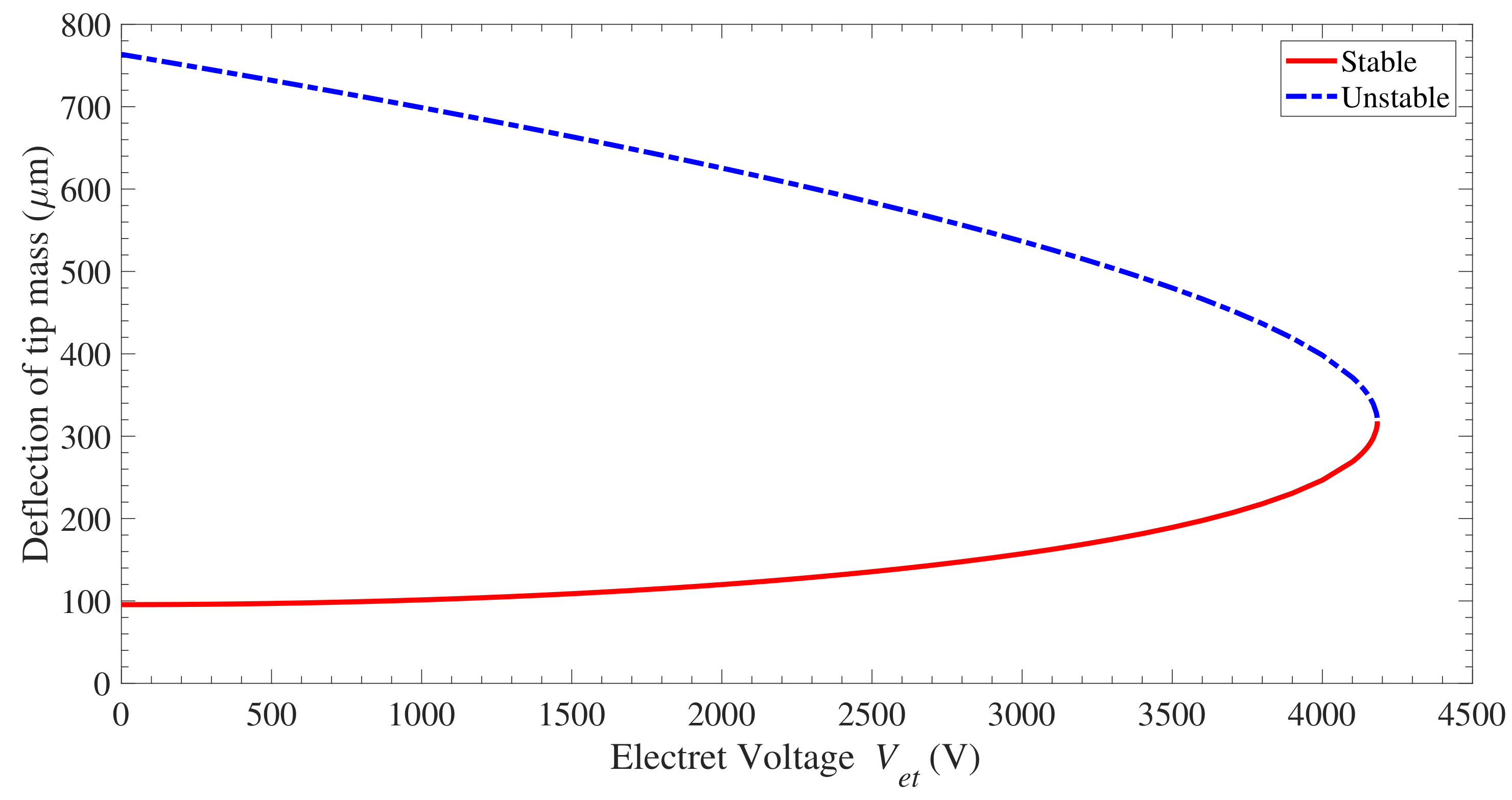
3.1. Static Analysis and Pull-in Instability
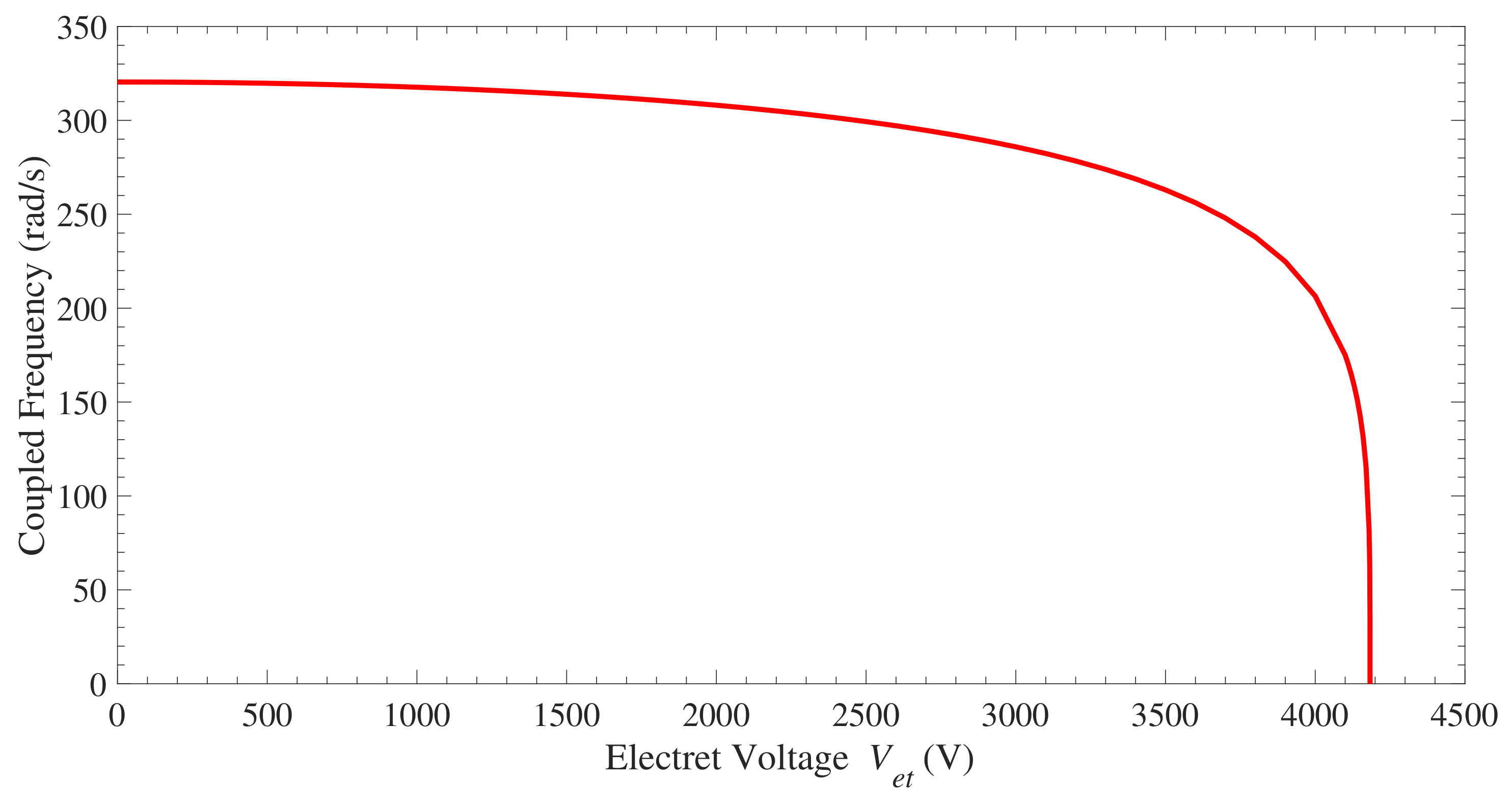
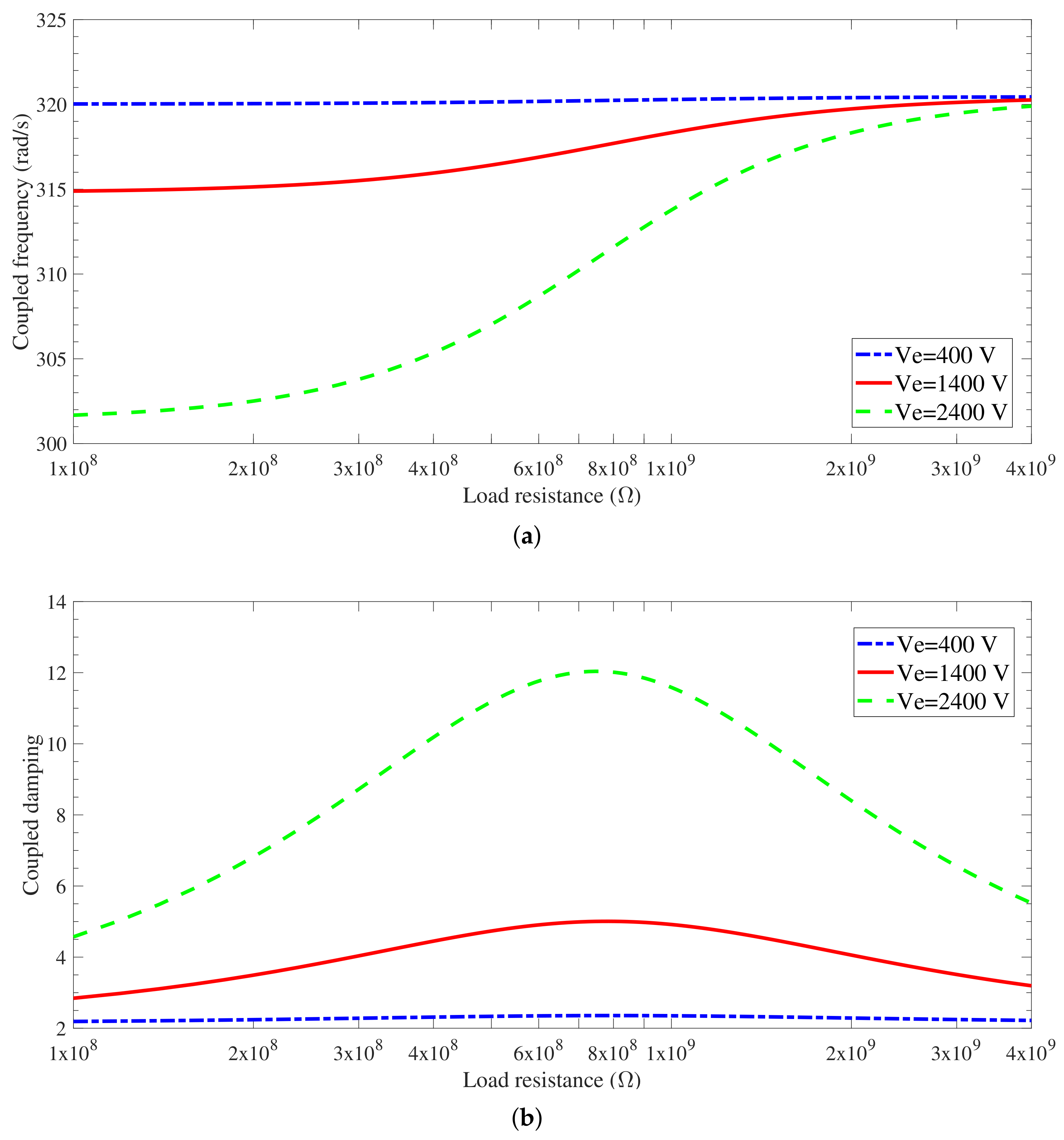
3.2. Coupled Frequency and Electromechanical Damping
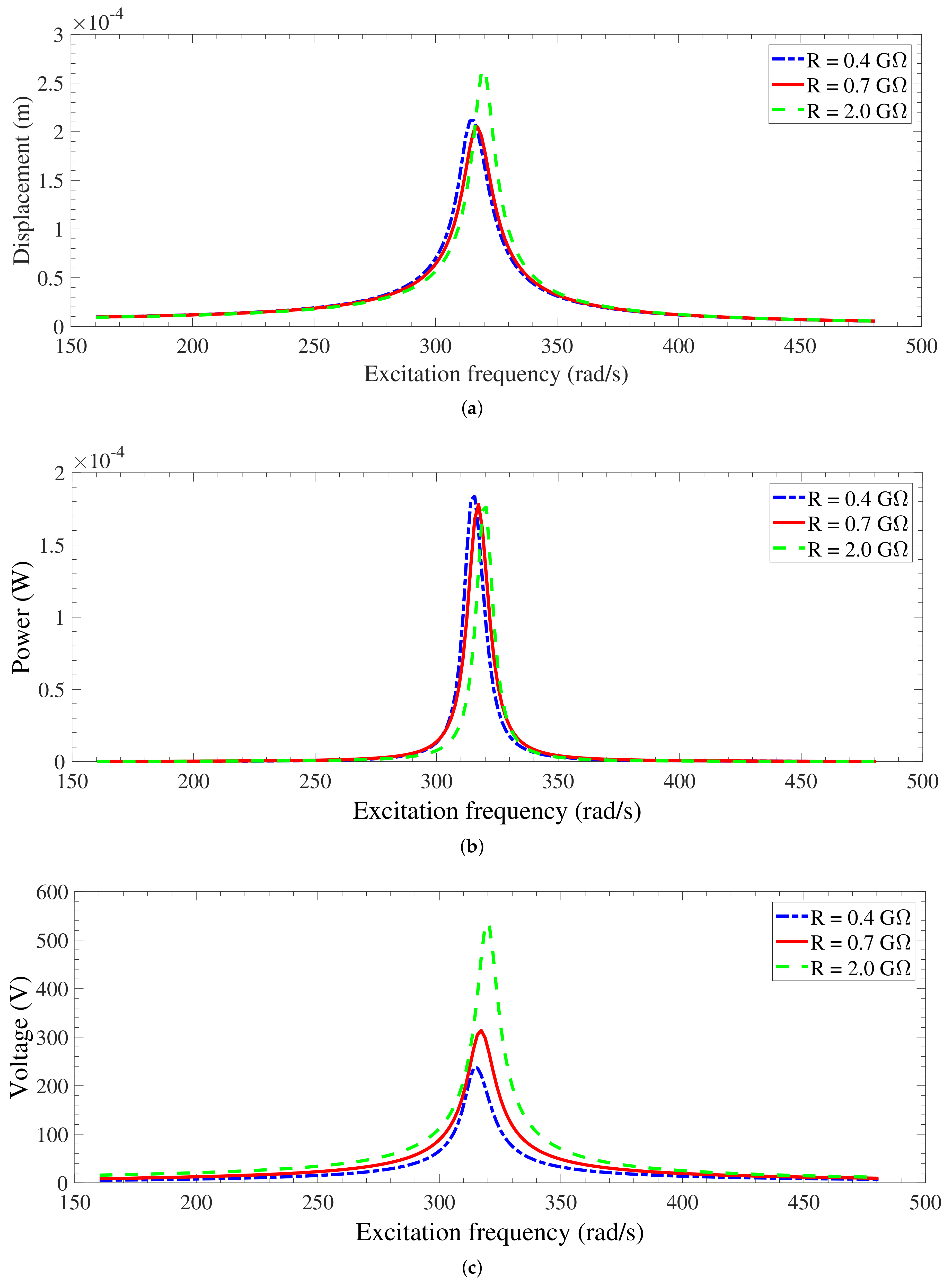
3.3. Energy Harvester Performance and Nonlinear Characteristics
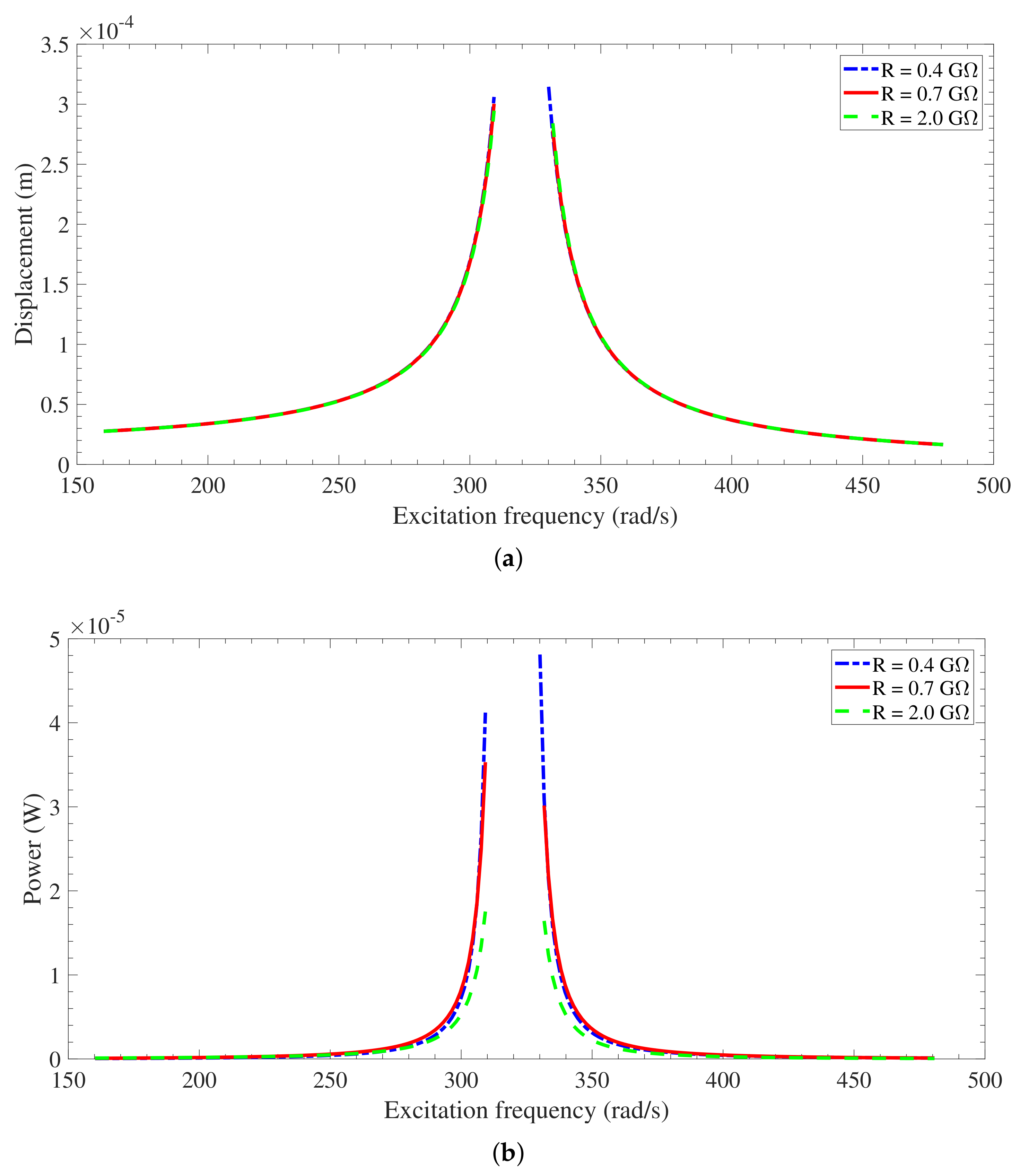
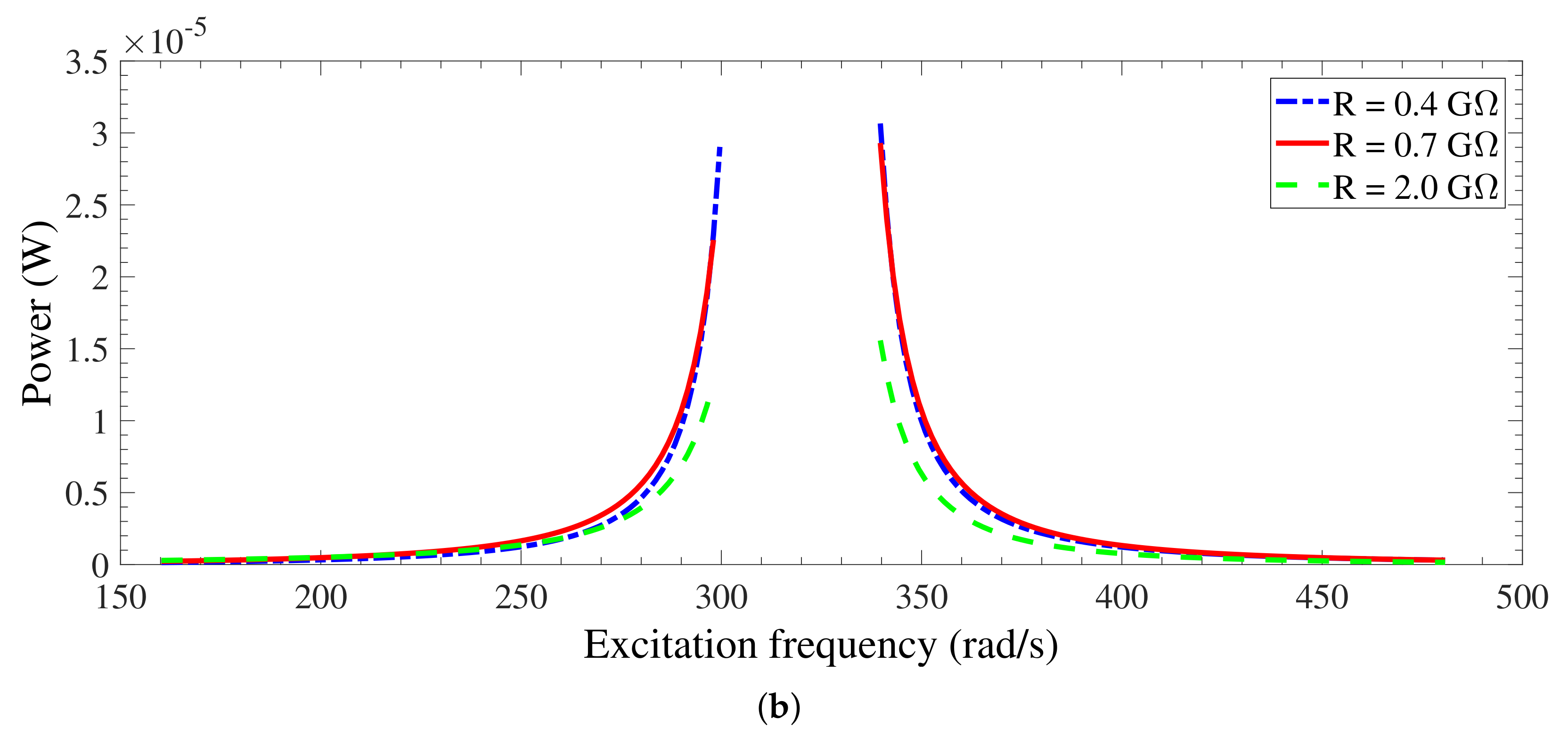
3.3.1. Effects of the electret surface voltages on the system performance
3.3.2. Optimal Performance of the Energy Harvester
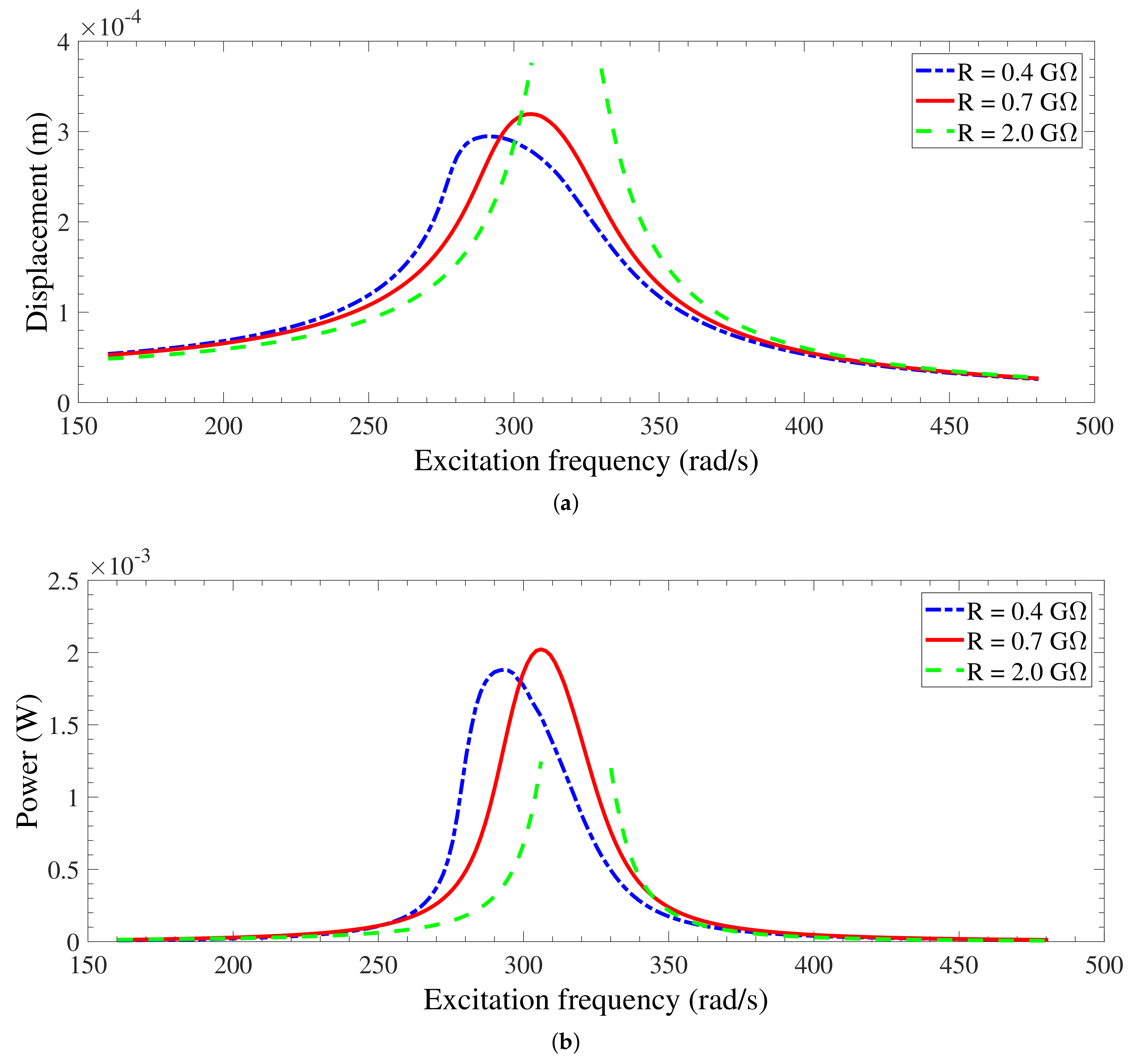
3.3.3. Base Acceleration Effects and Dynamic Pull-In
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bhatnagar, V.; Owende, P. Energy harvesting for assistive and mobile applications. Energy Sci. Eng. 2015, 3, 153–173. [Google Scholar] [CrossRef]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar] [CrossRef]
- Wei, C.; Jingi, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Modeling and analysis of piezoaeroelastic energy harvesters. Nonlinear Dyn. 2012, 67, 925–939. [Google Scholar] [CrossRef]
- Abdelkefi, A. Aeroelastic energy harvesting: A review. Int. J. Eng. Sci. 2016, 100, 112–135. [Google Scholar] [CrossRef]
- Firoozy, P.; Khadem, S.E.; Pourkiaee, S.M. Broadband energy harvesting using nonlinear vibrations of a magnetopiezoelastic cantilever beam. Int. J. Eng. Sci. 2017, 111, 113–133. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahmud, S.; Heyst, B.V. A review of the state of the science on wearable thermoelectric power generators (TEGs) and their existing challenges. Renew. Sustain. Energy Rev. 2017, 73, 730–744. [Google Scholar] [CrossRef]
- Arnaud, A.; Boisseau, S.; Monfray, S.; Puscasu, O.; Despesse, G.; Boughaleb, J.; Sanchez, Y.; Battegay, F.; Fourel, M.; Audran, S.; et al. Piezoelectric and electrostatic bimetal-based thermal energy harvesters. J. Phys. Conf. Ser. 2013, 476, 012062. [Google Scholar] [CrossRef]
- Perez, M.; Boisseau, S.; Gasnier, P.; Willemin, J.; Geisler, M.; Reboud, J.L. A cm scale electret-based electrostatic wind turbine for low-speed energy harvesting applications. Smart Mater. Struct. 2016, 25, 045015. [Google Scholar] [CrossRef]
- Bryant, M.; Garcia, E. Modeling and Testing of a Novel Aeroelastic Flutter Energy Harvester. J. Vib. Acoust. 2011, 133, 011010. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Watkins, S.; Deivasigamani, A.; John, S. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Sun, W.; Jo, S.; Seok, J. Development of the optimal bluff body for wind energy harvesting using the synergetic effect of coupled vortex induced vibration and galloping phenomena. Int. J. Mech. Sci. 2019, 156, 435–445. [Google Scholar] [CrossRef]
- Nabavi, S.F.; Farshidianfar, A.; Afsharfard, A.; Khodaparast, H.H. An ocean wave-based piezoelectric energy harvesting system using breaking wave force. Int. J. Mech. Sci. 2019, 151, 498–507. [Google Scholar] [CrossRef]
- Huang, H.-H.; Chen, K.-S. Design, analysis, and experimental studies of a novel PVDF-based piezoelectric energy harvester with beating mechanisms. Sens. Actuators Phys. 2016, 238, 317–328. [Google Scholar] [CrossRef]
- Franco, V.; Varoto, P. Parameter uncertainties in the design and optimization of cantilever piezoelectric energy harvesters. Mech. Syst. Signal Process. 2017, 93, 593–609. [Google Scholar] [CrossRef]
- Yanga, Z.; Erturkb, A.; Zua, J. On the efficiency of piezoelectric energy harvesters. Extrem. Mech. Lett. 2017, 15, 26–37. [Google Scholar] [CrossRef]
- Su, W.-J.; Zu, J.; Zhu, Y. Design and development of a broadband magnet-induced dual cantilever piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 430–442. [Google Scholar] [CrossRef]
- Staaf, L.G.H.; Smith, A.D.; Lundgren, P.; Folkow, P.D.; Enoksson, P. Effective piezoelectric energy harvesting with bandwidth enhancement by assymetry augmented self-tuning of conjoined cantilevers. Int. J. Mech. Sci. 2019, 150, 1–11. [Google Scholar] [CrossRef]
- Tan, Y.; Dong, Y.; Wang, X. Review of MEMS Electromagnetic Vibration Energy Harvester. J. Microelectromech. Syst. 2017, 26, 1–16. [Google Scholar] [CrossRef]
- Naifar, S.; Bradai, S.; Viehweger, C.; Kanoun, O. Survey of electromagnetic and magnetoelectric vibration energy harvesters for low frequency excitation. Measurement 2017, 106, 251–263. [Google Scholar] [CrossRef]
- Gilani, S.F.-U.-H.; Khir, M.H.B.M.; Ibrahim, R.; Kirmani, U.H.; Gilani, S.I.-U.-H. Modelling and development of a vibration-based electromagnetic energy harvester for industrial centrifugal pump application. Microelectron. J. 2017, 66, 103–111. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Zhanga, Y.; Caoa, J. A batch-fabricated electromagnetic energy harvester based on flex-rigid structures. Sens. Actuators Phys. 2017, 263, 571–579. [Google Scholar] [CrossRef]
- Yang, Z.; Tan, Y.; Zu, J. A multi-impact frequency up-converted magnetostrictive transducer for harvesting energy from finger tapping. Int. J. Mech. Sci. 2017, 126, 235–241. [Google Scholar] [CrossRef]
- O’Riordan, E.; Galayko, D.; Basset, P.; Blohinaa, E. Complete electromechanical analysis of electrostatic kinetic energy harvesters biased with a continuous conditioning circuit. Sens. Actuators Phys. 2016, 247, 379–388. [Google Scholar] [CrossRef]
- Jeong, B.; Kim, M.-O.; Lee, J.-I.; Eun, Y.; Choi, J.; Kim, J. Development of MEMS multi-mode electrostatic energy harvester based on the SOI process. Micromachine 2017, 8, 51. [Google Scholar] [CrossRef]
- Le, C.P.; Halvorsen, E.; Søråsen, O.; Yeatman, E.M. Microscale electrostatic energy harvester using internal impacts. J. Intell. Mater. Syst. Struct. 2012, 23, 1409–1421. [Google Scholar] [CrossRef]
- Kaur, S.; Halvorsen, E. Parameter sensitivity of an in-plane gap closing electrostatic energy harvester with end-stop impacts. J. Intell. Mater. Syst. Struct. 2017, 28, 1640–1650. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Dynamics and performance evaluation of a novel tristable hybrid energy harvester for ultra-low level vibration resources. Int. J. Mech. Sci. 2019, 156, 123–136. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar] [CrossRef]
- Boisseau, S.; Despesse, G.; Sylvestre, A. Optimization of an electret-based energy harvester. Smart Mater. Struct. 2010, 19, 075015. [Google Scholar] [CrossRef][Green Version]
- Boisseau, S.; Despesse, G.; Ricart, T.; Defay, E.; Sylvestre, A. Cantilever-based electret energy harvesters. Smart Mater. Struct. 2011, 20, 105013. [Google Scholar] [CrossRef]
- Jefimenko, O.D.; Walker, D.K. Electrostatic Current Generator Having a Disk Electret as an Active Element. IEEE Trans. Ind. Appl. 1978, IA-14, 537–554. [Google Scholar] [CrossRef]
- Perez, M.; Boisseau, S.; Gasnier, P.; Willemin, J.; Reboud, J.L. An electret-based aeroelastic flutter energy harvester. Smart Mater. Struct. 2015, 24, 035004. [Google Scholar] [CrossRef]
- Lu, Y.; O’Riordan, E.; Cottone, F.; Boisseau, S.; Galayko, D.; Blokhina, E.; Marty, F.; Basset, P. A batch-fabricated electret-biased wideband MEMS vibration energy harvester with frequency-up conversion behavior powering a UHF wireless sensor node. J. Micromech. Microeng. 2016, 26, 124004. [Google Scholar] [CrossRef]
- Tao, K.; Lye, S.W.; Miao, J.; Tang, L.; Hu, X. Out-of-plane electret-based MEMS energy harvester with the combined nonlinear effect from electrostatic force and a mechanical elastic stopper. J. Micromech. Microeng. 2015, 25, 104014. [Google Scholar] [CrossRef]
- Tao, K.; Chang, H.; Wu, J.; Tang, L.; Kottapalli, A.; Hu, L.; Lye, S.; Miao, J. Enhanced performance of electrostatic energy harvester with integrated opposite-charged electrets. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017. [Google Scholar]
- Pondrom, P.; Sessler, G.M.; Bös, J.; Melz, T. Compact electret energy harvester with high power output. Appl. Phys. Lett. 2016, 109, 053906. [Google Scholar] [CrossRef]
- Halvorsen, E.; Westby, E.R.; Husa, S.; Vogl, A.; Ostbo, N.P.; Leonov, V.; Sterken, T.; Kvisteroy, T. An electrostatic energy harvester with electret bias. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Denver, CO, USA, 21–25 June 2009. [Google Scholar]
- Genter, S.; Langhof, T.; Paul, O. Electret-based Out-Of-Plane Micro Energy Harvester with Parylene-C Serving as the Electret and Spring Material. Procedia Eng. 2015, 120, 341–344. [Google Scholar] [CrossRef][Green Version]
- Chiu, Y.; Lee, Y.-C. Flat and robust out-of-plane vibrational electret energy harvester. J. Micromech. Microeng. 2013, 23, 015012. [Google Scholar] [CrossRef]
- Le, C.P.; Halvorsen, E. Equivalent-circuit models for electret-based vibration energy harvesters. Smart Mater. Struct. 2017, 26, 085042. [Google Scholar] [CrossRef]
- Suzuki, Y.; Miki, D.; Edamoto, M.; Honzumi, M. A MEMS electret generator with electrostatic levitation for vibration-driven energy-harvesting applications. J. Micromech. Microeng. 2010, 20, 104002. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Ranasinghe, D.C.; Al-Sarawi, S.F. Analytical modeling and optimization of electret-based microgenerators under sinusoidal excitations. Microsyst. Technol. 2017, 23, 5855–5865. [Google Scholar] [CrossRef]
- Ghavami, M.; Azizi, S.; Ghazavi, M.R. On the dynamics of a capacitive electret-based micro-cantilever for energy harvesting. Energy 2018, 153, 967–976. [Google Scholar] [CrossRef]
- Hammad, B.; Abdel-Rahman, E.; Mahmoud, M. Micro Cantilever Electrostatic Energy Harvester. In Proceedings of the IDETC/CIE International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
- Erturk, A.; Inman, D. On Mechanical Modeling of Cantilevered Piezoelectric Vibration Energy Harvesters. J. Intell. Mater. Syst. Struct. 2008, 19, 1311–1325. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson: Harlow, UK, 2010. [Google Scholar]
- Kotrappa, P. Long term stability of electrets used in electrect in chambers. J. Electrost. 2008, 66, 407–409. [Google Scholar] [CrossRef]
- Leonov, V.; Fiorini, P.; Van Hoof, C. Stabilization of positive charge in SiO2/Si3N4 electrets. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y. Numerical and analytical study on the pull-in instability of microstructure under electrostatic loading. Sens. Actuators A 2006, 127, 366–380. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Abdelkefi, A. Ultra-wide bandwidth improvement of piezoelectric energy harvesters through electrical inductance coupling. Eur. Phys. J. Spec. Top. 2015, 224, 2733–2753. [Google Scholar] [CrossRef]
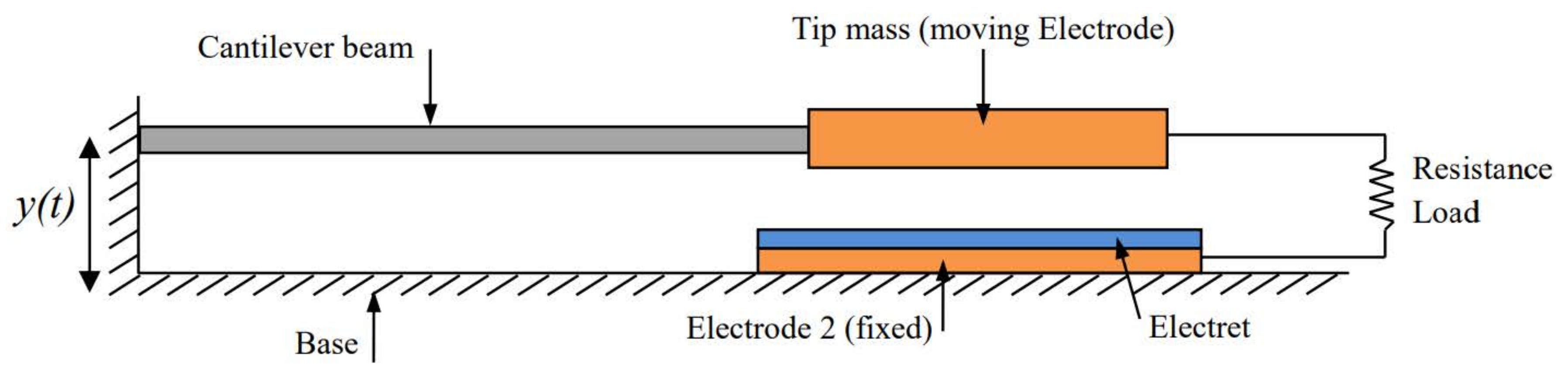
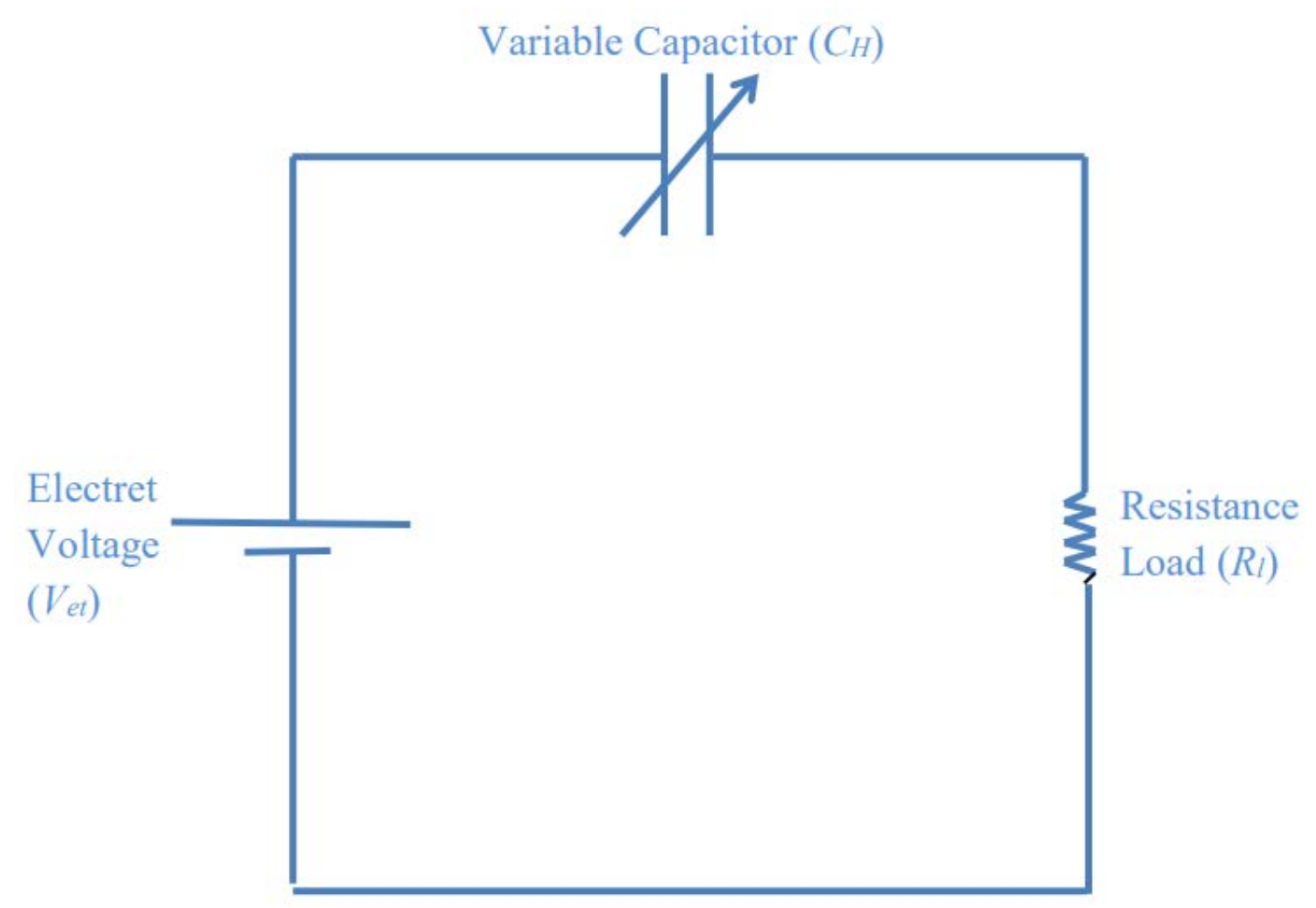
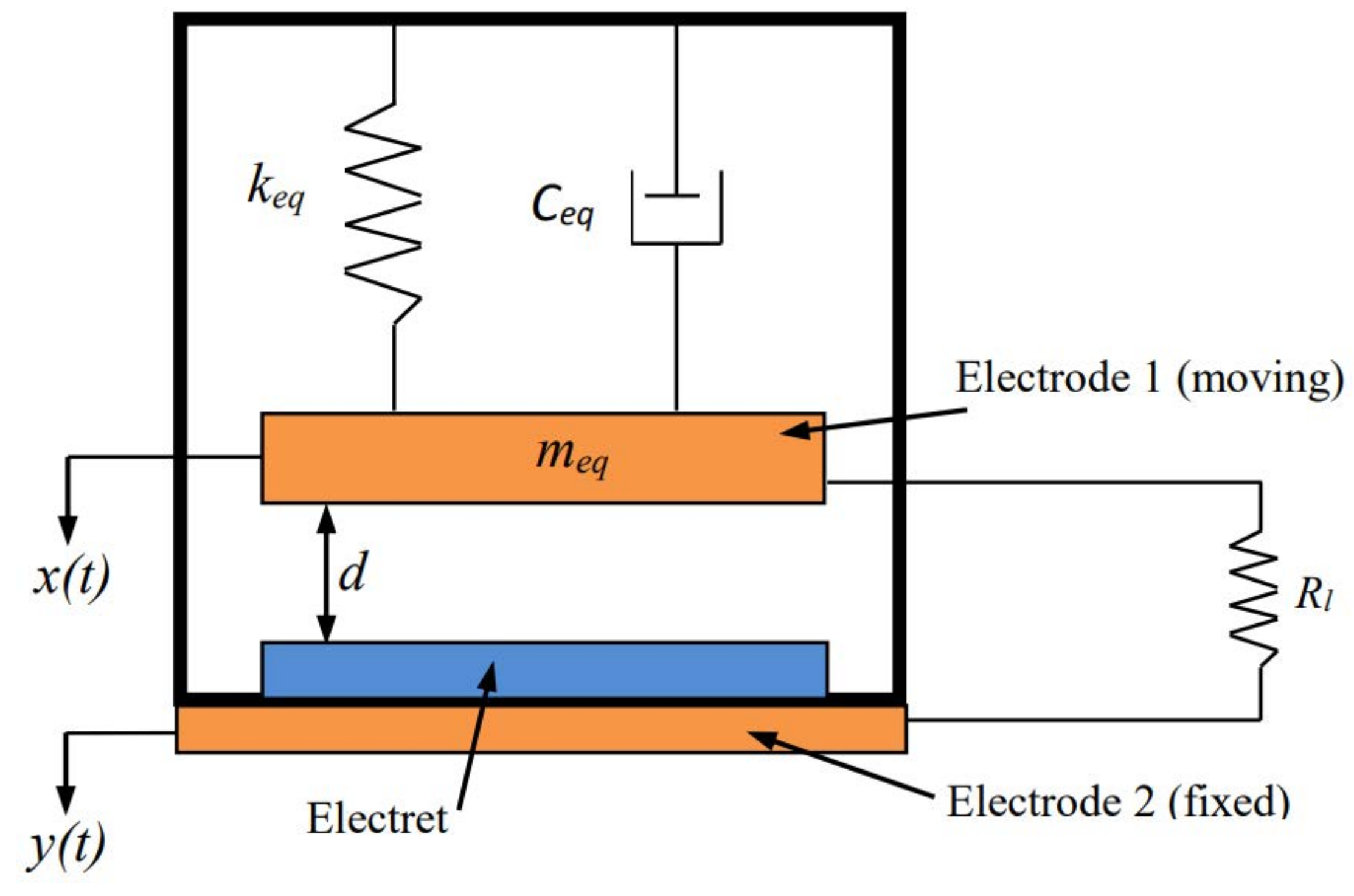
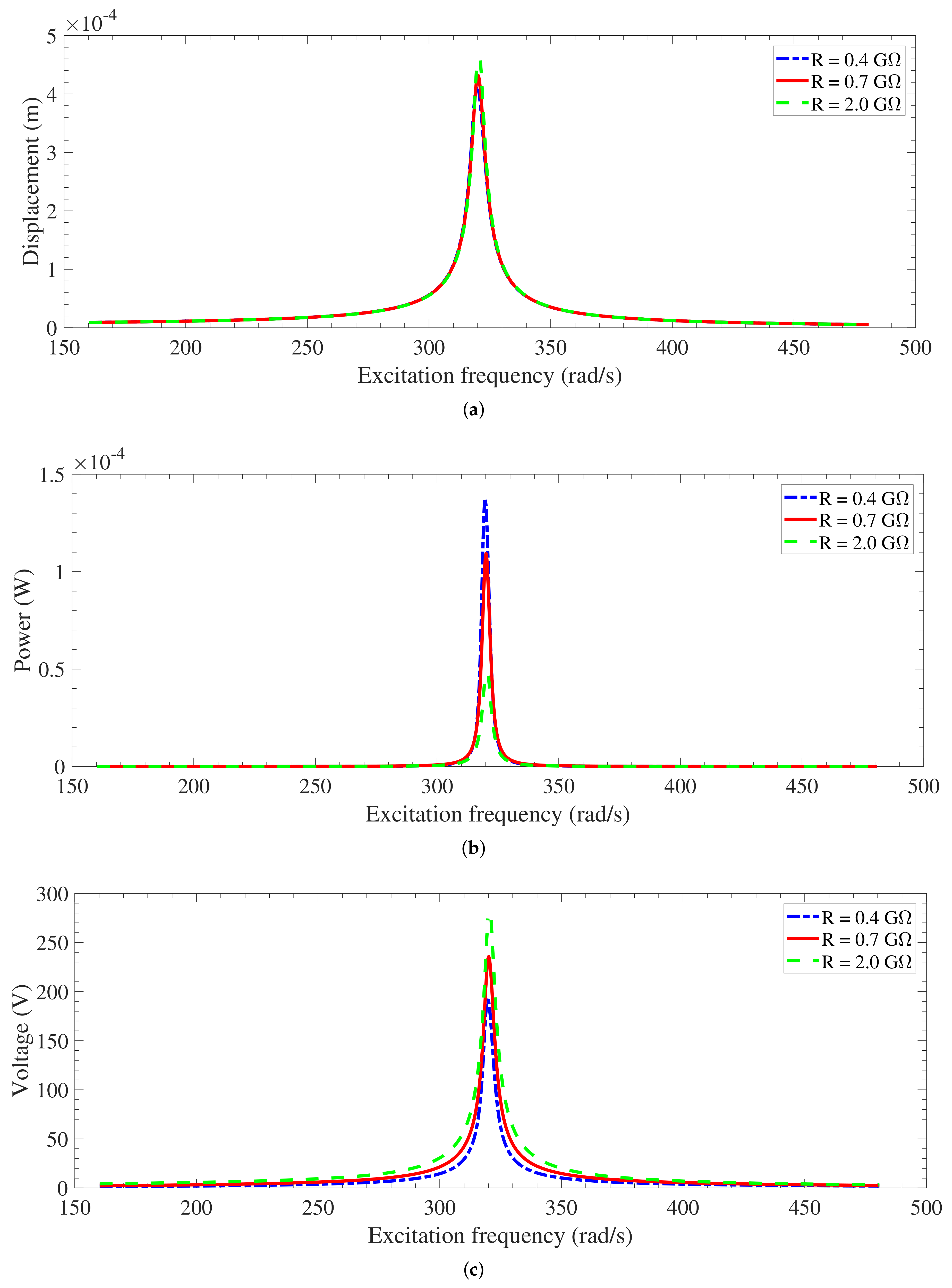
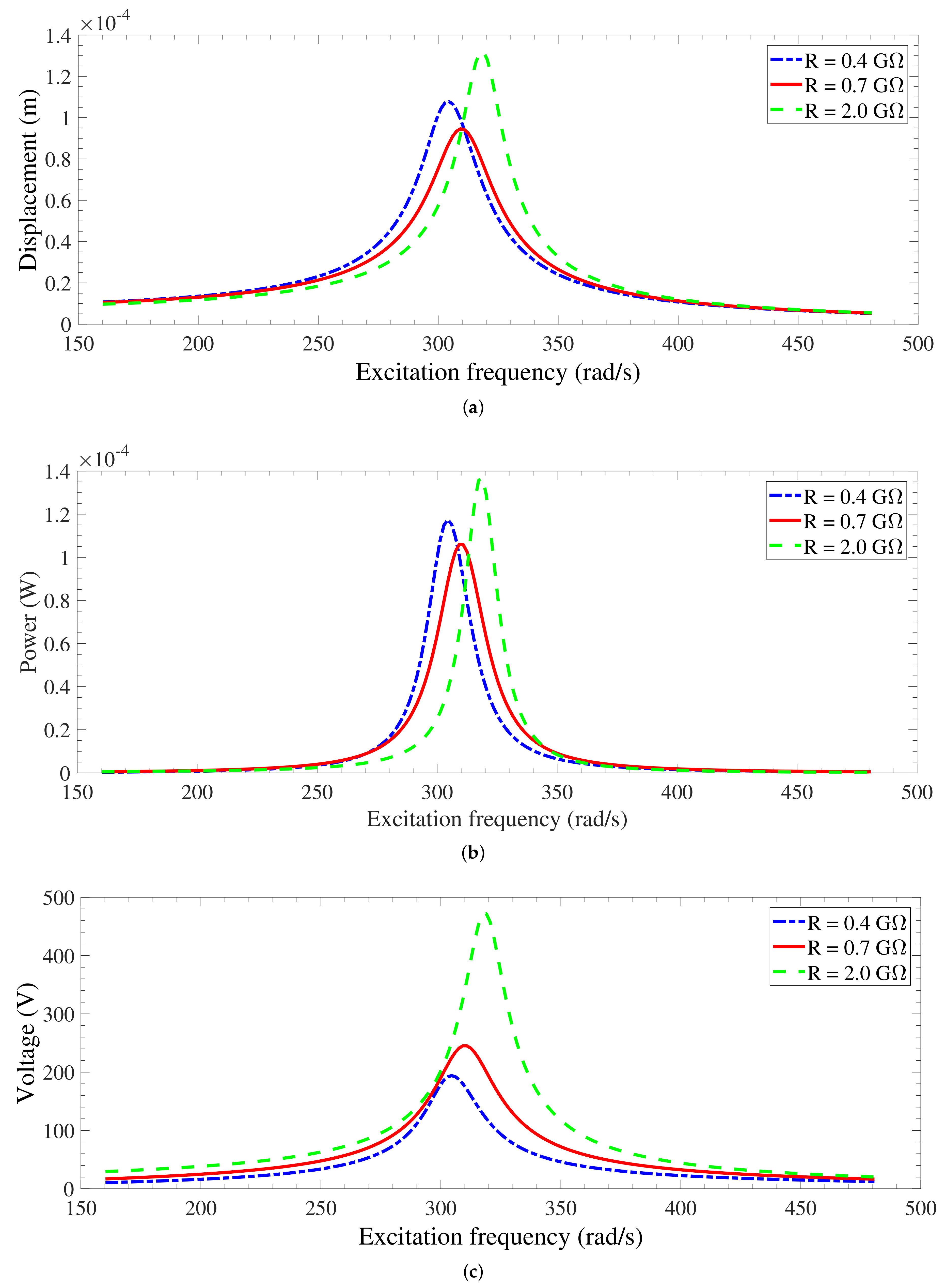

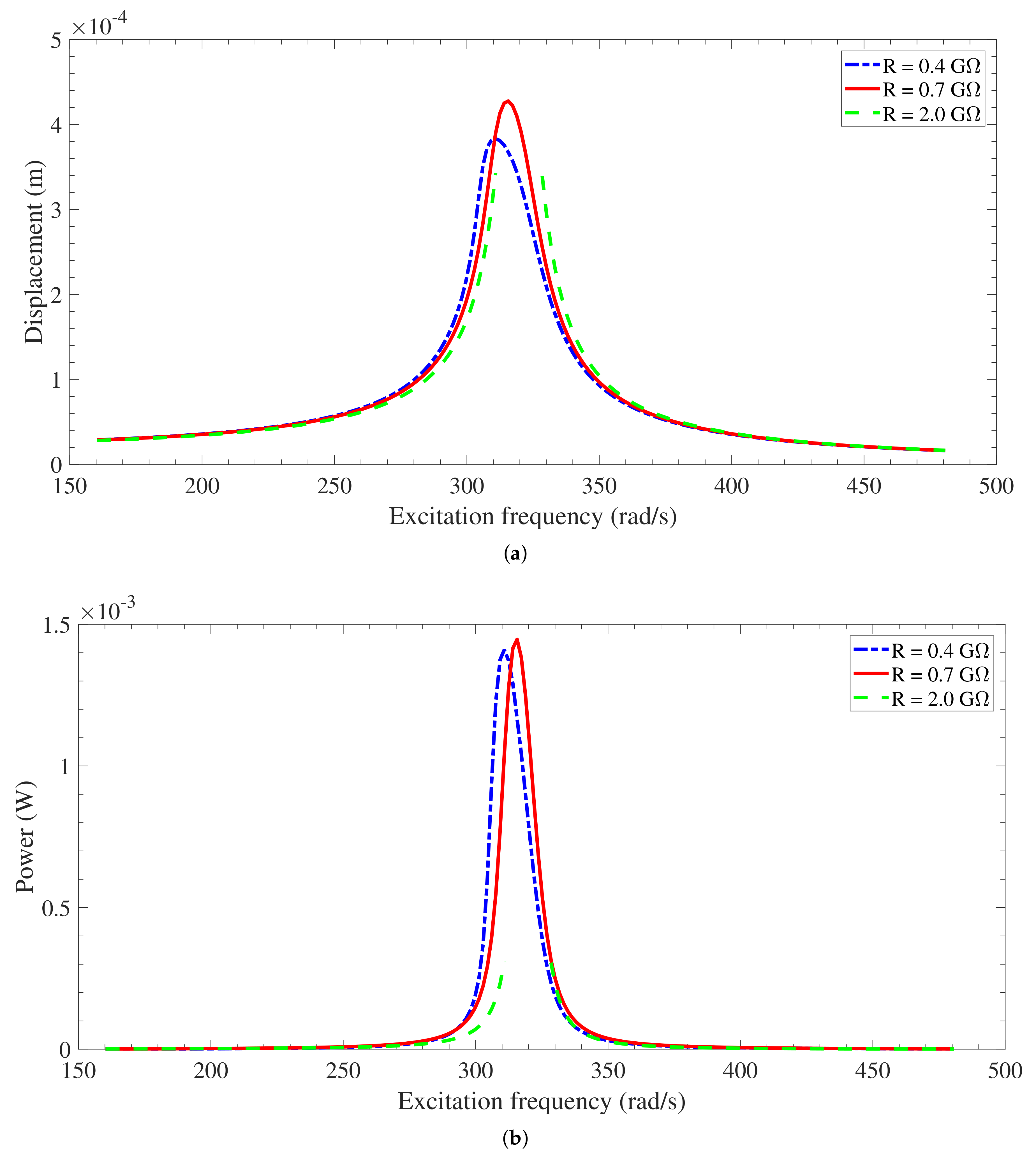
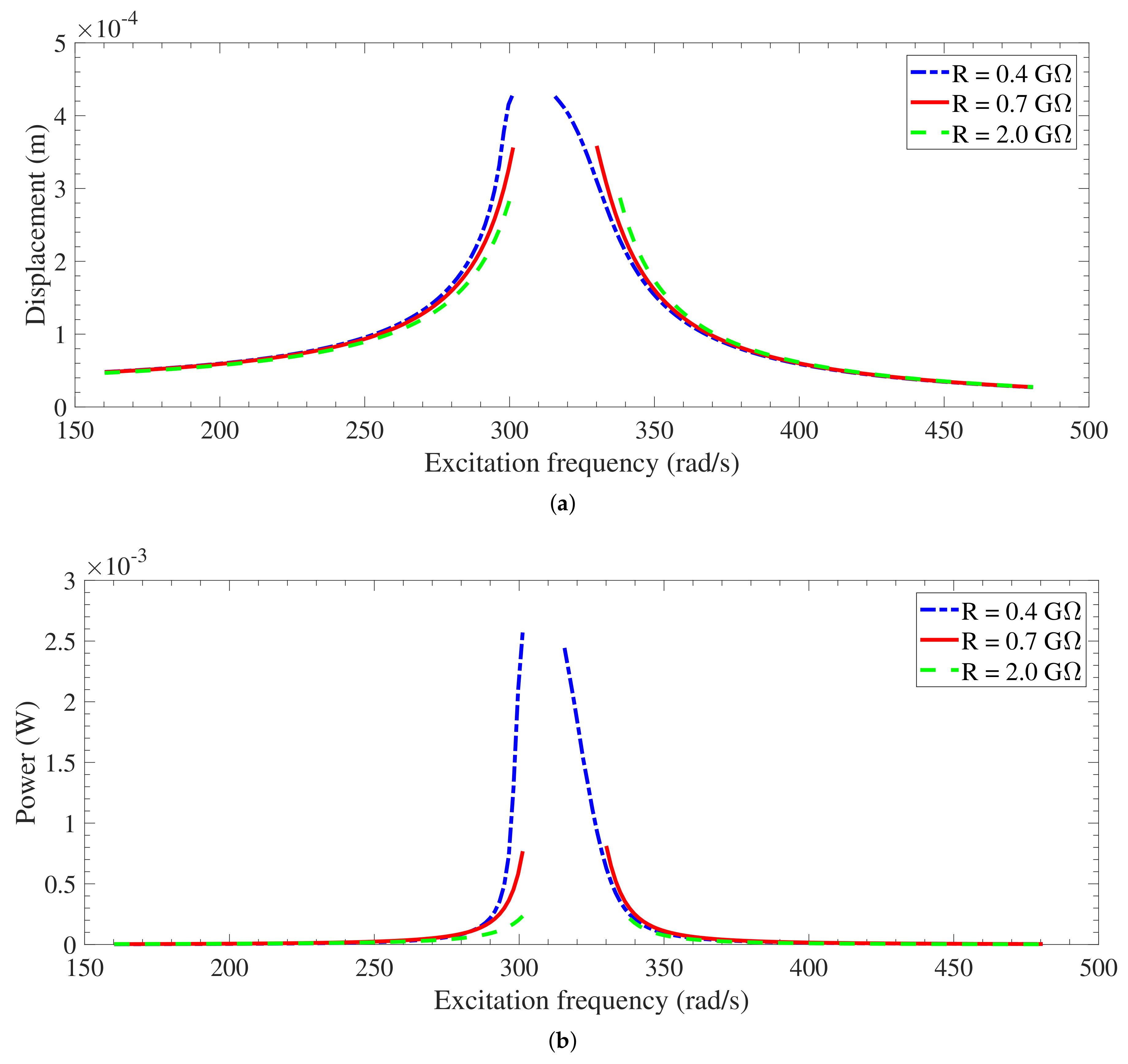


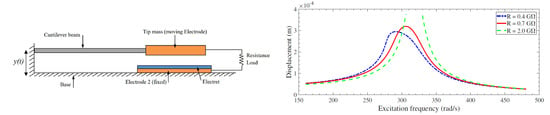
| Parameter | Value |
|---|---|
| Cantilever beam length, L (mm) | 30 |
| Cantilever beam thickness, (m) | 300 |
| Cantilever beam width, (mm) | 13 |
| Electrode length, (mm) | 22.8 |
| Electret thickness, (m) | 127 |
| Dielectric constant of electret, | 2 |
| Tip mass, () | 5 |
| Gap between electret and cantilever, (m) | 700 |
| Cantilever beam material | Silicon |
| Silicon Young’s Modulus, E (GPa) | 160 |
| Silicon density, (kg/m) | 2300 |
| damping ratio, | 1/150 |
| Vet | Base Acceleration | Resistance | Lower Limit | Upper Limit | Snap-through Range |
|---|---|---|---|---|---|
| (V) | (m/s) | (G) | (rad/s) | (rad/s) | (rad/s) |
| 400 | 1 | 2.0 | 319.8 | 321.1 | 1.3 |
| 3 | 0.4 | 309.2 | 330.1 | 20.9 | |
| 0.7 | 309.2 | 331.7 | 22.5 | ||
| 2.0 | 309.2 | 331.7 | 22.5 | ||
| 5 | 0.4 | 299.6 | 339.7 | 40.1 | |
| 0.7 | 298.0 | 339.7 | 41.7 | ||
| 2.0 | 298.0 | 339.7 | 41.7 | ||
| 1400 | 3 | 2 | 310.9 | 328.5 | 17.6 |
| 5 | 0.4 | 301.2 | 315.7 | 14.5 | |
| 0.7 | 301.2 | 330.1 | 28.9 | ||
| 2.0 | 301.2 | 338.1 | 36.9 | ||
| 2400 | 5 | 2.0 | 306.0 | 330.1 | 24.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammad, B.; Abdelmoula, H.; Abdel-Rahman, E.; Abdelkefi, A. Nonlinear Analysis and Performance of Electret-Based Microcantilever Energy Harvesters. Energies 2019, 12, 4249. https://doi.org/10.3390/en12224249
Hammad B, Abdelmoula H, Abdel-Rahman E, Abdelkefi A. Nonlinear Analysis and Performance of Electret-Based Microcantilever Energy Harvesters. Energies. 2019; 12(22):4249. https://doi.org/10.3390/en12224249
Chicago/Turabian StyleHammad, Bashar, Hichem Abdelmoula, Eihab Abdel-Rahman, and Abdessattar Abdelkefi. 2019. "Nonlinear Analysis and Performance of Electret-Based Microcantilever Energy Harvesters" Energies 12, no. 22: 4249. https://doi.org/10.3390/en12224249
APA StyleHammad, B., Abdelmoula, H., Abdel-Rahman, E., & Abdelkefi, A. (2019). Nonlinear Analysis and Performance of Electret-Based Microcantilever Energy Harvesters. Energies, 12(22), 4249. https://doi.org/10.3390/en12224249