Dynamic Modeling and Structural Optimization of a Bistable Electromagnetic Vibration Energy Harvester
Abstract
:1. Introduction
2. BEMH Configuration and Modeling
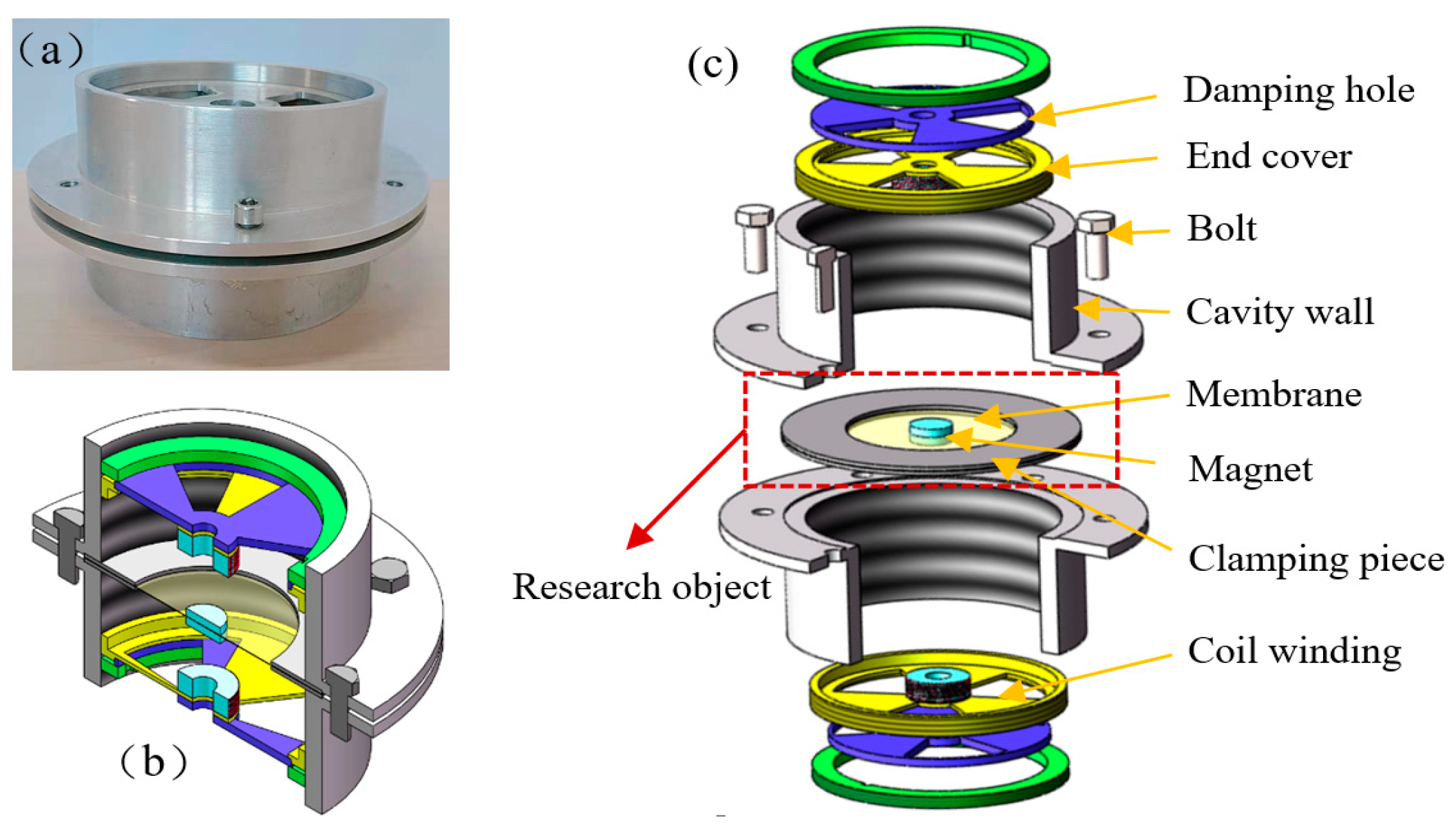
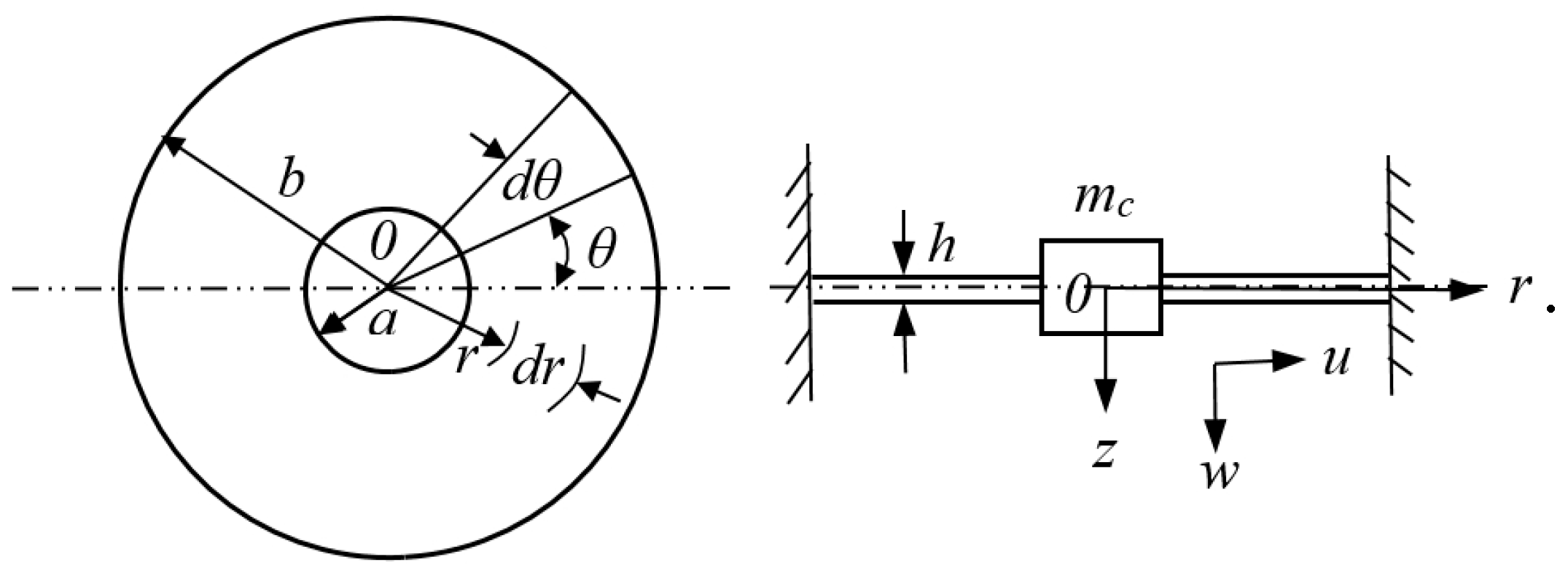
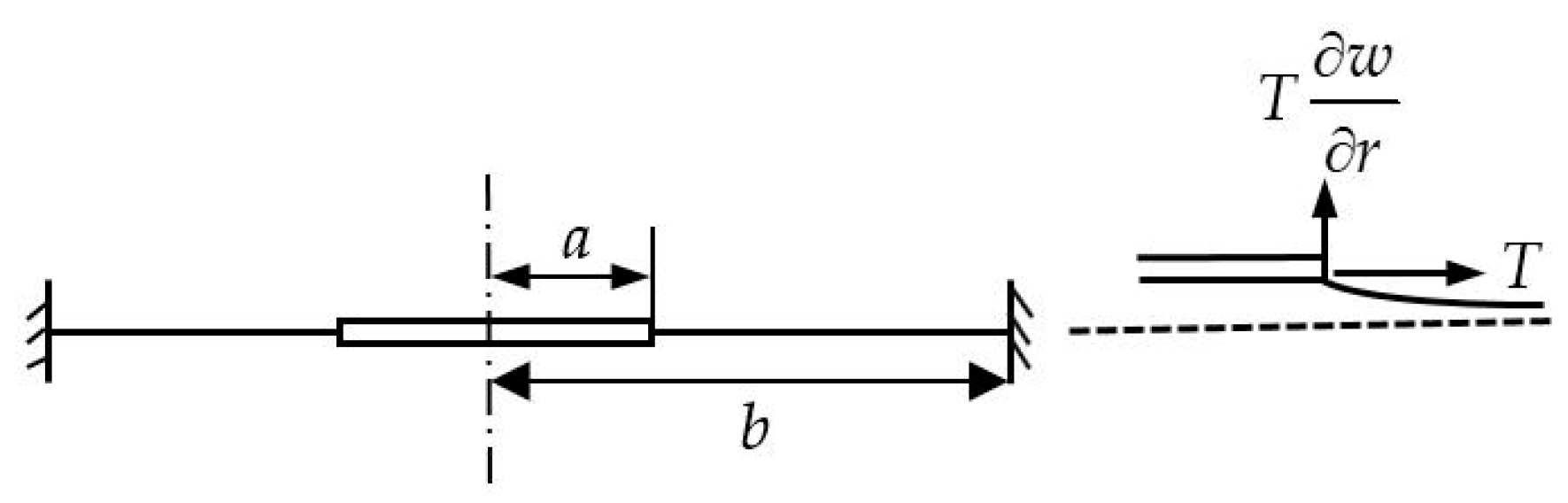
2.1. BEMH Architecture and Mathematical Model of the Main System
2.2. Reduced-Order Model
3. Model Validation and Result Analysis
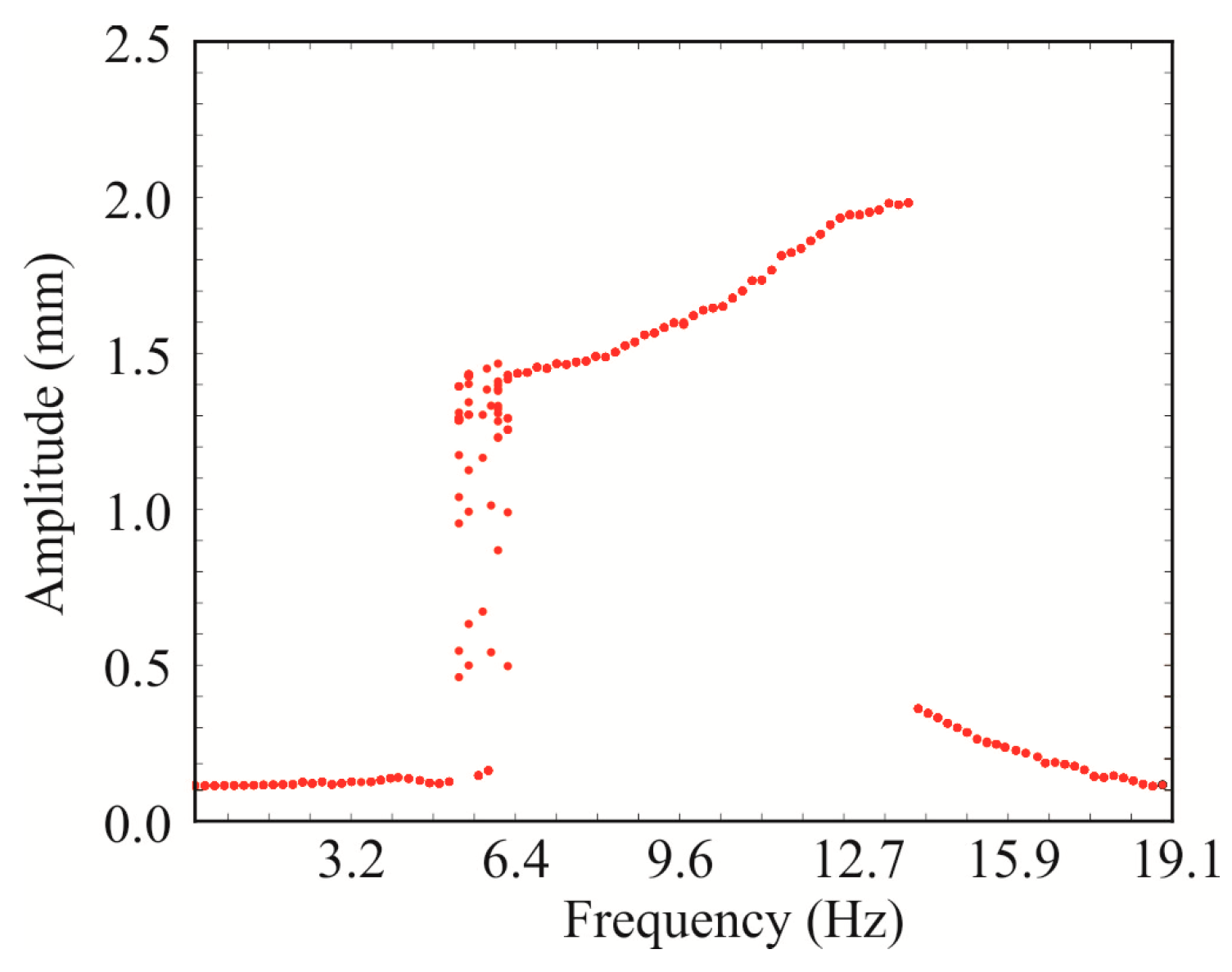
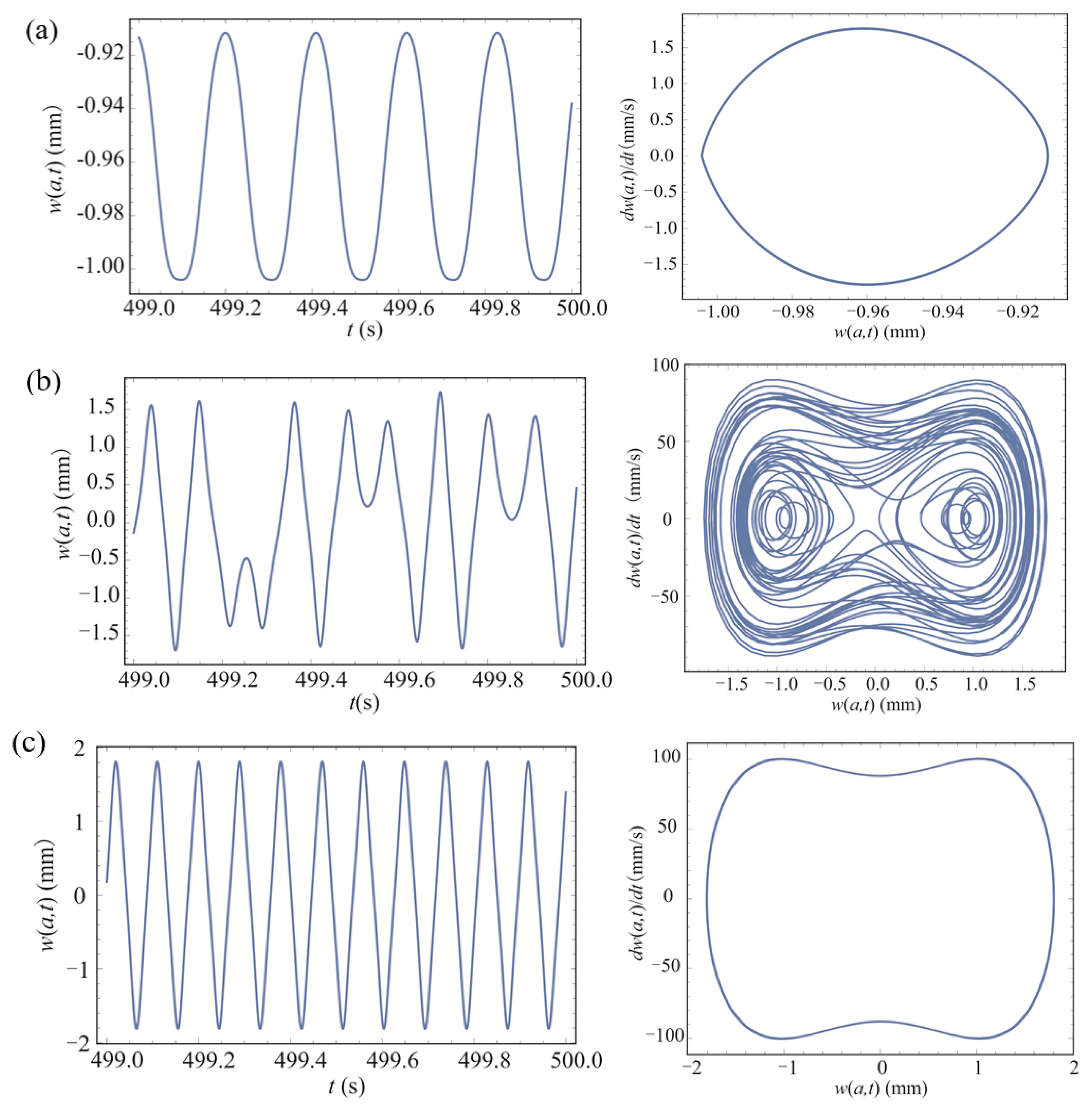
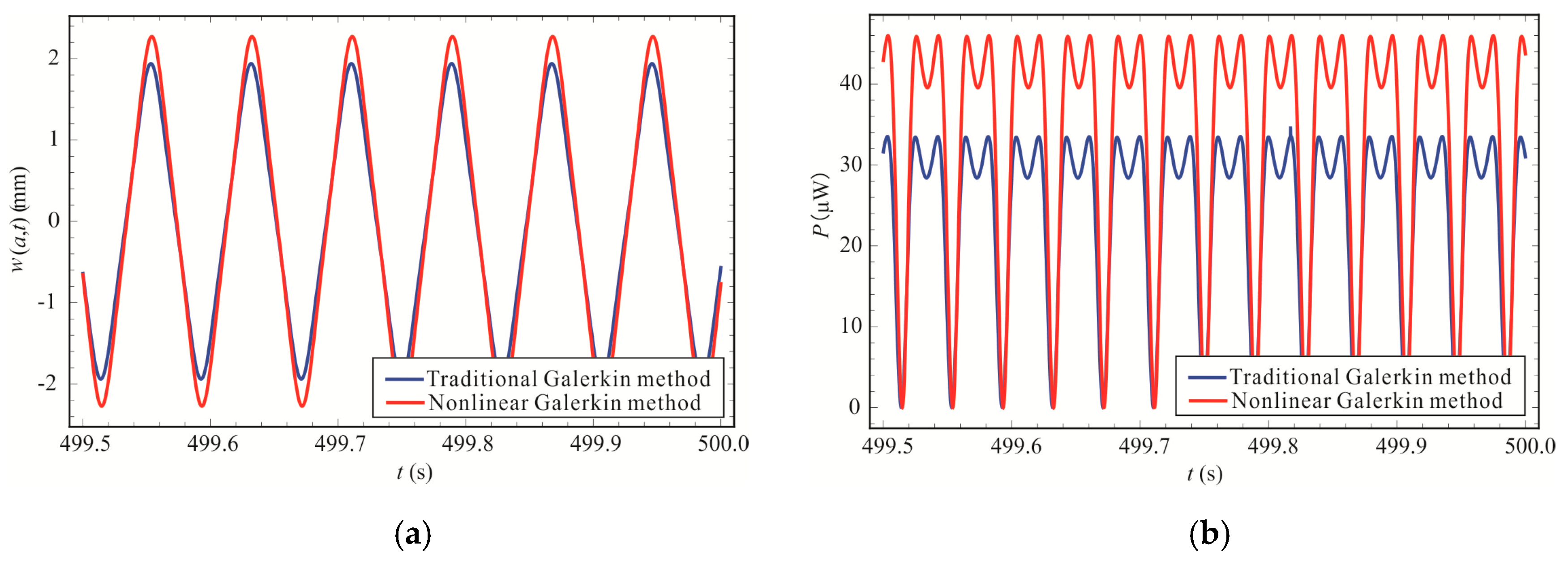
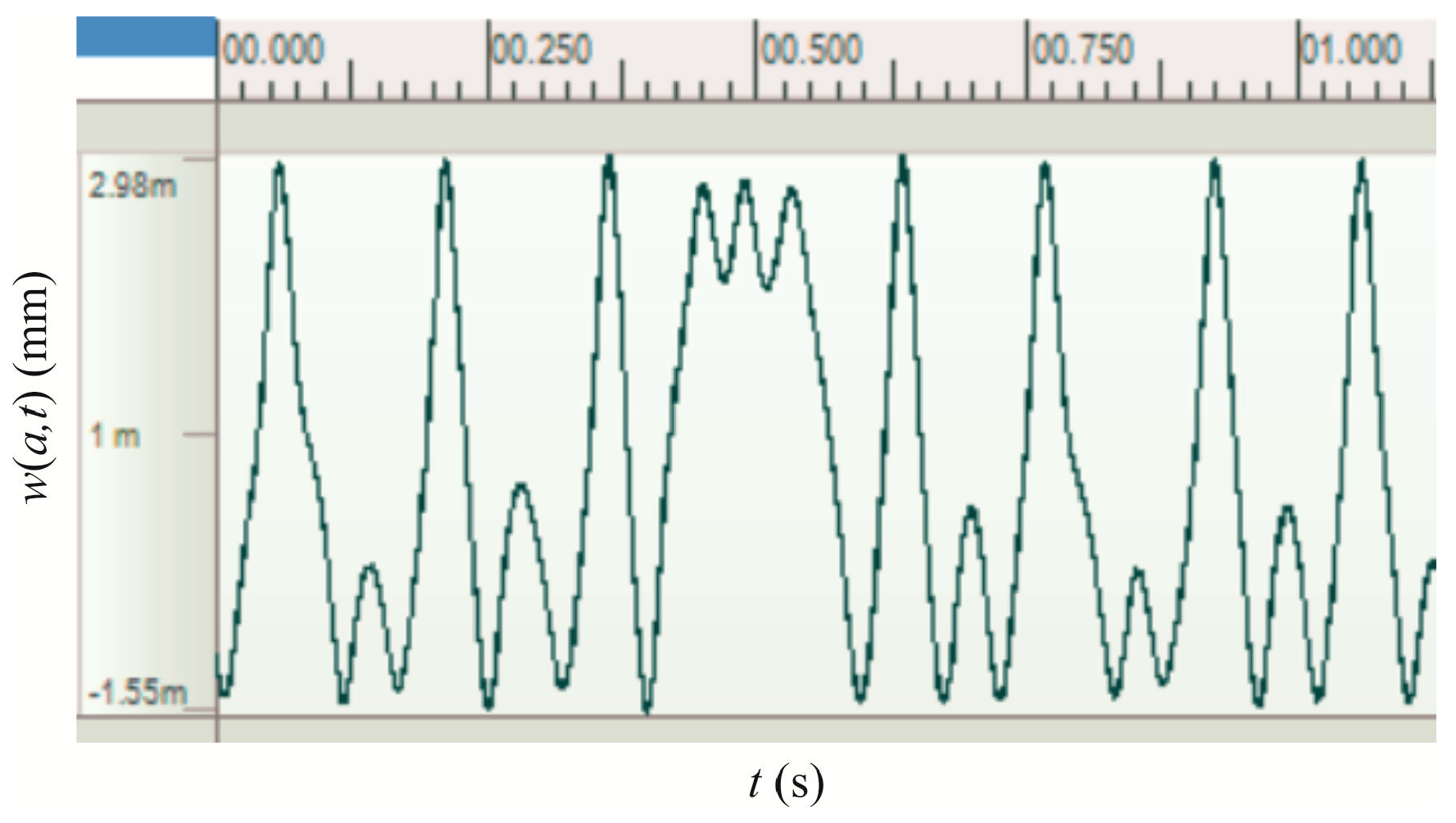
3.1. The Output Displacement Response and Power of the BEMH
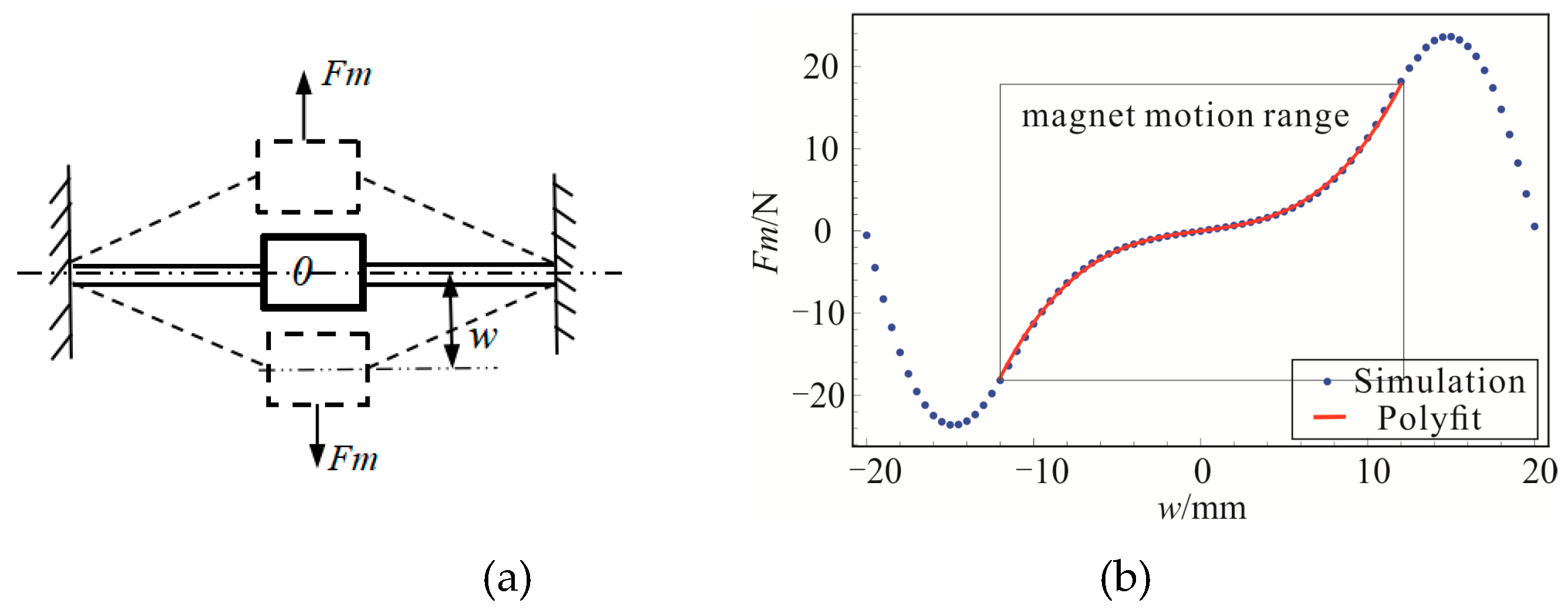
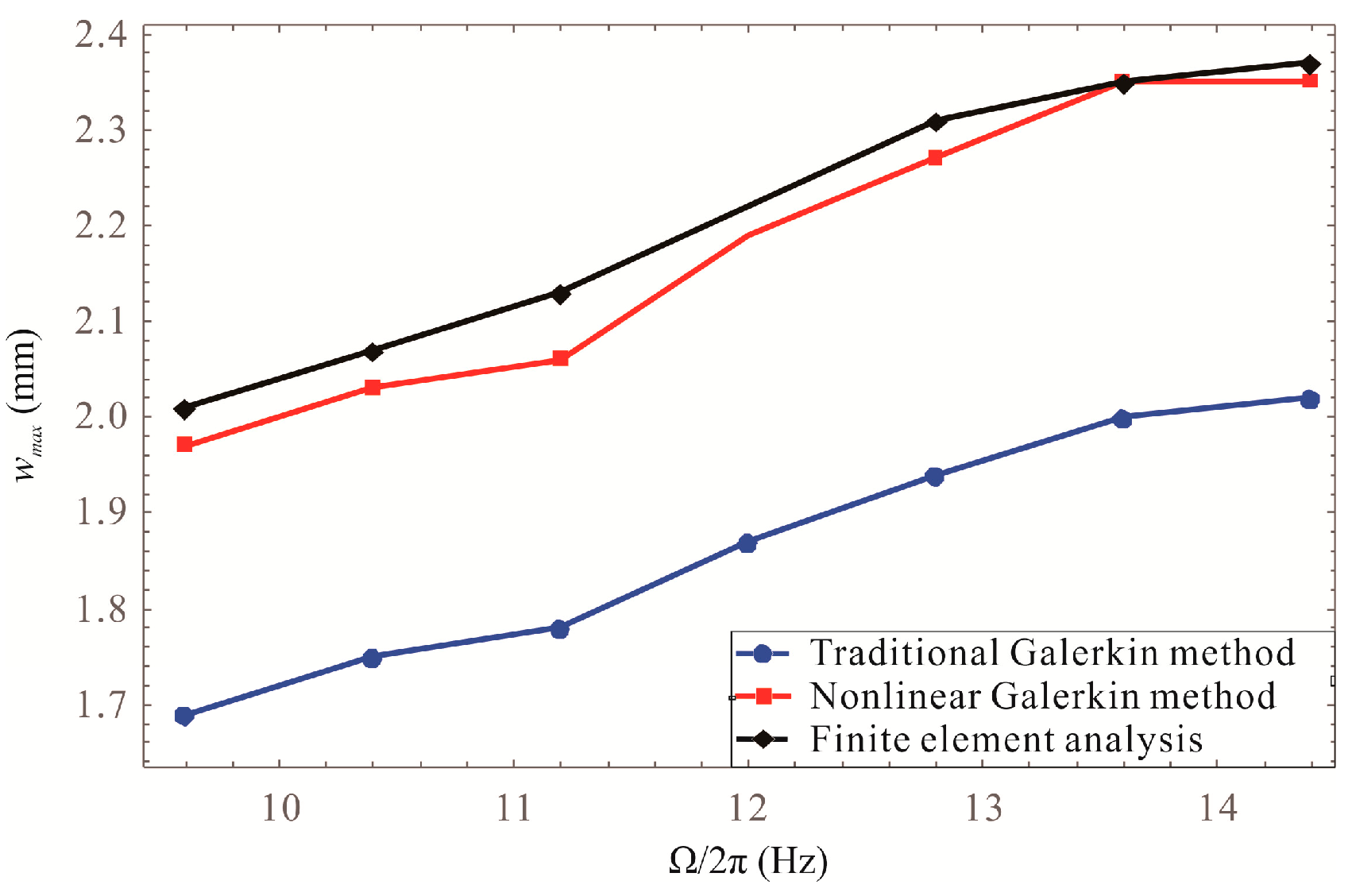
3.2. Finite Element Simulation Validations and Numerical Results
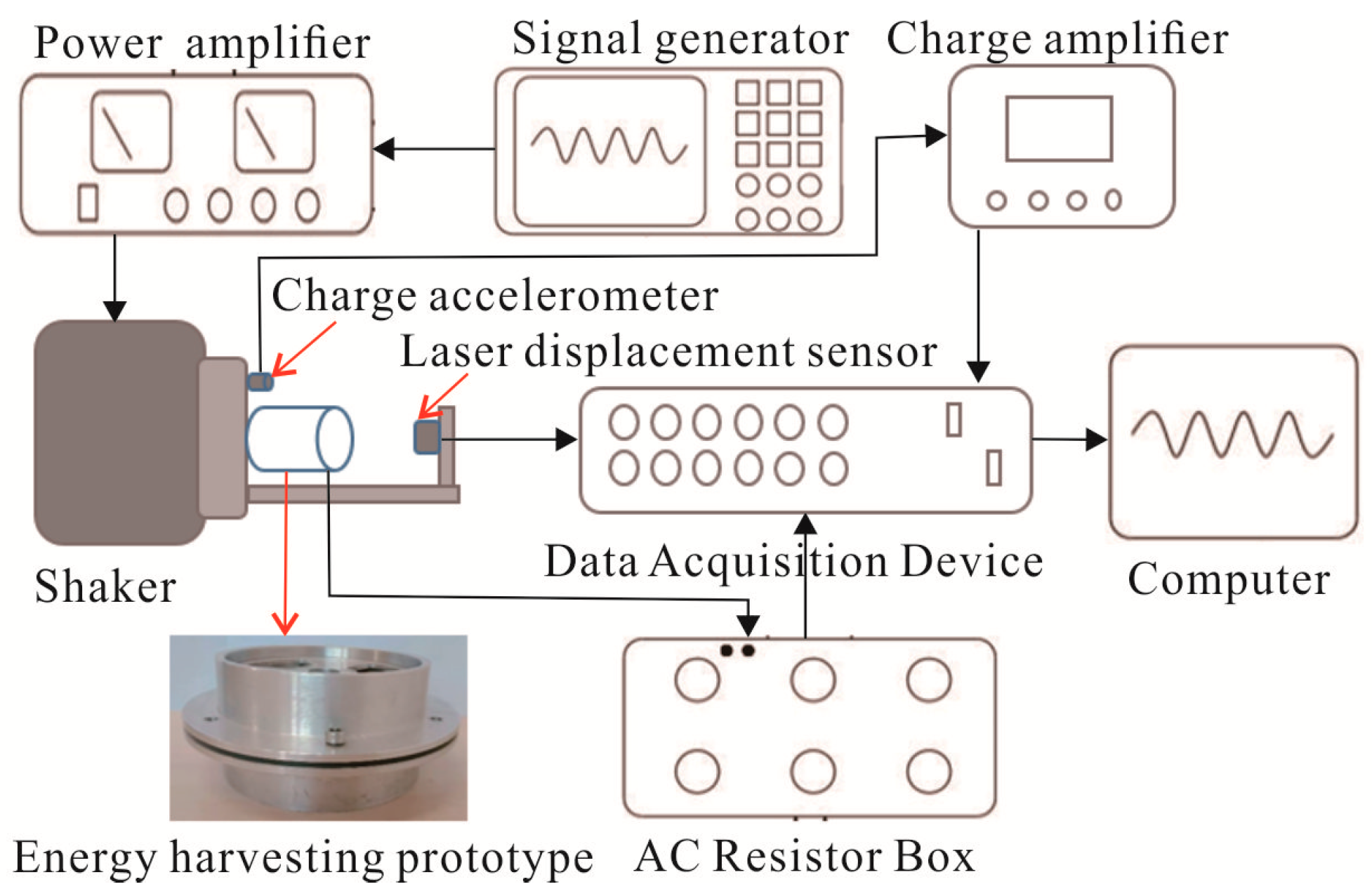
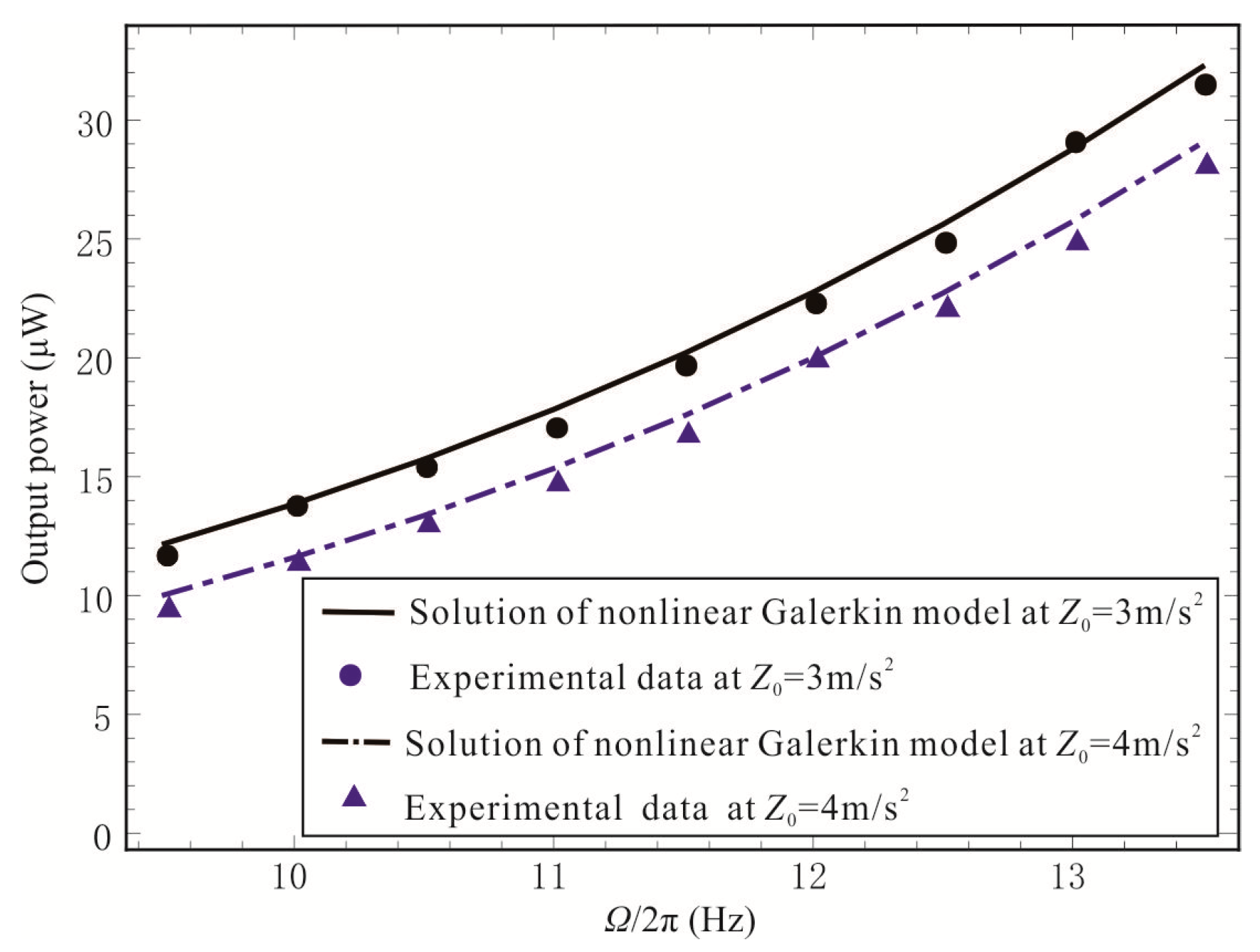
3.3. Experimental Results
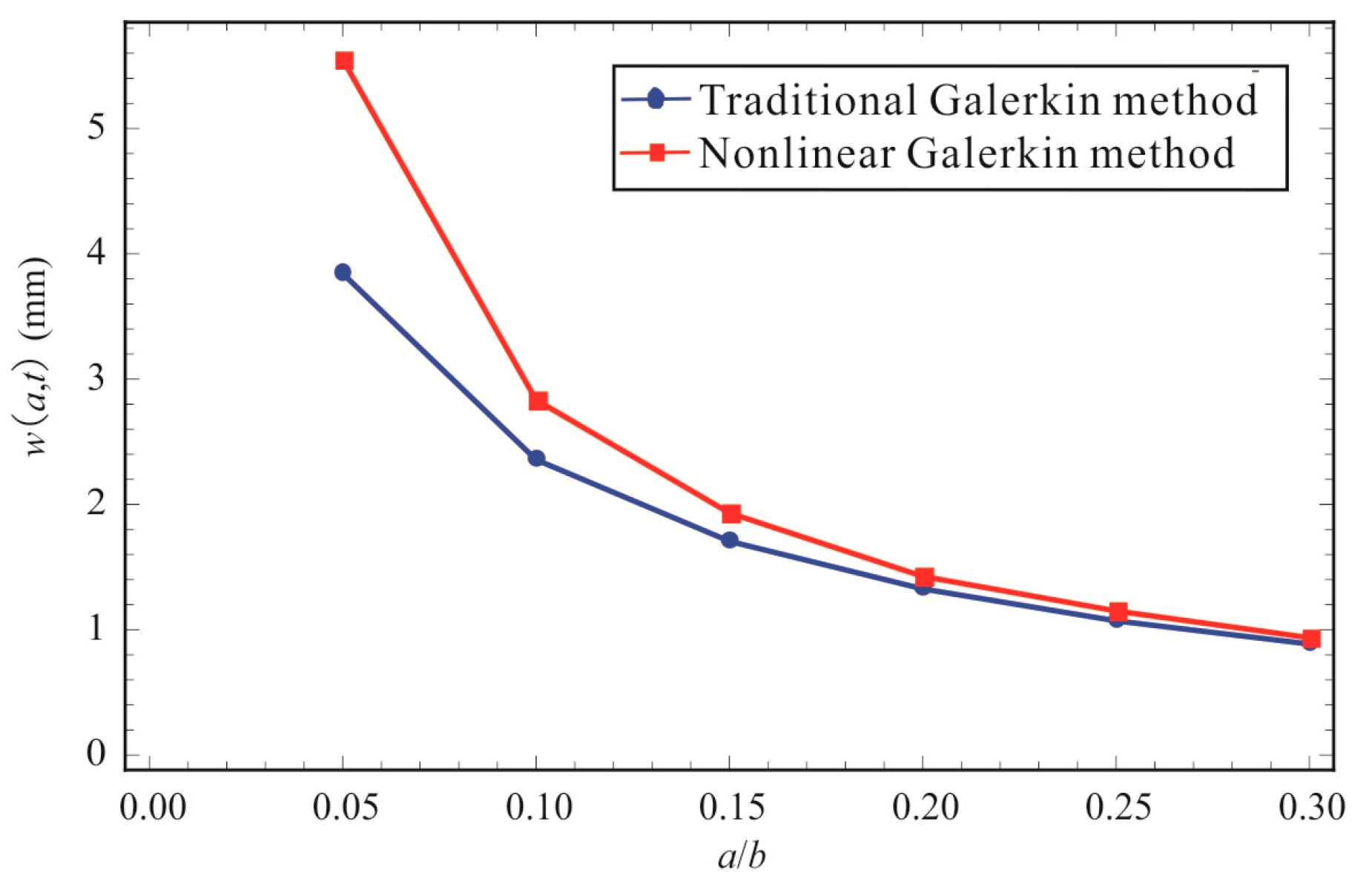
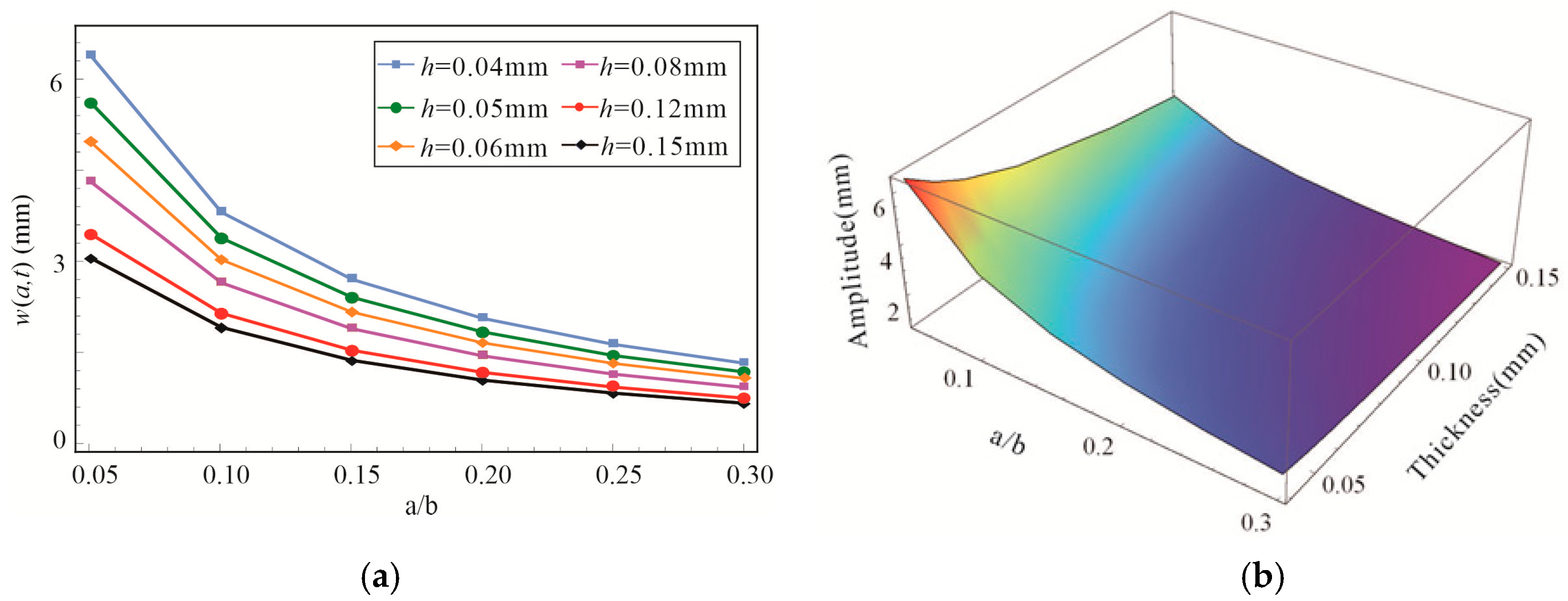
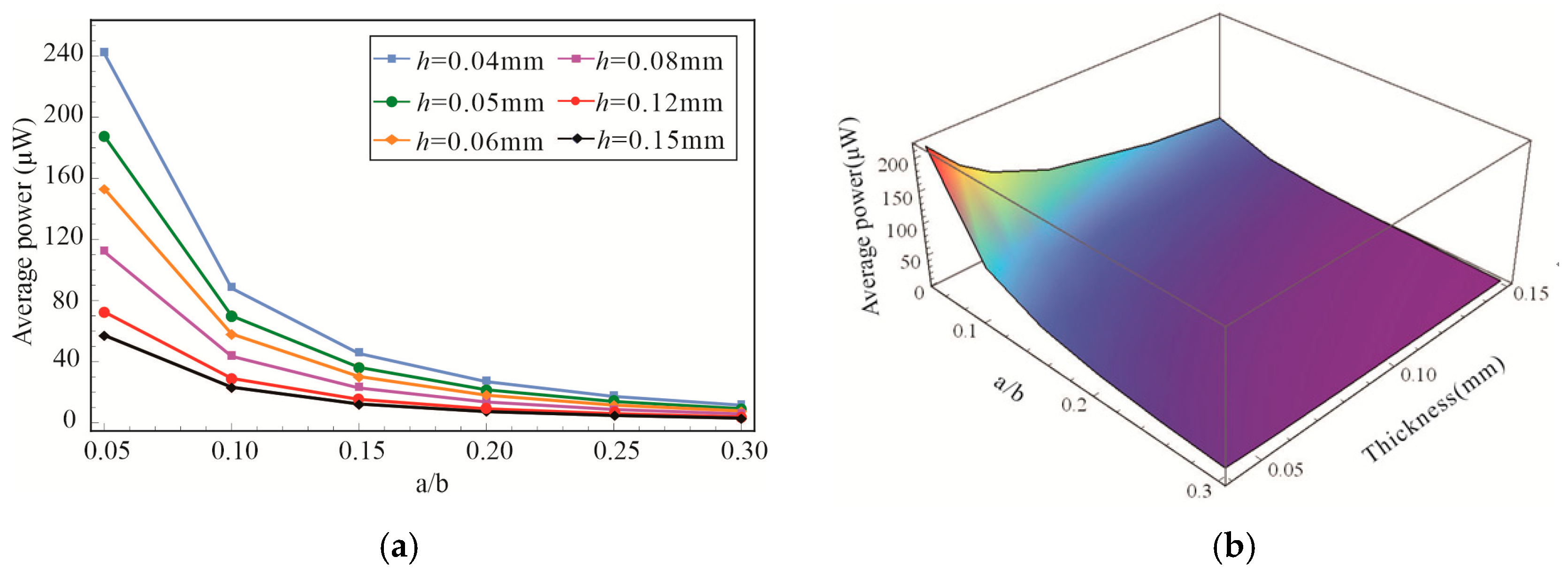
4. Parametric Study of the BEMH
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ranjith, B.; Halder, P.; Samad, A. High-performance ocean energy harvesting turbine design—Detailed flow analysis with blade leaning strategy. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 233, 379–396. [Google Scholar] [CrossRef]
- White, A.J.; McTigue, J.D.; Markides, C.N. Analysis and optimisation of packed-bed thermal reservoirs for electricity storage applications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 739–754. [Google Scholar] [CrossRef]
- Qiu, Q.; Xiao, L.Y.; Xin, S.Q.; Huang, T.B. Research progress of vibration micro-generator. J. Vib. Shock 2010, 29, 191–195. [Google Scholar]
- Yen, K.T. Energy Collection of Autonomous Sensor System: Design, Analysis and Practical Application; China Machine Press: Beijing, China, 2014. [Google Scholar]
- Chang, S.; Wang, Q.; Hu, H.; Ding, Z.; Guo, H. An NNwC MPPT-Based Energy Supply Solution for Sensor Nodes in Buildings and Its Feasibility Study. Energies 2019, 12, 101. [Google Scholar] [CrossRef]
- Gunduz, D.; Stamatiou, K.; Michelusi, N.; Zorzi, M. Designing Intelligent Energy Harvesting Communication Systems. IEEE Commun. Mag. 2014, 52, 210–216. [Google Scholar] [CrossRef]
- Akbari, S. Energy Harvesting for Wireless Sensor Networks Review. Com. SIS Consortium 2014, 2, 987–992. [Google Scholar]
- Elvin, N.G.; Elvin, A.A. Vibrational Energy Harvesting From Human Gait. IEEE/ASME Trans. Mechatron. 2013, 18, 637–644. [Google Scholar] [CrossRef]
- Orphée, C.; Jérôme, D.; Raisigel, H. Permanent magnet planar micro-generators. Sens. Actuators A Phys. 2006, 30, 438–444. [Google Scholar]
- Abdelmoula, H.; Sharpes, N.; Abdelkefi, A.; Lee, H.; Priya, S. Low-frequency Zigzag energy harvesters operating in torsion-dominant mode. Appl. Energy 2017, 204, 413–419. [Google Scholar] [CrossRef]
- Cooley, C.G. Vibration properties of and power harvested by a system of electromagnetic vibration energy harvesters that have electrical dynamics. Mech. Syst. Sig. Process. 2017, 94, 237–252. [Google Scholar] [CrossRef] [Green Version]
- Truong, B.D.; Le, C.P.; Halvorsen, E. Analysis of Electrostatic Energy Harvesters Electrically Configured as Bennet’s Doublers. IEEE Sens. J. 2017, 17, 5180–5191. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.C.; Wang, W. Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity. J. Sound Vib. 2017, 399, 169–181. [Google Scholar] [CrossRef]
- Wu, Y.P.; Ji, H.L.; Qiu, J.H.; Zhang, H. Nonlinear piezoelectric vibration energy harvester with the adjustable resonance frequency. J. Vib. Shock 2017, 36, 12–16. [Google Scholar]
- Li, H.T.; Qin, W.Y.; Deng, W.Z.; Lan, H.B.; Tian, R.L. Dynamics and coherent resonance of composite bistable energy acquisition system. J. Vib. Shock 2016, 35, 119–124. [Google Scholar]
- 16 Yao, M.H.; Li, Y.B.; Zhang, W. Nonlinear dynamics of longitudinal auxiliary magnetism bistable piezoelectric cantilever beam. J. Beijing Univ. Technol. 2015, 41, 1756–1760. [Google Scholar]
- Naifar, S.; Bradai, S.; Viehweger, C.; Kanoun, O. Survey of electromagnetic and magnetoelectric vibration energy harvesters for low frequency excitation. Measurement 2017, 106, 251–263. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; Harris, N. Increasing output power of electromagnetic vibration energy harvesters using improved Halbach arrays. Sens. Actuators A Phys. 2013, 203, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Ayala-Garcia, I.N.; Mitcheson, P.D.; Yeatman, E.M.; Zhu, D.; Tudor, J.; Beeby, S.P. Magnetic tuning of a kinetic energy harvester using variable reluctance. Sens. Actuators A Phys. 2013, 189, 266–275. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Zimmerman, S.; Abdelkefi, A. Accurate modeling, comparative analysis, and performance enhancement of broadband piezoelectric energy harvesters with single and dual magnetic forces. Int. J. Nonlinear Mech. 2017, 95, 355–363. [Google Scholar] [CrossRef]
- Spreemann, D.; Manoli, Y. Electromagnetic Vibration Energy Harvesting Devices. Advanced Microelectronics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, L.B.; Abdelkefi, A.; Dai, H.L.; Naseer, R.; Wang, L. Design and experimental analysis of broadband energy harvesting from vortex-induced vibrations. J. Sound Vib. 2017, 408, 210–219. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, A.; Hu, H.; Zhu, H. Hybrid Electromagnetic and Triboelectric Nanogenerators with Multi-Impact for Wideband Frequency Energy Harvesting. Energies 2017, 10, 2024. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Theoretical analysis of multi-stable energy harvesters with high-order stiffness terms. Commun. Nonlinear Sci. 2019, 69, 270–286. [Google Scholar] [CrossRef]
- Naseer, R.; Dai, H.L.; Abdelkefi, A.; Wang, L. Piezomagnetoelastic energy harvesting from vortex-induced vibrations using monostable characteristics. Appl. Energy 2017, 203, 142–153. [Google Scholar] [CrossRef]
- Yan, B.; Zhou, S.; Litak, G. Nonlinear Analysis of the Tristable Energy Harvester with a Resonant Circuit for Performance Enhancement. Int. J. Bifurcation Chaos. 2018, 28, 1850092. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Litak, G.; Lin, J. Numerical analysis and experimental verification of broadband tristable energy harvesters. Tm-Tech. Mess 2018, 85, 521–532. [Google Scholar] [CrossRef]
- Daqaq, M.; Masana, R.; Erturk, A.; Quinn, D.D. Closure: On the Role of Nonlinearities in Energy Harvesting: A Critical Review and Discussion. Appl. Mech. Rev. 2014, 66, 046001. [Google Scholar] [CrossRef]
- Dhakar, L.; Liu, H.; Tay, F.E.H.; Lee, C. A new energy harvester design for high power output at low frequencies. Sens. Actuators A Phys. 2013, 199, 344–352. [Google Scholar] [CrossRef]
- Paula, A.S.D.; Inman, D.J.; Savi, M.A. Energy harvesting in a nonlinear piezomagnetoelastic beam subjected to random excitation. Mech. Syst. Sig. Process. 2015, 54–55, 405–416. [Google Scholar] [CrossRef]
- Zhou, S. Harmonic balance analysis of nonlinear tristable energy harvesters for performance enhancement. J. Sound Vib. 2016, 373, 223–235. [Google Scholar] [CrossRef]
- Mann, B.P.; Owens, B.A. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Transient responses. J. Sound Vib. 2014, 333, 4859–4880. [Google Scholar] [CrossRef]
- Harne, R.L.; Thota, M.; Wang, K.W. Bistable energy harvesting enhancement with an auxiliary linear oscillator. Smart Mater. Struct. 2013, 22, 125028. [Google Scholar] [CrossRef]
- Fan, K.; Tan, Q.; Liu, H.; Zhang, Y.; Cai, M. Improved energy harvesting from low-frequency small vibrations through a monostable piezoelectric energy harvester. Mech. Syst. Sig. Process. 2019, 117, 594–608. [Google Scholar] [CrossRef]
- Mofidian, S.M.M.; Bardaweel, H. A dual-purpose vibration isolator energy harvester: Experiment and model. Mech. Syst. Sig. Process. 2019, 118, 360–376. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W.; Feng, J. A low-frequency, wideband quad-stable energy harvester using combined nonlinearity and frequency up-conversion by cantilever-surface contact. Mech. Syst. Sig. Process. 2018, 112, 305–318. [Google Scholar] [CrossRef]
- Man, X.B.; Wu, X.H.; Sun, Q. Research on order reduction of flexible beam model by nonlinear Galerkin method. J. Xi’an Jiaotong Univ. 2015, 49, 113–119. [Google Scholar]
- Mirkhalaf, M.; Najafizadeh, M.M. Vibration analysis of circular plates with an eccentric circular perforation with a free edge and attached concentrate. Aust. J. Basic Appl. Sci. 2016, 12, 3052–3058. [Google Scholar]
- Lin, W.J.; Chen, S.H. Finite element analysis of transverse vibration of membranes. J. Appl. Mech. 2011, 28, 44–49. [Google Scholar]
- Rubin, M.B.; Nadler, B. An Eulerian Formulation for Large Deformations of Elastically Isotropic Elastic-Viscoplastic Membranes. J. Mech. Mater. Struct. 2016, 11, 197–216. [Google Scholar] [CrossRef]
- Yamada, S.; Ijima, K.; Obiya, H.; Zakaria, M.N.; Abd Rahman, N.; Mohd Jaini, Z.; Yunus, R.; Rahmat, S.N. An Orthotropic Membrane Model for the Large Deformation Analysis and Snapping Phenomena of the Dome Inflated. MATEC Web Conf. 2016. [Google Scholar] [CrossRef]
- Hansbo, P.; Larson, M.G.; Larsson, F. Tangential differential calculus and the finite element modeling of a large deformation elastic membrane problem. Comput. Mech. 2015, 56, 87–95. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Halvorsen, E. Harmonic-Balance Analysis of Nonlinear Energy Harvester Models. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014. [Google Scholar]
- Berger, H.M. A new approach to the analysis of large deflections of plates. Ph.D. thesis, California Institute of Technology, Pasadena, California, 1954. [Google Scholar]
- Pennisi, G.; Mann, B.P.; Naclerio, N.; Stephan, C.; Michon, G. Design and experimental study of a Nonlinear Energy Sink coupled to an electromagnetic energy harvester. J. Sound Vib. 2018, 437, 340–357. [Google Scholar] [CrossRef]
- Zheng, Z.L.; Guo, J.J.; Song, W.J.; He, X.T.; Lu, F.M.; Xie, C.X.; Sun, J.Y. Nonlinear free vibration analysis of axisymmetric polar orthotropic circular membranes under the fixed boundary condition. Math. Prob. Eng. 2014, 651356. [Google Scholar] [CrossRef]
- Wang, C.Y. Vibration of an annular membrane attached to a free, rigid core. J. Sound Vib. 2003, 260, 776–782. [Google Scholar] [CrossRef]
- Alper, E.; Daniel, J.I. Piezoelectric Energy Harvesting; National Defense Industry Press: Beijing, China, 201; pp. 308–312. [Google Scholar]
- Marion, M.; Temam, R. Nonlinear Galerkin methods: The finite elements case. Numer. Math. 1990, 57, 205–226. [Google Scholar] [CrossRef]
- Alevras, P.; Theodossiades, S.; Rahnejat, H. On the dynamics of a nonlinear energy harvester with multiple resonant zones. Nonlinear Dyn. 2018, 92, 1271–1286. [Google Scholar] [CrossRef] [Green Version]
- Priya, S.; Inman, D.J. Energy Harvesting Technologies; Spring US: New York, NY, USA, 2009; pp. 84–89. [Google Scholar]
- Soares, R.M.; Gonçalves, P.B. Nonlinear vibrations and instabilities of a stretched hyperelastic annular membrane. Int. J. Solids Struct. 2012, 49, 514–526. [Google Scholar] [CrossRef] [Green Version]





| Parameters | Symbol | Values |
|---|---|---|
| Radius of center magnet | 7.5 mm | |
| Radius of membrane | 60 mm | |
| Thickness of membrane | 0.05 mm | |
| Mass of center magnet | 10.6 × 10–3 Kg | |
| Density of membrane | 1420 Kg/m3 | |
| Elasticity modulus | 90 MPa | |
| Poisson’s ratio | 0.3 | |
| Tension of membrane | 1 N/m | |
| Linear stiffness coefficient | 2.700 N/mm | |
| Nonlinear stiffness coefficient | 8.432 × 10−3 N/mm3 | |
| Damping ratio | 0.011 | |
| Electromagnetic coupling coefficient | 6.68 Vs/m | |
| Load resistance | 20 KΩ | |
| Coil resistance | 8.2 Ω |
| Excitation Frequency (Hz) | Excitation Maximum Value of Model Prediction (m/s2) | Excitation Maximum Value of Experiment (m/s2) |
|---|---|---|
| 8 | 6.9 | 7.1 |
| 9 | 4.6 | 4.9 |
| 10 | 2.7 | 2.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Zhang, Q.; Wang, W.; Han, J.; Tang, X.; Gu, F.; Ball, A.D. Dynamic Modeling and Structural Optimization of a Bistable Electromagnetic Vibration Energy Harvester. Energies 2019, 12, 2410. https://doi.org/10.3390/en12122410
Zhang B, Zhang Q, Wang W, Han J, Tang X, Gu F, Ball AD. Dynamic Modeling and Structural Optimization of a Bistable Electromagnetic Vibration Energy Harvester. Energies. 2019; 12(12):2410. https://doi.org/10.3390/en12122410
Chicago/Turabian StyleZhang, Bei, Qichang Zhang, Wei Wang, Jianxin Han, Xiaoli Tang, Fengshou Gu, and Andrew D. Ball. 2019. "Dynamic Modeling and Structural Optimization of a Bistable Electromagnetic Vibration Energy Harvester" Energies 12, no. 12: 2410. https://doi.org/10.3390/en12122410
APA StyleZhang, B., Zhang, Q., Wang, W., Han, J., Tang, X., Gu, F., & Ball, A. D. (2019). Dynamic Modeling and Structural Optimization of a Bistable Electromagnetic Vibration Energy Harvester. Energies, 12(12), 2410. https://doi.org/10.3390/en12122410








